1 Introduction

This study tested the hypothesis that Asian weather and climate in a given winter can be predicted 1 year in advance. A persistent cold wave and heavy snowfall during the winter in East Asia have social, economic, and psychological impacts on Japan because of the lack of atomic power stations in the post-Fukushima accident era. The colder the winter, the more electricity Japan needs. A cold wave is associated with an anomaly in hemispheric atmospheric circulation. One of the most important components of atmospheric circulation correlated with surface air temperature (SAT) teleconnections over Eastern Asia is the Western Pacific (WP) pattern identified by Wallace and Gutzler (1981). The negative phase of the WP pattern affects the Eastern Asian monsoon and leads to abnormally cool temperatures over Eastern Asia and Eastern Siberia in the winter (Gong et al. 2001; Zhang et al. 2009). Prediction of the WP pattern in advance is thus important for Japanese society. However, knowledge of the long-term variation of the WP pattern and its prediction is much less advanced than understanding and prediction of other large-scale atmospheric modes.

Honda et al. (2009) have hypothesized that winter weather in East Asia is related to ice reduction in the Barents–Kara Seas during the previous autumn. Their atmospheric general circulation model (AGCM) results indicate that a decrease of the extent of sea ice in summer and autumn strengthens the Siberian anticyclone in the following winter and in this way brings about a cold anomaly over East Asia. Honda et al. (2009) did not specifically take note of the WP pattern, but the extent of ice cover in autumn may be a key metric for long-term forecasting of the severity of the winter in East Asia, and specifically in Japan. Takano et al. (2008) have also shown that the Siberian-Japan pattern, which is similar to the WP pattern, favors heavy snowfall in Japan, and Hori et al. (2011) have pointed out that arrival of a cold wave in East Asia is related to an anticyclonic anomaly formed in association with the decline of sea ice in the Barents–Kara Seas.

Ogi et al. (2003) have shown that the extent of sea ice during the summer in the Barents Sea and summertime weather in East Asia are related to the North Atlantic Oscillation (NAO) during the winter of the previous year. Rodwell et al. (1999) have also pointed out the impact of the NAO on Arctic Sea ice cover in the Barents Sea. Collectively, these previous studies suggest that the winter cold wave in East Asia is associated with the NAO during the previous winter. However, no previous studies have examined whether the NAO during the winter can be used to predict the WP pattern in the next winter. The first goal of the present study was to determine whether there was an association between the WP pattern during the winter and the NAO during the previous winter.

El Niño/Southern Oscillation (ENSO) is another well-known key factor needed for long-term prediction of the

WP pattern. The WP pattern is known to be one of the most influential teleconnection patterns excited by ENSO (e.g., Horel and Wallace 1981; Mo and Livezey 1986; Kodera 1998). For example, Horel and Wallace (1981) have shown that El Niño events during the winter and the negative phase of the Southern Oscillation Index (SOI) are associated with the positive phase of the winter WP.

For the prediction of East Asian weather in the winter, the influence of both the tropics (e.g., ENSO) and the Arctic (e.g., sea ice) should therefore be considered. As the previous studies have suggested, the WP pattern during the winter can be related to both the NAO and ENSO. If interannual variation of the NAO is somehow related to ENSO, the mechanism responsible for the connection among the WP, NAO, and ENSO might be complicated. For example, if the NAO influences ENSO, or if ENSO influences the NAO, these influences would need to be carefully taken into account. Some studies have demonstrated that the Arctic Oscillation (AO) during the spring influences ENSO in the following winter (Nakamura et al. 2006, 2007; Chen et al. 2014). Because the AO and NAO have similar structures in the northern hemisphere over the Atlantic Ocean, the NAO may also influence ENSO. It is important to distinguish cause and effect in the interactions between the NAO, WP, and ENSO. The second goal of the present study was therefore to test the hypothesis that the NAO influences ENSO. Finally, we discuss the physical processes responsible for the NAO-WP linkage at both low and high latitudes. The methodology of this study primarily involved statistical analyses of a reanalysis dataset from the latter half of the twentieth century.

2 Data and methods

The atmospheric dataset used in this study was the National Centers for Environmental Prediction and National Centers for Atmospheric Research (NCEP/NCAR) reanalysis dataset (Kalnay et al. 1996). The extent of sea ice cover and sea surface temperature (SST) data used in this study came from the sea ice and sea surface temperature dataset version 1 (HadISST1) of the Met Office of the Hadley Center (Rayner et al. 2003). The snow depth data from 1979 through 2010 in the Japan Meteorological Agency Climate Data Assimilation System reanalysis (JCDAS) (Onogi et al. 2007) were also used in this study. We used monthly mean data from 1960 to 2010, except for the snow data.

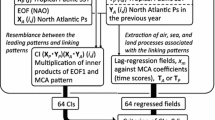
We performed an empirical orthogonal function (EOF) analysis to derive indices of the NAO, WP, and ENSO. Time series of the first leading mode (i.e., EOF1 score) of the December geopotential height at 500 hPa (Z500) in the North Atlantic region, December Z500 in the western Pacific region, and December SST in the tropical Pacific region were used as NAO, WP, and ENSO indices, respectively. Table 1 provides detailed definitions of the corresponding regions. Furthermore, a combined (extended) EOF was found to be useful for deriving time series that represented interannual variations coherent with the dominant mode among multiple variables in multiple regions. We can thus signify the coherency of multiple dominant modes by using EOF scores of combined EOFs as indices. On the basis of our hypothesis that there is a linkage between the NAO in the winter and the WP and ENSO in the following winter, we calculated two types of combined EOFs. One was an EOF of the December Z500 in the North Atlantic combined with the one-year-lagged December Z500 in the western Pacific. We defined the NAO + WP index as the EOF1 score of this combined EOF. The other was the same as the NAO + WP EOF, but the 1-year-lagged December SST in the tropical Pacific region was also included. We defined the NAO + WP + ENSO index to be the EOF1 score of this combined EOF. Corresponding regions used for the combined EOF were the same as those used for individual EOFs. Table 1 provides a description of the lead-lag relationships among the different regions. Note that in the EOF calculations, area-weighted values were applied, because the density of grid points increases with latitude. Furthermore, because different variables (here, geopotential height and SST fields) have different variances, EOF analysis was performed using a correlation matrix. The definitions of the NAO, WP, and ENSO indices therefore differed from the ones conventionally used: the NAO index from Jones et al. (1997), the WP index from Wallace and Gutzler (1981), and El Niño SST anomalies, respectively. However, the indices used in this study were highly correlated with these conventional indices, and the substantive results of this paper would not be changed if conventional indices were used.

Table 1 Definitions of indices used in this study
Full size table

To examine the possible linkages among the NAO and one-year-lagged WP and ENSO as well as the underlying mechanisms, we carried out a lead-lag linear regression of the atmospheric variables, SST, sea ice concentration, and snow depth against EOF1 scores. Because of the time scales of SST variability associated with ENSO and sea ice variability, both indices and response variables were normalized and detrended. The indices and variables were then divided into high-, middle-, and low-frequency variations. The high-, middle-, and low-frequency data were obtained by 3-year high-pass, 3–7-year band-pass, and 7-year low-pass filters, respectively. The low-pass data were obtained by 7-year running mean, the high-pass data were obtained by subtracting a 3-year running mean, and the band-pass data were determined by subtracting the 7-year low-pass data from the 3-year running mean data.

3 Results and discussion

3.1 The winter WP and the previous winter NAO

Figure 1a is a simultaneous correlation map of Z500 with the WP index in December. A significant north–south dipole pattern is apparent over the western part of the North Pacific; positive anomalies are apparent over Japan, and there are negative anomalies over the Russian Far East. Figure 1b shows a simultaneous correlation map of temperature at 1,000 hPa (T1000) with the WP index. The temperature is anomalously high over Japan and East Asia and anomalously low over the Russian Far East. These anomaly fields of height and temperature are quite similar to the field of the original WP pattern first defined by Wallace and Gutzler (1981), in which two-point correlation was applied. The contributions of the first and second modes of our EOF analysis were 39.5 and 22.6 %, respectively. These results thus confirm that the WP pattern is the mode that most influences the East Asian climate in December. In this study, the positive phase of the WP index was defined as cold north and warm south, as shown in Fig. 1. Because a negative WP is the opposite of this pattern, cold winters in Japan tend to occur during the negative phase of the WP.

Fig. 1
figure 1

Simultaneous regression fields of a geopotential height anomaly at 500 hPa (m) and b temperature at 1,000 hPa (K) with the WP index in December. Contours indicate regression coefficients. Light, moderate, and heavy shading indicate statistical significance greater than 80, 90, and 95 %, respectively. Red and blue indicate positive and negative correlations, respectively

Full size image

Figure 2a is a lag correlation map of Z500 in December of the previous year with the WP index. Significant positive correlations over Iceland and negative correlations over the North Atlantic Ocean are apparent. This pattern of geopotential height anomaly is somewhat similar to the negative phase of the NAO pattern defined by Wallace and Gutzler (1981). Figure 2b is the same as Fig.2a but for T1000. Negative correlations (i.e., cold anomalies) are apparent over Europe and the Barents–Kara Seas, consistent with anomalous temperature signatures in the negative phase of the NAO. The significant lagged correlation indicates that when the winter NAO is in a negative (positive) phase, a positive (negative) phase of the WP pattern appears 1 year later, and thus a warm (cold) anomaly tends to appear over East Asia in the following winter as shown in Fig. 1. To assess this one-year-lag relationship objectively, we performed an EOF analysis of December Z500 fields. This analysis combined spatially and temporally separated areas, specifically the North Atlantic area and the one-year-lagged Western Pacific area (see details in Sect. 2). Figure 3 shows the first mode of this coupled EOF analysis. The contributions of the first and second modes were 26.7 and 16.5 %, respectively, the indication being that successive occurrences of the negative phase of the NAO and the positive phase of the WP in the following winter were dominant. The result of this EOF analysis is consistent with the 1-year-lag relationship apparent in Fig. 2. We therefore define the EOF1 score of this coupled EOF as the NAO + WP index. Here, the positive NAO + WP index corresponds to the negative phase of the NAO and the positive phase of the WP, and vise versa.

Fig. 2
figure 2

Lag-regression fields of a geopotential height anomaly at 500 hPa (m) and b temperature at 1,000 hPa (K) in December (0 year) against the WP index in 1 year later (+1 yr). Contours and shading have the same meaning as in Fig. 1

Full size image
Fig. 3
figure 3

Spatial pattern of 1st mode of EOF applied to December Z500 in North Atlantic region and December Z500 the following year in the Western Pacific region (NAO + WP, see text and Table 1)

Full size image

3.2 The path from the winter NAO to the winter WP the following year

Some mechanisms that connect the winter NAO and the WP in the following winter are not apparent. The mechanisms cannot involve the atmosphere, because the atmosphere cannot retain information long enough to connect phenomena in successive winters. Candidate mechanisms may involve the ocean, land, and sea ice, because their heat capacities are much larger than that of the atmosphere. Here we point out some processes that may modulate the internal variability of the atmosphere and play roles in connecting these two atmospheric patterns.

3.2.1 Arctic sea ice variations

We first examined the relationship between the NAO-WP linkage and Arctic sea ice variability. Figure 4 shows the correlation between the extent of Arctic sea ice cover in the spring (left), summer (middle), and autumn (right) and the NAO + WP index. There are clearly apparent positive correlations between the low-frequency variations (bottom row) on the Eurasian side of the Arctic Ocean, in particular the Barents Sea, in all seasons. These correlations mean that the low-frequency variations of a negative (positive) NAO during the winter and a positive (negative) WP during the next winter are associated with a decadal-scale increase (decrease) of sea ice in the Barents Sea in the extra-winter seasons. Figure 5 shows normalized time series of the NAO + WP index and the areal extent of summertime sea ice in the Barents–Kara Seas (the area surrounded by the green line in Fig. 4) separated into high-, middle-, and low-frequency variations. Whereas high-frequency variations were poorly correlated (r = 0.06) with a low confidence level (~31 %), middle- and low-frequency variations were much better correlated (r = 0.48 and 0.52, respectively) with relatively high confidence levels (~95 and 82 %, respectively). These results suggest that long-term variations of the extent of sea ice in extra-winter seasons is a key to explaining the two winter teleconnection patterns. The connection with the positive NAO during the winter and the negative WP during the following winter as a result of the decrease of the extent of sea ice in the Barents Sea in the spring and summer is consistent with the influences of the NAO on Arctic sea ice (Ogi et al. 2003). Furthermore, the implication that a decrease of the extent of Arctic sea ice in the summer brings a cold anomaly to the Far East in the winter is consistent with the results of Honda et al. (2009).

Fig. 4
figure 4

Lag-correlation maps of the extent of sea-ice in the (left) spring, (center) summer, and (right) autumn +1 yr against the NAO + WP index. Spring, summer, and autumn values are defined to be 3-month means of data for March–April–May, June–July–August, and September–October–November, respectively. The designation +1 yr indicates that the sea-ice field follows by 1 year the North Atlantic region of the EOF analysis of the NAO + WP. Correlations obtained from the sea-ice field and NAO + WP indices determined by applying a 3-year high-pass filter, 3–7-year band-pass filter, and 7-year low-pass filter are shown in the top, middle, and bottom rows. Blue (red) indicates positive (negative) correlation

Full size image
Fig. 5
figure 5

Time series of (black) NAO + WP index and (red) extent of sea-ice area in Barents–Kara Seas in JJA of the following year (25–75ºE and 65–85ºN: area surrounded by green line in bottom-center panel of Fig. 4). The indices were normalized and applied a a 3-year high pass filter, b 3–7-year band-pass filter, and c 7-year low-pass filter. The correlation coefficient between the two time series is displayed at the upper right-hand corner of each panel

Full size image

3.2.2 Tropical SST variations

The NAO and WP might be linked not only by Arctic sea ice but also by the SST in the rest of the ocean. In particular, the variations of tropical SSTs caused by phenomena such as ENSO have large impacts on East Asian winter weather. We therefore next examined the relationship between the NAO-WP linkage and tropical SST variability. Figure 6a shows regression coefficients of the high-frequency variations of SST in December against the high-frequency variations of the NAO + WP index during the previous year. A positive SST anomaly is apparent in the central-to-eastern tropical Pacific. Figure 6c, e shows the same coefficients as Fig. 6a, but for middle- and low-frequency variations, respectively. Whereas there is a positive anomaly of the middle-frequency SST variations in the tropical Pacific resembling ENSO, the low-frequency SST variations do not show a noticeable signature. The distributions of these SST anomalies associated with high- and middle-frequency variations somewhat resemble the anomalous SST patterns of ENSO. Figure 6b, d, f shows the evolutions of the high-, middle-, and low-frequency tropical SST anomalies, respectively, regressed against the NAO + WP index. For the high-frequency variations in the central to eastern tropical Pacific (90–180°W), negative anomalies are apparent in January-March of the following year, and positive anomalies are apparent in September-December of the following year. For the middle-frequency variations, positive SST anomalies extend toward the east from the central tropical Pacific in January of the following year to the eastern tropical Pacific in December of the following year. The structures of these anomalies in the evolution of the tropical SST also resemble the development of ENSO on a similar time scale. In contrast, low-frequency variations showed no significant evolution. This result indicates that El Niño (La Niña) and the positive (negative) phase of the WP tend to occur 1 year after the negative (positive) phase of the winter NAO. This pattern is obvious on the typical timescale of ENSO (about 2–6 years), but not on a decadal timescale. That is, neither the decadal ENSO nor the Pacific decadal oscillation (PDO) is associated with a link to the NAO or WP.

Fig. 6
figure 6

(left) Lag-regression fields of the SST (K) in December of the following year against the NAO + WP index. (right) Same as left, but for evolution of the equatorial SST from January of the following year to December of the following year. Correlations calculated using a a, b 3-year high-pass filter, c, d 3–7-year band-pass filter, and e, f 7-year low-pass filter are displayed in the top, middle, and bottom rows, respectively. The meaning of the contours and shading are the same as in Fig. 1

Full size image

To estimate the strength of the relationship between the winter NAO in one year and ENSO and the WP in the following year, we executed a combined EOF analysis, NAO + WP + ENSO (see Sect. 2; Table 1). Figure 7 shows the horizontal pattern of the first mode of the EOF. The contributions of EOF1 and EOF2 were 25.5 and 16.1 %, respectively. This EOF1 pattern signifies the occurrence of the negative phase of the NAO and the positive phase of both the WP and El Niño, with a lag of 1 year after the NAO. The same relationship between the NAO-WP linkage and the tropical SST anomaly illustrated in Fig. 6 is apparent in the first mode of this EOF analysis. We defined the NAO + WP + ENSO index to be the score of the first mode of this combined EOF. Figure 8 shows an unfiltered time series of three individual EOF1 scores (i.e., NAO, WP, and ENSO indices) and two combined EOF1 scores (i.e., the NAO + WP and NAO + WP + ENSO indices). All of the indices are positively correlated with each other. The correlation coefficients among the five indices are shown in Table 2. The correlations between the NAO and ENSO indices are relatively low, because there was no consideration of the time scale. Although the NAO-ENSO correlation is low, the NAO + WP + ENSO index was highly correlated with the three individual indices (Table 2), the indication being that there was good coherence among the three phenomena. This is because the most suitable spatial pattern and time scale was chosen by EOF to make covariance among three fields the largest. We thus confirmed that the NAO, WP, and ENSO are closely connected with each other.

Fig. 7
figure 7

Spatial pattern of 1st mode of EOF applied to the December Z500 in the North Atlantic, December of the following year Z500 in the Western Pacific, and December of the following year SST in the tropical Pacific Ocean (NAO + WP + ENSO: see text and Table 1)

Full size image
Fig. 8
figure 8

Time series of normalized indices obtained by EOF analyses. Each curve is explained in the note in the lower left-hand portion of the figure. Note that only the NAO index is drawn with a reversed sign

Full size image
Table 2 Correlation coefficients among indices
Full size table

3.2.3 Possible mechanism

We have shown that the winter NAO is likely associated with the WP during the winter of the following year, and that WP is strongly connected to the temperature anomaly in Japan. In addition, we have shown that there are two processes, one involving high latitudes, and the other involving low latitudes.

The high-latitude process involves Arctic sea ice variations. The negative (positive) phase of the winter NAO changes oceanic currents in the North Atlantic and weakens (strengthens) oceanic heat transport into the Arctic (Wohlleben and Weaver 1995; Kwok and Rothrock 1999; Sandø et al. 2010; Schlichtholz 2011). This weakened (strengthened) heat transport also slows down (speeds up) the reduction of sea ice in the spring. A condition of more (less) ice than normal then persists until the season of ice freezing in autumn. In winter, all of the Arctic Ocean is covered by sea ice, regardless of the autumn ice area. Less (more) ice production during the freezing season reduces (increases) the heat released from the ocean to the atmosphere in the Arctic. An anomalously small (large) heat flux excites stationary Rossby wave propagation, which induces warm (cold) advection to Japan, as shown by Honda et al. (2009). The influence of the NAO on this mechanism is more obvious at low-frequency time scales, such as a decadal time-scale. This scenario is reasonable, because sea ice and the ocean have large heat capacities.

The low-latitude process involves variations of tropical Pacific SSTs on a timescale typical of ENSO. As mentioned above, El Niño (La Niña) induces positive (negative) WP in the winter (e.g., Horel and Wallace 1981; Mo and Livezey 1986; Kodera 1998). It is thus necessary to examine processes that connect the winter NAO and the subsequent ENSO. An El Niño outbreak tends to start in the late winter/early spring (Philander 1985; Barnett et al. 1989; Yu and Rienecker 1998; Yu et al. 2003). We thus focus on the impacts of the winter NAO on the tropics in late winter/early spring. Some studies have pointed out the relationship between an NAO-associated snow anomaly on the Eurasian continent and tropical atmospheric variations. Clark et al. (1999) and Hori and Yasunari (2003), for example, have shown that there is an anomalous increase (decrease) of snowfall in western Eurasia in association with a negative (positive) winter NAO. Barnett et al. (1989) have shown that winter snow on the Eurasian continent is associated with the summer Indian monsoon and ENSO. In addition, Nakamura et al. (2006, 2007) have shown that an outbreak of cold air from Asia to the tropics intensifies the westerly wind burst over the western tropical Pacific and triggers El Niño. The winter NAO thus has the potential to intensify a cold air outbreak through its effect on the snow anomaly in the western Eurasian continent. We therefore hypothesize that tropical atmospheric variations, which are related to El Niño outbreaks, can respond to the Eurasian snow anomaly associated with the wintertime NAO. To test this hypothesis, we examined the Eurasian snow anomaly and associated atmospheric processes by regression against the NAO + WP + ENSO index. We focused on only the 3–7-year band-pass timescale, because the regression of SST anomaly in the central-to-eastern tropical Pacific against the NAO + WP index was highest on this timescale (Fig. 6).

Figure 9 shows the correlation of the middle-frequency variations (3–7-year band-pass-filtered) of snow depth (upper) and SAT (lower) in December of 1 year (a, c) and in January of the following year (b, d) with the winter NAO + WP + ENSO. It should be noted that January of the following year indicates January of the next calendar year, namely 1 month after December of the current year. Positive correlations with snow anomalies and negative correlations with surface temperature anomalies are apparent for the western Eurasian continent. In addition, areas highly correlated with snow depth widen toward the east from December to January. These results signify that a negative NAO widens the area of anomalous snow cover in association with a cold anomaly in the western Eurasian continent. Figure 10 shows a normalized time series of the NAO + WP + ENSO index and snow depth during January of the following year averaged over western Eurasia (the area surrounded by the green line in Fig. 9). In Fig. 10, all of the time series are separated into high-, middle-, and low-frequency variations. Whereas the NAO + WP + ENSO index and western Eurasian snow are significantly correlated for high- and middle-frequency variations (r = 0.54 and 0.51, respectively), the correlation coefficient for low-frequency variations was not significant (r = 0.14). This result indicates that western Eurasian snow varies coherently with the NAO and ENSO on a timescale typical of ENSO, the suggestion being that western Eurasian snow is important to the NAO-WP-ENSO linkage.

Fig. 9
figure 9

The correlation of (upper) snow depth and (lower) temperature at 1,000 hPa in (a, c) December and in (b, d) January of the following year against the NAO + WP + ENSO index. Correlations obtained from the snow and temperature fields with the NAO + WP + ENSO index are all based on use of a 3–7-year band-pass filter. Light, moderate, and heavy shading indicate statistical significance greater than 80, 90, and 95 %, respectively. Blue (red) indicates positive (negative) correlations in (a) and (b), and negative (positive) correlation in (c) and (d). Contours in (c) and (d) indicate regression coefficient of temperature (K)

Full size image
Fig. 10
figure 10

Time series of (black) NAO + WP index and (red) snow depth averaged in central Europe in January of the next year (0–40°E and 40–60°N: area surrounded by the green line in Fig. 9). Indices were normalized and applied a 3-year high-pass filter, b 3–7-year band-pass filter, and c 7-year low-pass filter. The correlation coefficient between the two time series after 1979 is displayed at the upper right-hand corner of each panel

Full size image

Figure 11a shows the regression field of the middle-frequency variations (3–7-year band-pass-filtered) of the geopotential height at 300 hPa in January of the following year against the NAO + WP + ENSO index. In addition to the negative NAO-like anomaly in the North Atlantic, a negative anomaly in western Russia (around 60°E, 60°N) and a positive anomaly around Mongolia (100°E, 40°N) are apparent. The associated wave activity flux, which has been developed by Takaya and Nakamura (2001) and is an indicator of the group velocity of the quasi-geostrophic Rossby wave, indicates that a stationary Rossby wave propagates from Europe to Mongolia. Figure 11b shows a vertical cross section of the geopotential height anomaly and associated wave activity flux along with the path of Rossby wave propagation (brown line in Fig. 11a). Upward and eastward propagation of the stationary Rossby wave is apparent around 30°E. The wave originates from a near-surface wave source where strong baroclinicity exists because of the negative heat released with the large snow anomaly (i.e., high-pressure anomaly around 30°E below 500 hPa). Downward propagation of the Rossby wave is apparent around 90°E, and an anticyclonic anomaly extends toward near the surface, although their signals are insignificant. Figure 11c shows regressions of the geopotential height and horizontal wind vector at 850 hPa in February of the following year against the NAO + WP + ENSO index. A positive geopotential anomaly is apparent from Mongolia to Southeast Asia. An anomalous westerly wind over the maritime continent is apparent. The results suggest that changes in the tropical circulation of the western equatorial Pacific may occur because of the NAO-related snow anomaly. In other words, a high-pressure anomaly in the lower troposphere in Southeast Asia brings a cold surge from the continent to the equatorial Pacific (Yu and Rienecker 1998; Yu et al. 2003; Nakamura et al. 2007), and thus the Asian cold surge often intensifies the westerly wind burst over the maritime continent. The anomalous westerly wind found in our results may be a signature of the intensification of the westerly wind burst. These processes, which start with a negative NAO, can induce the occurrence of an El Niño from summer to winter. The timescale of this NAO influence is 3–7 years, which agrees well with the typical timescale of an ENSO. Because the WP is excited by the ENSO (e.g., Horel and Wallace 1981; Mo and Livezey 1986; Kodera 1998), ENSO plays a role in connecting the NAO and WP on a timescale of about 3–7 years.

Fig. 11
figure 11

Regression fields of a geopotential height anomaly at 300 hPa (m) in January of the following year against the NAO + WP + ENSO index and the corresponding wave activity flux indicated by the green arrow. An arrow length corresponding to 0.1 m2 s−2 is displayed at the upper right-hand corner of the panel. b Vertical cross section of the regression of geopotential height along the brown line in (a). The green arrow is the vector of the zonal and vertical components of the corresponding wave activity flux. c Regression fields of geopotential height anomaly at 850 hPa (m) in February of the following year against the NAO + WP + ENSO index and horizontal wind vector at 850 hPa (green arrow). An arrow length corresponding to 0.5 m s−1 is shown at the top right-hand portion of the panel. The meaning of the shading and contour is the same as in Fig. 1

Full size image

4 Conclusions

We have used statistical analyses to show for the first time that a positive (negative) phase of the WP pattern during the winter, which brings a warm (cold) anomaly to East Asia, including Japan, is related to a negative (positive) phase of the NAO in the previous winter. Exploiting this interannual linkage may facilitate long-term weather prediction. In this study we have proposed two mechanisms responsible for this interannual linkage. One mechanism involves the Arctic, and the other involves the tropics. The key factor in the case of the Arctic mechanism is Arctic sea ice. The Arctic mechanism is more obvious at low-frequency timescales, such as decadal or multi-decadal time-scales. The other mechanism involves variations of tropical SSTs. We found that a negative winter NAO induced an El Niño-like SST anomaly in the following winter. Because El Niño excites the WP pattern remotely, a NAO in one winter can induce a WP pattern in the following winter. A process that may link a negative NAO during the winter to El Niño is the following. Unusually extensive snow cover on the western Eurasian continent as the result of the influence of the negative phase of the NAO during the winter, which brings about cold winters in Europe, makes the air temperature in the region low. The negative heat release associated with the cold surface generates a wave, and the propagation of the wave excites an anticyclonic circulation over the Tibetan plateau. This anticyclonic circulation brings about an outbreak of cold air from Asia to the western tropical Pacific Ocean, which intensifies the western wind burst over the western tropical Pacific Ocean. This burst of westerly winds can excite El Niño from summer to winter in the following year.

Both the long-term and short-term variations of the winter NAO therefore act to induce a WP in the following winter. The phase of the NAO during the winter could therefore be a predictor of the WP the following year. We have proposed two processes to account for the connectivity of the NAO and WP. Other processes that are not apparent may also influence the WP in the following winter. For example, the winter WP might have an influence on the NAO in the following winter because the time scales of the discovered linkage between the NAO and WP is in 3–5 years or decadal. This possibility must be explored in future studies. Because this study was based on statistical analysis of the reanalysis dataset, the true cause of the relationships between the NAO, Arctic sea ice, ENSO, and WP is still uncertain. In the case of the tropics in particular, the impacts of the NAO on El Niño outbreaks should be examined in more detail. To confirm the proposed processes, we performed a multi-model ensemble analysis using the Coupled Global Climate Model (CGCM) from the Coupled Model Intercomparison Project phase 3 (CMIP3) of the World Climate Research Programme (Meehl et al. 2007; Randall et al. 2007) in Part II (Nakamura et al. 2014 Footnote 1) as a counterpart of this study.