Abstract
The predictability of the Arctic sea ice is investigated at the interannual time scale using decadal experiments performed within the framework of the fifth phase of the Coupled Model Intercomparison Project with the CNRM-CM5.1 coupled atmosphere–ocean global climate model. The predictability of summer Arctic sea ice extent is found to be weak and not to exceed 2 years. In contrast, robust prognostic potential predictability (PPP) up to several years is found for winter sea ice extent and volume. This predictability is regionally contrasted. The marginal seas in the Atlantic sector and the central Arctic show the highest potential predictability, while the marginal seas in the Pacific sector are barely predictable. The PPP is shown to decrease drastically in the more recent period. Regarding sea ice extent, this decrease is explained by a strong reduction of its natural variability in the Greenland–Iceland–Norwegian Seas due to the quasi-disappearance of the marginal ice zone in the center of the Greenland Sea. In contrast, the decrease of predictability of sea ice volume arises from the combined effect of a reduction of its natural variability and an increase in its chaotic nature. The latter is attributed to a thinning of sea ice cover over the whole Arctic, making it more sensitive to atmospheric fluctuations. In contrast to the PPP assessment, the prediction skill as measured by the anomaly correlation coefficient is found to be mostly due to external forcing. Yet, in agreement with the PPP assessment, a weak added value of the initialization is found in the Atlantic sector. Nevertheless, the trend-independent component of this skill is not statistically significant beyond the forecast range of 3 months. These contrasted findings regarding potential predictability and prediction skill arising from the initialization suggest that substantial improvements can be made in order to enhance the prediction skill.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Decadal climate prediction is a major issue in the development of strategies for societal adaptation to the changing climate. This new domain of research, initiated by societal demand and enabled by recent achievements of ocean reanalysis, goes beyond the simple production of confident climate predictions. Still in its infancy, the achievement of decadal prediction objectives requires, as a primary step, a sufficient understanding of the mechanisms of interannual to decadal variability of the climate system, as well as improved simulations of those mechanisms in climate models (Latif and Keenlyside 2011).
Predictability arising from initial conditions knowledge, i.e. predictability of the first kind according to Lorenz (1975) addresses the question of which long term evolving variables have an impact on the characteristics of the probability distribution function of shorter time scale events (from seasonal means to weather events). These long-term evolving variables, as well as the physical mechanisms leading to effects on shorter time scale, can be seen as predictability sources. For near-term climate predictions, these long-term evolving modes need to be correctly phased with observations, implying a good initialization. The ocean, characterized by strong inertia and, more particularly, oceanic variability modes such as the Atlantic Meridional Overturning Circulation (AMOC), have been shown to be the major source of predictability in the climate system (Griffies and Bryan 1997; Boer 2004; Pohlmann et al. 2004; Knight et al. 2006; Solomon et al. 2011; Doblas-Reyes et al. 2011). Accordingly, initialization of the ocean state improves some aspects of climate forecast (Smith et al. 2007; Pohlmann et al. 2009; Mochizuki et al. 2010), especially in the North Atlantic sector (Keenlyside et al. 2008; Garcia-Serrano et al. 2012; Yeager et al. 2012; Doblas-Reyes et al. 2013). Sea ice, which is strongly influenced by the ocean (Bitz et al. 2005), exhibits multiannual time scale variability (Gloersen et al. 1996; Deser et al. 2000; L’Hévéder and Houssais 2001; Ukita et al. 2007), and has a strong impact on the surface atmosphere and large-scale atmospheric circulation (Royer et al. 1990; Alexander et al. 2004; Kvamstø et al. 2004; Deser et al. 2004; Magnusdottir et al. 2004; Balmaseda et al. 2010a; Bader et al. 2011; Orsolini et al. 2012), is expected to play an essential role in decadal climate predictability. Its link with the ocean suggests that it is potentially predictable up to several years, and because of its impact on the atmosphere, especially at the ice edge, sea ice predictability might, in return, be a source of predictability for the polar climate.
The Arctic sea ice predictability has, until now, been investigated mostly at the seasonal time scale, dominated by the initial-value predictability. Most of analyses dealing with the Arctic sea ice cover seasonal predictability are based on statistical relationships (Walsh et al. 1980; Johnson et al. 1985; Drobot and Maslanik 2002; Drobot 2007), giving relatively good prediction scores. It seems, however, that non-observable variables–such as, for example, sea ice thickness (SIT) distribution–appear to be the best predictors of sea ice cover (extent or volume) (Chevallier and Salas y Mélia 2012). Further, considering the rapid changes in the Arctic environment, statistical relationships may not remain valid in the future (Holland and Stroeve 2011), justifying the increasing use of physical models. Models can be used together with observations to reconstruct the past sea ice cover and further investigate statistical precursors of the sea ice (Lindsay et al. 2008; Chevallier and Salas y Mélia, 2012), or be used individually to produce ensemble hindcast-forecasts (Blanchard-Wriggleworth et al. 2011a; Holland et al. 2011; Chevallier et al. 2013; Sigmond et al. 2013; Merryfield et al. 2013). Note that previously mentioned reconstructions constitute very good tools for initializing these hindcasts-forecasts. Despite its relatively short prediction time scale, the seasonal predictability is assessed (with statistical methods as well as coupled model experiments) over several decade-long periods, therefore exhibiting some long-evolving trends. This raises the question of the impact of this trend, due to changes in boundary conditions, on the total predictability assessment. For decadal prediction, this is even more crucial. Indeed, initial values account for this trend and complicate the assessment of the predicted trend in response to the change in forcing during the hindcasts, which constitutes a large part of the predictability.
Longer-term Arctic sea ice predictability has been investigated using perfect model assumption, in which Global Climate Models (GCMs) ensemble integrations are initialized from a reference model integration (Koenigk and Mikolajewicz 2009; Holland et al. 2011; Koenigk et al. 2012; Tietsche et al. 2013). These studies examined the upper limit of initial-value predictability and its sensitivity to the Arctic sea ice mean state (Holland et al. 2011), which is an important issue in the observed rapidly changing Arctic sea ice conditions. Koenigk and Mikolajewicz (2009) found that the Arctic SIT annual mean is predictable up to 2 years ahead while the annual mean sea ice concentration (SIC) shows no predictability in the ECHAM5-MPI-OM GCM. However, for the seasonal mean, they found some significant predictability of the SIC for a few months to 2 years in the Subarctic seas of the Atlantic sector. In examining the monthly means of spatially integrated indices, i.e. sea ice volume (SIV) and sea ice area (SIA), Holland et al. (2011) found similar predictability time scales of 2 and 1 year, respectively, in the CCSM3 GCM. Blanchard-Wriggleworth et al. (2011b) found an even longer predictability time scale for both SIA and SIV monthly means. They show that the sea ice cover predictability is dominated by boundary-condition predictability rather than initial-value predictability beyond 3 years. The higher predictability of SIT, i.e. volume with respect to that of sea ice concentration (i.e. area or extent), found in all seasonal to interannual predictability studies seems to disappear when considering longer time scales, as shown by the very weak predictability of SIV, in contrast to the highly predictable sea ice extent (SIE) found on decadal means by Koenigk et al. (2012).
The Arctic SIA, SIE and SIV are indices that integrate a large variety of regions influenced by different physical mechanisms. Therefore, the understanding of their variability and predictability requires consideration at a smaller spatial scale in order to highlight regional discrepancies. A few studies have investigated the spatial distribution of the sea ice cover predictability, concluding that the sea ice cover is more predictable in the Atlantic sector than in the rest of the Arctic (Koenigk and Mikolajewicz 2009; Koenigk et al. 2012). This higher predictability is attributed to sea ice anomalies advection processes in the transpolar drift stream impact area, i.e. the east Greenland current (ECG) and the Labrador Sea (Koenigk and Mikolajewicz 2009) and to a stronger sea ice link with the ocean variability through the Atlantic meridional overturning circulation (AMOC) in the Labrador, Greenland and Barents Seas (Koenigk et al. 2012).
Due to incomplete climate state observations and model errors, the perfect-model assumption gives only an upper limit of the predictability, to which a good initialization scheme and a good interannual to multi-decadal variability simulation, as well as a correct response of the model to external forcings, must be added in order to produce real decadal climate forecasts. A decadal prediction protocol has been designed within the framework of the fifth phase of the Coupled Model Intercomparison Project (CMIP5) to examine the ability of individual dynamical models to simulate and predict decadal climate variability, and to test the benefits and limitations of different initialization schemes (Meehl et al. 2009; Taylor et al. 2012). No initialization technique was imposed to contribute to the CMIP5 decadal exercise. Therefore, in addition to the intercomparison of the predictability skills of coupled models, CMIP5 decadal simulations should be individually analyzed in detail in order to document the preliminary issues previously introduced. Focusing on one of the CMIP5 coupled models, the CNRM-CM5.1 AOGCM, this analysis contributes to those objectives, addressing the following questions:
-
Assessment of the Arctic sea ice initial-value predictability in the model.
-
Identification of predictability sources of the Arctic Sea Ice (where/why?)
-
Time evolution of this potential predictability in a changing climate.
-
Assessment of prediction scores of the model initialized with our specific method.
A detailed description of the simulations used in this analysis is given in Sect. 2, with a brief description of CNRM-CM5.1. Responses to previously mentioned questions are detailed in Sect. 3. Finally, results are summarized and discussed in Sect. 4.
2 Description of the model and experiments
2.1 CNRM-CM5.1 coupled model
The simulations used in this analysis are performed with the CNRM-CM5.1 atmosphere–ocean general circulation model (AOGCM), which was developed jointly by CNRM-GAME and CERFACS to contribute to the CMIP5 database. A full description and a basic evaluation of the system can be found in Voldoire et al. (2013).
CNRM-CM5.1 includes the global spectral atmospheric model ARPEGE-Climat (v5.2), operated on a T127 truncation (roughly 1.4° resolution in both longitude and latitude). Land-surface processes and air-sea turbulent exchanges are simulated through the SURFEX platform. The ocean component is based on the ocean part of the NEMO model. The ORCA-1° global tripolar quasi-isotropic grid is used: its nominal horizontal resolution is 1°, with a latitudinal refinement of 0.5° in the Arctic Ocean and 0.3 along the equator. 42 vertical levels are used (10 in the uppermost 100 m). The GELATO5 dynamic-thermodynamic sea ice model is directly embedded into the ocean component and uses the same horizontal grid. It includes elastic-viscous-plastic rheology, semi-lagrangian advection of ice slabs, ridging and rafting, parametrization of lead processes, snow-ice formation, prognostic salinity, and an advanced snow cover scheme which represents the effect of snow ageing on snow density. In the present study, 4 thickness categories are used: 0–0.3, 0.3–0.8, 0.8–3.0, and over 3 m. For the treatment of the vertical heat diffusion of ice, every slab of ice is divided into 9 vertical layers, and may be covered with one snow layer. All components are coupled through the OASIS(v3) system (Valcke 2006).
2.2 Experimental design
2.2.1 Historical simulations (HIST)
To investigate the added value of the ocean initialization on the decadal predictability and prediction, we use, for comparison, CMIP5 historical experiments (Taylor et al. 2012), performed with CNRM-CM5.1. Ten members have been computed for the period 1850–2012. They differ in their initial conditions, taken from different dates of the 1000-year control simulation under preindustrial conditions performed with the model. The internal variability of those historical simulations is not synchronized with observations. They will therefore be referred to as “non-initialized” experiments in contrast with decadal simulations.
The sea ice cover simulated by CNRM-CM5.1 is partially described in Voldoire et al. (2013). The Arctic geographical distribution of sea ice has been shown to be correctly simulated, especially in winter, despite a slight overestimation of 1.1 × 106 km2 of the total Arctic SIE (Table 1) over the period 1979–2008. This bias comes from an overestimation of sea ice concentration in the Sea of Okhotsk and east of the Kuril Islands (Voldoire et al. 2013). During the summer, the total Arctic SIE is underestimated due to spurious loss in the eastern part of the Siberian Basin. The comparison of simulated SIT with the Pan-Arctic-Ice-Ocean-Modeling-System (PIOMAS) (Zhang et al. 2008; Schweiger et al. 2011) highlights a strong negative bias, especially north of Greenland. As a consequence, sea ice transport through the Fram Strait is underestimated by 42 % when compared to observational estimations by Kwok et al. (2004).
2.2.2 Decadal hindcasts (DEC)
Analyses of the sea ice predictability in this paper are based on a set of ten-year-long, ten-member ensemble decadal hindcasts performed within the framework of CMIP5 (Taylor et al. 2012) with CNRM-CM5.1. Hindcasts were initialized on January 1st of every 0, 1, 5 and 6 calendar years of a given decade spanning the 1960–1996 period, which corresponds to 16 start dates. The choice to limit our analysis to this period is based on the 1958–2008 coverage period of the target used as a reference for prediction skill assessment. Hindcasts starting after 2000 cannot be compared to the reference for the whole integration period and are therefore treated as forecasts. For a given start date, members share the exact same ocean/sea ice initial state, while that of the atmosphere/land differs. The latter are randomly selected during January. This set of decadal hindcasts will henceforth be referred to as DEC.
Initial states are extracted from a coupled experiment, hereafter referred to as NUD, performed with the same coupled model, in which the ocean temperature and salinity are nudged towards the full fields from the ECMWF ocean reanalysis NEMOVAR–COMBINE (Balmaseda et al. 2010b). This reanalysis was performed with the same NEMO version at the same horizontal and vertical resolution as in CNRM-CM5.1. The constraint consists of a 3D Newtonian damping toward the NEMOVAR–COMBINE temperature and salinity with a vertical dependence of the relaxing time-scale ranging from 10 days below the mixed layer to 360 days at the bottom of the ocean. No nudging is applied within the mixed layer, and the sea surface temperature and salinity are restored through flux formulation with coefficients equal to −40 W m2 K−1 and −167 mm day−1, respectively. The 3D damping is applied outside a broad equatorial band (15° latitude) in which the subsurface is free to evolve while the surface restoring is active everywhere. No constraint is applied directly to sea ice, atmosphere and land. This preliminary experiment aims to produce ocean initial states compatible with the observations and the model mean state. The use of NUD, performed with the same coupled model as DEC, allows us to initialize all dynamical and thermodynamical sea ice variables, especially those related to the four ice categories of the GELATO model.
Table 1 presents the evaluation of Arctic sea ice simulated by NUD and HIST. We used the National Snow Ice Data Center (NSIDC) sea ice index (Fetterer et al. 2002) as a reference for SIE. As no equivalent long-term and spatial sample observations of the SIT exist, the SIV is compared to the PIOMAS SIV reconstruction time series (Zhang et al. 2008; Schweiger et al. 2011), which stands as a reference in Arctic SIV reconstruction. This evaluation is performed on datasets overlapping period, namely 1979–2008. Clearly, the sea surface temperature and salinity restoring impose a strong constraint on sea ice edge position during winter, leading to a SIE very close to observations. This indirect constraint is no more efficient during summer, when a negative bias in SIE is observed, in accordance with the free coupled model mean state. In contrast, the ocean surface restoring does not impose any constraints on SIT, giving free rein to the known intrinsic underestimation of SIV in CNRM-CM5.1 (Voldoire et al. 2013). Accordingly, a very strong negative bias is found in SIV during both winter and summer. During winter, this bias is even stronger than in the free coupled model, due to the correction of the CNRM-CM5.1 SIE overestimation (Voldoire et al. 2013) mentioned previously. The winter and summer downward trends of both SIE and SIV are correctly represented, as shown by the correlation coefficients of interannual time series. The NUD simulation also performs well in reproducing the interannual variability around the trend for the SIE, with significant correlation coefficients of the detrended time series in both winter and summer. On the other hand, it clearly fails to reproduce the Arctic SIV interannual variability around the linear trend. In conclusion, the sea ice initial states provided by NUD are close to observations in terms of SIE, but strongly underestimate the SIV, which is much closer to the free coupled model attractor.
All external radiative forcings (natural and anthropogenic) are the same in all simulations, following the CMIP5 historical protocol until 2005 and the RCP8.5 scenario thereafter. The use of the same coupled model for all 3 sets of experiments (NUD, DEC, and HIST) is clearly one of the strengths of this analysis, as no uncertainties arise from the model version when comparing datasets.
3 Results
3.1 Prognostic potential predictability
DEC ensemble members which share the same ocean/sea ice initial state diverge as the forecast range increases due to the chaotic nature of the climate system. The DEC ensemble spread (\({\sigma_{d} }\)) increases accordingly and a measure of the predictability relies on the comparison of the latter to an estimation of the natural variability of the system (\({\sigma_{h} }\)). Predictability is assumed when the former is smaller than the latter, following the so-called prognostic potential predictability (PPP) approach (Pohlmann et al. 2004; Koenigk and Mikolajewicz 2009) defined as:
In most studies, the expected spread due to natural variability is assessed using stationary control run integrations (Pohlmann et al. 2004; Koenigk and Mikolajewicz 2009; Holland et al. 2011). As DEC start dates span several decades and climate conditions change rapidly, especially over the Arctic, we decided to use the HIST ensemble spread to obtain an estimate of the spread associated with the natural variability of a given year. HIST is preferred to a pre-industrial control run because it accounts for changes in natural variability, which are crucial in the Arctic. Note that HIST ensemble spread is computed on the exact same date as DEC, meaning that for each start date and forecast range, it is computed as the ensemble member standard deviation of the prediction date. Figures 1, 3, 4, 5 and 6 show ensemble spread as a function of lead time for both DEC (in red) and HIST (in black) simulations for several physical quantities with a seasonal distinction. Those spreads are averaged over all start dates, thus giving an evaluation of the “mean” PPP over the second half of the twentieth century. A zero spread of DEC simulations corresponds to a perfectly predictable system (no divergence of the ensemble members at the given time). Conversely, a spread equal to HIST spread implies no predictability coming from ocean/sea ice initialization. The null hypothesis that the two spreads are indistinguishable is tested according to a Fisher test at 95 % level with Nsd*(Nmb − 1) − 1 degrees of freedom, where Nsd is the number of start dates and Nmb is the number of members. Significantly distinguishable spreads are indicated in full circles in Figs. 1, 3, 4, 5 and 6. In those figures, we can see small variations of the HIST ensemble spread with the forecast range. Those variations could be externally forced by brief events such as volcanic eruptions or, as will be shown in the following section for regional indices, by the long-term GreenHouse Gases (GHGs) evolution. In addition to these effects, uncertainties due to the HIST ensemble size may lead to small variations. These uncertainties can be reduced by averaging this spread over several years.
Ensemble standard deviation of a March SIE b September SIE c March SIV, and d September SIV for DEC experiment (in red) and HIST experiment (in black). The standard deviation of each lead time is averaged over all start dates. Years for which HIST ensemble variance is significantly higher than the DEC ensemble variance according to a fisher test at 95 % confident level are indicated in full circles
Unlike HIST, the DEC ensemble spread might depend on how the ensemble is generated (Du et al. 2012). The generation ensemble methodology and its impact on predictability and prediction skill is a main issue of near-term climate prediction but is not the focus of this paper. Nevertheless, a very short analysis testing our atmospheric-only perturbation against an atmosphere–ocean perturbation technique performed on a few start dates (not shown) leads us to conclude that atmospheric-only perturbation was sufficient to generate the Arctic SIE and SIV ensemble spread, though it gives an upper limit of potential predictability. Note that this PPP measure addresses initial-value predictability only. The lead time is from 0 for the year of the initialization to 9 for the tenth year of simulation. Therefore, lead time 0 year corresponds to a lead time of 3(9) months for March (September) SIE and SIV.
3.1.1 Global Arctic
March global Arctic SIE ensemble spread (Fig. 1a) for DEC is lower than for HIST up to 6 years, suggesting that there is some memory of initial conditions during the first years of forecast. The same conclusion can be drawn for March SIV (Fig. 1c), which exhibits a significant PPP up to a lead time of 8 years. The summer sea ice cover seems to be much less predictable (Fig. 1b, d) in terms of PPP, with September SIE showing no significant predictability after the first 3 years of integration. Summer SIV shows some predictability up to 4 years and suggests predictability up to 6 years.
In the Arctic, the transition zones between the interior ice pack and the open ocean, known as Marginal Ice Zones (MIZ), capture most of the seasonal and longer term SIC variability. During winter, the Arctic SIE and Arctic SIA interannual variability arises from the MIZ, present in all peripheral seas. This is highlighted by the interannual SIC standard deviation distribution of the historical simulations (Fig. 2a). Thus, understanding of the Arctic sea ice cover predictability requires a regional approach because of the different driving mechanisms of variability at work, which depend on location. These peripheral seas also play an important role in Arctic SIV variability, as shown by interannual SIT standard deviation (Fig. 2b). However, in contrast with SIC, SIT exhibits some interannual variability in the ice pack, showing that the interior basin should not be neglected when explaining Global Arctic SIV variability and predictability. As Arctic sea ice cover is confined to the Central Arctic during summer, we limit the following regional investigation to the winter season.
3.1.2 Regional sea ice cover
The winter SIC of the marginal seas exhibits a covariability known as the double dipole pattern (Walsh and Johnson 1979; Fang and Wallace 1994; Deser et al. 2000), which is linked to the North Atlantic Oscillation (NAO). This link associates positive (negative) SIC anomalies in the Labrador and Bering Seas (Nordic and Okhotsk Seas) with a positive NAO phase (Deser et al. 2000; Ukita et al. 2007). Superimposed on the large scale covariability of the North Hemisphere sea ice, regional contrasts between peripheral seas have been also identified over the full historical period (Mysak and Manak 1989) and the more recent period of satellite observations (Parkinson et al. 1999). Bitz et al. (2005) identified a strong influence from solar radiation as well as the convergence of heat transported by the ocean on the ice edge position. The latter process differs significantly from one marginal sea to the other, as it is influenced by the fluctuations of different water masses. For example, Schlichtholz (2011) identified a strong control of the Nordic Seas winter SIA by the summer temperature in the Atlantic water core in the Barents Sea opening area. Those regionally contrasted oceanic influences are expected to play a crucial role in sea ice cover predictability.
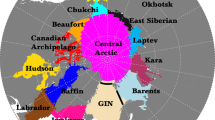
In this section, we investigate regional PPP in six regions, shown in Fig. 2c. The three Atlantic sector regions, namely the Labrador, Greenland-Iceland-Norwegian (GIN) and Barents Sea regions, along with the Pacific sector region of the Bering Sea, correspond to the NSIDC regional index computation domains (Parkinson et al. 1999; Parkinson and Cavalieri 2008). The Okhotsk Sea region is chosen larger than the NSIDC computation domain in order to be more consistent with the Pacific MIZ distribution in CNRM-CM5.1, which is displaced slightly southward compared to observations (Voldoire et al., 2013). Finally, we consider the Central Arctic domain in order to investigate the significant SIT variability there.
The evolution of SIE ensemble spread as a function of lead time and domain highlights strong regional constrasts in PPP (Fig. 3). The most striking result occurs for the GIN Seas SIE, which exhibits some significant PPP up to 9 years lead time, 3 years longer than the Global Arctic SIE PPP. Moreover, the fact that the GIN SIE DEC ensemble spread never catches up with the HIST ensemble spread suggests some predictability beyond the 10 years of simulation. The same conclusion can be drawn for the Labrador Sea. Note, however, that the Labrador SIE variability is underestimated in CNRM-CM5.1 (not shown), suggesting that some key processes that might affect the PPP might be not correctly simulated in this region. In comparison, other marginal seas exhibit a very low initial value predictability limit, equal to 1 year at most, suggesting that the winter Arctic SIE PPP comes mostly from the Atlantic sector, and more specifically from the GIN Seas.
March regional SIE ensemble standard deviation for a the GIN Seas, b the Labrador Sea, c, the Barents Sea, d the Central Arctic, e the Bering Sea, and f the Okhotsk Sea. Regional domain locations are shown on Fig. 2c
Similar conclusions can be drawn from the regional SIV (Fig. 4). Indeed, the GIN and Labrador Seas exhibit SIV PPP limits quite similar to the Global Arctic SIV PPP limit, while the Bering and Okhotsk Seas show no SIV PPP beyond a lead time of 2 years. Note that, although not significant beyond 2 years, the Barents Sea SIV exhibits some PPP up to 4 years, although it cannot be identified at all on SIE. SIV shows some significant PPP in the Central Arctic domain of the order of 8 years (Fig. 4d). The Global Arctic SIV PPP thus comes mostly from the central Arctic domain, as well as the Atlantic domain. The Pacific sector shows very weak predictability. Those results are in accordance with Koenigk and Mikolajewicz (2009).
March regional SIV ensemble standard deviation for a the GIN Seas, b the Labrador Sea, c, the Barents Sea, d the Central Arctic, e the Bering Sea, and f the Okhotsk Sea. Regional domain locations are shown on Fig. 2c
3.1.3 Period dependence of the PPP
As mentioned at the beginning of this section, DEC start dates span several decades where rapid climate condition changes occur, implying the need to take into account changes of internal variability in the PPP estimation. In this section, the period dependence of PPP is evaluated. We separate the 16 start dates into two disjoint sets: the first containing the 8 start dates prior to 1979, and the second the most recent 8 start dates after 1979. This split is constrained by the limited number of available start dates and the need for sufficient sampling in order to obtain statistically significant conclusions.
Repeating the previous analysis on both disjoint periods leads us to conclude that the winter Arctic SIE and both winter and summer Arctic SIV have less predictability due to initialization in the recent period than during the 1960–1979 period (not shown). The summer Arctic SIE, which already exhibited poor predictability in the analysis of the whole period (Fig. 1b) shows no PPP variation between the two periods. The most striking PPP differences between the two periods occur for the GIN Seas SIE (Fig. 5). In this region, when we restrict the PPP assessment to the start dates prior to 1979, SIE is highly predictable due to initialization during the 10 years of hindcast (Fig. 5a) while the PPP limit drops to 6 years when considering the period after 1979 (Fig. 5b), and the difference between HIST and DEC spread is much weaker beyond the first 3 years. No similar PPP sensitivity can be identified in other Arctic regions (not shown), suggesting that the PPP variation identified on Arctic SIE comes mostly from the GIN Seas. Note, however, that the Labrador Sea SIE shows opposite PPP variations, with higher potential predictability in the recent period. The same results are found for SIV in both domains. Additionally, the Central Arctic and Barents Sea SIV PPP behave similarly to the GIN Seas PPP, with weaker initial-value predictability after 1979 (Fig. 6).
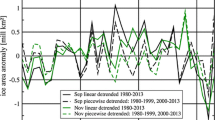
The decrease of the GIN Seas PPP for both SIV and SIE in the recent period is not associated with a faster divergence of DEC ensemble members, but comes from a decrease of internal variability captured by the decrease of HIST ensemble spread between the two periods (Fig. 5b compared to Fig. 5a). As discussed by Goosse et al. (2009), a reduction of mean state could explain a linear decrease of the variance. However, the decrease found in HIST is strongly non-linear, with a first drop occurring around 1986 and a second around 2000 (Fig. 7). These drops in both SIE and SIV variance between HIST members are not associated with drops in mean state, as would be expected if the simple model of Goosse et al. (2009) could be applied here. To understand this non-linearity, the ocean water masses distribution and their impact on sea ice cover in this region are now documented. The two surface oceanic fronts, namely the Arctic front separating the so-called Arctic Intermediate Water of the interior of the Greenland Sea from the warm Atlantic water to the east, and the polar front separating the cold and fresh polar water to the west, strongly influence the sea ice distribution (Swift 1986; Comiso et al. 2001). The Arctic and Polar fronts delimit three areas exhibiting contrasted SIC distribution and variability (Comiso et al. 2001; Germe et al. 2011). The first, west of the polar front and coinciding more or less with the East Greenland shelf, is characterized by highly compact sea ice cover and weak interannual variability. The second, between the two fronts, is covered by less compact, but much more variable, ice cover. The last, east of the Arctic front, is never covered by sea ice as the result of the influence of warm Atlantic water. These three regions will be referred to hereafter as “Polar,” “Arctic,” and “Atlantic” areas respectively, following the Swift (1986) denomination. This spatial pattern–that is, the two fronts, as well as the corresponding contrasted sea ice cover areas–is well simulated in CNRM-CM5.1 despite a slight shift toward Iceland, as shown by the mean sea surface temperature distribution (Fig. 8) and the SIC variability on Fig. 2a. In light of the context of oceanic influence, the drop in SIE variance that occurs in 1986 obviously comes from the quasi-disappearance of sea ice in the “Arctic area,” as shown by the 15 and 95 % sea ice concentration contour positions on Fig. 8a, b. The second drop is due to the delayed disappearance of sea ice cover in this area for two HIST members. With no sea ice cover in the Arctic area, the GIN Seas sea ice cover is reduced to the Polar area, where the constant influence of polar water prevents strong interannual variability of the sea ice concentration. The sea ice concentration variability therefore mostly comes from slight variations in the polar front position, which does not have a significant impact on the total GIN Seas SIE and SIV. This narrowing of Greenland Sea MIZ has been observed and described by Strong (2012) using the NSIDC satellite dataset, showing that this changing state is not limited to our climate model but is noticeable in observations. No such narrowing of the GIN Seas MIZ could be identified in DEC in accordance with the similar spread behavior for the two periods. DEC seems to be attracted by a “colder” state than HIST. This might come from a lower climate sensitivity of DEC experiments as suggested by Meehl and Teng (2012). In any case, the GIN Seas MIZ in DEC remain in a mean state close to the HIST pre-1986 state. This large MIZ in DEC, which is not associated with a fast divergence of ensemble members, supports the hypothesis of a high sea ice cover potential predictability in this area.
For the central Arctic domain, the decrease of winter SIV PPP between the earlier and more recent periods is partially explained by the faster rate of divergence of DEC members together with the decrease of internal variability, which is also a contributing factor. In contrast to the GIN SIE, this decrease is more or less regular and shows no strikingly abrupt drop (not shown). As the Central Arctic is completely covered by sea ice during winter, with no reduction of SIE, the reduction of SIV variability is only due to a reduction of SIT variability. Interestingly, the pattern of the trend of the SIT spread differs from that of the SIT trend (Fig. 9). The SIT trend is negative in the whole Arctic domain (Fig. 9a), while the trend of the SIT spread is less homogeneous (Fig. 9b). In the Bering Sea, as well as the Barents Sea, regional dipoles mark a shift of the MIZ associated with the shift of the sea ice edge position. By construction, variance disappears where the sea ice disappears, while the variance increases in the new MIZ area. In the GIN Seas, as already mentioned, the MIZ is reduced rather than shifted, explaining the absence of a dipole. In the central Arctic domain, the decrease is maximal near the Siberian coast and weakened when moving toward the pole. An increase is observed near the Greenland and Canadian Archipelago, although not significant at the 95 % level. The dipolar pattern between Laptev/East Siberian Seas and north of Greenland cannot be associated with a similar dipole in the SIT trend, showing that the evolution of the spread cannot be explained by thickness evolution alone. Moreover, the decrease of SIT in the Central Arctic is not sufficient to affect the variance by the proximity of the zero boundary. In addition, stronger spread decrease and increase both occur in areas covered by thick ice, suggesting that dynamical processes are involved in these spread variations. But the explanation of this variability changes has yet to be understood. The thinning of the sea ice cover in the Central Arctic can explain the faster rate of divergence of DEC members in the more recent period in comparison to the earlier one by a stronger sensitivity of sea ice cover to atmospheric fluctuations, as discussed by Holland et al. (2011).
3.2 Prediction skills
In order to quantify the hindcasts’ skill in capturing the sea ice cover evolution, we use the so-called Anomaly Correlation Coefficient (ACC) skill score defined as:
where \(t\) is the lead time and j is the start date. Anomalies are computed relative to the 1958–2008 period. DEC skill scores are compared with those of HIST in order to highlight the added value of ocean/sea ice initialization on predictions. Recall that all external forcing and model components are identical; the differences between DEC and HIST thus arise purely from initialization. Note that for DEC predictions, some skill arises from the trend present in initial conditions, in addition to the direct and instantaneous climate response to evolving forcings. Therefore, we look at the “residual” skill associated with internal ocean/sea ice variability, obtained by removing the long-term trend, following the approach of Oldenborgh et al. (2012). This trend is computed by linear regression on CO2 concentration evolving time series. The sensitivity of the ACC to the detrending technique has been analyzed by comparing our definition of the trend to the use of a 2nd order polynomial fit. No significant impact of the detrending method on the ACC has been identified except for winter total Arctic indices. For those indices, the ACC are slightly overestimated by our method. However, the higher sensitivity of the polynomial fit to the sampling leads us to reject this technique. Due to the lack of observed SIV time series and uncertainties in SIV PIOMAS reconstruction (Schweiger et al. 2011), we use NUD as a target for all the ACC computations, including those of SIE, in order to be consistent. Note that NUD is biased against observations (Table 1). Therefore, ACC, as presented here, does not perfectly reflect the prediction skill (i.e. correspondence between forecast and observations) of our model. DEC and HIST ACC are computed from ensemble mean. Before ACC computation, the model drift is removed following the CLIVAR recommendations relevant for full field initialization (CLIVAR 2011).
3.2.1 Global Arctic
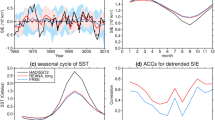
Figure 10 shows global Arctic sea ice indices ACC with (solid lines) and without (dashed lines) trend, for DEC (red lines), HIST (black lines) and persistence (blue lines). Here, persistence prediction is taken as the March (September) anomaly (in NUD) of the year before the initialization date for March (September) prediction at a given lead time. For all indices, DEC exhibits significant scores up to a lead time of 10 years. However, HIST ACC of a similar order of magnitude, obtained before detrending, show that those skills are mostly due to external forcing. This is confirmed by the much lower skill of the hindcasts once the linear regression on the CO2 time series has been removed. No added value from the initialization can be identified except for the first lead time (3 months lead time indicated as lead time 0 year on the Fig. 10) of winter SIV, and, to a lesser extent, the winter SIE.
Anomaly correlation coefficients (ACC) of a March SIE, b September SIE, c March SIV, and d September SIV for Decadal experiment (in red), Historical experiment (in black) and persistence evaluated from NUD (in light blue). Solid and dashed lines correspond to anomalies from the mean and long evolving trend, respectively. The trend is assessed by a linear regression onto the CO2 concentration external forcing time series. In c the purple dotted line corresponds to the number of years impacted by the Pinatubo eruption or a strong SIV anomaly in the 70 s in NUD (i.e. years included in the following list: 1977, 1978, 1979, 1993, 1994, 1995) taken into account in the ACC computation
Considering the persistence predictions of summer sea ice indices, the rather constant scores with lead time before detrending, in addition to the insignificant scores after detrending, suggest that this persistence prediction skill comes purely from the trend. Indeed, in summer, this long-term trend is substantial when compared to natural variability (83 % of the variance for SIE as well as SIV in NUD) and is present in the initial conditions in both DEC and HIST. Remember that the latter is not synchronized with observations in terms of internal variability and therefore is not initialized in that sense (see Sect. 2.2). A similar conclusion can be drawn for winter SIV, for which the linear trend explains 80 % of the variance. In contrast, for winter SIE, the externally forced linear trend explains only 48 % of the total variance. The winter SIE persistence ACC varies with lead time and is not very sensitive to detrending. This suggests that those scores come from a memory of the system and not purely from the trend.
The weak PPP of the summer Arctic sea ice cover identified in Sect. 3.1.1 is in accordance with the lack of prediction skill found here after detrending. In contrast, the low ACC of detrended winter SIE, and even more of winter SIV compared to the significant PPP previously mentioned, show that strong improvements could be made. Those improvements would require a better initialization and simulation of sea ice variability driving mechanisms.
Finally, one can notice an oscillatory behavior of ACC along the forecast time axis with a period around 4–5 years. This is most striking for the winter SIV. It comes from the start date sampling and does not reflect a physical reemergence of skill. For example, if an event of strong anomaly appears in the target NUD in a given year, but is not predicted by HIST or DEC, the ACC will be weakened at lead times that take into account this peculiar year. Due to the start dates sampling, those lead times will be distributed as n, n + 1, n + 4 and n + 5. One can have the opposite case of strong anomaly in DEC and HIST (for example, due to a volcanic eruption such as the Pinatubo in 1991) that does not appear in NUD. In that case, the ACC will be impacted in the same way for HIST and DEC, while the persistence will not be impacted. For winter SIV ACC, the oscillations can be explained by the combined effects of the Pinatubo eruption and a strong positive anomaly event in 1970s (in NUD) which is not predicted by HIST or DEC. This is highlighted by the number of “polluted” points (i.e. the points impacted by the Pinatubo eruption or the 70 s SIV anomaly) taken into account for the ACC computation, indicated by the purple line in Fig. 10c. This recurrence of a single event signal on ACC at different forecast range was already observed by Garcia-Serrano and Doblas-Reyes (2012) on ACC of surface atmospheric temperature for the occurrence of ENSO events. Note that for persistence, in addition to the “polluted” predicted years, the lead time predicted by these peculiar events will also be impacted. Therefore the purple line does not perfectly reflect the impact of those events on the persistence computation.
3.2.2 Regional sea ice cover
As could be expected from the previously documented PPP discrepancies, regional prediction scores are higher in the Atlantic than in the Pacific sector (not shown). However, even in the Atlantic subdomains, no significant scores are obtained beyond 2 years. For the SIE, the best prediction scores are obtained for the GIN Seas domain (Fig. 11a). DEC ACC are higher than those of HIST for the first three lead times, which suggests some added value of the initialization. Those ACC are much weaker after detrending. However, the fact that they remain positive and higher than the persistence ACC, in addition to the large PPP of this region identified in the previous section, gives some confidence about the usefulness of the DEC protocol. Beyond 3 years, HIST’s ACC exceed those of DEC, showing that there is no improvement (and even possible degradation) from the initialization at those lead times. Higher scores for DEC compared to HIST are also found for the two first lead times of the Labrador and Barents SIE, and the first lead time (lead time 0 year) of the Bering Sea (not shown). For those regions, the scores are not strongly affected by the detrending, which again increases confidence in added predictive skills coming from the initialization.
The GIN Seas SIV ACC exhibit the same overall behavior as those of the SIE (Fig. 11b); i.e., rather constant and significant HIST ACC with lead times, again showing some prediction skill coming from boundary condition changes, but higher DEC ACC up to 1 year lead time, with or without detrending. The best prediction skill of the SIV is obtained for the central Arctic domain (Fig. 12). In that case, the comparable ACC of HIST and DEC clearly suggest that those skills come purely from the boundary condition changes. However, despite a strong decrease after detrending, DEC exhibits positive and higher ACC than HIST for lead times exceeding 3 years. This highlights a possible delayed added value of the initialization that could come from a delayed impact of the ocean initialization on the SIT in the central Arctic.
Although insignificant, the Labrador Sea exhibits very interesting ACC (Fig. 13). Indeed, especially for SIV, DEC ACC are much higher than those of HIST for the first lead times. Those ACC remain nearly unchanged after detrending, which clearly shows an added value of the initialization at those lead times. In contrast, after the first DEC ACC drop, for lead times exceeding 6 years, DEC and HIST ACC rise together for SIV (and to a lesser extent for SIE for lead time exceeding 7 years). These long lead time skill disappears after detrending, showing that the recovered prediction skill comes from the boundary conditions. The Labrador sea SIV trend is strongly non linear and affects much more the recent period from the 90 s in both DEC and HIST. As the last DEC initial date starts in 1996, this trend is only captured by the last lead times, hence explaining the rise of the skill.
4 Conclusion and discussion
Based on the CMIP5 protocol for decadal experiments, the prognostic potential predictability (PPP) of the Arctic sea ice at interannual timescale was investigated in the CNRM-CM5.1 model. The standard CMIP5 historical twentieth century experiment performed with the same coupled model was also used to investigate the added value of the ocean initialization for the sea ice interannual potential predictability and prediction skill. Our results show that the CNRM-CM5.1 Arctic SIE (SIV) PPP is significant for approximately 6(8) years and 2(4) years for winter time and summer time, respectively. The interannual predictability of Arctic sea ice beyond 2 years’ lead time has been poorly investigated so far. The SIE was found to be potentially predictable for a shorter time in summer than in winter, in accordance with the findings of Holland et al. (2011) for SIA, although the potential predictability was found to be longer in our model. The long time scale of potential predictability found for SIV is in accordance with previous studies, which showed that the winter SIT is predictable for at least 2 years on annual mean (Koenigk and Mickolajewitz 2009) and for both winter and summer (Holland et al. 2011). However, as for SIE, the SIV potential predictability in CNRM-CM5.1 is very long compared to the findings from those previous analyses. This predictability time scale depends partly on the generation ensemble technique, along with the chosen metric, and further analysis investigating the sensitivity of our results to those aspects would be useful.
We found that the potential predictability of the winter Arctic SIE comes predominantly from the Atlantic sector, especially from the GIN Seas, while the Pacific sector seems unpredictable beyond the first year. In addition to the Atlantic Sector, the Central Arctic also plays a substantial role in total Arctic SIV potential predictability. The contrasted potential predictability of sea ice between the two oceanic sectors has been observed in other coupled models, such as ECHAM5/MIP-OM (Koenick and Mickolajewitz 2009), and EC-Earth (Koenigk et al. 2012). This is in accordance with the high initial-value predictability of North Atlantic variability (Kim et al. 2012; Doblas-Reyes et al. 2013), especially in the subpolar gyre (Hazeleger et al. 2013), and with the poor predictability of the North Pacific in state-of-the-art climate models (Kim et al. 2012; Guemas et al. 2012; Doblas-Reyes et al. 2013).
The period dependence of the PPP—in other words, its stationarity—was also investigated. This analysis highlights a decrease of PPP in the more recent period. This decrease is attributed to the thinning of the ice cover, as well as the disappearance of sea ice in areas where the SST and SSS exhibit a strong variability such as the convection zone in the Greenland Sea. Concerning the Central Arctic SIV PPP, its reduction comes from the combined effect of a faster divergence of DEC members and a reduction of the internal variability estimated by HIST member spread. The faster rate of divergence can be attributed to the thinning of the sea ice cover, making it more sensitive to atmospheric fluctuations. This lower PPP associated with a thinner ice regime has already been mentioned in previous studies, such as Holland et al. (2011), showing that this finding is not restricted to the CNRM-CM5.1 model. The thinning and associated rise of sensitivity to atmospheric fluctuations will have also a strong impact on the summer SIE variability and predictability. Indeed, studies focusing on seasonal Arctic sea ice predictability have already emphasized the important role of thick winter sea ice in SIE predictability of the following summer. (Holland et al. 2011; Chevallier and Salas y Mélia 2012). This is consistent with the faster DEC ensemble divergence of summer Arctic SIE found in the recent period for the first lead time (i.e. 9 months lead time, not shown).
Interestingly, the Labrador Sea seems to behave differently from the rest of the Arctic, with an increase of the PPP during the recent period. However, this result should be interpreted with caution, as the Labrador sea ice cover variability is underestimated in the model. This underestimation prevents to reproduce the negative correlation between sea ice extent in the Labrador and GIN Seas regions associated with the observed Atlantic sea ice seesaw (Fang and Wallace 1994; Ukita et al. 2007). However, this negative correlation found in observations suggests the existence of a common driving mechanism exhibiting opposite impacts on sea ice variability and sea ice PPP in the two regions. A good candidate would be the North Atlantic Oscillation (NAO). Positive NAO dominance, together with the associated northerly winds through the Fram Strait, creates favorable conditions for large sea ice export (Vinje 2001; Kwok et al. 2004; kwok et al. 2009; Kwok et al. 2013). According to Mysak et al. (1990), and Koenigk et al. (2006), this sea ice export causes fresh water, and therefore SIE, anomalies, in the Labrador Sea a few years later. This export also depends on the propagation of SIT anomalies across the Arctic, through the Transpolar Drift stream to the Fram Strait. This link with sea ice advection anomalies formed several years earlier near the Siberian coast, strengthened by favorable export conditions, could explain the larger predictability of the sea ice cover in the Labrador Sea during long positive NAO periods. Note that the northerly winds that create favorable conditions of sea ice export also drive a westward Ekman drift along the East Greenland Current (EGC) that tends to push the sea ice toward the Greenland coast, preventing it from penetrating into the Greenland Sea (Germe et al. 2011). This could explain the disappearance of sea ice cover in the central Greenland Sea during the recent period, as well as the weak impact of the export on the interannual variability of the GIN Seas SIE. Döscher et al. (2010) also associated a multiyear negative trend of summer SIE ensemble spread with a positive trend of the NAO winter index. This summer SIE, restricted to the Central Arctic, shows that a positive NAO trend would also impact the Central Arctic internal variability. Therefore, a positive trend of the NAO index in HIST could explain most of the PPP evolution in the Central Arctic as well as in the GIN and Labrador Seas. Unfortunately, individual HIST members exhibit greatly varying trends of the NAO index (taken as the first principal component of the winter averaged sea level pressure over the North Atlantic domain used by Hurrell et al. (2003)), showing that the evolution of sea ice variability in the Labrador and GIN Seas cannot be explained by a boundary-forced positive NAO trend. However, the link between the Fram Strait sea ice and freshwater export and the NAO has been identified in observations, and might differ in CNRM-CM5.1. Furthermore, some studies showed that this link is strongly dependent on the period (Vinje 2001; Hilmer and Jung 2000; Schmith and Hansen 2003) and that other large-scale circulation patterns involving northerly winds across the Fram Strait might play a more important role in this export (Koenigk 2006; Wu et al. 2006; Tsukernik et al. 2009). A significant positive trend of both freshwater and sea ice mass annual export through the Fram Strait has been found over the 1958–2008 period in HIST, giving some confidence as to the impact of the Fram Strait export on observed PPP variations in the GIN and Labrador Seas. A more detailed analysis of the mechanisms involved in this export, as well as in sea ice cover variability in Atlantic marginal Seas in CNRM-CM5.1, and their eventual evolution according to the boundary forcing in the recent period, would be needed to answer properly to this question. This analysis goes beyond the scope of this paper, and will be the subject of future work.
The very high potential predictability of the GIN Seas before 1986, and the higher potential predictability of the Atlantic sector compared to the Pacific sector in general, has yet to be understood. The persistence of anomalies in SIE, as well as in SIV, evaluated from NUD, is very weak (no more than 2 years) in all six regional domains (not shown). Furthermore, this persistence is not longer in the Atlantic sector, even in the GIN seas, and cannot explain the longer PPP observed in this area. This low persistence of the sea ice cover anomalies in the GIN Seas suggests that the PPP results from a dynamical effect. In addition to the already mentioned Arctic sea ice or freshwater export role (Griffies and Bryan 1997; Koenigk et al. 2006; Koenigk and Mikolajewicz 2009), Atlantic water temperature and salinity anomalies advection might be a significant source of predictability of the sea ice cover in this region, as suggested by Schlichtholz (2011). In the GIN Seas, the reemergence of oceanic anomalies due to the proximity of the deep water formation zone might also play an important role in sea ice cover variability and predictability (Roach et al. 1993; Bitz et al. 2005; Schlichtholz 2011). Finally, the correlation found by Koenigk et al. (2012) between the sea ice cover in the GIN and Labrador Seas and the MOC suggests an influence of the large scale oceanic circulation as well. In conclusion, the Atlantic Subarctic Seas undergo strong antagonist oceanic influences, leading to a complex local variability which is very difficult to understand, but clearly strongly linked to the long-term evolving ocean.
In contrast to the high PPP of Arctic sea ice, it has been shown that the DEC prediction skill evaluated from ACC of the whole Arctic SIE/SIV is mostly due to external forcing, with no improvement from initialization. In accordance with the PPP analysis, this result is contrasted when we examine regional indices. An added value of the initialization protocol has been found for the Labrador and GIN Seas SIE predictions during the first 2 years. In the GIN Seas, the prediction skill seems to be dominated by the boundary condition changes beyond this timescale, while the boundary-condition prediction skill rises only for timescales exceeding 6 years in the Labrador Sea. The Labrador and GIN Seas SIV exhibit the same added value of the initialization during the first 2 and 1 year of integration, respectively. In contrast, central Arctic SIV predictions show an additional value of the initialization protocol only during the first few months, and this added value is noticeable only after detrending. This shows that, despite its large PPP, the central Arctic SIV prediction skill is dominated by climate external forcing rather than initial conditions. This is consistent with the large part of variance explained by the trend taken as the linear regression on the CO2 time series (80 % in NUD). Regarding SIE, these results seem robust, as they remain quasi-unchanged when using HadISST dataset as a target instead of NUD (not shown). The contrasted findings regarding potential predictability and prediction skill might be partially due to an overestimation of the potential predictability coming from the generation ensemble technique, or the metric; however, it suggests that substantial improvements could be made in order to enhance the prediction skill.
The Arctic is changing rapidly. This change affects the mean state of various components of the Arctic system, but this analysis shows that the variability of those components changes as well. Variability changes will have a strong impact on predictability. Therefore, long-term changes of seasonal to interannual variability and associated interactions among components could be better understood, with the aim of possible near-term climate predictions. Another important aspect highlighted in this paper is that the common interpretation of larger internal variability implying reduced predictability might be incomplete. Indeed, an increase of internal variability is not necessarily associated with a faster divergence of initialized ensemble spread, which would, indeed, lead to a reduction of the potential predictability. On the contrary, such an increase, without any increase in the chaotic nature of the system (DEC rate of divergence), will lead to higher potential predictability. In the same way, a decrease of internal variability, without any decrease of the chaotic nature of the system, will lead to weaker potential predictability. Of course, if the internal variability tends to zero (as observed, for instance for the GIN Seas SIE in recent years), the PPP will tend to zero as well, but this PPP will no longer be relevant. Therefore, PPP time evolution analysis should always take into account whether its changes were induced by the internal variability or the rate of divergence.
References
Alexander MA, Bhatt US, Walsh JE, Timlin MS, Miller JS, Scott JD (2004) The atmospheric response to realistic Arctic sea ice anomalies in an AGCM during winter. J Clim 17:890–905
Bader J, Mesquita MDS, Hodges KI, Keenlyside N, Østerhus S, Miles M (2011) A review on north hemisphere sea-ice, storminess and the North Atlantic Oscillation: observations and projected changes. Atmos Res 101:809–834
Balmaseda, M., K. Mogensen, F. Molteni, A. T. Weaver (2010b) The NEMOVAR-COMBINE ocean reanalysis, COMBINE Technical report no 1 (http://www.combine-project.eu/Technical-Reports.1668.0.html)
Balmaseda MA, Ferranti L, Molteni F, Palmer T (2010) Impact of 2007 and 2008 Arctic ice anomalies on the atmospheric circulation: implications for long-range predictions. Q J R Meteorol Soc 136:1655–1664
Bitz CM, Holland MM, Hunke EC, Moritz RE (2005) Maintenance of the sea-ice edge. J Clim 18:2903–2921. doi:10.1175/JCLI3428.1
Blanchard-Wrigglesworth E, Armour KC, Bitz C, DeWeaver E (2011a) Persistence and inherent predictability of Arctic sea ice in a GCM ensemble and observations. J Clim 24:231–250. doi:10.1175/2010JCL13775.1
Blanchard-Wrigglesworth E, Bitz CM, Holland MM (2011b) Influence of initial conditions ans climate forcing on predicting Arctic sea ice. Geophys Res Let 38(L18503):1029. doi:10.1029/2011GL048807
Boer GJ (2004) Long time-scale potential predictability in an ensemble of coupled climate models. Clim Dyn 23:29–44. doi:10.1007/s00382-004-0419-8
Chevallier M, Salas y Mélia D (2012) The role of sea ice thickness distribution in the Arctic sea ice potential predictability: a diagnostic approach with a coupled GCM. J Clim 25(8):3025–3038. doi:10.1175/JCLI-D-11-00209.1
Chevallier M, Salas y Mélia D, Voldoire A, Dequé M (2013) Seasonal forecasts of the Pan-Arctic sea ice extent using a GCM-based seasonal prediction system. J Clim 26:6092–6104. doi:10.1175/JCLI-D-12-00612.1
CLIVAR (2011) Data and bias correction for decadal climate predictions. CLIVAR Publ. Series, 150, International CLIVAR Project Office, 4 pp
Comiso JC, Wadhams P, Pedersen LT, Gersten RA (2001) Seasonal and interannual variability of the Odden ice tongue and a study of environmental effects. J Geophys Res 106:9093–9116. doi:10.1029/2000JC000204
Deser C, Walsh JE, Timlin MS (2000) Arctic sea ice variability in the context of recent atmospheric circulation trends. J Clim 13:617–633
Deser C, Magnusdottir G, Saravanan R, Philips A (2004) The effects of North Atlantic SST and sea ice anomalies on the winter circulation in CCM3. Part II: Direct and indirect components of the response. J Clim 17(5):877–889
Doblas-Reyes FJ, Balmaseda MA, Weisheimer A, Palmer TN (2011) Decadal climate predictions with the european center for medium-range weather forecasts coupled forecast system: impact of ocean observations. J Geophys Res 116:D19111. doi:10.1029/2010JD015394
Doblas-Reyes FJ, Andreu-Burillo I, Chikamoto Y, Garcia-Serrano J, Guemas V, Kimoto M, Mochizuki T, Rodrigues LRL, Van Oldenborgh GJ (2013) Initialized near-term regional climate change predictions. Nat Commun 4:1715. doi:10.1038/ncomms2704
Döscher R, Wyser K, Meier HEM, Qian M, Redler R (2010) Quantifying Arctic contributions to climate predictability in a regional coupled ocea-ice-atmosphere model. Clim Dyn 34:1157–1176. doi:10.1007/s00382-009-0567-y
Drobot SD (2007) Using remote sensing data to develop seasonal outlooks for Arctic regional sea ice minimum extent. Remote Sens Environ (Remote sensing of the cryosphere Special issue) 111(2–3):136–147. doi:10.1016/j.rse.2007.03.024
Drobot SD, Maslanik J (2002) A practical method for long-range forecasting of ice severity in the Beaufort Sea. Geophys Res Let 29(8). doi:10.1029/2001GL014173
Du H, Doblas-Reyes FJ, Garcia-Serrano J, Guemas V, Soufflet Y, Wouters B (2012) Sensitivity of decadal predictions to the initial atmospheric and oceanic perturbations. Clim Dyn 23 (7–8). doi: 10.1007/s00382-011-1285-9
Fang Z, Wallace J (1994) Arctic sea ice variability on a time-scale of weeks and its relation to atmospheric forcings. J Clim 13:1897–1914
Fetterer F, Knowles K, Meier W, Savoie M (2002) Sea ice index. National Snow and Ice Data Center, Boulder, CO, digital media. http://nsidc.org/data/g02135.html
Garca-Serrano J, Doblas-Reyes FJ, Coelho AS (2012) Understanding Atlantic multi-decadal variability prediction skill. Geophys Res Let 39:L18708. doi:10.1029/2012GL053283
Garcia-Serrano J, Doblas-Reyes FJ (2012) On the assessment of nea-surface global temperature and North Atlantic multi-decadal variability in the ENSEMBLES decadal hindcast. Clim Dyn 39:2025–2040. doi:10.1007/s00382-012-1413-1
Germe A, Houssais M-N, Herbaut C, Cassou C (2011) Greenland Sea sea ice variability over 1979-2007 and its link to the surface atmosphere. J Geophys Res 116:C10034. doi:10.1029/2011JC006960
Gloersen P, Yu J, Mollo-Christensen E (1996) Oscillatory behavior of Arctic sea ice concentrations. J Geophys Res 101(C3):6641–6650
Goosse H, Arzel O, Mitz CM, De Montety A, Vancoppenolle M (2009) Increased variability of the Arctic summer ice extent in a warmer climate. Geophys Res Lett 36(L23702):1029. doi:10.1029/2009GL040546
Griffies SM, Bryan K (1997) A predictability study of simulated North Atlantic multidecadal variability. Clim Dyn 13:459–487. doi:10.1007/s003820050177
Guemas V, Doblas-Reyes FJ, Lienert F, Soufflet Y, Du H (2012) Identifying the causes of the poor decadal climate prediction skill over the North Pacific. J Geophys Res 117(D20111):1010. doi:10.1029/2012JD018004
Hazeleger W, Wouteres B, van Oldenborgh GJ, Corti S, Palmer T, Smith D, Dunstone N, Kröger J, Pohlmann H, von Storch J-S (2013) Predicting multiyear North Atlantic Ocean variability. J Geophys Res 118:1087–1098. doi:10.1002/jgrc.20117
Hilmer M, Jung T (2000) Evidence for recent change in the link between the North Atlantic Oscillation and Arctic sea ice export. Geophys Res Lett 27(7):989–992
Holland MM, Stroeve J (2011) Changing seasonal predictor relationships in a changing Arctic Climate. Geophys Res Lett 38:L18501. doi:10.1029/2011GL049303
Holland MM, Baily DA, Vavrus S (2011) Inherent sea ice predictability in the rapidly changing Arctic environment of the Community Climate System Model, version3. Clim Dyn 36(1239–1253):1007. doi:10.1007/s00382-010-0792-4
Hurrell J, Kushnir Y, Ottersen G, Visbeck M (2003) An overview of the North Atlantic Oscillation in The North Atlantic Oscillation: Climatic Significance and Environmental Impact, Geophys Monogr Ser 134:1–36, edited by J. W. Hurrell et al., AGU, Washington, DC
Johnson CM, Lemke P, Barnett TP (1985) Linear predictions of sea ice anomalies. J Geophys Res 90(D3):5665–5675
Keenlyside NS, Latif M, Jungclaus J, Kornblueh L, Roeckner E (2008) Advancing decadal-scale climate predictions in the North Atlantic Sector. Nature 453:84–88. doi:10.1038/nature06921
Kim H-M, Webster PJ, Curry JA (2012) Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys Res Let 39:L10701. doi:10.1029/2012GL051644
Knight JR, Folland CK, Scaife AA (2006) Climate impacts of the Atlantic multidecadal oscillation. Geophys Res Let 33:L17706. doi:10.1029/2006GL026242
Koenigk T, Mikolajewicz U (2009) Seasonal to interannual climate predictability in mid and high northern latitudes in a global coupled model. Clim Dyn 32(783–798):1007. doi:10.1007/s00382-008-0419-1
Koenigk T, Mikolajewicz U, Haak H, Jungclaus J (2006) Variability of Fram strait sea ice export: causes, impacts and feedbacks in a coupled climate model. Clim Dyn 26:17–34. doi:10.1007/s00382-005-0060-1
Koenigk T, Beatty CK, Caian M, Döscher R, Wyser K (2012) Potential decadal predictability and its sensitivity to sea ice albedo parameterization in a global coupled model. Clim Dyn 38:2389–2408. doi:10.1007/s00382-011-1132-z
Kvamstø NG, Skeie P, Stephenson DB (2004) Impact of Labrador Sea ice extent on the North Atlantic Oscillation. Int J Climatol 24:603–612. doi:10.1002/joc.1015
Kwok R (2009) Outflow of Arctic ocean sea ice into the Greenland ans Barents Seas: 1979–2007. J Clim 22:2438–2457. doi:10.1175/2008JCLI2819.1
Kwok R, Cunningham GF, Pang SS (2004) Fram Strait sea ice outflow. J Geophys Res 109:C01009. doi:10.1029/2003JC001785
Kwok R, Spreen G, Pang S (2013) Arctic sea ice circulation and drift speed: decadal trends and ocean currents. J Geophys Res Oceans 118:2408–2425. doi:10.1002/jgrc.20191
Latif M, Keenlyside NS (2011) A perspective on decadal climate variability and predictability. Deep Sea Res II 58:1880–1894. doi:10.1016/j.dsr2.2010.10.066
L’Hévéder B, Houssais M-N (2001) Investigating the variability of the Arctic sea ice thickness in response to a stochastic thermodynamic atmospheric forcing. Clim Dyn 17:107–125. doi:10.1007/s003820000096
Lindsay RW, Zhang J, Schweiger AJ, Steele MA (2008) Seasonal predictions of ice extent in the Arctic ocean. J Geophys Res 113(C2). doi:10.1029/2007JC004259
Lorenz EN (1975) Climate Predictability. In: The physical bases of climate and climate modelling. WMO GARP Ser. No. 16. World Meteorol Organ, Geneva, Switzerland, pp 132–136
Magnusdottir G, Deser C, Saravanan R (2004) The effects of North Atlantic SST and sea ice anomalies on the winter circulation in CCM3. Part I: Main features and storm track characteristics of the response. J Clim 17(5):857–876
Meehl GA, Teng H (2012) Case studies for initialized decadal hindcasts and predictions for the Pacific region. Geophys Res Lett 39:L22705. doi:10.1029/2012GL053423
Meehl GA, Goddard L, Murphy JM, Stouffer RJ, Boer G, Danasoglu G, Dixon KW, Giorgetta MA, Greene AM, Hawkins E (2009) Decadal prediction. Can it be skillfull? Bull Am Meteorol Soc 90:1467–1485. doi:10.1175/2009BAMS2778.1
Merryfield WJ, Lee W-S, Wang W, Chen M, Kumar A (2013) Multi-system seasonal predictions of Arctic sea ice. Geophys Res Lett 40:1551–1556. doi:10.1002/grl.50317
Mochizuki T, Ishii M, Kimoto M, Chikamoto Y, Watanabe M, Nozawa T, Sakamoto TT, Shiogama H, Awaji T, Sugiura N, Toyoda T, Yasunaka S, Tatebe H, Mori M (2010) Pacific decadal oscillation hindcasts relevant for near-term climate predictions. PNAS 107:1833–1837. doi:10.1073/pnas.0906531107
Mysak LA, Manak DK (1989) Arctic sea-ice extent and anomalies, 1953–1984. Atmos Ocean 27:376–405. doi:10.1080/07055900.1989.9649342
Mysak LA, Manak DK, Marsden RF (1990) Sea ice anomalies observed in the Greenland and Labrador Seas during 1901-1984 and their relation to an interdecadal Arctic climate cycle. Clim Dyn 5:111–113. doi:10.1007/BF00207426
Oldenborgh GJV, Doblas-Reyes FJ, Wouters B, Hazeleger W (2012) Decadal prediction in a multi-model ensemble. Clim Dyn 38:1263–1280. doi:10.1007/s00382-012-1313-4
Orsolini YJ, Senan R, Benestad RE, Melsom A (2012) Autumn atmospheric response to the 2007 low Arctic sea ice extent in coupled ocean-atmosphere hindcasts. Clim Dyn 38:2437–2448. doi:10.1007/s00382-011-1169-z
Parkinson CL, Cavalieri DJ (2008) Arctic sea ice variability and trends: 1979-2006. J Geophys Res 113:C07003. doi:10.1029/2007JC004558
Parkinson CL, Cavalieri DJ, Gloersen P, zwally HJ, Comiso JC (1999) Arctic sea ice extents, areas and trends: 1978–1996. J Geophys Res 104(C9):20837–20856
Pohlmann H, Botzet M, Latif M, Roesch A, Wild M, Tschuck P (2004) Estimating the decadal predictability of a coupled AOGCM. J Clim 17:4463–4472. doi:10.1175/3209.1
Pohlmann H, Junglaus JH, Köhl A, Stammer D, Marotzke J (2009) Initializing decadal climate predictions with the GECCO Oceanic synthesis: effects on the North Atlantic. J Clim 22:3926–3938. doi:10.1175/2009JCLI2535.1
Roach A, Aagaard A, Carsey F (1993) Coupled ice-ocean variability in the Greeland Sea. Atmos Ocean 31:319–337. doi:10.1080/07055900.1993.9649474
Royer JF, Planton S, Déqué M (1990) A sensitivity experiment for the removal of Arctic sea ice with the French spectral general circulation model. Clim Dyn 5:1–17. doi:10.1007/BF00195850
Schlichtholz P (2011) Influence of oceanic heat variability on sea ice anomalies in the Nordic Seas. Geophys Res Lett 38:L05705. doi:10.1029/2010GL045894
Schmith T, Hansen C (2003) Fram strait ice export during the nineteenth and twentieth centuries reconstructed from a multiyear sea ice index from southwester Greenland. J Clim 16:2782–2791
Schweiger A, Lindsay R, Zhang J, Steel M, Sternans H, Kwok R (2011) Uncertainty in modeled Arctic sea ice volume. J Geophys Res. 116:C00D06. doi:10.1029/2011JC007084
Sigmond M, Fyfe JC, Flato GM, Kharin VV, Merryfield WJ (2013) Seasonal forecast skill of Arctic sea ice area in a dynamical forecast system. Geophys Res Lett 40(3):529–534. doi:10.1002/grl.50129
Smith DM, Cusack S, Colman AW, Folland CK, Harris GR, Murphy JM (2007) Improved surface temperature prediction for the coming decade from a global climate model. Science 317:796. doi:10.1126/science.1139540
Solomon A, Goddard L, Kumar A, Carton JA, Deser C, Fukumori I, Greene AM, Hegerl GC, Kirtman B, Kushner Y, Newman M, Smith D, Vimont D, Delworth TL, Meehl GA, Stockale TN (2011) Distinguishing the roles of natural and anthropogenically forced decadal climate variability: implications for prediction. Bull Am Meteorol Soc 92:141–156. doi:10.1175/2010BAMS2962.1
Strong C (2012) Atmospheric influence on Arctic marginal ice zone position and width in the Atlantic sector, February-April 1979-2010. Clim Dyn 39:3091–3102. doi:10.1007/s00382-012-1356-6
Swift J (1986) The arctic waters. The Nordic Seas. Springer, New York, pp 124–156
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. doi:10.1175/BAMS-D-11-00094.1
Tietsche S, Notz D, Jungclaus JH, Marotzke J (2013) Predictability of large interannual Arctic sea-ice anomalies. Clim Dyn. doi:10.1007/s00382-013-1698-8
Tsukernik M, Deser C, Alexander M, Tomas R (2009) Atmospheric forcing of Fram Strait sea ice export: a closer look. Clim Dyn 35:1349–1360. doi:10.1007/s00382-009-0647-z
Ukita J, Honda M, Nakamura H, Tachibana Y, Cavalieri D, Parkinson C, Koide H, Yamamoto K (2007) Northern hemisphere sea ice variability: lag structure and its implications. Tellus 59A:261–272. doi:10.1111/j.1600-0870.2006.00223.x
Valcke S (2006) OASIS user guide (prism_2-5). Technical-report TR/CMGC/06/73, CERFACS, Toulouse, France, 60 pp
Vinje T (2001) Fram strait ice flux and atmospheric circulation, 1950-2000. J Clim 14:3508–3517
Voldoire A, Sanchez-Gomez E, Salas y Mélia D, Decharme B, Cassou C, Sénési S, Valcke S, Beau L, Alias A, Chevallier M, Déqué M, Deshayes J, Douville H, Fernandez E, Madec G, Maisonnave E, Moine M-P, Planton S, Saint-Martin D, Szopa S, Tyteca S, Alkama R, Belamari S, Braun A, Coquart L, Chauvin F (2013) The CNRM-CM5,1 global climate model: description and basic evaluation. Clim Dyn 40(9-10):2091–2121. doi:10.1007/s00382-011-1259-y
Walsh J (1980) Empirical orthogonal functions and the statistical predictability of sea ice extent. In: Pitchard R (ed) Sea ice processes and models. University of Washington Press, Seattle, pp 373–384
Walsh JE, Johnson CM (1979) An analysis of Arctic sea ice fluctuations, 1953-1977. J Phys Oceanogr 9:580–591. doi:10.1175/1520-0485(1979)009<0580:AAOASI>2.0.CO;2
Wu B, Wang J, Walsh E (2006) Dipole anomaly in the winter arctic atmosphere and its association with sea ice motion. J Clim 19:210–225. doi:10.1175/JCLI3619.1
Yeager S, Karspeck A, Danabasoglu G, Tribbia J, Teng H (2012) A decadal prediction case study: late twentieth century North Atlantic ocean heat content. J Clim 25:5173–5189. doi:10.1175/JCLI-D-11-00595.1
Zhang J, Steele M, Lindsay R, Schweiger A, Morison J (2008) Ensemble 1-year predictions of Arctic sea ice for the spring and summer of 2008. Geophys Res Lett 35:L08502. doi:10.1029/2008GL033244
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Germe, A., Chevallier, M., Salas y Mélia, D. et al. Interannual predictability of Arctic sea ice in a global climate model: regional contrasts and temporal evolution. Clim Dyn 43, 2519–2538 (2014). https://doi.org/10.1007/s00382-014-2071-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-014-2071-2