Abstract
We investigate the ability of a global atmospheric general circulation model (AGCM) to reproduce observed 20 year return values of the annual maximum daily precipitation totals over the continental United States as a function of horizontal resolution. We find that at the high resolutions enabled by contemporary supercomputers, the AGCM can produce values of comparable magnitude to high quality observations. However, at the resolutions typical of the coupled general circulation models used in the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, the precipitation return values are severely underestimated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Very extreme weather events are important due to their potential to have serious impacts on human and ecological systems. As the mean climate changes due to anthropogenic causes, such rare events are also expected to change (CCSP3.3 2008). The intensity of the extreme precipitation is expected to increase with the availability of atmospheric moisture, which follows the Clausius-Clapeyron relationship (Allen and Ingram 2002).
To make credible predictions of future changes in extreme weather events, it is reasonable to ask a model to accurately simulate the observations of the recent past.
Precipitation is generally not as well simulated as air temperature in global climate models. One reason is that precipitation is influenced by vertical motions on scales smaller than the model grid. These motions, as well as relevant cloud microphysical processes, are parameterized in typical climate models. Furthermore, precipitation is often influenced by orography, which is smoothed by the finite grid sizes used in climate models. Despite these issues, climate models can have good skill in simulating large scale patterns of mean precipitation such as the zonal mean distribution. However, models generally lack skill in accurately simulating regional distributions of precipitation and vary greatly from one model to another (Covey et al. 2000).
Very extreme precipitation events are well described by the statistical formalism of the Generalized Extreme Value (GEV) theory. The statistical character of the very extreme portion of a distribution is determined by relatively few events in samples of any reasonable size. In the case of precipitation, these events are highly localized in both space and time due to the episodic nature of strong storms. In this paper, we investigate the ability of climate models to simulate the very extreme tails of the distribution of precipitation events. By varying the horizontal resolution of a model, we quantify the effect of better representing the local nature of individual storms on the statistics of very extreme precipitation. Duffy et al. (2003) and Iorio et al. (2004) showed that high-resolution simulations using the NCAR Community Climate Model version 3 produce spatial patterns of seasonal-mean precipitation that agree more closely with observed precipitation patterns than do results from the same model at coarse resolution. Iorio et al. (2004) further find that higher-resolution simulations have more realistic daily precipitation statistics in North America.
2 Methodology
The climate model used in this study is the Community Atmospheric Model version 2 (CAM2). We use the finite volume dynamics version of the model (fvCAM), for our simulations (Lin and Rood 1996). CAM2 is the fifth generation of the NCAR atmospheric GCM (http://www.ccsm.ucar.edu/models/atm-cam/docs/cam2.0/description/index.html). As used in this study, this global atmospheric model was configured according to the protocol dictated by the Atmospheric Model Intercomparison Project (AMIP) (Gates et al. 1999) using prescribed time varying values of the sea surface temperature and sea ice extent. Although the details of a stand alone atmospheric model simulation can differ from that of a fully coupled ocean atmosphere general circulation model simulation (Covey et al. 2003), we believe that the effect of changing horizontal atmospheric resolution is similar in the two classes of climate models. We performed fvCAM AMIP integrations over the period 1979–1994 under three different horizontal grid resolutions. The first used a 2.0° × 2.5° mesh, the second used a 1.0° × 1.25° mesh, and the third used 0.5° × 0.625° mesh. No model tuning specific to resolution was involved. The initial conditions were simply regridded to each of the meshes and the surface boundary conditions (sea surface temperature and sea ice extent) were obtained by a standard AMIP request. These correspond, respectively, to roughly 240, 120 and 60 km grid spacing at the equator. For reference, the CMIP3 database of coupled climate model simulations prepared for the IPCC AR4 report ranged from 400 to 110 km at the equator (http://www-pcmdi.llnl.gov).Vertical resolution was unaltered and kept at the default 26 levels. Daily precipitation totals were saved and extracted from each integration.
High quality observations of accumulated daily precipitation for this study were taken from the “NOAA CPC (Climate Prediction Center) .25 × .25 Daily US Unified Precipitation” dataset (Higgins et al. 2000). These observations are confined to the continental United States land areas and are aggregated from three sources of station rain gauge data gridded to a 0.25°× 0.25° grid. Between 8,000 and 13,000 stations were quality controlled and gridded to about 18000 grid points using a modified Cressman (1959) scheme. Hence, there are likely many grid points with no stations as well as many with multiple stations. The density of station data is least in the Western mountainous and desert regions. The model representation of a storm is meant as an average over a grid cell. This transformed observational dataset is the closest comparison that can be made to the models and is far superior to comparison to individual station data. Data used in this study was limited to the same time period as the simulations.
We analyzed the tails of the parent distributions of the simulated and observed daily mean precipitation datasets using a block maxima Generalized Extreme Value theory formalism. In our application of the block maxima formalism, the annual (or seasonal) maximum of the daily averaged precipitation is found at each grid point, forming another random variable that can be shown to be well described by the GEV distribution function (Zwiers and Kharin 1998; Kharin and Zwiers 2000, 2005; Kharin et al. 2007). In fact, GEV theory is an asymptotic treatment of the tails of distributions with relatively few restrictions on its validity (Coles 2001; Castillo et al. 2004). Hence, GEV theory has broad applicability to climate and other natural systems. The GEV distribution, F(x), is a three parameter function,
where ξ, α and k are called the location, scale and shape factors. The Gumbel distribution is a special case where the shape parameter, k, is zero. Formally, F(x) is the limiting cumulative distribution function of the maxima of a sample of independently and identically distributed random variables (Leadbetter et al. 1983). The three parameters of the GEV distribution may be quickly and accurately estimated from a sample of extreme values using a technique based on L-moments (Hosking and Wallis 1997) or a number of other techniques such as maximum likelihood. Here, F(x) represents the probability that the annual maximum of daily mean precipitation is less than x.
By further considering the tail of the appropriate GEV distribution function, one is truly describing rare events. The return value of a random variable, X T is that value which is exceeded, on average, once in a period of time, T. For example, when considering annual maxima of daily averaged variables, there is a 1/T chance of any daily average exceeding X T in a given year (where T is in years). Formally, this is straightforwardly defined as
where T 0 is a characteristic time whose value is 1 if T is measured in years. Solving for X T using the above definition of the GEV distribution yields (Castillo et al. 2004),
Hence, return values of annual or seasonal extrema are readily obtained by this inversion of the GEV distribution function after its three parameters have been estimated.
3 Results
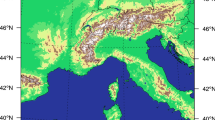
In Fig. 1, we show the 20-year return value of the annual maximum daily precipitation for each of the three simulation resolutions and the observations determined from the appropriate L-moments and GEV parameters calculated on each dataset’s native grid. The return value calculated from the observed precipitation (lower right panel) reveals a large amount of spatial structure with the highest values over the southeastern states and the lowest values over the Midwest. Interesting structure is also found along the Pacific coast reflecting the complex orography of the region. However, we note that the station data may be sparse in wilderness regions. Not surprisingly, the coarsest-resolution simulation considered (upper left panel) does not reproduce the highly detailed spatial structure of the observations. More importantly, at this resolution, the return value is systematically underpredicted by a factor of two or more. However, the large scale pattern of low western and high eastern return values with a secondary maximum on the West Coast is generally reproduced. At the intermediate model resolution (upper right panel), the simulated return values are significantly larger than at the coarsest resolution but still 50% or more lower than the observations. The West Coast maximum is significantly improved. At the highest model resolution considered in this study (lower left panel), the difference between simulation and observation is further reduced. The West Coast orographically determined structures are beginning to appear. The large values over the Southeastern states are still somewhat low and the values over the Rocky Mountain states have become too large although this is a region of sparser observations. However, the location of the sharp east–west gradient occurring in the middle of the country is well reproduced.
Since the spatial scale of precipitation events is often less than all the grid sizes considered here, the coarser model versions should have smaller return values. Hence it is useful to compare model results to observations that have been regridded to the model’s native grid before statistics (annual maxima, return values) are calculated. In Fig. 2, we show the 20 year return value of the observed annual maximum daily precipitation calculated by first regridding the daily data onto the three model grids shown in Fig. 1. This step is then followed by the calculation of the L-moments and GEV parameters for each of the regridded observations. At the coarsest resolution considered (upper left panels), the observed precipitation return value is indeed reduced but still exceeds the simulated return value at this resolution in Fig. 1. Agreement on the West Coast is reasonable, but the sharp east–west gradient in the middle of the country remains in the regridded observed result. The simulated result does not resemble the regridded observations particularly well. At the intermediate resolution (upper right panels), agreement is improved but simulated return values are still too low compared to the observations. At the highest resolution (lower left panels), the simulated return values actually exceed the observed return values in some regions, especially California and Florida.
4 Discussion
We find that the ability of the atmospheric general circulation model, fvCAM, to simulate the extreme precipitation over the continental United States is strongly dependent on horizontal resolution. Even when the observed daily precipitation rates are regridded to the model’s native mesh, the simulated return values are substantially lower than the observations at coarse resolutions. At the highest resolutions that we were able to integrate, approximately 60 km at the equator, the simulated 20 year return value of the annual maximum daily precipitation approaches or even exceeds the observed return value when calculated on the model grid. We interpret this as somewhat of a breakthrough resolution. On coarser meshes, the resolution itself is limiting the intensity of these extreme events, rather than any particular model parameterization defect. At the 60 km scale, resolution certainly still limits precipitation intensity, particularly for tropical cyclones. However, at least for fvCAM, this resolution has allowed simulated extreme rainfall over the continental US to be at least as intense as the observations on the same mesh. This allows the model defects to be exposed whether they are circulation errors or more localized model formulation problems.
Greater model fidelity changes the distribution of simulated daily precipitation. Part of the change is a simply a shift in the distribution, improving the simulation of longer term averages of precipitation toward observations (Duffy et al. 2003). However, another part of the change is the enabling of substantially stronger precipitation events due to better resolution of the atmospheric fluid dynamics and the surface boundary conditions. By analyzing the relative amounts of cumulus convective precipitation and large scale precipitation on the days when total precipitation is the annual maximum, we find that over the continental US, either process can be responsible for the extreme values depending on the location. The large scale precipitation parameterization produces the largest precipitation rates over the Western regions while cumulus convective parameterization does so over the Southeastern US. This is likely a reflection of the nature of the most intense storms in the different regions: large scales systems coming off the Pacific Ocean for the Western US and Atlantic tropical cyclones for the Southeastern US. Higher horizontal resolution increases the realism of both processes.
While the computational burden associated with high-resolution climate models is significantly higher than that of current generation production climate models (http://www.pcmdi.llnl.gov), recent technological trends are making such simulations feasible. Worley (2007) has measured the simulation rate of fvCAM (in a beta version 3) in the 60 km configuration to be about 3,650 times faster than real time on approximately 1,000 processors of a Cray XT4 supercomputer. This compares with the simulation rate of about 1,600 times faster than real time realized on US-based computers when the Community Climate System Model (CCSM3.0) was run for the IPCC AR4 report. In fact, we estimate that for a 0.25° × 0.375° version of fvCAM, a simulation rate of about 900 times faster than real time could be presently obtained on 2,000 processors of a Cray XT4 (Wehner et al. 2008). This corresponds to about a 30 km grid spacing at the equator and is an appealing high resolution as it is still coarse enough that statistical issues in cumulus cloud process parameterization are avoided (Arakawa, private communication 1999). Also, the hydrostatic approximation employed in many current climate models is generally valid at this grid spacing.
The benefits of increased horizontal resolution to the quality of global atmosphere simulations extend well beyond those presented here for very extreme precipitation events. For instance, tropical cyclones are simulated well enough at these high resolutions to permit a direct investigation of the effect of anthropogenic climate change on these storms (Oouchi et al. 2006). Also, larger scale processes have been demonstrated (Duffy et al. 2003) to be very sensitive to horizontal grid spacing, with significant improvements to seasonal averages obtained at ~60 km resolutions over typical current production models. Regional scale climate change projections and societal impacts assessments also require higher resolution than is provided by the current typical global models. Since temporal extremes have disproportionate societal impacts, it is convenient that models using finer spatial grids also represent these extremes better.
References
Allen MR, Ingram WJ (2002) Constraints on future changes in climate and the hydrologic cycle. Nature 419:224–232
Castillo E, Hadi AS, Balakrishnan N, Sarabia JM (2004) Extreme value and related models with applications in engineering and science. Wiley, New York
CCSP3.3 (2008) Weather and Climate Extremes in a Changing Climate Regions of Focus: North America, Hawaii, Caribbean, and U.S. Pacific Islands, Synthesis and Assessment Product 3.3, US Climate Change Science Program, Washington, DC. http://www.climatescience.gov
Coles S (2001) An introduction to statistical modeling of extreme values. Springer, London
Covey C, AchutaRao KM, Lambert SJ, Taylor KE (2000) Intercomparison of Present and Future Climates Simulated by Coupled Ocean–Atmosphere GCMs, Program for Climate Model Diagnosis and Intercomparison Report #66, Lawrence Livermore National Laboratory UCRL-ID-140325
Covey C, AchutaRao KM, Gleckler PJ, Phillips TJ, Taylor KE, Wehner MF (2003) Coupled ocean–atmosphere vs. prescribed-SST simulations: effect of a “perfect” ocean. Glob Planet Change 41:1–14
Cressman GF (1959) An operational objective analysis system. Mon Weather Rev 87:367–374
Duffy PB, Govindasamy B, Milovich J, Taylor K, Wehner M, Lamont A, Thompson S (2003) High resolution simulations of global climate, Part 1: present climate. Clim Dyn 21:290–371
Gates WL, Boyle JS, Covey C, Dease CG, Doutriaux CM, Drach RS, Fiorino M, Gleckler PJ, Hnilo JJ, Marlais SM, Phillips TJ, Potter GL, Santer BD, Sperber KR, Taylor KE, Williams DN (1999) An overview of the results of the Atmospheric Model Intercomparison Project (AMIP). Bull Am Meteorol Soc 80:29–55
Gutowski WJ, Hegerl GC, Holland GJ, Knutson TR, Mearns LO, Stouffer RJ, Webster PJ, Wehner MF, Zwiers FW (2008) Causes of observed changes in extremes and projections of future changes in weather and climate extremes in a changing climate. Regions of focus: North America, Hawaii, Caribbean, and U.S. Pacific Islands. In: Karl TR, Meehl GA, Miller CD, Hassol SJ, Waple AM, Murray WL (eds) A Report by the U.S. Climate Change Science Program and the Subcommittee on Global Change Research, Washington, DC
Higgins RW, Shi W, Yarosh E, Joyce R (2000) Improved US Precipitation Quality Control System and Analysis. NCEP/Climate Prediction Center ATLAS No. 7, National Centers for Environmental Prediction, Climate Prediction Center, Camp Springs, Maryland. Available at http://www.cpc.ncep.noaa.gov/research_papers/ncep_cpc_atlas/7/index.html. Data is available at http://www.cdc.noaa.gov/cdc/data.unified.html
Hosking JRM, Wallis JR (1997) Regional frequency analysis, an approach based on L-moments. Cambridge University Press, New York
Iorio JP, Duffy PB, Govindasamy B, Thompson SL, Khairoutdinov M, Randall D (2004) Effects of model resolution and subgrid-scale physics on the simulation of precipitation in the continental United States. Clim Dyn 23:243–258
Kharin VV, Zwiers FW (2000) Changes in the extremes in an ensemble of transient climate simulation with a coupled atmosphere–ocean GCM. J Clim 13:3760–3788
Kharin VV, Zwiers FW (2005) Estimating extremes in transient climate change simulations. J Clim 18:1156–1173
Kharin VV, Zwiers FW, Zhang X, Hegerl GC (2007) Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J Clim 20:1419–1444
Leadbetter MR, Lindgren G, Rootzen H (1983) Extremes and related properties of random sequences and processes. Springer, New York, 336 pp
Lin S-J, Rood RB (1996) Multidimensional flux-form semi-Lagrangian transport schemes. Mon Weather Rev 124:2046–2070
Oouchi K, Yoshimura J, Yoshimura H, Mizuta R, Kusunoki S, Noda A (2006) Tropical cyclone climatology in a global-warming climate as simulated in a 20 km-mesh global atmospheric model: frequency and wind intensity analysis. J Meteorol Soc Japan 84:259–276
Wehner MF (2005) Changes in daily precipitation and surface air temperature extremes in the IPCC AR4 models. US CLIVAR Variations 3:5–9
Wehner MF, Oliker L, Shalf J (2008) Towards ultra-high resolution models of climate and weather. Int J High Perform Comput Appl 22:149–165
Worley P (2007) Comparison of XT3 and XT4 Scalability CUG 2007 Seattle, WA, 7–10 May 2007. http://www.csm.ornl.gov/~worley/talks/CUG2007_Worley.pdf
Zwiers FW, Kharin VV (1998) Changes in the extremes of the climate simulated by CCC GCM2 under CO2 doubling. J Clim 11:2200–2222
Acknowledgment
This work was performed under the auspices of the U.S. Department of Energy (DOE) by the Lawrence Berkeley National Laboratory (LBNL) under contract No. DE-AC03-76SF00098 (LBNL) and with support from the DOE Climate Change Prediction Program. CPC US Unified Precipitation data provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their web site at http://www.cdc.noaa.gov/.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
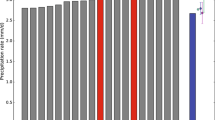
Uncertainty in the return values shown in Figs. 1 and 2 comes from at least two sources. Estimation of the GEV parameters comes from 15-year samples of daily precipitation. The robustness of GEV parameters fitted to samples of 15 annual maxima can be ascertained following a methodology outlined by Hosking and Wallis (1997). In this method, GEV parameters are first estimated from the actual available sample data. Then, a set of random samples distributed according to this GEV distribution is generated. GEV parameters and associated return values are then calculated for each of these random samples (of the same size as the actual sample). Standard accuracy measures can be straightforwardly obtained from this “sampling distribution” of the return value. To illustrate the magnitude of the return value uncertainty due to parameter estimation, we generated 50 random samples of 15 annual maxima from the GEV parameters estimated from the observations. In the top panel of Fig. 3, we show a map of the 20-year return value uncertainty in this sample at the 95% confidence level expressed as a percentage of the return value fitted to the actual observations. We note that over the US this uncertainty due to parameter estimation is less than 10% and mostly in the 3–4% range.
Uncertainties in the 20 year return value of annual maximum daily precipitation at the 95% confidence level expressed as a percentage of the actual calculated return value. Upper Panel: Percent uncertainty calculated from 50 samples of 15 years length generated randomly according to the GEV distribution fitted to the actual observational record. This uncertainty is due to the GEV parameter estimation. Lower Panel: Percent uncertainty calculated from 13 continuous 15-year periods of the T85 spectral version of CCSM3.0. This uncertainty is due to the climate model’s unforced internal variability
A second source of uncertainty in our estimates of return value comes from the internal variability of the climate system itself. In order to best quantify this uncertainty, long temporal records are required. Unfortunately, we have neither sufficiently long records of observed daily precipitation nor high-resolution model simulations. However, long control runs of lower resolution coupled climate models from the CMIP3 database can serve as a proxy for the model runs considered here. Daily precipitation values stored from 230 years of a pre-industrial control run of the T85 spectral version of CCSM3.0 provide a dataset long enough to analyze decadal scale variability. In a manner similar to that in the previous paragraph, we construct a sampling distribution by drawing 15-year periods from this 230-year population. We again calculate GEV parameters and return values for each of these 15-year samples to produce the map of return value uncertainty shown in the lower panel of Fig. 3. We note that the uncertainty due to unforced internal climate variability is considerably larger than the uncertainty due to parameter estimation. However, the magnitude over the US does not exceed 12% and ranges from 5 to 9% over most of the region.
Finally, a key assumption in the application of GEV theory as outlined above is that the data be independently and identically distributed. As the simulations and observations considered here are subject to anthropogenically induced climate change, the quasi-stationarity of the distribution of precipitation is in question. As the climate warms, extreme precipitation events are expected to become more severe (Kharin and Zwiers 2000; Allen and Ingram 2002; Wehner 2005; Kharin et al. 2007) although the changes are relatively less than for extreme temperature events (Gutowski et al. 2008). The issue then becomes choosing an analysis period long enough that the GEV parameters are estimated to the required accuracy and short enough that changes are not statistically significant. Analysis of the observations and all the simulations reveals that changes in the annual maximum daily precipitation over the 16-year period (1979–1994) are not statistically significant. Nonetheless, we have applied a linear detrending to the annual maxima to remove the small positive trend found in each of the datasets. Our conclusions regarding the effect of resolution are the same whether the trend is included or not. Differences in the return values shown in Figs. 1 and 2 stemming from this small trend are just barely noticeable.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Wehner, M.F., Smith, R.L., Bala, G. et al. The effect of horizontal resolution on simulation of very extreme US precipitation events in a global atmosphere model. Clim Dyn 34, 241–247 (2010). https://doi.org/10.1007/s00382-009-0656-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-009-0656-y