Introduction

Gaseous nitrogen (N) losses from agricultural soils, mainly in form of ammonia (NH3), and the denitrification products nitrous oxide (N2O), and dinitrogen (N2), significantly reduce fertilizer N use efficiency. Despite N2 emissions represent in most situations the largest gaseous N loss pathway (e.g., Barton et al. 1999; Qasim et al. 2022; Scheer et al. 2020; Zistl-Schlingmann et al. 2019), they are still little constrained. This is because notorious challenges arise by directly measuring soil N2 emissions due to denitrification in front of high atmospheric background concentrations and atmospheric fluctuations in field studies (Friedl et al. 2020; Groffman et al. 2007). Hence, magnitudes and temporal patterns of denitrification and thus, total N balances, in most terrestrial ecosystems still are not fully understood and accurately constrained (Groffman et al. 2007). Therefore, an improved quantification of soil N2 emissions is essential to better understand the fates and environmental impacts of reactive N used in agriculture (Galloway and Cowling 2002; Westhoek et al. 2015), including the emissions of the N2 precursor N2O, a potent greenhouse gas and ozone-depleting substance (Davidson and Kanter 2014; Ravishankara et al. 2009; Zhang et al. 2023).

Currently, there are basically only two state-of-the-art methods for directly measuring the denitrification products N2 and N2O from terrestrial soils as well as their stoichiometry (Friedl et al. 2020; Micucci et al. 2023), the 15NGF and the Helium soil core method. The latter is based on direct N2 flux measurements in an artificial He-O2 atmosphere and does therefore not require the addition of an N isotopic tracer that may strongly stimulate denitrification in particular if applied to N-limited ecosystems (Friedl et al. 2020). However, unlike the 15NGF method, the Helium soil core technique is confined to laboratory incubation studies, requiring an exceptionally gas-tight incubation system (Butterbach-Bahl et al. 2002; Cárdenas et al. 2003; Senbayram et al. 2020) to reduce atmospheric N2 concentration to a few ppmv. It further requires minimal and constant system inherent leakage rates to allow for the quantification of small N2 fluxes. Solving these challenges requires large engineering efforts and working with larger soil cores leads to substantial He consumption and associated costs.

In contrast to the He-O2 soil core method, the 15NGF method has been applied in both laboratory and field studies. Large amounts of highly enriched mineral N, typically 15NO3−, are added to the soil, enabling the detection of 15N enrichment not only in N2O but also in N2, despite the significant atmospheric N2 background (Friedl et al. 2020; Mosier and Klemedtsson 1994; Siegel et al. 1982). The fluxes are typically measured by using a static chamber approach, which is based on temporal increases in 15N2 headspace gas concentrations over time and subsequent isotopic analysis of gas samples for 15N enrichment in N2O and N2 (Friedl et al. 2020; Micucci et al. 2023).

Despite the first field studies on N2 emissions from fertilized agricultural systems, using the 15NGF, date back to the 1970s, relatively few studies have followed until today, with reported N2 emissions ranging from 0.4 to 40.2 kg N ha− 1, i.e., 0.3–26% of the applied fertilizer N (Baily et al. 2012; Buchen-Tschiskale et al. 2023; Čuhel et al. 2010; Lindau et al. 1990; Liu et al. 2022; Mosier et al. 1989; Pan et al. 2022a; Rolston et al. 1978). It is still unclear to what extent this large variability is driven by different fertilizer types (organic vs. mineral), agricultural systems (e.g., crop vs. grassland), physicochemical soil parameters or climatic conditions, or also by methodological uncertainties.

Major methodological innovation was achieved by Warner et al. (2019), who tested a mobile continuous-flow isotope ratio mass spectrometry (IRMS) system for online in situ measurements of N2 and N2O fluxes. Furthermore, Well et al. (2019a) strongly increased the sensitivity of the 15NGF method under field conditions by reducing the ambient N2 concentration during the chamber measurements through soil flushing with He. Yet, despite being the only method to directly quantify field denitrification rates from upland soils in situ, its use is still relatively limited. This is, probably, due to the high costs associated with isotope additions and the limited availability of delicate analytics, such as isotope ratio mass spectrometry (IRMS) with suitable pre-treatment peripherals, that are required to obtain sufficient sensitivity for 15N2 analysis (Galloway and Cowling 2002; Westhoek et al. 2015).

A further challenge is that the method involves a range of inherent uncertainties that are difficult to constrain (Friedl et al. 2020; Micucci et al. 2023), while a successful verification with an alternative and fully independent approach to measuring field N2 emissions in situ is still missing. There have been a number of studies that compared the N2 and N2O fluxes, using the 15NGF method and the acetylene inhibition technique (AIT), respectively (Aulakh et al. 1991; Malone et al. 1998; Mosier et al. 1986a; Sgouridis et al. 2016). Such method comparisons are not promising in view of the widely demonstrated weaknesses of the AIT technique (Butterbach-Bahl et al. 2013). Yang et al. (2011) developed an N2O labelling-based 15N2O pool dilution method, where gross 15N2O consumption in soil headspace was proposed to equal soil N2 formation. However, Wen et al. (2016) showed, for various soils, that this approach strongly and irreproducibly underestimates N2 formation (see also Well and Butterbach-Bahl 2013). A comparison of the 15NGF technique with the He-O2 soil core technique hitherto also failed to reveal similar results for N2 emissions (Kulkarni et al. 2014). Furthermore, the He-O2 soil core technique is not applicable under in situ conditions.

Nitrogen mass balance studies with 15N-labelled fertilizers are a more promising option to constrain gaseous N2 losses, given that all 15N fates are quantified (plant uptake, soil storage, all gaseous N losses, leaching N losses), so that the unrecovered 15N should equal N2 losses. Such approaches, however, typically suffer from the huge uncertainty in unrecovered fertilizer 15N that accumulates from the quantification of the numerous N balance components (Micucci et al. 2023; Rolston et al. 1979). This uncertainty can be reduced by the use of lysimeters. They provide spatially well-constrained setups that are targeted to optimize the accuracy of isotope tracing, N leaching and gaseous N loss measurements (e.g. Kiese et al. 2018; Zistl-Schlingmann et al. 2020). Finally, lysimeters also provide good opportunities to study soil gas concentration changes, which can serve to estimate soil-atmosphere exchange via the gradient method (e.g., Wolf et al. 2011). Interestingly, the latter approach has not yet been used in the context of soil N2 emissions.

Hence, our objectives were to (1) quantify N2 emissions and their importance for the fertilizer N mass balance of a winter wheat rotation using the 15NGF method for a quantitative comparison with unrecovered 15N of the 15N fertilizer mass balance approach, and (2) to compare the temporal N2 emission dynamics at the soil-atmosphere interface by dynamics of 15N enrichment of N2 in the vertical soil profile in order to assess the potential of soil air 15N2 measurements to serve as alternative method to constrain soil N2 emissions. For this, we cultivated winter wheat on lysimeters, homogenously applied highly 15N enriched mineral fertilizers via drip fertigation at three dates during the cropping period (together 171 kg N ha− 1) and analyzed gaseous (NH3, N2O, 15N2) and hydrological N losses as well as fertilizer N fates in plant and soil, and 15N2 enrichment in soil air. Drip fertigation was chosen to achieve homogenous 15N labelling and decrease the role of NH3 in the N mass balance in favor of N2. We hypothesized that field N2 emissions measured by the 15NGF method would be equal to the unrecovered 15N of the total fertilizer 15N mass balance. We further hypothesized that temporal changes in 15N enrichment of N2 in the soil profile are closely correlated with measured N2 fluxes at the soil-atmosphere interface.

Materials and methods

Experimental design and lysimeters

To test these hypotheses, we combined a lysimeter experiment with three weighed lysimeters (1 m2 area each) with a 15N fertilizer tracing experiment over an entire winter wheat cycle. The experimental setup included the determination of N leaching, soil 15N storage and plant 15N export, and the quantification of gaseous N2O and NH3 losses to obtain a particularly precise estimate of the unrecovered 15N fertilizer which is related to N2 losses. Furthermore, we directly quantified soil N2 emissions with high temporal resolution and for the entire lysimeter areas using the 15NGF method, accompanied by measurements of the dynamics of soil air 15N2 enrichment over the entire experimental period.

The lysimeters (Fig. 1) were manufactured according to Pütz et al. (2016) by UGT (Umwelt Geräte Technik, Müncheberg, Germany). The lysimeters were constructed of stainless-steel cylinders with a surface area of 1 m2 and a depth of 1.5 m. A stainless-steel plate that was tightly bolted to the cylinder served as the cylinder’s bottom closure. The lysimeters were filled with intact soil monoliths extracted from an agricultural field close to the town of Bad Rotthalmünster, Germany, on March 27, 2020. On April 1st, 2020, the lysimeters were delivered to the lysimeter field site of Campus Alpin of the Karlsruhe Institute of Technology (IMK-IFU), Garmisch-Partenkirchen (185 km southwest of the soil sampling). The original, undisturbed soil structure was carefully preserved during soil extraction and transport. On April 8, 2020, the installation of the lysimeters was completed. The soil was classified as a Luvisol derived from loess, containing 10% sand, 71% silt, and 19% clay in the ploughing layer. Its pH (CaCl2) was measured to be 6.7 (Rethemeyer 2004; Rohe et al. 2021).

Various sensors and probes were installed at different depths of the lysimeter (Fig. 1). Combined soil moisture/soil temperature sensors (SMT-100, UGT GmbH, Germany) were placed at 10, 20, 30, 50 and 120 cm depths to determine the temperature and volumetric water content of the soil. Soil water content and soil temperature were recorded by data loggers (DT85, DataTaker-Thermo Fisher Scientific Australia Pty Ltd., Scoresby, VIC, Australia) every ten minutes. For soil water sampling, the lysimeters were supplied with suction cups with ceramic tips at the same depths (UGT GmbH, Munich, Germany), in conjunction with a vacuum control unit (VS, UMS, Munich, Germany) operating at 100 hPa. The vacuum was applied on sampling bottles for each sampling depth that collected soil water through the suction cups. For sampling of soil air, custom-made semi-permeable polypropylene membrane (PP V8/2 HF membrane, Accurel®, Akzo Nobel Faser AG, Wuppertal, Germany) gas lances with a nominal pore size of 0.2 μm, inner diameters of 5.5 mm, and lengths of 80 cm were installed horizontally at depths of 10, 20, 30, 50, and 120 cm.

Fig. 1
figure 1

(a) Lysimeter filled with Rotthalmünster soil, equipped with the sensors and tubing, ready for the installation at IMK-IFU. (b) Scheme of lysimeter sensor equipment: TS1: tensiometer; SMT: soil moisture/soil temperature probes; Suction cups for water sampling; Gas tubes for soil gas concentration measurements; Suction rake for water exchange at the lower boundary layer between lysimeter and drainage tank

Full size image

Since a natural hydraulic gradient and water flow would normally be hampered by the closure at the bottom of the lysimeters, a suction rake formed out of six silicon carbide porous cups (SIC40, UMS AG, Munich, Germany) was installed at the lower boundary of the lysimeter (in 140 cm soil depth), to establish in situ hydrological field conditions within the lysimeters. For this, a bidirectional pump was employed to adjust the water content of the lower lysimeter boundary via the suction rake. To maintain consistent water tension both within and outside the lysimeters, water was either extracted from or introduced into them. A tensiometer, specifically the TS1 model (UMS AG, Munich, Germany), was positioned within the lysimeter at a depth of 140 cm for this purpose. In addition, three reference tensiometers were placed at the same depth outside, in direct vicinity to the lysimeters in the field. Water flow out of or into the lysimeters was adjusted according to the matric potential measured at the reference field tensiometers. This setup ensured that the lysimeter simulated an “infinite” soil column. To assess the water balance, the lysimeters were positioned on three load cells (Model 3510, Tedea-Huntleigh, Canoga Park, CA, USA) that had a resolution of 1 g (equivalent to 0.001 mm precipitation and a water flux of 0.001 l). The leaching water extracted from 140 cm depth was collected and stored in water tanks that were positioned on a plateau balance with a resolution of 1 g (equivalent to a water flux of 0.001 l (Pütz et al. 2016). Data on load cells and plateau balance were stored every minute on the data logger.

Management history of soil, winter wheat cultivation, and 15N labelled drip fertigation

The agricultural field, from which the soil monoliths were extracted, was utilized as grassland from 1961 to 1969. Subsequently, it was converted into a wheat field, and maize has been grown on the field since 1979. Immediately prior to the lysimeter extraction procedure in 2020, an oil radish cover crop was growing on the site. After the installation of the lysimeters at IMK-IFU, the soil was left fallow for one complete vegetative cycle to allow for the germination of residual seeds and weeds, followed by their removal. Campesino winter wheat (Triticum sp.), recommended for farmers in Bavarian regions (Bayerisches Staatsministerium für Ernährung 2021), was planted on the 28th of September 2020 in the lysimeters. We also grew winter wheat in the area surrounding the lysimeters (at least 5 m width) to protect the wheat plants inside the lysimeters from wind shear effects. Before planting, we performed manual tilling of the soil. The total wheat planting area was ca. 100 m2 (including the wind shear protection zone around the lysimeters). In total, 171 kg N ha-1 mineral fertilizer NH4NO3 was applied: on the 20th of April (55 kg N ha-1), the 1st (56 kg N ha-1) and the 21st of June 2021 (60 kg N ha-1). The sowing procedure, amounts of fertilizer and application intervals matched those used by conventional farmers. The 15N enrichment was similar for NH4+-N and NO3--N and amounted to 71.66 atom% so as to determine recovery rates of the fertilizer N in various N pools (soil, plant biomass, roots, soil water, and gaseous emissions). The homogenous application of fertilizer in the lysimeters was achieved through a recently developed drip fertigation method (Tenspolde et al. 2023). To accomplish this, 219 bottles were used for fertigation of each lysimeter, with a water addition through the drip system of 22 l per lysimeter within a time span of 2 hours. During the 3rd fertilization, the wheat growth was dense and tall, which allowed for using only a reduced number of 102 bottles with extensions to pass the plants, equaling to application of 10.2 l through drip fertigation per lysimeter. Consequently, we added an additional 30 l of water in 5-liter pulses over 2 hours using a watering can. This approach was optimized to ensure the best possible 3-dimensional distribution of the 15N tracer in the topsoil.

Sampling design

The timeline for sampling is presented in Fig. 2. Prior to the initial fertilizer application, soil samples were randomly collected from each lysimeter at sampling depths 0–5 cm and 5–30 cm. These samples were then homogenized and analyzed to determine the natural abundance isotopic enrichment of 15N in total soil N. In addition to this, the natural abundance of 15N in both aboveground biomass and roots of the plants growing on the lysimeters was also determined prior to fertilization. Following the application of 15N labelled fertilizer, soil samples were collected from three replicates per lysimeter at depths of 0–5 cm and 5–30 cm, at four different time points (t1 to t4). For this, augers with inner diameters of 5 cm were used. On the same days of soil sampling, entire representative wheat plants, including roots, were harvested and analyzed (N = 1 for the first three, N = 5 for the final sampling). For the final sampling, motor-driven drilling equipment with plastic tube inliners (inner diameter 4.7 cm) was used to collect soil samples down to a depth of 1 m, as described by Zistl-Schlingmann et al. (2020). The five replicate soil cores per lysimeter were divided into depths of 0–30 cm, 30–60 cm, and 60–100 cm. Gravimetric soil water content was measured by drying freshly collected soil at each sampling time at 105 °C for 24 h.

Fig. 2
figure 2

The experimental timeline, including the sowing, fertilization, and sampling events for both soil and plant biomass. The frequency of different measurements is illustrated using grey, red, and blue colors. 15NGF: 15N gas flux method to measure N2 emissions

Full size image

Analytics

Measurement of N2 emissions using the 15NGF method

The 15NGF method to quantify N2 losses was applied daily in periods after fertilization, and on a weekly basis when the N2 emissions had declined (Fig. 2). The chamber closure time varied between 120 and 270 min, depending on the chamber’s height and proximity to the fertilization event. The static chambers, which covered the entire lysimeters (1 m2), were equipped with a fan and initially had a height of 30 cm. As the wheat plants grew after the second fertilization, the chamber height was increased to 60 cm to prevent damage to the plants. Gas samples were collected (0 min, 60 min, and at the end of the closure time) using a syringe through a septum opening in the chamber and were subsequently inserted into a 12 ml pre-evacuated double septum exetainer (Labco Ltd. High Wycombe, UK) for analysis. Gas samples were analyzed for 15N-N2O and 15N-N2 using an Isoprime PrecisION isotope ratio mass spectrometer (Elementar UK Ltd. Stockport, UK), coupled to an iso FLOW GasBench (Elementar UK Ltd. Stockport, UK).

The calculation of N2 and N2O produced via denitrification was done using the 15NGF method following the procedure described by Mulvaney (1984). Assuming that all of the N2 and N2O produced by denitrification come from the same pool of NO3−, the 15N enrichment of the NO3− pool undergoing denitrification was derived from 15N-N2O. The ion currents (I) at m/z 44, 45, and 46 enabled the molecular ratios 45R (45I/44I) and 46R (46I/44I) to be calculated for N2O. The 15N enrichment of the NO3− pool undergoing denitrification (aD) was then calculated from the non-random distribution of N2O isotopologues using 45R and 46R as described by (Stevens and Laughlin 2001).

Fluxes of N2 were calculated using aD and the increase of 15N-N2 in the chamber headspace following denitrification. The ion currents at m/z 28, 29 and 30 enabled the molecular ratios 29R (29I/28I) and 30R (30I/28I) to be calculated for N2. The differences between ambient and enriched atmospheres were expressed as Δ29R and Δ30R. The fraction of N2 attributable to denitrification (d) in the chamber headspace was calculated according to Mulvaney and Kurtz (1984) using Δ30R and the enrichment of the denitrifying pool aD (Stevens and Laughlin 2001). Fluxes of N2 were corrected for temperature and expressed on a surface basis in kg ha− 1 day− 1. The fraction of fertilizer-derived N2 (FD N2) was calculated as the ratio of 15N atom excess % of N2 emitted and the 15N atom excess % of the N fertilizer applied following the procedure described in Friedl et al. (2023).

The detection limit (DL) for N2 emissions was determined by measuring Δ29R and Δ30R in atmospheric air samples using the method described in Friedl et al. (2020). The DL was calculated by multiplying the standard deviation (SD) of ambient air samples (n = 17) by the t-value at a confidence level of 95%. The SD for 29R and 30R of ambient air samples for each IRMS analysis, was 5.2448 × 10− 6 and 1.6755 × 10− 6, respectively. The resulting DL values were 1.1067 × 10− 5 for Δ29R and 3.5354 × 10− 6 for Δ30R. These DL values were used to set a lower limit of quantification for subsequent N2 flux measurements, and fluxes below the DL were considered background fluxes. N2 fluxes with negative Δ30R values were discarded, corresponding to approximately 35% of the fluxes. The N2 flux calculation, based on aD, which showed a uniform distribution of 15N after the fertilizer applications (Fig. S1), resulted in a detection limit of the method (MDL) of 0.003 g N m− 2 day− 1 (i.e., 0.03 kg N ha− 1 day− 1) for a closure time of 3 h and chamber height of 0.3 m and 0.006 g N m− 2 day− 1 for a chamber height of 60 cm. If N2 fluxes were below the DL, fluxes were set to 0.5 MDL following the procedure used by Friedl et al. (2023).

Linear interpolation was employed to estimate flux values for days when no measurements were conducted. During periods when the fluxes were not detectable, which typically occurred more than 2 weeks after fertilization events, the fluxes were assumed to be equal to 0.5 MDL for linear interpolation and cumulative flux calculation.

Measurement of other gaseous N losses

Ammonia losses were estimated using one cylindric manual chamber (150 mm diameter) per lysimeter. The chamber design is by Jantalia et al. (2012), and the underlying principle is NH3 absorption in an acid trap. The chamber is formed of a rigid PVC cylinder that is 200 mm high. The open top is protected against rain with a roof 70 mm above the cylinder. Two polyurethane plastic foams (25 mm thick) acting as acid traps were soaked in 50 ml of a sulfuric acid solution (1 M H2SO4 and 4% (v/v) glycerol) and fixed in the chamber at 50 and 155 mm height above the soil surface. To facilitate the measurement of NH3 emissions, three PVC frames (5 cm in height) were permanently installed on each lysimeter as a base for the ammonia chamber. Monitoring of NH3 emissions occurred over a two-week period, commencing one day after each fertilization event. In the initial three days of measurement, the foam was replaced every 12 h. Subsequently, the foam switch frequency was adjusted to once a day for the following 7 days. Finally, the foams were changed every two days until the conclusion of the measurement period. For each NH3 measurement, the chamber was set on a different basement to minimize chamber effects on soil and plants. At foam retrieval, the foam was vigorously compressed in a bag containing 150 ml of a 2 M potassium chloride (KCl) solution to extract the NH4+ cations and the foam extract was transferred into 50 ml falcon tubes and frozen for further analysis. The contents of NH4+-N in the extracts were measured using a colorimetric technique according to Kempers and Zweers (1986). The residual acid in the samples had to be neutralized, as the procedure requires alkaline conditions. We assumed that NH4+-N accumulations from the bottom foam equaled the NH3-N emissions from the soil area covered by the chamber. 15N enrichment could not be determined due to low NH4+ concentrations of the acid trap extract. We assumed that all NH3 emissions were fertilizer-derived, which appears justified given that significant NH3 emissions only occurred shortly after fertilization.

Nitrous oxide emissions were measured on a daily up to weekly basis, depending on the proximity to the fertilization events. For this, the large manual chambers covering the entire lysimeter that had been described earlier for N2 emission measurements, were used. The chamber was connected to an Ultraportable Greenhouse Gas Analyzer (Los Gatos Research, San Jose, USA). The flux calculation relied on the N2O concentration change inside the chamber as continuously measured over a period of 10–15 min, following the approach outlined by Ma et al. (2021a).

When the Greenhouse Gas Analyzer was unavailable, manual gas sampling from the chamber was conducted using a syringe, and the collected samples were placed into evacuated screw-cap Exetainers (12 ml), following the method described by Rehschuh et al. (2019). The chamber was then closed for a duration of 2 h. Subsequently, the samples were analyzed using a gas chromatograph connected to an autosampler (SRI 8610 C, SRI Instruments, Torrance, USA), as detailed in Rehschuh et al. (2019).

Soil air N2O concentrations and δ15N in N2

To quantify soil air N2O concentrations, we collected air samples from the semi-permeable membrane tubes (PP V8/2 HF membrane, Accurel®, Akzo Nobel Faser AG, Wuppertal, Germany), which were in equilibrium with soil air inside the lysimeters (Wolf et al. 2010), using a syringe, and then they were transferred into pre-evacuated screw-cap Exetainers (12 ml) through a septum (Wolf et al. 2010). The samples were subsequently analyzed by gas chromatography as described above. Using the same semi-permeable membrane tubes and sampling procedures, we also assessed 15N enrichment in N2 enrichment in the vertical soil air profile and analyzed the samples by Gasbench-IRMS as described above. To ensure the re-establishment of equilibrium with the soil air, we maintained a minimum time interval of 6 h between subsequent sampling events of the membrane tubes. Sampling frequency for N2O concentrations and δ15N in N2 ranged from daily after fertilization events to weekly in periods of background fluxes.

Inorganic N in soil water and N leaching

Mineral N in the soil solution was determined by collecting soil water samples from the bottles connected to suction cups (Fu et al. 2017). We collected water samples on a weekly basis or when sufficient water had accumulated in the bottles. The volume of water collected at each depth was determined, and a subsample of 50 ml was then filtered using a 0.45 μm hydrophilic cellulose acetate membrane (Sartorius Stedim Biotech GmbH, Göttingen, Germany) and a syringe. The filtered subsample was poured into Falcon tubes and stored in a frozen state until further analysis. Dissolved NH4+-N and NO3−-N concentrations were determined colorimetrically using a microplate spectrometer (BioTek Instruments, Inc. USA) according to Kempers and Zweers (1986) and Pai et al. (2021). The amount of leached water was calculated based on the mass changes in the drainage tank of each lysimeter, while the threshold of 100 g min− 1 was set to exclude occasionally observed outliers from the mass records. The amount of leached N was calculated by multiplying the cumulative water amount leached between two water sampling dates by the concentration of NH4+-N and NO3−-N at 120 cm depth. In addition, subsamples were analyzed for δ15N in NH4+-N and NO3−-N using sequential diffusion (Wu et al. 2011).

Plant uptake and soil fates of fertilizer N

The aboveground (AGB) and belowground (BGB) biomass of the crop were calculated by multiplying the mean dry weight of wheat plant AGB/BGB (N = 3 for the first two samplings, N = 15 for the final sampling) by the lysimeter-specific number of plants counted at each sampling period. To analyze N concentrations and 15N enrichment in plant, root and soil, samples were dried at 60 °C according to Zistl-Schlingmann et al. (2020). The dry soil and plant samples were then ground using a pebble mill and subsequently packed into tin capsules. The concentration and isotope ratio of N was determined using an elemental analyzer (Flash EA, Thermo Scientific, Waltham, MA, USA) coupled to an isotope ratio mass spectrometer (Delta PlusXP, Thermo Scientific, Waltham, MA, USA) as described in detail by Zistl-Schlingmann et al. (2020).

The excess 15N amount in plant and soil pools was calculated using the following equation:

$${N}_{pool}\times \left(\frac{APE}{100}\right) \left(1\right)$$

where \({N}_{pool}\) is the amount of N in mg, found in the soil or plant pool and \(APE\) (atomic percent excess) is the 15N excess enrichment of the respective pool. \(APE\) is determined by subtracting the natural abundance 15N enrichment (atom% 15N) from the measured value of atom% 15N of the associated N pool.

Recovery of the fertilizer N in investigated N pools was calculated by dividing the 15N excess amount of the respective N pool by the cumulative amount of fertilizer 15N excess added to the lysimeters at the corresponding sampling time. For scaling of soil 15N recovery to the lysimeter level, sampling depth, volume and bulk density were considered (Zistl-Schlingmann et al. 2020). We then multiplied 15N excess recovery (% of added 15N excess) by fertilizer N addition rate (kg N ha− 1) to obtain the flow of fertilizer-N into the investigated N pools. More detailed calculation procedures for the 15N tracing approach into plant and soil N pools are provided by Dannenmann et al. (2016, supplementary material).

Fertilizer N balance

The cumulative emissions of N2, N2O, and NH3 were calculated for single sampling dates, and over the entire duration of the study. To account for days when no measurements of NH3, N2O, and N2 were taken, a linear interpolation was applied (see above for details on N2 interpolation). The “unaccounted fertilizer N” – which may be interpreted as N2 emissions - was calculated by subtracting the fertilizer N flows into soil N, plant N, leaching water N, and gaseous emissions (excluding N2) from fertilizer N addition. These fertilizer N balances were set up separately for all four sampling dates where plant, soil and 15NGF data were available.

Statistical analysis

The statistical analyses were conducted using the open-source programming language Python (version 3.6.0, Python Software Foundation) and R version 4.2.0 (R Core Team 2019). The graphs were made using Origin, version 2020b (OriginLab Corporation 2020). The three lysimeters were used as replications in the experiment, making the lysimeter the statistical unit. The five replicated soil cores or plants obtained during each harvest were treated as pseudoreplicates. Mean values and standard error of the mean were calculated using N = 3 lysimeters. To assess the statistical difference between the results obtained with the 15NGF method and the 15N mass balance approach, the Wilcoxon Signed Ranks Test was used.

Results

N2, N2O and NH3 emissions, and soil water nitrate

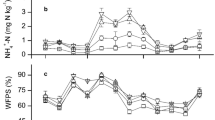
The emissions of N2 (Fig. 3a) showed large variations across the three instances of fertilization. Largest N2 fluxes were observed with delays ranging from a few days to 3 weeks after the first fertilization event (April 21st), with a maximum flux of > 3 kg N ha− 1 day− 1 on May 8. These delayed N2 emission peaks occurred with warming soil (Fig. 3g), and in particular, after precipitation events that increased WFPS in topsoil (Fig. 3f). It should also be noted that these high N2 emission peaks were observed at a time when plant N acquisition, with cumulative uptake of 14 ± 2 kg N ha− 1, was still relatively low (Table 1a). In addition to the increased topsoil NO3− concentrations originating from the 15N-labelled fertilizer, we also observed high NO3− concentrations at depths greater than 50 cm (Fig. 3e). High subsoil NO3− concentrations originated from downward movement of NO3− during the preceding winter (data not shown), which finally reached depths of > 100 cm at the end of the growing season. This was also confirmed by only insignificant 15N enrichment in leached NO3− at 120 cm depth, while NH4+ was at the detection limit in the leachate. The total amount of leached NO3− during the measurement period accounted for 3.1 ± 0.3 kg N ha− 1 (detailed monthly water and NO3− leaching data are provided in Table S1). However, the leaching of recent fertilizer N during the monitored period was with only 0.04 ± 0.02 kg N ha− 1 very small (Table 1a).

Unlike the emissions observed after the first fertilization, the N2 emissions following the 2nd fertilization exhibited a brief peak-like response, remained smaller than 0.42 kg N ha− 1 day− 1 and returned to background levels within 6 days (Fig. 3a). The increase in N2 emissions was observed already within 2–3 h after fertilizer application. Dinitrogen emissions were lowest after the 3rd fertilization, despite higher soil temperatures compared to earlier fertilization events (Fig. 3a, g). These lower N2 peak emissions after the 2nd and 3rd fertilization corresponded to periods of large plant N uptake, i.e., up to half of fertilizer N was recovered in plant biomass (Table 1a, b).

The total cumulative N2 losses at the end of the experiment were 21 ± 3 kg N ha− 1 (Table 1a). Among these losses, the N2 losses derived from the fertilizer accounted for 13 ± 2 kg N ha− 1, equivalent to 7.5 ± 0.9% (Table 1a, b) of the applied fertilizer.

Table 1(a) Fertilizer N balances for the different sampling times (t1 to t4), as calculated from respective 15N recovery rates (Table 1b). The table shows N inputs by fertilizer addition, as well as fertilizer N fates, soil storage, plant uptake (including roots), N leaching, as well as N2O and NH3 emissions. This information then is used to calculate the unaccounted fate of fertilizer N, which should equal fertilizer-derived N2 emissions. The last two lines then provide the directly measured cumulative N2 emissions by use of the 15NGF method, separately for fertilizer-derived emissions and total emissions. Uncertainty is provided as the standard error of the mean of N = 3 lysimeters
Full size table
Table 1(b) Fertilizer N fates expressed in % of fertilizer applied until the respective sampling dates (t1-t4). Error bars represent the standard error of the mean. The percentage of unrecovered fertilizer N loss was not statistically different compared to directly measured fertilizer-derived N2 emissions, expressed in % of applied fertilizer. Note that t1 and t2 samplings were after the first 15N application, t3 after already two, and t4 after all three 15N applications. This explains e.g., the increase of fertilizer N recovery in soil between t3 and t4
Full size table

The N2O flux pattern after the first fertilization in April equaled that of N2 emissions, i.e., showed sporadic emissions over ca. three weeks with occasionally high variability across lysimeters. Following the 2nd fertilization, N2O emissions exhibited a sharp peak response, with the highest emissions observed one day after fertilization amounting to 0.008 ± 0.002 kg N ha− 1 day− 1. Following the peak emission, the N2O emissions quickly decreased and returned to background levels in the subsequent days. After the 3rd fertilization on June 21, N2O emissions were of similar magnitude compared to the second fertilization, but lasted longer. Throughout the measurement period of 2.5 months, a total of 0.15 ± 0.01 kg N2O-N ha− 1 was emitted. Given the small N2O emissions in contrast to the significant N2 emissions the resulting N2:(N2O + N2) ratio was on average 0.94 ± 0.06, with a maximum of 1.001 and a minimum of 0.75.

Fig. 3
figure 3

Soil N2 emissions as measured by the 15NGF method from the entire 1 m2 lysimeter areas (N = 3). The black symbols represent the total N2 soil emissions (T N2), the green symbols represent fertilizer N derived N2 flux (FD N2) (a); 15N enrichment profile of soil air N2 (b); Total soil N2O emissions measured from the entire lysimeter area and daily precipitation (including drip fertigation) (c); soil air N2O concentrations profile (d), soil water NO3--N concentrations profile in mg N l-1 (e); soil water-filled pore space profile, in % (f); soil temperature profile, in °C (g). All values provided are mean values of the 3 analyzed lysimeters. The error bars for fluxes indicate SE. Fertigation events are visually represented in the flux graphs by vertical dashed lines

Full size image

After the first fertilization event, NH3 emissions peaked at 0.228 ± 0.006 kg N ha− 1 day− 1 on day 5 and then rapidly declined, becoming undetectable until the next fertilization event (Fig. 4). After subsequent fertilization events, similar patterns of NH3 emissions were observed. Following the 2nd fertilization event, peak emissions reached only 0.04 kg N ha− 1 day− 1, while after the 3rd fertilization, emissions peaked at 0.15 ± 0.01 kg N ha− 1 day− 1 on days 1 and 2 following fertilization, before gradually declining within 7 days to values below the detection limit. The cumulative emissions of NH3 after the first fertilization event were 1.1 ± 0.1 kg N ha− 1, while the total cumulative emissions for the entire intensive measurement period were 1.5 ± 0.1 kg N ha− 1 or 0.87 ± 0.03% of the applied fertilizer (Table 1a, b). Hence, both NH3 and N2 emissions mainly occurred after the first fertilization, but were of lower importance later in the growing season, when temperature was higher, but large proportions of fertilizer N were allocated to plants.

Fig. 4
figure 4

Ammonia emissions in kg N ha-1 day-1 after each fertigation event. The fertigation events are represented by dashed lines. The error bars indicate the standard error (SE) of the mean

Full size image

Fertilizer N mass balance and comparison of unaccounted fertilizer N fates with directly measured N2emissions

Across all four sampling dates, between 32% and 64% (equivalent to 21–78 kg N ha− 1) of the applied fertilizer N was recovered in the soil, making it the primary sink for the fertilizer N (Table 1a, b). Plant uptake was of equal importance, with 26–52% (14–73 kg N ha− 1) of the added fertilizer N being taken up by the plants at the respective sampling dates (Table 1a, b). In contrast, cumulative NH3 losses were only 1.5 kg N ha− 1 over the entire period (less than 1% of added fertilizer N), which still was much larger than the cumulative N2O emissions, which only accounted for 0.1% of added fertilizer N. Leaching of fertilizer N was even lower compared to N2O emissions, and thus negligible for the fertilizer mass balance.

Based on these fertilizer N fates, 8–33% of fertilizer N remained unaccounted across the sampling dates (Table 1b). This translates to an unaccounted fertilizer N loss that increased from 4 ± 2 to 18 ± 13 kg N ha− 1 over time (Table 1a). Parallel direct measurements of N2 losses using the 15NGF method revealed fertilizer N2 losses of 2.4 ± 0.5 kg N ha− 1 that increased to 13 ± 2 kg N ha− 1 and total N2 losses that increased from 3.3 ± 0.7 kg N ha− 1 to 21 ± 3 kg N ha− 1. Both directly measured fertilizer N2 emissions and total N2 emissions were not statistically different compared to unaccounted fertilizer N loss of the mass balance approach. Directly measured cumulative fertilizer N2 emissions increased in particular between May 5 and May 28, i.e., from 2.4 ± 0.5 to 10 ± 1 kg N ha− 1, with little increase in the remaining experimental period (Table 1a). Also, this was in excellent agreement with the findings of the fertilizer mass balance approach, which during the same time indicated an increase in N2 emissions (via unrecovered fertilizer 15N) from 4 ± 2 to 18 ± 9 kg N ha− 1. Hence, the mass balance approach did not only represent directly measured cumulative N2 emissions at the end of the measuring period, but also identified the highest N2 emissions in the same time span as observed by the 15NGF measurements.

While N2 and N2O emissions represent fluxes between the soil and the atmosphere for 1 m2 area of the lysimeters, vertical soil information on 15N enrichment in N2 and on N2O concentration was obtained from the installed semi-permeable membrane tubes that reflect a smaller fraction of the lysimeters soil air (Fig. 3b and d). Nonetheless, the patterns of δ15N2 in lysimeter soil air generally reflected the temporal dynamics of measured N2 emissions. Specifically, this included the delayed response and the extended overall length of N2 emission after the first fertilization. Unfortunately, on the day of the highest N2 emissions beginning of May, we did not measure corresponding soil profile data of δ15N2. This is because the sampling frequency had declined as we did not expect high emissions to occur weeks after the fertilization event. After the 2nd fertilization, peak N2 fluxes were accompanied by clear increases of δ15N2 values in the soil air right over the duration of the N2 emissions peak. Finally, the only very low N2 emissions after the 3rd fertilization were also hardly visible in form of δ15N2 increases in the topsoil. However, it needs to be noted that the highest soil air δ15N2 values did not necessarily correspond to the highest N2 emissions at the soil-atmosphere interface. This was also reflected by the results of a regression analysis, which on the one hand indicated a significant positive relationship between N2 flux and δ15N in soil air at 10–50 cm depths (p < 0.01) (Fig. 5a). On the other hand, the regression model only explained up to 52% of the variability observed in N2 emissions across the measurements, with a further strongly decreasing explanatory power at greater depths. Very similar results were obtained for the relationships between soil air N2O concentrations and N2O emissions at the soil-atmosphere interface (Figs. 3c and d and 5b). The dynamics of soil air N2O concentrations generally corresponded to the peaks in N2O emissions following the 2nd and 3rd fertilization events, while the magnitude of N2O concentrations varied significantly despite comparable emissions. Additionally, the sporadic N2O emissions observed after the first fertilization event did not result in commensurate increases in soil air N2O concentrations. The results of regression analysis indicated a strong correlation between the N2O flux and N2O concentration in three depths- 10, 20 and 30 cm (p = 0.000, p = 0.01, p = 0.013, respectively), while the R2 at 10 cm depth was the highest and decreased with depth, similar to the pattern observed for N2 emissions vs. δ15N2 in soil air (R2 = 0.48, R2 = 0.32 and R2 = 0.21, respectively) (Fig. 5b).

Fig. 5
figure 5

(a) Regression analysis of the mean fertilizer-derived N2 flux and δ15N2 values for various depths (10 cm, 20 cm, 30 cm, 50 cm, and 120 cm), only when were measured at the same day; (b) Regression analysis of the mean total N2O flux and N2O concentrations in ppb in all the depths. Each data point represents the average value for a specific depth and time point. The fluxes are in kg N ha-1 day-1. The solid lines represent linear regression lines fitted to the data. The p-values provide statistical significance of the relationships

Full size image

Discussion

The role of N2 emissions in the fertilizer N balance of fertigated winter wheat

Total N2 emissions (including those not from applied fertilizer) in our study were the dominating N loss and exceeded NH3 emissions by approximately one order of magnitude, and N2O emissions by two orders of magnitude, while overall fertilizer N losses remained low with about 12% of applied fertilizer compared to plant uptake and soil storage (Table 1).

Denitrification losses from agricultural soils and its product stoichiometry, as well as NH3 emissions are governed by climate and soil properties, but to a large extent also by management, which might be of particular importance in our study as the fertilization was done in conjunction with irrigation, i.e., by fertigation. Total NH3 emissions in our study were about 1% of applied fertilizer N and, thus, much smaller than the global NH3 emission factor for the use of synthetic fertilizer N (12.56%), the NH3 emission factor for use of synthetic N in Europe (6%) or the global NH3 emission factor for wheat cultivation (12.05%) (Ma et al. 2021b). Nitrous oxide emissions measured during our monitoring period accounted for only ca. 0.1% of fertilizer N, which is also low compared to the German national emission factor for direct N2O emissions from synthetic fertilizers, which is 0.6% (Mathivanan et al. 2021).

In contrast to NH3 and N2O emissions, much less is known on fertilizer-induced N2 emissions. Recently, Pan et al. (2022b) provided estimates of emission factors of denitrification (N2 + N2O) based on a global synthesis and obtained a global mean value of 4.7% of applied fertilizer. However, the dataset in this study is strongly dominated by AIT studies so that this emission factor might be underestimated. The total N2 losses in this study were found to be 21 ± 3 kg N ha− 1 in 2.5 months (or fertilizer-derived N2 losses of 13 ± 2 kg N ha− 1 season− 1, i.e., 7.5 ± 0.9% of fertilizer N input). These values are comparable to the results of Rolston et al. (1978), who used the 15NGF method to evaluate field N2 fluxes in summer-period (23 °C) cropped plots (perennial ryegrass) in Typic Xerorthent, fertilized with enriched KNO3 under two water regimes close to saturation. In the latter study, the cumulative N2 flux was 7–30 kg N ha− 1 accounting for 3–14% of the fertilizer N. Mosier et al. (1986b), measured N2 fluxes from barley and corn miniplots in Nunn clay loam during the summer season in Colorado. They used the 15NGF method to assess N2 seasonal emissions of 1.5 and 0.7 kg N ha− 1 for corn and barley, respectively, after the application of enriched (NH4)2SO4. These emissions accounted for only around 1–2% of the applied N, possibly because of high N use efficiency of the crop. Recent studies conducted in Germany, on Haplic Luvisol crop systems using cattle slurry organic fertilizer and enriched K15NO3, reported N2 emissions of 0.4 to 3 kg N ha− 1 or 0.6–3.9% of the total N input (Buchen-Tschiskale et al. 2023). The study’s findings of minor N2 + N2O losses but high NH3 emissions of up to 8 kg N ha− 1 are typical for the application of liquid cattle slurry fertilizer. In a study conducted by Pan et al. (2022a) in northeastern China, characterized by a cool temperate, sub-humid continental monsoon climate and cultivated black soil, similarly low N2 emissions of 1.6 ± 0.5 kg N2-N ha− 1 were reported, accounting for only 0.7% of the applied (15NH4)2SO4-N input. In the latter case, with measurements in the spring season, low temperatures might explain the N2 emissions. Vice versa, N2 emissions can be particularly high in tropical regions. For instance, Takeda et al. (2023) investigated denitrification emissions in intensively managed tropical sugarcane farms, revealing exponentially increasing denitrification losses (ranging from 12 to 87 kg N ha− 1 season− 1) with increasing N fertilizer rates from 0 to 250 kg N ha− 1. These emissions accounted for as much as 31–78% of the mineral fertilizer 15N losses, with the primary component being N2.

We attribute the fertilizer N fate patterns of our study, characterized by high plant N uptake and soil storage along with low overall gaseous N losses that are dominated by N2 emissions rather than NH3 emissions, to the drip fertigation management. While our primary motivation for using drip fertigation was to achieve homogenous 15N labelling, decreased leaching and reduced NH3 emissions, our findings indicate a range of beneficial effects of drip fertigation in the temperate climate conditions of this study where its application is not common. However, a control with normal fertilization was not included in this study. Recent research confirmed that drip fertigation does not only strongly increase water use efficiency, but also N use efficiency (Anas et al. 2020). It reduces NH3 and N2O emissions and NO3− leaching (Zheng et al. 2023), but possibly increases the relative importance of denitrification over NH3 emissions (Qasim et al. 2022). A significant and unresolved question in this context is the extent to which N2O losses are mitigated by complete denitrification until the terminal product N2. In our study, with a pH value of 6.7, high WFPS and low soil NO3−, there were several factors that promote denitrification until the terminal product N2 and thus might explain the large importance of N2 emissions over N2O emissions (Butterbach-Bahl et al. 2013).

Comparison of unrecovered fertilizer N with directly measured N2 emissions to verify field 15NGF measurements

Fertilizer-derived N2 emissions as obtained from the 15NGF method are subject to method-inherent bias that is difficult to constrain, e.g., underestimation of N2 losses due to heterogeneous tracer application and 15N2 subsoil diffusion and storage (Arah 1992; Friedl et al. 2020; Micucci et al. 2023; Vanden Heuvel et al. 1988). Also, the 15N fertilizer mass balance approach is subject to uncertainty, given the many components of the N mass balance that need to be considered such as uncertainty in quantifying above and belowground biomass N or N compounds along the soil profile.

In this context, the most striking finding of this study was that directly measured fertilizer-derived N2 emissions were statistically similar to the unaccounted fertilizer N fates of the 15N fertilizer mass balance approach for all four sampling dates conducted during three fertigation events. Still, the total cumulative fertilizer-derived N2 emissions persistently showed smaller numbers (by 28–44%) than the gap in the 15N fertilizer mass balance. It could be argued that this discrepancy might be attributed to the aforementioned issues of the 15NGF method, leading to an underestimation of N2 formation. However, this remains generally speculative, given the remaining uncertainties of the fertilizer N mass balance approach.

The experimental design of this study was optimized in several regards to facilitate this method comparison. In our study, only NO emissions and DON leaching were not accounted for in the 15N mass balance, which however are expected to be negligible (a) given the high N2:N2O ratios and very low N2O emissions, which suggest a small role of NO as well (Butterbach-Bahl et al. 2013) and (b) the very low NO3- leaching losses in our study. Consequently, we were able to reduce uncertainty in 15N fertilizer mass balance, largely attributed to its fates in plants and soil, which significantly improved the overall accuracy of the approach. Despite this, the uncertainty in constraining unrecovered 15N based on lysimeter triplication remained larger compared to that obtained for direct N2 measurements using the 15NGF method. Furthermore, the slow drip fertigation application method did not only maximize the homogeneity of 15N application (Tenspolde et al. 2023) and thus, the representativeness of soil sampling, but likely reduced NH3 emissions and their role in the fertilizer N mass balance. The latter, together with the low NO3- leaching from fertilizer strongly reduced the accumulation of uncertainty in the 15N fertilizer mass balance. Such uncertainty often prevents the setup of an accurate 15N fertilizer budget under field conditions (Micucci et al. 2023; Myrold 1990).

To enhance the accuracy of 15NGF measurements, we employed closed lysimeter systems, that might limit underestimation of N2 emissions due to 15N subsoil diffusion (Friedl et al. 2020; Well et al. 2019b). This underestimation may be in the order of magnitude of 1/3 or more (Micucci et al. 2023) and might possibly be smaller in our approach as 15N enriched gases could not leave the closed bottom of the lysimeters. Additionally, as we set up our experiments in lysimeters we avoided typical weaknesses associated with the 15N fertilizer mass balance approach such as unclear spatial boundaries (Micucci et al. 2023), and difficult quantification of N leaching losses. To further optimize the accuracy of the 15NGF method, we applied high 15N fertilizer enrichment with optimized homogeneity (Tenspolde et al. 2023). We minimized the chamber height according to the current crop height to enhance the detection limit of the 15NGF method during the early stages of plant growth (Friedl et al. 2020; Micucci et al. 2023). In our study, the N2 flux detection limit varied based on chamber height (30 to 60 cm) between 0.003 g N m-2 day-1 for 30 cm height and 0.006 g N m-2 day-1 for 60 cm chamber height. Recently, Liu et al. (2022) reported similar detection limits for in situ 15NGF method application in maize and wheat fields, which was as low as 0.001–0.006 g N m− 2 day− 1 for six hours of chamber closure, while for two hours the detection limit was 0.004–0.037 g N m− 2 day− 1. It is worth noting that the chamber used had a height of 3 cm in that study, which prevented the inclusion of plants within the chamber. Similar ranges of detection limits were reported in other studies (0.003–0.022 g N m− 2 day− 1), however, they all used lower chamber heights (Bergsma et al. 2001; Buchen et al. 2016; Tauchnitz et al. 2015).

In our study, the static chambers used to directly measure N2 emissions extended to the entire lysimeter area of 3 m2. This approach was chosen to prevent the risk of overlooking small-scale denitrification hot spots (see e.g., Parkin 1987). In contrast to spatial resolution, we attribute significant uncertainty of direct N2 emission measurements in our study to the restricted temporal resolution, which leads to uncertainties during interpolation and cumulation of N2 emissions. This may explain the relatively low cumulative fertilizer-derived N2 emissions compared to the mass balance approach between May 5th and May 28th (Table 1a), i.e., further sporadic N2 emission peaks were probably missed. On the other hand, the highest directly measured N2 emissions measurements between t1 and t2 were accompanied by a concomitant increase in unrecovered fertilizer N in that period, again demonstrating that results of the 15NGF method aligned well with the 15N fertilizer mass balance approach. Considering the low plant N uptake in this period (Table 1a), the relatively high N2 emissions were likely facilitated by low competition by plants, while fertilizer-induced increases in topsoil NO3- concentrations were already diminishing (Fig. 3e).

Similar to our work, Rolston et al. (1979) compared the 15NGF method to quantify N2 emissions with a fertilizer mass balance approach under field conditions. This study reported direct measurements of total denitrification to be generally much smaller compared to estimates obtained from the mass balance approach (up to 65 kg N ha− 1). The difficulties to compare the two approaches were assigned to both methods – the large detection limit of the 15NGF method to quantify N2 (0.1 g N m− 2day− 1), the limited temporal resolution of direct flux measurements, and huge uncertainties in the quantification of the different 15N fertilizer fates such as leaching and soil storage. Recently, Buchen-Tschiskale et al. (2023) compared directly measured N2 emissions from the 15NGF method under reduced ambient N2 atmosphere with a 15N mass balance approach using organic slurry fertilizer applied to winter wheat. This study revealed that for certain slurry application treatments, N2 + N2O losses matched well with the 15N recovery, while for others, they did not, with the large NH3 emissions possibly being the dominating source of uncertainty. These earlier studies thus illustrate that it was essential that in this study the uncertainty of both methods could be reduced.

Kulkarni (2014) compared the 15NGF method with the He gas-flow soil core method under laboratory conditions using unfertilized forest soils. This comparison did not reveal comparable or related rates of N2 loss, which was likely related to the use of different soil samples and addition of N amounts to unfertilized soil only in the 15NGF method. Generally, the application of the 15NGF method to unfertilized forest soils appears questionable due to the need to add large 15NO3− amounts which will perturbate denitrification processes (Friedl et al. 2020). Furthermore, the He gas-flow soil core method reveals total N2 emissions, irrespective of source processes, fertilizer-N and other sources, and from all origins along the entire vertical soil profile. In contrast, the 15NGF method only reveals total N2 emissions from NO3− pools that were well mixed with 15N-enriched NO3−, i.e., do not include emissions from unlabeled NO3− in subsoil. Given the significant subsoil NO3− concentrations, accompanied by persistently high WFPS (Fig. 3), we might indeed have underestimated total N2 emissions in this study. This however does not affect our comparison between fertilizer-derived N2 emissions and unaccounted 15N of the 15N fertilizer mass balance.

In conclusion, due to our targeted lysimeter setup, we were able to reduce the uncertainty of the 15N fertilizer mass balance to an extent that allowed for a direct comparison with directly measured N2 losses obtained from the 15NGF method. This provided independent confirmation of the 15NGF measurements under ambient atmospheric conditions for multiple soil and plant sampling dates.

Relationships between measured N emissions and soil air measurements

In our second hypothesis, we expected a link between changes in 15N enrichment of N2 in the soil profile and measured N2 fluxes at the soil-atmosphere interface. This was partly confirmed due to the general but not universal relationships between variations in δ15N enrichment of N2 in the soil profile and measured N2 emissions at the soil-atmosphere interface (Fig. 5a), which were also reflected in significant correlations. Analogously to N2 emissions, a positive correlation of N2O emissions with N2O concentrations in the soil at 10–30 cm depth was found. These similarities in the relationships between soil air data and fluxes observed for N2O and N2 emissions indicate the presence of a relationship between soil air of δ15N2 and N2O concentrations to associated fluxes at the soil atmosphere interface.

To our knowledge, no comparable study is available on soil air δ15N dynamics. However, our N2O-related findings align well with the results of Li et al. (2021), who demonstrated a comparable association between surface N2O emissions and elevated N2O concentrations in the top soil layer of 0–15 cm in a cotton field. In our study, up to 52% of the variation of the data was explained by the regression models for N2 and N2O (Fig. 5a, b). Additionally, the statistical significance of the N2 regression models was stronger than for N2O.

The observed spatiotemporal dynamics of measured vertical δ15N patterns in N2 generally support the observed temporal dynamics of N2 measurements. This encourages the development and testing of new methods to better constrain field N2 emissions based on in situ sampling of soil N gases. E.g., in future applications, our data could serve to validate 15N2 diffusion modelling approaches targeted to constrain underestimation of denitrification by 15N subsoil diffusion and storage (Well et al. 2019b). Furthermore, the gradient method, considering diffusivity (Maier and Schack-Kirchner 2014), could be used to derive vertical fluxes of N2 to be compared with chamber fluxes, at least when N2 sources are not too close to the soil surface so that a relevant enrichment gradient can form. Given that the detection limit for denitrification is lower in soil air compared to chamber fluxes, soil air δ15N analyses, including analyses of soil air N2:N2O product ratios might serve to reveal sound flux estimates in phases when chamber fluxes are below the detection limit. In this context, the presented dataset is an excellent prerequisite for developing and testing such a potential new method to assess field N2 emissions based on in situ sampling of soil N gases.

Conclusions

This study provides a unique combination of field N2 flux measurements and lysimeter-based 15N fertilizer mass balances, thereby successfully demonstrating that the 15NGF method delivers realistic estimates of N2 flux under field conditions in ambient atmosphere. The soil air δ15N2 data, along with the profile data of environmental controls of denitrification, further support the trustworthiness of measured N2 emissions at the soil-atmosphere interface. Additionally, these findings suggest that combining such measurements with soil gas diffusion modeling and the gradient method could offer an alternative approach to constrain soil N2 emissions. With its high temporal resolution of environmental data, encompassing all key components of the N cycle in a winter wheat rotation, we present a benchmark dataset for testing process-based biogeochemical ecosystem models. Furthermore, the successful cross-comparison of the 15NGF method with the 15N mass balance approach calls for a broader application of the 15NGF method across various agricultural ecosystems in order to create more reliable N2 emission data as a solid basis for the development of strategies to mitigate N losses from agriculture.