Critical Subgraphs of Schrijver Graphs for the Fractional Chromatic Number

Abstract

Schrijver graphs are vertex-color-critical subgraphs of Kneser graphs having the same chromatic number. They also share the value of their fractional chromatic number but Schrijver graphs are not critical for that. Here we present an induced subgraph of every Schrijver graph that is vertex-critical with respect to the fractional chromatic number. These subgraphs turn out to be isomorphic with certain circular complete graphs. We also characterize the critical edges within this subgraph.

1 Introduction

Kneser graphs $\textrm{KG}(n,k)$ are defined for every pair of positive integers n, k satisfying $n\ge 2k$. Kneser [11] observed (using different terminology) that their chromatic number is not more than $n-2k+2$ and conjectured that this upper bound is tight. This was proved by Lovász in his celebrated paper [13] using the Borsuk-Ulam theorem. Soon afterwards Schrijver [16] found that a certain induced subgraph $\textrm{SG}(n,k)$ of $\textrm{KG}(n,k)$, now called Schrijver graph, still has chromatic number $n-2k+2$ and is also vertex-critical for this property, that is, deleting any of its vertices the chromatic number becomes smaller. It is also well-known that the fractional chromatic number of $\textrm{KG}(n,k)$ is $\frac{n}{k}$, a consequence of the vertex-transitivity of these graphs and the Erdős–Ko–Rado theorem. (For the definition of the fractional chromatic number, see Sect. 2.) Proving a conjecture of Holroyd and Johnson [6], Talbot [19] gave the exact value of the independence number of Schrijver graphs that easily implies, as already observed in [17], that their fractional chromatic number is also $\frac{n}{k}$. Most Schrijver graphs are not vertex-critical for this property (the only exceptions are the trivial cases when $k=1$, $n=2k$, or $n=2k+1$, cf. Corollary 14 in Sect. 3) and this suggests the problem of finding critical subgraphs of Schrijver graphs for the fractional chromatic number. In this paper we present such a subgraph for all values of n and k with $n\ge 2k$. These subgraphs, that turn out to be isomorphic to the circular (also called rational) complete graphs $K_{n'/k'}$ for $n'=\frac{n}{\gcd (n,k)}, k'=\frac{k}{\gcd (n,k)}$, are vertex-transitive, so deleting any of their vertices the value of the fractional chromatic number drops to the same smaller value. We also locate the edges of these special subgraphs that are critical for the fractional chromatic number and show that their deletion already results in the same decrease of the fractional chromatic number as the deletion of a vertex.

The paper is organized as follows. In the next section we give the necessary definitions to define the above mentioned vertex-critical subgraph and state our main theorem. A proposition is also given there claiming the relation to circular complete graphs. From the latter the theorem will easily follow via known results about circular cliques. Section 3 contains the proof of the mentioned proposition thus completing the proof of our main result. The last section is devoted to characterizing the critical edges of circular complete graphs for the fractional chromatic number.

2 Well-Spread Subsets and the Subgraph Q(n, k)

Definition 1

For positive integers $n\ge 2k$ the Kneser graph $\textrm{KG}(n,k)$ is defined on the vertex set that consists of the ${\left( {\begin{array}{c}n\\ k\end{array}}\right) }$ k-element subsets of $[n]=\{1,\dots n\}$ with two such subsets forming an edge if and only if they are disjoint. A k-subset X of [n] is called r-separated if for any two of its elements x, y we have $r\le |x-y|\le n-r$. The Schrijver graph $\textrm{SG}(n,k)$ is the subgraph of $\textrm{KG}(n,k)$ induced by vertices representing 2-separated sets.

Notice that arranging the elements of the basic set [n] around a cycle, the r-separated sets are exactly those any two elements of which have at least $r-1$ elements on both of the two arcs between them on this cycle.

The following theorem is a condensed version of the well-known results in [13, 16].

Theorem 1

(Lovász–Kneser theorem [13]; Schrijver theorem [16]) For every $n\ge 2k$ we have

$$\begin{aligned} \chi (\textrm{SG}(n,k))=\chi (\textrm{KG}(n,k))=n-2k+2. \end{aligned}$$

Moreover, $\textrm{SG}(n,k)$ is vertex-color-critical, i.e.,

$$\begin{aligned} \forall X\in V(\textrm{SG}(n,k)):\ \chi (\textrm{SG}(n,k) {\setminus }\{X\})=n-2k+1. \end{aligned}$$

The graphs $\textrm{KG}(n,k)$ and $\textrm{SG}(n,k)$ are widely investigated, cf. e.g. [1,2,3,4, 8,9,10, 12, 14, 18] to mention just a few more of the results related to them.

A graph homomorphism from graph F to graph G is an edge-preserving map $f:V(F)\rightarrow V(G)$, that is one for which $\{u,v\}\in E(F)$ implies $\{f(u),f(v)\}\in E(G)$. The existence of a graph homomorphism from F to G is denoted by $F\rightarrow G$.

Definition 2

The fractional chromatic number $\chi _f(G)$ of a graph G is

$$\begin{aligned} \chi _f(G)=\min \left\{ \frac{n}{k}: G\rightarrow \textrm{KG}(n,k)\right\} . \end{aligned}$$

Note that it follows from the definition that $F\rightarrow G$ implies $\chi _f(F)\le \chi _f(G)$, in particular this is always the case if F is a subgraph of G.

It is well-known that, denoting the independence number of graph G by $\alpha (G)$, one always has

$$\begin{aligned} \chi _f(G)\ge \frac{|V(G)|}{\alpha (G)} \end{aligned}$$

and equality holds whenever the graph is vertex-transitive, see e.g. [15] for this and other basic facts about the fractional chromatic number.

The independence number of Kneser graphs is given by the famous Erdős–Ko–Rado theorem.

Theorem 2

(Erdős–Ko–Rado [7])

$$\begin{aligned} \alpha (\textrm{KG}(n,k))={\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }. \end{aligned}$$

Moreover, for $n>2k$ the only independent sets of this size are the ones whose vertices represent k-element subsets that all contain a fixed element $i\in [n]$.

Corollary 3

(cf. e.g. [15])

$$\begin{aligned} \chi _f(\textrm{KG}(n,k))=\frac{n}{k}. \end{aligned}$$

Holroyd and Johnson [6] conjectured that a similar phenomenon to the one expressed by the Erdős–Ko–Rado theorem is also true for Schrijver graphs and more generally, for families of r-separated sets. This conjecture was proved by Talbot [19], below we state his result only for $r=2$.

Theorem 4

(Talbot [19])

$$\begin{aligned} \alpha (\textrm{SG}(n,k))={\left( {\begin{array}{c}n-k-1\\ k-1\end{array}}\right) }. \end{aligned}$$

Moreover, for $n>2k, n\ne 2k+2$ the only independent sets of this size in $\textrm{SG}(n,k)$ are the ones whose vertices represent k-element subsets that all contain a fixed element $i\in [n]$. For $n=2k+2$ other independent sets of this size exist, too.

Since $|V(\textrm{SG}(n,k))|=\frac{n}{k}{\left( {\begin{array}{c}n-k-1\\ k-1\end{array}}\right) }$ and obviously $\chi _f(\textrm{SG}(n,k))\le \chi _f(\textrm{KG}(n,k))$ the above theorem has the following immediate consequence already noted in [17].

Corollary 5

$$\begin{aligned} \chi _f(\textrm{SG}(n,k))=\frac{n}{k}. \end{aligned}$$

Let $C_n$ denote the cycle on vertex set [n] where the edges are formed by the pairs of vertices $\{i,i+1\}$ for $i\in \{1,\dots ,n-1\}$ and $\{1,n\}.$ In particular, the vertices of $\textrm{SG}(n,k)$ are exactly the independent sets of size k in $C_n$. (We will refer to this cycle as the defining cycle for $\textrm{SG}(n,k)$.)

Definition 3

We call a subset U of $V(C_n)$ well-spread if for any two sets $A,B\subseteq [n]$ with $|A|=|B|\le n-1$ satisfying that both induce a (connected) path in $C_n$ we have

$$\begin{aligned} \left| |A\cap U|-|B\cap U|\right| \le 1. \end{aligned}$$

The induced subgraph of $\textrm{SG}(n,k)$ on all well-spread k-subsets will be denoted by Q(n, k).

Example 1

For $n=11$ the set $U=\{1,4,8\}$ is well-spread but the set $U'=\{1,4,9\}$ is not as the size of its intersection with the 4-element sets $\{1,2,3,4\}$ and $\{5,6,7,8\}$ of consecutive vertices of $C_n$ differs by 2.

Now we state a basic property of the graphs Q(n, k).

Proposition 6

Let $n\ge 2k$ and $\ell \ge 2$ be any positive integer. Then the graphs Q(n, k) and $Q(\ell n,\ell k)$ are isomorphic.

Proof

Let $U \subseteq V(C_{\ell n})=[\ell n]$ be a well-spread set of size $\ell k$. We will show that rotating the set U n times along the cycle $C_{\ell n}$ it will map to itself and that will easily imply the statement.

Consider the n-element sets $A_i\subseteq [\ell n], i\in [\ell n]$ defined by

$$\begin{aligned} A_i:=\{i,i+1,\dots ,i+n-1\}, \end{aligned}$$

where the addition is intended modulo $\ell n$ (and 0 is represented by $\ell n$), that is the sets $A_i$ are exactly those subsets of $[\ell n]$ that induce a path of length $n-1$ in $C_{\ell n}$. First we show that the number of pairs in the set

$$\begin{aligned} \{(j, A_i):i\in [\ell n], j\in A_i\cap U\}, \end{aligned}$$

where $j\in [\ell n]$ and $A_i$ is one of the sets just defined is $\ell kn$. Indeed, since each $j\in U$ will appear in exactly n distinct $A_i$’s and $|U|=\ell k$, this claim follows. Since there are $\ell n$ distinct $A_i$’s, this means that if any $A_i$ would contain less than k elements of U, then some other $A_{i'}$ should contain more than k elements of U. However, this would imply that these two sets, $A_i$ and $A_{i'}$ are of the same size, both induce a path of $C_{\ell n}$ and the size of their intersection with U differs by at least 2. This would contradict the well-spread property of U, so this is impossible. The situation is similar if any $A_i$ would contain more than k elements of U, therefore we have

$$\begin{aligned} \forall i:|A_i\cap U|=k. \end{aligned}$$

This implies that we have $j\in U$ if and only if $j+n$ (mod $\ell n$) $\in U$ for every $j \in V(C_{\ell n})$ (otherwise $|A_j\cap U|=|A_{j+1}\cap U|$ would not be satisfied). Hence, if we have $X \in V(Q(\ell n,\ell k))$, that is X is a well-spread $(\ell k)$-subset of $[\ell n]$, and we rotate the defining cycle $C_{\ell n}$ exactly n times, then we get a vertex $Y \in Q(\ell n, \ell k)$, that is identical to X.

Let $g:V(C_{\ell n})\rightarrow V(C_n)$ be defined by

$$\begin{aligned} g: i\mapsto i-n\left\lfloor \frac{i-1}{n}\right\rfloor \end{aligned}$$

and for a subset $X=\{x_1,\dots ,x_{\ell k}\}\in {\left( {\begin{array}{c}[\ell n]\\ \ell k\end{array}}\right) }$ we let $\hat{g}(X)$ denote the set $\{g(x_1),\dots , g(x_{\ell k})\} \subseteq V(C_n)$. The foregoing implies that if $X\in V(Q(\ell n,\ell k))$ then $\hat{g}(X)\in V(Q(n,k))$. It also follows that for $X,Y\in V(Q(\ell n,\ell k))$ we have $\hat{g}(X)\cap \hat{g}(Y)=\emptyset \Leftrightarrow X\cap Y=\emptyset$. The latter means that $Q(n,k)\cong Q(\ell n,\ell k)$ and this proves the statement. $\square$

Example 2

Let $n=7, k=3$ and $\ell =2$. Then the statement of Proposition 6 is that Q(14, 6) is isomorphic to Q(7, 3). The vertices of Q(7, 3) are the 3-element sets

$$\begin{aligned} \{1,3,5\}, \{2,4,6\}, \{3,5,7\}, \{4,6,1\}, \{5,7,2\}, \{6,1,3\}, \{7,2,4\}. \end{aligned}$$

The vertices of Q(14, 6) are

$$\begin{aligned}{} & {} \{1,3,5,8,10,12\}, \{2,4,6,9,11,13\}, \{3,5,7,10,12,14\},\\{} & {} \{4,6,8,11,13,1\}, \{5,7,9,12,14,2\}, \{6,8,10,13,1,3\}, \{7,9,11,14,2,4\}. \end{aligned}$$

Note that the latter seven sets have the form $\{i,i+2,i+4,i+7,i+9,i+11\}$. Thus if we identify i and $i+7$ for every $i\in \{1,2,\dots ,7\}$ (the mapping g defined in the proof of Proposition 6 does essentially this by mapping both to i), then the seven vertices of Q(14, 6) become identical to the seven vertices of Q(7, 3).

Note that Proposition 6 implies that $Q(n,k)\cong Q\left( \frac{n}{\gcd (n,k)},\frac{k}{\gcd (n,k)}\right)$, therefore when discussing the properties of Q(n, k) we may assume that $\gcd (n,k)=1$.

Now we can already state our result on the vertex-criticality of Q(n, k) for the fractional chromatic number.

Theorem 7

Assume $n\ge 2k$, $\gcd (n,k)=1$ and let a and b be the smallest positive integers for which $ak=bn-1.$ The graph $Q(n,k)\subseteq \textrm{SG}(n,k)$ satisfies the following properties.

• $\chi _f(Q(n,k))=\frac{n}{k}=\chi _f(\textrm{SG}(n,k)).$

• $\forall U\in V(Q(n,k))\ \ \chi _f(Q(n,k){\setminus }\{U\})=\frac{a}{b}<\frac{n}{k}$, that is Q(n, k) is vertex-critical for the fractional chromatic number.

• Q(n, k) contains an induced subgraph isomorphic to Q(a, b).

For an example see Example 3 after Proposition 8.

For proving Theorem 7 it will be enough to show that if $\gcd (n,k)=1$ then the Q(n, k) subgraph is isomorphic to the circular (also called rational) complete graph $K_{n/k}$ that we define next.

Definition 4

The circular complete graph $K_{n/k}$ is defined as follows:

$$\begin{aligned}{} & {} V(K_{n/k}) = \{0,1, \dots , n-1 \}\\{} & {} E(K_{n/k}) = \{ \{i,j\}: k \le |i-j| \le n-k. \} \end{aligned}$$

The name circular complete graph refers to the central role of $K_{n/k}$ in the following definition.

Definition 5

The circular chromatic number $\chi _c(G)$ of a graph G is

$$\begin{aligned} \chi _c(G)=\min \left\{ \frac{p}{q}: p\le |V(G)|, G\rightarrow K_{p/q}\right\} . \end{aligned}$$

For detailed accounts on the circular chromatic number see the survey articles [20, 21] or Section 6.1 of the book [5].

Some important properties of the graphs $K_{n/k}$ are that they are vertex-transitive, that $K_{n/k}$ is homomorphically equivalent to $K_{n'/k'}$ whenever $\frac{n}{k} = \frac{n'}{k'}$ and that $\chi (K_{n/k}) = \bigg \lceil \frac{n}{k}\bigg \rceil$ (for these and further properties, see [5]). Note that the just stated homomorph equivalence cannot be an isomorphism if $n\ne n'$ since then $|V(K_{n/k})|=n\ne n'=|V(K_{n'/k'})|$. This is a crucial difference between the graphs $K_{n/k}$ and Q(n, k) and shows that the condition $\gcd (n,k)=1$ cannot be dropped in the following statement from which Theorem 7 already easily follows.

Proposition 8

Q(n, k) is isomorphic with the circular complete graph $K_{n/k}$ whenever $\gcd (n,k)=1$.

Proof of Theorem 7 from Proposition 8

It is known that the fractional chromatic number of $K_{n/k}$ is n/k since it is vertex transitive and has n vertices, while its independence number is k (cf. [5]). This already implies the first statement of Theorem 7. It is also known that removing any vertex x from $K_{n/k}$, the remaining graph $K_{n/k} - \{x\}$ is homomorphically equivalent to $K_{a/b}$, where a and b are the unique solution for $nb-ka = 1$, see Lemma 6.6 in [5], where a retract of $K_{n/k} - \{x\}$ which is isomorphic to $K_{a/b}$ is shown. This implies the second and third statements of Theorem 7. $\square$

Example 3

Let $n=8, k=3$. Figure 4 (see it at the end of Sect. 3) illustrates the vertices of Q(8, 3) and its isomorphism with $K_{8/3}$. The values of a and b as defined in Theorem 7 will be $a=5$, $b=2$. Deleting, say vertex $X_0 = \{1,3,6\}$ (cf. Figure 4 for the labeling of the vertices as $X_i$’s) the remaining graph admits a homomorphism to its subgraph induced by the vertices $X_2=\{3,5,8\}$, $X_3=\{1,4,6\}$, $X_4=\{2,5,7\}$, $X_5=\{3,6,8\}$, $X_6=\{1,4,7\}$ which is isomorphic to $Q(5,2) \cong K_{5/2} \cong C_5$ having fractional chromatic number 5/2.

Thus our main task is to prove Proposition 8. This is done in the next section.

3 Q(n, k) and $K_{n/k}$

Our argument will need the following alternative characterization of well-spread k-subsets.

Lemma 9

Let $U\subseteq V(C_n)$ be fixed and let $A,B\subseteq V(C_n)$ be any two sets inducing a path in the graph $C_n$ both starting and ending with vertices of $C_n$ that belong to U. The subset $U\subseteq V(C_n)$ is well-spread if and only if for any two such sets A, B that also satisfy $|A\cap U|=|B\cap U|$ we have

$$\begin{aligned} ||A|-|B||\le 1. \end{aligned}$$

Proof

Assume to the contrary that for two sets A, B as in the statement $||A|-|B|| \ge 2$ and w.l.o.g. assume that $|A|-2 \ge |B|$. Then, we can modify the subset A by removing its two extremal (that is starting and ending) vertices and $|A|-|B|-2$ more vertices from one end. This way we obtain a path $A'$ for which $|A'| = |B|$ but $||A'\cap U|-|B\cap U|| \ge 2$ which means that U is not well-spread by Definition 3.

For the other direction suppose that U is not well-spread. Then there exist $A,B\subseteq V(C_n)$ both inducing a path in $C_n$ for which $|A| = |B|$ but $||A\cap U|-|B\cap U|| \ge 2$. W.l.o.g. assume, that $|A\cap U| \ge |B\cap U|+2$. We may assume that A induces a path in $C_n$ that both starts and ends with elements of U because otherwise we can make both A and B shorter so that $|A\cap U|$ does not change while $|B\cap U|$ may only become smaller, so the relations $|A\cap U| \ge |B\cap U|+2$ and $|A|=|B|$ remain valid. Now extend B at both of its ends until it will contain a new element of U at both ends, that is we obtain a $B'$ which induces a path of $C_n$ that both starts and ends with elements of U and intersects U in $|B\cap U|+2$ elements. If this number is still less than $s:=|A\cap U|$ then extend $B'$ further (on one end) to make it a similar path containing exactly s elements of U. Since in the first step we extended B at both ends we certainly have $|B'|\ge |A|+2$, so A and $B'$ are two sets satisfying the conditions in the statement for which $||A|-|B'||\le 1$ does not hold. This completes the proof. $\square$

Example 4

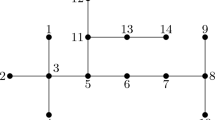
Let $n=11$ and $U=\{1,4,8\}$ which is easy to check to be well-spread according to Definition 3. Also, if $A=\{1,2,3,4\}$ and $B=\{4,5,6,7,8\}$, then they satisfy the conditions in Lemma 9 and also satisfy $||A|-|B||\le 1$. On the other hand, $U'=\{1,4,9\}$ is not well-spread as we already have seen in Example 1 as its intersection with the 4-element sets $\{1,2,3,4\}$ and $\{5,6,7,8\}$ differs by 2. Accordingly, the sets $A=\{1,2,3,4\}$ and $B':=\{4,5,6,7,8,9\}$ satisfy $|A\cap U'|=|B'\cap U'|$, they both start and end with elements of U, but do not satisfy $||A|-|B'||\le 1$. (See Fig. 1 for an illustration.)

Fig. 1

This figure shows sets U and $U'$ along with the sets A, B and $B'$ described in Example 4

Note that a set $U\subseteq V(C_n)$ need not be 2-separated for being well-spread. Moreover, the following observations hold for U and $\overline{U}:=V(C_n){\setminus } U$.

Observation 1

U is well-spread if and only if $\overline{U}$ is well-spread.

Proof

If $A,B\subseteq V(C_n),|A|=|B|$ and both of them induce a path, then

$$\begin{aligned} ||A\cap \overline{U}|-|B\cap \overline{U}||=||(|A|-|A\cap U|)| -|(|B|-|B\cap U|)||=||B\cap U|-|A\cap U||, \end{aligned}$$

so $||A\cap \overline{U}|-|B\cap \overline{U}||\le 1$ is equivalent to $||A\cap U|-|B\cap U||\le 1$. $\square$

Observation 2

If U is well-spread and $\gcd (n,|U|)=1$ (and $n > 2$) then exactly one of U and $\overline{U}$ is a 2-separated set.

Proof

Assume U is well-spread, then so is $\overline{U}$ as well by Observation 1. If $|U| = |\overline{U}| = n/2$ (in which case both |U| and $|\overline{U}|$ are 2-separated, alternatingly containing the vertices of $C_n$), then $\gcd (n,|U|)=n/2 \ne 1$. So w.l.o.g. U has less than n/2 elements. Then $\overline{U}$ must contain two adjacent vertices of the cycle $C_n$, say $\overline{u}_1$ and $\overline{u}_2$. If U would also contain two adjacent vertices of $C_n$, say $u_1$ and $u_2$ then taking $A=\{u_1, u_2\}$ and $B=\{\overline{u}_1, \overline{u}_2\}$ we would have two sets with $|A|=|B|=2$ for which $|A\cap U|=2$ and $|B\cap U|=0$, so U cannot be well-spread, a contradiction. $\square$

In what follows we denote by $f_i$ the i-fold clockwise rotation of the defining cycle. In particular, for $j\in V(C_n)$ we let $f_i(j)=i+j$, where addition is meant modulo n and 0 is represented by n. For a set $X=\{x_1,\dots ,x_h\}\subseteq V(C_n)$ $f_i(X)=\{f_i(x_1),\dots ,f_i(x_h)\}$.

Lemma 10

Let $U, W\subseteq V(C_n)$ be two well-spread sets of the same size k. Then there is a bijection between the elements of U and W that is given by a rotation of the cycle $C_n$. The graph Q(n, k) is vertex-transitive for any n and k and if $\gcd (n,k)=1$ then $|V(Q(n,k))|=n$.

Proof

Let U be a well-spread set of size k on the cycle $C_n$. If $gcd(n,k)\ne 1$ then we have already seen in the proof of Proposition 6 that every well-spread set maps to itself when we rotate the defining cycle $C_n$ by $\frac{n}{gcd(n,k)}$ elements. In particular, there are only $|V(Q(\frac{n}{gcd(n,k)},\frac{k}{gcd(n,k)}))|$ distinct well-spread subsets of $V(C_n)$ and they behave exactly as the well-spread sets we obtain on $V(C_{\frac{n}{gcd(n,k)}})$ when identifying every element of $V(C_n)$ that are $\frac{n}{gcd(n,k)}$ distance apart. This means that we may assume, that we do from now on, that $gcd(n,k)=1$.

A pair $x,y \in U$ will be called U-consecutive if one of the arcs between them does not contain any other $z \in U$. By Lemma 9 if $x,y\in U$ are U-consecutive, then x and y should be $q_0:= \left\lfloor \frac{n}{k}\right\rfloor$ or $\left\lfloor \frac{n}{k}\right\rfloor + 1$ distance apart on $V(C_n)$, that is, they are separated by $q_0-1$ or $q_0$ other elements of the cycle. If $n=q_0k+r_1$ then we have exactly $r_1$ U-consecutive pairs whose distance is $q_0+1$ and $k-r_1$ U-consecutive pairs that have distance $q_0$. Let $U=\{x_1,x_2,\dots ,x_k\}$, where the indices are chosen so that the pair formed by $x_i$ and $x_{i+1}$ is U-consecutive for all $i\in \{1,\dots ,k-1\}$ (and the indices increase as we go along the cycle $C_n$ in the clockwise direction). Let $(a_1,a_2,,\dots ,a_k)$ be the sequence of numbers that denote the distances of U-consecutive elements, that is, $a_i$ is the distance of $x_{i+1}$ from $x_i$ (in the clockwise direction) for each $i\in \{1,\dots ,k-1\}$ and $a_k$ is the (also clockwise) distance of $x_1$ from $x_k$. We identify two sequences $(a_1,\dots ,a_k)$ and $(b_1,\dots ,b_k)$ if one can be obtained from the other by cyclically permuting its elements, that is, if $(a_1,a_2,\dots ,a_k)=(b_{i+1},b_{i+2}\dots ,b_k,b_1,\dots ,b_i)$ for some i and call it the placement pattern of U. In case U has only 1 element, we consider its placement pattern to be (n). Notice that if two k-element subsets U and W of $V(C_n)$ have the same placement pattern then they must be rotations of each other, so to prove the first statement of the Lemma it is enough to prove that any two well-spread k-subsets of $V(C_n)$ should have the same placement pattern. This is what we do next.

Remove $q_0-1$ vertices of $C_n$ from the arcs between every pair of U-consecutive elements. This way we obtain a shorter cycle $C_{n-(q_0-1)k}$ on which U is still well-spread and $\overline{U} = V(C_{n-(q_0-1)k}) {\setminus } U$ is also well-spread by Observation 1. On this shorter cycle U is not 2-separated any more (since there were U-consecutive elements in U separated by exactly $q_0-1$ other elements that are now removed), so $\overline{U}$ is a 2-separated set by Observation 2. Using the notation $n_1:=n-(q_0-1)k=k+r_1$ we have $|\overline{U}|=n_1-|U|=r_1$ and the $\overline{U}$-consecutive elements of $\overline{U}$ are separated by $q_1:=\left\lfloor \frac{k+r_1}{r_1}\right\rfloor$ or by $q_1-1$ elements of U. Now performing the previous removal process with $C_{n_1}$ in the place of $C_n$ and its $r_1$-element subset $U_1:=\overline{U}$ in place of U is essentially performing a second step of the Euclidean algorithm with $k+r_1$ and $r_1$ (instead of k and $r_1$ but this is not an essential difference since $gcd(k+r_1,r_1)=gcd(k,r_1)=gcd(n,k)=1$). This means that now we remove $q_1-1$ elements of the current cycle between any two $U_1$-consecutive elements of $U_1$. That results in a cycle $C_{n_2}$ of length $n_2:=n_1-|U_1|(q_1-1)=n_1-(q_1-1)r_1$ and we have $U_1$ as its subset that is not 2-separated any more (since it did have $U_1$-consecutive elements separated by exactly $q_1-1$ other elements). Thus by Observation 2$U_2:=V(C_{n_2}){\setminus } U_1$ is 2-separated. It has size $n_2-|U_1|=n_1-q_1r_1=:r_2$, that is, $n_2=r_1+r_2$ and we clearly have $gcd(r_1+r_2,r_2)=gcd(r_1,r_2)=1$. We can go on iterating this process. Let $U_i$ be a 2-separated well-spread set on $C_{n_i}$ with $U_i$-consecutive elements having distance $q_i$ and $q_i+1$ on $V(C_{n_i})$. We remove $q_i-1$ elements not belonging to $U_i$ between any two $U_i$-consecutive elements of $U_i$. This way we obtain the cycle $C_{n_{i+1}}$ with $n_{i+1}=n_i-|U_i|(q_i-1)$, and assuming $gcd(n_i,|U_i|)=1$ we will have $gcd(n_{i+1},|U_i|)=1$. Define $U_{i+1}:=V(C_{n_{i+1}}){\setminus } U_i$. Then $U_{i+1}$ is 2-separated on $C_{n_{i+1}}$ and $gcd(n_{i+1},|U_{i+1}|)=1$ also holds, so we can continue until we will arrive to a situation where we have a cycle $C_m$ for some $m=n_h$ and our current 2-separated set $U_h$ will have only $\gcd (n,k)=1$ element. This process is illustrated on Fig. 2 for $n=14, k=5$.

We can place the remaining 1-element set on our final cycle $C_m$ into m different points, but the m different sets we can get this way are obviously just rotations of each other. In other words, their placement pattern is the same for every possible choice. Now observe that our removal process was completely deterministic, thus so is also its reversed process. This means that if at every step we make a note of how many elements were removed between two $U_i$-consecutive elements of the current $U_i$ on $C_{n_i}$ (these are simply the numbers $q_i-1$) to obtain the shorter cycle $C_{n_{i+1}}$ and $U_{i+1}=[n_{i+1}]{\setminus } U_i$, then getting back $U_i$ on $C_{n_i}$ from $U_{i+1}$ is also determined. It simply means that we should put back the appropriate number of removed elements between any pair of $U_i$-consecutive elements of $U_i$ on $C_{n_{i+1}}$. (This is also illustrated on Fig. 2 if we follow the three pictures from right to left.)

The foregoing implies that if the placement pattern of $U_{i+1}$ is uniquely determined, then so is the placement pattern of $U_i$. As we have seen the placement pattern of our final 1-element set $U_h$ is uniquely determined, thus the placement pattern of U itself on the original $C_n$ is also uniquely determined. This proves the first statement in the Lemma and implies $|V(Q(n,k))|\le n$.

We still have to prove the two statements in the last sentence of the Lemma, that is that $\gcd (n,k)=1$ also implies $|V(Q(n,k))|= n$ from which vertex-transitivity follows also for the other cases via Proposition 6.

If U is well-spread, then so is $f_i(U)$, so the latter is also a vertex of Q(n, k). Let t be the smallest positive integer i for which $f_i(U)=U$ for some vertex $U\in V(Q(n,k))$. Since we have $t\le n$, it is enough to prove that if $gcd(n,k)=1$, then t cannot be smaller than n. Thus we assume $gcd(n,k)=1$ and first we show that t is a divisor of n. Indeed, let $n=\ell t+r$, where $r<t$. Then for some vertex U we have $f_{\ell t}(U)=U$ and $f_r(U)=f_r(f_{\ell t}(U))=f_n(U)=U$ implying $r=0$ by the minimality of t. Thus t divides n.

Now we show that $\ell =\frac{n}{t}$ also divides k. Assume $f_t(u_1)=u_s$. Then we must have $f_t(u_i)=u_{i+s-1}$ for every $i\in \{1,\dots ,k\}$ (addition in the indices intended modulo k with k identified to 0) otherwise we could not have $f_t(U)=U$. Therefore $u_1=f_n(u_1)=f_{\ell t}(u_1)=u_{1+\ell (s-1)}$ showing $\ell (s-1)=k$ meaning that $\ell$ divides k. (Here we used that $f_n$ “winds around” $C_n$ exactly once.) Since $\ell$ also divides n, it should be 1, therefore $t=n$. $\square$

Fig. 2

The process in the proof of Lemma 10 performed for $n=14, k=5$. In the first picture we see the defining cycle $C_{14}$ where the elements of a well-spread 5-subset U are illustrated by empty circles. The second picture shows the situation after removing one of the one or two elements we have between any pair of U-consecutive elements of U. This results in the cycle $C_9$ of the second picture where the empty circles still denote the elements of U, while the elements of $U_1=[9]{\setminus } U$ are shown by the remaining 4 black dots. Then we remove one element of the original set U from between any pair of $U_1$-consecutive elements of $U_1$ to obtain the third picture with $C_{n_2}=C_5$ and the 1-element set $U_2$

The following Corollary is essentially implicit already in the proof of the previous Lemma, yet we state it separately for further reference.

Corollary 11

If $\gcd (n,k)=1$ then for every $X,Y\in V(Q(n,k))$ there is a unique rotation of $C_n$ that maps X to Y.

Proof

We have $|V(Q(n,k))| = n$, where the vertices can only be different by some rotation and we have exactly n possible rotations for each vertex. $\square$

Lemma 12

Let $\gcd (n,k)=1$ and $X,Y\in V(Q(n,k))$ be such that $XY\notin E(Q(n,k))$, that is, $X\cap Y\ne \emptyset$. Let $f:V(C_n)\rightarrow V(C_n)$ be the unique clockwise rotation moving X to Y and let i be an element of $X\cap Y$. Then the number of elements of Y on the arc of $C_n$ between i and f(i) (moving from i to f(i) in the clockwise direction) is independent of the choice of $i\in X\cap Y$.

Proof

Let $i, j \in X\cap Y$ and let A and B be the arcs of $C_n$ between i and f(i) and between j and f(j), respectively (i, f(i) and j, f(j) included). We obviously have $|A| = |B|$. Assume to the contrary of the statement that w.l.o.g. $|A \cap Y| + 1 \le |B \cap Y|$. Add the minimal number of consecutive vertices to A from $C_n$ in the same (clockwise) direction to get $A'$, such that $|A' \cap Y| = |B \cap Y|$. As $Y \in V(SG(n,k))$, we have that Y is a 2-separated set. So, since A ended with $f(i)\in Y$, $|A'| \ge |A| +2 = |B| +2$. Since $A'$ and B are arcs starting and ending with elements of Y and also containing the same number of elements of Y, this gives a contradiction by Lemma 9 with the well-spreadness of Y. $\square$

Definition 6

Under the conditions of Lemma 12 we call vertex $Y\in V(Q(n,k))$ a right j-jumper of vertex $X\in V(Q(n,k))$ if the number of elements of Y on the arc of $C_n$ strictly between i and f(i) for some $i\in X\cap Y$ (moving from i to f(i) in the clockwise direction) is $j-1$.

Fig. 3

This figure shows the well-spread set $X=\{1,4,8,11,15,18,22\}$ in the defining cycle $C_{24}$ together with its two right 4-jumpers Y and Z as discussed in Example 5. The elements $1\in X$ and $15\in Y$ are darkened on the first pair of pictures to emphasize that 1 will be mapped to 15 by the unique rotation moving X to Y. Similarly, $4\in X$ and $17\in Z$ are darkened in the second pair of pictures, because the unique rotation moving X to Z maps 4 to 17

Note that by Lemma 12 the previous definition is meaningful as it does not depend on the choice of $i\in X\cap Y$.

Example 5

Let $n=24, k=7$. Then $X=\{1,4,8,11,15,18,22\}$ and $Y=\{1,5,8,12,15,18,22\}$ are two intersecting well-spread subsets of [24], therefore two non-adjacent vertices of Q(24, 7). The unique rotation that moves X to Y is $f_{14}$, the 14-fold clockwise rotation of the defining cycle. In particular, it maps element 1 to 15 and Y has three other elements on the arc between these two, so Y is a right 4-jumper of X. There is one more right 4-jumper of X, namely $Z=\{4,7,11,14,17,21,24\}$. We have $Z=f_{13}(X)$, in particular, element 4 is moved to 17 and there are three other elements of Z on the clockwise arc connecting 4 to 17. (See Fig. 3 for an illustration.)

Corollary 13

If $gcd(n,k)=1$ then the degree of every vertex in Q(n, k) is $n-2k+1$.

Proof

We show that each vertex is non-adjacent to exactly $2k-2$ vertices different from itself from which the statement follows. By vertex-transitivity it is enough to show this to an arbitrary vertex $X\in V(Q(n,k))$.

If Y is another vertex for which $\{X,Y\}\notin E(Q(n,k))$, then there is some $u\in X\cap Y$, so Y is a right j-jumper of X for some j. Since any two vertices of Q(n, k) are rotations of each other, we know that $Y=f_i(X)$ for some i. We claim that if $gcd(n,k)=1$ and j is fixed then there are exactly two distinct values i can take in the set $\{1,2,\dots ,n-1\}$. Indeed, by Lemma 9 the length of the clockwise arc from u to $f_i(u)$ can take only two different values (differing by 1) and if $gcd(n,k)=1$ then two such distinct values exist indeed. (Otherwise for some $0<i<n$ and $U\in V(Q(n,k))$ we would have $f_i(u)\in U$ for every $u\in U$ implying $f_i(U)=U$. But we have already seen in the proof of Lemma 10 that this is impossible if $gcd(n,k)=1$.) Lemma 12 implies that j will not depend on the choice of $u\in X\cap Y$ which also implies that we cannot get the same $f_i$ for two different j’s. This means that the number of non-neighbors of an $X\in V(Q(n,k))$, not counting X itself, is exactly twice the number of possible values of j, that is $2(k-1)$ as claimed. $\square$

Now we show that $\textrm{SG}(n,k)$ itself is critical for the fractional chromatic number only in the cases already mentioned in the Introduction.

Corollary 14

We have $Q(n,k)=\textrm{SG}(n,k)$ if and only if $k=1, n=2k$, or $n=2k+1$. In particular, $\textrm{SG}(n,k)$ is vertex-critical for the fractional chromatic number in exactly these cases.

Proof

We know from Schrijver’s theorem, that $\chi (\textrm{SG}(n,k))=n-2k+2$. By Corollary 13 this is exactly one more than the (maximum) degree of Q(n, k). Thus, since $\textrm{SG}(n,k)$ is connected, Brooks’ theorem implies that in case $\textrm{SG}(n,k)=Q(n,k)$ we must have that $\textrm{SG}(n,k)$ is a complete graph or an odd cycle. This happens only in the cases listed in the statement and in those cases we indeed have $Q(n,k)=\textrm{SG}(n,k)$. $\square$

Now we have all the necessary lemmas to prove that our Q(n, k) graph is isomorphic to the circular complete graph $K_{n/k}$ whenever $\gcd (n,k)=1$.

Proof of Proposition 8

As $|V(Q(n,k))| = |V(K_{n/k})| = n$ and in both graphs each vertex has degree $n-2k+1$ it is enough to show a bijection between the vertex sets that maps non-adjacent vertices to non-adjacent vertices.

Fix a vertex $X_0\in V(Q(n,k))$ and let for every $i\in \{1,\dots ,n-1\}$ $X_i=f_i(X_0)$. Let $\varphi : V(Q(n,k)) \rightarrow V(K_{n/k})$ be defined by

$$\begin{aligned} \varphi : X_u \mapsto uk \ (\textrm{mod}\ n) \end{aligned}$$

This is a one-to-one function since $\gcd (n,k) = 1$. Now look at $X_u \ne X_v$ arbitrary non-adjacent vertices in Q(n, k). Let $\ell := |u-v|$ be their distance measured in rotations. If they are not adjacent, then one of them must be a right j-jumper of the other for some $j \in \{1,\dots ,k-1\}$. Since all right j-jumpers in Q(n, k) have to be either $\ell$ or $\ell -1$ rotations apart, or they all have to be $\ell$ or $\ell +1$ rotations apart one of the equations $(k-x)\ell +x(\ell +1) = jn$ or $(k-x)\ell +x(\ell -1) = jn$ has an integral solution with $0<x<k$. (This is because if we consider the clockwise arc from each $z\in X_u$ to the $z'\in X_u$ for which this arc contains j elements of $X_u$ including $z'$ but excluding z, then we cover $C_n$ exactly j times.) That means that $k\ell$ must belong to the same congruence class modulo n as x or $-x$, meaning that in the image the vertices $uk \ (\textrm{mod}\ n)$ and $vk \ (\textrm{mod}\ n)$, whose distance is $|u-v|k=\ell k$, should be either less than k, or more than $n-k$ apart, i.e., they are indeed non-adjacent in $K_{n/k}$. $\square$

Example 6

Let $n=8, k=3$. The vertices of Q(n, k) are the sets $\{1,3,6\}$, $\{2,4,7\}$, $\{3,5,8\}$, $\{1,4,6\}$, $\{2,5,7\}$, $\{3,6,8\}$, $\{1,4,7\}$, $\{2,5,8\}.$ Choosing $X_0$ to be $\{1,3,6\}$ the mapping given in the proof of Proposition 8 above sends the above vertices into vertices 0, 3, 6, 1, 4, 7, 2, 5 of $K_{8/3}$, respectively. Vertices belonging to disjoint sets in V(Q(8, 3)) are mapped to adjacent vertices of $K_{8/3}$. Since both graphs are 3-uniform, this shows that they are isomorphic. (For an illustration see Fig. 4.)

Fig. 4

This figure shows how the sets $X_i$ are mapped to the vertices of $K_{8/3}$ as described in Example 6

With the above we have completed the proof of Theorem 7. The following is an easy consequence of Proposition 8.

Corollary 15

For all $n\ge 2k$ we have

$$\begin{aligned} \chi (Q(n,k))=\bigg \lceil \frac{n}{k}\bigg \rceil . \end{aligned}$$

Proof

From Proposition 8 and the properties of the circular complete graphs it follows that

$$\begin{aligned} \chi (Q(n,k)) =\chi (K_{n'/k'}) =\bigg \lceil \frac{n'}{k'}\bigg \rceil =\bigg \lceil \frac{n}{k}\bigg \rceil , \end{aligned}$$

where $n'=\frac{n}{\gcd (n,k)}, k'=\frac{k}{\gcd (n,k)}$. $\square$

Note that Corollary 15 gives a second proof for Corollary 14 as $Q(n,k)=\textrm{SG}(n,k)$ implies the equality of their chromatic number and $n-2k+2 =\bigg \lceil \frac{n}{k}\bigg \rceil$ also implies that we must have $n=2k, n=2k+1$ or $k=1$.

4 Critical Edges

Here we are going to prove a strengthening of the second statement of Theorem 7.

Definition 7

An edge $\{i,j \}\in E(K_{n/k})$ of the circular complete graph $K_{n/k}$ is called a shortest edge if $|i-j|=k$ or $|i-j|=n-k$.

We remark that in terms of Q(n, k) a shortest edge of $K_{n/k}$ (when $gcd(n,k)=1$) belongs to one that connects a vertex $X\in V(Q(n,k))$ to a vertex that can be obtained by one rotation along the defining cycle. This can be read out from the proof of Proposition 8.

Theorem 16

An edge of $K_{n/k}$ is critical for the fractional chromatic number if and only if $gcd(n,k)=1$ and e is a shortest-edge. The same statement holds also if we change the word “fractional” to “circular” in the previous sentence. More precisely, if $\gcd (n,k)=1$, $e\in E(K_{n/k})$ and a, b are defined as in Theorem 7 then

$$\begin{aligned} \chi _f(K_{n/k}{\setminus }\{e\})=\chi _c(K_{n/k}{\setminus }\{e\}) =\left\{ \begin{array}{lll} \frac{a}{b}&{}&{}\text {if}\ e\ \text {is a shortest edge}\\ \frac{n}{k}&{}&{}\text {otherwise.} \end{array}\right. \end{aligned}$$

Proof

For both parameters $\chi _f(K_{n/k}) = \chi _c(K_{n/k}) =\frac{n}{k}$ is a trivial upper bound and $\chi _f(K_{a/b}) =\chi _c(K_{a/b}) = \frac{a}{b}$ is a lower bound, because $K_{a/b}$ is a subgraph of $K_{n/k}$ (see Lemma 6.6 in [5]). It is well-known that $\chi _f(G)\le \chi _c(G)$ holds for any graph G (cf. [5]), so it is enough to prove that if $gcd(n,k)>1$ or e is not a shortest edge then $\chi _f(K_{n/k}{\setminus }\{e\}) \ge \frac{n}{k}$, while if $gcd(n,k)=1$ and e is a shortest edge then $\chi _c(K_{n/k}{\setminus }\{e\}) \le \frac{a}{b}.$

If $gcd(n,k)>1$ then $K_{n/k}$ is homomorphically equivalent to $K_{n'/k'}$ for $n'=\frac{n}{gcd(n,k)}, k'=\frac{k}{gcd(n,k)}$ and since $|V(K_{n'/k'})|=n'<n=|V(K_{n/k})|$ in this case, $K_{n/k}$ cannot have any critical edges. Thus from now on we assume $gcd(n,k)=1$.

It is well-known that the independence number $\alpha (K_{n/k})=k$ (see this as a Claim within the proof of Theorem 6.3 in [5]). One can also easily show that if $n>2k$ (and for $n\ge 2k, gcd(n,k)=1$ this is always the case) the only independent sets of $K_{n/k}$ with size exactly k consist of k cyclically consecutive elements. That is, a largest independent set must have the form $\{i,i+1,\dots ,i+k-1\}$, where addition is intended modulo n. Indeed, if S is an independent set in $K_{n/k}$ having size k and $j\in S$ then $S\subseteq \{j-k+1,j-k+2,\dots ,j,j+1,\dots ,j+k-1\}$ and since $\forall h\in \{1,\dots ,k-1\}: \{j-h,j-h+k\}\in E(K_{n/k})$, $|S|=k$ implies that exactly one of the vertices $j-h$ and $j-h+k$ must belong to S for every $h\in \{1,\dots ,k-1\}$. If S was not a set of cyclically consecutive vertices, then we must have a $h\in \{2,\dots ,k-1\}$ for which $j-h\in S$ and $j-h+1\notin S$. Then $|S|=k, j-h+1\notin S$ implies $j-h+k+1\in S$ by the foregoing. However $j-h$ and $j-h+k+1$ are adjacent in $K_{n/k}$ (whenever $n>2k$) contradicting that S is an independent set.

Since $\chi _f(G)\ge \frac{|V(G)|}{\alpha (G)}$ and for $K_{n/k}$ we have equality because $K_{n/k}$ is vertex-transitive, $\chi _f(K_{n/k}{\setminus }\{e\})<\chi _f(K_{n/k})$ is possible only if $\alpha (K_{n/k}{\setminus }\{e\})>\alpha (K_{n/k})=k$. This requires that $e=\{x,y\}$ for two vertices x, y for which there exists a set $U\subseteq V(K_{n/k})$ of size $|U|=k-1$ for which $x,y\notin U$ and both $U\cup \{x\}$ and $U\cup \{y\}$ are k-element independent sets of $K_{n/k}$. Since k-element independent sets are formed by cyclically consecutive elements, this means that w.l.o.g. we must have $U=\{x+1,\dots ,x+k-1\}$ and $y=x+k$, in which case $\{x,y\}$ is a shortest edge.

What is left to prove is that if $gcd(n,k)=1$ and $e=\{x,x+k\}$ is a shortest edge then we have $\chi _c(K_{n/k}{\setminus }\{e\})\le \frac{a}{b}$. To show this we give a homomorphism from $K_{n/k}{\setminus }\{e\}$ to $K_{n/k}{\setminus }\{x\}$. By Lemma 6.6 in [5] we know that a retract of $K_{n/k}{\setminus }\{x\}$ is isomorphic to $K_{a/b}$, so by transitivity of the existence of homomorphisms we get that $K_{n/k}{\setminus }\{e\} \rightarrow K_{a/b}$. Let $f: V(K_{n/k}{\setminus }\{e\}) \rightarrow V(K_{n/k}{\setminus }\{x\})$ be the function $f(x) = x+1$ and $f(i) = i$ $\forall i\in [n]{\setminus }\{x\}$. Since the neighborhood of x in $V(K_{n/k}{\setminus }\{e\})$ is $\{x+k+1, \dots , x+n-k\}$ which is a subset of $\{x+k+1, \dots , x+n-k+1\}$, the neighborhood of $x+1$ in $V(K_{n/k}{\setminus }\{e\})$ and also in $V(K_{n/k}{\setminus }\{x\})$, f is indeed a homomorphism. $\square$