Abstract
In this paper, we consider the problem of path planning in a weighted polygonal planar subdivision. Each polygon has an associated positive weight which shows the cost of path per unit distance of movement in that polygon. The goal is to find a minimum cost path under the Manhattan metric for two given start and destination points. First, we propose an \(O(n^2)\) time and space algorithm to solve this problem, where n is the total number of vertices in the subdivision. Then, we improve the time and space complexity of the algorithm to \(O(n \log ^2 n)\) and \(O(n \log n)\), respectively, by applying a divide and conquer approach. We also study the case of rectilinear regions in three dimensions and show that the minimum cost path under the Manhattan metric is obtained in \( O(n^2 \log ^3 n) \) time and \( O(n^2 \log ^2 n) \) space.
Similar content being viewed by others
1 Introduction
Path planning (PP) problem is one of the fundamental problems in computer science and robotics. This problem is an interesting and challenging problem, and many variations of it have been studied (e.g., multi-robot path planning [2, 3], bi-objective path planning [4, 5], path planning among transient obstacles [6], etc.). In the classical version of PP, a workspace contains a set of obstacles, two start and destination points s and t are given, and the objective is to find an optimal path with minimum length from s to t which avoids all obstacles [7, 8]. However, in a general formulation of PP—called Weighted Region Problem (WRP)—which was first introduced by Mitchell and Papadimitriou [9], each obstacle has an associated weight and a path is allowed to enter them at extra costs. In fact, these weights represent the cost per unit distance of movement in the obstacles (or say weighted regions). This generalization of PP has a lot of applications, e.g., it can be used in self-driving cars navigation, robot motion planning [10], military purposes [11], crowd simulation and gaming applications [12]. An important theoretical result on WRP [13] has shown that this problem cannot be solved in the algebraic computation model over the rational numbers under the Euclidean metric. This result justifies the search for approximate solutions as opposed to exact ones. Motivated by this result, we provide a solution for WRP under the Manhattan metric, which is also an approximate solution for the Euclidean case.
Mitchell and Papadimitriou [9] introduced an \(\epsilon \)-optimal algorithm with running time of \( O(n^8 L) \), where n is the total number of vertices of polygonal regions, and L is the precision of problem’s instance. Precisely, \( L = O(\log (nNW/ \epsilon w)) \), where N is the maximum integer coordinate of any vertex of the subdivision, W and w are the maximum non-infinite and minimum non-zero integer weights assigned to the faces of the subdivision, and \(\epsilon \) > 0 is a user-specified error tolerance. The output is the shortest path from the starting point s to all vertices of the polygons with an error tolerance \(\epsilon \) under the Euclidean metric. Mata and Mitchell [11] have proposed an algorithm based on constructing a relatively sparse graph—called pathnet—that can search for paths that are close to optimal. They have proved that a pathnet of size O(nk) can be constructed in \( O(kn^3) \) time. As a matter of fact, the pathnet limits the paths that can extend from vertices with k cones at each vertex. Searching for a path on the constructed pathnet yields a path whose weighted length is at most (1 + \(\epsilon \)) of the optimal path. Precisely, \(\epsilon = \frac{W/w}{k\Theta _{min}} \), where W/w is the ratio of the maximum non-infinite weight to the minimum non-zero weight, and \(\theta _{min}\) is the minimum internal face angle of the subdivision. Moreover, Aleksandrov et al. [14] have introduced a data structure—called All points query (APQ)—which is used for finding \(\epsilon \)-optimal paths (\(\epsilon \in (0, 1)\)) for all-pairs queries on an instance of the WRP. Since APQ has a high construction time, it is mostly useful for answering many queries on the same scene. Also, one of the common techniques for obtaining approximate shortest paths is to position Steiner points for discretizing the edges of the triangular regions and then constructing a graph by connecting them. Finally, by using graph search algorithms such as Dijkstra [15, 16], an approximate minimum cost path is computed [17,18,19]. Among the approximation algorithms for solving WRP, a few of them compute paths whose lengths are close to optimal. On the other hand, these algorithms are theoretical algorithms. A recent work on WRP [20] has proposed a new practical method for solving this problem. The proposed method exploits Snell’s law of physical refraction and is able to return a path in a reasonable time that is very close to the optimum weighted shortest path. Furthermore, Aleksandrov et al. [21] have presented a (1 + \(\epsilon \))-approximation algorithm (\(\epsilon \in (0, 1)\)) for computing shortest paths in a weighted three-dimensional environment. Given n tetrahedra with positive weights in a polyhedral domain \({\mathcal {D}}\), their algorithm constructs (1 + \(\epsilon \))-approximation paths in \({\mathcal {D}}\) from a fixed source vertex to all vertices of \({\mathcal {D}}\) in \(O({\mathcal {C}}({\mathcal {D}})\frac{n}{\epsilon ^{2.5}}\log \frac{n}{\epsilon }\log ^3 \frac{1}{\epsilon })\) time, where \({\mathcal {C}}({\mathcal {D}})\) is a geometric parameter related to the aspect ratios of tetrahedra. Also, Tran et al. [22] have studied WRP in a three-dimensional environment. They present a path close to the optimal path, based on a user-defined parameter \(\delta \), between two points using Snell’s law of physical refraction. In addition, a recent work on WRP [23] has established an \(\Omega (n^d)\) lower bound on the maximum number of cell crossings a weighted shortest path could take in a d-dimensional polyhedral environment consisting of a linear number of O(n) polyhedral cells and cell faces.
There are several variants of WRP due to the metric and the shape of weighted regions. Lee et al. [24] have solved the problem in the presence of isothetic (rectilinear) obstacles (the boundary edges of obstacles are either vertical or horizontal line segments). They have presented two algorithms for finding the shortest path under the Manhattan metric. The first algorithm runs in \( O(n \log ^2 n) \) time and \( O(n \log n) \) space, and the second one runs in \( O(n \log ^{3/2} n) \) time and space. Also, Chen et al. [25] have presented some techniques for processing single-source and two-point rectilinear shortest path queries among disjoint rectilinear obstacles. If the starting point s is fixed, and the termination point t is arbitrary, then the query is called a single-source query, and if both s and t are arbitrary points, then the query is called a two-point query. For the single-source case, they construct a data structure in \( O(n \log ^{3/2} n) \) time and \( O(n \log n) \) space, where n is the number of vertices of the obstacles. This data structure is able to report the length of a shortest path between s and any query point in \( O(\log n) \) time and the actual shortest path in \( O(\log n + k) \) time, where k is the number of edges on the output path. For the two-point case, a data structure is constructed in \( O(n^2 \log ^2 n) \) time and space which is able to report the length of a shortest path between two arbitrary query points in \( O(\log ^2 n) \) time and the actual shortest path in \( O(\log ^2 n + k) \) time. Gewali et al. [26] have considered a special case of this problem in which there are only three types of regions: regions with weight of \(\infty \), regions with weight of 0 and regions with weight of 1. They have presented an algorithm in \( O(m + n \log n) \) time, where \( m \in O(n^2)\) is the number of visibility edges. Furthermore, they have presented an algorithm for the case that linear feathers are added. Precisely, edges of the subdivision are allowed to have arbitrary weights. Their algorithm for this case takes \( O(n^2) \) time for constructing a graph of size \( O(n^2) \) for searching the shortest path. In fact, it takes \( O(n^2 \log n) \) time for finding the shortest path. Gheibi et al. [27] have discussed the problem in an arrangement of lines. Due to the fact that this special case of the problem has unbounded regions, they have presented a minimal region—called SP-Hull—to bound the regions. This minimal region contains the minimum cost path from s to t. They construct SP-Hull in \( O(n \log n) \) time, where n is the number of lines in the arrangement. After constructing SP-Hull, an approximate minimum cost path is obtained by applying the existing approximation algorithms within bounded regions. Jaklin et al. [12] have analyzed the problem when the weighted regions are cells of a grid. They have also presented a new hybrid method—called vertex-based pruning—which is able to compute paths that are \(\epsilon \)-optimal inside a pruned subset of the scene.
In this paper, we consider a planar subdivision with arbitrary positive weights. First, we present an algorithm that constructs a planar graph in \( O(n^2) \) time with \( O(n^2) \) vertices and edges, where n is the total number of vertices of the subdivision. The constructed graph contains the minimum cost path between two points s and t in the plane, where the distances are measured under the weighted Manhattan metric—the length of a path is the weighted sum of Manhattan lengths of the sub-paths within each region. Then, we propose an improved algorithm based on a divide and conquer approach which constructs a graph in \(O(n \log ^2 n)\) time with \(O(n \log n)\) vertices and edges, which also contains the minimum cost path between s and t under the weighted Manhattan metric. Thus, we present two different algorithms for constructing two different graphs. In the second algorithm, the time and space complexity have been improved; however, the first one is a simple, easy to understand, and easy to implement algorithm. It has been shown that WRP is unsolvable over the rational numbers when the distances are measured under the weighted Euclidean metric [13]. To the best of our knowledge, this is the first result that presents exact algorithms for solving WRP under the Manhattan metric in a case where the regions are arbitrary simple polygons with positive weights. For finding the minimum cost path under the weighted Manhattan metric in the plane, our algorithms take \( O(n^2) \) and \(O(n \log ^2 n)\) time, respectively. These algorithms are also \(\sqrt{2}-\)approximation algorithms for the Euclidean metric. Also, we study WRP in three dimensions under the Manhattan metric. It has been shown that the problem of finding a shortest path under any \( L^P \) metric in a three-dimensional polyhedral environment is NP-hard [28]. Here, we consider a specific variation where the regions are rectilinear and show that the minimum cost path under the Manhattan metric is obtained in \( O(n^2 \log ^3 n) \) time and \( O(n^2 \log ^2 n) \) space.
This paper is organized in six sections. In Sect. 2, we provide some preliminaries and definitions related to WRP. In Sect. 3, we present the first algorithm for constructing a graph that contains the minimum cost path in a two dimensional work space. In Sect. 4, we present the improved algorithm based on a divide and conquer approach. In Sect. 5, we generalize the proposed algorithms for the case of rectilinear regions in three dimensions, and in Sect. 6, we draw a conclusion.
2 Preliminaries and Definitions
The problem of weighted region path planning, WRP, considered in this paper is defined as follows. Let \( {\mathcal {S}} \) be a subdivision of the plane into polygonal regions with n vertices and \( s, t \in {\mathcal {S}} \) be two start and destination points in the plane. Each region of \( {\mathcal {S}} \) has an associated positive weight. The weight of an edge \( e \in {\mathcal {S}} \) (boundary of regions) is assumed to be min\( \lbrace w_r, w_{r'} \rbrace \), where \( w_r \) and \( w_{r'} \) are the weights of regions incident to e. The goal is to find a minimum cost path between s and t, where the distances are measured under the weighted Manhattan metric—the length of a path is the weighted sum of Manhattan lengths of the sub-paths within each region.
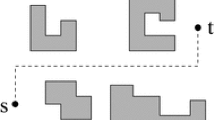
Let \(\pi _{st}\) denote a path between s and t which consists of some sub-paths between consecutive breakpoints. A breakpoint is a point on the path in which the path turns. We also consider s and t (two endpoints of the path) as breakpoints (see Fig. 1). Let \( \rho _1,\rho _2,\ldots , \rho _k \) be sub-paths between consecutive breakpoints of a path \(\pi _{st}\) in which each \( \rho _i \), for \(i = 1, 2, \ldots , \textit{k}\) lies completely within one region. If a part of a path \(\pi _{st}\) does not lie totally in one of the regions, we decompose it to some sub-paths. We denote \( d(\rho _i) \) as the Manhattan distance between two endpoints of \( \rho _i \). The weighted length of a path \(\pi _{st}\) under the Manhattan metric, denoted by \( d_w(\pi _{st}) \), is defined as:
where \( w_i \) is the weight of the region in which \(\rho _i\) lies.
A path \(\pi _{st}\) is called a horizontal (resp., vertical) path if it has a horizontal (resp., vertical) sub-path between only two consecutive breakpoints. Also, we say two horizontal (resp., vertical) paths are consecutive if and only if they have the same starting and termination points. This definition is used in Lemma 1.
The basic idea behind the proposed algorithms is to reduce the problem to a graph searching problem. Therefore, we first provide an algorithm for constructing a graph \( {\mathcal {G}}_1 \) that contains the minimum cost path under the weighted Manhattan metric. The constructed graph is a planar graph with \( O(n^2) \) vertices and edges, where n is the total number of vertices of the subdivision. For planar graphs with positive edge weights, Henzinger et al. [29] have given a linear-time algorithm to compute single-source shortest paths. By running this algorithm on \( {\mathcal {G}}_1 \), the minimum cost path between s and t under the Manhattan metric is obtained in \( O(n^2) \) time. Then, we propose an improved algorithm based on a divide and conquer approach for constructing a graph \( {\mathcal {G}}_2 \) that contains the minimum cost path under the weighted Manhattan metric. This graph has \( O(n \log n) \) vertices and edges and is not a planar graph (unlike the first graph). Dijkstra’s algorithm [15, 16] is able to find a shortest path on a graph between s and t in \( O(m + n \log n) \), where m and n are the number of edges and vertices of the graph, respectively. Thus, by running Dijkstra’s algorithm on \( {\mathcal {G}}_2 \), the minimum cost path between s and t under the Manhattan metric is obtained in \( O(n \log ^2 n) \) time.
For constructing \( {\mathcal {G}}_1 \), a horizontal line and a vertical line are considered passing through every vertex of the subdivision (s and t are also included in the set of vertices of the subdivision). By intersecting these horizontal and vertical lines with each other, at most two direct rectilinear paths between every two vertices of the subdivision on \( {\mathcal {G}}_1 \) are obtained. A rectilinear path is said to be a direct rectilinear path if it consists of at most three breakpoints (two of the breakpoints are two endpoints of the path). Precisely, If two vertices of the subdivision have the same x-coordinates or y-coordinates, there exists only one direct rectilinear path between them with two breakpoints; otherwise, there exist two direct rectilinear paths between them on \( {\mathcal {G}}_1 \), and each path has three breakpoints. First, we will prove that \( {\mathcal {G}}_1 \) contains the minimum cost path between s and t under the weighted Manhattan metric. Then, we will show that for every direct rectilinear path \( \pi _1 \) among the vertices of the subdivision on \( {\mathcal {G}}_1 \), there exists a path \( \pi _2 \) on \( {\mathcal {G}}_2 \) such that \( d_w(\pi _2) \le d_w(\pi _1) \). We say \( \pi _2 \) is an equivalent path of \( \pi _1 \).
Since a simple polygon with n vertices can be triangulated in \( O(n \log n) \) time and O(n) space [30], w.l.o.g. we assume all the regions to be triangular regions in all parts of the paper. The set \( V_{\mathcal {S}} \) indicates the set of vertices of the subdivision throughout the paper, which includes s, t, and the vertices of the triangular regions.
3 The First Algorithm: \( O(n^2) \) Time and Space
3.1 The Algorithm
For constructing a graph \( {\mathcal {G}}_1 = (V, E) \), which contains the minimum cost path between s and t under the Manhattan metric, a vertical line, denoted by \( VL(\alpha _i) \), and a horizontal line, denoted by \( HL(\alpha _i) \), are considered passing through every vertex \( \alpha _i \), for \(i = 1, 2, \ldots , \textit{n}\) in \( V_{\mathcal {S}} \). More precisely, for passing the horizontal lines through the vertices in \( V_{\mathcal {S}} \), we sort the vertices by y-coordinates first, and for passing the vertical lines, we sort the vertices in \( V_{\mathcal {S}} \) by x-coordinates. The set V consists of the vertices in \( V_{\mathcal {S}} \) and the intersection points among \( HL(\alpha _i) \) and \( VL(\alpha _j) \), for \(i, j = 1, 2, \ldots , \textit{n}\). Also, the intersection points among \( HL(\alpha _i) \) (resp., \( VL(\alpha _i) \)), for \(i = 1, 2, \ldots , \textit{n}\) and the edges of the triangular regions are added to V. The set E consists of the line segments between adjacent vertices in V that lie on the considered horizontal lines, vertical lines, or the edges of the triangular regions. For an edge \( (u, v) \in E \) which lies in a region with weight \( w_i \), let d(u, v) denote the Manhattan distance between two endpoints of the edge. The weight of the edge is equal to the product of d(u, v) and \( w_i \). Note that each edge lies completely within one region. This algorithm is described below.
The basic idea of the proposed algorithm is to extend four rays to the up, down, right and left directions (horizontal and vertical lines) at every vertex of the subdivision (\( V_{\mathcal {S}} \)). This idea has similarities to the vertical cell decomposition (VCD) method [8]. In this method, the free space is partitioned into a finite collection of one-dimensional and two-dimensional cells by extending rays upward and downward through free space. In this method, the rays are not allowed to enter obstacles, however, in our algorithm, the rays are extended to all parts of the subdivision since the paths are allowed to enter weighted regions at extra costs. Also, we extend rays to the four directions at every vertex, however, in the VCD method the rays are extended only upward and downward. In both methods, the motion planning problem is reduced to a graph search problem. In VCD method, a roadmap is constructed by selecting sample points from the cell centroids, however, in our algorithm, the graph is constructed by intersecting the rays with each other and also by the edges of the triangles.
Some of the edges of \({\mathcal {G}}_1\) which lie on an edge of a triangle are oblique. These edges are useful when two triangular regions are close to each other and the region among them has a lower weight than these triangles. A path that passes between these two triangles cannot be completely horizontal or vertical since it will enter the triangles. So it will be oblique and lie on one of the edges of the triangles (see the sub-path between \( b_4 \) and \( b_5 \) on Fig. 1).
According to the construction of the graph, some vertices and edges are added to the graph by vertical and horizontal lines passing through vertices in \( V_{\mathcal {S}} \). We call the part of the workspace which lies between two horizontal lines \( HL(\alpha _i) \) and \( HL(\alpha _{i+1}) \) (resp., two vertical lines \( VL(\alpha _i) \) and \( VL(\alpha _{i+1}) \)), for some i, a horizontal lane (resp., vertical lane) denoted by LH (resp., LV). So each LH (resp., LV) is bounded by two consecutive horizontal (resp., vertical) lines. Therefore, when we say the lines of an LH (resp., an LV), we mean these two lines.
The constructed graph of Fig. 1
For constructing the graph, we can use one of the line segments intersections algorithms [31, 32] which computes all k intersections among n line segments in the plane in \( O(n \log n + k) \) time. These intersection points are vertices of \({\mathcal {G}}_1\). After specifying the set of vertices of \({\mathcal {G}}_1\), the set of edges of \({\mathcal {G}}_1\) can be specified. It takes \( O(n^2) \) time to construct \({\mathcal {G}}_1\) since the graph has \( O(n^2) \) vertices and edges. The constructed graph of the workspace in Fig. 1 is shown in Fig. 2. For simplicity, we do not triangulate the white regions with weight 1 in these figures. Precisely, we can apply the proposed algorithm in a polygonal subdivision in which the regions are not triangular. The triangulation of the regions just helps us for showing that \({\mathcal {G}}_1\) contains the minimum cost path between s and t.
For computing the minimum cost path under the Manhattan metric between s and t, we can apply Dijkstra’s algorithm to \({\mathcal {G}}_1\). In this case, the minimum cost path is obtained in \( O(n^2 \log n) \) time. However, since \({\mathcal {G}}_1\) is a planar graph with positive edge weights, we can apply the algorithm presented by Henzinger et al. [29], which is a linear-time algorithm, to \({\mathcal {G}}_1\). Therefore, the minimum cost path is obtained in \( O(n^2) \) time.
3.2 Correctness Proof
Now, we show that the constructed graph contains the minimum cost path between s and t under the Manhattan metric. Since our metric for measuring the distance is Manhattan, we can convert any arbitrary path between s and t to a path that consists of vertical and horizontal line segments. In other words, when a sub-path between two consecutive breakpoints is oblique, we can replace it with two horizontal and vertical line segments where the cost of movement on these horizontal and vertical line segments is equal to the cost of movement along the oblique line segment. In a case where a sub-path lies between two close triangular regions and the region between these two triangular regions has a lower weight than these triangles, by applying this conversion, some parts of the horizontal and vertical line segments may lie in the triangular region with higher weight. In this case, we can replace the part which lies in a triangular region with higher cost with a line segment that lies on an edge of the triangles (see the sub-path between \( b_4 \) and \( b_5 \) on Fig. 1). Since the weight of each of the edges of the workspace is equal to the minimum weight of the regions that are incident to that edge, the cost of movement between two breakpoints on the replaced line segments is equal to the cost of movement along the oblique line segment. Therefore, a path between s and t can only consist of horizontal, vertical, and oblique line segments, the latter of which are located on the edges of the triangles. As a result, all the paths that we consider in the following lemmas consist of the above mentioned line segments. Our first objective is to prove the following lemma.
Lemma 1
Let \( \pi _1 \), \( \pi _2 \) and \( \pi _3 \) be three consecutive horizontal (or vertical) sub-paths from \( s' \) to \( t' \) which lie inside an LH (resp., an LV) and pass through \( k>0 \) triangular regions. If \( d_w(\pi _2 )< d_w(\pi _1 ), \ then\ d_w(\pi _3 ) < d_w(\pi _2 )\).
Proof
We consider the case \(k=2\), the proof is similar for any \(k>0\). For simple comparison among the sub-paths, let the points \( s' \) and \( t' \) lie on the same horizontal line segment. Assume w.l.o.g. that both triangles have vertical edges (see Fig. 3). The weighted lengths of \(\pi _1\), \(\pi _2\) and \(\pi _3\) are defined as follows (refer to Fig. 3 for the notations):
According to Fig. 3, \( a_1 = b_1 + x_1 \) and \( a_2 = b_2 - z_2 \). Due to the assumption that \( d_w (\pi _2) < d_w (\pi _1) \), we have the following inequality:
and due to the triangle similarity theorems, we have the following equations:
By applying the triangle similarity equations in the mentioned inequality and adding \( (w_1\times c_1) + (w_2\times b_2) \) to both sides of the inequality we get:
Thus, the weighted length of \(\pi _3\) is less than \(\pi _2\). In fact, the proof is based on the following equation:
and since \( \frac{h}{h'} \) is constant, we can generalize the proof for any \(k>0\) triangular regions between \( s' \) and \( t' \). Therefore, the lemma holds. \(\square \)
Note that inside an LH (resp., an LV), we can consider all the triangles to have vertical (resp., horizontal) edges since vertical (resp., horizontal) lines are considered passing through vertices in \( V_{\mathcal {S}} \). The result of this lemma helps us to show that there exists a shortest path between s and t under the Manhattan metric such that all the horizontal (resp., vertical) sub-paths between consecutive breakpoints in LHs (resp., LVs) lie on the lines of the LHs (resp., LVs). We call such a path, a perfect shortest path between s and t, denoted by \( \pi ^p_{st} \). Note that according to the principle of optimality, since \( \pi ^p_{st} \) is optimal in length, all of its sub-paths in LHs and LVs are also optimal in length.
Lemma 2
There exists a shortest path between s and t under the Manhattan metric such that, for any sub-path of the shortest path in an LH (resp., an LV), all the horizontal (resp., vertical) sub-paths between consecutive breakpoints lie on the lines of the LH (resp., LV).
Proof
Suppose the lemma for the case of a horizontal lane. Similarly, the lemma holds for a vertical lane. We consider \( s' \) as the entrance point to the LH and \( t' \) as the exit point. W.l.o.g. we consider that \( s' \) is on the left side of \( t' \). Due to the assumption that the path between s and t is optimal in length, any sub-path of this path is also optimal in length. Thus, the path between \( s' \) and \( t' \) is optimal in length. We consider a path between \( s' \) and \( t' \) where a horizontal sub-path between two consecutive breakpoints does not lie on the lines of the LH. We show that there exists an equivalent path between \( s' \) and \( t' \) such that all the horizontal sub-paths between consecutive breakpoints lie on the lines of the LH. We assume c and d as two consecutive breakpoints such that the horizontal sub-path between them does not lie on the lines of the LH (see Fig. 4). There are k triangular regions between c and d and the sub-path between these two breakpoints must pass through all k triangular regions (w.l.o.g. assume c and d are located on the edges of the triangles). We also assume that the path between \( s' \) and \( t' \) contains other two breakpoints—we call them a and b—which are on the lower line of the LH (these two breakpoints are also located on the edges of the triangles). For passing these triangles, a path can directly go from a to b. Since the path between \( s' \) and \( t' \) is optimal in length, the path which contains c and d (\(\pi _2\)) has less than or equal length to the case in which it goes directly from a to b (\(\pi _1\)). If \( d_w (\pi _1) = d_w (\pi _2) \), an equivalent path that does not contain the horizontal sub-path between c and d exists. If \( d_w (\pi _1) < d_w (\pi _2) \), it contradicts our assumption that the path between s and t is optimal in length. For the other case where \( d_w (\pi _2) < d_w (\pi _1) \), we consider another path that goes from a to e (a breakpoint on the upper line of the LH and on the edge of the left-most triangle) and then from e to f (a breakpoint on the upper line of the LH and on the edge of the right-most triangle) and then to b (\(\pi _3\)). According to Lemma 1, since \( d_w (\pi _2) < d_w (\pi _1) \), therefore, \( d_w (\pi _3) < d_w (\pi _2) \) and this contradicts our assumption that the path between s and t is optimal in length. Thus, the lemma holds. \(\square \)
According to Lemma 2, a path between the entrance (\( s' \)) and exit point (\( t' \)) of an LH (resp., an LV) is not optimal in length, unless there exists an optimal path in length such that all the horizontal (resp., vertical) sub-paths between consecutive breakpoints lie on the lines of the LH (resp., LV). Precisely, there is always a path \( \pi ^p_{s't'} \) in an LH (resp., an LV). According to the construction of the graph, lines of an LH (resp., an LV) are edges of \({\mathcal {G}}_1\), and a horizontal (resp., vertical) sub-path of a path \( \pi ^p_{s't'} \) between two consecutive breakpoints in an LH (resp., an LV) lies on the edges of \({\mathcal {G}}_1\).
Corollary 3
For any path \( \pi ^p_{s't'} \) in an LH (resp., an LV), the sub-paths between consecutive breakpoints cannot be simultaneously horizontal (resp., vertical) and lie between two lines of the LH (resp., LV).
Lemma 4
A breakpoint of a path \( \pi ^p_{s't'} \) in an LH (resp., an LV) is located on a line of an LH or an LV or possibly both.
Proof
We assume that b is a breakpoint in an LH which is not located on a line of the LH or a LV. According to Corollary 3, the line segment that is incident to b cannot be horizontal. Therefore, one of the line segments is vertical and the other one is located on an edge of a triangle. Since b is also located in an LV and is not located on one of the lines of the LV, the vertical line segment incident to b lies between the left and right lines of the LV, which contradicts Corollary 3. Thus, the lemma holds. \(\square \)
Lemma 4 shows that the breakpoints of the perfect shortest paths in LHs (resp., LVs) must lie on the lines of the LHs and LVs, meaning that they lie on the edges of \({\mathcal {G}}_1\) (since the lines of LHs and LVs are edges of \({\mathcal {G}}_1\)). The next step is to show that these breakpoints are located on the vertices of \({\mathcal {G}}_1\).
Lemma 5
For a path \( \pi ^p_{s't'} \) in an LH (resp., an LV), the breakpoints of the path are located on the vertices of \({\mathcal {G}}_1\).
Proof
According to Lemma 4, a breakpoint of a path \( \pi ^p_{s't'} \) in an LH (resp., an LV) is located on a line of an LH or an LV or possibly both. If a breakpoint is located on both a line of an LV and a line of an LH, it is on the intersection point of these two lines. Thus, it is on a vertex of \({\mathcal {G}}_1\). If it is only located on a line of an LH or an LV, and one of the incident line segments lies on a triangle edge, then the breakpoint is located on a vertex of \({\mathcal {G}}_1\) (since the intersection of an LH or LV line with a triangle edge is a vertex of \({\mathcal {G}}_1\)). Therefore, the breakpoints of a path \( \pi ^p_{s't'} \) are on the vertices of \({\mathcal {G}}_1\). \(\square \)
Lemma 5 shows that the breakpoints of a path \( \pi ^p_{s't'} \) in an LH (resp., an LV) are located on the vertices of \({\mathcal {G}}_1\). The next step is to show that a path \( \pi ^p_{s't'} \) under the Manhattan metric in an LH (resp., an LV) is on \({\mathcal {G}}_1\). To this end, we need to show that the edges of the path \( \pi ^p_{s't'} \) are on the edges of \({\mathcal {G}}_1\).
Lemma 6
A path \( \pi ^p_{s't'} \) in an LH (resp., an LV) is on \({\mathcal {G}}_1\).
Proof
According to Lemma 5, the breakpoints of a path \( \pi ^p_{s't'} \) in an LH (resp., an LV) are on the vertices of \({\mathcal {G}}_1\). Let e be an edge between two consecutive breakpoints. If e is on an edge of a triangle, it is on \({\mathcal {G}}_1\). Now we assume that e is in an LH and is not on \({\mathcal {G}}_1\). According to Corollary 3, e cannot be horizontal since it must lie on one of the lines of the LH, and the lines of LHs are edges of \({\mathcal {G}}_1\). Therefore, it is a vertical edge. Since it is also located in an LV and is not on \({\mathcal {G}}_1\), it is not on a line of the LV. Therefore, it contradicts Corollary 3. Thus, e is on \({\mathcal {G}}_1\). \(\square \)
According to Lemma 6, perfect shortest paths in LHs and LVs which are sub-paths of a path \( \pi ^p_{st} \) are on the constructed graph. Note that in all the lemmas, a path between s and t only consists of horizontal, vertical, and oblique line segments, the latter of which are located on the edges of the triangles. In the continuous workspace, an arbitrary path between s and t consists of line segments that are not in the form of the mentioned line segments. Finally, we prove that there exists a shortest path between s and t on \({\mathcal {G}}_1\).
Theorem 7
For a shortest path \(\pi _1\) under the weighted Manhattan metric in the continuous work space from s to t, there exists a path \(\pi _2\) from s to t on \({\mathcal {G}}_1\) such that \( d_w (\pi _2) \le d_w (\pi _1) \).
Proof
It is obvious that when the metric for measuring the distance is Manhattan, any arbitrary path in the continuous workspace can be converted to a path that consists of the three mentioned line segments without increment in the cost of the path. Thus, we convert \(\pi _1\) to \(\pi _1'\) such that the line segments in \(\pi _1'\) are in the form of the mentioned line segments. Obviously, \( d_w (\pi _1') = d_w (\pi _1) \). According to the principle of optimality, each sub-path of an optimal path in length is also optimal. Therefore, \( \pi _1' \) consists of optimal sub-paths in length in LHs and LVs. According to Lemma 2, for any shortest path in an LH (resp., an LV), there exists a path \( \pi ^p_{s't'} \), and due to the Lemma 6, perfect shortest paths in LHs and LVs are on \({\mathcal {G}}_1\). Thus, \( \pi _1' \) can be converted to a perfect shortest path \(\pi _2\) without increment in the cost of the path. Therefore, a path from s to t on \({\mathcal {G}}_1\) exists (\(\pi _2\)) whose weighted length is not greater than \(\pi _1\). \(\square \)
According to Theorem 7, \({\mathcal {G}}_1\) contains a shortest path from s to t under the weighted Manhattan metric. Since simple polygons can be triangulated in \( O(n \log n) \) time and O(n) space [30], workspaces with simple polygonal regions can be discretized by using the mentioned graph construction algorithm. Thus, the proposed algorithm solves WRP under the Manhattan metric.
Theorem 8
The weighted region problem in a planar polygonal subdivision with positive weights can be solved in \( O(n^2) \) time and space under the Manhattan metric, where n is the total number of vertices of the subdivision.
4 The Second Algorithm: \( O(n \log ^2 n) \) Time and \( O(n \log n) \) Space
By considering vertical and horizontal lines passing through vertices in \( V_{\mathcal {S}} \), we built a planar graph \( {\mathcal {G}}_1 \), which has \( O(n^2) \) vertices and edges. In this section, we will show that a graph \( {\mathcal {G}}_2 \), which contains the minimum cost path between two points s and t under the Manhattan metric, can be constructed by using a divide and conquer approach. The graph \( {\mathcal {G}}_2 \) has \( O(n \log n) \) vertices and edges.
4.1 The Algorithm
The basic idea for constructing a graph \({\mathcal {G}}_2 = (V, E)\), which contains the minimum cost path between s and t under the Manhattan metric, is using a divide and conquer approach. To be precise, at each recursive step of the algorithm, a vertical line \( x_{mid} \) is considered passing through the median of the x-coordinates of the vertices in \( V_{\mathcal {S}} \). This vertical line is called a vertical cut line. Let \( P_L \) and \( P_R \) denote the set of vertices in \( V_{\mathcal {S}} \) which are located on the left side and right side of the \( x_{mid} \), respectively. For each vertex \( p \in P_R \cup P_L\), the perpendicular projection \( p' \) on \( x_{mid} \) is computed and is added to V. Also, the edge \( (p, p') \) is added to E. Then, the intersection points among \( x_{mid} \) and the edges of the triangles are added to V. This procedure is done recursively on the set \( P_R \) and \( P_L \), respectively, until all the vertices in \( V_{\mathcal {S}} \) are located on a vertical cut line. (Note that the vertices in \( V_{\mathcal {S}} \) are included in V.) The above procedure is also done horizontally. Finally, an edge for every two consecutive vertices on all considered vertical and horizontal cut lines is created and added to E. Also, we create an edge for every two adjacent vertices in V where the line segment between them lies on an edge of a triangle. This algorithm is described below.
Note that for computing the perpendicular projections of the points in \( P_R \) and \( P_L \), the vertices in \( V_{\mathcal {S}} \) which are located on \( x_{mid} \) are also considered.
In the above algorithm, some edges which are added to E pass through more than one region. Precisely, an edge between a vertex in \( P_R \) or \( P_L \) and its perpendicular projection on \( x_{mid} \) may pass through more than one region. At the end of the algorithm, these edges are replaced with the edges which lie completely within one region and lie on these edges. For instance, suppose vertex p and its perpendicular projection \( p' \) on the vertical cut line \( x_{mid} \). The edge \( (p, p') \) passes through more than one region. In the horizontal procedure of the algorithm, a horizontal cut line passes through p and lies on the edge \( (p, p') \). According to the above algorithm, the intersection points among this horizontal cut line and the edges of the triangular regions are added to V. Also, an edge for every two consecutive vertices on this horizontal cut line is created. Therefore, we can replace the edge \( (p, p') \) with other edges which lie on \( (p, p') \) and lie completely within one region. Thus, each edge in E lies completely within one region. The weights of the edges in E are calculated similar to the first algorithm.
This algorithm is based on a divide and conquer approach which is similar to the algorithm SRP0 presented by Lee et al. [24]. In both algorithms, vertical and horizontal cut lines are considered passing through the median of the x-coordinates and y-coordinates of all the vertices of the subdivision, respectively. Also, in both algorithms, distances are measured under the weighted Manhattan metric. In SRP0, the edge \( (p, p') \) is added to E if it lies totally in one of the regions, however, in the proposed algorithm, the perpendicular projection of all the vertices on the right side and left side of the vertical cut lines (or above and below the horizontal cut lines) are computed and the edge between each vertex and its perpendicular projection is added to E. In SRP0, all the regions are isothetic, however, in the proposed algorithm, all the regions are triangular. Therefore, the proposed algorithm solves WRP under the Manhattan metric in a case where regions are arbitrary simple polygons (since a simple polygon with n vertices can be triangulated in \( O(n \log n) \) time and O(n) space [30]).
The set V consist of the set of vertices of the subdivision (\( V_{\mathcal {S}} \)), the set of the perpendicular projection points, and the set of the points that are generated by intersecting vertical cut lines and horizontal cut lines with the edges of the triangles. The set \( V_{\mathcal {S}} \) is of size O(n) . For constructing the graph, there exist \( O(\log n) \) recursive steps, each of which gives rise to O(n) perpendicular projection points and intersection points with the edges of the triangles. Therefore, \( {\mathcal {G}}_2 \) has \( O(n \log n) \) vertices and edges.
By sorting and sweeping sweep lines over the vertices in \( V_{\mathcal {S}} \), the set of vertices of the graph is obtained. For specifying the set of edges of the graph, the set V needs to be sorted. Therefore, it takes \( O(n \log ^2 n) \) time to construct \( {\mathcal {G}}_2 \). The vertical procedure of the algorithm of the workspace on Fig. 5a is shown in Fig. 5b–e. Also, the constructed graph of the workspace in Fig. 5a, based on the second algorithm, is shown in Fig. 5h. Note that, vertical and horizontal recursions are not done separately in the algorithm. Precisely, horizontal recursions are done after the termination of vertical recursions. However, for the sake of clarity, the final horizontal recursion of the workspace on Fig. 5a, is shown on Fig. 5h separately. In fact, the final horizontal recursion, based on the algorithm, is shown in Fig. 5g. Finally, by applying Dijkstra’s algorithm to \( {\mathcal {G}}_2 \), the minimum cost path between s and t under the Manhattan metric is obtained in \( O(n \log ^2 n) \) time.
4.2 Correctness Proof
In the first algorithm, by considering horizontal and vertical lines passing through vertices in \( V_{\mathcal {S}} \) and then adding their intersection points to the set of vertices of the graph, we built at most two direct rectilinear paths between every two vertices in \( V_{\mathcal {S}} \). In the second algorithm, there are no direct rectilinear paths between vertices in \( V_{\mathcal {S}} \) that are located on the left and right side of the vertical (resp., above and below the horizontal) cut lines. To be precise, at each recursive step of the second algorithm, these vertices are connected to each other by some points on the vertical and horizontal cut lines. Therefore, we will show that for every direct rectilinear path \( \pi _1 \) among the vertices in \( V_{\mathcal {S}} \) on \( {\mathcal {G}}_1 \), there exists a path \( \pi _2 \) on \( {\mathcal {G}}_2 \) such that \( d_w(\pi _2) \le d_w(\pi _1) \). In addition to direct rectilinear paths on \( {\mathcal {G}}_1 \), there exist other oblique sub-paths between vertices in \( V_{\mathcal {S}} \), which are on the edges of the triangles. Since both graphs contain these sub-paths, we will only consider rectilinear paths in the correctness proof.
Observation 9
The intersection point of a vertical cut line \( C_V \) and a horizontal cut line \( C_H \) is a vertex of \( {\mathcal {G}}_2 \) if and only if two vertices \( v_1 \) and \( v_2 \) in the set \( V_{\mathcal {S}} \) are on different sides of these two cut lines.
Proof
According to the second algorithm, vertical and horizontal cut lines are considered passing through vertices in \( V_{\mathcal {S}} \). Therefore, there is a vertex in \( V_{\mathcal {S}} \) above or below \( C_H \) which is located on \( C_V \). Due to the second algorithm, the perpendicular projection of this vertex on \( C_H \), which is on the intersection point of these two cut lines, is in the set of vertices of \( {\mathcal {G}}_2 \). \(\square \)
Lemma 10
For two vertices \( v_1 \) and \( v_2 \) in the set \( V_{\mathcal {S}} \) which are located on different sides of a vertical cut line \( C_V \) and a horizontal cut line \( C_H \), there exists a path between them on \( {\mathcal {G}}_2 \) such that the weighted length of this path under the Manhattan metric is not greater than the weighted length of the direct rectilinear path between them.
Proof
Let o be the intersection point of \( C_V \) and \( C_H \) and C(o) denote the translated coordinate system with o as the origin. W.l.o.g. assume \( v_1 \) and \( v_2 \) are located in the third and first quadrant of C(o) , respectively. The perpendicular projection of \( v_1 \) on \( C_V \) generates \( v'_1 \) and the perpendicular projection of \( v_2 \) on \( C_H \) generates \( v'_2 \). Also, let x be the intersection point of the horizontal line passing through \( v_1 \) and the vertical line passing through \( v_2 \), which is located in the fourth quadrant of C(o) (see Fig. 6). We will show that there is a path between \( v_1 \) and \( v_2 \) on \( {\mathcal {G}}_2 \) whose weighted length under the Manhattan metric is not greater than the direct rectilinear path between them (\( v_1 x v_2 \)). According to the second algorithm, the edges \( (v_1, v'_1) \) and \( (v_2, v'_2) \) are in the set of edges of \( {\mathcal {G}}_2 \). Therefore, we will only show that there exists a path between \( v'_1 \) and \( v'_2 \) on \( {\mathcal {G}}_2 \) whose weighted length under the Manhattan metric is not greater than \( v'_1 x v'_2 \). We consider the following cases.
Different cases in Lemma 10
Case 1. There is no vertex of \( V_{\mathcal {S}} \) in the fourth quadrant of C(o) . Therefore, \( v'_1 o v'_2 \) is an equivalent path of \( v'_1 x v'_2 \). According to Observation 9, since o is a vertex of \( {\mathcal {G}}_2 \), the edges \( (v'_1, o) \) and \( (v'_2, o) \) are in set of edges of \( {\mathcal {G}}_2 \).
Case 2. There is only one vertex y of \( V_{\mathcal {S}} \) in the fourth quadrant of C(o) which is located above \( v'_1 x \) and on the left side of \( v'_2 x \). The perpendicular projections of y on \( C_V \) and \( C_H \) generate points a and b, respectively, which are in the set of vertices of \( {\mathcal {G}}_2 \) (see Fig. 7a). In this case, \( v'_1 a y b v'_2 \) is an equivalent path of \( v'_1 x v'_2 \).
Case 3. There is only one vertex y of \( V_{\mathcal {S}} \) in the fourth quadrant of C(o) which is located above the line passing through \( v'_1 x \) and on the right side of \( v'_2 x \). The perpendicular projections of y on \( C_V \) and \( C_H \) generate points a and b, respectively. Also, the perpendicular projection of y on the line passing through \( v'_1 x \) generates point c (see Fig. 7b). These three points are in the set of vertices of \( {\mathcal {G}}_2 \). According to Lemma 1, \( v'_2 b c x \) or \( v'_2 o v'_1 x \) has less than or equal length to \( v'_2 x \). Therefore, \( v'_1 c b v'_2 \) or \( v'_1 o v'_2 \) is an equivalent path of \( v'_1 x v'_2 \).
Case 4. There is only one vertex y of \( V_{\mathcal {S}} \) in the fourth quadrant of C(o) which is located below \( v'_1 x \) and on the left side of the line passing through \( v'_2 x \). The perpendicular projections of y on \( C_V \) and \( C_H \) generate points a and b, respectively. Also, the perpendicular projection of y on the line passing through \( v'_2 x \) generates point c (see Fig. 7c). These three points are in the set of vertices of \( {\mathcal {G}}_2 \). According to Lemma 1, \( v'_1 a c x \) or \( v'_1 o v'_2 x \) has less than or equal length to \( v'_1 x \). Therefore, \( v'_1 a c v'_2 \) or \( v'_1 o v'_2 \) is an equivalent path of \( v'_1 x v'_2 \).
Case 5. There is only one vertex y of \( V_{\mathcal {S}} \) in the fourth quadrant of C(o) which is located below the line passing through \( v'_1 x \) and on the right side of the line passing through \( v'_2 x \). The perpendicular projections of y on \( C_V \) and \( C_H \) generate points a and b, respectively, which are in the set of vertices of \( {\mathcal {G}}_2 \) (see Fig. 7d). According to Lemma 1 and similar to Case 3 and Case 4, \( v'_1 a y b v'_2 \) or \( v'_1 o v'_2 \) is an equivalent path of \( v'_1 x v'_2 \).
Case 1 in Lemma 10 in which a part of an equivalent path between \( v'_1 \) and \( v'_2 \) lies on an edge of a triangle
In all the above cases, if the equivalent path between \( v'_1 \) and \( v'_2 \) enters a triangular region such that the weighted length of the path increases, we replace the part which lies in a triangular region with higher cost with a line segment which lies on an edge of the triangle. For instance, suppose case 1 in which an edge of a triangle intersects \( C_V \) and \( C_H \) in points a and b in the fourth quadrant of C(o) , respectively (see Fig. 8). In this case, \( v'_1 a b v'_2 \) is an equivalent path of \( v'_1 x v'_2 \) (since the weighted length of \( v'_1 o v'_2 \) under the Manhattan metric, is more than \( v'_1 x v'_2 \)). Note that, the weight of each of the edges of the triangles is equal to the minimum weight of the regions that are incident to that edge, and the intersection points of the vertical and horizontal cut lines with the edges of the triangles are vertices of \( {\mathcal {G}}_2 \).
For the other cases in which there are more than one vertex of \( V_{\mathcal {S}} \) in the fourth quadrant of C(o) , similar to the above cases, it is easy to show that there exists an equivalent path on \( {\mathcal {G}}_2 \). \(\square \)
According to the first algorithm, there are at most two direct rectilinear paths between every two vertices of \( V_{\mathcal {S}} \) on \( {\mathcal {G}}_1 \). Precisely, If two vertices in \( V_{\mathcal {S}} \) have different x-coordinates and y-coordinates, there are two direct rectilinear paths between them on \( {\mathcal {G}}_1 \). In Lemma 10, we showed that these paths have an equivalent path on \( {\mathcal {G}}_2 \). If two vertices in \( V_{\mathcal {S}} \) have the same x-coordinates or y-coordinates, there is only one direct rectilinear path between them on \( {\mathcal {G}}_1 \). According to the second algorithm, it is obvious that \( {\mathcal {G}}_2 \) contains these paths (since both vertices are located on the same horizontal or vertical cut line).
Theorem 11
For a shortest path \(\pi _1\) under the weighted Manhattan metric in the continuous work space from s to t, there exists a path \(\pi _2\) from s to t on \({\mathcal {G}}_2\) such that \( d_w (\pi _2) \le d_w (\pi _1) \).
Proof
According to Theorem 7, a path \(\pi '_2\) from s to t on \({\mathcal {G}}_1\) exists such that \( d_w (\pi '_2) \le d_w (\pi _1) \). \({\mathcal {G}}_1\) contains three kinds of paths between vertices in \( V_{\mathcal {S}} \): oblique paths, which are located on the edges of the triangles, direct rectilinear paths with two breakpoints, and direct rectilinear paths with three breakpoints. It is obvious that \({\mathcal {G}}_2\) contains direct rectilinear paths with two breakpoints. In Lemma 10, we showed that \({\mathcal {G}}_2\) contains equivalent paths for direct rectilinear paths with three breakpoints. Also, both graphs \({\mathcal {G}}_1\) and \({\mathcal {G}}_2\) contain oblique paths. Therefore, there exists a path \(\pi _2\) from s to t on \({\mathcal {G}}_2\) such that \( d_w (\pi _2) \le d_w (\pi '_2) \). Thus, \({\mathcal {G}}_2\) contains the minimum cost path under the Manhattan metric from s to t. \(\square \)
According to Theorem 11, \({\mathcal {G}}_2\) contains a shortest path from s to t under the weighted Manhattan metric. Thus, the proposed algorithm solves WRP under the Manhattan metric.
Theorem 12
The weighted region problem in a planar polygonal subdivision with positive weights can be solved in \( O(n \log ^2 n) \) time and \( O(n \log n) \) space under the Manhattan metric, where n is the total number of vertices of the subdivision.
By using the triangular inequality, it is easy to see that the length of a path under the Manhattan metric is at most \( \sqrt{2} \) times of the length of the path under the Euclidean metric. Thus, the proposed algorithms are also \( \sqrt{2} \)-approximation algorithms for solving WRP under the Euclidean metric.
Corollary 13
The first algorithm in \( O(n^2) \) time and space and the second algorithm in \( O(n \log ^2 n) \) time and \( O(n \log n) \) space are \( \sqrt{2} \)-approximation algorithms for solving the weighted region problem in a planar polygonal subdivision with positive weights under the Euclidean metric.
5 The Three-Dimensional Case
In this section, we consider WRP in three dimensions. It has been shown that the problem of finding a shortest path under any \( L^P \) metric in a three-dimensional polyhedral environment is NP-hard [28]. So, here we consider a specific variation where the regions are rectilinear.
Since the metric for measuring the distance is Manhattan, any oblique path between two consecutive breakpoints in three-dimensional space can be converted to three parallel line segments to x, y, and z axes without increment in the cost of the path. Thus, we consider all the paths to be rectilinear. First of all, we generalize the first algorithm for constructing a graph \( {\mathcal {G}}'_1 \) in three dimensions, which contains the minimum cost path between two points s and t. Then, we show that the second algorithm can also be generalized for constructing a graph \( {\mathcal {G}}'_2 \) in the case of rectilinear regions in three dimensions.
Let n be the total number of vertices of the subdivision and let (\( x_i \), \( y_i \), \( z_i \)), for \(i = 1, 2, \ldots , \textit{n}\) be the coordinates of the vertices of the regions (and of s and t) in sorted order (these points are sorted three times by x-, y- and z-coordinates). Let \( {\mathcal {P}} \) be the set of planes \( x = x_i \), \( y = y_i \), \( z = z_i \), for \(i = 1, 2, \ldots , \textit{n}\). The set of vertices of \( {\mathcal {G}}'_1 \) consists of the intersection points among at least three planes in \( {\mathcal {P}} \), and the set of edges of \( {\mathcal {G}}'_1 \) consists of the line segments between two adjacent vertices of the graph which lie on the intersection lines between at least two planes in \( {\mathcal {P}} \). The constructed graph has \( O(n^3) \) vertices and edges, and by applying Dijkstra’s algorithm to it, the minimum cost path under the Manhattan metric is obtained in \( O(n^3 \log n) \) time.
Similar to the definitions of LH and LV in the planar case, we define notations for the three-dimensional case. Let XYC denote a part of the workspace which is bounded by two planes \( p_i \) and \( p_{i+1} \) orthogonal to the x-axis and two planes \( p_j \) and \( p_{j+1} \) orthogonal to the y-axis in \( {\mathcal {P}} \), for some i and j, which is called an \( XY-container \). Note that an XYC is not bounded along the z-axis. XZC and YZC notations are defined similarly. Since all the paths are considered to be rectilinear, for any path in an XYC, there exists an equivalent path such that all the sub-paths between consecutive breakpoints along the z-axis are located on the planes bounding XYC. Precisely, according to the graph construction algorithm of \( {\mathcal {G}}'_1 \), each XYC consists of some cuboids where the cost of movement in every part of a cuboid is the same. Therefore, the sub-paths along the z-axis in a cuboid have the same cost when they are located either on the planes bounding XYC or inside the cuboid. Similar results hold for an XZC and a YZC. Thus, an equivalent path between s and t exists where all the sub-paths between consecutive breakpoints are located on the considered planes in \( {\mathcal {P}} \). Arguments similar to the ones used in Theorem 7 show that \( {\mathcal {G}}'_1 \) contains the minimum cost path between s and t under the Manhattan metric.
To construct \( {\mathcal {G}}'_2 \), first, some additional points are added to the set of vertices of the subdivision. These points are obtained by intersecting planes in \( {\mathcal {P}} \) with the edges of the regions. Since the number of such points is \( O(n^2) \), the number of vertices of subdivision becomes \( O(n^2) \) as well. This step is similar to the one that is used in the algorithm for computing a shortest path in three-dimensions between two points s and t among three-dimensional non-intersecting rectilinear obstacles under the Manhattan metric presented by Clarkson et al. [33]. Similar to the planar case, we denote the set of vertices of the subdivision by \( V_{\mathcal {S}} \). Then, the vertices in \( V_{\mathcal {S}} \) are added to the set of vertices of \( {\mathcal {G}}'_2 \). Next, \( {\mathcal {G}}'_2 \) is constructed as follows.
Let \( px_{mid} \) be the plane perpendicular to the x-axis passing through the median of the x-coordinates of the vertices in \( V_{\mathcal {S}} \). The vertices in \( V_{\mathcal {S}} \) on either side of \( px_{mid} \) are projected on this plane. Also, the line-segments between the vertices in \( V_{\mathcal {S}} \) on either side of \( px_{mid} \) and their projections on \( px_{mid} \) are added to the set of edges of \( {\mathcal {G}}'_2 \). Moreover, the edges and vertices of \( {\mathcal {G}}'_2 \) on the plane \( px_{mid} \) are computed using the planar algorithm. We then recursively do the above procedure on the set of vertices of the subdivision on either side of \( px_{mid} \) until all the vertices in \( V_{\mathcal {S}} \) are located on a plane perpendicular to the x-axis. The above procedure is repeated two more times according to the y-coordinates and z-coordinates of the vertices in \( V_{\mathcal {S}} \). The constructed graph has \( O(n^2 \log ^2 n) \) vertices and edges. To be precise, there are \( O(\log n) \) recursive steps, each of which gives rise to \( O(n^2 \log n) \) vertices and edges. Finally, by applying Dijkstra’s algorithm to \( {\mathcal {G}}'_2 \), the minimum cost path under the Manhattan metric is obtained in \( O(n^2 \log ^3 n) \) time.
In the generalization of the first algorithm, the workspace is partitioned into cuboids, and all of the vertices of the cuboids are in the set of vertices of \( {\mathcal {G}}'_1 \). Therefore, we only showed that an equivalent path between s and t exists such that all the sub-paths between consecutive breakpoints are located on the considered planes in \( {\mathcal {P}} \), and according to Theorem 7, the sub-paths on these planes are located on \( {\mathcal {G}}'_1 \). In the generalization of the second algorithm, by considering planes perpendicular to the x, y, and z axes in the divide and conquer procedure, the workspace is partitioned into cuboids as well. (Note that the planes that we consider in the divide and conquer procedure are the planes in \( {\mathcal {P}} \).) The difference here lies in the fact that some vertices of the cuboids are not in the set of vertices of \( {\mathcal {G}}'_2 \). Thus, we need to show that an equivalent path between s and t exists such that all the sub-paths between consecutive breakpoints are located on the considered planes in the divide and conquer procedure (or \( {\mathcal {P}} \)), and each breakpoint of the path between two sub-paths on two different planes is on \( {\mathcal {G}}'_2 \). Precisely, a breakpoint of the equivalent path where the path enters another plane should be on \( {\mathcal {G}}'_2 \).
The considered planes in the divide and conquer procedure are the planes in \( {\mathcal {P}} \). Therefore, according to the arguments in the generalization of the first algorithm, an equivalent path \( \pi '_{st} \) between s and t exists where the sub-paths between consecutive breakpoints are located on the considered planes in the divide and conquer procedure. Thus, we only need to show that an equivalent path \( \pi ''_{st} \) of \( \pi '_{st} \) exists where each breakpoint of \( \pi ''_{st} \) between two sub-paths on two different planes is on \( {\mathcal {G}}'_2 \).
Lemma 14
For a shortest path \( \pi '_{st} \), such that the sub-paths between consecutive breakpoints in \( \pi '_{st} \) are located on the considered planes in the divide and conquer procedure of the generalization of the second algorithm, there exists an equivalent path \( \pi ''_{st} \) such that each breakpoint of \( \pi ''_{st} \) between two sub-paths on two different planes is on \( {\mathcal {G}}'_2 \).
Proof
Since we considered all the paths to be rectilinear, there exist three kinds of sub-paths between consecutive breakpoints: sub-paths along the x-axis, sub-paths along the y-axis, and sub-paths along the z-axis. All these sub-paths in \( \pi '_{st} \) are located on the considered planes in the divide and conquer procedure. W.l.o.g. suppose the case where a sub-path of \( \pi '_{st} \) along the x-axis (\( s_x \)) is located on a plane perpendicular to the z-axis (\( p_z \)) and a sub-path along the z-axis (\( s_z \)) is located on a plane perpendicular to the x-axis (\( p_x \)). These two sub-paths are connected to each other in a breakpoint called b. We will show that b is located on a vertex of \( {\mathcal {G}}'_2 \) in the equivalent path \( \pi ''_{st} \). The sub-path \( s_z \) is also located in an XYC. Therefore, it can be moved inside the XYC without an increment in the cost of the path. If an edge of the XYC is located on an edge of a region at a point which is located on the plane \( p_z \), we can locate the sub-path \( s_z \) on that edge in the equivalent path \( \pi ''_{st} \). Therefore, b is located on an edge of a region, and since the intersections of the plane \( p_z \) with the edges of the subdivision are vertices of the subdivision, b is located on a vertex of \( {\mathcal {G}}'_2 \). Otherwise, the XYC is inside a region on the plane \( p_z \), and according to the graph construction algorithm, there exists a perpendicular projection which is located on the plane \( p_z \) and also on one of the planes that surrounds the XYC. Thus, b can be located on that point (the perpendicular projection) in the equivalent path \( \pi ''_{st} \). \(\square \)
According to Lemma 14 and arguments in the generalization of the first algorithm, there exists an equivalent path between s and t such that all the sub-paths between consecutive breakpoints are located on the considered planes in the divide and conquer procedure, and each breakpoint of the path between two sub-paths on two different planes is on \( {\mathcal {G}}'_2 \). Thus, arguments similar to the ones used in Theorem 11 show that \( {\mathcal {G}}'_2 \) contains the minimum cost path between s and t under the Manhattan metric.
Theorem 15
The weighted region problem in a three-dimensional workspace among rectilinear regions with positive weights can be solved in \( O(n^2 \log ^3 n) \) time and \( O(n^2 \log ^2 n) \) space under the Manhattan metric, where n is the total number of vertices of the subdivision.
6 Conclusion
In this paper, we considered a generalization of path planning problem—called weighted region problem (WRP). While the unsolvability of WRP over the rational numbers under the Euclidean metric has been proved [13], we proposed two polynomial time algorithms for solving WRP under the Manhattan metric, which are also \( \sqrt{2} \)-approximation solutions for the Euclidean case. The first one is a simple, easy to understand and easy to implement algorithm, however, in the second algorithm, the time and space complexity have been improved. In fact, it takes \( O(n \log ^2 n) \) time and \( O(n \log n) \) space to compute the minimum cost path between two start and destination points s and t under the Manhattan metric, where n is the total number of vertices in the subdivision. We also considered the case of rectilinear regions in three dimensions and generalized our algorithms for this case. It has been shown that \( \Omega (n \log n) \) is a lower bound for the shortest rectilinear path problem from s to t in the presence of disjoint isothetic rectangles [34]. Therefore, the lower bound of the problem considered in this paper is also \( \Omega (n \log n) \). Improving the time complexity and providing a better approximation factor for the Euclidean metric remain open.
References
Davoodi, M., Enamzadeh, H., Safari, A.: Path planning in a weighted planar subdivision under the Manhattan metric. In: CCCG, pp. 80–86 (2020)
Olcay, E., Schuhmann, F., Lohmann, B.: Collective navigation of a multi-robot system in an unknown environment. Robot. Auton. Syst. 132, 103604 (2020)
Davoodi, M., Abedin, M., Banyassady, B., Khanteimouri, P., Mohades, A.: An optimal algorithm for two robots path planning problem on the grid. Robot. Auton. Syst. 61(12), 1406–1414 (2013)
Davoodi, M.: Bi-objective path planning using deterministic algorithms. Robot. Auton. Syst. 93, 105–115 (2017)
Davoodi, M., Rouhani, A., Sanisales, M.: Path planning with objectives minimum length and maximum clearance. In: International Conference on Topics in Theoretical Computer Science, pp. 101–115. Springer (2020)
Maheshwari, A., Nouri, A., Sack, J.-R.: Shortest paths among transient obstacles. J. Combin. Optim. 43, 1036–1074 (2020)
Choset, H.M., Hutchinson, S., Lynch, K.M., Kantor, G., Burgard, W., Kavraki, L.E., Thrun, S.: Principles of Robot Motion: Theory, Algorithms, and Implementation. MIT press, Cambridge (2005)
LaValle, S.M.: Planning Algorithms. Cambridge University Press, Cambridge (2006)
Mitchell, J.S., Papadimitriou, C.H.: The weighted region problem: finding shortest paths through a weighted planar subdivision. J. ACM (JACM) 38(1), 18–73 (1991)
Chestnutt, J., Nishiwaki, K., Kuffner, J., Kagami, S.: An adaptive action model for legged navigation planning. In: 2007 7th IEEE-RAS International Conference on Humanoid Robots, pp. 196–202. IEEE (2007)
Mata, C.S., Mitchell, J.S.: A new algorithm for computing shortest paths in weighted planar subdivisions. In: Proceedings of the Thirteenth Annual Symposium on Computational Geometry, pp. 264–273 (1997)
Jaklin, N., Tibboel, M., Geraerts, R.: Computing high-quality paths in weighted regions. In: Proceedings of the Seventh International Conference on Motion in Games, pp. 77–86 (2014)
De Carufel, J.-L., Grimm, C., Maheshwari, A., Owen, M., Smid, M.: A note on the unsolvability of the weighted region shortest path problem. Comput. Geom. 47(7), 724–727 (2014)
Aleksandrov, L., Djidjev, H.N., Guo, H., Maheshwari, A., Nussbaum, D., Sack, J.-R.: Algorithms for approximate shortest path queries on weighted polyhedral surfaces. Discrete Comput. Geom. 44(4), 762–801 (2010)
Dijkstra, E.W., et al.: A note on two problems in connexion with graphs. Numer. Math. 1(1), 269–271 (1959)
Fredman, M.L., Tarjan, R.E.: Fibonacci heaps and their uses in improved network optimization algorithms. J. ACM (JACM) 34(3), 596–615 (1987)
Aleksandrov, L., Lanthier, M., Maheshwari, A., Sack, J.-R.: An \(\varepsilon \)-approximation algorithm for weighted shortest paths on polyhedral surfaces. In: Scandinavian Workshop on Algorithm Theory, pp. 11–22. Springer (1998)
Aleksandrov, L., Maheshwari, A., Sack, J.-R.: Determining approximate shortest paths on weighted polyhedral surfaces. J. ACM (JACM) 52(1), 25–53 (2005)
Sun, Z., Reif, J.H.: On finding approximate optimal paths in weighted regions. J. Algorithms 58(1), 1–32 (2006)
Tran, N., Dinneen, M.J., Linz, S.: Computing close to optimal weighted shortest paths in practice. In: Proceedings of the International Conference on Automated Planning and Scheduling, vol. 30, pp. 291–299 (2020)
Aleksandrov, L., Djidjev, H., Maheshwari, A., Sack, J.-R.: An approximation algorithm for computing shortest paths in weighted 3-d domains. Discrete Comput. Geom. 50(1), 124–184 (2013)
Tran, N., Dinneen, M.J., Linz, S.: Close weighted shortest paths on 3d terrain surfaces. In: Proceedings of the 28th International Conference on Advances in Geographic Information Systems, pp. 597–607 (2020)
Bauernöppel, F., Maheshwari, A., Sack, J.-R.: An \(\omega (nd)\) lower bound on the number of cell crossings for weighted shortest paths in d-dimensional polyhedral structures. Comput. Geom. 107, 101897 (2022)
Lee, D., Yang, C.-D., Chen, T.: Shortest rectilinear paths among weighted obstacle. Int. J. Comput. Geom. Appl. 1(02), 109–124 (1991)
Chen, D.Z., Klenk, K.S., Tu, H.-Y.T.: Shortest path queries among weighted obstacles in the rectilinear plane. SIAM J. Comput. 29(4), 1223–1246 (2000)
Gewali, L.P., Meng, A.C., Mitchell, J.S., Ntafos, S.: Path planning in 0/1/\(\infty \) weighted regions with applications. ORSA J. Comput. 2(3), 253–272 (1990)
Gheibi, A., Maheshwari, A., Sack, J.-R.: Weighted region problem in arrangement of lines. In: CCCG, pp. 123–128 (2013)
Canny, J., Reif, J.: New lower bound techniques for robot motion planning problems. In: 28th Annual Symposium on Foundations of Computer Science (SFCS 1987), pp. 49–60. IEEE (1987)
Henzinger, M.R., Klein, P., Rao, S., Subramanian, S.: Faster shortest-path algorithms for planar graphs. J. Comput. Syst. Sci. 55(1), 3–23 (1997)
de Berg, M., van Kreveld, M., Overmars, M., Schwarzkopf, O.C.: Polygon triangulation. In: Computational Geometry, pp. 45–61. Springer, Berlin (2000)
Balaban, I.J.: An optimal algorithm for finding segments intersections. In: Proceedings of the Eleventh Annual Symposium on Computational Geometry, pp. 211–219 (1995)
Chazelle, B., Edelsbrunner, H.: An optimal algorithm for intersecting line segments in the plane. J. ACM (JACM) 39(1), 1–54 (1992)
Clarkson, K., Kapoor, S., Vaidya, P.: Rectilinear shortest paths through polygonal obstacles in o (n (log n) 2) time. In: Proceedings of the Third Annual Symposium on Computational Geometry, pp. 251–257 (1987)
de Rezende, P.J., Lee, D., Wu, Y.-F.: Rectilinear shortest paths in the presence of rectangular barriers. Discrete Comput. Geom. 4(1), 41–53 (1989)
Funding
The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Also, the authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A very preliminary version appeared at CCCG 2020 [1].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Davoodi, M., Safari, A. Path Planning in a Weighted Planar Subdivision Under the Manhattan Metric. Graphs and Combinatorics 40, 16 (2024). https://doi.org/10.1007/s00373-023-02744-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00373-023-02744-7