Shortest Directed Networks in the Plane

Abstract

Given a set of sources and a set of sinks as points in the Euclidean plane, a directed network is a directed graph drawn in the plane with a directed path from each source to each sink. Such a network may contain nodes other than the given sources and sinks, called Steiner points. We characterize the local structure of the Steiner points in all shortest-length directed networks in the Euclidean plane. This characterization implies that these networks are constructible by straightedge and compass. Our results build on unpublished work of Alfaro, Campbell, Sher, and Soto from 1989 and 1990. Part of the proof is based on a new method that uses other norms in the plane. This approach gives more conceptual proofs of some of their results, and as a consequence, we also obtain results on shortest directed networks for these norms.

1 Introduction

In the well-studied Euclidean Steiner problem, a finite set of points in the plane is given, and the problem is to find a shortest network interconnecting all points. Its fascinating history is given a definitive treatment by Brazil et al. [4]. What distinguishes this problem from the well-known Minimal Spanning Tree problem, is that such a network (necessarily a tree) may contain new points, called Steiner points. The degree of such a Steiner point is always 3, and the angle between any two incident edges is $120^\circ$. In fact, any such tree is constructible using straightedge and compass. Despite the simplicity of this local structure, it is NP-hard to compute such a shortest network. On the other hand, there is an exact algorithm (GeoSteiner) that can feasibly compute these networks for given point sets of size in the thousands. For more detail, see Chapter 1 of Brazil and Zachariasen [5].

A directed version of this problem was introduced by Frank Morgan for undergraduate research at Williams College in the late 1980s [1,2,3]. In this problem, a set of sources and a set of sinks in the plane are given, and the object is to find a shortest directed network containing a directed path from each source to each sink. As these directed networks are not necessarily trees, they are much harder to study, and even their existence is non-trivial [2]. See Fig. 4(b) for an example of a shortest directed network that has a cycle. There is no known algorithm for finding such networks, and as a first step, the local structure of such networks has to be described. There are some partial results in [1, 3]. The main contribution of this paper is to complete their results with a complete description of the local structure of the directed edges incident to a Steiner point in a shortest directed network (Theorem 1). We also find new proofs of some of their results. Our characterization easily implies that any shortest directed network in the plane is constructible by straightedge and compass (Corollary 2), and that there exists an algorithm (even though prohibitively inefficient) that can compute them (Corollary 3).

We make use of norms other than the Euclidean, which on the one hand gives conceptually simpler proofs of some of the results in [1], and on the other hand also give examples of shortest directed networks for these norms.

2 Main Results

The digraphs $G=(V,E)$ in this paper will be simple, that is, they are without loops. We call the elements of V nodes. The elements of E, which we call directed edges or just edges, are directed pairs of distinct nodes, and denoted by $x\mathord {\rightarrow }y$, where x is the tail and y the head of the directed edge. The indegree of a node x is the number $\text{deg} ^-(x)$ of directed edges in E with head x, and the outdegree the number $\text{deg} ^+(x)$ of directed edges in E with tail x. The degree of x is the ordered pair $\text{deg} (x)=(\text{deg} ^-(x),\text{deg} ^+(x))$.

Given a digraph $G=(V,E)$ and nodes $a,b\in V$, a directed path from a to b is a finite sequence of distinct vertices $a=x_1,x_2,\ldots ,x_n=b$ ($n\ge 1$) such that $x_i\mathord {\rightarrow }x_{i+1}\in E$ for each $i=1,\ldots ,n-1$. We allow a path with a single vertex. We call any directed path in G from a to b an (a, b)-path. Given subsets $A,B\subseteq V$, we say that G is an (A, B)-network if G contains an (a, b)-path for each $a\in A$ and $b\in B$. We do not require A and B to be disjoint. The nodes in $V\setminus (A\cup B)$ are called the Steiner points of the (A, B)-network. We call an (A, B)-network simple if for each Steiner point $s\in V$, $\text{deg} ^-(s)\ge 1$, $\text{deg} ^+(s)\ge 1$ and $\text{deg} ^-(s)+\text{deg} ^+(s)\ge 3$.

Let $X=(\mathbb {R}^d,\Vert \cdot \Vert )$ be a d-dimensional normed space. A directed network or geometric digraph in X is an embedding of a digraph $G=(V,E)$ into X such that each node in V is represented as a point in X and where each directed edge is drawn as a straight-line segment from its tail to its head. We allow distinct nodes in V to be represented by the same point in X. The length of a directed edge $x\mathord {\rightarrow }y$ in a directed network is its length in the norm $\Vert x\mathord {\rightarrow }y\Vert :=\Vert x-y\Vert$. The length of a network G is the sum of the lengths of its directed edges and denoted $\Vert G\Vert := \sum _{x\mathord {\rightarrow }y\in E} \Vert x\mathord {\rightarrow }y\Vert$. We will sometimes work with the same network in $\mathbb {R}^d$ but with more than one norm. To avoid confusion, we will always use subscripts to distinguish between different norms. These norms are all introduced in Sect. 3.

Note that any (A, B)-network in X can be modified into a simple (A, B)-network without increasing its length. Indeed, given any Steiner point s of the (A, B)-network G, if $\text{deg} ^-(s)=0$ or $\text{deg} ^+(s)=0$, then s and its incident directed edges can be removed from G, and the new directed graph remains an (A, B)-network. Also, if $\text{deg} ^-(s)=\text{deg} ^+(s)=1$, then s and its incident directed edges $x\mathord {\rightarrow }s$ and $s\mathord {\rightarrow }y$ can be replaced by a single directed edge $x\mathord {\rightarrow }y$ to obtain an (A, B)-network $G'$ with $\Vert G'\Vert \le \Vert G\Vert$. By applying these two procedures repeatedly, we obtain a simple (A, B)-network after finitely many steps.

Given finite sets A and B of points from X, a shortest (A, B)-network is an (A, B)-network of minimum length among all (A, B)-networks in X. From the remarks in the previous paragraph, we only have to consider simple (A, B)-networks when finding shortest ones. It is not obvious that any finite sets of points A and B in a finite-dimensional normed space X has a shortest (A, B)-network, as an (A, B)-network can have cycles and there is no immediate upper bound for the number of Steiner points in such a network. However, it has been shown that the number of Steiner points in a simple (A, B)-network is bounded by $O(|A|+|B|)$ in the Euclidean plane [2] and $O(|A|^2|B|+|A||B|^2)$ in any normed space (or indeed, any metric space) [8]. This, together with a compactness argument, shows that for any given finite subsets A and B of a finite-dimensional normed space, there always exists at least one shortest (A, B)-network.

Fig. 1

$\text{deg} (s)=(1,2)$ or (2, 1)

Fig. 2

$\text{deg} (s)=(2,2)$: two possibilities

Fig. 3

$\text{deg} (s)=(2,3)$ or (3, 2)

Partial results on the local structure of Steiner points in a shortest (A, B)-network in the Euclidean plane can be found in [1, 3]. Our main result is a completion of these partial results into a full characterization.

Theorem 1

The following is a complete list of all possibilities for the local geometric structure of a Steiner point s in a shortest (A, B)-network G in the Euclidean plane.

• 1. ${deg} (s)=(1,2)$ or (2, 1). The three directed edges incident to s are pairwise at $120^\circ$ angles (Fig. 1).

• 2. ${deg} (s)=(2,2)$. One of the following two cases:

  • (a) Opposite pairs of directed edges lie on two straight lines, with directed edges alternating between incoming and outgoing (Fig. 2(a)).

  • (b) Opposite pairs of directed edges lie on two straight lines, directed edges do not alternate between incoming and outgoing,  and the angles between the two incoming directed edges and between the two outgoing directed edges are $\ge 120^\circ$(Fig. 2(b)).

• 3. ${deg} (s)=(2,3), (3,2)$.

  In the case (2, 3),  the three outgoing directed edges are pairwise at $120^\circ$ degrees,  and the two incoming directed edges lie on a straight line (Fig. 3(a)). The case (3, 2) is exactly opposite: the three incoming directed edges are pairwise at $120^\circ$ degrees,  and the two outgoing directed edges lie on a straight line (Fig. 3(b)).

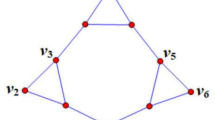
• 4. ${deg} (s)=(3,3)$. The incoming and outgoing edges alternate,  with consecutive directed edges at $60^\circ$ angles (Fig. 4(a)).

Fig. 4

Sources and sinks are alternating vertices of a regular hexagon. Since the directed network in a with $\text{deg} (s)=(3,3)$ is shortest, the directed network in b is also shortest and contains a cycle [1]

Case 1 in the above theorem was well known and follows easily from classical results in elementary geometry (see Lemmas 15 and 16). Case 2(b) was known [3, Theorem 2.4] and we do not prove it in this paper, but case 2(a) is new, and is proved as Theorem 19 in Sect. 4. We present a proof that uses a different norm on $\mathbb {R}^2$ and that gives as a byproduct results for the $\ell _1$-plane (Corollaries 20 and 21 below).

Case 3 is new and the hardest part of the theorem. We devote Sect. 6 to its proof. It was known in the special case where the two incoming directed edges (where $\text{deg} (s)=(2,3)$) are orthogonal to one of the outgoing directed edges [1]. Case 4 was known [1], but we give a different proof in Sect. 5, this time using the norm with the regular hexagon as unit ball (Theorem 23), and again with a corollary for shortest direct networks in this norm (Corollary 24).

An immediate consequence of Theorem 1 is that shortest directed networks can be constructed with straightedge and compass.

Corollary 2

Given two finite sets A and B of points in the Euclidean plane,  any shortest (A, B)-network can be constructed from A and B by straightedge and compass.

Proof

Consider the underlying graph G of a shortest (A, B)-network. Since we can easily construct a Steiner point of degree (2, 2) from its neighbours, we may without loss of generality replace each Steiner point of degree 4 and its incident edges by two edges joining opposite neighbours. We can similarly replace the incoming (outgoing) edges of a Steiner point of degree (2, 3) (degree (3, 2), respectively) by an edge joining the two neighbours. What remains are Steiner points with three neighbours joined by edges that are pairwise at $120^\circ$. It is then clear that we can decompose G into a union of full Steiner trees (trees in which each non-Steiner point has degree 1) such that any two full Steiner trees intersect in only finitely many points. Each of these trees is constructible by the Melzak–Hwang algorithm [5, Section 1.2.1]. $\square$

Corollary 3

Given finite sets A and B of points with rational coordinates in the Euclidean plane,  there is an algorithm that constructs a shortest (A, B)-network.

We leave open the following problems.

Problem 4

Find an algorithm that can feasibly compute shortest directed networks in the Euclidean plane, at least for a small number of sources and sinks.

The main difficulty in finding an algorithm lies in the enumeration of all possible digraph structures. Note that if there is only one source or one sink, then a shortest network has to be a minimum Steiner tree, which can be computed with the GeoSteiner algorithm [5, Section 1.4].

Problem 5

Find a characterization of the local structure of sources or sinks of shortest directed networks in the Euclidean plane analogous to that for Steiner points in Theorem 1.

Note that such a characterization is known in the undirected case: In a Steiner minimal tree, a given node either has degree 3 with all angles between incident edges equal to $120^\circ$, or has degree 2 with the angle between the two edges $\ge 120^\circ$, or has degree 1 [5, Theorem 1.2].

Problem 6

Find characterizations of the local structure of nodes (Steiner points, sources or sinks) of shortest directed networks in higher-dimensional Euclidean space analogous to that for Steiner points in Theorem 1.

Corollary 18 below gives some partial results on the above two problems.

Problem 7

Find characterizations of the local structure of nodes (Steiner points, sources or sinks) of shortest directed networks in other normed planes and spaces.

The undirected case of Problem 7, namely to characterize the local structure of Steiner points and terminals in Steiner minimal trees in normed planes, is known [9].

We also draw attention to the following attractive conjecture of Alfaro.

Conjecture 8

(Alfaro [1]) In the Euclidean plane,  suppose that the set A of sources and set B of sinks are the same. Then a shortest (A, B)-network does not have Steiner points and is a union of cycles.

3 Basic Lemmas

By a norm defined on $\mathbb {R}^d$, we mean a function $\Vert \cdot \Vert :\mathbb {R}^d\rightarrow \mathbb {R}$ such that $\Vert x\Vert \ge 0$ for all $x\in \mathbb {R}^d$, $\Vert \lambda x\Vert =\left|\lambda \right|\Vert x\Vert$ for all $\lambda \in \mathbb {R}$ and $x\in \mathbb {R}^d$, and $\Vert x+y\Vert \le \Vert x\Vert +\Vert y\Vert$ for all $x,y\in \mathbb {R}^d$. The unit ball of a norm is defined to be the set $\{x\in \mathbb {R}^d:\Vert x\Vert \le 1\}$. We will compare norms, and to do this, it is useful to keep in mind that $\Vert x\Vert _a\ge \Vert x\Vert _b$ for all $x\in \mathbb {R}^d$ if and only if the corresponding unit balls $B_a\subseteq B_b$.

We denote the d-dimensional Euclidean space by $\mathbb {E}^d$, that is, the d-dimensional normed space with norm

$$\begin{aligned} \Vert (x_1,\ldots ,x_d)\Vert _2 = \sqrt{x_1^2+\cdots +x_d^2}. \end{aligned}$$

We will work with a variety of norms in the plane $\mathbb {R}^2$ apart from the Euclidean norm $\Vert \cdot \Vert _2$ with unit ball $B_2$. The $\ell _1$-norm is defined by $\Vert (x,y)\Vert _1=|x|+|y|$. Its unit ball $B_1$ is the convex hull of the four points $\pm e_1$ and $\pm e_2$, where $e_1=(1,0)$ and $e_2=(0,1)$ form the standard unit basis of $\mathbb {R}^2$. Since $B_1\subseteq B_2$, it follows that $\Vert x\Vert _2\le \Vert x\Vert _1$ for all $x\in \mathbb {R}^2$. Alternatively,

$$\begin{aligned} \Vert (x,y)\Vert _2^2 = x^2+y^2 \le \left|x\right|^2 + 2\left|x\right|\left|y\right|+\left|y\right|^2 = (\left|x\right|+\left|y\right|)^2 = \Vert (x,y)\Vert _1^2. \end{aligned}$$

For any $\theta \in (0,90^\circ )$ we define the norm $\Vert \cdot \Vert _{1(\theta )}$ on $\mathbb {R}^2$ by

$$\begin{aligned} \Vert (x,y)\Vert _{1(\theta )}=\left|x\right|\cos \theta +\left|y\right|\sin \theta . \end{aligned}$$

Lemma 9

For any $\theta \in (0^\circ ,90^\circ )$ and $(x,y)\in \mathbb {R}^2$, $\Vert (x,y)\Vert _2\ge \Vert (x,y)\Vert _{1(\theta )}$.

Proof

By the Cauchy–Schwarz inequality,

$$\begin{aligned} \Vert (x,y)\Vert _{1(\theta )}&= \left\langle (\left|x\right|,\left|y\right|), (\cos \theta ,\sin \theta ) \right\rangle \\&\le \Vert (\left|x\right|,\left|y\right|)\Vert _2\Vert (\cos \theta ,\sin \theta )\Vert _2 = \Vert (x,y)\Vert _2. \end{aligned}$$

$\square$

The inequality in Lemma 9 is sharp with equality attained at the points $(\pm \cos \theta ,\pm \sin \theta )$. This lemma can also be seen by noting that the unit ball $B_{1(\theta )}$ of $\Vert \cdot \Vert _{1(\theta )}$ is a parallelogram circumscribing the Euclidean unit ball $B_2$, and touching $B_2$ at the four points $(\pm \cos \theta ,\pm \sin \theta )$. See Fig. 5 for the case $\theta =60^\circ$, where the four points are labelled $a_2$, $a_3$, $b_2$, $b_3$.

Fig. 5

The unit balls of $\Vert \cdot \Vert _h$, $\Vert \cdot \Vert _2$, $\Vert \cdot \Vert _H$ and $\Vert \cdot \Vert _{1(60^\circ )}$

Define the norm

$$\begin{aligned} \Vert (x,y)\Vert _H = \max \left\{ \left|x\right|,\tfrac{1}{2}\left|x\right|+\tfrac{\sqrt{3}}{2}\left|y\right|\right\} = \max \left\{ \left|x\right|, \Vert (x,y)\Vert _{1(60^\circ )}\right\} . \end{aligned}$$

Its unit ball $B_H$ is a regular hexagon $a_1'b_1'a_2'b_2'a_3'b_3'$ with vertices $a_1'=-b_2'=(-1,1/\sqrt{3})$, $a_2'=-b_3'=(0,-2/\sqrt{3})$, $a_3'=-b_1'=(1,1/\sqrt{3})$, circumscribing the Euclidean unit circle and touching it at $a_1,a_2,a_3,b_1,b_2,b_3$ (Fig. 5), where $a_1=-b_1=(1,0)$, $a_2=-b_2=(-1/2,\sqrt{3}/2)$, $a_3=-b_3=(-1/2,-\sqrt{3}/2)$. Also define the norm

$$\begin{aligned} \Vert (x,y)\Vert _h = \max \left\{ \tfrac{2}{\sqrt{3}}\left|y\right|,\left|x\right|+\tfrac{1}{\sqrt{3}}\left|y\right|\right\} . \end{aligned}$$

Its unit ball $B_h$ is the regular hexagon $a_1b_3a_2b_1a_3b_2$ inscribed in the Euclidean unit circle (Fig. 5). Note that although the normed plane $(\mathbb {R}^2,\Vert \cdot \Vert _h)$ is not the same as $(\mathbb {R}^2,\Vert \cdot \Vert _H)$, they are isometric.

Lemma 10

For any $(x,y)\in \mathbb {R}^2,$$\Vert (x,y)\Vert _h\ge \Vert (x,y)\Vert _2\ge \Vert (x,y)\Vert _H$.

Proof

For the first inequality, note that if $3x^2\le y^2$ then $x^2+y^2\le \frac{4}{3}y^2$, while if $3x^2\ge y^2$, then $x^2+y^2\le (\left|x\right|+\frac{1}{\sqrt{3}}\left|y\right|)^2$. For the second inequality, note that by Lemma 9, $\Vert (x,y)\Vert \ge \Vert (x,y)\Vert _{1(60^\circ )}$, and trivially, $\Vert (x,y)\Vert =\sqrt{x^2+y^2}\ge \left|x\right|$. $\square$

This lemma also follows from the fact that the unit balls $B_h\subseteq B_2\subseteq B_H$.

Lemma 11

For any $a,b\in \mathbb {R}^2,$ if $a'$ and $b'$ are the orthogonal projections of a and b onto the x-axis,  then $\Vert a-b\Vert _H\ge \Vert a'-b'\Vert _H=\Vert a'-b'\Vert _2$.

Proof

Note that $\Vert (x,y)\Vert _H\ge \left|x\right|=\Vert (x,0)\Vert _H=\Vert (x,0)\Vert _2$. $\square$

Lemma 12

Suppose that the unit ball B of the norm $\Vert \cdot \Vert$ on $\mathbb {R}^2$ is a polygon with edges $p_ip_{i+1},$$i=1,\ldots ,2n-1,$ where $p_{n+i}=-p_i,$$i=1,\ldots, n$ and $p_{2n}=p_0$. Then for any segment vw in the plane there exists a point c such that the segments vc and cw are each parallel to $p_i$ and $p_{i+1}$ for some $i=1,\ldots ,n-1$ and $\Vert v-w\Vert =\Vert v-c\Vert +\Vert c-w\Vert$.

Proof

Let $i=1,\ldots ,2n-1$ be such that the unit vector $\Vert w-v\Vert ^{-1}(w-v)$ lies on the edge $p_ip_{i+1}$ of B. Then $w-v = \alpha p_i + \beta p_{i+1}$ for some $\alpha ,\beta \ge 0$. It is then easy to see that $c=w-\beta p_{i+1} = v+\alpha p_i$ is the required point. $\square$

We call the union of the segments $vc\cup cw$ in the above lemma a broken segment that has the same length as vw. Likewise, we call the directed path consisting of the edges $v\mathord {\rightarrow }c$ and $c\mathord {\rightarrow }w$ a broken edge. Note that if we replace the directed edge $v\mathord {\rightarrow }w$ in an (A, B)-network by the broken edge $v\mathord {\rightarrow }c$, $c\mathord {\rightarrow }w$, then we still have an (A, B)-network of the same length.

We next note that only the directions of the directed edges incident to a vertex are important in characterizing the local structure of a node.

Lemma 13

Let $A=\{a_1,\ldots ,a_m\}$ and $B=\{b_1,\ldots ,b_n\}$ be sources and sinks in a d-dimensional normed space X. Suppose that the (A, B)-network G with directed edge set $E=\{a_i\mathord {\rightarrow }o:a_i\ne o, i=1,\ldots ,m\}\cup \{o\mathord {\rightarrow }b_j:b_j\ne o, j=1,\ldots ,n\}$ is a shortest (A, B)-network. Let $a_i'$ be any point on the ray from o to $a_i$ and $b_j'$ any point on the ray from o to $b_j$. Let $A'=\{a_1',\ldots ,a_m'\}$ and $B'=\{b_1',\ldots ,b_n'\}$. Then the network $G'$ with directed edge set $E'= \{a_i'\mathord {\rightarrow }o:a_i'\ne o, i=1,\ldots ,m\}\cup \{o\mathord {\rightarrow }b_j':b_j'\ne o, j=1,\ldots ,n\}$ is a shortest $(A',B')$-network.

Proof

By scaling, we may assume that each $\Vert a_i'\Vert \le \Vert a_i\Vert$ and each $\Vert b_j'\Vert \le \Vert b_j\Vert$. If $G'$ is not a shortest (A, B)-network, then G can be shortened by replacing the part of G that coincides with $G'$ by a shorter network, which gives a contradiction. $\square$

Lemma 14

All vertices and directed edges of a shortest (A, B)-network in Euclidean space $\mathbb {E}^d$ are contained in the convex hull of $A \cup B$.

Proof

It is sufficient to prove that each Steiner point of the (A, B)-network G is contained in ${{\,\mathrm{conv}\,}}(A\cup B)$. Suppose that some Steiner point $s\notin {{\,\mathrm{conv}\,}}(A\cup B)$. Let H be a hyperplane that strictly separates s from all other nodes of G. Each directed edge e incident to s intersects H in some point $p_e$. If we project s, together with the part $e'$ joining s and $p_e$ of each edge e orthogonally onto H, then we obtain a shorter network, which is a contradiction. $\square$

The following is a well-known geometric result that goes back to Fermat and Torricelli [6, Problem 91].

Lemma 15

Let a, b, c be three points in Euclidean space $\mathbb {E}^d$. Then there is a unique point s that minimizes the sum of distances $\Vert a-s\Vert _2 + \Vert b-s\Vert _2 + \Vert c-s\Vert _2$ to the given points. If $\sphericalangle abc, \sphericalangle bca, \sphericalangle cab < 120^\circ ,$ then s is in the relative interior of ${{\,\mathrm{conv}\,}}\{a,b,c\},$ and $\sphericalangle asb = \sphericalangle bsc = \sphericalangle csa = 120^\circ$. If,  on the other hand,  $\sphericalangle abc \ge 120^\circ ,$ say,  then $s=b$.

A proof of the following lemma can be found in [7, p. 22].

Lemma 16

Let a, b, c be three points in Euclidean space $\mathbb {E}^d$ distinct from the origin o. Suppose that all three angles $\sphericalangle aob, \sphericalangle boc, \sphericalangle coa\ge 120^\circ$. Then a, b, c, o lie in the same 2-dimensional plane,  and $\sphericalangle aob = \sphericalangle boc = \sphericalangle coa = 120^\circ$.

As a consequence of the previous two lemmas, we obtain the following properties of shortest directed networks in Euclidean space.

Lemma 17

Let $G=(V,E)$ be a shortest (A, B)-network in Euclidean space $\mathbb {E}^d$.

• 1. Let $v\in V$. Then the angle at v between any two incoming directed edges or any two outgoing directed edges at v is $\ge 120^\circ$. Consequently,  $\text{deg} ^-(v), \text{deg} ^+(v)\le 3$.

• 2. Let $v\in V\setminus B$ satisfy $\text{deg} ^+(v)=1$. Then the angle at v between the outgoing directed edge and any incoming directed edge is $\ge 120^\circ$. Consequently,  $\text{deg} ^-(v)\le 2$.

• 3. Let $v\in V\setminus B$ satisfy $\text{deg} ^-(v)=1$. Then the angle at v between the incoming directed edge and any outgoing directed edge is $\ge 120^\circ$. Consequently,  $\text{deg} ^+(v)\le 2$.

Proof

1. By Lemma 15, if some angle between two incoming directed edges is $<120^\circ$, then we can replace these two directed edges by three directed edges joined to a Steiner point, oriented appropriately, to obtain a shorter (A, B)-network. It then follows from Lemma 16 that there cannot be more than three incoming edges.

2. Let the outgoing directed edge be $v\mathord {\rightarrow }b$ and consider any incoming directed edge $c\mathord {\rightarrow }v$ with $\sphericalangle bvc<120^\circ$. Note that by minimality of G, since v is not a sink and has only one outgoing directed edge, any directed path from a source to a sink that uses $c\mathord {\rightarrow }v$ also has to use $v\mathord {\rightarrow }b$. We can then replace $v\mathord {\rightarrow }b$ and $c\mathord {\rightarrow }v$ by a Steiner point s from Lemma 15 and directed edges $c\mathord {\rightarrow }s$, $v\mathord {\rightarrow }s$ and $s\mathord {\rightarrow }b$, to obtain a shorter (A, B)-network.

3. Similar to 2 by changing the directions of all directed edges. $\square$

Corollary 18

[1, Theorem 3.1] The only possible degrees of a node in a simple (A, B)-network in any Euclidean space of dimension at least 2 are (1, 2),  (2, 1),  (2, 2),  (2, 3),  (3, 2) and (3, 3).

4 Steiner Points of Degree 4

Theorem 19

Let $a_1b_1a_2b_2$ be a convex quadrilateral in the Euclidean plane with diagonals $a_1a_2$ and $b_1b_2$ intersecting in o. Let $A=\{a_1,a_2\}$ be the set of sources and $B=\{b_1,b_2\}$ the set of sinks. Then the network with directed edges $a_i\mathord {\rightarrow }s$ and $s\mathord {\rightarrow }b_i,$$i=1,2,$ is a shortest (A, B)-network if,  and only if $s=o$.

Proof

We first note that by the triangle inequality it follows that if the network with edge set $\left\{ a_1\mathord {\rightarrow }s,a_2\mathord {\rightarrow }s,s\mathord {\rightarrow }b_1,s\mathord {\rightarrow }b_2\right\}$ is shortest, then $s=o$.

We next show the converse. By Lemma 13, it is sufficient to prove the theorem with $a_1b_1a_2b_2$ a rectangle. From now on we assume that $a_1b_1a_2b_2$ is a rectangle with half diagonals of length $\Vert a_1\Vert _2=\Vert a_2\Vert _2=\Vert b_1\Vert _2=\Vert b_2\Vert _2=1$. We choose coordinates such that o is the origin, $a_1$ is in the first quadrant, and the axes bisect the four angles created by the diagonals $a_1a_2$ and $b_1b_2$ at o. Let $\theta$ be the angle that $oa_1$ makes with the positive x-axis (see Fig. 6.)

Fig. 6

Proof of Theorem 19

Let N be any given (A, B)-network. We have to show that the total length $\Vert N\Vert _2\ge 4$. Create a new (A, B)-network $N'$ by replacing each edge $v\mathord {\rightarrow }w$ of N by a broken edge, that is, an edge $v\mathord {\rightarrow }s$ parallel to the x-axis, joined to an edge $s\mathord {\rightarrow }w$ parallel to the y-axis, where s is a new Steiner point of degree (1, 1). Then

$$\begin{aligned} \Vert N\Vert _2\ge \Vert N\Vert _{1(\theta )}=\Vert N'\Vert _{1(\theta )}, \end{aligned}$$

(1)

by Lemmas 9 and 12. Each edge in $N'$ is in one of 4 directions: the positive and negative x- and y-axes. Consider any $(a_1,b_1)$-path P in the new network $N'$. The total $\Vert \cdot \Vert _{1(\theta )}$-length of all the edges of P in the direction of the negative x-axis is at least $\Vert a_1-b_1\Vert _{1(\theta )} = (2\cos \theta )\cos \theta + 0\sin \theta = 2\cos ^2\theta$. Similarly, the total $\Vert \cdot \Vert _{1(\theta )}$-length of all the edges of an $(a_2,b_2)$-path in the direction of the positive x-axis is also at least $2\cos ^2\theta$. In the same way, the total $\Vert \cdot \Vert _{1(\theta )}$-length of all the edges of an $(a_2,b_1)$-path in the direction of the positive y-axis is at least $2\sin ^2\theta$, and of all the edges of an $(a_1,b_2)$-path in the direction of the negative y-axis is also at least $2\sin ^2\theta$. Since we did not count any edge twice, we arrive at a lower bound for the $\Vert \cdot \Vert _{1(\theta )}$-length of $N'$ of

$$\begin{aligned} \Vert N'\Vert _{1(\theta )} \ge 2\cos ^2\theta +2\cos ^2\theta +2\sin ^2\theta +2\sin ^2\theta = 4. \end{aligned}$$

This, together with (1), finishes the proof that $\Vert N\Vert _2\ge 4$. $\square$

As corollaries of the above Euclidean result, we obtain two results in the $\ell _1$-plane.

Corollary 20

Consider the $\ell _1$-plane with unit ball with vertices $\pm e_1, \pm e_2$. Let $A=\left\{ \pm e_1\right\}$ be the set of sources and $B=\left\{ \pm e_2\right\}$ the set of sinks. Then the directed (A, B)-network with edge set $\left\{ e_1\mathord {\rightarrow }o,-e_1\mathord {\rightarrow }o,o\mathord {\rightarrow }e_2,o\mathord {\rightarrow }-e_2\right\}$ is shortest.

Proof

Let $N_0$ denote the network described in the corollary, and let N be any (A, B)-network. Note that $\Vert N\Vert _2\le \Vert N\Vert _1$ for any network N. By Theorem 19, $\Vert N\Vert _2\ge \Vert N_0\Vert _2$. It follows that $\Vert N\Vert _1\ge \Vert N_0\Vert _2=\Vert N_0\Vert _1$. $\square$

Since $\Vert x\Vert _2\le \Vert x\Vert _1$, and because we can replace edges of shortest directed networks in the $\ell _1$-plane by broken edges without changing the length, it follows that in any shortest directed network in the $\ell _1$-plane, each vertex, including Steiner points, has indegree and outdegree at most 4 each. This can be attained.

Corollary 21

In the $\ell _1$-plane,  let $A=B=\left\{ \pm e_1,\pm e_2\right\}$. Then the (A, B)-network with the 8 edges $\left\{ o\mathord {\rightarrow }\pm e_1, \pm e_1\mathord {\rightarrow }o, o\mathord {\rightarrow }\pm e_2, \pm e_2\mathord {\rightarrow }o\right\}$ is shortest.

Proof

The proof is the similar to that of Theorem 19: Consider all edges in the direction of the positive x-axis from $-e_1$ to $e_1$, etc. $\square$

5 Steiner Points of Degree 6

In this section we prove part 4 of Theorem 1. Proposition 22 shows necessity of the angle condition on a Steiner point of degree (3, 3). Then Theorem 23, originally shown in [1], shows sufficiency.

Proposition 22

Let $A=\left\{ a_1,a_2,a_3\right\}$ and $B=\left\{ b_1,b_2,b_3\right\}$ be two sets of three points each in the Euclidean plane such that $o\notin A\cup B$, and suppose that the network with edge set $\left\{ a_1\mathord {\rightarrow }o,a_2\mathord {\rightarrow }o,a_3\mathord {\rightarrow }o,o\mathord {\rightarrow }b_1,o\mathord {\rightarrow }b_2,o\mathord {\rightarrow }b_3\right\}$ is a shortest (A, B)-network. Then the incoming and outgoing edges alternate, with consecutive directed edges at $60^\circ$ angles.

Proof

By Lemma 13 we may assume that each edge has unit length. By Lemma 17.1 we know that the incoming edges are at $120^\circ$ angles, and the outgoing edges are at $120^\circ$ angles. Denote the smallest angle between an incoming and outgoing edge by $\theta$. Then $\theta \le 60^\circ$. We show that $\theta =60^\circ$ by contradiction. If $\theta < 60^\circ$, then the network can be shortened, as shown in Fig. 7. In particular, we then have that the intersections $s_1$ of $a_2b_2$ and $a_3b_3$, $s_2$ of $a_1b_1$ and $a_3b_3$, and $s_3$ of $a_1b_1$ and $a_2b_2$ are distinct and distinct from o, and it follows from the triangle inequality that the network with edge set

$$\begin{aligned} \left\{ a_1\mathord {\rightarrow }s_2,a_2\mathord {\rightarrow }s_3,a_3\mathord {\rightarrow }s_1,s_3\mathord {\rightarrow }b_1,s_1\mathord {\rightarrow }b_2,s_2\mathord {\rightarrow }b_3,s_1\mathord {\rightarrow }s_2,s_2\mathord {\rightarrow }s_3,s_3\mathord {\rightarrow }s_1\right\} \end{aligned}$$

is strictly shorter than the original network. $\square$

Fig. 7

Shortening a network with a Steiner point of degree (3, 3) if some angle is $<60^\circ$

Theorem 23

[1, Theorem 3.2] Let $A=\left\{ a_1,a_2,a_3\right\}$ and $B=\left\{ b_1,b_2,b_3\right\}$ be sets of points in the Euclidean plane such that

$$\sphericalangle a_1ob_2 = \sphericalangle b_2oa_3 = \sphericalangle a_3ob_1 = \sphericalangle b_1oa_2 = \sphericalangle a_2ob_3 = \sphericalangle b_3oa_1 = 60^\circ.$$

Then the network with edge set $\left\{ a_1\mathord {\rightarrow }o,a_2\mathord {\rightarrow }o,a_3\mathord {\rightarrow }o,o\mathord {\rightarrow }b_1,o\mathord {\rightarrow }b_2,o\mathord {\rightarrow }b_3\right\}$ is shortest among all directed (A, B)-networks.

Proof

By Lemma 13, we may assume that the lengths $\Vert a_i-o\Vert _2$ and $\Vert b_i-o\Vert _2$ are all the same. Thus $a_1b_2a_3b_1a_2b_3$ is a regular hexagon. We may also assume without loss of generality that o is the origin and $\Vert a_i\Vert _2=\Vert b_i\Vert _2=1$, $i=1,2,3$, as in Fig. 5. Denote the (A, B)-network described in the statement of the theorem by $N_0$. Let N be any given (A, B)-network. We have to show that $\Vert N\Vert _2\ge \Vert N_0\Vert _2$.

By Lemma 10, $\Vert N\Vert _2\ge \Vert N\Vert _H$, and by Lemma 12, we can replace each edge of N by a broken edge consisting of two edges parallel to one of the main diagonals $a_1'b_2'$, $a_2'b_3'$, $a_3'b_1'$ of $B_H$ (Fig. 5) to create a new network $N'$ with all edges in one of the 6 directions $a_i', b_i'$, and of the same length $\Vert N\Vert _H=\Vert N'\Vert _H$.

Consider any $(a_1,b_1)$-path P in $N'$. The only vectors on this path with negative x-component are those in the directions of $a_1'$ and $b_1'$. If we project this path orthogonally onto the x-axis, the $\Vert \cdot \Vert _H$-distance does not increase, by Lemma 11. It follows that the total $\Vert \cdot \Vert _H$-length of the edges in the directions of $a_1'$ and $b_1'$ is at least 2. By symmetry, the total $\Vert \cdot \Vert _H$-length of the edges on an $(a_2,b_2)$-path in the directions of $a_2'$ and $b_2'$ is at least 2, and the total $\Vert \cdot \Vert _H$-length of the edges on an $(a_3,b_3)$-path in the directions of $a_3'$ and $b_3'$ is at least 2. Since we did not count any edge more than once, we obtain that $\Vert N'\Vert _H\ge 6$. If we put all the inequalities together, we obtain $\Vert N\Vert _2\ge 6 = \Vert N_0\Vert _2$. $\square$

Corollary 24

Consider the normed plane $(\mathbb {R}^2,\Vert \cdot \Vert _h)$ with unit ball the regular hexagon $B_h=a_1b_2a_3b_1a_2b_3$. Let $A=\left\{ a_1,a_2,a_3\right\}$ and $B=\left\{ b_1,b_2,b_3\right\}$. Then the network with edge set $\left\{ a_1\mathord {\rightarrow }o,a_2\mathord {\rightarrow }o,a_3\mathord {\rightarrow }o,o\mathord {\rightarrow }b_1,o\mathord {\rightarrow }b_2,o\mathord {\rightarrow }b_3\right\}$ is shortest among all directed (A, B)-networks in $(\mathbb {R}^2,\Vert \cdot \Vert _h)$.

Proof

The proof is similar to that of Corollary 20. Since $B_h\subseteq B_2$, we have that $\Vert x\Vert _2\le \Vert x\Vert _h$ for all $x\in \mathbb {R}^2$. Let $N_0$ denote the network described in the corollary, and let N be any (A, B)-network. By Lemma 10, $\Vert N\Vert _2\le \Vert N\Vert _h$. By Theorem 23, $\Vert N\Vert _2\ge \Vert N_0\Vert _2$. It follows that $\Vert N\Vert _h\ge \Vert N_0\Vert _2=\Vert N_0\Vert _h$. $\square$

6 Steiner Points of Degree 5

Theorem 25

Let $a_1, a_2, a_3, b_1, b_2, s$ be points in the Euclidean plane. Let $A=\{a_1,a_2,a_3\}$ and $B=\{b_1,b_2\}$. Then the network with edges $a_i\mathord {\rightarrow }s,$$i=1,2,3$ and $s\mathord {\rightarrow }b_i$, $i=1,2,$ is a shortest (A, B)-network if and only if $\sphericalangle a_isa_j=120^\circ$ for all $1\le i < j\le 3$ and $\sphericalangle b_1sb_2=180^\circ$.

Proof

We first show that the condition is necessary for a Steiner point s of degree (3, 2). By Lemmas 16 and 17, the three incoming directed edges $a_i\mathord {\rightarrow }s$ are pairwise at $120^\circ$ angles, and the two outgoing directed edges $s\mathord {\rightarrow }b_i$ have to be at an angle of $\ge 120^\circ$. Therefore, $s\mathord {\rightarrow }b_1$ and $s\mathord {\rightarrow }b_2$ lie in different (closed) angles spanned by pairs of incoming edges. If $\sphericalangle b_1sb_2\ne 180^\circ$, then, assuming without loss of generality that the segment $b_1b_2$ intersects the segment $a_1s$ at a point $s'$, the network can be shortened by replacing $s\mathord {\rightarrow }b_1$, $s\mathord {\rightarrow }b_2$ and $a_1\mathord {\rightarrow }s$ by $s\mathord {\rightarrow }s'$, $a_1\mathord {\rightarrow }s'$, $s'\mathord {\rightarrow }b_1$, $s'\mathord {\rightarrow }b_2$ as in Fig. 8. Therefore, $\sphericalangle b_1sb_2 = 180^\circ$.

Fig. 8

If $b_1,s,b_2$ are not collinear, the network can be shortened

To show the converse, suppose that $a_1,a_2,a_3$ satisfy $\sphericalangle a_isa_j=120^\circ$ for all distinct i, j, and $b_1,b_2$ satisfy $\sphericalangle b_1sb_2=180^\circ$. By Lemma 13, we may assume that the neighbours of s lie on the unit circle centred at s. By relabelling, we may also assume that $b_1$ lies inside $\sphericalangle a_1 o a_2$ and $b_2$ inside $\sphericalangle b_2 o a_3$. By a limit argument we may assume that $A=\{a_1,a_2,a_3\}$ and $B=\{b_1,b_2\}$ are disjoint. We want to show that the network with directed edges $a_i\mathord {\rightarrow }s$, $i=1,2,3$ and $o\mathord {\rightarrow }b_j$, $j=1,2$, is a shortest (A, B)-network. Let G be a simple shortest (A, B)-network. We will show that $\Vert G\Vert _2\ge 5$. (We will only use the assumption that G is shortest in Case 2.3 in the last part of the proof).

If the underlying undirected graph of G has a cycle, then we can reorient some edges of the cycle in G so that the resulting digraph stays an (A, B)-network. Among all reorientations of G that are still (A, B)-networks, we choose one with an $(a_2,b_2)$-path P that minimizes the area of the region ${\Gamma }$ bounded by P and the segments $a_2a_3$ and $a_3b_2$ (Fig. 9). Let Q be an $(a_3,b_1)$-path. By Lemma 14, Q crosses P. Let p be the first vertex on Q that is also on P. Let $Q_1$ be the subpath of Q from from $a_3$ to p. Let $P_1$ be the part of P from $a_2$ to p. Let q be the last vertex on Q that is also on the part of P from p to $b_2$. Let $P_2$ be the part of P from p to q, and $P_3$ the part of P from q to $b_2$. We choose Q such that the part of Q from p to q coincides with $P_2$. Let $Q_3$ be the part of Q from q to $b_1$. Then no edge of $Q_3$ can be in the interior of the region ${\Gamma }$, otherwise $Q_3$ will cross P again, thus making a cycle which can be reoriented to make ${\Gamma }$ smaller, which would contradict the minimality of ${\Gamma }$. It is possible for vertices of $Q_3$ other than q to lie on $P_1$. Let R be an $(a_1,b_2)$-path without repeated vertices. Let r be the first point on R that is on $P_3\cup Q_3$. We distinguish between two cases, depending on whether r is on $P_3$ (Fig. 10) or $Q_3$ (Fig. 11).

Fig. 9

Analysing the network G

Fig. 10

Case 1

Case 1: r is on $P_3$ (including the case $r=q$). See Fig. 10. Then without loss of generality, the part of R from r to $b_2$ coincides with P. We may also assume that among all $(a_1,b_2)$-paths hitting $P_3\cup Q_3$ first in $P_3$, we have chosen one with r closest to q on the path $P_3$. Let S be an $(a_1,b_1)$-path without repeated vertices, and let s be the last point on S that is also on R. Then s has to be on the part of R from $a_1$ to r, otherwise s would be on the part of $P_3$ from r to $b_2$, not including r, and then S would either have to cross itself or enter the interior of ${\Gamma }$, which would contradict either the choice of S or the minimality of ${\Gamma }$. Again, because S does not cross itself, the part of S from s to $b_1$ cannot enter the polygon ${\Delta }$ bounded by the part of R from $a_1$ to r, the part of $P_3$ from r to $b_2$ and the segment $a_1b_2$. Let t be the first point of S that is on $Q_3$. We have now described all $(a_i,b_j)$-paths, so by minimality of G we have that G consists of the directed edges of non-zero length among $a_1\mathord {\rightarrow }s, s\mathord {\rightarrow }t, q\mathord {\rightarrow }t, q\mathord {\rightarrow }r, s\mathord {\rightarrow }r, t\mathord {\rightarrow }b_1, r\mathord {\rightarrow }b_2, p\mathord {\rightarrow }q, a_2\mathord {\rightarrow }p, a_3\mathord {\rightarrow }p$. By applying the triangle inequality four times, we find that the perimeter of the quadrilateral qrst is at least the sum of its diagonals $\Vert s-q\Vert _2+\Vert t-r\Vert _2$. We now forget the directions of the directed edges, and replace the perimeter of qrst by the diagonals to obtain a geometric graph that splits into a tree that connects $a_1,a_2,a_3$ and an edge-disjoint path that connects $b_1$ and $b_2$. By Lemma 15 and the triangle inequality, the tree will have length bounded below by the length of the tree with edges $a_1o$, $a_2o$, $a_3o$, which equals 3. The path between $b_1$ and $b_2$ is bounded below by the distance $\Vert b_1-b_2\Vert _2=2$. That is,

$$\begin{aligned} \Vert G\Vert _2&\ge \Vert a_1-s\Vert _2 + (\Vert s-t\Vert _2 + \Vert q-t\Vert _2 + \Vert q-r\Vert _2 + \Vert s-r\Vert _2)\\&\quad + \Vert t-b_1\Vert _2 + \Vert r-b_2\Vert _2 + \Vert p-q\Vert _2 + \Vert a_2-p\Vert _2 + \Vert a_3-p\Vert _2\\&\ge \Vert a_1-s\Vert _2 + (\Vert s-q\Vert _2 + \Vert t-r\Vert _2) + \Vert t-b_1\Vert _2 + \Vert r-b_2\Vert _2\\&\quad + \Vert p-q\Vert _2 + \Vert a_2-p\Vert _2 + \Vert a_3-p\Vert _2\\&= (\Vert a_1-s\Vert _2+\Vert s-q\Vert _2+\Vert p-q\Vert _2+\Vert a_2-p\Vert _2+\Vert a_3-p\Vert _2)\\&\quad + (\Vert t-b_1\Vert _2+\Vert t-r\Vert _2+\Vert r-b_2\Vert _2)\\&\ge (\Vert a_1-p\Vert _2 + \Vert a_2-p\Vert _2 + \Vert a_3-p\Vert _2) + \Vert b_1-b_2\Vert _2\\&\ge (\Vert a_1-o\Vert _2 + \Vert a_2-o\Vert _2 + \Vert a_3-o\Vert _2) + \Vert b_1-b_2\Vert _2 = 1+1+1+2, \end{aligned}$$

where we have used Lemma 15 in the last inequality and the triangle inequality in the others.

Fig. 11

Case 2

Case 2: r is on $Q_3$ (and $r\ne q$). See Fig. 11. Let s be the last point of R on $Q_3$. Without loss of generality, the part of R from r to s coincides with $Q_3$. By Lemma 14, the region ${\Gamma }_{\!0}$ bounded by the part of R from $a_1$ to s, the part of $Q_3$ from s to $b_1$ and the segment $a_1b_1$, is connected. The directed edge e on R following s cannot be in ${\Gamma }_{\!0}$, because R does not have repeated vertices and s is the last point of R on $Q_3$. Therefore, e is in the interior of either the region ${\Gamma }_{\!2}$ bounded by $Q_3$, the segment $b_1a_2$, and the part of P from $a_2$ to q, or the region ${\Gamma }_{\!4}$ bounded by the part of R from $a_1$ to r, the part of $Q_3$ from q to r, $P_3$ and the segment $a_1b_2$ (and then $s=r$). Let t be the first point on R that is also on P. Without loss of generality, the part of R from t to $b_2$ coincides with P. If e is in the interior of ${\Gamma }_{\!2}$, then t is either in $P_1$ or $P_2$, or the path from s to t hits Q in the part from q to r before passing into ${\Gamma }_{\!4}$.

We thus have three subcases, depending on whether t is on $P_1$, $P_2$, or $P_3$.

Fig. 12

Case 2.1

Case 2.1: $t\in P_2$. See Fig. 12. By minimality of G, its edges are the ones of non-zero length among $a_1\mathord {\rightarrow }r$, $r\mathord {\rightarrow }s$, $s\mathord {\rightarrow }b_1$, $s\mathord {\rightarrow }t$, $a_2\mathord {\rightarrow }p$, $p\mathord {\rightarrow }t$, $t\mathord {\rightarrow }q$, $q\mathord {\rightarrow }r$, $q\mathord {\rightarrow }b_2$, $a_3\mathord {\rightarrow }p$. Then we finish as in Case 1 by replacing the perimeter of the quadrilateral rstq by its diagonals.

Fig. 13

Case 2.2

Case 2.2: $t\in P_3$. Then R hits the part of $Q_3$ from q to r before hitting $P_3$ at t. Let u be the point on $Q_3$ where R hits $Q_3$ first and let v be the last point of R on the part of $Q_3$ from u to r (Fig. 13). By minimality of G, its edges are the ones of non-zero length among $a_1\mathord {\rightarrow }r$, $r\mathord {\rightarrow }s$, $s\mathord {\rightarrow }b_1$, $s\mathord {\rightarrow }u$, $u\mathord {\rightarrow }v$, $v\mathord {\rightarrow }r$, $v\mathord {\rightarrow }t$, $t\mathord {\rightarrow }b_2$, $a_2\mathord {\rightarrow }p$, $p\mathord {\rightarrow }q$, $q\mathord {\rightarrow }u$, $q\mathord {\rightarrow }t$, $a_3\mathord {\rightarrow }p$. As before, we finish as in Case 1 by replacing the perimeter of the quadrilateral rsuv by its diagonals.

Fig. 14

Case 2.3

Case 2.3: $t\in P_1$ (Fig. 14). This case is slightly more complicated since we now have a pentagon pqrst instead of a quadrilateral. However, we show that in this case, at least one of the edges of the pentagon must be degenerate, and then we finish as before by replacing the edges of the resulting quadrilateral by its diagonals. Suppose to the contrary that all five edges of pqrst have non-zero lengths. Since $\sphericalangle b_1a_1b_2=90^\circ <120^\circ$, $\text{deg} ^+(a_1)=1$ and $\text{deg} ^-(a_1)=0$ by Lemmas 14 and 17. Thus $a_1\ne r$, hence $\sphericalangle qrs=120^\circ$ by Lemma 15. Since $\sphericalangle b_1a_2a_3=180^\circ -\sphericalangle b_1a_1a_3=120^\circ -\sphericalangle b_1a_1a_2<120^\circ$, and similarly, $\sphericalangle b_2a_3a_3<120^\circ$, we obtain in the same way that $\sphericalangle qpt=\sphericalangle pts=120^\circ$. Finally, we either have that $b_1\ne s$ and then also $\sphericalangle tsr=120^\circ$, or $b_1=s$, and then $\sphericalangle tsr=\sphericalangle tb_1r\ge 120^\circ$ by Lemma 17. (In fact, equality has to hold since $\sphericalangle a_1b_1a_2=120^\circ$.) Similarly, $\sphericalangle rqp\ge 120^\circ$. It follows that the interior angle sum of pqrst is at least $5\cdot 120^\circ$, a contradiction.

Therefore, we have that at least one of the edges of pqrst has zero length. If either $p=q$, $p=t$ or $s=t$, then we replace the perimeter of the quadrilateral by its diagonals and finish as in Case 1. If on the other hand, $r=q$ or $r=s$, then we can already split the underlying graph into two edge-disjoint connected subgraphs, one joining $a_1,a_2,a_3$, and the other a path joining $b_1$ and $b_2$. $\square$