Abstract
In this paper, we propose to work in the 2.5D space of the scene to facilitate composition of new spherical panoramas. For adding depths to spherical panoramas, we extend an existing method that was designed to estimate relative depths from a single perspective image through user interaction. We analyze the difficulties to interactively provide such depth information for spherical panoramas, through three different types of presentation. Then, we propose a set of basic tools to interactively manage the relative depths of the panoramas in order to obtain a composition in a very simple way. We conclude that the relative depths obtained by the extended depth estimation method are enough for the purpose of compositing new photorealistic panoramas through a few elementary editing tools.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A spherical panorama is a photography that captures a view of 360 degrees horizontally and 180 degrees vertically. Such image stores a projection of the 3D world on a sphere whose center is the observer position. These images are used as resources for immersing the user in a given environment, which is known as Virtual Reality Photography [11]. Nowadays, there are a wide variety of consumer cameras at very affordable prices that allow to obtain spherical panoramic images and video, with resolutions even higher than 5K. Additionally, Street View [17] provides a vast amount of spherical panoramas around the world.
Spherical panorama compositing through depth estimation. We first obtain the relative depth maps for the source panoramas and then, the user interactively modifies depth ranges to obtain the desired composition, shown at the right (Source of panoramas: Street View [17])
Despite the proliferation of these type of visual resources, composition of new spherical panoramas has been scarcely addressed. Image editing software (e.g., Photoshop) is able to manage spherical panoramas and allows users to select a viewing direction and manually isolate contents in layers in order to, for instance, insert an object partially occluded. However, this procedure is time consuming, usually requires a skilled user and must be repeated for each view direction. The use of depths has been proposed as an effective way to make image composition easy. Depth availability allows users to work in the 2.5D space of the image, and tasks like the insertion of partially occluded objects are automatically managed [22]. Other uses where depths are helpful include, for example, shadow mapping, 3d reconstruction, depth of field simulation or stereoscopic vision.
Depth estimation from a single image has been widely studied [3, 21]. Some of the proposed solutions in the literature obtain relative depths exploiting user knowledge by requiring some input information [16, 23, 24]. In these methods, depths are obtained through an optimization process subject to a set of constraints extracted from user input (scribbles or points). The estimated depth values represent an ordering of depths between contiguous pixels, and therefore, these are not real distances from objects to the viewer. They are called relative depths [3], because they mean whether a pixel is farther or closer than its neighbor. Our goal is to obtain the relative depths from a spherical panorama by taking advantage of these solutions for single images. In particular, we selected DfSI [16], although other methods based on depth constraints may also be used. However, there are two main issues that prevent to directly apply these methods to spherical panoramas:
-
Some assumptions inherent to these works are suitable for perspective projections, but not for spherical projections.
-
Spherical panoramas show image deformations that make difficult to exploit the natural human ability to interpret perspective images.
To overcome these issues, we consider in this paper three different ways to present the spherical panorama to the user. First, we analyze the advantages and drawbacks of each presentation for introduction of depth-related information. From that, we propose to convert the spherical panorama to a cube map representation, that is, six perspective views resulting from the projection of the spherical image in six orthogonal directions and obtain the relative depths from each of the six views.
However, the application of DfSI to each view of the cube map separately produces relative depths that present discontinuities at image boundaries when depths are stitched together to create the panorama depth map. To deal with this problem, we propose to use relative depths calculated for a given view as new constraints for depth estimation of its adjacent views, thus favoring coherence among them and, consequently, on the final depth map of the spherical panorama.
We validate the obtained depth maps by creating new compositions, with outdoor panoramas. The user can interactively adjust the relative depth ranges to obtain the objects of interest, while occlusions are managed automatically. Although relative depths do not provide an accurate 3D model of the scene, the experiments show that they can be used to create new spherical panoramas. Figure 1 shows an example with two spherical panoramas together with their calculated depth maps, where the user has interactively adjusted the depth ranges to create a new spherical panorama. In summary, the main contributions of this paper are:
-
A qualitative analysis of the advantages and drawbacks of three different presentations of spherical panoramas, regarding the acquisition of user input about depth (Sect. 3).
-
A new method to obtain relative depths from panoramas by exploiting depth-related user input (Sect. 4).
-
The use of relative depths to interactively compose new spherical panoramas (Sect. 5).
2 Related work
2.1 Image synthesis based on photograph collections
The classic pipeline of a graphical system is based on creating geometric models that are algorithmically transformed and displayed to finally obtain synthetic images. In the last decade, several works propose the use of image collections as a new way to generate image synthesis [12, 19]. Among the benefits of this approach, we can highlight first that the process of synthesis is more simple, and second, that it is accessible to inexperienced users. The first approaches worked in the 2D space of the image. First, the user provides a photograph and specifies the area to be modified, then the system searches in an image database to find the more adequate options, and finally the user decides among these options [1, 5, 10, 14]. Some methods are able to perform a composition starting from an empty canvas. The user, through labels, specifies what they want to show in the final composition, and then, the system searches for pieces that are stitched or glued together [4, 6, 13].
However, working in the 2D space of the image produces visibility problems (i.e., occlusions) [15] and inconsistent scales [4, 10], which make the composition difficult. Photo Clip Art [15] proposed to make image manipulation in the 3D space of the scene, to automate object scaling based on distances to the camera. However, the objects used to modify the photography are planar impostors that are placed parallel to the image plane. The problem with occlusions is solved only among the inserted objects, but not with the background image. Buildup [20], however, is fully 3D. The user starts from an empty canvas, and the system allows to modify the camera parameters slightly (position, orientation and focus). In the composition process, the user selects a 3D scene position and the system provides the more adequate objects. Thanks to the use of 3D coordinates, the problems of scale inconsistency and occlusions are correctly solved. As a drawback, a lot of manual interaction are required to build the 3D object library.
2.2 Depth estimation
An image is a projection of a three-dimensional scene on a plane. When the scene is projected on a 2D plane, the third dimension, that is, objects depth, is lost. There are different approaches to recover them. First, there are systems with multiple cameras or special cameras that capture additional views or information, that allow to calculate depths [9]. For example, structured-light-based systems, time-of-flight cameras and stereoscopic systems. These systems require specific hardware: one or more additional cameras (stereoscopic vision), a light projector that applies a light pattern on the scene (structured light), or a range detection system based on time of flight of a light beam. They often recover quite accurately the scene geometry, which is their main advantage. The main drawback is the acquisition time and the equipment cost. In the case of panoramic images, this kind of systems has been used successfully. The work in [2] uses a system based on structured light to acquire geometry together with the image, with the help of a camera operator who inspects, during the acquisition, the 3D model being obtained. However, in many cases either such a system is not available or it can not be used (e.g., a drawing). Zioulis et al. [25] propose to estimate the depth map by training a CNN directly from spherical panoramas, in a supervised manner, and its applicability is limited to indoor scenes.
For perspective images, there are several approaches to estimate depths automatically: some proposals are based on learning [21], and others are based on Gestalt [3]. Other approaches tackle the problem in a semiautomatic way, by exploiting human ability to interpret 2D images. The extension of traditional photography editing tools to 3D is the most straightforward solution and provides excellent accuracy, but it requires a lot of user interaction and a high level of skill. Therefore, many approaches tried to reduce drastically this effort by designing tools based on sketches, scribbles or points provided by the user [16, 23, 24] and then transforming this inaccurate information into depths, resulting in dense relative depth maps [3]. In general, these methods use information interactively provided by the user to estimate the depth values of every pixel, guided by the image contents. The result is a relative depth map, that is, a depth ordering between neighboring pixels. Stereobrush [23] uses scribbles to assign absolute depth values, which are propagated to the rest of the image through an optimization algorithm. Yücer et al. [24] use pairs of scribbles that represent depth inequalities, which are included as relative constraints to guide the optimization. Lopez et al. [16] use points, pairs of points and scribbles to represent depth relationships. Considering the variety of the input data as well as how easy is for the users to provide the depth constraints, we selected the method DfSI [16] to estimate depths from a single perspective image.
2.3 Review of DfSI
DfSI permits to apply different types of constraints simultaneously. It performs an optimization process where all these constraints, which are derived from user input, are applied. The user can introduce the following elements:
-
Points with a given depth value (called seeds). The user is asked to select points in the farthest part of the image and points close to the observer, so that they are assigned the maximum and minimum depth value. However, DfSI admits seeds with any depth value. The resulting depths will typically vary between these maximum and minimum values. DfSI requires at least two seeds with different initial depth values.
-
Pairs of points with equal depth. When the user adds one of these pairs, the depths in these points are restricted to be equal.
-
Pairs of points with different depth. When the user adds one of these pairs, the depth in the first point is restricted to be closer than the second point, in at least an amount which can be configured. In the experiments, we used a minimum difference of 20 for depths ranging from 0 to 255.
-
Floor plane. The user draws the horizon line, and a scribble with points in the floor plane. These are used to constrain the location of the floor points to be in a plane that goes through the horizon.
DfSI uses convex optimization to find a depth map subject to depth constraints. The function to be minimized involves image gradients and constraints obtained from the input provided by the user. DfSI requires at least two points, the nearest and the furthest; however, depth estimation is considerably improved when additional input is provided. The optimization process encourages depth discontinuities at higher gradients and depth smoothness at lower gradients, and it consists of an iterative process that finishes when a solution with the desired accuracy has been obtained.
With the appropriate user input, DfSI can obtain a relative depth map for perspective images, but it has limitations with other types of images, such as spherical panoramas. First, the pixel connectivity of a spherical panorama is different than perspective images. The last column of the panorama is connected to the first column, the first row converges in an only point (zenith) and so does the last row (nadir). Therefore, certain areas of the sphere are more densely represented than others. Second, the geometry of the projection is different: under perspective projection, straight lines in the 3D world project as straight lines in the 2D image plane, while in general they project as curves in the spherical panorama.
3 Interaction with spherical panoramas
For visualization of a spherical panorama, we considered the following three methods.
Panoramic view. The entire scene is displayed in a rectangular area (Fig. 2). The X axis represents the azimuthal angle, \(\theta \), and the Y axis represents the polar angle, \(\phi \) [26]. Therefore, the left upper corner corresponds to \((0^{\circ },0^{\circ })\) and the right lower corner corresponds to \((360^{\circ },180^{\circ })\). In the panoramic view, a large number of straight lines of the scene appear as curves in the image, for example, driveways and sidewalks.
Cube map. The spherical panorama is rearranged into six square images, each resulting from the projection of the spherical image in six orthogonal directions. This kind of representation is a very popular resource in real-time graphics because it is widely supported by graphic hardware. Figure 3 shows the six images that form the cube map of the panorama in Figure 2.
Cube map. The panorama of Figure 2 is displayed through six images, by projecting on six planes perpendicular to orthogonal directions
Spherical projection. Four views of panorama in Figure 2. Left: direction \(\theta = 90^{\circ }\) and \(\phi = 90^{\circ }\), and the rest result from slightly rotating towards right and bottom
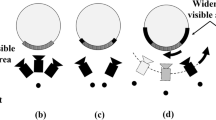
Spherical projection. The scene is partially displayed, depending in the view direction, and the result is a projection of the spherical image on a plane perpendicular to that direction. This type of presentation requires interaction to change the camera direction in order to observe other parts of the scene. This mechanism is widely used in image editing tools, videogames and other interactive applications. Figure 4 shows several views of the panorama in Figure 2, obtained with different view directions: the left view looks towards \(\theta = 90^{\circ }\) and \(\phi = 90^{\circ }\), and the others are obtained by slightly changing the view direction.
3.1 Qualitative analysis
In order to test user interaction with panoramas, we implemented conversions between the three types of presentation, so that any element (e.g., a point, a scribble) can be introduced in any presentation and then drawn in all the presentations. We aim to analyze the advantages and drawbacks of these presentations when considered for introduction of elements that contain information about depths. We consider the input reviewed in Sect. 2.3, except the horizon line, which we can assume to be in the central row of the panorama. In summary:
-
Points: either distant or nearby.
-
Pairs of points: with either equal or different depths.
-
Scribbles: The user selects a undetermined number of points considered to be lying on the same plane.
Distortion. Let us suppose that an inexperienced user wants to enter a pair of points with equal depth. Probably, the presentation that is most comfortable is the spherical projection, due to the human ability to interpret perspective images. The views in the cube map would be equally comfortable, except when the points lay on different views, given that they are projected under different perspectives. The most uncomfortable presentation to relate two points is the panoramic view, due to the distortion of the scene objects, which can be prone to error.
Continuity. With appropriate scroll tools, in the spherical projection, we always see all the elements without discontinuities. However, in the cube map, even if we can apply a rotation to put the most interesting part for example in the front, there will still be discontinuities in some areas of the scene. In the panoramic view, the discontinuity appears in a meridian of the sphere, that is, the first and last pixels of each row are contiguous in the sphere.
Completeness. The main drawback of the spherical projection is partiality: it does not provide a complete view of the scene at the same time, which is usually very convenient for the user to obtain a global comprehension of all the interaction. For example, in Figure 5c we need six different projections to show the six elements drawn, while they can be displayed all together in any of the other presentations.
We conclude that, to consider the use of spherical projection for user interaction, it should be accompanied by another type of presentation that offers a global view of the scene. When considering completeness, the fewer discontinuities of the panoramic view gain advantage over the cube map, but the distortion is a disadvantage. The natural human ability to recognize the 3D structure of the scene loses accuracy when the projection is not perspective. Nevertheless, interaction with the cube map is also difficult. The user should be aware of, not only the discontinuities between the cube faces, but also the differences in the perspective projection. Both presentations would require some user training for proper interaction, specially in the case of the panoramic view, unless new specialized tools were developed, which needs a deeper evaluation of user interaction with panoramas. Table 1 summarizes the pros and cons of each type of presentation. The pros are highlighted in bold.
4 Depth estimation
DfSI can be applied directly to each view of the corresponding cube map representation, but the coherence of the obtained depths across the six views is not guaranteed. Figure 6 shows depth discontinuities in boundaries of consecutive views when DfSI is applied separately. In this paper, we propose a method that uses DfSI for depth estimation of spherical panorama while maintaining coherence between the depth maps (bottom row of Fig. 6). We first apply DfSI to obtain the depth map for any of the views in X or Z directions. We have proceed in our experiments starting from the front view \(+Z\) (Sect. 4.1). Second, depths for the other three views are obtained in horizontal order, that is, right, back and left views in our experiments (Sect. 4.2). Then, we get depth maps for bottom and top views (Sect. 4.3). Finally, we convert the six depth maps into a panorama depth map. This process is summarized in Fig. 7.
4.1 Depth estimation for the front view (+Z)
Let us consider the panorama in Figure 2, whose front view (+Z) is shown in the left image in Figure 8. For this example, we selected a series of points of each type, shown in the center of Figure 8: far points in red, and near points in dark blue. We also added depth equalities, which are represented by connected pairs of points in green. Each of these pairs of points produces a constraint in the optimization process that forces the depth of both points to be equal.
Analogously, we added depth inequalities, which are represented by connected pairs of points in yellow and green. Each inequality produces a constraint in the process that forces the point in green to be further than the point in yellow by an amount that can be configured (in our experiments, 10% of the total range of depths). Finally, we added a scribble indicating some points of the floor in order to constrain depths in these points to be in a plane (scribble in light blue, Fig. 8). Using these data as input, DfSI obtains the depth map shown in the right side of Figure 8, where light means near and dark means far, which is commonly used in the literature to represent depths [3, 23, 24].
4.2 Depth for right, back and left views (\(+X, -Z, -X\))
We first process the right view \(+X\). In order to maintain coherence with the \(+Z\) depth map, the +X view is extended one column in its left side, which is filled using the last column of the +Z view. We add the estimated depths of this column as additional constraints, which together with that from the user input, allows DfSI to obtain a depth map which is coherent to +Z.
For the back view (\(-Z\)), we proceed analogously, by considering the last column of \(+X\).
For the left view (\(-X\)), we add constraints from two columns: last column of \(-Z\) and first column of \(+Z\). Figure 9 shows the user input and the resulting depth maps obtained for these images of the cube map.
4.3 Depth for top and bottom views (\(+Y, -Y\))
For processing the bottom face (\(-Y\)), we extend it with two columns and two rows such that we can add additional constraints about depth around the whole image, by using depths from the previous four cube map images. Figure 10a shows the alignments needed for this task. Each face is rotated in the figure to show the relationships with the bottom face. In this figure, faces are rotated for the sake of understanding (there is no need to perform such rotation to images).
We process the top face (\(+Y\)) proceeding analogously with the depths from the first (upper) rows of the four faces. Faces in Figure 10b are rotated to show the alignments between the neighboring pixels.
We usually find that in outdoor scenes the top view is just sky and the bottom view is just the floor plane, and the user does not provide any input depth, as in the current example. In these cases, DfSI depth estimation uniquely depends on the additional depth constraints, provided by the neighboring views. For the top view, it is not uncommon that all the pixels involved in the constraints are estimated to be at the furthest depth. In this case, we can even skip the optimization process for the top view. For the bottom view, when there is no user input and we apply only the depth constraints in the contour of the image, DfSI obtains a depth map which ranges between the minimum and maximum values of these constraints.
4.4 Depth panorama
Finally, we convert the six depth maps into a spherical panorama (Fig. 11 left). Depth values in the cube map are equivalent to the z coordinate in a (x, y, z) coordinate system. But, to display a panorama through a spherical projection, these coordinates do not take into account the user location. Therefore, we compute a panorama distance map (Fig. 11 right), which represents distances of each pixel to the center of the spherical projection. For simplicity, from now on, we will call depths to both depths and distances.
5 Panorama compositing
Relative depths obtained by the process explained above provides a depth ordering that makes sense within one panorama, but it may not when compared to another panorama. If we just merge two panoramas with their depth maps, the result will probably not match with the user’s desire. For example, the mere combination of the two panoramas of Figure 1 produces artifacts in the result (Fig. 12).
To obtain an appropriate composition, we propose to adjust the relative depths through simple scaling and translation operations. Scaling consists of multiplying the depth values by a factor in range [0..2]: values greater than 1 produce a widening of the range, while values less than 1 produce a shortening. Translation consists of adding a factor in range \([-1..1]\) to all depth values to equally move away or move closer the whole depth map.
With all depth values normalized to [0..1], both operations are applied, first scaling and then translation, to every pixel in both panoramas, so that the closest pixel after adjustment is selected for the composition. As this operation is performed in the fragment shader of the OpenGL pipeline, we can interactively adjust these parameters and the result is shown in real time. In the experiments, we often obtained satisfactory results by using only the scaling, whereas the translation transformation was rarely useful.
This procedure does not work well when both panoramas contain very distant areas like the sky, where normalized values are very close to 0. For this particular case, the user can expressly choose one of the skies. The selected one is prioritized in the composition without modifying the depth ranges. Additionally, horizontal and vertical panning operations provide flexibility to the composition. Panning does not resolve artifacts, but it helps in the aesthetics of the final composition. Figure 13 shows the application pipeline to compose panoramas.
Panorama of Mestalla Stadium (Source: Google Street View [17])
6 Experimental setup and results
We obtained depths of real panoramas from different sources (Street View [17] and the website Humus [18]). In this section, we show a few examples that pose challenges to our system. Figure 14 shows a panorama example with the resulting depths. In this example, the left face of the cube map lacks sky, due to the stadium, which is also visible in the top face. However, depth constraints from other faces and adequate user input provide a coherent result. The Coit Tower (Fig. 15) is a difficult example, due to the high number of windows. In addition, the lights and shadows of this panorama make depth estimation difficult. With the appropriate user input, the method can relate depths of the sky and the windows’ inside. Figure 16 shows an example with the CN Tower in the background, which appears in two different faces (front and top) of the cube map.
Coit Tower panorama (Source: Emil Persson (Humus) [18])
CN Tower panorama (Source: Emil Persson (Humus) [18])
For depth estimation, we used Matlab and CVX, a package for specifying and solving convex programs [7, 8]. All the experiments were performed with a cube edge length of 200 pixels. The computation times of the experiments shown along this paper range from 9.1 to 10.8 minutes using a i7 processor. Most of this time (around 97%) is spent in the front view of the cube map, because the addition of variables to represent the ground plane requires more processing in the optimization step. The average number of iterations is 51.7. The example used to illustrate this method (Figs. 2 to 11) took 50 iterations distributed as follows: front 10, right 10, back 11, left 10, bottom 9, and top 0. The example of the CN Tower (Fig. 16) took 9.1 minutes and 58 iterations: front 10, right 10, back 10, left 10, bottom 9 and top 9. In the case of scenes where the floor is not flat (mainly natural scenes), the computation time is higher, up to four times if the ground plane is also estimated in the right, back and left views, as the optimization process for each of these views can be as hard as for the front view.
We also created synthetic scenes for the experiments. For all these scenes, we computed the ground truth depth maps. Figures 17 and 18 show some of these synthetic panoramas and their depth maps. In some examples, we omitted the background (Fig. 18).
Figure 19 shows the combination of two synthetic panoramas. These panoramas are combined using the editing tools on the ground truth depth calculated from creation. We also experimented the combination of real and a synthetic panoramas. Figure 20 shows one of these combinations. The differences in the character of depths (ground truth absolute depths versus relative estimated depths) do not pose a problem when generating the composition. Through these tools, we can add synthetic objects to the real panorama, add real background to synthetic panorama, and so on.
Finally, we experimented combinations of two real panoramas. Figure 21 shows the original panoramas and the results of the compositions. By these combinations, we can add a building to a scene (top-left example), change the floor (top-right), or the background (the two bottom examples).
7 Conclusions
We conclude that scene depths help to edit and combine outdoor panoramas to create new spherical panoramas. Moreover, relative depths can be used for this purpose. This is remarkable, because we do not require specialized capture systems that obtain accurate absolute depths. We obtained satisfactory results by combining different panoramas, although we left composition with indoor panoramas as future work. We used basic compositing tools, which obtained results that seem real in a very simple way.
For obtaining relative depths, we extended a state-of-the-art method that estimates depths from user input, by applying the process to the six views of the cube map while maintaining coherence among contiguous views. There are several future research lines related to this topic: compare different strategies of depth propagation, including multiple (iterative) refinement, adapt the depth estimation method to spherical coordinates, etc.
We used relative depths to obtain new panoramas by combining real and synthetic panoramas. However, if the user does not provide the adequate input, they may need to repeat the procedure. To obtain acceptable results, some examples require the user to know what information should be provided and through which elements. For spherical panoramas, to interactively provide depth information is a bigger challenge than for perspective images. Another interesting research line consists of exhaustively evaluating interaction through the different panorama presentations, in order to find out which elements and views are the most appropriate. A more exhaustive study, including user studies, could help us to provide the user more understandable and more effective tools for this purpose. Finally, we would like to improve the composition tools, by developing more immersive view types, to observe and even play with the generated panorama, through either a spherical projection, or a virtual reality application.
References
Agarwala, A., Dontcheva, M., Agrawala, M., Drucker, S., Colburn, A., Curless, B., Salesin, D., Cohen, M.: Interactive digital photomontage. ACM Trans. Graph. 23(3), 294–302 (2004)
Bahmutov, G., Popescu, V., Mudure, M., Sacks, E.: Depth Enhanced Panoramas. In: M. Chantler (ed.) Vision, Video, and Graphics (2005). The Eurographics Association (2005). https://doi.org/10.2312/vvg.20051017
Calderero, F., Caselles, V.: Recovering Relative Depth from Low-Level Features Without Explicit T-junction Detection and Interpretation. Int. J. Comput. Vision 104, 38–68 (2013)
Chen, T., Cheng, M.M., Tan, P., Shamir, A., Hu, S.M.: Sketch2photo: internet image montage. ACM SIGGRAPH Asia 28(5), 124:1–124:10 (2009)
Diakopoulos, N., Essa, I., Jain, R.: Content based image synthesis. In: Proc. of International Conference on Image and Video Retrieval, pp. 299–307 (2004)
Eitz, M., Richter, R., Hildebrand, K., Boubekeur, T., Alexa, M.: Photosketcher: interactive sketch-based image synthesis. IEEE Computer Graphics and Applications (2011)
Grant, M., Boyd, S.: Graph implementations for nonsmooth convex programs. In: V. Blondel, S. Boyd, H. Kimura (eds.) Recent Advances in Learning and Control, Lecture Notes in Control and Information Sciences, pp. 95–110. Springer-Verlag Limited (2008). http://stanford.edu/~boyd/graph_dcp.html
Grant, M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx (2014)
Hartley, R.I., Zisserman, A.: Multiple View Geometry in Computer Vision, 2nd edn. Cambridge University Press, Cambridge (2004)
Hays, J., Efros, A.A.: Scene completion using millions of photographs. ACM Transactions on Graphics (SIGGRAPH) 26(3) (2007)
Highton, S.: Virtual Reality Photography (2003). http://www.vrphotography.com/. Last visited May 30, 2021
Hu, S.M., Chen, T., Xu, K., Cheng, M.M., Martin, R.R.: Internet visual media processing: A survey with graphics and vision applications. Visual Comput. 29(5), 393–405 (2013)
Johnson, M., Brostow, G.J., Shotton, J., Arandjelović, O., Kwatra, V., Cipolla, R.: Semantic photo synthesis. Comput. Graph. Forum 25(3), 407–413 (2006)
Johnson, M.K., Dale, K., Avidan, S., Pfister, H., Freeman, W.T., Matusik, W.: Cg2real: Improving the realism of computer generated images using a large collection of photographs. IEEE Trans. Visual Comput. Graphics 17(9), 1273–1285 (2011)
Lalonde, J.F., Hoiem, D., Efros, A.A., Rother, C., Winn, J., Criminisi, A.: Photo clip art. ACM SIGGRAPH 2007 26(3) (2007)
Lopez, A., Garces, E., Gutierrez, D.: Depth from a Single Image Through User Interaction. In: A. Munoz, P.P. Vazquez (eds.) Spanish Computer Graphics Conference (CEIG). The Eurographics Association (2014). https://doi.org/10.2312/ceig.20141109
Maps, G.: Street View (2021 (last visited February 1st, 2021)). https://www.google.com/streetview/
Persson, E.: Humus (2018). http://www.humus.name/index.php?page=3D. Last visited May 30, 2021
Reinhard, E., Efros, A.A., Kautz, J., Seidel, H.P.: On visual realism of synthesized imagery. Proc. IEEE 101(9), 1998–2007 (2013)
Ribelles, J., Gutierrez, D., Efros, A.: Buildup: interactive creation of urban scenes from large photo collections. Multimedia Tools Appl. 76(10), 12757–12774 (2017). https://doi.org/10.1007/s11042-016-3658-x
Saxena, A., Sun, M., Ng, A.Y.: Make3D: learning 3D scene structure from a single still image. PAMI 31(5), 824–840 (2009)
Tan, X., Xu, P., Guo, S., Wang, W.: Image Composition of Partially Occluded Objects. Computer Graphics Forum (2019). https://doi.org/10.1111/cgf.13867
Wang, O., Lang, M., Frei, M., Hornung, A., Smolic, A., Gross, M.: Stereobrush: interactive 2d to 3d conversion using discontinuous warps. In: Proc. of the 8th Eurographics Symposium on Sketch-Based Interfaces and Modeling (SBIM), pp. 47–54. ACM (2011)
Yücer, K., Sorkine-Hornung, A., Sorkine-Hornung, O.: Transfusive weights for content-aware image manipulation. In: Proc. of the Vision, Modeling and Visualization Workshop (VMV), pp. 57–64 (2013)
Zioulis, N., Karakottas, A., Zarpalas, D., Daras, P.: Omnidepth: Dense depth estimation for indoors spherical panoramas. In: Proceedings of the European Conference on Computer Vision (ECCV) (2018)
Zwillinger, D.: CRC Standard Mathematical Tables and Formulae, 31st Edition. Advances in Applied Mathematics. Chapman & Hall/CRC (2003)
Acknowledgements
The authors would like to thank the Department of Computer Science and Engineering of Universitat Jaume I for the scholarship received by Miguel Saura-Herreros, during his studies at the Master’s Degree on Intelligent Systems. In addition, we would like to thank the Institute of New Imaging Technologies, for supporting this work. Finally, we also would like to thank the anonymous referees for their useful suggestions.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: The funding note was missing.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saura-Herreros, M., Lopez, A. & Ribelles, J. Spherical panorama compositing through depth estimation. Vis Comput 37, 2809–2821 (2021). https://doi.org/10.1007/s00371-021-02239-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-021-02239-7