Skip to main content
SpringerLink
Log in

MPIPN: a multi physics-informed PointNet for solving parametric acoustic-structure systems

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

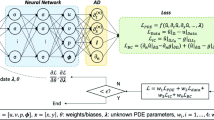
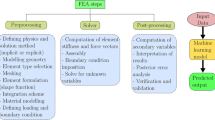
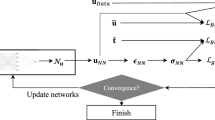
Machine learning is employed for solving physical systems governed by general nonlinear partial differential equations (PDEs). However, complex multi-physics systems such as acoustic-structure coupling are often described by a series of PDEs that incorporate variable physical quantities, which are referred to as parametric systems. There are lack of strategies for solving parametric systems governed by PDEs that involve explicit and implicit quantities. In this paper, a deep learning-based Multi Physics-Informed PointNet (MPIPN) is proposed for solving parametric acoustic-structure systems. First, the MPIPN introduces an enhanced point-cloud architecture that encompasses explicit physical quantities and geometric features of computational domains. Then, the MPIPN extracts local and global features of the reconstructed point-cloud as parts of solving criteria of parametric systems, respectively. Besides, implicit physical quantities are embedded by encoding techniques as another part of solving criteria. Finally, all solving criteria that characterize parametric systems are amalgamated to form distinctive sequences as the input of the MPIPN, whose outputs are solutions of systems. The proposed framework is trained by adaptive physics-informed loss functions for corresponding computational domains. The framework is generalized to deal with new parametric conditions of systems. The effectiveness of the MPIPN is validated by applying it to solve steady parametric acoustic-structure coupling systems governed by the Helmholtz equations. An ablation experiment has been implemented to demonstrate the efficacy of physics-informed impact with a minority of supervised data. The proposed method yields reasonable precision across all computational domains under constant parametric conditions and changeable combinations of parametric conditions for acoustic-structure systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data availability

The data will be available if the corresponding author receives any appropriate request. We are pleased and delighted to offer any help and access to the data we use in this research.

References

  1. Liao G, Wang Z, Luan C, Liu J, Yao X, Fu J (2021) Broadband controllable acoustic focusing and asymmetric focusing by acoustic metamaterials. Smart Mater Struct 30:045021

    Article  Google Scholar 

  2. Popa B-I, Zigoneanu L, Cummer SA (2011) Experimental acoustic ground cloak in air. Phys Rev Lett 106:253901

    Article  Google Scholar 

  3. Almeida GN, Vergara EF, Barbosa LR, Lenzi A, Birch RS (2021) Sound absorption metasurface with symmetrical coiled spaces and micro slit of variable depth. Appl Acoust 183:108312

    Article  Google Scholar 

  4. Sahai AK, Kaur M, Joseph S, Dey A, Phani R, Mandal R, Chattopadhyay R (2021) Multi-model multi-physics ensemble: a futuristic way to extended range prediction system. Front Clim 3:655919

    Article  Google Scholar 

  5. Renardy M, Rogers RC (2006) An introduction to partial differential equations. Springer Science & Business Media, Berlin

    Google Scholar 

  6. Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707

    Article  MathSciNet  Google Scholar 

  7. Cai S, Wang Z, Wang S, Perdikaris P, Karniadakis GE (2021) Physics-informed neural networks for heat transfer problems. J Heat Transfer 143:060801

    Article  Google Scholar 

  8. Haghighat E, Raissi M, Moure A, Gomez H, Juanes R (2021) A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput Methods Appl Mech Eng 379:113741

    Article  MathSciNet  Google Scholar 

  9. Lou Q, Meng X, Karniadakis GE (2021) Physics-informed neural networks for solving forward and inverse flow problems via the Boltzmann-BGK formulation. J Comput Phys 447:110676

    Article  MathSciNet  Google Scholar 

  10. Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L (2021) Physics-informed machine learning. Nat Rev Phys 3:422–440

    Article  Google Scholar 

  11. Meng X, Li Z, Zhang D, Karniadakis GE (2020) PPINN: parareal physics-informed neural network for time-dependent PDEs. Comput Methods Appl Mech Eng 370:113250

    Article  MathSciNet  Google Scholar 

  12. Wu J, Feng X, Cai X, Huang X, Zhou Q (2022) A deep learning-based multi-fidelity optimization method for the design of acoustic metasurface. Eng Comput 2:1–19

    Google Scholar 

  13. Qi CR, Su H, Mo K, Guibas LJ (2017) Pointnet: deep learning on point sets for 3d classification and segmentation. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 652–660

  14. Kashefi A, Rempe D, Guibas LJ (2021) A point-cloud deep learning framework for prediction of fluid flow fields on irregular geometries. Phys Fluids 33:2

    Article  Google Scholar 

  15. Lagari PL, Tsoukalas LH, Safarkhani S, Lagaris IE (2020) Systematic construction of neural forms for solving partial differential equations inside rectangular domains, subject to initial, boundary and interface conditions. Int J Artif Intell Tools 29:2050009

    Article  Google Scholar 

  16. Gao N, Wang M, Cheng B (2022) Deep auto-encoder network in predictive design of Helmholtz resonator: on-demand prediction of sound absorption peak. Appl Acoust 191:108680

    Article  Google Scholar 

  17. Wang B, Zhang W, Cai W (2020) Multi-scale deep neural network (MscaleDNN) methods for oscillatory stokes flows in complex domains. Commun Comput Phys 28:2139–2157

    Article  MathSciNet  Google Scholar 

  18. Liu Z, Cai W, Xu Z-QJ (2020) Multi-scale deep neural network (MscaleDNN) for solving Poisson-Boltzmann equation in complex domains. arXiv preprint arXiv:2007.11207

  19. Sirignano J, Spiliopoulos K (2018) DGM: A deep learning algorithm for solving partial differential equations. J Comput Phys 375:1339–1364

    Article  MathSciNet  Google Scholar 

  20. Kissas G, Yang Y, Hwuang E, Witschey WR, Detre JA, Perdikaris P (2020) Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput Methods Appl Mech Eng 358:112623

    Article  MathSciNet  Google Scholar 

  21. Zhu Y, Zabaras N, Koutsourelakis P-S, Perdikaris P (2019) Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J Comput Phys 394:56–81

    Article  MathSciNet  Google Scholar 

  22. Geneva N, Zabaras N (2020) Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. J Comput Phys 403:109056

    Article  MathSciNet  Google Scholar 

  23. Hesthaven JS, Rozza G, Stamm B (2016) Certified reduced basis methods for parametrized partial differential equations. Springer, Berlin

    Book  Google Scholar 

  24. Im J, de Barros FP, Masri SF (2023) Data-driven identification of partial differential equations for multi-physics systems using stochastic optimization. Nonlinear Dyn 111:1987–2007

    Article  Google Scholar 

  25. Im J, de Barros FP, Masri S, Sahimi M, Ziff RM (2023) Data-driven discovery of the governing equations for transport in heterogeneous media by symbolic regression and stochastic optimization. Phys Rev E 107:L013301

    Article  MathSciNet  Google Scholar 

  26. Berner J, Dablander M, Grohs P (2020) Numerically solving parametric families of high-dimensional Kolmogorov partial differential equations via deep learning. Adv Neural Inf Process Syst 33:16615–16627

    Google Scholar 

  27. Chen Y, Dong B, Xu J (2022) Meta-mgnet: meta multigrid networks for solving parameterized partial differential equations. J Comput Phys 455:110996

    Article  MathSciNet  Google Scholar 

  28. Gasick J, Qian X (2023) Isogeometric neural networks: A new deep learning approach for solving parameterized partial differential equations. Comput Methods Appl Mech Eng 405:115839

    Article  MathSciNet  Google Scholar 

  29. Gao H, Sun L, Wang J-X (2021) PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. J Comput Phys 428:110079

    Article  MathSciNet  Google Scholar 

  30. Kashefi A, Mukerji T (2022) Physics-informed PointNet: a deep learning solver for steady-state incompressible flows and thermal fields on multiple sets of irregular geometries. J Comput Phys 468:111510

    Article  MathSciNet  Google Scholar 

  31. Lu L, Jin P, Pang G, Zhang Z, Karniadakis GE (2021) Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 3:218–229

    Article  Google Scholar 

  32. Lu L, Meng X, Cai S, Mao Z, Goswami S, Zhang Z, Karniadakis GE (2022) A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data. Comput Methods Appl Mech Eng 393:114778

    Article  MathSciNet  Google Scholar 

  33. Goswami S, Yin M, Yu Y, Karniadakis GE (2022) A physics-informed variational DeepONet for predicting crack path in quasi-brittle materials. Comput Methods Appl Mech Eng 391:114587

    Article  MathSciNet  Google Scholar 

  34. Li Z, Kovachki NB, Azizzadenesheli K, Bhattacharya K, Stuart A, Anandkumar A (2020) Fourier neural operator for parametric partial differential equations. In: International Conference on Learning Representations

  35. Tripura T, Chakraborty S (2023) Wavelet neural operator for solving parametric partial differential equations in computational mechanics problems. Comput Methods Appl Mech Eng 404:115783

    Article  MathSciNet  Google Scholar 

  36. Feng J, Zheng X, Wang H, Wang H, Zou Y, Liu Y, Yao Z (2013) Low-frequency acoustic-structure analysis using coupled FEM-BEM method. Math Prbl Eng 20:13

    Google Scholar 

  37. Misra D (2019) Mish: a self regularized non-monotonic activation function, arXiv preprint arXiv:1908.08681

  38. Zangeneh-Nejad F, Fleury R (2019) Active times for acoustic metamaterials. Rev Phys 4:100031

    Article  Google Scholar 

  39. Song H, Ding X, Cui Z, Hu H (2021) Research progress and development trends of acoustic metamaterials. Molecules 26:4018

    Article  Google Scholar 

  40. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, Gaburro Z (2011) Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334:333–337

    Article  Google Scholar 

  41. Givoli D, Neta B (2003) High-order non-reflecting boundary scheme for time-dependent waves. J Comput Phys 186:24–46

    Article  MathSciNet  Google Scholar 

  42. Liu L, Jiang H, He P, Chen W, Liu X, Gao J, Han J (2019) On the variance of the adaptive learning rate and beyond. arXiv preprint arXiv:1908.03265

  43. Zhang M, Lucas J, Ba J, Hinton GE (2019) Lookahead optimizer: k steps forward, 1 step back. Adv Neural Inf Process Syst 32:2

    Google Scholar 

Download references

Acknowledgements

This research has been partially supported by the National Natural Science Foundation of China (NSFC) under Grant no. 52175231.

Author information

Authors and Affiliations

  1. School of Aerospace Engineering, Huazhong University of Science & Technology, Wuhan, 430074, Hubei, China

    Chu Wang, Jinhong Wu, Yanzhi Wang, Zhijian Zha & Qi Zhou

Authors
  1. Chu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinhong Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yanzhi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhijian Zha
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Qi Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Chu Wang: Conceptualization, Data curation, Methodology, Software, Writing – original draft. Jinhong Wu: Investigation, Writing – review & editing. Yanzhi Wang: Investigation, Validation. Zhijian Zha: Validation. Qi Zhou: Funding acquisition, Writing – review & editing.

Corresponding author

Correspondence to Qi Zhou.

Ethics declarations

Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, C., Wu, J., Wang, Y. et al. MPIPN: a multi physics-informed PointNet for solving parametric acoustic-structure systems. Engineering with Computers (2024). https://doi.org/10.1007/s00366-024-01998-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00366-024-01998-w

Keywords

Search

Navigation