Enforcing local boundary conditions in peridynamic models of diffusion with singularities and on arbitrary domains

Abstract

Imposing local boundary conditions and mitigating the surface effect at free surfaces in peridynamic (PD) models are often desired. The fictitious nodes method (FNM) “extends” the domain with a thin fictitious layer of thickness equal to the PD horizon size, and is a commonly used technique for these purposes. The FNM, however, is limited, in general, to domains with simple geometries. Here we introduce an algorithm for the mirror-based FNM that can be applied to arbitrary domain geometries. The algorithm automatically determines mirror nodes (in the given domain) of all fictitious nodes based on approximating, at each fictitious node, the “generalized” (or nonlocal) normal vector to the domain boundary. We tested the new algorithm for a peridynamic model of a classical diffusion problem with a flux singularity on the boundary. We show that other types of FNMs exhibit “pollution” of the solution far from the singularity point, while the mirror-based FNM does not and, in addition, shows a significantly faster rate of convergence to the classical solution in the limit of the horizon going to zero. The new algorithm is then used for mirror-based FNM solutions of diffusion problems in domains with curvilinear boundaries and with intersecting cracks. The proposed algorithm significantly improves the accuracy near boundaries of domains of arbitrary shapes, including those with corners, notches, and crack tips.

Graphical Abstract

Appendices

Appendix A Numerical implementation of peridynamic diffusion model with the fictitious nodes method

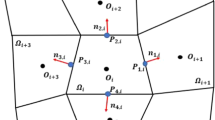
For spatial discretization, we discretize the whole PD interaction region $\Omega \cup \widetilde{\Omega }$ uniformly [2] into cells with nodes in the center of those cells. Figure 

Fig. 24

Uniform discretization for a peridynamic model. The circular region is the horizon region of node ${{\varvec{x}}}_{i}$

24 shows a 2D uniform discretization with grid spacing $\Delta x$ around a node ${{\varvec{x}}}_{i}$. Non-uniform grids are also possible [23, 55, 56], which may conform better to shapes with, for example, rounded boundaries [57], but this is not pursued in this work. Although only 2D problems are considered here, the extension to 3D cases should be straightforward.

To approximate the peridynamic integral operator, we use a meshfree method with one-point Gaussian quadrature [2], with a modification to account for partial nodal volumes covered by the horizon region of a node [4, 58, 59]. Faster numerical methods such as boundary-adapted spectral methods, [35, 51] can be alternative options.

The discretized PD Laplace’s equation (see Eqs. (3) and (4)) for each ${{\varvec{x}}}_{i}\in\Omega$ at ${n}^{{\text{th}}}$ load step becomes:

$$\sum_{\begin{array}{c}j\in {\mathcal{H}}_{i}\\ j\ne i\end{array}}\frac{{u}_{j}^{n}-{u}_{i}^{n}}{{\xi }_{ij}^{2}}\Delta {A}_{ij}=0$$

(22)

where the superscript $n$ means ${n}^{{\text{th}}}$ load step; the subscripts $i$ and $j$ denote the current node ${{\varvec{x}}}_{i}$ and its family node ${{\varvec{x}}}_{j}$ respectively, in the discretized domain; ${\mathcal{H}}_{i}$ is the horizon region of node ${{\varvec{x}}}_{i}$ and $j\in {\mathcal{H}}_{i}$ includes all the nodes covered by ${\mathcal{H}}_{i}$ (fully or partially); ${\xi }_{ij}=\Vert {{\varvec{x}}}_{j}-{{\varvec{x}}}_{i}\Vert$ and $\Delta {A}_{ij}$ is the area of node ${{\varvec{x}}}_{j}$ covered by ${\mathcal{H}}_{i}$. The discretized versions for other equations are similar to Eq. (22).

In Taylor-based and mirror-based fictitious nodes methods, the equilibrium system can be solved iteratively using the linear Conjugate Gradient (CG) solver combined with additional criteria to check for the convergence of the solution. At each iteration or solution step, the CG solver is called and the solution in the domain and fictitious region is updated. To minimize the overall computational cost, the tolerance in the CG solver is set to be ${10}^{-2}$ at first and then decreased with solution steps by a factor until it reaches ${10}^{-6}$. This treatment can lead to simulations that are 50% more efficient than fixing the tolerance in the CG solver to be ${10}^{-6}$ from the start of the simulation. The system converges when the solutions in the domain obtained for two sequential solution steps, differ, in terms of norm-2 of their relative difference, by less than a given tolerance (${10}^{-6}$ was used in this work). The detailed workflow for a complete simulation is shown in Fig. 

Fig. 25

Workflow for the peridynamic simulation with Taylor/mirror FNM

25.

Appendix B FEM modeling of the steady-state diffusion problem in a disk with a crack

To obtain the classical FEM-based solution for the problem shown in Fig. 18, the ANSYS Workbench Steady-State Thermal solver is used. In the FE model, the two crack surfaces are generated by two arcs with the same small curvature and the maximum space between them is $0.01$, which equals the grid size in the corresponding PD model. For the mesh, as shown in Fig. 

Fig. 26

FEM mesh (a) over the whole disk; (b) near the crack tip

26, the element order is selected to be program-controlled and all elements are quadratic triangles with a maximum size equal to 0.05. The total number of nodes and elements are 9312 and 4548, respectively, and reduced integration is selected. All other options in the solver are set to their default values.