1 Introduction

The bandgap property in periodic microstructural materials, e.g., photonic crystals (PtCs) and phononic crystals (PnCs), can confine the propagation of photonic, elastic, and acoustic waves with specific frequencies. This unique property has received extensive research interest in the past few decades and has given rise to widespread applications such as wave isolators and waveguides [1, 2], imaging [3, 4], beam splitters [5], beam bending [6], optical fibers [7], and signal processing [8]. The recent discovery of topological insulators [9] that obey the conventional bulk-boundary correspondence [10, 11] has brought new insights into the novel application of bandgap materials. Among the structures in acoustic systems, phononic bandgap crystals are ideal for realizing topologically protected states [12,13,14,15,16,17,18,19,20].

The traditional intuition and parameter design methods have provided an excellent understanding of bandgap crystals [21,22,23,24]. Nevertheless, they were limited to the regular shape and arrangement of scatters and resonators, and it was a challenge to manipulate acoustic and mechanical waves efficiently. With the development of computer technology, e.g., topology optimization, deep learning, and addictive manufacturing, efficient approaches have been exploited to pursue structures or metamaterials with desired properties, e.g., photonic or phononic bandgaps [25,26,27,28,29,30,31,32], structural frequency response [33], wave field manipulation [34,35,36], thermal performance [37, 38], shell-infill composites [39, 40], and robust design with uncertainties [41,42,43].

The bandgap size in crystalline structures does not monotonically increase or decrease with the volume fraction of the constituent material. Therefore, a volume fraction constraint is often imposed in topology optimization algorithms to stabilize the optimization process [44, 45]. Actually, the bandgap width is the priority of topology optimization, and the volume fraction is less critical for the design of bandgap crystals. More seriously, topology optimization constrained by a given volume fraction of the solid often leads to an impractical design, as shown in Fig. 1a, which does not contain air channels for the propagation of acoustic waves. Numerically, the band diagram displays a wide bandgap where flat bands are caused by the pseudo-air resonant modes [46]. Such a design reflecting all acoustic waves is impractical and should be avoided during topology optimization. In this paper, we will establish a new topology optimization approach for acoustic bandgap crystals constrained by air connectivity based on the floating projection topology optimization (FPTO) method [40, 47,48,49], where the traditional volume constraint is replaced by the non-zero permeability constraint to ensure air connectivity. As a result, the optimized design shown in Fig. 1b always contains penetrable air channels for the propagation of acoustic waves outside the bandgap.

Fig. 1
figure 1

Topology optimization for maximizing the 3rd-order band gap constrained by the a volume fraction and b relative permeability. The schematic design diagrams contain 3 × 3 periodic units, where the red dashed box indicates one unit cell. The solid is colored white, and the air is black. The band diagrams include calculated bands (black lines), the optimized gap range, and simulated results (red dots)

Full size image

Topology optimization methods have also been applied in realizing topological insulators, leading to outstanding discoveries. Christiansen et al. [50] optimized the transmission properties of functional devices, e.g., the backscattering-protected acoustic energy transport, by density-based topology optimization. This approach does not require the pre-existence of pseudospin states nor the Chern numbers of topological phases but relies on an initial guess structure. By specifying different frequencies for the dipolar and quadrupolar modes to break the double Dirac cones, Chen et al. [51] obtained the design of photonic topological insulators, which was then further extended to the acoustic topological insulators [52]. However, the previous research focuses only on the odd-order bandgap structures, and the success of the proposed method relies highly on the initial guess design and the manually selected frequencies for the dipolar and quadrupolar modes. By customizing Dirac cones with optimized local density of states (LDOS) [53,54,55] in acoustic PnCs via the genetic algorithm, Dong et al. [56] constructed topological insulators exhibiting unique functionalities, such as zigzag transmission and one-way transport. Du et al. [57] developed the quantum valley Hall insulators by engineering the Berry curvature and tailoring the band structure, which skipped the manual introduction and tuning of the Dirac cone feature. Since the crystalline symmetry is highly related to the topological property, Fu et al. [58] proposed the parity of eigenstates to indicate nontrivial unit cells. Luo et al. [59] proposed the explicit topology optimization method for designing photonic topological insulators by constraining the symmetry indicators.

In all cases, the bandgap properties of trivial and nontrivial crystals are fundamental for topologically protected states. Meanwhile, the optimized crystalline structures provide a wide operational bandwidth for forming the topological phase of matter. This paper presents novel acoustic PnCs achieved with a maximized frequency gap on any specified band order. From bandgap crystal design to topologically protected structure design, two approaches based on the parity inversion are suggested for PnCs with a maximized odd/even-order bandgap, respectively.

The rest of the paper is organized as follows. Section 2 presents the acoustic eigenvalue problem based on Bloch’s theorem. Section 3 formulates the bandgap optimization problem constrained by air permeability. The three-field FPTO method is demonstrated, followed by the numerical implementation procedure. Section 4 presents some numerical results, and conclusions are drawn in Sect. 5.

2 Finite element analysis of acoustic unit cell

The propagation of acoustic waves is generally governed by the following Helmholtz equation

$$-\nabla \bullet \left[\frac{1}{\rho \left(\mathbf{r}\right)}\nabla p\left(\mathbf{r}\right)\right]+\frac{{\partial }^{2}}{\partial {t}^{2}}\left[\frac{p\left(\mathbf{r}\right)}{B\left(\mathbf{r}\right)}\right]=0$$
(1)

where p(r) is the pressure field. r = (x, y) denotes the position vector. ρ is the material mass density, and B is the bulk modulus. Given the periodicity of PnCs, the pressure distribution p(r) can be taken in the form of Bloch wave expansion

$$p\left(\mathbf{r},\mathbf{k}\right)={p}_{k}\left(\mathbf{r}\right){\text{exp}}\left(j\mathbf{k}\bullet \mathbf{r}\right){\text{exp}}\left(j\omega t\right)$$
(2)

where \({p}_{{\text{k}}}\left({\varvec{r}}\right)\) is a periodic function with the same periodicity as the crystal lattice, i.e., \({p}_{{\text{k}}}\left({\varvec{r}}+\mathbf{a}\right)={p}_{{\text{k}}}\left({\varvec{r}}\right)\) with the lattice vector a. k = (kx, ky) denotes the Bloch wave vector. j is the imaginary number, i.e., \({j}^{2}=-1\). By substituting Eq. (2) into Eq. (1), we can obtain the typical eigenvalue problem under the framework of finite element analysis

$$\left({\varvec{K}}-{\omega }^{2}{\varvec{M}}\right){\varvec{p}}=0$$
(3)

where the global stiffness matrix K and mass matrix M can be calculated by the following equations.

$${\varvec{K}}=\sum_{{\varvec{e}}}\frac{1}{{\rho }_{{\varvec{e}}}}\left({{\varvec{K}}}_{e}^{1}+j{k}_{x}{{\varvec{K}}}_{e}^{2}+j{k}_{y}{{\varvec{K}}}_{e}^{3}+\left({k}_{x}^{2}+{k}_{y}^{2}\right){{\varvec{K}}}_{e}^{4}\right)$$
(4a)
$${\varvec{M}}=\sum_{{\varvec{e}}}\frac{1}{{B}_{{\varvec{e}}}}{{\varvec{M}}}_{{\varvec{e}}}$$
(4b)

where the elemental stiffness and mass matrices \({\mathbf{K}}_{{\varvec{e}}}\) and \({\mathbf{M}}_{{\varvec{e}}}\) \((e=\mathrm{1,2},\cdots )\), can be expressed as

$${{\varvec{K}}}_{e}^{1}={\int }_{\Omega }\left(\frac{\partial {{\varvec{N}}}^{T}}{\partial x}\frac{\partial {\varvec{N}}}{\partial x}+\frac{\partial {{\varvec{N}}}^{T}}{\partial y}\frac{\partial {\varvec{N}}}{\partial y}\right)\mathrm{d\Omega }$$
(4c)
$${{\varvec{K}}}_{e}^{2}={\int }_{\Omega }\left(\frac{\partial {{\varvec{N}}}^{T}}{\partial x}{\varvec{N}}-{{\varvec{N}}}^{T}\frac{\partial {\varvec{N}}}{\partial x}\right)\mathrm{d\Omega }$$
(4d)
$${{\varvec{K}}}_{e}^{3}={\int }_{\Omega }\left(\frac{\partial {{\varvec{N}}}^{T}}{\partial y}{\varvec{N}}-{{\varvec{N}}}^{T}\frac{\partial {\varvec{N}}}{\partial y}\right)\mathrm{d\Omega }$$
(4e)
$${{\varvec{K}}}_{e}^{4}={\int }_{\Omega }\left({{\varvec{N}}}^{T}{\varvec{N}}\right)\mathrm{d\Omega }$$
(4f)
$${{\varvec{M}}}_{e}={\int }_{\Omega }\left({{\varvec{N}}}^{T}{\varvec{N}}\right)\mathrm{d\Omega }$$
(4g)

where Ω denotes an element domain, and N is the shape function matrix of a linear four-node element.

This paper focuses on the design of acoustic bandgap crystals with a square lattice under the C4v symmetry (see Fig. 2a), even though the proposed design approach can be equally extended to other lattice types. The wave vector can be restricted to the first irreducible Brillouin zone (FIBZ) [60] due to the periodicity, as shown in Fig. 2b. To this end, the mth eigenfrequency, \({\omega }_{m}\) (\(m=\mathrm{1,2}, \dots )\) and eigenvector \({{\varvec{p}}}_{{\varvec{m}}}\) can be calculated for the specified wave vector k along the boundaries (M-Γ-X-M) of the FIBZ [61].

Fig. 2
figure 2

a An illustrated primitive unit cell of 2D acoustic crystals with the C4v symmetry, where the blue dash lines denote the symmetric axis. b The reciprocal space. The yellow area and its boundaries (M-Γ-X-M) indicate the first irreducible Brillouin zone

Full size image

3 Design of acoustic bandgap structures via topology optimization

3.1 Problem statement

To achieve a wide bandgap and ensure air connectivity, the optimization problem for the design of acoustic crystals can be stated as follows

$${\text{max}}:f=\frac{{\text{min}}{\omega }_{m+1}\left(\mathbf{k}\right)-{\text{max}}{\omega }_{m}\left(\mathbf{k}\right)}{\frac{1}{2}\left({\text{min}}{\omega }_{m+1}\left(\mathbf{k}\right)+{\text{max}}{\omega }_{m}\left(\mathbf{k}\right)\right)}$$
(5)
$${\text{s}}.{\text{t}}.:\begin{array}{c}\\ {\kappa }^{H}={\kappa }^{*}\\ {x}_{e}={x}_{{\text{min}}} or 1, (e=\mathrm{1,2},\cdots )\end{array}$$
(5a)

where the objective function aims to maximize the normalized bandgap size (the ratio between the bandwidth and the mid-band frequency). The design domain is discretized into fixed-mesh elements, and xe is the design variable for the eth element. Physically, xe can be viewed as the volume fraction of air within the eth element, and xe = 1 denotes that element e is filled with the air and xe = xmin with the solid. xmin is a small positive value to avoid the numerical singularity, e.g., xmin = 10–9 in this paper. \({\kappa }^{H}\) and \({\kappa }^{*}\) are the effective permeability and the corresponding constraint value. As explained in the introduction, the imposed permeability constraint aims to ensure the connected air channels. In particular, the problem does not contain a volume constraint used in the traditional topology optimization approaches. Based on the homogenization theory [62], the effective permeability \({\kappa }^{H}\) for a given design can be calculated by

$${\kappa }^{H}=\frac{1}{\Omega }{\int }_{\Omega }\kappa ({x}_{e})(\mathbf{I}-{\varvec{\upmu}})d\Omega$$
(6)

where \(\kappa ({x}_{e})\) is the artificial permeability within the element e. I is the identity matrix, and µ is the solution computed by finite element analysis of the periodic unit cell under a uniform test function, e.g., [1, 0]T and [0, 1]T.

However, the topology optimization problem in Eq. (5) is challenging to be solved mathematically due to involving a large amount of discrete design variables. To circumvent this difficulty, the variables are relaxed with the continuous ones, i.e., \({x}_{{\text{min}}}\le {x}_{e} \le 1\). Meanwhile, the discrete (or called 1/0) constraints of the design variables will be simulated by the floating projection constraint [40], which will be illustrated in the next section. Due to the relaxation of the design variables, all material properties should also be interpolated between \({x}_{{\text{min}}}\) and 1. The material properties involved in this topology optimization problem include bulk modulus, mass density and relative permeability. To assign material properties within intermediate elements, we can apply the interpolation scheme as

$$\left\{\begin{array}{c}\frac{1}{B}=\frac{1}{{B}_{a}}{x}_{e}\\ \frac{1}{\rho }=\frac{1}{{\rho }_{a}}{x}_{e}\\ \kappa ={\kappa }_{a}{x}_{e}\end{array}\right.$$
(7)

where Ba and \({\rho }_{a}\) are material constants of the air, and \({\kappa }_{a}\)= 1 denotes the relative air permeability. The solid medium can then be represented by the lower limit, i.e., xe = xmin. Note that the significant contrast in material properties between the air and solid is to ensure the solid parts are ‘hard’ enough despite the equivalent fluid assumption. An enormous material density for the solid medium is not necessary for an actual application. For instance, the scatters in PnCs can be made of epoxy, a light material that perfectly reflects sound waves.

3.2 Sensitivity analysis

The sensitivity, defined as the variation of the objective and constraint functions with respect to the design variables, is crucial to guide the optimization in the density-based methods. However, the objective function in Eq. (5a) is non-differentiable since the upper and lower bounds of the frequency gap, \({\text{min}}{\omega }_{m+1}\left({\varvec{k}}\right)\) and \({\text{max}}{\omega }_{m}\left({\varvec{k}}\right)\), vary with different wave vector points ki during the optimization process. To calculate the sensitivity, the bounds are modified by the p-norm approximation as follows.

$$\left\{\begin{array}{l}{\text{max}}{\omega }_{m}\left({\varvec{k}}\right)={\left[\sum_{i=1}^{nk}{\omega }_{m}^{s}\left({{\varvec{k}}}_{i}\right)\right]}^{1/s}\\ {\text{min}}{\omega }_{m+1}\left({\varvec{k}}\right)={\left[\sum_{i=1}^{nk}{\omega }_{m+1}^{-s}\left({{\varvec{k}}}_{i}\right)\right]}^{-1/s}\end{array}\right.$$
(8)

where ki is the wave vector evenly distributed on the boundary of FIBZ. When s tends to infinity, Eq. (8) will be strictly held. In our numerical implementation, s = 8 is applied. Then, the sensitivity of the modified objective function can be expressed as

$$\frac{df}{d{x}_{e}}=4\frac{{\text{max}}{\omega }_{m}\left({\varvec{k}}\right)\frac{\partial {\text{min}}{\omega }_{m+1}\left({\varvec{k}}\right)}{\partial {x}_{e}}-{\text{min}}{\omega }_{m+1}\left({\varvec{k}}\right)\frac{\partial {\text{max}}{\omega }_{m}\left({\varvec{k}}\right)}{\partial {x}_{e}}}{{\left[{\text{min}}{\omega }_{m+1}\left({\varvec{k}}\right)+{\text{max}}{\omega }_{m}\left({\varvec{k}}\right)\right]}^{2}}$$
(9)

According to Huang et al. [63], the partial derivative of the mth eigenfrequencies can be computed as

$$\frac{\partial {\omega }_{m}\left({\varvec{k}}\right)}{\partial {x}_{e}}=\frac{1}{2{\omega }_{m}}{\varvec{p}}{({\varvec{k}})}_{m}^{T}\left(\frac{\partial {\varvec{K}}}{\partial {x}_{e}}-{\omega }_{m}^{2}\frac{\partial {\varvec{M}}}{\partial {x}_{e}}\right){\varvec{p}}{\left({\varvec{k}}\right)}_{m}$$
(10)

where \({\varvec{p}}{\left({\varvec{k}}\right)}_{m}\) is the corresponding eigenvector. The partial derivative of the bounds under the p-norm approximation can be calculated as

$$\left\{\begin{array}{l}\frac{\partial {\text{max}}{\omega }_{m}\left({\varvec{k}}\right)}{\partial {x}_{e}}={\sum_{i=1}^{nk}\left[{\omega }_{m}^{s-1}\left({{\varvec{k}}}_{i}\right)\bullet \frac{\partial {\omega }_{m}\left({{\varvec{k}}}_{i}\right)}{\partial {x}_{e}}\right]\bullet \left[\sum_{i=1}^{nk}{\omega }_{m}^{s}\left({{\varvec{k}}}_{i}\right)\right]}^{s-1}\\ \frac{\partial {\text{min}}{\omega }_{m+1}\left({\varvec{k}}\right)}{\partial {x}_{e}}={\sum_{i=1}^{nk}\left[{\omega }_{m+1}^{-s-1}\left({{\varvec{k}}}_{i}\right)\bullet \frac{\partial {\omega }_{m+1}\left({{\varvec{k}}}_{i}\right)}{\partial {x}_{e}}\right]\bullet \left[\sum_{i=1}^{nk}{\omega }_{m+1}^{-s}\left({{\varvec{k}}}_{i}\right)\right]}^{-\frac{1}{s}-1}\end{array}\right.$$
(11)

The sensitivity of the effective permeability constraint can be expressed as

$$\frac{d{\kappa }^{H}}{d{x}_{e}}=\frac{1}{\Omega }{\int }_{\Omega }{({\varvec{I}}-{\varvec{\mu}})}^{T}\frac{\partial \kappa ({x}_{e})}{{x}_{e}}({\varvec{I}}-{\varvec{\mu}})d\Omega$$
(12)

3.3 Topology optimization approach and numerical implementation

The three-field FPTO method [40] defines the design field (\({\overline{x} }_{e}\)), the filter field (\({\widetilde{x}}_{e}\)) and the physical field (\({x}_{e}\)) based on variable substitution [64]. This method seeks optimal solutions in the design field, which are transferred to the filter field according to the filtering scheme [65] as

$${\widetilde{x}}_{j}=\frac{\sum_{j}{w}_{ej}{\overline{x} }_{e}}{\sum_{j}{w}_{ej}}$$
(13)

where wej is a weight factor determined by the distance rej between the centers of elements e and j as

$${w}_{ej}=\left\{\begin{array}{cc}\frac{{r}_{{\text{min}}}-{r}_{ej}}{\sum_{j}\left({r}_{{\text{min}}}-{r}_{ej}\right)}& e\in {\Omega }_{j}\\ 0& e\notin {\Omega }_{j}\end{array}\right.$$
(14)

where the filter support domain Ωj is defined by a specific radius rmin. Optimization without the filter may lead to the checkerboard pattern in the optimized structure. To solve this problem and avoid numerical instability, the above filter is adopted in our numerical implementation. The weight factors for different meshes can be computed in advance of the optimization process to save the computational cost. Then the solution is transferred to the physical field by the projection scheme [66] as

$${x}_{e}=\frac{{\text{tanh}}\left({\beta }_{1}\bullet \eta \right)+{\text{tanh}}\left[{\beta }_{1}\bullet \left({\widetilde{x}}_{e}-\eta \right)\right]}{{\text{tanh}}\left({\beta }_{1}\bullet \eta \right)+{\text{tanh}}\left[{\beta }_{1}\bullet \left(1-\eta \right)\right]}$$
(15)

where β1 can be determined by the steepness β of the floating projection constraint in Eq. (15), e.g., β1 = 1.2 × β, and the threshold η = 0.5 is adopted. This projection function can suppress the grayscale resulting from the substitution filter. Based on the substitution between the three fields of variables, the sensitivities of the objective and constraint functions can be derived by using the chain rule as

$$\frac{df}{d{\overline{x} }_{e}}=\sum_{j}\left(\frac{df}{d{x}_{j}}\frac{\partial {x}_{j}}{{\partial }_{{\widetilde{x}}_{j}}}\frac{\partial {\widetilde{x}}_{j}}{{\partial }_{{\overline{x} }_{e}}}\right)$$
(16)
$$\frac{d{\kappa }^{H}}{d{\overline{x} }_{e}}=\sum_{j}\left(\frac{d{\kappa }^{H}}{d{x}_{j}}\frac{\partial {x}_{j}}{{\partial }_{{\widetilde{x}}_{j}}}\frac{\partial {\widetilde{x}}_{j}}{{\partial }_{{\overline{x} }_{e}}}\right)$$
(17)

where \(\frac{\partial {\widetilde{x}}_{j}}{{\partial }_{{\overline{x} }_{e}}}\) and \(\frac{\partial {x}_{j}}{{\partial }_{{\widetilde{x}}_{j}}}\) can be derived from the substitution filtering scheme in Eq. (13) and the projection scheme in Eq. (15), respectively. The derivative of the objective and the constraint functions with respect to the physical variables are given in Eqs. (9) and (12), respectively. The design variables can then be updated according to the modified Optimality Criteria (OC) as

$${\overline{x} }_{e}={\overline{x} }_{e}^{k-1}\left(1+\frac{df}{d{\overline{x} }_{e}}+\lambda \frac{d{\kappa }^{H}}{d{\overline{x} }_{e}}\right)$$
(18)

where λ is the Lagrange multiplier determined by the permeability constraint. The superscript k − 1 indicates the number of the last iteration. Meanwhile, the upper and lower bounds of \({\overline{x} }_{e}\) are enforced.

To simulate the 0/1 constraints in the original problem, the implicit floating projection constraint [46] is imposed on the design field as

$${\overline{x} }_{e}=\frac{{\text{tanh}}\left(\beta \bullet \psi \right)+{\text{tanh}}\left[\beta \bullet \left({\widetilde{x}}_{e}-\psi \right)\right]}{{\text{tanh}}\left(\beta \bullet \psi \right)+{\text{tanh}}\left[\beta \bullet \left(1-\psi \right)\right]}$$
(19)

where the floating threshold \(\psi\) can be determined by ensuring the summation of design variables \(\sum_{e}{\overline{x} }_{e}\) after the projection remains the same as before. β starts from a small positive value, e.g., \({10}^{-6}\) until a convergent element-based design is achieved, indicated by the maximum variation of the design variables being small enough as

$${\text{max}}({\overline{x} }_{e}^{k}-{\overline{x} }_{e}^{k-1})\le 0.01$$
(20)

Then, β increases with \(\Delta \beta\) (e.g., = 1) until the difference between the element-based design and its post-processed smooth design is acceptable, as illustrated below.

The smooth design is extracted from the convergent element-based design under a given β through image post-processing [40]. However, regarding the performance demonstrated by the objective functions, there might be a significant difference between an optimized element-based design and the corresponding post-processed smooth design. Thus, we shall calculate the relative difference in their objective values as

$${\text{tol}}=\frac{\left|{f}_{{\text{smooth}}}-f\right|}{\left|f\right|}$$
(21)

where the objective value of the smooth design can be calculated by projecting the pixel-based smooth representation back to the original mesh and computing one more finite element analysis.

If the relative difference in Eq. (21) is larger than the acceptable value, such as 1% in this paper, it denotes that the current element-based design does not meet the desired 0/1 level. As mentioned above, β in Eq. (19) increases by a specified value Δβ to impose a stricter 0/1 constraint, and the optimization continues. Otherwise, the whole optimization process is stopped, and the final convergent element-based design can be accurately represented by the smooth design for possible fabrication.

In summary, the optimization procedure can be outlined as follows.

Step 1: Discretize the design domain with fixed-mesh finite elements. Initial physical variables \({{\varvec{x}}}_{e}^{0}\) are randomly assigned for each element, and then design variables and filtering variables are initialized as \({\widetilde{{\varvec{x}}}}_{e}^{0}={\overline{{\varvec{x}}} }_{e}^{0}={{\varvec{x}}}_{e}^{0}\).

Step 2: Assemble global matrices K and M according to the standard finite element formulation.

Step 3: Solve the eigenvalue problem in Eq. (3) to obtain eigenfrequencies and eigenvectors.

Step 4: Calculate the sensitivities for the objective and constraint functions.

Step 5: Update physical variables according to Eq. (15) and design variables according to Eqs. (18) and (19).

Step 6: Repeat Steps 2–5 until the topology converges.

Step 7: Extract a post-processed smooth design from the convergent element-based design.

Step 8: Conduct finite element analysis for the smooth design and calculate the relative difference defined in Eq. (21). If the difference exceeds 1%, repeat steps 2–8. Otherwise, the whole optimization is stopped.

Our numerical experience indicates that the optimization problem can also be solved by the method of moving asymptotes (MMA) [67] by introducing two inequality constraints for the original equality permeability constraint.

4 Results and discussion

4.1 Topology optimization of acoustic bandgap crystals

In this section, we demonstrate the effectiveness of the proposed topology optimization method. The PnCs are composed of solid inclusions and air matrix, represented by white and black in the figures. The material parameters are ρa = 1.21 kg/m3 and Ba = 1.42 × 10–4 GPa. The speed of sound waves propagating in the air is 343 m/s. The design domain is first discretized with 64 × 64 four-node bilinear elements, and the filter radius rmin = 3 is applied.

The evolutionary histories of the objective value, relative air permeability and element-based topology for maximizing the 1st band gap are shown in Fig. 3. Starting from an initial structure with randomly assigned design variables, the negative objective value indicates no band gap exists. To satisfy the constraint \({\kappa }^{H}=0.3\), the relative air permeability value drops rapidly from about 0.6 in a few steps while the objective value increases slowly. After the 8th iteration, the air connectivity constraint is strictly satisfied, and then the target band gap opens and enlarges significantly. The topology first converges in the 36th iteration without 0/1 constraints on design variables (\(\beta ={10}^{-6}\)). Thus, many intermediate elements exist on the boundaries between solids and the air. To gradually impose the implicit floating projection constraint, β increases by Δβ = 1 after achieving a new convergent topology. The optimization process stops after 66 iterations when the calculated relative difference of the bandgap between the element-based design and its smooth design is smaller than 1%. The final design, consisting of four maraca-like bars and four connected air chambers, has a wide band gap of 82% in normalized gap size. Together with the 64 × 64 mesh, the problem is also solved by using the 96 × 96 and 128 × 128 meshes. The evolution histories of the bandgap size and corresponding element-based results are shown in Fig. 4. It can be seen that the gapsize converges at almost the same level, demonstrating that the optimized design depends weekly on the mesh size.

Fig. 3
figure 3

Evolution histories of PnCs maximizing the 1st bandgap. The insets depict the element-based designs at the 1st and 15th iterations and four convergent solutions corresponding to different values of β

Full size image
Fig. 4
figure 4

Evolution histories of the 1st bandgap by using different meshes and corresponding element-based results

Full size image

Optimized results for seeking maximized gaps on the specified band orders are listed in Fig. 5. For the 128 × 128 mesh, the processing time of these examples varies from 1459 to 7236 s, depending on the target band order. The acceptable relative difference value in Eq. (21) is easy to be satisfied for a low-order (i.e., m = 1, 2) bandgap structure so that the optimization stops within significantly fewer iterations than that for a high-order PnC with complex structures. The mid-gap frequency increases as the target band order rises, decreasing the relative bandgap size, while the optimized structures of solid scatters become more complex. To ensure the optimized design contains air channels with solid scatters, \({\kappa }^{H}=0.3\) is applied. Moreover, the maximum band gap size relies highly on the relative permeability.

Fig. 5
figure 5

PnC unit cells with a maximized gap on the 1st–6th bands, respectively

Full size image

Figure 6 gives the optimized results for maximizing the first bandgap under different constraint values, where 128 × 128 mesh and rmin = 5 are applied. As the constraint value increases, the volume fraction of solids in the optimized PnCs and the resulting band gap sizes gradually decrease. Generally, a lower permeability gives a topology with larger solid inclusions and narrower air channels, making it easier to confine sound waves. The corresponding band gap is broader than that with a higher constraint value. However, a too-small constraint value will lead to impractical results with local resonance. In contrast, the too-large constraint value will make it difficult to open a band gap. Thus, the constraint value \({\kappa }^{*}\) should be selected appropriately. In our numerical implementation, we find that it is easier to achieve optimized results with air channels when \(\kappa^{*} = 0.3{-}0.4\). The maximized gap sizes for the 1st to 6th bands are listed in Table 1, where N/A indicates that the optimization fails to obtain practical bandgap crystals with specific constraint values.

Fig. 6
figure 6

Optimized results for PnCs with the first-order band gap varying with the specified air connectivity constraint \({\kappa }^{*}\)

Full size image
Table 1 Maximized gap sizes subjected to different air permeability values
Full size table

4.2 Topological insulators with a gap above the odd-order band

The topological property can be indicated by the 2D polarization P = (Px, Py) [18, 58, 68]. Py = Px due to the mirror symmetries of the C4v lattice, and Px can be calculated by

$${P}_{x}=\frac{1}{2}\left(\sum_{n}{q}^{n}{\text{mod}} 2\right), n=\mathrm{1,2},\dots ,m$$
(22)
$${\left(-1\right)}^{{q}^{n}}=\frac{{\eta }_{n}({\text{X}})}{{\eta }_{n}(\Gamma )}$$
(23)

where \({\eta }_{n}\) represents the odd parity (−) or even parity ( +) at the high symmetric points of FIBZ, which can be determined by the modal symmetries of the nth eigenmodes. \({\eta }_{n}({\text{X}})\)/\({\eta }_{n}(\Gamma )\) =  − 1 denotes one pair of opposite parities. Thus, we can get P = (1/2, 1/2) when the UC has odd pair(s) of opposite parities, indicating a nontrivial topological phase. In contrast, P = (0, 0) is for the trivial UC having even pairs of opposite parities.

The key to constructing TIs by PnCs lies in seeking the topological nontrivial units, which can be realized by translating the periodic unit cell along specific paths. For a PnC hosting an odd-order band gap, e.g., m = 3, UC2 can be obtained by translating the UC1 with (a/2, a/2), as shown in Fig. 7a. It can be proved that the translation leads to the parities preserving at point Γ but reversing at point X. As a result, UC1 and UC2 will have different (i.e., even/odd) pairs of opposite parities. As shown in Fig. 6b, UC1 has two pairs of opposing parties, while UC2 has only one pair. Therefore, UC1 is topological trivial, and UC2 is nontrivial.

Fig. 7
figure 7

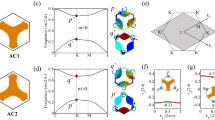
Translation of PnCs with a 3rd band gap. a The optimized unit cell UC1 and its translated counterpart UC2. b The band diagrams and polarization parities, ‘ + ’ for even and ‘ −’ for odd parity. The insets show the sound pressure distribution of the first three eigenmodes. The translation reverses the parities of eigenstates at point X, while those preserve at point Γ

Full size image

Then, a second-order topological insulator can be formed by combining the nontrivial and trivial UCs [69,70,71]. As shown in Fig. 8, we built the slab-like supercells with 12 × 12 unit cells, where 6 × 6 Nontrivial unit cells are located at the top right corner, and others are trivial. The unit cell size is a = 18.9 mm, and computational domain is 12a × 12a. Plane Wave Radiation conditions are imposed on the boundaries. In the calculated eigenspectra, we can find wide gaps between the edge and the bulk states, where topological corner states can potentially emerge. The absolute sound pressure fields with different frequencies corresponding to the gapped edge and in-gap corner states are given in insets(i)–(vi) of Fig. 8, where the sound localization at corners has a higher sound pressure level than that propagating through edges.

Fig. 8
figure 8

The calculated eigenspectra (left), gapped edge states (middle), and in-gap corner states (right) of topological insulators by optimized PnCs with the 1st (a), 3rd (b), and 5th (c) band gaps, respectively. The inset of the eigenspectra indicates the combination of topological trivial and nontrivial units

Full size image

4.3 Topological insulators with a gap above the even-order band

The above approach to creating topological insulators is only practical for PnCs hosting an odd-order band gap. The parity inversion at X will not change the topological phase of the unit cell having even bands below the bandgap. For an optimized PnC with an even-order band gap, e.g., m = 2, we can translate the unit cell with (a/2, 0), which reverses the parties at point M as shown in Fig. 9a and b. This character can generate acoustic TIs with quantum-spin-Hall [19, 72] edge states. Here, we create a ribbon-like numerical model with eight UC1 and eight UC2, and the computational domain is 16a × a. The projected band diagram is illustrated in Fig. 9c. The topological edge states emerge in the bulk band gap, where the group velocities are opposite within the domains kx = (0, 1) × π/a and kx = (1, 2) × π/a. The pressure phase profiles at states at f0 = 10.476 kHz with kx = (1 ± 0.2)π/a are plotted in Fig. 9d, where the winding directions of phase vortices (green arrows) indicate the pseudospin-up and pseudospin-down states.

Fig. 9
figure 9

Translation of PnCs with a 2nd band gap. a The optimized design (UC1) and its translated counterpart (UC2). b The first four bands and parities at point M. c Projected band diagram of the ribbon-like supper cell for the pseudospin-up(red) and pseudospin-down(blue) edge states along the x direction. d The pressure phase profiles of two units on the interface, indicating the edge states at f0 = 10.476 kHz with kx = (1 ± 0.2)π/a. The green arrows represent the winding directions of phase vortices, and the black arrows denote the acoustic intensity flow

Full size image

At last, we formed the topological insulators by the acoustic crystals with an even-order bandgap. The calculated eigenspectra in Fig. 10 illustrate edge states filling bulk bandgaps without the potential existence of corner states, which agrees with the gapless edge bands in Fig. 9c. The wave-localized modes at different frequencies are shown in insets (i)–(vi) of Fig. 10.

Fig. 10
figure 10

The calculated eigenspectra (left), gapless edge states of topological insulators by optimized PnCs with the 2nd (a), 4th (b) and 6th (c) band gaps, respectively

Full size image

5 Conclusion

This paper establishes an FPTO-based optimization algorithm for designing acoustic bandgap crystals. The relative air permeability constraint is introduced to ensure the connectivity of the acoustic medium during the optimization process. The constraint value significantly impacts the size of the optimized structure and corresponding bandgap width. Numerical examples demonstrate the effectiveness of the proposed algorithm in opening and enlarging the gap on any specified band order.

The band inversion by translating the optimized unit cells provides a platform for investigating the topological phases of matter. We can build second-order topological insulators with gapped edge states and in-gap corner states using the optimized PnCs with an odd-order bandgap. In contrast, the ones with an even-order bandgap can be applied in topological insulators with gapless edge states. The maximized band gap size enables a wide range of frequencies for the potential existence of edge and corner states. The proposed method can be extended to electronic or elastic systems and designing three-dimensional crystalline structures for high-order topological insulators.