Coupling of bond-based peridynamics and continuous density-based topology optimization methods for effective design of three-dimensional structures with discontinuities

Abstract

This study proposes continuous density-based three-dimensional topology optimization (TO) approaches developed by coupling the peridynamic theory (PD) with optimality criteria (OC) and proportional approach (PROP). These frameworks, abbreviated as PD-OC-TO and PD-PROP-TO, can be practically utilized to enhance the fracture toughness of the structures during the optimization process by taking critical regions into account as pre-defined cracks. Breaking the non-local interactions (bonds) between relevant PD particles enables us to readily model cracks. Utilizing this advantage, we solve several benchmark optimization problems including different numbers, positions, and alignments of the cracks. The major differences between the proposed methods are examined by comparing optimum topologies for various cracked scenarios. Moreover, the mechanical behaviour of the optimized structures is investigated under dynamic loads to prove the significant improvements achieved by the present approach in the final designs. The results of dynamic analyses reveal the viability of both PD-TO methods for increasing the fracture toughness of the structure in the optimization stage. Overall, the proposed approach is confirmed as a superior design and optimization tool for future engineering structures.

Graphical abstract

1 Introduction

Topology optimization (TO), a powerful structural design method for improving critical engineering structures, has been mostly utilized in the automotive and aerospace industries, where the weight-to-stiffness ratio is a crucial factor for the best design [1,2,3,4,5,6,7,8,9,10,11,12]. TO methods mainly focus on minimizing an objective function (i.e., compliance) while satisfying the problem constraints such as volume fraction, stress, and minimum dimensions. However, reducing the weight of geometries while minimizing compliance or stress leads to a considerable increase in manufacturing complexity. Such a complex design brought the utilization of additive manufacturing (AM) for the fabrication of optimized structures [13,14,15,16,17,18,19]. Additive manufacturing of those complex structures has been criticized for having residual stress concentrations thereby leading to local process-induced damages [20,21,22,23,24]. The current study majorly focuses on modelling those local damages effectively utilizing state-of-the-art nonlocal theory, peridynamics (PD), as pre-defined surface cracks before optimization and investigation of their effects on the optimized topologies.

Among the myriad of TO methods, a homogenization-based method [25] is one of the first studies followed by many researchers [26]. Considering the homogenization method is one class of TO method, the other approaches can be classified [27] as the level-set-based methods [28,29,30] and the solid isotropic material with penalization (SIMP) [31,32,33] based methods. In the SIMP approach, design variables correspond to the elemental densities where a density value of 1 and 0 represent solid material and void, respectively. This model utilizes the so-called power-law scheme to update the material properties (elastic modulus) of the elements by a penalization factor [33]. Thus, the SIMP method enables TO iterations by changing the material properties of each element according to the design variables. Utilizing the SIMP as the material interpolation scheme, several discrete density-based TO algorithms are proposed such as simulated annealing optimization [34], evolutionary structural optimization (ESO) [35, 36], and bi-directional evolutionary structural optimization (BESO) [37,38,39,40] as an improved version of ESO, where the design variables only take binary values. Until the volume constraint is satisfied, the materials with low strain energy are removed in each iteration of the ESO approach whereas BESO can both eliminate/add those elements during the optimization. Besides, continuous density-based TO methods were proposed, providing less computational cost and higher efficiency than discrete density-based algorithms, and allowing intermediate densities in TO process [41].

Optimality criteria (OC) is a popular continuous density-based TO approach [42,43,44]. Instead of direct optimization of an objective function, pre-defined analytical criteria are satisfied during the OC process. The algorithm uses the material interpolation scheme of the SIMP and utilizes sensitivities in every iteration [43]. Thus, the design variables are not updated using only the strain energy of elements, but the relative change of the elemental compliances with respect to densities. The sensitivities and previous elemental densities are incorporated with a bi-section algorithm in the inner loop of the OC to update the design variables [44]. Another important TO approach based on SIMP is the proportional topology optimization algorithm [45]. This method calculates the strain energy proportion of each element to the whole domain at the beginning of each iteration. Then, the desired amount of density is allocated to the elements based on their calculated proportion value. This increases computational efficiency by excluding the sensitivities. Both OC and PROP allow intermediate densities by utilizing continuous design variables and achieve optimal topologies with the integration of filtering schemes.

Most of the current TO approaches utilize mesh-based methods such as the finite element method (FEM) to conduct structural analysis during the optimization. However, these methods have been found to be limited in the presence of structural discontinuities due to the need for re-meshing and elimination of elements to embed cracks in a design domain. Thus, in the case of structural discontinuities, they are very computationally demanding and prone to local optima. Recently, several studies have been conducted to overcome the limitations of mesh-based methods in fracture modelling [46, 47]. Surpassing the fracture barrier in the TO process can immensely contribute to the design of optimum structures for AM production. This is because the additive manufacturing processes involve heating and cooling repeatedly, resulting in concentrated local residual stresses, which create cracking during/after manufacturing [48, 49]. Hence, there is an urgent need to address the challenges of embedding cracks in the TO process, which is crucial to improve the designs and prevent residual stress concentrations during AM.

Peridynamics (PD) has the potential to practically overcome the issues related to mesh-based methods for crack modelling [50,51,52]. The PD discretizes structures with particles and utilizes integrodifferential equations so is singularity-free in case of structural discontinuities. Kefal et al. [53] pioneered the first research effort to take advantage of PD to solve the topology optimization problem of cracked structures. This approach was based on BESO and later was extended to consider continuous density-based algorithms namely optimality criteria (OC) and proportional approach (PROP) [54]. After that, the multi-material optimization of structures with cracks was performed based on PD-TO [55]. Furthermore, a comparative study between FEM-TO and PD-TO was conducted by Motlagh and Kefal [56], where the advantages of the PD-TO approach were demonstrated in modelling cracks during the TO of two-dimensional structures. The PD-TO approach was also utilized to investigate the effect of micro-cracks in topology optimization [57]. These PD-TO approaches were presented in 2D and showed that the cracked structures can be modelled easily without any re-meshing and eliminating particles [58]. The method simply achieved accurate results by breaking the bonds between PD particles in any region where residual stress potentially concentrates. Recently, Kendibilir et al. [59] proposed an enhanced PD-TO for optimizing three-dimensional structures with embedded surface cracks based on the BESO algorithm. Most recently, this robust PD-TO method has been utilized for the 3D lightweight design of marine structures [60, 61].

In this study, we propose a continuous density-based peridynamics topology optimization framework for improving the fracture toughness of the topologically optimized structures. To the best of our knowledge, there is not any reported study in the literature that performs 3D PD-TO with continuous density-based topology optimization methods. Investigating the performance of OC and PROP algorithms with PD for the 3D structures involving surface cracks for the first time in the literature is one of the motivations and novelty of the present study. The capabilities of the proposed approach are presented by optimizing various 3D structures involving different crack scenarios with both offered methods which are named PD-OC-TO and PD-PROP-TO. Another significant novel contribution of this study is to enhance the fracture toughness of TO designs utilizing PD-TO methods. To this end, the locations of the surface cracks on the optimized structures are detected under dynamic loads for the first time. Then, the optimization procedure is performed once more to create tougher structures against the same load. Therefore, this framework can be performed in the preliminary design stage to assess the performance of topologically optimized designs and improve the toughness under operation loads. In addition, this study can be utilized in the design of additively manufactured structures, where the residual-stress-induced defects can be minimized in the TO process.

This paper is structured as follows. PD formulation is summarized for 3D analysis and crack modelling in Sect. 2. Then, Sect. 3 describes the optimality criteria and proportional topology optimization algorithms with the relevant filtering scheme. Numerical examples are presented in Sect. 4 for four different crack scenarios. Results of dynamic PD analyses are provided in Sect. 5 to compare the load-bearing capacity of optimized structures with/without cracks. In the end, the concluding remarks of this study are included in Sect. 6.

2 Peridynamics formulation and crack modelling

2.1 PD formulation for 3D structures

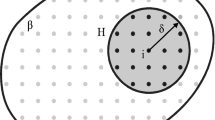
Peridynamics, a recent theory of solid mechanics, utilizes integral equations as an alternative to partial differential equations in the classical continuum mechanics formulation, which gained high potential for effective modelling of discontinuities in computational mechanics. Here, we employed a bond-based PD formulation for the coding implementation of the PD-TO framework. In a three-dimensional domain, peridynamic theory may be considered a continuum form of molecular dynamics considering the non-local interactions between the material particles as shown in Fig. 1b.

Fig. 1

a Illustration of peridynamic modelling in three-dimensional space. b Non-local interactions of a material point $i$ within its horizon

In PD, we first discretize the given domain into equally spaced uniform particles (Fig. 1a) and then create PD bonds between a material point $i$ and all the material points within its horizon where each one is called point $j$ as illustrated in Fig. 1b. Therefore, each particle can only interact with the material points in its family or horizon, $H$, which is a length scale that defines the range of the non-local relations, represented by a radius of $\delta$ for the sphere. The PD equation of motion for a material point located at point ${\mathbf{x}}$ in reference configuration at the time $t$ can be written as:

$$\rho \left( {\mathbf{x}} \right)\,{\mathbf{\ddot{u}}}\left( {{\mathbf{x}},t} \right)\, = {\mathbf{L}}_{u} \left( {{\mathbf{x}},t} \right) + {\mathbf{b}}\left( {{\mathbf{x}},t} \right)\,\,\,\,\,\,\forall x \in \beta \,,\,\,t \ge 0,$$

(1)

$${\mathbf{L}}_{u} \left( {{\mathbf{x}},t} \right) = \int\limits_{H} {\left( {{\mathbf{t}}\left( {{\mathbf{u^{\prime}}} - {\mathbf{u}},{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right) - {\mathbf{t^{\prime}}}\left( {{\mathbf{u}} - {\mathbf{u^{\prime}}},{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right)} \right)\,} dH,$$

(2)

where $\rho$ is the material density and $\beta$ represents the reference configuration of the body. Also, ${\mathbf{u}}$ and ${\mathbf{b}}$ vectors contain the displacements and body force densities, respectively. ${\mathbf{L}}_{u}$ corresponds to the internal force density per unit volume that is applied on a particle ${\mathbf{x}}$ by other material points. Another term given in Eq. (2), ${\mathbf{t}}$, is the force density vector which has opposite direction but equal magnitude according to bond-based PD in a deformed state for two interacting points ${\mathbf{x}}$ and ${\mathbf{x^{\prime}}}$ in two-dimensional space as depicted in Fig. 2. Here, the force density vector can be given as follows:

$${\mathbf{t}} \equiv {\mathbf{t}}\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right) = \frac{1}{2}f\frac{{{\mathbf{y^{\prime}}} - {\mathbf{y}}}}{{\left| {{\mathbf{y^{\prime}}} - {\mathbf{y}}} \right|}},$$

(3)

$${\mathbf{t^{\prime}}} = {\mathbf{t^{\prime}}}\left( { - {{\varvec{\upeta}}}, - {{\varvec{\upxi}}}} \right) = - \frac{1}{2}f\frac{{{\mathbf{y^{\prime}}} - {\mathbf{y}}}}{{\left| {{\mathbf{y^{\prime}}} - {\mathbf{y}}} \right|}},$$

(4)

where the magnitude of pairwise force density is represented by $f$. Here, ${{\varvec{\upeta}}} = {\mathbf{u^{\prime}}} - {\mathbf{u}}$ and ${{\varvec{\upxi}}} = {\mathbf{x^{\prime}}} - {\mathbf{x}}$ define the relative displacement and position vectors of two particles. When we add the initial position vector and displacement vector together, we reach the final position vector of the relevant particle. Therefore, the final position vectors can be written as ${\mathbf{y^{\prime}}} = {\mathbf{x^{\prime}}} + {\mathbf{u^{\prime}}}$ and ${\mathbf{y}} = {\mathbf{x}} + {\mathbf{u}}$.

Fig. 2

Two-dimensional illustration of interactions of a PD particle in before and after deformation

Considering that ${\mathbf{t^{\prime}}}\left( { - {{\varvec{\upeta}}}, - {{\varvec{\upxi}}}} \right) = - {\mathbf{t}}\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right)$ satisfies the conservation rule of linear and angular momentum, the general PD equation of a motion can be rewritten in terms of the pairwise force density vector as:

$$\rho \left( {\mathbf{x}} \right)\,{\mathbf{\ddot{u}}}\left( {{\mathbf{x}},t} \right)\, = \int\limits_{H} {{\mathbf{f}}\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right)dH} + b\left( {{\mathbf{x}},t} \right),$$

(5)

where the pairwise density function is defined as:

$${\mathbf{f}}\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right) \equiv {\mathbf{f}} = f\frac{{{\mathbf{y^{\prime}}} - {\mathbf{y}}}}{{\left| {{\mathbf{y^{\prime}}} - {\mathbf{y}}} \right|}} = cs\frac{{{{\varvec{\upxi}}} + {{\varvec{\upeta}}}}}{{\left| {{{\varvec{\upxi}}} + {{\varvec{\upeta}}}} \right|}},$$

(6)

where $s$ is the stretch and $c$ is the bond constant that defines the strength of the direct physical interaction of the material points, which can be considered as spring in the elastic region. The stretch between two body points and bond constant for elastic material can be calculated as given in Eqs. (7) and (8), respectively.

$$s = \frac{{\left| {{\mathbf{y^{\prime}}} - {\mathbf{y}}} \right| - \left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|}}{{\left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|}} = \frac{{\left| {{{\varvec{\upxi}}} + {{\varvec{\upeta}}}} \right| - \left| {{\varvec{\upxi}}} \right|}}{{\left| {{\varvec{\upxi}}} \right|}},$$

(7)

$$c = \frac{12E}{{\pi \delta^{4} }}.$$

(8)

It is important to remind that the interactions are non-local but restricted by a predefined horizon size, $\delta$, thus it follows:

$${\mathbf{f}}\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right) = 0\,\,\,\,\,\forall {{\varvec{\upeta}}}\,\,\,\,\,\,{\text{whenever}}\,\,\,\,\,\,\left| {{\varvec{\upxi}}} \right|\, > \delta ,$$

(9)

which states that a particle ${\mathbf{x}}$ cannot communicate with a point beyond its horizon. Accordingly, the micro-potential between two interacting points can be formulated to compute the total strain energy density of a point at ${\mathbf{x}}$ as

$$w\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right) = \frac{1}{2}{\mathbf{f}}\left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right)\left( {\left| {{{\varvec{\upxi}}} + {{\varvec{\upeta}}}} \right| - \left| {{\varvec{\upxi}}} \right|} \right) \equiv \frac{1}{2}cs^{2} \left| {{\varvec{\upxi}}} \right|,$$

(10)

$$W\left( {{\mathbf{x}},t} \right) = \frac{1}{2}\int\limits_{H} w \left( {{{\varvec{\upeta}}},{{\varvec{\upxi}}}} \right)dH.$$

(11)

Consequently, one can calculate the compliance (i.e., total strain energy) of the structure by integrating the strain energy densities of the particles over the whole domain $\beta$ as

$$C = \int\limits_{\beta } {W\left( {{\mathbf{x}},t} \right)} \,d\beta .$$

(12)

Next, general formulations can be restated in explicit forms for computational implementation purposes as

$$\rho \left( {{\mathbf{x}}_{i} } \right)\,{\mathbf{\ddot{u}}}\left( {{\mathbf{x}}_{i} ,t} \right)\, = \,\sum\limits_{j = 1}^{{N_{f} }} {{\mathbf{f}}_{ij} V_{j} } \, + {\mathbf{b}}\left( {{\mathbf{x}}_{i} ,t} \right),$$

(13)

where $i$ is the index of the particle located at ${\mathbf{x}}$ which has the interactions between $j$ points with the total number of $N_{f}$, and $V_{j}$ is the volume of a material point. The summation term on the right-hand side in Eq. (13) calculates the total PD force acting on the point $i$, whereas the second term is the body force acting on the same point. PD force density can be linearized to obtain a direct solution for the TO implementation as

$${\mathbf{f}}_{ij} \equiv {\mathbf{f}}\left( {{{\varvec{\upeta}}}_{ij} ,{{\varvec{\upxi}}}_{ij} } \right) = \frac{{c_{ij} }}{{\left| {{{\varvec{\upxi}}}_{ij} } \right|}}{\mathbf{T}}_{ij} {{\varvec{\upeta}}}_{ij} ,$$

(14)

where the pairwise force density vector and transformation matrix are represented by ${\mathbf{f}}_{ij}$ and ${\mathbf{T}}_{ij}$, respectively. The use of a transformation matrix is necessary for mapping the relative displacement from the bond direction to the direction of the global axes in the initial configuration. This process can be defined as

$${\mathbf{T}}_{ij} = \left[ {\begin{array}{*{20}c} {n_{x} n_{x} } & {n_{x} n_{y} } & {n_{x} n_{z} } \\ {n_{x} n_{y} } & {n_{y} n_{y} } & {n_{y} n_{z} } \\ {n_{x} n_{z} } & {n_{y} n_{z} } & {n_{z} n_{z} } \\ \end{array} } \right],$$

(15)

$$n_{\chi } = \frac{{\chi_{j} - \chi_{i} }}{{\left| {{{\varvec{\upxi}}}_{ij} } \right|}}\,\,\,\left( {\chi \, = x,y,z} \right).$$

(16)

Note that the ${{\varvec{\upxi}}}_{ij}$,${{\varvec{\upeta}}}_{ij}$ vectors as well as ${\mathbf{x}}_{\chi }$ and ${\mathbf{u}}_{\chi }$ vectors for determining the position and deformation vectors of two body points in the global orthogonal Cartesian coordinate (x, y, z) system can be defined as

$${{\varvec{\upxi}}}_{ij} = {\mathbf{x}}_{j} - {\mathbf{x}}_{i} \,\,,\,\,\,{{\varvec{\upeta}}}_{ij} = {\mathbf{u}}_{j} - {\mathbf{u}}_{i} ,$$

(17)

$${\mathbf{x}}_{\chi } = \left[ {x_{\chi } \,\,\,y_{\chi } \,\,\,z_{\chi } } \right]^{T} \,\,\,\left( {\chi = i,j} \right),\,\,{\mathbf{u}}_{\chi } = \left[ {\overline{u}_{\chi } \,\,\,\overline{v}_{\chi } \,\,\,\overline{w}_{\chi } } \right]^{T} \,\,\left( {\chi = i,j} \right).$$

(18)

Considering the changing material properties of the particles during the optimization process, the bond constant, $c_{ij}$, can be calculated by harmonically averaged elastic modulus, $E_{ij}$, of the bonds as

$$c_{ij} = \frac{{12E_{ij} }}{{\pi \delta^{4} }},$$

(19)

$$E_{ij} = \frac{{2E_{i} E_{j} }}{{E_{i} + E_{j} }}.$$

(20)

One can perform quasi-static analysis by the setting acceleration to zero in the general linear matrix–vector form of PD equation defined as

$$\sum\limits_{j = 1}^{{N_{f} }} {\frac{{c_{ij} V_{j} }}{{\left| {{{\varvec{\upxi}}}_{ij} } \right|}}} \left[ {{\mathbf{T}}_{ij} \,\,\,\, - {\mathbf{T}}_{ij} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{i} } \\ {{\mathbf{u}}_{j} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {b_{x} } \\ {b_{y} } \\ {b_{z} } \\ \end{array} } \right\}_{i} \,\,\, \Rightarrow \,\,\,{\mathbf{s}}_{i} {\mathbf{d}}_{i} = {\mathbf{b}}_{i} m$$

(21)

$$\,{\mathbf{s}}_{i} = \left[ {\sum\nolimits_{j = 1}^{{N_{f} }} {{\mathbf{T}}_{ij} \frac{{c_{ij} V_{j} }}{{\left| {{{\varvec{\upxi}}}_{ij} } \right|}}} \,\,\,\,\, - {\mathbf{T}}_{i1} \frac{{c_{i1} V_{1} }}{{\left| {{{\varvec{\upxi}}}_{i1} } \right|}}\,\,\,\,\, - {\mathbf{T}}_{i1} \frac{{c_{i2} V_{2} }}{{\left| {{{\varvec{\upxi}}}_{i2} } \right|}}\,\,\,\,\,...\,\,\,\,\, - {\mathbf{T}}_{{iN_{f} }} \frac{{c_{{iN_{f} }} V_{n} }}{{\left| {{{\varvec{\upxi}}}_{{iN_{f} }} } \right|}}} \right],$$

(22)

$${\mathbf{d}}_{i} = \left[ {{\mathbf{u}}_{i} \,\,\,{\mathbf{u}}_{1} \,\,\,...\,\,\,\,{\mathbf{u}}_{{N_{f} }} } \right]^{T} {\text{and }}{\mathbf{b}}_{i} = \left[ {\begin{array}{*{20}c} {b_{x} } & {b_{y} } & {b_{z} } \\ \end{array} } \right]_{i}^{T} .$$

(23)

In Eqs. (22) and (23), the stiffness matrix and displacement vector of a body-point, ${\mathbf{s}}_{i}$ and ${\mathbf{d}}_{i}$, are given in the explicit form. Moreover, ${\mathbf{b}}_{i}$ is the force vector of a particle and includes the body force components along the $x -$, $y -$, $z -$axes. Note that, the displacement vector ${\mathbf{d}}_{i}$ contains all the displacement vectors of the family points of $i$. The displacement vector of a family member is then represented by ${\mathbf{u}}_{i}$, which consists of three components of the displacement in the Cartesian coordinate system as ${\mathbf{u}}_{i} = \left[ {\begin{array}{*{20}c} {u_{x} } & {u_{y} } & {u_{z} } \\ \end{array} } \right]_{i}$. Since a set of equations has been established on a single point, one can construct a single compact matrix–vector equation for the entire domain,$\beta$, by the given assembly process, $\cup$, for the global stiffness matrix, displacement and force vectors ${\mathbf{S}}$, ${\mathbf{D}}$, and ${\mathbf{B}}$:

$${\mathbf{SD}} = {\mathbf{B}},$$

(24)

$${\mathbf{S}} = \bigcup\limits_{i = 1}^{N} {{\mathbf{s}}_{i} } ,\,\,\,\,{\mathbf{D}} = \bigcup\limits_{i = 1}^{N} {{\mathbf{d}}_{i} ,} \,\,\,\,{\mathbf{B}} = \bigcup\limits_{i = 1}^{N} {{\mathbf{b}}_{i} } ,$$

(25)

where $N$ is the total number of particles in the domain. In this system, we can solve a quasi-static problem by applying the relevant boundary and loading conditions. In PD, it is crucial to apply the forces as body force density on each particle in the region of interest. Moreover, the relevant points should be constrained according to the pre-defined boundary conditions. Consequently, the PD problem can be directly solved by performing a similar procedure as the conventional finite element does. Namely, taking the inverse of the reduced global stiffness matrix and solving the system of PD equations, the displacements of all particles can be determined. Hence, the strain energy densities needed for the optimization process can be calculated by pair-wise interactions of particles as

$$W_{i} = \frac{1}{2}\sum\limits_{j = 1}^{{N_{f} }} {\frac{{c_{ij} \left( {\left| {{{\varvec{\upxi}}}_{ij} + {{\varvec{\upeta}}}_{ij} } \right| - \left| {{{\varvec{\upxi}}}_{ij} } \right|} \right)^{2} }}{{2\left| {{{\varvec{\upxi}}}_{ij} } \right|}}} V_{j} .$$

(26)

To calculate the objective function (compliance) at the beginning of each TO iteration, a summation of the energy densities can be performed as

$$C = \sum\limits_{i = 1}^{N} {W_{i} \,V_{i} } .$$

(27)

2.2 Crack modelling

To generate a surface crack, all the bonds passing through the crack must be broken. For this purpose, we search all interactions and evaluate them geometrically to understand whether they are intersecting with the crack or not. This process can be investigated visually from Fig. 3. As shown in the illustration, 8 particles are interacting with the total number of 28 PD bonds before a crack (Fig. 3a). Then, the embedded crack cuts some of these interactions (8 bonds) from the intersecting points (Fig. 3b). In the final state, as depicted in Fig. 3c, the remaining bonds continue to play a role in the PD model.

Fig. 3

Surface crack modelling in a three-dimensional PD domain. a PD particles and their interactions before the crack, b Intersection points of the bonds and a surface crack, c Interactions of the same particles after crack involvement

A scalar-valued failure function defining the failure parameter $\gamma_{ij}$ between points and $j$ can be defined explicitly as

$$\gamma_{ij} = \left\{ \begin{gathered} \,\,0\,\,\,\,\,{\text{if}}\,\,\,\,s_{ij} > s_{c} \hfill \\ \,\,1\,\,\,\,\,\,{\text{otherwise}} \hfill \\ \end{gathered} \right.,$$

(28)

where 0 and 1 values correspond to a broken or unbroken bond, respectively. Thus, to involve the failure in the PD model, the failure parameter of the relevant interactions should be updated to zero. In addition, the critical stretch value,$s_{c}$, is the decisive parameter that defines a critical stretch limit in a dynamic PD analysis to break the bond when a stretch value between two points, $s_{ij}$, exceeds the pre-defined limit. The critical stretch can be calculated for 3D bodies as

$$s_{c} = \sqrt {\frac{{5G_{c} }}{6E\delta }} ,$$

(29)

where $G_{c}$, is the critical energy release rate which is a characteristic of materials related to fracture behaviour. Moreover, the damage parameter, $\phi_{i}$, represents the amount of damage at a material point, which can be utilized to monitor crack propagation in time.

The damage is associated with the failure function such that an increasing number of broken bonds leads to the damage value of 1 as

$$\phi_{i} = 1 - \frac{{\sum\limits_{j = 1}^{{N_{f} }} {\gamma_{ij} } V_{j} }}{{\sum\limits_{j = 1}^{{N_{f} }} {V_{j} } }}.$$

(30)

Finally, to obtain converged results in the dynamic PD analysis, the time step size is calculated by utilizing the standard von Neumann stability analysis [62] as

$$dt = 0.8\sqrt {\frac{\rho }{{2\pi b\delta^{3} }}} ,$$

(31)

where $b = {{15\mu } \mathord{\left/ {\vphantom {{15\mu } {2\pi \delta^{5} }}} \right. \kern-0pt} {2\pi \delta^{5} }}$ is a PD parameters related to the shear modulus of material, $\mu$, which can be calculated as $\mu = {{2E} \mathord{\left/ {\vphantom {{2E} 5}} \right. \kern-0pt} 5}$ using Poisson’s ratio value of $v = 1/4$ for 3D bond-based PD. Elimination of the PD bonds in the cracked region gives rise to the relevant particles the chance of moving independently. To reveal this mechanical effect, the total displacements of a cantilever beam problem are given in Fig. 4. It is observed that the particles in the zoomed region are aligned in a regular arrangement in a crack-free state (Fig. 4a) whereas these particles are looking separated in the cracked model (Fig. 4b).

Fig. 4

Displacement contours of a simple bending problem a without crack, and b with crack where the results are 300 times exaggerated for a better representation

3 Optimization procedure

3.1 Optimization problem definition

Compliance minimization is the most widely preferred objective function in topology optimization literature. A pre-defined target volume is the constraint of the optimization problem. Utilizing the strain energy values calculated by PD, the compliance of the structure can be minimized with the following scheme:

$$\mathop {\min }\limits_{{\kappa_{i} }} \,\,C\left( {\kappa_{i} } \right)\,\,\,\,s.t.\left\{ \begin{gathered} SD = B \hfill \\ \sum\limits_{i = 1}^{N} {\kappa_{i} V_{i} } = \mathop V\limits^{ - } \sum\limits_{i = 1}^{N} {V_{i} } \hfill \\ \kappa_{\min } \le \kappa_{i} \le 1\, \hfill \\ \end{gathered} \right..$$

(32)

Each PD particle has a design variable, $\kappa_{i}$, that determines its density and thereby its material property. In this study, we utilize two different continuous density based TO algorithms, namely optimality criteria (OC) and proportional topology optimization (PROP) methods. The design variable can take a value between 0 and 1, continuously. Therefore, a particle in the design domain can be placed as void, solid, or even as a material with an intermediate density. Material properties are updated using the power-law interpolation which depends on elastic moduli of solid and void material in addition to the design variable as:

$$E_{i} \equiv E_{i} \left( {\kappa_{i} } \right) = E^{v} + \left( {\kappa_{i} } \right)^{p} \left( {E^{s} - E^{v} } \right),$$

(33)

where solid and void materials have the elastic moduli of $E^{s}$ and $E^{v}$, respectively. The power of the design variable, penalization parameter, p, is used to achieve distinct values. Setting the elastic modulus of void material to $E^{v} = 0$, simplifies Eq. (33) into

$$E_{i} = \left( {\kappa_{i} } \right)^{p} E^{s} .$$

(34)

A minimum value of the design variable can be defined in the range of $0 < \kappa_{\min } < 10^{ - 3}$ which ensures that the elastic modulus of void material is not equal to zero. Moreover, the penalty parameter can be selected in between $1 \le p \le 5$. We adjust the optimization parameters as $\kappa_{\min } = 10^{ - 3}$ and $p = 3$ in this study.

3.2 Proportional topology optimization method

Proportional topology optimization algorithm (PROP), originally introduced in [45], is a non-sensitivity approach that distributes material in the domain by assigning the design variables to particles proportionally to their compliance value. Unlike optimality criteria (OC), sensitivity calculations are not included in this method, so it is both a computationally cheaper approach and prevents the complexities due to sensitivities. In addition, like OC, PROP employs continuous density variables resulting in intermediate densities and enhanced search performance during the optimization. PROP distributes the densities according to the strain energy of the particles as

$$\kappa_{i}^{{{\text{opt}}}} = \frac{{R_{m} \,C\left( {\kappa_{i} } \right)^{q} }}{{\sum\limits_{i = 1}^{N} {\left( {C\left( {\kappa_{i} } \right)V_{i} } \right)^{q} } }},$$

(35)

$R_{m}$ is the amount of remaining material, $\kappa_{i}^{{{\text{opt}}}}$ corresponds to optimal particle densities in the current iteration, and $q$ represents the proportion exponent. The actual material distributed to the particles is calculated after applying the filter on $\kappa_{i}^{{{\text{opt}}}}$. Then, the design variables are updated for the next iteration as

$$\kappa_{i}^{new} = \alpha \kappa_{i}^{prev} + \left( {1 - \alpha } \right)\kappa_{i}^{opt} ,$$

(36)

where $\kappa_{i}^{{{\text{new}}}}$, particle densities in the next iteration, is calculated by linearly blending the $\kappa_{i}^{opt}$ and $\kappa_{i}^{prev}$, design variables from the last iteration. The history coefficient, $\alpha$, is utilized to control the impact of the last iteration on the current one.

The pseudo-code of the PROP method is given in Algorithm 1. After the structural analysis and strain energy calculation, the algorithm starts with the determination of the target volume (desired total volume), and the remaining volume (target volume–actual volume) is set to the target volume initially. Then, the algorithm calculates the proportional compliance of each element so that the available volume can be distributed to the elements accordingly. These values are used at the beginning of each inner loop iteration to distribute the remaining material, and this loop continues until there is no remaining volume.

The distributed densities are filtered through weighted local averaging using a prescribed $R_{min}$ (minimum filter radius) distance and the density limits $\left( {10^{ - 3} ,\,1} \right)$ are enforced. At the end of the inner loop, the current volume obtained after the distribution, filtering, and density limits is subtracted from the target volume to update the remaining volume which will be used for redistribution. Finally, outside of the inner loop, the elemental densities are updated by linearly mixing the design variables computed at the current iteration and the ones from the previous iteration. Since elements can take all values between 0 and 1 proportionally in PROP results, the design variables are sorted descending after each optimization iteration. Afterward, only the design variables until the predefined target volume are taken into consideration while writing the result files. Thus, clear demonstrations are achieved and presented in desired volume fractions for the PROP results. This is also the reason behind the presented scales of the PROP results starting from a value greater than 0.001, unlike the ones of OC.

Algorithm 1

Pseudo code of the proportional approach

3.3 Optimality criteria method

Optimality criteria (OC), a sensitivity-based topology optimization approach, utilize filtered sensitivities to distribute the elemental densities and provides intermediate densities by continuous design variables. The method updates the design variables based on the following equation:

$$\kappa_{i}^{new} = \left\{ \begin{gathered} \max \left( {0,\,\,\,\,\,\kappa_{i} - mv} \right)\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\,\,\,\kappa_{i} B_{i}^{0.5} \le \max \left( {0,\,\,\kappa_{i} - mv\,} \right)\, \hfill \\ \min \,\,\left( {1,\,\,\,\,\,\,\kappa_{i} + mv} \right)\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\,\,\,\kappa_{i} B_{i}^{0.5} \ge \,\,\min \,\left( {1,\,\,\,\kappa_{i} + mv\,} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\kappa_{i} B_{i}^{0.5} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{otherwise}} \hfill \\ \end{gathered} \right.,$$

(37)

where the move limit ($mv$) is defined as 0.2 and $B_{i}$ is computed with the optimality condition:

$$B_{i} = \frac{{ - \frac{{\partial C\left( {\kappa_{i} } \right)}}{{\partial \kappa_{i} }}}}{{\lambda \frac{{\partial V\left( {\kappa_{i} } \right)}}{{\partial \kappa_{i} }}}},$$

(38)

where $\lambda$ is a Lagrangian multiplier which is found by a bi-sectioning algorithm. The sensitivity of a compliance value, $\omega_{i}$, can be calculated as follows:

$$\omega_{i} = \frac{{\partial C\left( {\kappa_{i} } \right)}}{{\partial \kappa_{i} }} = - p\left( {\kappa_{i} } \right)^{p - 1} C_{i}^{{}} ,$$

(39)

where the compliance of any particle is represented by $C_{i}^{{}}$, can be calculated using Eq. (27).

Algorithm 2

Pseudo code of the optimality criteria

The pseudo-code of the OC method is given in Algorithm 2. The method starts with using the current strain energies and previous design variables to calculate the sensitivity of each element which is the key factor to determine the new elemental densities. Then, the sensitivity values are filtered by weighted local averaging within a sphere horizon with $R_{min}$ radius to prevent checkerboard patterns and instabilities in the optimized topologies. The algorithm continues with initializing the volume threshold, lower and upper bounds, and move limits that will be used in the inner loop while updating the elemental densities. The inner loop uses the lower and upper bounds for the termination criterion and starts with calculating the middle value between the bounds. Afterward, the algorithm recalculates the densities using Eq. (37). At the end of each inner loop iteration, the bounds are updated with the bi-sectioning algorithm. Finally, when the inner loop terminates, the design variables are assigned to the calculated densities.

3.4 Filter scheme and stabilization

The main numerical instabilities to consider in the optimization process are the checkerboard pattern and mesh dependency. In OC, the filter is employed for the sensitivities, whereas PROP filters the particle densities to eliminate these numerical difficulties. To identify the nearby particles inside this sub-domain, a circular domain with a set radius, $R_{\min }$, is specified at the center of the material point $i{\text{th}}$. The modified sensitivity number in OC, $\mathop {\mathop \omega \limits^{ \sim } }\nolimits_{i}$, and the filtered density in PROP, $\mathop {\mathop \kappa \limits^{ \sim } }\nolimits_{i}^{{opt}}$, can be calculated by Eqs. (40) and (41), respectively.

$$\mathop \omega \limits^{\sim } _{i} = \frac{{\sum\limits_{{j = 1}}^{{N_{i} }} {\psi \left( {R_{{ij}} } \right)\omega _{j} } }}{{\sum\limits_{{j = 1}}^{{N_{i} }} {\psi \left( {R_{{ij}} } \right)} }},$$

(40)

$$\mathop {\mathop \kappa \limits^{ \sim } }\nolimits_{i}^{{opt}} = \frac{{\sum\limits_{{j = 1}}^{{N_{i} }} {\psi \left( {R_{{ij}} } \right)\kappa _{j}^{{opt}} } }}{{\sum\limits_{{j = 1}}^{{N_{i} }} {\psi \left( {R_{{ij}} } \right)} }},$$

(41)

where $N_{i}$ represents the total number of particles in the horizon of the particle $i$, $R_{ij} = \left| {{\mathbf{x}}_{j} - {\mathbf{x}}_{i} } \right|$ is the distance between the particle $i$ and $j$, and $\psi \left( {R_{ij} } \right)$ is a weight factor given as:

$$\psi \left( {R_{ij} } \right) = \left\{ \begin{gathered} \,\,R_{\min } - R_{ij} \,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,R_{ij} \le R_{\min } \hfill \\ \,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,R_{ij} > R_{\min } \,\, \hfill \\ \end{gathered} \right.\,\,\,\,\,\,.$$

(42)

In Sect. 2 and Sect. 3, the mathematical formulations of the proposed PD-PROP-TO and PD-OC-TO methods are introduced. A general framework of these methods is given in Fig. 5.

Fig. 5

The general framework of PD-TO methods

4 Topology optimization examples

In this chapter, we optimize two examples of TO problems from the literature to prove the accuracy and abilities of the proposed optimization methods. Several crack-involving domain scenarios are created to examine the location and orientation effect of crack/cracks. All the numerical results are generated by an in-house MATLAB code. Unless otherwise stated, the Poisson’s ratio and modulus of elasticity of the material are $v = 0.25$ and $E = 200\,\,GPa$, respectively. Additionally, the minimum filter radius and PD horizon size are kept remained as $R_{\min } = 3{\text{dx}}$ and $\delta = 3.015{\text{dx}}$ for all the optimization problems. In the design variable updating scheme, the penalization parameter is set to 3.

4.1 Cantilever beam

The most famous benchmark problem in topology optimization literature, the 3D cantilever beam, is chosen as the first case study. Figure 6 presents the five scenarios including several crack conditions where the length ${\text{L}} = 1\,{\text{m}}$. Particle spacing is chosen as ${\text{dx = L/30}}$ which results in a discretization of 54,000 particles in total (${60} \times {30} \times {30}$ along $x - y - z$ axes). Applied boundary and loading conditions are clamping on the left face and a concentrated downward load of ${\text{F = 100 kN}}$ divided into 4 PD particles at the center of the right face, respectively. The total volume of this geometry during the optimization process is constrained to $\overline{V} = 0.25$. The embedded square-shaped cracks are formed with an edge length of $l_{c} { = 0}{\text{.2L}}$. The mesh dependency analysis is given in Appendix A.

Fig. 6

Design domain and loading condition of the Cantilever Beam problem for five scenarios in total including with/without crack conditions, namely a without crack; b back crack; c front crack; d double parallel crack; e double perpendicular crack. Single or multiple cracks are embedded into different locations. Cases (b), and (c) are designed to investigate the location effect of a single crack by positioning at varying distances to the applied force. In cases (d) and (e), we intend to examine the reaction of the optimizers in the existence of multiple cracks in different orientations

The optimum designs obtained by PD-PROP and PD-OC with the results of reference PD-BESO [59] are presented in Fig. 7 (isometric view). Here, there are remarkable geometric differences observed between the optimum design of continuous (PROP, and OC) and discrete (BESO) density-based approaches. This comparison is made to reveal the difference between the proposed methods and the previously published method in [59]. In the remainder of the study, only the results of the two proposed methods will be compared. For the back crack case, both optimization methods displayed a similar reaction creating a hole in the normal direction while preserving material at the crack tips. As depicted in Fig. 7c, PROP and OC maintained material at the back like the crack-free scenario, but more material accumulated in the width around the cracked regions (front). The hole at the back crack region and increased width of the front crack region can be observed in PROP result (Fig. 7d). Likewise, by removing material from the normal direction of the cracks and accumulating the materials in the crack tips, a combination of back and front crack cases is revealed in optimum OC design (Fig. 7d). Changing only the orientation resulted in totally different topologies as compared to the double parallel case. However, as seen in Fig. 7(a, e), double perpendicular case results are like the first case as if there is no crack at all. As a result, this problem shows that the perpendicular cracks cannot easily propagate in this loading condition and thus do not lead to a considerable increase in strain energy. Therefore, it can be inferred that the TO methods do not react to such cracks that are not creating any moment with the applied force.

Fig. 7

Optimal material distributions of the Cantilever Beam obtained by PROP, OC, and BESO for all the cases with/without cracks: a without crack; b back crack; c front crack; d double parallel cracks; e double perpendicular cracks. Here, the results are presented in an isometric view to show the geometrical details. Note that, for PROP results, the colour scale contains green and blue colours to represent the minimum and maximum values of the design variables, respectively. For the results of OC, yellow corresponds to the minimum value of the design variable whereas red colour represents the solid material where the design variable of the particle is equal to 1. The design variable is equal to 1 for all particles shown in the BESO results

4.2 Hanger beam

In this problem, a 3D domain shaped like a hanger is modelled as depicted in Fig. 8 where all the edges have the same length of ${\text{L}}\,{ = }\,{60}\,{\text{mm}}$. The model is discretized into 69,120 particles with a uniform particle diameter of ${\text{dx}}\,{ = }\,{2}{\text{.5}}\,{\text{mm}}$. The hanger is fully clamped on its back whereas a concentrated downward load ${\text{F}}\,{ = }\,{500}\,\,{\text{N}}$ is applied on the edges shown in Fig. 8. This load is distributed to 4 PD particles located in the middle of the upper edges. The target volume is set to $\overline{V} = 0.15$. All the square-shaped surface cracks shown in Fig. 8 have an edge length of $l_{c} = {\text{L/6}}$. A thorough analysis of horizon size dependency is presented in Appendix B.

Fig. 8

Design domain and loading condition of the Hanger problem for five scenarios in total including with/without crack conditions, namely: a without crack; b back crack; c front crack; d double crack; e triple crack. Single or multiple cracks are embedded into different locations. Cases (b) and (c) are designed to investigate the location effect of a single crack by positioning at varying distances from the applied force. In cases (d) and (e), we intend to examine the reaction of the optimizers in the existence of multiple cracks near the clamping and loading regions

Figure 9 presents the optimum topologies obtained by PD-PROP and PD-OC in two different isometric views. It can be revealed that the regions close to the crack tips are strengthened. Although the back crack and front crack cases have similar distributions in the clamping region, the front part of the hanger is changed as compared to the crack-free state. PROP and OC results are quite similar for the back crack scenario as depicted in Fig. 9b. Contrarily, the reactions of the methods in the front crack case (Fig. 9c) differ in a way that OC opens a hole in the normal direction of the crack whereas the PROP stacks material directly into the crack position.

Fig. 9

Optimal material distributions of the Hanger obtained by PD-PROP and PD-OC for all the cases with/without cracks: a without crack; b back crack; c front crack; d double crack; e triple crack. Here, the results are presented in two isometric views to show the geometrical details as much as possible. Note that, for PROP results, the colour scale contains green and blue colours to represent the minimum and maximum values of the design variables, respectively. For the results of OC, yellow corresponds to the minimum value of the design variable whereas red colour represents the solid material where the design variable of the particle is equal to 1

In the next crack scenario (double crack), the material distribution in the cracked region is affected by the left and right cracks. Accordingly, it can be seen in Fig. 9d that the PROP method enlarges the existing hole in this region. Likewise, OC opens a new hole at the same location. Additionally, the PROP method fills the gap between separate arms in the clamping region. Another change appearing on the top side of the back part is the shrinkage of the large hole in the middle. In the other case (triple crack), we embedded two additional cracks into similar positions at the other blocks of the hanger. That is why the results of the triple crack case are compared with those of the front crack case. While the PROP results seem almost identical, the OC method alters the design remarkably (Fig. 9c, e). The back, front, and triple crack cases include a longer base plate along the bottom side. A potential reason for this effect could be that the cracks closer to the loading points (front, back, and triple crack) are more affected by tension in the upper portion, the PROP method changed the bottom side to prevent the crack opening at the top.

5 Dynamic analyses for the assessment of fracture toughness enhancement

5.1 Dynamic analysis setup

In the previous section, two benchmark geometries have been optimized for various crack locations to assess the effect of the crack numbers/locations and alignments utilizing the proposed PD-TO methods. The final shapes are compared with each other mostly in their shapes under static loading conditions. However, one may desire to know the dynamic behaviour of these structures where the major concern is crack modelling. Therefore, we here conduct a comparison study between the final topologies under the same dynamic loads. This comparison would be effective to reveal whether the fracture toughness of the geometry is increased in the cracked region or not. For the dynamic analysis, we apply the displacement boundary condition to the loading points defined in the previous section for the cantilever beam and hanger problem. The loading points have a velocity of ${\text{v = 2 m/s}}$ in the negative z-direction for both problems. The size of a time step is calculated as ${\text{dt = 6}}{\text{.53e - 6 s}}$, and ${\text{dt = 4}}{\text{.90e - 7 s}}$ using Eq. (31) for the cantilever beam and hanger geometries, respectively. Additionally, critical stretch values are determined by Eq. (29).

5.2 Comparison strategies

We determine two different strategies for the comparison of the dynamic behaviour of the optimized structures. The first strategy is the initiation of the crack as defined in Sect. 4.1. After that, the structures obtained for the case of with and without cracks are analysed under dynamic load. Here, we selected the front crack for crack initiation and compare the dynamic behaviour and damage patterns of the structure. To be clear, Fig. 10(a–b) represent the placement of the front crack into the optimized topologies without an initial crack for OC and PROP, respectively. Moreover, in Fig. 10(c–d), we consider the topologies optimized with the pre-defined front crack and embed this crack into these topologies for dynamic analysis.

Fig. 10

The structures utilized in dynamic analysis correspond to the results of a OC-without crack b PROP-without crack c OC-front crack d PROP-front crack. Note that the relevant bonds are broken to introduce the front crack in the given domain before the dynamic load is applied

For the second strategy, we perform dynamic analysis for a topology without initiating any discontinuities in the structure. An optimized structure is first dynamically loaded until it is broken thus the fracture pattern can be tracked. Hence, the knowledge of possible cracked regions because of operating conditions can be achieved. The following stage herein is to initiate necessary cracks in the initial domain into the regions where the fracture begins. Then, the structure containing these cracks should be re-optimized by the PD-TO methods. Thereafter, the dynamic behaviour of the initial topology (once optimized) and re-optimized topology (optimized considering possible cracks) can be widely compared to search the fracture toughness enhancement. In this regard, we employ the second strategy on the hanger geometry as depicted in Fig. 11. Here, Fig. 11(a–b) show the fracture patterns of the optimized topologies (without crack) of OC-TO and PROP-TO, respectively, which are obtained under dynamic load. Then, we determine the possible crack regions from Fig. 11(a–b). Finally, the new cracks are embedded in these locations for the next optimization. In this respect, Fig. 11(c–d) depict the design domain with possible cracks for the second optimization to strengthen the critical regions by the proposed TO methods.

Fig. 11

Fracture patterns obtained for the topologies of a OC-without crack, and b PROP-without crack under dynamic load. Observing the patterns, new cracks are embedded in the initial design domain in (c) and (d) for OC and PROP, respectively

5.3 Numerical results: dynamic behaviour of the optimized structures

After applying dynamic load to the structures for the first strategy, some of the critical time steps ($300{\text{th}},\,\,400{\text{th}},\,\,500{\text{th}},\,\,600{\text{th}}$) of the analyses are captured to compare the fracture behaviour. In this context, damage contours are given for the selected instants as shown in Fig. 12. It can be concluded from Fig. 12 that both optimizers generate more resistant topologies in the existence of an induced crack in the structure. There is no crack propagation in the front crack results at the parallel time steps (Fig. 12). It is expected that the crack will propagate after a certain amount of time under the increasing load. Eventually, critical damage accumulation started about the ${\text{700th}}$ time step as shown in Fig. 13. This figure shows the maximum total displacement values with respect to the time step.

Fig. 12

Damage plots at the certain time steps for PD-OC-TO and PD-PROP-TO results during dynamic PD analysis. Note that total displacements are reflected in these pictures by the magnification factor of 50

Fig. 13

Maximum displacements for cantilever beam during dynamic analysis. The starting point of crack propagation is clarified by showing the status of critical regions at relevant time steps

In Fig. 13, the displacement regime is linear up to the instant when crack propagation starts. The separation of the material points in the damaged region can be observed as highlighted by zoomed pictures. Moreover, the maximum displacement values of the structures right before the crack propagates are compared to evaluate the load-bearing capacity of the structures. These displacement values right before the failure are listed in Table 1. It is shown that the structures optimized considering the induced crack can deform $85\%$ and $80\%$ more before it fails with PD-OC and PD-PROP, respectively, which can be attributed to the enhanced fracture toughness under the same loading.

Table 1 Maximum displacements just before the crack propagates

In the second strategy, the demonstrated cracks (Fig. 11c–d) are embedded in the initial domain for re-optimization. The resultant topologies after the second optimization are tested under the same load, and their dynamic behaviour is depicted in Fig. 14 together with the results of the initial scenario without crack. As clearly shown in the figure, re-optimized geometries by considering the critical regions become more resilient to breakage. According to damage contours, the re-optimized PD-OC result shows the best performance as compared to the others in the given time interval (Fig. 14). In addition, PD-PROP brings an improvement in the critical region but fails in another region. Nevertheless, both methods lead to a delay in the failure time when we introduce a crack in a critical region.

Fig. 14

Damage plots at the certain time steps for PD-OC-TO and PD-PROP-TO results during dynamic PD analysis. Note that total displacements are reflected in these pictures by the magnification factor of 10

The maximum displacement values of the optimized topologies are compared in Fig. 15 where the failed points are demonstrated in zoomed pictures. It is observed that more resistant structures can be achieved by considering the cracks in critical regions at the optimization stage. Another observation is that the PD-OC reacts more sensitively and produces better results relative to PD-PROP in the context of fracture toughness. Furthermore, the maximum total displacements of the structures just before they fail are compared in Table 2. As a result, PD-OC increased the maximum displacement that the structure can resist by ${9}{\text{.24\% }}$. The improvement provided by PD-PROP is ${7}{\text{.16\% }}$ which is relatively lower than what PD-OC offers. Consequently, it is strongly proved that the proposed TO methods would achieve better designs to bear more load.

Fig. 15

Maximum displacements for the hanger during dynamic analysis. The starting point of crack propagation is clarified by showing the status of critical regions at relevant time steps

Table 2 Maximum displacements just before the cracks propagate

6 Conclusions

In this research effort, two novel three-dimensional topology optimization methods named PD-OC-TO and PD-PROP-TO are developed for the optimization of structures containing defects. In addition, we present a novel strategy for enhancing the fracture toughness of the topologically optimized structures utilizing the proposed TO methods. Two different benchmark problems are optimized to demonstrate their capabilities. Moreover, various crack locations, numbers, and alignment options are created to investigate the effect of cracking scenarios on the optimized geometries. Accordingly, two main concluding remarks are obtained:

• The final geometries obtained by PD-OC, and PD-PROP methods for all the scenarios are examined comprehensively. Although both methods show improvement in the optimized results to avoid crack propagation, it is revealed that the OC method is more sensitive to structural discontinuities and PROP creates fewer sub-branches between the main support arms.

• The performance of the PD-TO methods in fracture toughness enhancement is investigated. In this regard, the damage contours and fracture patterns of the optimized geometries are compared at certain time steps under dynamic load. These comparisons revealed that the suggested methods would produce superior designs that could support a greater load than the initial TO results by just embedding hypothetical (predicted by simulations) cracks into the regions that are determined to be critical under dynamic loading.

Overall, it is proved that the proposed methods are favourable and practical to be utilized in the lightweight design of various engineering structures. For instance, the defects caused by the thermal-residual stresses during additive manufacturing processes could be modelled by these methods to avoid failures. Moreover, observing the fracture patterns that happen in the operating period of the critical engineering parts would be essential inputs. Hence, these methods would enable a designer to enhance the fracture toughness of the relevant structures through optimized designs.

Albeit being generally applicable to many design/optimization problems, the proposed PD-TO methods involve several limitations for specific applications. These can be potentially addressed in future studies. First, the current PD-TO algorithm is based on bond-based formulation, which restricts the Poisson ratio of material to 0.25. This limitation can be addressed by ordinary state-based formulation for the TO problems that Poisson’s ratio plays a critical role. Another drawback can be attributed to the uniform particle discretization of the PD-TO, which can be resolved by employing dual horizon peridynamics (DH-PD) [63, 64] in the TO process. This would reduce the computational cost of the present method in optimizing complex geometry with intricate shapes such as holes.

Appendix

1.1 Mesh dependency analysis on cantilever beam problem

Computational simulations involving numerical discretization are usually subjected to mesh dependency studies to show that the result obtained by the utilized method does not depend on the discretization size. Therefore, four different models with the discretization of the domain as ${32} \times {16} \times {16}$ (coarse), ${40} \times {20} \times {20}$ (medium), ${60} \times {30} \times {30}$ (fine), and ${80} \times {40} \times {40}$ (finest) are created to select the optimum resolution in terms of accuracy and computational cost. The compliance results obtained by the PD-PROP and PD-OC methods are illustrated in Figs. 16 and 17, respectively. The result is affected by the particle size up to a certain resolution limit. Especially, coarse, and medium discretization lead to considerably higher compliance values as compared to the fine and finest discretization for both methods. For the sake of clarity, their relative differences among varying resolutions are listed in Table 3. The domain which includes 54,000 (${60} \times {30} \times {30}$) particles is selected for our analysis by considering both the optimum result and computational effort. Even though mesh dependency analyses are not explicitly given for the other case, we determine their discretization sizes with the same methodology.

Fig. 16

Compliance values and final topologies obtained by PD-PROP for different discretization options

Fig. 17

Compliance values and final topologies obtained by PD-OC for different discretization options

Table 3 Mesh-dependency study based on compliance values

1.2 Horizon size dependency analysis on hanger beam problem

The horizon radius is an important PD parameter that limits the extent of interactions between two particles. Therefore, the horizon size affects the solution in various aspects such as optimum material distribution, time cost, compliance, and so on. The optimized topologies obtained for four different horizon sizes are presented in Fig. 18. Average time consumption for a solution step and total strain energy are listed for both methods in Table 4. The elapsed time for each optimization analysis is achieved using a workstation having Intel(R) Xeon(R) Silver 4215R CPU 3.20 GHz with 16 cores. The average time can be considered the most influenced parameter as the increasing horizon radius causes high computational costs. Compliance also increases as the horizon is expanded. Decreasing the radius causes thinner sub-branches in the final designs which certainly leads to difficulties in the manufacturing step. Consequently, 3dx, is utilized as the optimum size of the horizon radius in this study.

Fig. 18

Final topologies obtained by PD-OC and PD-PROP for varying horizon size

Table 4 Mesh-dependency study based on compliance values