An improved plane strain/plane stress peridynamic formulation of the elastic–plastic constitutive law for von Mises materials

Abstract

A two-dimensional ordinary state-based peridynamic formulation is proposed for the analysis of elastic–plastic plane structures. Selecting appropriate relation for isotropic extension state, the deviatoric strain energy formulation is derived for plane strain/plane stress cases. Simple formulas to calculate peridynamic equivalent von Mises stress and its equivalent plastic strain are proposed. New yield function and flow rule are introduced. Implicit backward Euler time integration is used to obtain the increment of deviatoric plastic extension. Two example problems of grooved plate specimen and perforated plate under uniform tensile loading are considered to verify the accuracy of the present model in plane strain and plane stress situations respectively. The obtained results had a good agreement with those obtained by finite-element method. Results of displacements, von Mises stress, equivalent plastic strain, and plastic zone area are demonstrated. The effect of influence function on the results is also studied.

Appendices

Appendix A

In Eq. (C2) of Mousavi et al. [40], it is claimed that since $\underline{t}^{d}$ ignores the out of plane component in deviatoric stress tensor; thus, one can write (without any justification)

$$\frac{{3\pi l_{z} \delta^{4} }}{8}\frac{{\left\| {\underline{t}^{d} } \right\|^{2} }}{2} = \frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right).$$

(43)

On the other hand, the square of von Mises stress is given by

$$\sigma_{VM}^{2} = \frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + \left( {\sigma_{33}^{d} } \right)^{2} 2\left( {\sigma_{12}^{d} } \right)^{2} } \right).$$

(44)

Comparing these two equations, they concluded that by adding missing out of plane component $\frac{3}{2}\left( {\sigma_{33}^{d} } \right)^{2}$ to the both sides of Eq. (43), the von Mises stress can be obtained as

$$\sigma_{VM}^{2} = \frac{{3\pi l_{z} \delta^{4} }}{8}\frac{{\left\| {\underline{t}^{d} } \right\|^{2} }}{2} + \frac{3}{2}\left( {\sigma_{33}^{d} } \right)^{2} .$$

(45)

They proved that $\sigma_{33}^{d} = - \left( {\underline{t}^{d} \bullet \underline{x} } \right)$ and the final form of von Mises stress is given as

$$\sigma_{VM}^{2} = \frac{{3\pi l_{z} \delta^{4} }}{8}\frac{{\left\| {\underline{t}^{d} } \right\|^{2} }}{2} + \frac{3}{2}\left( {\underline{t}^{d} \bullet \underline{x} } \right)^{2} .$$

(46)

For $\omega = 1$, the weighted volume in PD can be written as $m = {{\pi l_{z} \delta^{4} } \mathord{\left/ {\vphantom {{\pi l_{z} \delta^{4} } 2}} \right. \kern-0pt} 2}$. Thus, Eq. (46), can be written in general form as

$$\sigma_{VM}^{2} = \frac{3m}{8}\left\| {\underline{t}^{d} } \right\|^{2} + \frac{3}{2}\left( {\underline{t}^{d} \bullet \underline{x} } \right)^{2} .$$

(47)

According to the above explanations, they considered that the term ${{\left\| {\underline{t}^{d} } \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {\underline{t}^{d} } \right\|^{2} } 2}} \right. \kern-0pt} 2}$ does not have any contribution from $\sigma_{33}^{d}$. However, we will show that $\frac{{3\pi l_{z} \delta^{4} }}{8}\frac{{\left\| {\underline{t}^{d} } \right\|^{2} }}{2}$ does not equal to $\frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right)$ and it has a contribution from $\sigma_{33}^{d}$ as

$$\frac{3m}{8}\left\| {\underline{t}^{d} } \right\|^{2} = \frac{{3\pi l_{z} \delta^{4} }}{8}\frac{{\left\| {\underline{t}^{d} } \right\|^{2} }}{2} = \frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right) + \eta \left( {\sigma_{33}^{d} } \right)^{2} .$$

(48)

To show this, from Eq. (29), we have

$$W_{PD}^{d} = \frac{5}{4}\mu \left( {\varepsilon_{33}^{d} \,} \right)^{2} + \frac{\alpha }{2}\left( {\underline{\omega } \underline {e}^{d} \bullet \underline {e}^{d} } \right).$$

(49)

Considering $\underline{t}^{d} = \alpha \omega \underline{e}^{d}$ and $\sigma_{ij}^{d} = 2\mu \,\varepsilon_{ij}^{d}$ and substituting for $\varepsilon_{33}^{d}$ and $\underline {e}^{d}$ in terms of $\sigma_{33}^{d}$, $\underline{t}^{d}$, one can write

$$W_{PD}^{d} = \frac{5}{\mu }\left( {\sigma_{33}^{d} \,} \right)^{2} + \frac{1}{2\alpha }\omega^{ - 1} \underline{t}^{d} \bullet \underline{t}^{d} .$$

(50)

Using Eq. (50) in Eq. (26), we have

$$\overline{\sigma }_{PD} = \sqrt {30\left( {\sigma_{33}^{d} \,} \right)^{2} + \frac{3m}{8}\omega^{ - 1} \underline{t}^{d} \bullet \underline{t}^{d} } .$$

(51)

The von Mises stress in continuum mechanics is defined as

$$\sigma_{VM}^{CM} = \sqrt {\frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + \left( {\sigma_{33}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right)} .$$

(52)

Equating Eqs. (51) and (52), we have

$$\begin{gathered} 30\left( {\sigma_{33}^{d} \,} \right)^{2} + \frac{3m}{8}\omega^{ - 1} \underline{t}^{d} \bullet \underline{t}^{d} = \frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + \left( {\sigma_{33}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right) \hfill \\ \omega^{ - 1} \underline{t}^{d} \bullet \underline{t}^{d} = \frac{4}{m}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right) - \frac{76}{m}\left( {\sigma_{33}^{d} } \right)^{2} . \hfill \\ \end{gathered}$$

(53)

Considering $\underline{\omega } = 1$, substituting from Table 1 for $m = {{\pi h\delta^{4} } \mathord{\left/ {\vphantom {{\pi h\delta^{4} } 2}} \right. \kern-0pt} 2}$ in Eq. (53), we have

$$\frac{3m}{8}\left\| {\underline{t}^{d} } \right\|^{2} = \frac{{3\pi l_{z} \delta^{4} }}{8}\frac{{\left\| {\underline{t}^{d} } \right\|^{2} }}{2} = \frac{3}{2}\left( {\left( {\sigma_{11}^{d} } \right)^{2} + \left( {\sigma_{22}^{d} } \right)^{2} + 2\left( {\sigma_{12}^{d} } \right)^{2} } \right) - \frac{57}{2}\left( {\sigma_{33}^{d} } \right)^{2} \frac{1}{2}\left\| {\underline{t}^{d} } \right\|^{2} .$$

(54)

From Eq. (54), $\eta$ can be obtained as $- \frac{57}{2}$. Thus, the relationship claimed in Eq. (43) is not correct.

Figure 

Fig. 13

Comparison of two formulations for vertical central axis displacement (left) and horizontal central axis von Mises stress (right) distribution in perforated plate

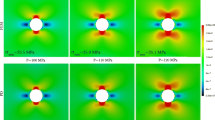
13 shows the comparison of the results with Mousavi et al.’s [40] formulation and present study for von Mises stress distribution and vertical displacement in plane stress case. As it can be seen, the Mousavi et al.’s [40] formulation cannot predict the von Mises stress and vertical displacement accurately.

Appendix B

In 3D PD, yield function is given by $F\left( {\underline{t}^{d} } \right) = \frac{1}{2}\underline{\omega }^{ - 1} \underline{t}^{d} \bullet \underline{t}^{d} - t_{0}$. Taking Freshet derivative with respect to $\underline{t}^{d}$, one can get

$${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t}^{d} = }}} \right. \kern-0pt} {\partial \underline{t}^{d} = }}\underline{\omega }^{ - 1} \underline{t}^{d} .$$

(55)

Knowing that $\underline{t}^{d} = \underline{t} - \frac{{\underline{t} \bullet \underline{x} }}{m}\underline{\omega x}$ and replacing in yield function, one can write the $F\left( {\underline{t} } \right)$ as

$$F\left( {\underline{t} } \right) = \frac{1}{2}\underline{\omega }^{ - 1} \left( {\underline{t} - \frac{{\underline{t} \bullet \underline{x} }}{m}\underline{\omega x} } \right) \bullet \left( {\underline{t} - \frac{{\underline{t} \bullet \underline{x} }}{m}\underline{\omega x} } \right) = \frac{1}{2}\left( {\underline{\omega }^{ - 1} \underline{t} \bullet \underline{t} - 2\frac{{\left( {\underline{t} \bullet \underline{x} } \right)^{2} }}{m} + \frac{{\left( {\underline{t} \bullet \underline{x} } \right)^{2} }}{m}} \right) - t_{0} .$$

(56)

${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} }}} \right. \kern-0pt} {\partial \underline{t} }}$ can be written as

$${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} = }}} \right. \kern-0pt} {\partial \underline{t} = }}\underline{\omega }^{ - 1} \underline{t} - \frac{{\left( {\underline{t} \bullet \underline{x} } \right)}}{m}\underline{x} = \underline{\omega }^{ - 1} \underline{t}^{d} .$$

(57)

Comparing Eqs. (55) and (57), it can be concluded that ${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t}^{d} = }}} \right. \kern-0pt} {\partial \underline{t}^{d} = }}{{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} }}} \right. \kern-0pt} {\partial \underline{t} }}$.

Appendix C

Considering the yield function in Eqs. (16) and (17), taking ${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t}^{d} }}} \right. \kern-0pt} {\partial \underline{t}^{d} }}$, one can get

$$\begin{gathered} F\left( {\underline{t}_{d} ,{t}_{0} } \right) = {{\left( {\underline{\omega }^{ - 1} \underline{t}^{d} } \right) \bullet \underline{t}^{d} } \mathord{\left/ {\vphantom {{\left( {\omega^{ - 1} \underline{t}^{d} } \right) \bullet \underline{t}^{d} } 2}} \right. \kern-0pt} 2} + E\left( {\underline{t}^{d} \bullet \underline{x} } \right)^{2} - {t}_{0}, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,E = {5 \mathord{\left/ {\vphantom {5 {2m}}} \right. \kern-0pt} {2m}} \hfill \\ \hfill \\ {{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t}^{d} }}} \right. \kern-0pt} {\partial \underline{t}^{d} }} = \underline{\omega }^{ - 1} \underline{t}^{d} + 2E\left( {\underline{t}^{d} \bullet \underline{x} } \right)\underline{x} = \underline{\omega }^{ - 1} \underline{t}^{d} + 5\left( {\underline{t}^{d} \bullet \underline{x} } \right){{\underline{x} } \mathord{\left/ {\vphantom {{\underline{x} } m}} \right. \kern-0pt} m}. \hfill \\ \end{gathered}$$

(58)

Substituting for $\underline{t}^{d}$ and $\underline{t}^{d} \bullet \underline{x}$ in terms of $\underline{t}$ and $\underline{t} \bullet \underline{x}$ from Eqs. (10) and (13), one can get the yield function in terms of $\underline{t}$ as

$$F\left( {\underline{t} ,\underline{t}_{0} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\underline{\omega }^{ - 1} \underline{t} \bullet \underline{t} - \frac{E}{15}\,\left( {\underline{t} \bullet \underline{x}} \right)^{2} - {t}_{0} } {\left( {{\text{2D}}\,{\text{plane}}\,{\text{stress}}} \right)} \\ {\frac{1}{2}\underline{\omega }^{ - 1} \underline{t} \bullet \underline{t} - \frac{E}{5}\frac{{\left( {9\kappa^{2} + 6\mu \kappa - 5\mu^{2} } \right)}}{{\left( {\kappa + {\mu \mathord{\left/ {\vphantom {\mu 3}} \right. \kern-0pt} 3}} \right)^{2} }}\left( {\underline{t} \bullet \underline{x} } \right)^{2} - {t}_{0} } {\left( {{\text{2D}}\,{\text{plane}}\,{\text{strain}}} \right)} \\ \end{array} } \right.,$$

(59)

Taking ${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} }}} \right. \kern-0pt} {\partial \underline{t} }}$, one can get

$$\begin{gathered} {{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} }}} \right. \kern-0pt} {\partial \underline{t} }} = \left\{ \begin{gathered} \underline{\omega }^{ - 1} \underline{t} - \frac{1}{3}\,\left( {\underline{t} \bullet \underline{x} } \right)\frac{{\underline{x} }}{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{2D}}\,{\text{plane}}\,{\text{stress}}} \right) \hfill \\ \underline{\omega }^{ - 1} \underline{t} - \frac{{\left( {9\kappa^{2} + 6\mu \kappa - 5\mu^{2} } \right)}}{{9\left( {\kappa + {\mu \mathord{\left/ {\vphantom {\mu 3}} \right. \kern-0pt} 3}} \right)^{2} }}\left( {\underline{t} \bullet \underline{x} } \right)\,\frac{{\underline{x} }}{m}\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{2D}}\,{\text{plane}}\,{\text{strain}}} \right) \hfill \\ \end{gathered} \right.. \hfill \\ \hfill \\ \end{gathered}$$

(60)

Substituting for $\underline{t}$ and $\underline{t} \bullet \underline{x}$ in terms of $\underline{t}^{d}$ and $\underline{t}^{d} \bullet \underline{x}$ from Eqs. (10) and (13), the following relations can be obtained:

$${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} }}} \right. \kern-0pt} {\partial \underline{t} }} = \left\{ {\begin{array}{*{20}c} {\underline{\omega }^{ - 1} \underline{t}^{d} + \left( {\underline{t}^{d} \bullet \underline{x} } \right)\frac{{\underline{x} }}{m}\,} {\left( {{\text{2D}}\,{\text{plane}}\,{\text{stress}}} \right)} \\ {\underline{\omega }^{ - 1} \underline{t}^{d} + \frac{{ - \kappa + {{5\mu } \mathord{\left/ {\vphantom {{5\mu } 3}} \right. \kern-0pt} 3}}}{{\kappa + {\mu \mathord{\left/ {\vphantom {\mu 3}} \right. \kern-0pt} 3}}}\left( {\underline{t}^{d} \bullet \underline{x} } \right)\frac{{\underline{x} }}{m}} {\left( {{\text{2D}}\,{\text{plane}}\,{\text{strain}}} \right)} \\ \end{array} } \right..$$

(61)

Comparing Eqs. (61) and (58), it is found that ${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t}^{d} \ne }}} \right. \kern-0pt} {\partial \underline{t}^{d} \ne }}{{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{t} }}} \right. \kern-0pt} {\partial \underline{t} }}$ for both of plane strain and plane stress cases.

Appendix D

Consider the following uniaxial tension loading condition (which satisfy dilatation zero behavior of von Mises plasticity) for plan strain problem:

$${{\varvec{\upvarepsilon}}}^{dp} = \left[ {\begin{array}{*{20}c} \varepsilon & 0 & 0 \\ 0 & { - \varepsilon } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right].$$

(62)

Using the above strain field, plastic extension state $\underline {e}^{dp}$ can be represented as

$$\underline {e}^{dp} = \left| {\underline{Y} } \right| - \left| {\underline{x} } \right| = \frac{{\left( {x_{1}^{2} - x_{2}^{2} } \right)}}{{\sqrt {x_{1}^{2} + x_{2}^{2} } }}\varepsilon .$$

(63)

Using Eq. (63), the $\underline{\omega } \underline {e}^{dp} \bullet \underline {e}^{dp}$ term can be calculated as

$$\underline{\omega } \underline {e}^{dp} \bullet \underline {e}^{dp} = \frac{m}{2}\varepsilon^{2} .$$

(64)

Knowing that $\theta_{Plastic} = 0$ for plan strain case $\overline{\varepsilon }_{PD}$ is calculated as

$$\overline{\varepsilon }_{PD} = \sqrt {\chi \frac{m}{2}\varepsilon^{2} } \,.$$

(65)

The equivalent plastic strain should recover the axial plastic strain in uniaxial tension loading. Thus, the parameter $\chi$ can be calculated as

$$\chi = \frac{2}{m}.$$

(66)

For plane stress case, the following strain field is considered:

$${{\varvec{\upvarepsilon}}}^{dp} = \varepsilon \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} & 0 \\ 0 & 0 & { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \\ \end{array} } \right].$$

(67)

Similar to the procedure for plane strain loading, one can obtain the $\underline{\omega } \underline {e}^{dp} \bullet \underline {e}^{dp}$, $\theta_{Plastic}$ as

$$\underline{\omega } \underline {e}^{dp} \bullet \underline {e}^{dp} = m\varepsilon^{2} ,\,\,\,\,\,\,\theta_{Plastic} = 2\varepsilon .$$

(68)

Considering $\chi = {2 \mathord{\left/ {\vphantom {2 m}} \right. \kern-0pt} m}$ from previous case, $\gamma$ can be obtained as

$$\gamma = \frac{5}{4}.$$

(69)

Thus, unified formulation for $\overline{\varepsilon }_{PD}$ in both cases can be shown as

$$\overline{\varepsilon }_{PD} = \sqrt {\gamma \left( {\theta_{Plastic} \,} \right)^{2} + \frac{2}{m}\left( {\underline{\omega } \underline {e}^{dp} \bullet \underline {e}^{dp} } \right)} \,\,\,\,\,\gamma = \left\{ {\begin{array}{*{20}c} {5/4} & {\left( {{\text{2D}}\,{\text{plane}}\,{\text{stress}}} \right)} \\ 0 & {\left( {{\text{2D}}\,{\text{plane}}\,{\text{strain}}} \right)} \\ \end{array} } \right..$$

(70)