1 Introduction

Over the next decades, the wastewater industry will continue to be subjected to unprecedented challenges, as worldwide demands for food and clean water are expected to rise by 50% and 30% respectively [1]. Furthermore, implementation of the EU Water Framework Directive (WFD) is driving an increase of energy consumption by up to 60% in wastewater treatment works (WwTWs) over the next 10–15 years [2], due to tighter discharge requirements. The wastewater-energy link must be clearly addressed in order to mitigate, and adapt towards, climate change.

Since 2009, wastewater treatment works across each major European country have produced over 1 M tonnes sludge per country per year [3]. The preferred method to treat sludge is mesophilic (22–41 \(^{\circ }\)C) anaerobic digestion with mixing occurring through biogas injection. Through this process, sludge is degraded by anaerobic bacteria into stable digestate and biogas (a mixture of mainly methane and carbon dioxide). Biogas is usually directed to a combined heat and power unit for energy recovery. Mixing is necessary for correct digestion and can be responsible for anywhere between 17% and 73% of digester energy consumption [4]. This level of consumption is largely suboptimal, as experimental evidence [5] shows that input mixing power can be reduced by to 50% without affecting the digestion process. To address mitigation and adaptation to climate change, it is therefore necessary to rethink mixing design practices and operation protocols, with the goal of balancing input mixing energy against output biogas production, rather than merely considering digestate quality.

Over the years, (segregated) Finite-Volume (FV) Computational Fluid Dynamics (CFD) has been successfully employed to model gas-mixed anaerobic digesters [6,7,8,9,10,11,12,13,14,15,16,17,18,19]. A CFD approach to design and system analysis offers multiple benefits, including a saving of time and money arising from avoiding lengthy and time-consuming experiments, and providing an insight to flow patterns which are unattainable from optical visualisation techniques (sludge is opaque) or tracer-response methods (which provide no more than a black-box description of the system). This progress has enabled the development of structured modelling protocols to significantly improve energy performance of both new and existing full-scale digester [20]. However, limitations in the industrial applicability of this approach persist, as long simulation runtimes (\(\ge 2\) days) render the deployment of the above-mentioned strategies excessively time-consuming. Furthermore, the multi-core parallel run of most common Finite-Volume schemes (viz., up to second-order) is hampered by poor parallel performance [21], mainly due to the high proportion of non-scalable inter-core communication operations involved in solving the Poisson pressure equation [22]. Indeed, previous Finite-Volume models of full-scale anaerobic digesters [17, 20, 23] could not scale up beyond 36 cores. As such, traditional Finite-Volume CFD cannot benefit from the on-going evolution of high-performance computing. In turn, this makes it impractical, or very time-consuming, to employ accurate but resource-intensive methodologies, e.g., the Large Eddy Simulations (LES). Indeed, no LES model for full-scale gas-mixed anaerobic digestion has been developed so far: only [24] has developed a LES Finite-Volume model for full-scale anaerobic digestion, but for mechanical, not gas, mixing, and concluded that LES is impractical due to the excessive computational expense required.

A potential solution to both the problems listed above is offered by the Lattice-Boltzmann (LB) method, a relatively recent CFD alternative to the Finite-Volume approach with recent industrial applications comprising, among other things, Ball-Grid-Array encapsulation process, heat flux inside refrigerated vehicles, internal-combustion engine and 3D-printed wet-scrubber nozzle [25,26,27,28]. Lattice-Boltzmann is essentially a Finite-Difference method equipped with tunable diffusivity [29]. Lattice-Boltzmann presents tangible advantages over the traditional Finite-Volume approach, such as: (i) full explicitness free from internal loops, resulting in a well-defined, limited number of floating-point operations per timestep; and (ii) strong parallelizability due to reduced non-scalable inter-core communication thanks to a formal and implementational distinction between non-local and non-linear parts of the algorithm and non-local access usually limited to first-neighbour cells only. Furthermore, the Lattice-Boltzmann method has the advantage over other models suitable to parallel computing (viz., high-order Finite-Volume, [21]), of (iii) implementational simplicity, as its structured grid approach and first-neighbour-only non-local access allow it to avoid complex stencils and to implement boundary conditions in a straightforward manner. Multiphase models, both Euler–Euler [30] and Euler–Lagrange [31,32,33,34,35], are available. A comparison between a Lattice-Boltzmann LES model and its Finite-Volume counterpart applied to a internal-combustion engine [27] showed that the former ran 32 times faster, thus making the usage of LES much more practical: “The faster calculation speed for NWM-LES using LBM is advantageous to address industrial applications and to enable ‘overnight’ calculations that previously took weeks. Therefore, faster design cycles and operating condition tests are feasible”. Coming to anaerobic digestion, a Lattice-Boltzmann model for a laboratory-scale gas-mixed digester [34] has been shown to perform around 180 times faster than its Finite-Volume analogue [14] whilst being able to run on ten times more processors without appreciable efficiency decrease. Thus, Lattice-Boltzmann’s superior numerical efficiency and parallelizability allow much finer grids than Finite-Volume at comparable numerical expense and runtimes, amply compensating for the errors arising from the traditional lack of local mesh refinement, unstructured and body-fitted grids in the traditional Lattice-Boltzmann implementations. It is therefore clear that Lattice-Boltzmann models can deliver a significant benefit to the operation of numerical modelling anaerobic digestion with gas mixing.

The topic of mixing improvement in full-scale anaerobic digestion has been widely investigated through CFD despite severe limitations in validation procedure: the intrinsically opaque and hazardous nature of sludge, as well as the impracticability of taking digesters out of production for experimental purposes, means that no experimental data concerning full-scale anaerobic digesters for wastewater treatment are available in the literature. As a result, there are examples in the literature where researchers provide unvalidated results in full-scale anaerobic digestion [8,9,10, 13]; rely on full-scale validation conducted on black-box measurements such as impeller power number [36]; or validate a model against flow patterns from a lab-scale setup, and then apply it to the full-scale [14, 17, 20, 23, 37].

Despite the advantages of CFD and, to a greater extent, Lattice-Boltzmann method, for anaerobic digestion modelling, only a limited amount of work has been dedicated to modelling the gas mixing processes [6, 10, 14, 17, 20, 23, 34, 35, 38]; among this, only [34, 35] employed the Lattice-Boltzmann; and finally, none reports full-scale Lattice-Boltzmann models with gas mixing. Dapelo et al. [34] introduced the first-ever multiphase Lattice-Boltzmann model for gas-mixed anaerobic digestion in a laboratory-scale set-up, and [35] demonstrated that the sub-grid Euler–Lagrange Lattice-Boltzmann method can be successfully employed to model laboratory and full-scale anaerobic digesters. In both [34, 35], the models were validated against laboratory-scale experiments conducted by [14]. However, a knowledge gap persists as no Lattice-Boltzmann model for gas-mixed industrial-scale digesters has been reported in the literature.

Within the work reported here, the sub-grid method developed and validated lab-scale in [35] is used for the first time to model a full-scale setup reproducing a real wastewater treatment digester, applying the same approach towards validation of [14, 17, 20, 23, 37] and thereby filling the above-mentioned knowledge gap. Flow and viscosity patterns are analysed, and the degree of mixing is evaluated through the Uniformity Index (\(\textrm{UI}\)) method proposed by [9]. The effect of different modelling parameters on the simulation outcome is assessed. The results are discussed and compared to previous second-order Finite-Volume work on a similar design [17, 20, 23]. It is shown how the Lattice-Boltzmann method offers advantages over the method used therein, and has a clear potential to overcome the issues concerning industrial applicability of CFD-based mixing-improvement strategies described above. Likewise, it is shown that the introduction of a Lattice-Boltzmann-based model makes the application of LES to full-scale anaerobic digestion practically feasible to industries and consultancies.

This paper is structured as follows. Sludge is modelled in Sect. 2: the assumptions underlying the multiphase model are laid down in Sect. 2.1; then, the model is described within the Lattice-Boltzmann framework in Sects. 2.2 and 2.3; finally, the pseudocode algorithm is reported in Sect. 2.4. The model’s implementation in OpenLB is reported in Sect. 3, and a short description of OpenLB and the innovation it has brought in the field of parallel computing is offered in Sect. 3.1. then, the results are reported in Sect. 4, and specifically: flow patterns (Sect. 4.1); grid independence (Sect. 4.2); mixing efficiency (Sect. 4.3); dependence of the results from the choice of Lagrangian subcycles (Sect. 4.4) and bubble size (Sect. 4.5); and scaling-up (Sect. 4.6). Then, a discussion is performed (Sect. 5), and conclusions are drawn (Sect. 6).

2 Modelling of sludge

Within this work, one of the models described in [35], with the geometry of [17, 23] is used. It is summarised here for the sake of clarity.

2.1 Assumptions

Sludge is a complex mixture of organic and inorganic solids arranged in fragments of various dimensions (from colloid molecules to sand or gravel), water and biogas bubbles where gas mixing is employed. The range of inter-phase phenomena include bubble–liquid (two-way) and bubble–bubble (four-way) momentum transfer, solid–liquid interactions such as grit sedimentation and scum flotation, and complex liquid rheology characterised by shear thinning, shear banding, yield stress and thixotropy.

To simplify the problem of modelling sludge, a sub-grid, two-way coupled Euler–Lagrange model with non-Newtonian rheology and a large-eddy-simulation turbulence model is introduced. The assumptions and simplifications underlying the choice of this model, as well as the justifications underpinning them, are listed as follows.

  1. (i)

    Sedimentation and flotation are ignored because they respectively take place in years/months and days/weeks, whilst the timescale of the mixing is up to 2 h.

  2. (ii)

    Solid phase is considered as a suspension of liquid phase, and its effect on the latter is modelled as the liquid phase’s non-Newtonian pseudoplastic rheology [39], with more complex rheological phenomena being ignored. In a pseudoplastic power-law model, the apparent viscosity \(\mu\) is a function of the magnitude of the sear rate \(|\dot{\gamma }|\), as follows:

    $$\begin{aligned} \mu = K|\dot{\gamma }|^{n-1}, \end{aligned}$$
    (1)

    with K and n (\(0<n<1\)) being respectively the consistency and power-law coefficients. Although both K and n depend on temperature and total solids content [40], temperature dependence is ignored as K and n are considered constant at the fixed temperature of 35 \(^\circ \textrm{C}\), this being the ideal temperature for mesophilic conditions. Table 1 reports typical values of n and K at 35 \(^\circ \textrm{C}\). For the sake of simplicity, sludge density is set to 1000 \(\textrm{kg}\) \(\textrm{m}^{-3}\). Equation (1) returns unphysically high or low apparent viscosity values for low or high values of \(|\dot{\gamma }|\) respectively; this is avoided in a standard way by introducing a minimum and maximum cutoff value for the apparent viscosity, \(\mu _{\textrm{min}}\) and \(\mu _{\textrm{max}}\).

    Table 1 Power-law coefficients, cutoffs and density of sludge at T=35 \(^\circ \textrm{C}\). From [40]
    Full size table
  3. (iii)

    (iii) As reported in the following Results sections, the Reynolds number is found to be comprised between 3600 and 6100, and therefore, turbulence is modelled. A large eddy simulation (LES) model is chosen, and the Smagorinsky constant \(C_{\textrm{Smago}}\) is set to 0.14.

  4. (iv)

    Bubble–bubble interaction, bubble coalescence and breakup are ignored, as they were found not to occur in experimental work [14]. Conversely, mixing occurs because of the momentum of the buoyant bubbles being transferred to the surrounding liquid phase. Therefore, the bubble–liquid interaction must be modelled; i.e. bubble–liquid two-way coupling is considered whereby momentum is transferred from the liquid phase to the bubbles (“forward-coupling”); and from the bubbles to the liquid phase (“back-coupling”).

  5. (v)

    The smallest grid cells used in this work are cubes of 9 cm size, which are larger than the largest bubble diameter (5 cm). Previous work [35] showed that liquid phase flow patterns can be effectively reproduced through a sub-grid Euler–Lagrange model, and consequently, bubbles are considered as pointwise within this work. Bubbles are also assume to have the same density of air, i.e. 1 \(\textrm{kg}\) \(\textrm{m}^{-3}\).

2.2 Modelling and simulation: sub-grid Euler–Lagrange bubbly phase

The dispersed bubbly phase is modelled as a collection of sub-grid elements \(\mathscr {P}_K\), or “particles” [34, 41]—one (spherical) bubble per particle. As rotational effects and deviations from sphericity were found to be negligible in previous work [14, 34], it is possible to represent each \(\mathscr {P}_K\) as a tuple of numbers consisting of: coordinate \(\varvec{X}_K\), velocity \(\varvec{U}_K\), acceleration \(\varvec{A}_K\), nominal radius \(R_K\) and mass \(M_K\):

$$\begin{aligned} \mathscr {P}_K \equiv \left( \varvec{X}_K,\varvec{U}_K,\varvec{A}_K,\,R_K,\,M_K\right) . \end{aligned}$$
(2)

At any Lattice-Boltzmann update, each \(\mathscr {P}_K\) within the domain is updated separately via verlet integration of Newton’s second law [42] over a number s of “Lagrangian subcycles” with Lagrangian timestep \(\delta t/s\):

$$\begin{aligned} \varvec{F}_K = M_K\varvec{A}_K. \end{aligned}$$
(3)

The resultant \(\varvec{F}_K\) of the forces acting on \(\mathscr {P}_K\) is modelled as a sum of buoyancy \(\varvec{F}^{\textrm{b}}_K\), added mass \(\varvec{F}^{\textrm{a}}_K\) and gravity \(\varvec{F}^{\textrm{d}}_K\):

$$\begin{aligned} \varvec{F}_K = \varvec{F}^{\textrm{b}}_K + \varvec{F}^{\textrm{a}}_K + \varvec{F}^{\textrm{d}}_K. \end{aligned}$$
(4)

Forward-coupling is achieved by modelling \(\varvec{F}^{\textrm{b}}_K\), \(\varvec{F}^{\textrm{a}}_K\) and \(\varvec{F}^{\textrm{d}}_K\) in terms of the liquid phase’s local values of the macroscopic fields: in [35], different models were tested, and the best results in terms of both convergence and numerical expense were achieved when the values of the liquid phase density and velocity fields \(\rho\) and \(\varvec{u}\) at the Kth particle’s position \(\varvec{X}_K\) were determined through linear interpolation across the cells surrounding \(\mathscr {P}_K\); conversely, the value of the kinematic viscosity \(\nu\) was approximated to the nearest cell \(\varvec{X}^{\textrm{next}}_K\). The same approach is then adopted here. For buoyancy we have:

$$\begin{aligned} \varvec{F}^{\textrm{b}}_K = - \left[ \frac{4}{3}\pi R_K^3\rho \left( \varvec{X}_K\right) - M_K\right] \varvec{g} \end{aligned}$$
(5)

with \(\varvec{g}\) being the acceleration of gravity. Added mass is given by:

$$\begin{aligned} \varvec{F}^{\textrm{a}}_K= & {} -\frac{1}{2}\rho \left( \varvec{X}_K\right) \frac{4}{3}\pi R_K^3\,\frac{\hbox {d}}{\hbox {d} t}\left[ \varvec{U}_K - \varvec{u}\left( \varvec{X}_K\right) \right] \nonumber \\\simeq & {} - \frac{1}{2}\rho \left( \varvec{X}_K\right) \frac{\pi }{6}d_K^3A_K. \end{aligned}$$
(6)

The drag force is defined as:

$$\begin{aligned} \varvec{F}^{\textrm{d}}_K= & {} -\frac{1}{2}\rho \left( \varvec{X}_K\right) C_{\textrm{d}}\left( \hbox {Re}_{\textrm{P}}\right) \pi R_K^2\,|\varvec{U}_K - \varvec{u}\left( \varvec{X}_K\right) |\nonumber \\{} & {} \quad \left[ \varvec{U}_K - \varvec{u}\left( \varvec{X}_K\right) \right] . \end{aligned}$$
(7)

As in [35], Morsi’s drag coefficient [43] \(C_{\textrm{d}}\) is used. The particle Reynolds number \(\hbox {Re}_{\textrm{P}}\) is evaluated as:

$$\begin{aligned} {\hbox {Re}}_{\textrm{P}}= \frac{2R_K|\varvec{U}_k - \varvec{u}\left( \varvec{X}_K\right) |}{\nu \left( \varvec{X}^{\textrm{next}}_K\right) }. \end{aligned}$$
(8)

2.3 Modelling and simulation: Lattice-Boltzmann method for the fluid phase

The Lattice-Boltzmann model solves the one-particle density function \(f\left( \varvec{x},\,\varvec{c},\,t\right)\), which is defined as the probability of finding one ideally pointwise and indivisible portion of fluid with velocity in \(\left[ \varvec{c},\,\varvec{c}+d\varvec{c}\right]\) and position in \(\left[ \varvec{x},\,\varvec{x}+d\varvec{x}\right]\) at the time t. The method is mesoscopic insofar as the observable macroscopic fields of density \(\rho \left( \varvec{x},\,t\right)\), velocity \(\varvec{u}\left( \varvec{x},\,t\right)\) and shear stress \(\sigma \left( \varvec{x},\,t\right)\) are not directly resolved—rather, they are evaluated from f’s first three moments [44]:

$$\begin{aligned} \rho= & {} \int f\;\text {d}\varvec{c}; \end{aligned}$$
(9)
$$\begin{aligned} \rho \,\varvec{u}= & {} \int f\,\varvec{c}\;\text {d}\varvec{c};\end{aligned}$$
(10)
$$\begin{aligned} \rho \,\varvec{u}\otimes \varvec{u}= & {} \sigma + \int f\,\varvec{c}\otimes \varvec{c}\;\text {d}\varvec{c}. \end{aligned}$$
(11)

f’s continuity equation in the phase space \(\Phi \left( \varvec{x},\,\varvec{c}\right)\) takes the name of the Boltzmann equation:

$$\begin{aligned} \left( \partial _t + \varvec{c}\cdot \nabla \right) f = \mathscr {C}\left[ f\right] . \end{aligned}$$
(12)

The “collision operator” \(\mathscr {C}\) is a source-sink term, modelling the effect of f of inter-particle collisions taking place within the cube \(\left[ \varvec{x},\,\varvec{x}+\text {d}\varvec{x}\right]\) between t and \(\text {d}+\text {d}t\). Under the diluted gas assumption (which is considered to hold in the work presented here), only binary collisions are accounted for in \(\mathscr {C}\). Under the widely-adopted Bhatnagar–Gross–Krook (BGK) hypothesis [45], collisions occur isotropically and induce a relaxation of f towards an equilibrium distribution \(f^{\mathrm {(eq)}}\) with relaxation time \(\tau\):

$$\begin{aligned} \mathscr {C}\left[ f\right] = - \frac{f - f^{\mathrm {(eq)}}}{\tau }. \end{aligned}$$
(13)

The equilibrium distribution is the Maxwell equilibrium distribution [44]:

$$\begin{aligned} f^{\mathrm {(eq)}}\left( \varvec{x},\,t\right) := \rho \left( \varvec{x},\,t\right) \left( \frac{1}{2\pi c_{\textrm{s}}^2}\right) ^{3/2}\exp \left\{ -\frac{\left[ \varvec{u}\left( \varvec{x},\,t\right) \right] ^2}{2c_{\textrm{s}}^2}\right\} , \end{aligned}$$
(14)

where velocity and density are evaluated through Eqs. (9) and (10), and \(c_{\textrm{s}}\) is the speed of sound.

Simulations consist of trajectories on the discretized phase space, with constant timestep \(\delta t\). The phase space \(\Phi \left( \varvec{x},\,\varvec{c}\right)\) is discretized as follows. The (spatial) discretized computational domain is defined as a 3D cubic lattice, with \(\delta x\) being the distance between two first-neighbouring sites. The discretized velocity space is generated by a set of vectors \(\left\{ \varvec{c}_0,\,\ldots ,\,\varvec{c}_{q-1}\right\}\) not mutually independent. \(\varvec{c}_0\) is the zero vector; the others point from one lattice site to its first neighbour and have module \(\delta x/\delta t\); or to its second neighbour neighbour and have module \(\sqrt{2}\,\delta x/\delta t\); or to its third (module \(\sqrt{3}\,\delta x/\delta t\)). The different choices of discretization are conventionally labelled through a tag DdQq: d represents the spatial dimension (in this work, 3); q the number of vectors spanning the velocity space. In place of \(f\left( \varvec{x},\,\varvec{c},\,t\right)\) we now have the discretized set \(f_i\left( \varvec{x},\,t\right)\), where the latter is defined as the probability of finding one portion of fluid at the lattice site \(\varvec{x}\) with velocity \(\varvec{c}_i\) at the time t. The zeroth, first and second moments of f (Eqs. 9, 10 and 11) are evaluated as summations, in place of integrals, over the velocity set:

$$\begin{aligned} \rho= & {} \sum _i f_i; \end{aligned}$$
(15)
$$\begin{aligned} \rho \,\varvec{u}= & {} \sum _i f_i\,\varvec{c}_i; \end{aligned}$$
(16)
$$\begin{aligned} \rho \,\varvec{u}\otimes \varvec{u}= & {} \sigma + \sum _i f_i\,\varvec{c}_i\otimes \varvec{c}_i. \end{aligned}$$
(17)

Using a discretized velocity space induces a discretization error—however, this error source can be removed if the Maxwell equilibrium function (Eq. 14) is written as a linear combination of Hermite polynomials. To ensure density and momentum conservation, only the Hermite polynomials up to the second order are needed [44]. As such, the discretized equilibrium function reads as:

$$\begin{aligned} f^{\mathrm {(eq)}}_i = w_i\,\rho \left[ 1 + \frac{\varvec{u}\cdot \varvec{c}_i}{c_{\textrm{s}}^2} + \frac{\left( \varvec{u}\cdot \varvec{c}_i\right) ^2-c_{\textrm{s}}^2u^2}{2c_{\textrm{s}}^4}\right] . \end{aligned}$$
(18)

The values of the weights are set in a standard way depending of the specific DdQp lattice. Similarly, the speed of sound is defined as:

$$\begin{aligned} c_{\textrm{s}}:= \frac{1}{\sqrt{3}}\frac{\delta x}{\delta t}. \end{aligned}$$
(19)

The application of Eqs. (9) and (10) [44] allows evaluation of the macroscopic fields and recovery of the adiabatic dynamics with a Mach-number-dependent compressibility error of \(\textrm{Ma}^2\). If the BGK assumption (Eq. 13) is adopted the Boltzmann Eq. (12) is discretized into the Lattice-Boltzmann equation:

$$\begin{aligned} f_i\left( \varvec{x}+\varvec{c}_i\,\delta t,\,t+\delta t\right) = f_i\left( \varvec{x},\,t\right) - \frac{f_i\left( \varvec{x},\,t\right) - f^{\mathrm {(eq)}}_i\left( \varvec{x},\,t\right) }{\tau }. \end{aligned}$$
(20)

Implementation of Eq. (20) is split into two steps: a local, non-linear collision:

$$\begin{aligned} \Xi _i\left( \varvec{x},\,t\right) = f_i\left( \varvec{x},\,t\right) - \frac{f_i\left( \varvec{x},\,t\right) - f^{\mathrm {(eq)}}_i\left( \varvec{x},\,t\right) }{\tau }; \end{aligned}$$
(21)

and a linear, non-local streaming:

$$\begin{aligned} f_i\left( \varvec{x}+\varvec{c}_i,\,t+\delta t\right) = \Xi _i\left( \varvec{x},\,t\right) . \end{aligned}$$
(22)

A multiscale (“Chapman-Enskog”) expansion shows that the Lattice-Boltzmann Eq. (20) reproduces the incompressible Navier–Stokes equations under the limit \(\textrm{Ma} \ll 1\) [44]. Pressure and kinematic viscosity take the values:

$$\begin{aligned} p:=\rho c_{\textrm{s}}^2, \qquad \nu :=c_{\textrm{s}}^2\left( \tau -\frac{\delta t}{2}\right) . \end{aligned}$$
(23)

Non-Newtonian rheology and turbulence are accounted for following [34, 35]. The relaxation time is treated as a field \(\tau \left( \varvec{x},\,t\right)\) rather than a parameter; its value is stored alongside \(f_i\left( \varvec{x},\,t\right)\) and initialised at the first timestep by inverting the second of Eqs. (23) using a bespoke reference value \(\nu _{\textrm{ref}}\) for the kinematic viscosity (see Sect. 3). \(\tau\) is then updated locally at every timestep before the collision phase (Eq. 21), as follows:

  1. 1.

    Power-law rheology is modelled as in [46].The rate of shear tensor \(S_{\alpha \beta }\equiv \frac{1}{2}\left( \partial _\alpha u_\beta + \partial _\beta u_\alpha \right)\) is evaluated locally from the second momentum of the first-order multiscale term of f, defined as \(f^{\mathrm {(1)}}_i\) [44]:

    $$\begin{aligned} \begin{aligned} \varvec{S}\left( \varvec{x},\,t\right)&= -\frac{1}{2\rho \,c_{\textrm{s}}^2\,\tau \left( \varvec{x},\,t\right) }\sum _i f^{\mathrm {(1)}}_i\left( \varvec{x},\,t\right) \,\varvec{c}_i\otimes \varvec{c}_i \\&\simeq -\frac{1}{2\rho \,c_{\textrm{s}}^2\,\tau \left( \varvec{x},\,t\right) }\sum _i\left[ f_i\left( \varvec{x},\,t\right) - f^{\mathrm {(eq)}}_i\left( \varvec{x},\,t\right) \right] \varvec{c}_i\otimes \varvec{c}_i. \end{aligned} \end{aligned}$$
    (24)

    Dynamic viscosity \(\mu _{\textrm{PL}}\left( \varvec{x},\,t\right)\) and, consequently, kinematic viscosity \(\nu _{\textrm{PL}}\equiv \mu _{\textrm{PL}}/\rho\) are obtained from the power-law Eq. (1) through the substitution:

    $$\begin{aligned} |\dot{\gamma }|\equiv \sqrt{2\,\varvec{S}:\varvec{S}}, \end{aligned}$$
    (25)

    and then \(\tau\) is recalculated from the second of Eq. (23), with \(\nu _{\textrm{PL}}\) being used instead of \(\nu\).

  2. 2.

    Smagorinsky turbulence is modelled as in [47]. The shear rate magnitude \(|\dot{\gamma }|\) is calculated after power-law correction by reapplying Eqs. (24) and (25). The Smagorinsky closure with \(C_{\textrm{Smago}}=0.14\) is then applied in order to compute the turbulent linematic viscosity:

    $$\begin{aligned} \nu _{\textrm{turb}} = \nu _{\textrm{PL}} + C_{\textrm{Smago}}|\dot{\gamma }|. \end{aligned}$$
    (26)

    The final value of \(\tau\) is then calculated by inverting once more the second of Eq. (23), with \(\nu _{\textrm{turb}}\) in place of \(\nu\).

The momentum transfer from bubbles to liquid phase (viz., back-coupling) can be included by modifying the Lattice-Boltzmann Eq. (20) through a general procedure, due to [48]: a momentum source term due to a body force is added to the Lattice-Boltzmann Eq. (20):

$$\begin{aligned} f_i\left( \varvec{x}+\varvec{c}_i,\,t+\delta t\right)= & {} f_i\left( \varvec{x},\,t\right) - \frac{f_i\left( \varvec{x},\,t\right) - f^{\mathrm {(eq)}}_i\left( \varvec{x},\,t\right) }{\tau } \nonumber \\{} & {} + \left( 1 - \frac{1}{2\tau }\right) \mathscr {S}_i\left( \varvec{x},\,t\right) \end{aligned}$$
(27)

and consequently, the collision Eq. (21):

$$\begin{aligned} \Xi _i\left( \varvec{x},\,t\right)= & {} f_i\left( \varvec{x},\,t\right) - \frac{f_i\left( \varvec{x},\,t\right) - f^{\mathrm {(eq)}}_i\left( \varvec{x},\,t\right) }{\tau }\nonumber \\{} & {} + \left( 1 - \frac{1}{2\tau }\right) \mathscr {S}_i\left( \varvec{x},\,t\right) , \end{aligned}$$
(28)

where the source term \(\mathscr {S}_i\) is a function of a particle-dependent forcing term \(\varvec{\Phi }\):

$$\begin{aligned} \mathscr {S}_i:= w_i\left[ \frac{\varvec{c}_i - \varvec{u}}{c_{\textrm{s}}^2} + \frac{\left( \varvec{c}_i\cdot \varvec{u}\right) \varvec{c}_i}{c_{\textrm{s}}^4}\right] \cdot \varvec{\Phi }. \end{aligned}$$
(29)

For the specific case of implementing the back-coupling, [35] proposed different models. The best performing in terms of convergence and numerical expense consisted of equating the forcing \(\varvec{\Phi }\) (in Eq. 29) to \(-\varvec{F}_K\) (in Eq. 4) to the most near cell from \(\mathscr {P}_K\), and summing over the particles and the number of Lagrangian subcycles occurring within a Lattice-Boltzmann update:

$$\begin{aligned} \varvec{\Phi } = -\sum _s\sum _K\varvec{F}_K\;\delta ^3_{\varvec{x},\,\varvec{X}^{\textrm{next}}}. \end{aligned}$$
(30)

Finally, Eq. (16) is modified as follows:

$$\begin{aligned} \rho \,\varvec{u} = \sum _i f_i\,\varvec{c}_i + \frac{1}{2}\sum _i\mathscr {S}_i\,\varvec{c}_i. \end{aligned}$$
(31)

2.4 Simulation algorithm

The model follows Algorithm 1 below.

figure a

3 Numerical experiments: setup

Fig. 1
figure 1

Computational domain

Full size image

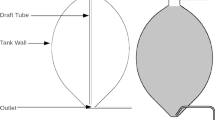
A cylindrical digester with an inclined base as [17, 23] is simulated (Fig. 1). A series of 12 nozzles, placed at equal distances along a circular manifold above the sloped bottom of the tank, is considered. Table 2 reports the geometric details. Mixing occurs through a circular manifold of 12 rectangular leaf-sparger nozzles with an equivalent diameter \(d_{\textrm{noz}}\). A set of material numbers is defined to facilitate boundary condition treatment—in other words, a n integer is assigned to a given portion of computational domain. Following Fig. 1b, c, material number 0 is assigned to out-of-domain cells which do not undertake any lattice operation; 1 to the bulk and is subjected to lattice update but not to boundary conditions; 2 to the wall and floor boundaries and is subjected to both lattice update and bespoke boundary conditions; 3 to the liquid phase’s free surface and is subjected only to bespoke boundary conditions.

Table 2 Details of the digester geometry, from [17, 23]
Full size table

The Reynolds number \(\textrm{Re}\) is evaluated as:

$$\begin{aligned} \textrm{Re}= \frac{U\,d_{\textrm{noz}}}{\nu _{\textrm{ref}}}. \end{aligned}$$
(33)

The reference velocity U is the theoretical asymptotic rising bubble velocity, obtained by imposing a static balance between buoyancy and drag force using Morsi’s model [43], multiplied by a heuristic correction set to 0.25 [35]. The reference kinematic viscosity \(\nu _{\textrm{ref}}\) is evaluated through substitution of the reference shear rate \(|\dot{\gamma }|_{\textrm{ref}}\) onto the rheology characteristic Eq. (1), with the former being defined as the shear rate occurring around an asymptotically rising bubble:

$$\begin{aligned} |\dot{\gamma }|_{\textrm{ref}} = \frac{U - u_{\textrm{surr}}}{2d} \simeq \frac{U}{2d} \end{aligned}$$
(34)

because the velocity of the portion of liquid phase surrounding a rising bubble \(u_{\textrm{surr}}\) is negligible if compared to the asymptotic rising bubble velocity U. \(\textrm{Re}\) was found to span between 3600 (15 mm bubble diameter) and 6100 (50 mm bubble diameter).

The simulations are performed on D3Q27 cubic lattices with linear dimension \(n_x\) spanning from 30 to 160 lattice sites across the diameter \(D_{\textrm{ext}}\), respectively corresponding to total numbers of cells spanning from 27,344 to 4,271,774. The dimensionless velocity \(U_{\textrm{LB}}\equiv \delta x/\delta t\cdot 1\,\textrm{s}/\textrm{m}\) is set according to diffusive scaling:

$$\begin{aligned} U_{\textrm{LB}} = U_{\textrm{LB}}^0\frac{n_x^0}{n_x}, \end{aligned}$$
(35)

with \(U_{\textrm{LB}}^0=0.15\) and \(n_x^0=60\). Simulated time spans between 600 and 3600 \(\textrm{s}\). Free-slip boundary condition is defined for the top free surface (material number 2), and Bouzidi no-slip for walls and bottom (material number 1). The maximum values of \(y^+\) around the walls are found to be 30, 13 and 5 for 2.5%, 5.4% and 7.5% TS respectively, and the average value were respectively 4, 0.16 and 0.08; as such, no wall function is implemented. At the initial timestep, the fluid phase is quiescent and no bubbles are present in the system. Bubbles of diameter \(15< d < 50\) \(\textrm{mm}\) are introduced in the computational domain (viz., a new tuple \(\mathscr {P}_K\) is defined) one at a time, at a position \(h_{\textrm{noz}}\) above the sloping base of the tank. The time interval between two bubble injection is defined as follows:

$$\begin{aligned} \Delta t_{\textrm{inj}} = \frac{\pi d^3}{6\,q_{\textrm{noz}}}. \end{aligned}$$
(36)

As \(\Delta t_{\textrm{inj}}\) is in general not a multiple of \(\delta t\), bubbles are in practice injected at the first subsequent timestep. The bubbles crossing the liquid surface are deleted.

3.1 OpenLB and Lattice-Boltzmann for platform-transparent saturation of modern HPC machines

The Lattice-Boltzmann is particularly suitable for extreme- and exa-scale simulations of fluid flows [49, 50] as, contrarily to conventional numerical techniques, close-to-optimal speedups are reachable. For example, LES of fluid flows in an injector with Lattice-Boltzmann-implemented in OpenLB (www.openlb.net) allow a speedup of 32 (simulation) and 424 (meshing) compared to Finite-Volume implementations in OpenFOAM (www.openfoam.org) on a similar setup with fixed accuracy [27].

The open-source C++ Lattice-Boltzmann framework OpenLB (https://www.openlb.net/) has been continuously developed since 2006. Krause (IANM/MVM/KIT). OpenLB contains a broad range of LBM implementations for several classes of partial differential equations (PDEs) for transport multi-physics including initial, boundary, and coupling methods [51]. Besides highly efficient simulations of turbulent, reactive, particulate and thermal fluid flow models, even coupled radiative transport or melting and conjugate heat transfer are realizable [27, 52,53,54,55].

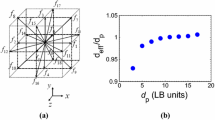
Specifically designed for large scale data generation, OpenLB supports efficient and platform-transparent executions, both on single-instruction-multiple-data (SIMD, vectorization) central processing units (CPUs), and general-purpose graphical processing units (GPGPUs) [56]. This is augmented by virtual memory manipulation and automatic code generation in order to reduce the arithmetic load per kernel [57], saturating the available memory bandwidth on current CPU and GPU targets [58]. The parallel efficiency of OpenLB was recently evaluated at up to perfect \(1.0\) (weak scaling) and very good \(0.94\) (strong scaling) on the HoreKa supercomputer (https://www.scc.kit.edu/dienste/horeka.php, 66/Top500 June 2022) at SCC (KIT), using both CPU-only and accelerated GPU partitions (Fig. 2). At the moment, a peak amount of \(1.3\times 10^{12}\) grid cell updates per second is realizable on 128 accelerator nodes with 4x NVIDIA A100 GPUs each.

Fig. 2
figure 2

OpenLB scaling-up on HoreKa

Full size image

4 Numerical experiments: results

The simulations are run on one 40-core Lenovo ThinkSystem SR65 CPU. The computational expense spans between 500 and 45,000 CPUs (cumulative figure summed across the cores), depending on the run. OpenLB (www.openlb.net) version 1.3 [51, 59], a generalistic open-source library for parallel Lattice-Boltzmann modelling, equipped with optimized load-balancing strategies [60] and a vectorised A–A streaming algorithm [61], is used.

4.1 Flow patterns

Fig. 3
figure 3

Flow patterns and vortex position, \(n_x=80\), \(50\,\textrm{mm}\) bubble size

Full size image

Figure 3 shows snapshots of flow patterns at different times (\(t=300\) and 600 s) for different values of TS. The numbers around the plots and in all the following refer to the spatial coordinates as Fig. 1a. Qualitatively, high-velocity narrow areas, with velocity directed vertically upwards, are observed above the nozzle locations; this corresponds to the drag effect exerted by rapidly-rising bubbles to the liquid phase. As the rapidly-rising flow approaches the liquid surface, it is deviated in a radial direction and then, as it approaches the walls, downwards. The flow is finally directed towards the rising columns, forming a toroidal vortex. Smaller-scale structures are also present, indicating the turbulent nature of the flow. The snapshots display fluctuations over time around this general description; this is in agreement with the fact that turbulence is modelled through LES. The large-scale flow patterns remain practically unchanged irrespective of the value of TS: the only qualitative aspect that varies depending of the value of TS is the relative prominence of the small-scale structures connected to turbulence; such structures tend to smooth out as the TS increases. This is in agreement with the fact that \(\textrm{Re}\) decreases (and therefore, the flow is less turbulent) as TS increases.

A quantitative description is offered by the coordinates of the vortex. For every timestep, the vortex is found by searching the x–y position minimizing the velocity magnitude within the square window \(\left[ 3.0,\;6.5\,\textrm{m}\right] \times \left[ 9.5,\;13.0\,\textrm{m}\right]\) starting from an initial guess of \(\left( 5.0,\;11.0\,\textrm{m}\right)\). The resulting vortex position is marked with a red cross in the snapshot of Fig. 3, and tracked over time in Fig. 4. As in the case of the flow patterns, the vortex position oscillates around an average value, as expected from a LES model. For all the TS values, the stationary-oscillating regime is reached after an initial transient period of around \(\sim 200\,\textrm{s}\). Both the average and the statistical standard error (the latter being computed on the same number of samples for all the runs) have similar values for all the values of TS, thereby confirming the qualitative observation of unchanging large-scale flow patterns irrespective of the value of TS.

Fig. 4
figure 4

Vortex coordinates over time, \(n_x=80\), \(50\,\textrm{mm}\) bubble size. Solid lines: instantaneous values. Dashed lines: averages, computed from 200 \(\textrm{s}\) onwards. Dotted lines: statistical standard errors computed from adapted standard deviations, computed from 200 \(\textrm{s}\) onwards

Full size image

In Fig. 5, snapshots of the apparent viscosity are reported. The viscosity patterns become more evident and less uniform as TS rises, indicating a more prominent power-law behaviour for higher values of TS.

Fig. 5
figure 5

Apparent viscosity over characteristic viscosity, \(n_x=80\), \(50\,\textrm{mm}\) bubble size

Full size image

4.2 Grid independence

Fig. 6
figure 6

Averaged vortex position and relative error, 2.5% TS sludge, \(50\,\textrm{mm}\) bubble size. Average performed for \(t\ge 200\,\textrm{s}\)

Full size image

The grid independence test is reported in Fig. 6. The test is performed over the vortex coordinate, with the average being taken for each run by averaging between the instantaneous values for \(200\,\textrm{s}\le t \le 600\,\textrm{s}\) and errorbars as in Fig. 4. The curves display rapid oscillations. Despite this, a best fit against a function of the type \(f\left( n_x\right) =a+b/n_x+c/n_x^2\) shows that the values oscillate around an approximatively horizontal asymptote for \(n_x\gtrsim 80\), with a relative error (defined as the absolute value of the relative difference between the datum and the series’ last value) comprised between 0.2 and 2%. It is therefore possible to consider the results as grid independent for \(n_x>80\), and the value of \(n_x=80\) is chosen for all the other runs reported in this work as the best compromise between accuracy and numerical expense.

4.3 Uniformity Index

In [20, 23], the uniformity index (\(\textrm{UI}\)), as introduced in [9], was found to be the best single-number quantitative criterion to assess mixing. Given a numerical macroscopic scalar field (“tracer”) \(\phi\) evolving according to an advection–diffusion equation with zero diffusivity:

$$\begin{aligned} \partial _t\phi + \left( \varvec{u}\cdot \varvec{\nabla }\right) \phi = 0, \end{aligned}$$
(37)

the uniformity index is defined in a cubic lattice as:

$$\begin{aligned} \textrm{UI}:= \frac{1}{2\left<\phi \right>}\left<|\phi -\left<\phi \right>|\right>, \end{aligned}$$
(38)

with \(\left<\cdot \right>\) being the average over the lattice sites. As a consequence of how it is defined, the value of \(\textrm{UI}\) varies between 0 for perfect mixing to 1 for complete inhomogeneity. The tracer \(\phi\) is solved through an explicit Finite-Volume method as in [62]. The first-order upwind scheme for the advection term is preferred over the central second-order for the sake of numerical stability. No negative-diffusivity correction is set [62].

Fig. 7
figure 7

“Sparse” results, 2.5% TS sludge, \(50\,\textrm{mm}\) bubble size

Full size image

Figure 7 shows the evolution of the tracer \(\phi\) over time up to \(t=600\) s, when \(\phi\) being initialised to 0 almost everywhere, and to 1 in single cells evenly distributed throughout the computational domain (Fig. 7a). This initial condition is labelled as “Sparse”. After 10 \(\textrm{s}\) from the start of the simulation (Fig. 7b), the positions of the pockets with non-zero \(\phi\) remain unaltered, showing that the flow patterns have not yet developed enough to displace them away from their original positions. However, numerical diffusion is evident, and no improvement is observed when negative anti-diffusion is set—this is the reason why anti-diffusion is not set in the work reported here. As a result, despite the evolution towards homogenisation (Fig. 7c, d) and decrease of the uniformity index (Fig. 7e), the latter displays an evident grid dependence with its value at given timesteps depends on grid size (Fig. 7f), as numerical diffusion depends on \(\delta x\) [62].

Fig. 8
figure 8

“Ball” results, 2.5% TS sludge, \(50\,\textrm{mm}\) bubble size

Full size image

In Fig. 8, another initial condition for the scalar tracer \(\phi\) is proposed, under the name of “Ball”. \(\phi\) is initialised to 0 everywhere and to 1 in a sphere sideways (Fig. 8a), around the location of the inlet [17, 23]. At the start of the run, the bulk of non-zero concentration field appears to be advected downwards by the flow patterns with marginal diffusion phenomena (Fig. 8b), until the tracer finally starts to be spread across the computational domain, after being brought in contact with the rising bubble column (Fig. 8c, d). Only at that point does the uniformity index start to fall significantly (Fig. 8e). This description is in agreement with [23], where new sludge just injected into the system finds itself in a position analogous to the scalar tracer described here and in the cited article, and initially undertakes only a poor level of mixing.

The observation of negligible diffusion phenomena (Fig. 8b) is corroborated by the analysis of the behaviour of the uniformity index for different values of \(n_x\) (Fig. 8f) fitted against a function of the type \(\sum _n n_x^{-n}\), \(0\le n \le 4\), and the corresponding relative error (Fig. 8g). Despite oscillations, a clear horizontal trend is observed at all the time snapshots for \(n_x\ge 80\), in agreement with the conclusions of Sect. 4.2. Above that threshold, the uniformity index appears to converge to approximately second order, and its relative error falls below 5%. This observation: (i) indicates that the “Ball” configuration is less affected by numerical diffusivity than the “Sparse”, and is therefore the most suitable to investigate the model’s behaviour under variation of its parameters; and (ii) further confirms mesh independence for \(n_x\ge 80\) wherever the initial conditions allow one to ignore numerical diffusivity.

4.4 Lagrangian subcycles

Fig. 9
figure 9

Flow patterns, vortex position, viscosity patterns and tracer for different numbers of Lagrangian subcycles at \(t=3600\,\textrm{s}\). 2.5% TS sludge, \(n_x=80\), \(50\,\textrm{mm}\) bubble diameter

Full size image

Figure 9 reports qualitative snapshots, taken at 3600 \(\textrm{s}\), of flow patterns, viscosity and scalar tracer field \(\phi\), for two different numbers of Lagrangian subcycles (viz., 20 and 400). No qualitative difference between the results of the different numbers of Lagrangian timesteps can be identified. Further, in Fig. 10, vortex position and the value of the uniformity index at different times are reported as a function of the number of Lagrangian subcycles, for both the “Sparse” and “Ball” initial conditions. A best fit of the form \(\textrm{UI}=\sum _i a_i s^{-n}\), \(0\le i \le 2\), is reported. Apart from local oscillations attributable to noise, the relevant parameters are observed to be independent from the number of Lagrangian subcycles, within a relative error of \(\sim 10^{-2}\).

Fig. 10
figure 10

Dependence on number of Lagrangian subcycles, \(n_x=80\), 2.5% TS sludge, \(50\,\textrm{mm}\) bubble size

Full size image

4.5 Bubble size

Fig. 11
figure 11

Flow patterns, vortex position, viscosity patterns and tracer for different bubble sizes at \(t=840\,\textrm{s}\). 2.5% TS sludge, \(n_x=80\), 100 Lagrangian subcycles

Full size image

Figure 11 reports qualitative snapshots, taken at 840 \(\textrm{s}\), of flow patterns, viscosity and scalar tracer field \(\phi\), for two different bubble sizes (viz., 15 and 50 \(\textrm{mm}\)). Flow patterns snapshots (Fig. 11a, b) display qualitatively more intense flow patterns in simulations with smaller bubble size. The latter also present a more prominent presence of small-scale structures, indicating a higher level of turbulence. Conversely, viscosity flow patterns (Fig. 11c, d) and final tracer \(\phi\) distribution (Fig. 11e, f) are not found to be affected by the choice of bubble size.

From these observations, it can be argued that smaller bubbles manage to mix the system faster thanks to more intense flow patterns and turbulence intensity, whilst the final level of mixing remains unaffected. This picture is confirmed by the quantitative picture (Fig. 12). The vortex positions (Fig. 12a, b) do not provide relevant information due to the large uncertainty bars. However, the uniformity index (Fig. 12c), for early timesteps (140 s) clearly shows that smaller bubble sizes produce lower \(\textrm{UI}\) values, with a difference of \(\textrm{UI}\) value between 50 and 15 mm bubble sizes of 0.083, corresponding to around 18% of 15 mm bubble size’s \(\textrm{UI}\) value. This difference decreases for further timesteps, with the relative error at the final timestep being below \(10^{-2}\).

Fig. 12
figure 12

Dependence on bubble size. “Sparse” results, \(n_x=80\), 2.5% TS sludge

Full size image

4.6 Scaling-up

Fig. 13
figure 13

Strong scaling, 2–12 nodes, each with 40 CPUs

Full size image

A strong scaling-up test was performed (Fig. 13) on up to 12 Intel Xeon Gold Skylake cores, each containing 40 CPU cores. The simulations were run selecting \(n_x=320\) (corresponding to over 32,113,000 cells), 50 \(\textrm{mm}\) bubble size, for 60 \(\textrm{s}\) simulated time. The scale-up clearly shows an increasing trend throughout the whole range of number of cores, with a loss of efficiency of less than \(25\%\) at the highest number of cores. Such loss of efficiency is likely due to the non-scalable inter-core communication taking place at the streaming phase; and to the Lagrangian particles. Indeed, within OpenLB, a Lagrangian particle is simulated by the CPU core responsible for the subdomain where the given particle is located; this means that non-scalable operations occur when a particle crosses a subdomain division as its data are communicated from the target to the destination CPU; and asymmetric load balancing occurs when the particles are not distributed uniformly throughout the computational domain (which is the case for the simulation work described within this article).

5 Discussion

The results reported in Sect. 4.2 show that the flow patterns are grid independent for \(n_x\gtrsim 80\). However, the noise manifesting itself as oscillations in Fig. 6 makes the determination of the order of convergence challenging. Similar considerations hold for the uniformity index: once the grid-dependent effect of numerical diffusion is singled out, \(\textrm{UI}\) displays grid independence for a similar value of \(n_x\gtrsim 80\), with analogue considerations about noise (Fig. 8f).

The results reported in Sect. 4.4 indicate that the simulations are independent of the number of Lagrangian subcycles. As such, the number of Lagrangian subcycles remains a non-physical tuning parameter, to be tuned depending on the particular application and the specific bubble size, to strike the best balance between numerical expense (i.e., the numerical expense is proportional to the number of Lagrangian subcycles), and stability (i.e., the Lagrangian solver becomes unstable if the number of Lagrangian timesteps falls below a threshold dependent on specific application and bubble size).

In Sect. 4.5, bubble size is shown to affect flow the patterns and the transient evolution of the uniformity index, but not the final value of \(\textrm{UI}\)—or in other words, the prediction of steady-state mixing quality. This is in agreement with the observations on the same geometry, applying a second-order Finite-Volume Reynolds-Averaged-Navier–Stokes model with Reynolds-stress turbulence model and the same power-law rheology model, on OpenFOAM 2.3.0 (www.openfoam.org/version/2-3-0) [17, 20, 23].

Overall, the Lattice-Boltzmann predictions of flow patterns, uniformity index and degree of mixing produced by the numerical work presented here are in agreement with observations from the above-mentioned Finite-Volume CFD work [17, 20, 23]. However, the Lattice-Boltzmann model presented here offers two critical advantages over the previous Finite-Volume, specifically:

  1. (i)

    Numerical efficiency. Lattice-Boltzmann runs with \(n_x=80\) need around 10,500 CPUs to run over grids of 536,171 cells for 600–3600 \(\textrm{s}\) simulated time, for a specific resource usage of 5.4–33\(\cdot 10^{-6}\) CPUs per \(\textrm{s}\) per cell. In contrast, the Finite-Volume analogue took around 13,500,000 CPUs for running over a grid of 394,400 cells for 300 \(\textrm{s}\) simulated time on 36 Intel Xeon E5-2690 v3 Haswell (2.6 GHz) cores, for a specific resource usage of 0.11 CPUs per \(\textrm{s}\) per cell. This makes the Lattice-Boltzmann model over 1000 times faster than the Finite-Volume model previously used in the literature to solve this problem. Similarly, the LES simulations performed in [24] for a full-scale mechanically-mixed digester were conducted on 188,289 cells for around 60 \(\textrm{s}\) simulated time and took 1,205,200 CPUs, for a specific resource usage of 0.11 CPUs per \(\textrm{s}\) per cell—the same value as [17, 20, 23]. Although the present Lattice-Boltzmann work and the previous Finite-Volume are conducted on different machines, the large performance difference between this and the previous models, as well as the similarity in performance between [17, 20, 23] and [24], allow us to confidently rule out any detrimental effect attributable to differences in hardware.

  2. (ii)

    Resolution. Lattice-Boltzmann’s best balance between numerical efficiency and precision was found to be \(n_x=80\), for 536,171 cells (Sect. 4.2). By contrast, the same balance returned 98,420 cells for a \(\pi /6\) wedge of the computational domain in the Finite-Volume model. This shows that the Lattice-Boltzmann model comfortably allows much finer grids than the Finite-Volume, thereby producing much more detailed predictions. In fact, the Lattice-Boltzmann model allowed a level of detail of the flow patterns, especially concerning smaller-scale turbulent patterns (Fig. 11a, b), which would be unachievable in the Finite-Volume results reported in [17, 23] because of the above-mentioned difference in numerical efficiency and Finite-Volume’s scaling-up problems [22].

  3. (iii)

    Scaleup. Scaling-up performance is discussed in Sect. 4.6. Despite the limiting factors discussed therein, the strong-scaling plot (Fig. 13) clearly shows an increasing trend, without reaching a plateau at 480 cores (it was not possible to perform simulations with more cores due to hardware limitations). This constitutes a notable improvement over previous Finite-Volume models, as the plateau was previously reached at 36 cores [17, 23].

Considering the usage of cache memory. Lattice-Boltzmann methods are memory-intensive: the model presented here uses 32 floats per lattice cell, much more than the previous Finite-Volume (which uses 5 floats per cell). This high memory usage does not usually pose a limitation to numerical performance as access to cache memory is fast—and indeed, it did not pose a limitation to the performance of the runs descripted here. However, care should be taken in checking that the available cache memory can meet a run’s memory requirement, before performing the run itself. OpenLB maps the computational domain into a lattice, or SuperLattice object, which is in turn divided into sub-lattices, or BlockLattice objects. Each BlockLattice is loaded onto the cache memory of a single CPU [51]. As such, increasing the number of cores usually resolves possible problems of shortage of memory. Considering the effectiveness of this strategy in preventing memory over-usage, and considering that memory usage does not constitute a bottleneck to numerical performance, we did not perform a comparison between memory usage of the model presented here, and its Finite-Volume predecessors [17, 23].

6 Conclusions

A Lattice-Boltzmann LES model of a full-scale, biogas-mixed anaerobic digester has been presented for the first time. Scaleup, convergence and the effects of bubble size and number of Lagrangian subcycles on the model predictions concerning the digester’s hydrodynamics have been assessed.

A comparison between Lattice-Boltzmann and Finite-Volume on an analogue applications shows that the former is over 1,000 times more computationally efficient, allows resolution of flow patterns in much more detail, and allow a feasible, resource-effective usage of LES in anaerobic digestion modelling for the first time. Thus, the work presented here is a comparison between two specific models being used to solve a problem of significant interest and relevance to the wastewater industry. It should not be considered as a benchmark in a strict sense—such benchmark work would require tests on a wide range of models being conducted on the same hardware running under the same conditions, and is out of the scope of this research. Notwithstanding this limitation, it can be concluded that the Lattice-Boltzmann is a more convenient modelling choice for full-scale gas mixing in anaerobic digestion, than the most common second-order Finite-Volume approaches.

Industries and consultancies will be able to use the results described here as guidance to improve full-scale digesters’ mixing efficiency via UI maximization. In this respect, the code used here will be available in a future official release of the OpenLB package.