1 Introduction

Domains with a tubular structure are featured in various applications, particularly in biomedically motivated ones, such as blood flow and bronchial airflow [1,2,3]. Such geometries can be reconstructed from medical imaging data for different applications, including computational fluid dynamics (CFD) (Fig. 1). The discretization of these domains is most often performed through unstructured mesh generation, supported by its capabilities to robustly capture complex geometries [4, 5]. The lack of control over the number of nodes and elements in the mesh, as well as the number of elements sharing a given node [6], are among the reasons one may prefer structured meshing approaches. The difficulties in structured mesh generation for nontrivial geometries are well-known, though they may be alleviated by providing sufficient topological and geometrical domain information, as well as a priori identification of potential singularities or sharp jumps arising in simulations.

A prominent example for special solution features, which should be considered in the mesh generation, are boundary layers in computational fluid dynamics [7], where one expects very strong velocity gradients. Special treatment of boundary layers is vital for any fluid simulation, and it should therefore be performed on the mesh level. Hexahedra are the imminently suitable element type in this regard, bolstered by the ability to induce anisotropy via mesh grading [8], with a 2D example in Fig. 2b. Thereby, tailored mesh refinement is obtained, inducing thinner elements near the domain boundary, capturing the aforementioned phenomenon whilst retaining the number of mesh elements. Alternatively, tetrahedra are a common choice, given their flexibility and popularity in unstructured mesh generation [5], though hex or hex-dominant unstructured approaches are also available [9]. Also, meshes may consist of both hexahedra and tetrahedra, including prisms and pyramids for transition [10].

Automatic structured hexahedral mesh generation is commonly performed on specific classes of domains. Herein, we restrict ourselves to healthy blood vessels, with the emphasis on patient-specific aortas. Such structures naturally admit a topological skeleton, i.e., a centerline abstracting the topology of the domain. Skeleton-based mesh generation includes a wide variety of approaches. One approach might be to consider so-called quad layout extraction [11], which was also extended to three dimensions in [12]. An important feature is the placement and subdivision of cubes at the junction points of the skeleton. Additional mesh optimization is performed to guarantee element validity. In [13], a hex mesh generation based on filling a triangular surface mesh was presented, providing a level of control between surface fitting and minimum mesh quality. Generation of explicit and smooth cylindrical maps, i.e., maps between a tubular domain and a cylinder in the polar coordinate system, was performed in [14]. A recent skeleton-reliant method for so-called face extrusion quad meshes is given in [15]. Semiautomatic approaches exist as well, e.g., for vascular modelling based on a block structure and a quadrilateral surface mesh [16]. High quality hexahedral meshing of large vascular structures based on a centerline input was performed by Ghaffari et al. [17]. A very recent and rather extensive survey of hex and hex-dominant mesh generation as well as mesh post-processing may be found in [18]. Furthermore, skeleton-based methods often go in the direction of quadrilateral scaffolds, i.e., coarse quadrilateral representations of the surface around the skeleton, such as scaffolding based on Voronoi diagrams [19], also mentioned by the same authors in [20], as well as a scaffolding approach in [21], citing a minimal number of quads for the given topological regularity. A somewhat similar three-dimensional concept is a block-structure, i.e., a division of the domain into coarse blocks. As the block structure captures the topology of the domain, and the skeleton is meant to abstract the very same topology, it was a natural choice to merge these two approaches. Relevant examples include a method based on a block structure enabling different element types presented in [22], and a survey of block-structured approaches in [23]. A comparison of computational fluid dynamics meshes generated based on various block structure generation methods was performed as well [24]. The block structure approach additionally enables the generation of rather coarse, but domain-conforming meshes. In particular, this enables applying the geometric multigrid method [25], a powerful iterative algorithm, which however requires the availability of several nested grids with varying spatial resolution of the same domain.

Most of the aforementioned work is focused on obtaining linear (first-order) meshes. Therein, geometric and approximation errors can be reduced by using more elements to discretise the domain, which is known as h-FEM. Instead of using more linear elements, one may rather improve the order of the elements, known as p-FEM [26]. Better performance is achieved by increasing the polynomial degree of the FE shape functions, and thus the number of nodes per element, as shown in Fig. 2c. A well-known example of a higher-order approach are the so-called Taylor-Hood elements [27]. They are particularly popular when solving incompressible flow problems, where we seek to determine pressure and velocity. Therein, elements of order k are used for velocity, and of order \(k-1\) for pressure, noting that equal orders lead to instabilities [28]. Many modern fluid flow solvers are turning to the higher-order paradigm as well [29]. Moreover, structured, higher-order, hexahedral meshes are the standard in isogeometric analysis [30, 31]. An early work by Zhang et al. offers a NURBS-based sweeping method for mesh generation [32]. The generation of truncated T-splines, showing desirable properties whilst enabling localized refinement, was the focus in [33]. Patient-specific flow with the focus on higher-order representation of realistic motion in a single lumen may be found in [34]. A review of patient-specific NURBS construction was given in [35]. Finally, the process of going from scanned images all the way to applicable geometrical models was covered in detail in a recent book [36], and earlier in the review paper [37]. Further advantages of higher-order approaches are discussed extensively in [38], wherein the lack of appropriate higher-order mesh generators was particularly emphasized.

The generation of higher-order meshes should be accompanied with a suitable shape representation method. Herein, we utilise convolution surfaces [39], relying heavily on the fact they offer a smooth representation. A more detailed overview of the topic of shape modelling, as well as accompanying details regarding convolution surfaces, are given in Sect. 2.

Fig. 1
figure 1

The overall pipeline: a the CT scan, b the CT scan with segmentation, c the extracted skeleton, d the convolution surface, e the block-structure, f the higher-order surface mesh on top of the block-structure, g the volumetric mesh, h velocity \({\varvec{u}}\) obtained via a fluid flow simulation

Full size image

Finally, we highlight topological restrictions of the domains we mesh. The tubular shapes we encounter in principle contain only bifurcations, and only rarely trifurcations. However, the algorithm is capable of resolving certain, modestly complex n-furcations where \(n\le 6.\) A particularly problematic situation of interest, to an extent already mentioned in [17], is the occurrence of multiple bifurcations very close to each other. This is only amplified by the potential large differences in the radii of the vessels. Similar to [12], we place cubes at junctions, but the present approach differs in the cube schemes, refinement strategies and re-orientation algorithms. In particular, our tactic for skeleton-based block structure generation is only locally dependent on the skeleton, thus loops (i.e., a skeleton, or parts of it, without any endpoints) do not present particular issues, as shown in examples in Sect. 4. The algorithm is furthermore capable of resolving loops in the skeleton, which might be encountered, e.g., when modelling the entire venal or arterial system. This aspect, however, is not of immediate interest within the present work.

1.1 Contribution

In this work, we introduce the following features:

  • Automatic generation of structured hexahedral meshes of arbitrary order, utilising the convolution surfaces for surface representation, as the fact that they are smooth perfectly complements the notion of higher-order meshes.

  • A skeleton-based block structure generation method yielding very coarse (valid) meshes, contained in an approach that is not limited to existing block structure templates, but instead flexible towards new ones.

  • A block-structured mesh generator that offers straightforward parametric control over mesh grading, through which the user easily controls the elements representing the boundary layers, without introducing new elements or affecting the surface representation quality.

Figure 1 showcases the entire pipeline from a CT scan to a structured volume mesh, and its application in a numerical simulation.

Fig. 2
figure 2

Demonstration of mesh features: a a structured quad mesh and an unstructured triangle mesh, b an isotropic mesh and an anisotropic graded mesh, and c a linear and a higher-order mesh, where both have the same amount of elements

Full size image

2 Shape modelling of vascular structures

This section provides an overview of shape modelling techniques to represent vascular structures with an emphasis on the method used in our workflow (Fig. 1a–d). The aim is to represent vascular structures as smooth and differentiable shapes, a common requirement of different numerical tasks, like gradient-based optimization, and that guarantees the absence of domain discontinuities in numerical simulations. For this, shape acquisition is a preliminary step and 3D imaging modalities like CTA represent the gold standard for acquisition and clinical assessment of deeper vascular structures [40]. After image acquisition, 3D reconstruction of such structures is done by segmenting the blood vessel in the CTA volume (Fig. 1a, b), typically after a windowing and denoising step as preprocessing [41]. The segmentation process generates a binary representation of the vascular structure inside the CTA grid. Recent reviews provide a broad overview of this topic [40, 41]. However, binary segmentations provide only a coarse and discrete representation. For visualisation purposes, it is common to build surface meshes by means of Marching Cubes (MC). However, MC is characterized by poor mesh quality [42] and supports only unstructured meshing (Fig. 3, left). Shape modelling can support the generation of higher quality meshes [43]. Distance transforms, which represent shapes as the distance from their surface, can be coupled with algorithms like Marching Tetrahedra to solve most issues of MC [44], yet the computed mesh is unstructured. Template deformations are a common technique to represent shapes with tailored meshes when topology is constant [45]. For tubular structures with variable topology, like blood vessels, skeleton-based representations are a valid alternative for shape representation and modelling [46]. Skeletons are generally 1D representations of the vascular structures that preserve their morphology. They can be combined with radial information to describe the cross-sectional shape of a blood vessel. Different cross-sectional priors have been considered, ranging from circles, to ellipses, polynomials, and Fourier descriptors [46, 47]. The skeleton provides information about blood flow direction and can support the generation of structured meshes. Sweeping and NURBS patches can be used to generate structured meshes from skeletal representations [32]. However, it can be challenging to connect different patches [43]. Alternatively, implicit modelling techniques can be used to reconstruct the cross-sectional shape and interpolate between two cross sections by means of blending [46] or convolution surfaces [48] (Fig. 3). Implicit models represent a shape by means of level sets:

$$\begin{aligned} f(x,y,z) - C = 0. \end{aligned}$$
(1)

In computational engineering, implicit descriptions of geometries and interfaces became popular under the label level-set method [49,50,51]. One may also incorporate (physical) concepts for the change or transport of the involved level-sets. Herein, we employ convolution surfaces for the implicit description of the geometry. The algorithm proposed herein also extends straightforwardly to other level-set representations, e.g, those based on signed distances.

Fig. 3
figure 3

Example of unstructured surface meshes of an Iliac bifurcation, representing the terminal part of the human aorta. From the left: Mesh explicitly generated using the Marching Cubes (MC) algorithm on the binary segmentation. Voxel artifacts are evident. The following mesh is generated using MC on a discrete distance function generated from the binary volume. Voxel artifacts are less evident. Eventually, a level set of the convolution surface (CS) is generated from the skeleton of the Iliac bifurcation. The CS also provides the normal vectors for algorithms like Poisson reconstruction at different resolutions. No voxel artifacts are evident

Full size image

2.1 Topological skeletons

After acquisition and segmentation, the topological skeleton provides the means to both model shape and structure (Fig. 1c). 3D shapes are typically represented either explicitly as surface meshes or implicitly as level sets. The latter also guarantee a degree of shape continuity, but neither representation provides information on shape topology. A way to analyze topology is to build the medial axis transform (MAT) of a given shape \(\Sigma\) [52]. The MAT is defined as the set of all spheres \((C_i,r_i)\) that are maximally inscribed in \(\Sigma .\) The MAT is sensitive to noise as even small perturbations can change the size, number, or origin of the maximally inscribed spheres. For tubular structures, the MAT is approximated as the set of segments [48]

$$\begin{aligned} \Gamma = \left\{ S_i = (C_i,C_j, r_{i},r_{j}) \,\,: \,\, (C_i,r_{i}),\,(C_j,r_{j}) \in \text{ MAT } \wedge i,j = 0,\ldots , N-1\right\} , \end{aligned}$$

where the number and length of the segments define the level of MAT approximation (Fig. 1c). While preserving the general shape, such shape representation allows easy identification of critical points such as bifurcations by analyzing the recurrence of a sphere origin \(C_i\) in the set. Bifurcation points are characterized by more than two occurrences, whereas an end point is characterized by a single occurrence. Different methods have been suggested to regress a shape to medial segments and build a topological skeleton [53], with mesh contraction being one of the most common ones [54].

2.2 Convolution surfaces

The MAT representation implicitly holds shape and topology information. While it is common to reconstruct shapes as the union of the medial axis spheres [55], implicit representations of the medial spheres can guarantee smoothness and differentiability (Fig. 1d) [48, 56]. Particular examples of implicit representations include metaballs [57], and convolution surfaces [48]. Metaballs are defined as the convolution of N spherical Gaussian functions over an Euclidean distance metric, centered in \(O_i\) [57]:

$$\begin{aligned} f(P) = \sum _{i=0}^{N-1} b_i {\textrm{e}}^{-\sigma _i \Vert P -O_i\Vert _2^2}. \end{aligned}$$
(2)

The chosen level C (Eq. 1) determines a geometric locus in the convolution domain. Convolution surfaces extend the concept of metaballs by replacing the sparse set of center points with a skeletal structure, which is often provided by a set of polylines [48] or Bézier curves [20] annotated with local thickness information along the skeleton. Given an arbitrary skeleton \(\Gamma ,\) a convolution surface can be defined as

$$\begin{aligned} f(P) = \int _{\Gamma } {\textrm{e}}^{-\frac{1}{2}\Vert P -s\Vert _2} \,{\textrm{d}}s. \end{aligned}$$
(3)

This formulation describes the locus of points \(P_i\) equally distant from \(\Gamma\) (Fig. 1d). Due to the linear properties of convolution, we can decompose \(\Gamma\) into non-overlapping regions such that \(\Gamma = \bigcup _i\,\Gamma _i,\) which lets us approximate the boundary surface of an arbitrary volume with a discrete set of primitives \(\Gamma _i\) (segments, curves, splines, etc.):

$$\begin{aligned} f(P) = \sum _i \int _{\Gamma _i} {\textrm{e}}^{-\frac{1}{2}\Vert P -s\Vert _2} \,{\textrm{d}}s. \end{aligned}$$
(4)

2.3 Convolution surface with radius control

For accurate shape reconstruction, it is crucial to have full control and matching between the radii associated with the topological skeleton and the reconstructed shape surface. In its original formulation, the convolution kernel is an exponential function, as shown in Eq. 4 [48]. To describe tubular structures using their skeleton and radial thickness, we rely on the convolution kernel proposed by Fuentes Suárez et al. [20]. Given a skeleton represented with polylines, for a single skeleton segment S defined by points \({\varvec{a}}, \,{\varvec{b}} \in {\mathbb {R}},\) the convolution surface at \({{\varvec{x}}}\in {\mathbb {R}}\) is given by

$$\begin{aligned}&C_{\Gamma }^{K}({{\varvec{x}}}) = \int _0^{1} K\left( g\left( \Gamma (s), {{\varvec{x}}} - \Gamma (s)\right) \right) g\left( \Gamma (s), \Gamma '(s)\right) \,{\textrm{d}}s, \\ &\quad C_{\Gamma }^{K}: {\mathbb {R}}^3 \rightarrow {\mathbb {R}}, \end{aligned}$$
(5)

where K denotes the kernel function and \(\Gamma\) denotes the parametrization of a skeleton segment \([{\varvec{a}},\, {\varvec{b}}]\) defined as

$$\begin{aligned} \Gamma _S(s) = (1-s){\varvec{a}} + s{\varvec{b}}, \quad \Gamma : [0,1] \rightarrow {\mathbb {R}}^3. \end{aligned}$$
(6)

We employ the same polynomial kernel function as Fuentes Suárez et al. [20], which is given by

$$\begin{aligned} K(x) = \left\{ \begin{array}{ll} \frac{35}{16} (1-x^2)^3,&{} \quad x \in [0,1],\\ 0, &{} \quad \text{otherwise}, \end{array}\right. \quad K: {\mathbb {R}}\rightarrow {\mathbb {R}}, \end{aligned}$$
(7)

as well as the same distance function g:

$$\begin{aligned} g({{\varvec{y}}}, {{\varvec{x}}}) = \sqrt{{{\varvec{x}}}^{\textrm{T}}\,G({{\varvec{y}}})\,{{\varvec{x}}}}, \end{aligned}$$
(8)

where G is a positive definite symmetric matrix, recovered from its eigendecomposition \(G = UDU^{\textrm{T}}.\) The matrix U is the frame of the skeletal curve determining the convolution surface. As the skeleton elements are segments, each segment defines a constant matrix U. Moreover, D is a constant diagonal matrix since our focus is on circular cross-sections. Otherwise, for ellipsoidal cross-sections, D would need to be modified accordingly. Finally, the total convolution surface function is obtained as the sum of convolution surface functions of individual segments:

$$\begin{aligned} C^K({{\varvec{x}}}) = \sum _{S\in {\mathbb {S}}} C_{\Gamma _S}^K({{\varvec{x}}}). \end{aligned}$$
(9)

The function \(C^K\) as well as \(\nabla _{{{\varvec{x}}}} C^K\) are computed through numerical integration, adopting the Clenshaw–Curtis quadrature [58]. An important property of this kernel function is its finite support, meaning that individual segments in the skeleton affect only nearby segments. Hence, a more precise radius control is obtained, as well as reduced aliasing effects, which are the main reasons for using the framework from [20] as opposed to the exponential kernel approach from Oeltze and Preim [48]. Finally, since the convolution surface function is a sum of independent segment functions, its implementation is straightforward to parallelize, with an example shown in Fig. 4.

Fig. 4
figure 4

Example of a convolution surface; firstly based on two separated segments, followed by two joined segments, to highlight the smooth blending effect

Full size image

3 Block-structured higher-order mesh generation

Having described the convolution surfaces employed herein for the boundary of the domain, the mesh generation process is described, which is divided into four main steps:

  1. 1.

    Topological description of the domain using a block structure.

  2. 2.

    Mesh grading towards the boundary.

  3. 3.

    Generation of a higher-order surface mesh through an iterative procedure combined with the convolution surface level-set approach.

  4. 4.

    Volumetric mesh generation from the block structure and the surface mesh.

Volumetric mesh generation requires information about the domain topology and geometry. The first step therefore consists of generating a block structure [59, 60], which is a coarse subdivision of the domain into blocks, such that its topology matches the topology of the domain. An example of a block structure is shown in Fig. 1e. Grading information is then assigned to the block-structure, to induce mesh anisotropy refining towards the boundary. To properly account for geometry information, we then generate a higher-order surface mesh of the domain. Finally, the three are combined through the volumetric mesh generator, with the pipeline illustrated in Fig. 5, as well as in Fig. 1e–g. In this paper, we utilise hexahedra as blocks and quadrilaterals as surface mesh elements.

The continuity at the boundary shared by two or more blocks is \(C^0.\) One has to distinguish the continuity of the geometry definition and the resulting (higher-order) hex-mesh. The geometry definition based on convolution surfaces may conceptionally be even \(C^\infty\) and a high level of continuity is an important asset for higher-order mesh generation, further justifying the choice of convolution surfaces in this work. On the other hand, no matter what the order of the resulting hex-mesh actually is, one can show that the resulting meshed geometry is only \(C^0\)-continuous, due to the \(C^0\)-continuous nature of the classical FEM shape functions. Of course, for higher orders, the kinks between element faces are extremely small. It is obvious that higher levels of continuity may not be achieved in a classical FEM framework but rather require novel approaches such as isogeometric analysis, coming with its own set of challenges.

Fig. 5
figure 5

Meshing pipeline demonstrated on the example of an aorta: a the skeleton where the point size indicates the relative radius at the given point, b the coarse block structure, c the higher-order surface mesh, and d the full volumetric mesh

Full size image

3.1 Block structure generation

The generation of the block structure (Fig. 5b) is done automatically, based on a classification of the tubular structure into a few prototype cases, to be outlined below. Although we show concrete schemes for our designated application, the general approach is not limited to tubular structures. Different domain shapes would only require devising new schemes, without further changes in the pipeline. The process may be summarized as:

  • Generation of blocks around junction points.

  • Generation of blocks around non-junction points.

  • Merging neighbouring junctions.

  • Iterative repositioning of surface nodes.

In the rest of this article, we refer to a skeletal point \(X\in \Gamma\) as a junction point if it has 3 or more neighbours, otherwise we refer to it as a non-junction point. The latter are dealt with as follows: a cross-section is generated around each point, as shown in Fig. 6a. They are then connected to form blocks, as shown in Fig. 6b. To determine the position of the cross-section around a skeleton point, three things are sufficient: the radius at the given point, the plane in which to place the cross-section, and its orientation inside that plane, i.e., torsion.

Fig. 6
figure 6

a An example of a cross-section formed around a single non-junction point of the skeleton, b five hexahedral blocks formed between two non-junction points (or two cross-sections) of the skeleton

Full size image

The radius of the cross-section is the input radius at the given skeleton point X. The plane is determined based on the neighbouring points of X. Assuming X is a non-junction point, it can have either one or two neighbours in the skeleton. For a point X with neighbours \(Y_1\) and \(Y_2,\) we denote the angle determined by those three points, with X being the central point, as \(\angle Y_1XY_2,\) i.e., the angle between \(\overline{XY_1}\) and \(\overline{XY_2}.\) We choose the plane that divides the angle in half, meaning that for any point P in the plane it holds that

$$\begin{aligned} (P\ne X) \implies (\angle PXY_1 = \angle PXY_2), \end{aligned}$$

as illustrated in Fig. 7a, b. If X has only one neighbour Y,  the plane is chosen to be perpendicular to the segment \(\overline{XY},\) as shown in Fig. 7c. Finally, the torsion of the cross-section is chosen to minimize the torsion with its neighbours. In case of a domain with no junctions, one torsion is set randomly, but due to the tubular shape this does not negatively impact the final mesh. Otherwise, at least one junction scheme has already been generated, and the torsion is propagated from there onwards.

Fig. 7
figure 7

Determining the plane for the cross-section depending on the number of neighbours of a non-junction skeleton point; a the plane determined by halving the angle between two segments, b the same situation in top-view and c the plane perpendicular to the segment

Full size image

We now consider a junction point X of the skeleton, with neighbours \(Y_1, Y_2 \text{ and } Y_3.\) Instead of a cross-section, a structured cube is generated around X,  as shown in Fig. 8a, consisting of seven hexahedral elements. The distance from X to the centers of the cube sides is the input radius at X. When connecting the cube with the cross-sections associated with non-junction points, the cube sides must be modified to yield conformal hexahedral blocks. The scheme is presented in Fig. 8b. It is worth noting, that subdividing the cube to accommodate a connection with a non-junction point affects only one of the original 7 hexahedra forming the cube, namely the hexahedron containing that very face. Thus, the junction cube refinement is not dependent on the order of the subdivisions. As each neighbouring point is assigned to one side of the cube, we seek to orient the cube based on an appropriate heuristic. It is oriented to maximize the angle formed by the segment connecting X to a given neighbour \(Y_i,\) and the segment connecting X to that side of the cube, which we seek to connect with the cross-section around \(Y_i.\) Ideally, the branch cross-section is facing the side of the cube perpendicularly. Additional weights may be added to favour neighbours with a larger radius.

Fig. 8
figure 8

a The scheme of a cube around a junction point, consisting of seven hexahedra. Each side that needs to be connected to a cross-section (see Fig. 6a) is equipped with a port, shown in b and c

Full size image

Due to the properties of convolution surfaces, we observe smooth blending between connecting objects, which fits well with the notion of anatomically motivated shapes [48]. Specifically, the smaller the angle between two branches at a junction, the stronger the effect from the smooth blending between them. To resolve this issue we subdivide the branch blocks into multiple parts, and connect them at the subdivision closest to the junction point, as shown in Fig. 9. The exact location is determined based on the convolution surface function.

Fig. 9
figure 9

The procedure of modifying the standard junction scheme shown in a to accommodate for a small angle between two branches; b the branches are subdivided depending on their length, and c connected depending on the location of the convolution surface blending

Full size image

In case of two junction cubes which are too close to each other or overlap, we merge them together and perform corrections to their inside schemes so as to account for the change caused by the merge. The overlap is shown in Fig. 10a, and the correction in Fig. 10b, c. Otherwise, blocks are formed between them in the same manner as between two cross-sections, see Fig. 6.

Fig. 10
figure 10

The resolution of two junction cubes which are overlapping; a the overlap in side view, b the merge in side view, and c the merge in 3D view

Full size image

After all of the blocks have been generated, the surface nodes of the block structure are corrected using an iterative process. A node \({{\varvec{x}}} = (x_1, x_2, x_3) \in {\mathbb {R}}^3\) is repositioned to the surface through an iterative procedure of finding a null-point, as described in Algorithm 1. The surface is represented as a level set \(\{{{\varvec{x}}}\in {\mathbb {R}}^3: \, f({{\varvec{x}}}) = C\},\) where \(f:{\mathbb {R}}^3\mapsto {\mathbb {R}}\) is the convolution surface function and \(C\in {\mathbb {R}}\) the chosen iso-value. However, within the presented framework, the block structure does not need to be aligned perfectly to the surface in the first step, since the convolution surface function and Algorithm 1 are afterwards used to rectify initial positioning errors. Herein lies another advantage of the convolution surface: the fact that the function defining the surface is smooth allows utilising its gradient.

figure a

3.2 Mesh grading

High-quality meshes for use in CFD must enable resolution of boundary layers, for which mesh grading is particularly useful [24, 38]. The goal is to obtain a tailored refinement of the mesh, with “thinner” elements near the boundary, as opposed to a standard uniform refinement. An example of a graded mesh compared to a uniformly refined mesh is shown in Fig. 2b. Most importantly, for the same number of elements, properly graded meshes lead to much better accuracy than uniform meshes.

An established approach to refining a hexahedron starts with subdividing each edge into n equal parts, to obtain uniform sub-hexahedra after refinement. To modify the uniform subdivision, a different scaling of the edges is introduced, thus resulting in a non-uniform refinement of the hexahedron. Here we use two types of scaling functions: quadratic and cubic. Assume that every edge is locally equipped with a coordinate t which linearly varies between \(-1\) and 1 along the edge. For an input scaling parameter \(m\in \langle -1,\,1\rangle\) the quadratic scaling transforms a value \(x\in {\mathbb {R}}\) with the function

$$\begin{aligned} f_m(t) = m\frac{t^2}{2} + t + \frac{m}{2}, \end{aligned}$$
(10)

and the cubic scaling with the function

$$\begin{aligned} f_m(t) = t - m\frac{t^3-t}{2}. \end{aligned}$$
(11)

We demonstrate the effects of the scaling using a simple discretisation of the interval \([-1,\, 1]\) into 20 subintervals, with the values of the input parameter \(m\in \{-0.9, -0.8,\ldots , 0.8, 0.9\},\) as well as the two extreme values close to \(-1\) and 1,  respectively, as shown in Fig. 11. For \(m=0\) no scaling occurs, in both aforementioned cases. Quadratic scaling moves the points closer to the left or the right edge of the interval, depending on whether the input parameter m is positive or negative. Cubic scaling is symmetric, where negative values of m imply a denser subdivision towards the edges of the interval, and positive values of m imply a denser subdivision towards the middle. Figure 12b shows which edges in the block structure are selected for grading, as well as an example of an ungraded and a graded mesh, in Fig. 12c, d.

Fig. 11
figure 11

The two examples of scaling the interval \([-1,1]\) uniformly discretised into 20 subintervals, by a quadratic and b cubic scaling. The uniform discretisation is achieved for \(m=0,\) in both scaling cases

Full size image
Fig. 12
figure 12

a Shows the block structure, and b highlights its edges which are selected for grading (blue), with indicated edge endings (magenta). As grading is not necessarily symmetrical, edges for grading need to be properly oriented. The ungraded mesh is shown in c, and a quadratically graded mesh, with \(m=0.9,\) in d (colour figure online)

Full size image

3.3 Higher-order surface mesh generation

Next, the convolution surface defined in Sect. 2, is converted (discretised) to a coarse, (very) high-order surface mesh, which is then used to drive the resulting volumetric mesh of any desired order. This is illustrated in Fig. 1f. Each element of the surface mesh is associated to the outer faces of the building blocks. The pipeline of the higher-order surface mesh generation consists of the following steps:

  • Generation of higher-order surface edges.

  • Repositioning the inner edge nodes to the surface.

  • Generation of higher-order surface faces from the edges.

  • Repositioning the inner face nodes to the surface.

A surface edge, i.e., a segment \(\overline{XY}\) lying on the surface of the block structure, may be viewed as a linear 1D finite element embedded in a three-dimensional space. As such, it can be converted to a higher-order 1D element, as illustrated in Fig. 13b. The end points of the higher-order edge are the same as the end points of the original segment it was obtained from, i.e., the end points are already on the domain surface. Therefore, only the inner nodes of the edge need to be repositioned, whilst keeping the edge a valid element. This is again performed using Algorithm 1, and illustrated step-by-step in Fig. 13.

Fig. 13
figure 13

The procedure of generating higher-order edges on the surface of the block structure: a a segment lying on the surface is treated as a 1D finite element, b then converted to a sixth order element followed by c iterative inner node repositioning to the convolution surface. d The final result after all edges have been processed is shown

Full size image

From the newly generated edges we obtain the faces through so-called transfinite mappings, which will be outlined in detail in Sect. 3.4. A face on the surface of the block structure may analogously be viewed as a two-dimensional element embedded in a three-dimensional space. The end points of the face are the nodes of the edges that form it, thus they already lie on the surface. Consequently, we reposition the inner nodes only, applying Algorithm 1 once again as illustrated in Fig. 14.

Fig. 14
figure 14

The procedure of generating higher-order faces on the surface of the block structure: a a surface face is treated as a 2D finite element, formed based on the four edges; in case the inner nodes are not perfectly aligned on the surface they get repositioned. b The final surface after all of the nodes have been repositioned

Full size image

As individual edges and, afterwards, individual faces get processed independently, the accompanying computations are performed in parallel. After we have the topology information in the form of a coarse block structure, mesh grading assignment, and the geometry information embedded in the higher-order surface mesh, we turn to the final volumetric meshing step.

3.4 Volumetric mesh generation

The main goal is now to generate a volumetric mesh based on the topology, geometry and grading information outlined above, as illustrated in Fig. 1g. The desired number of elements per building block \(n_{\textrm{el}}\) and their order p are user-defined. This specifies the number of nodes on every edge of the building block structure \(n_{\textrm{edge}}=n_{\textrm{el}} \cdot p+1\) and, thereby, also on every face, \(n_{\textrm{face}} =n_{\textrm{edge}}^{2},\) and block interior, \(n_{\textrm{block}} =n_{\textrm{edge}}^{3}.\) To place the \(n_{\textrm{block}}\) nodes inside every block, we need the concept of so-called transfinite maps.

3.4.1 Transfinite maps in quads

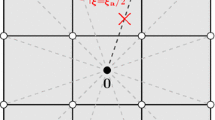
The rationale of transfinite maps is first outlined based on generic quadrilateral faces, later for hexahedral blocks. The approach chosen here is well-documented in [61,62,63] and is often called blending-function method. The starting point is a quadrilateral reference element as seen in Fig. 15a with associated \(\left( r,s\right)\)-coordinate system and vertex numbering; (b) shows the numbering of the edges. The corresponding (bi-linear) shape functions \(N_{i}\left( {{\varvec{r}}}\right)\) of this reference element are

$$\begin{aligned} N_{1}\left( {{\varvec{r}}}\right)&=\frac{1}{4}\left( 1-r\right) \cdot \left( 1-s\right) , \quad N_{2}\left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1+r\right) \cdot \left( 1-s\right) ,\\ N_{3}\left( {{\varvec{r}}}\right)&=\frac{1}{4}\left( 1+r\right) \cdot \left( 1+s\right) , \quad N_{4}\left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1-r\right) \cdot \left( 1+s\right) . \end{aligned}$$

One may then equip every edge with a ramp function \(R_{i}\left( {{\varvec{r}}}\right)\) being 1 along its edge

$$\begin{aligned}{} & {} R_{1}=N_{1}+N_{2},\quad R_{2}=N_{2}+N_{3}, \\{} & {} R_{3}=N_{3}+N_{4},\quad R_{4}=N_{4}+N_{1}. \end{aligned}$$

Next, let there be some point \({{\varvec{r}}}=(r,s)^{\textrm{T}}\) naturally related to each edge as seen in Fig. 15c. At these edge positions and the vertices, coordinate data \({{\varvec{x}}}_{i}^{\textrm{e}} \in {\mathbb {R}}^{3}\) and \({{\varvec{x}}}_{i}^{\textrm{v}} \in {\mathbb {R}}^{3}\) with \(i=1,\ldots ,4\) is given, respectively. These coordinates may, of course, also be interpreted in a Cartesian \(\left( x,y,z\right)\)-coordinate system as seen in Fig. 15d. The transfinite map according to the blending-function method defines the position \({{\varvec{x}}}\left( {{\varvec{r}}}\right)\) as follows:

$$\begin{aligned} {{\varvec{x}}}\left( {{\varvec{r}}}\right) =\sum _{i=1}^{4}R_{i}\left( {{\varvec{r}}}\right) \cdot {{\varvec{x}}}_{i}^{\textrm{e}}-\sum _{i=1}^{4}N_{i}\left( {{\varvec{r}}}\right) \cdot {{\varvec{x}}}_{i}^{\textrm{v}}. \end{aligned}$$
(12)

Interpreting this map \({{\varvec{x}}}\left( {{\varvec{r}}}\right)\) for any point \({{\varvec{r}}}\) reveals that this equation defines the smooth surface between 4 edge curves forming a closed contour in the three-dimensional space \({\mathbb {R}}^{3},\) see the black contour line in Fig. 15d and the resulting yellow surface.

Fig. 15
figure 15

Transfinite maps in quads: a local coordinate system \(\left( r,s\right)\) and vertex numbering, b edge numbering, c data points required to generate \({{\varvec{x}}}\left( {{\varvec{r}}}\right) ,\) d interpreting the data in a Cartesian coordinate system \(\left( x,y,z\right)\)

Full size image

Although this assessment mostly serves the purpose to pave the road to transfinite maps in hexahedra, it is also noted that the map in Eq. (12) is concretely used within the presented framework to generate start guesses for the face nodes of higher-order surface elements for the geometry definition as discussed in Sect. 3.3, see also Fig. 16.

Fig. 16
figure 16

a Transfinite maps based on 4 higher-order edge elements \((p=6)\) yield the black stars as start guesses for the inner face nodes. b These are then moved to the exact geometry via Algorithm 1 to generate the final higher-order surface element for the geometry definition

Full size image

3.4.2 Transfinite maps in hexas

We follow a similar outline as above and start with a hexahedral reference element as shown in Fig. 17a with local (r, s, t)-coordinate system and vertex numbering, (b) shows the numbering of the edges and faces. The (tri-linear) shape functions \(N_{i}\left( {{\varvec{r}}}\right)\) in the hexahedron are

$$\begin{aligned}&N_{1}\left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1-r\right) \cdot \left( 1-s\right) \cdot \left( 1-t\right) , \\ &N_{2} \left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1+r\right) \cdot \left( 1-s\right) \cdot \left( 1-t\right) ,\\ &N_{3}\left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1+r\right) \cdot \left( 1+s\right) \cdot \left( 1-t\right) , \\ &N_{4} \left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1-r\right) \cdot \left( 1+s\right) \cdot \left( 1-t\right) ,\\ &N_{5}\left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1-r\right) \cdot \left( 1-s\right) \cdot \left( 1+t\right) , \\ &N_{6} \left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1+r\right) \cdot \left( 1-s\right) \cdot \left( 1+t\right) ,\\ &N_{7}\left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1+r\right) \cdot \left( 1+s\right) \cdot \left( 1+t\right) , \\ &N_{8} \left( {{\varvec{r}}}\right) =\frac{1}{4}\left( 1-r\right) \cdot \left( 1+s\right) \cdot \left( 1+t\right) . \end{aligned}$$

Every edge is associated with a ramp function \(R_{i}^{\textrm{e}} \left( {{\varvec{r}}}\right)\)

$$\begin{aligned}{} & {} R_{1}^{\textrm{e}}=N_{1}+N_{2}, \quad R_{2}^{\textrm{e}}=N_{2}+N_{3}, \\{} & {} R_{3}^{\textrm{e}}=N_{3}+N_{4}, \quad R_{4}^{\textrm{e}}=N_{4}+N_{1},\\{} & {} R_{5}^{\textrm{e}}=N_{5}+N_{6}, \quad R_{6}^{\textrm{e}}=N_{6}+N_{7},\\{} & {} R_{7}^{\textrm{e}}=N_{7}+N_{8}, \quad R_{8}^{\textrm{e}}=N_{8}+N_{5},\\{} & {} R_{9}^{\textrm{e}}=N_{1}+N_{5}, \quad R_{10}^{\textrm{e}}=N_{2}+N_{6},\\{} & {} R_{11}^{\textrm{e}}=N_{3}+N_{7}, \quad R_{12}^{\textrm{e}}=N_{4}+N_{8}, \end{aligned}$$

and every face with a ramp function \(R_{i}^{\textrm{f}}\left( {{\varvec{r}}}\right)\)

$$\begin{aligned}{} & {} R_{1}^{\textrm{f}}=N_{1}+N_{4}+N_{5}+N_{8}, \quad R_{2}^{\textrm{f}}=N_{2}+N_{3}+N_{6}+N_{7},\\{} & {} R_{3}^{\textrm{f}}=N_{1}+N_{2}+N_{5}+N_{6}, \quad R_{4}^{\textrm{f}}=N_{3}+N_{4}+N_{7}+N_{8},\\{} & {} R_{5}^{\textrm{f}}=N_{1}+N_{2}+N_{3}+N_{4}, \quad R_{6}^{\textrm{f}}=N_{5}+N_{6}+N_{7}+N_{8}. \end{aligned}$$

It is easily verified that edge ramp functions \(R_{i}^{\textrm{e}} \left( {{\varvec{r}}}\right)\) are unity along their corresponding edges and face ramp functions \(R_{i}^{\textrm{f}}\left( {{\varvec{r}}}\right)\) on their corresponding faces.

For some point \({{\varvec{r}}}=(r,s,t)^{\textrm{T}},\) there is a related position on every edge and face according to Fig. 17c. At these face and edge positions and the vertices, coordinate data \({{\varvec{x}}}_{i}^{\textrm{f}} \in {\mathbb {R}}^{3},\) \(i=1,\ldots ,6,\) \({{\varvec{x}}}_{j}^{\textrm{e}} \in {\mathbb {R}}^{3},\) \(j=1,\ldots ,12,\) and \({{\varvec{x}}}_{k}^{\textrm{v}} \in {\mathbb {R}}^{3},\) \(k=1,\ldots ,8,\) is given, respectively. The interpretation of these coordinates in a Cartesian \(\left( x,y,z\right)\)-coordinate system is shown in Fig. 15d. The transfinite map according to the blending-function method for hexahedra defines the position \({{\varvec{x}}}\left( {{\varvec{r}}}\right)\) as follows:

$$\begin{aligned} {{\varvec{x}}}\left( {{\varvec{r}}}\right) =\sum _{i=1}^{6}R_{i}^{\textrm{f}} \left( {{\varvec{r}}}\right) \cdot {{\varvec{x}}}_{i}^{\textrm{f}} -\sum _{i=1}^{12}R_{i}^{\textrm{e}}\left( {{\varvec{r}}}\right) \cdot {{\varvec{x}}}_{i}^{\textrm{e}}+\sum _{i=1}^{8}N_{i} \left( {{\varvec{r}}}\right) \cdot {{\varvec{x}}}_{i}^{\textrm{v}}. \end{aligned}$$
(13)
Fig. 17
figure 17

Transfinite maps in hexas: a local coordinate system \(\left( r,s,t\right)\) and vertex numbering, b edge and face numbering, c data points required to generate \({{\varvec{x}}}\left( {{\varvec{r}}}\right) ,\) d interpreting the data in a Cartesian coordinate system \(\left( x,y,z\right)\)

Full size image

3.4.3 Mesh generation in a building block

With the transfinite maps defined above, the generation of a sub-mesh in every hexahedral building block may now be described as follows. Recall, that some of the faces of the building block may be equipped with a (very) high-order surface element defining the true geometry. Otherwise, the face is merely the bi-linear surface element from the building block itself. In any case, it is easily possible to map \(n_{\textrm{face}}=n_{\textrm{edge}}^{2}\) nodes to every surface element resulting in the coordinates \({{\varvec{x}}}_{i}^{\textrm{f}}.\) Simple compatibility requirements between the faces automatically yield the edge coordinates \({{\varvec{x}}}_{i}^{\textrm{e}}\) and vertex coordinates \({{\varvec{x}}}_{i}^{\textrm{v}}.\) Based on the transfinite map (13), every node inside the building block may now be generated, so that finally the coordinates of all \(n_{\textrm{block}}=n_{\textrm{edge}}^{3}\) nodes are specified.

The situation is exemplified in Fig. 18: (a) shows six higher-order surface elements with order \(p=4.\) The aim is to generate \(5\times 5\times 5=125\) elements with order \(p=2\) in this building block. This gives \(n_{\textrm{edge}}=5\cdot 2+1=11\) nodes per building block edge, \(n_{\textrm{face}}=11^{2}=121\) nodes per face and \(n_{\textrm{block}}=11^{3}=1331\) nodes for the whole sub-mesh in this building block. Figure 18b shows the \(n_{\textrm{face}}\) nodes per face (blue crosses) resulting from a simple finite element map based on the higher-order faces (black dots). The position of the final \(n_{\textrm{block}}\) nodes of this building block is plotted in Fig. 18c.

Finally, the \(n_{\textrm{block}}\) generated nodes must be associated with elements which is achieved by setting up a proper connectivity matrix. This, however, is a standard task in the finite element method [10, 61, 64] and not further outlined herein. Continuing the example from before, the final resulting sub-mesh is seen in Fig. 18d. Connecting all sub-meshes from the individual building blocks yields the desired volumetric mesh of the whole (tubular) geometry, to be used for FEM simulations and visualisations.

Fig. 18
figure 18

The generation of a higher-order sub-mesh in a building block: a the higher-order surface elements \((p=4)\) for the geometry definition, b placing \(n_{\textrm{face}}\) nodes on each face, c placing \(n_{\textrm{block}}\) nodes inside the building block via transfinite maps, d the resulting sub-mesh (\(5\times 5\times 5\) elements with order \(p=2\)) (colour figure online)

Full size image

4 Experiments and results

4.1 Mesh examples

Here we demonstrate several meshes obtained with our method, followed by examples of simulations performed on them. First, we showcase several synthetic examples, i.e., meshes generated based on manually constructed skeletons. The radius information of the skeleton points is shown in the form of relative point sizes, as in Fig. 5. Meshes are generated with different refinement levels and mesh orders.

Fig. 19
figure 19

Four examples of synthetic meshes, together with their skeletons, where the (relative) radius information is encoded in the size of the points. Further information relating to the meshes may be found in Table 1

Full size image
Table 1 Information about the skeletons and meshes shown in Fig. 19
Full size table

Particular situations of interest that occur in the synthetic meshes are neighbouring bifurcations in Fig. 19b, non-planar bifurcations in Fig. 19c and a six-furcation in Fig. 19d. The skeletons in the synthetic examples contain loops. Regarding this, the junction cubes are generated first, and not globally subdivided. More specifically, independent parts of the cube (each corresponding to one outer face of the cube) may be subdivided if a branch is coming into the aforementioned face, without affecting the other parts of the cube, as shown in Fig. 8b. Thus, the order of these subdivisions has no effect on the final configuration—the junction cube is the same in the end. Adding to this, the cross-sections around non-junction points are fully symmetric. Hence, no particular issues are encountered when the skeleton contains loops. Though they are not of immediate interest for this application, unless one wants to model the entire arterial and venal system, we encountered no issues in modeling them.

Furthermore, we highlight two patient-specific examples; an aorta and a coronary artery. To ease reproducibility, we performed our experiments on a publicly available CTA imaging and segmentation of the human aortic tree from the AVT dataset [65] as a representative tubular structure. The binary segmentation is first triangulated using Marching Cubes and the 1D vascular skeletons are generated by mesh contraction [54]. To limit the number of skeletal points, they are resampled at a minimum distance and radial information is computed as the distance between the skeletal point and the surface mesh.

We show the skeleton and the block structure, together with several meshes, for an aorta in Fig. 20, and a coronary artery in Fig. 21. Additionally, we show histograms of element-wise values of the scaled Jacobian [16] metric in Fig. 22. The values may be in the range \(\langle -\infty ,\, 1],\) where a negative value indicates an invalid element (hence an unusable mesh), and a value of 1 indicates an ideal element. The scaled Jacobian is computed on the meshes with increased refinement levels, as they are more suitable candidates for simulations.

Fig. 20
figure 20

An example of a patient-specific aorta: a the skeleton with radius information, b the block structure (320 blocks), c a coarse third-order mesh with 320 elements, d a refined first-order(linear) mesh with 69,120 elements, and e a refined second-order mesh with 69,120 elements

Full size image
Fig. 21
figure 21

An example of a patient-specific coronary artery: a the skeleton with radius information, b the block structure (432 blocks), c a coarse second-order mesh with 432 elements, d a refined first-order(linear) mesh with 93,312 elements, and e a refined second-order mesh with 93,312 elements

Full size image
Fig. 22
figure 22

Histograms of the values of the scaled Jacobian metric for the meshes of the aorta in Fig. 20d, e, followed by equivalent histograms for the meshes of the coronary artery given in Fig. 21d, e. Negative values indicate an invalid element, and a value of 1 indicates an ideal element

Full size image

Aside from the scaled Jacobian metric, another commonly utilised mesh quality metric is the equiangular skewness quality [16], defined as (for an element in the mesh)

$$\begin{aligned} S_{\textrm{elem}} = \max \left\{ \frac{\theta _{\textrm{max}}-\theta _{\textrm{ideal}}}{180^{\circ } -\theta _{\textrm{ideal}}}, \, \frac{\theta _{\textrm{ideal}} -\theta _{\textrm{min}}}{\theta _{\textrm{ideal}}} \right\} . \end{aligned}$$
(14)

Here, \(\theta _{\textrm{max}}\) and \(\theta _{\textrm{min}}\) denote the maximum and the minimum angle formed by edges of the element, respectively. It measures how far each element is from an ideal element, in the sense of angles between the edges of the element. In this regard, an ideal hexahedron is the one in which all of the aforementioned angles are exactly 90\(^{\circ }\), as it is the case in standard cubes or bricks. This is why \(\theta _{\textrm{ideal}} = 90^{\circ }.\) Unlike the Scaled Jacobian metric, values closer to zero are desirable, since an ideal element would satisfy \(\theta _{\textrm{max}}=\theta _{\textrm{min}}=\theta _{\textrm{ideal}}\) and thus \(S_{\textrm{elem}}=0\). The values of the equiangular skewness are shown in Fig. 23.

Fig. 23
figure 23

Histograms of the values of the equiangular skewness quality metric for the linear mesh of the aorta in Fig. 20d, and the linear mesh of the coronary artery given in Fig. 21d. Values closer to zero are desired

Full size image

4.2 Benchmarking higher-order accuracy

To demonstrate the higher-order accuracy of the proposed meshing technique and to reinforce the potential advantages of higher-order finite elements, we solve a Poisson equation with Dirichlet boundary conditions

$$\begin{aligned} -\Delta u&= f \quad \text{in } \Omega , \end{aligned}$$
(15)
$$\begin{aligned} u&= 0 \quad \text{on } \partial \Omega , \end{aligned}$$
(16)

on a domain \(\Omega .\) The skeleton with the radius information is constructed manually, leading to a convolution surface description of the domain. We then generate meshes ranging from order 1 to 5. The corresponding approximation errors are measured with respect to the energy norm,

$$\begin{aligned} E := \int _{\Omega } \nabla u \cdot \nabla u \,{\textrm{d}}{{\varvec{x}}}. \end{aligned}$$
(17)

The exact solution, and by extension the exact energy, are unknown. To evaluate the error with respect to energy, a reference value is thus required. Hence, we compute an overkill solution, i.e., we allow for significantly more degrees of freedom in a single simulation to diminish approximation errors. Performing a convergence study, we then proceed in computing energy norms for orders 1 to 5 under grid refinement, computing approximation errors taking the overkill solution’s value as reference. The mesh, the reference solution of the Poisson problem (15)–(16), and the convergence study in the energy error are shown in Fig. 24.

Fig. 24
figure 24

a The mesh of the domain, followed by b the values of the solution. c The convergence study for different p-FEM orders and refinement levels, where the error is measured with respect to the energy defined in Eq. 17

Full size image

4.3 Practical application in aortic blood flow

In a final example, we showcase the applicability of the proposed scheme in the context of cardiovascular flow, that is, pulsatile blood flow through the reconstructed arterial tree. Here, we choose a computational domain starting from the aortic root down to the common iliac arteries involving the aortic arch with the brachiocephalic trunk, left common carotid and left subclavian arteries as depicted in Fig. 5. Having such a spatial discretisation at hand, we can directly apply solvers for incompressible flow of generalised Newtonian fluids [66, 67]. Considering five cardiac cycles, we prescribe the volumetric flow rate at the aortic root adapting the temporal scale from [1], and recover realistic outlet pressures via lumped parameter models. All involved parameters and models are chosen in the physiological range, but are omitted here for the sake of brevity, referring the interested reader to [3, 68].

As the snapshots of the fluid velocity and pressure at the fifth cycle’s peak systole shown in Fig. 25 suggest, the hexahedral mesh constructed from medical image data via the proposed method is indeed capable of resolving the flow field properly. Here, we use a total of 40,000 hexahedral (trilinear) elements to accurately capture circulatory flow fields while showcasing applicability in the lower-order case, which is of high practical relevance as well. Note, however, that the discretisation order and selecting the number of elements is left entirely to the user, whom we provide with maximum freedom since coarse meshes involving merely 320 elements still resolving the current complex topology (but not the physical solution) can be constructed. Thus, one may use rather fine, but tailored pure hexahedral meshes for lower-order methods, or employ higher-order discretisations with much lower element counts, whereas the desired geometry is resolved accurately in both scenarios.

Fig. 25
figure 25

Physiological blood flow through the aorta using 40,000 trilinear elements: velocity vectors (left) and pressure fields including element edges (right) in aortic arch region (top) and at the iliac bifurcation (bottom) at peak systole as indicated by vertical line in the temporal inflow scale

Full size image

5 Conclusions and future work

Within this work, we presented a pipeline for block-structured generation of higher-order hexahedral meshes of tubular structures, starting from patient-specific CT scans, for use in fluid simulations. The focus of the paper lies on the generation of CFD-compliant higher-order meshes, resembling the domain with a spatial resolution as coarse or fine as required by the user. Future and ongoing work is centered around devising new block structure generation schemes and improving mesh quality, as well as resolving solid domains. These adaptations would pave the way for the application of the constructed meshes with an FSI framework, such as [3, 68].

The geometry is described by convolution surfaces, whose capabilities far encompass tubular structures. As the examples shown in the paper cover the healthy aorta, a next step could then involve pathological cases such as aneurysms, coarctations or aortic dissection. As mentioned, with modifications of the block structure, the entire pipeline could be straightforwardly expanded, e.g., to networks found in the respiratory system or in capillaries. Hence, a natural extension of this work consists of meshing structures that have no tubular-prior assumptions.