Skip to main content
SpringerLink
Log in

A novel optimization-based physics-informed neural network scheme for solving fractional differential equations

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

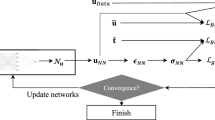
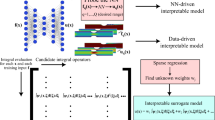
Abstract

Nowadays, the study of neural networks is one of the most interesting research topics. In this article, we introduce a novel scheme based on Physics Informed Neural Network (PINN) for solving Fractional Differential Equations (FDEs) in terms of Caputo derivative. We use a trial solution based on the Theory of Functional Connection called the constrained expression to obtain the approximate solution. The training is proposed using the recently introduced average and subtraction-based optimizer algorithm. We implement the proposed algorithm to obtain the approximate solutions of single as well as a system of FDEs. The proposed scheme eliminates the primary drawbacks of the standard PINN. With our scheme, we overcome the choice of additional parameters that affect the convergence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data availibility statement

The data used in this research is available/mentioned within the manuscript.

References

  1. McCulloch WS, Pitts W (1943) A logical calculus of the ideas immanent in nervous activity. Bull Math Biophys 5(4):115–133

    Article  MathSciNet  Google Scholar 

  2. Lagaris IE, Likas A, Fotiadis DI (1998) Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans Neural Networks 9(5):987–1000

    Article  Google Scholar 

  3. Kilbas A, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier Science

    Google Scholar 

  4. Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier

    Google Scholar 

  5. Losada J, Nieto JJ (2015) Properties of a new fractional derivative without singular kernel. Progress Fract Differ Appl 1(2):87–92

    Google Scholar 

  6. Kumar P, Govindaraj V, Erturk VS, Abdellattif MH (2022) A study on the dynamics of alkali-silica chemical reaction by using Caputo fractional derivative. Pramana 96(3):1–19

    Article  Google Scholar 

  7. Erturk VS, Ahmadkhanlu A, Kumar P, Govindaraj V (2022) Some novel mathematical analysis on a corneal shape model by using Caputo fractional derivative. Optik 261:169086

    Article  Google Scholar 

  8. Erturk V S, Alomari A K, Kumar P, Murillo-Arcila M (2022) Analytic solution for the strongly nonlinear multi-order fractional version of a BVP occurring in chemical reactor theory. Discrete Dyn Nat Soc 2022

  9. Kumar P, Erturk VS, Vellappandi M, Trinh H, Govindaraj V (2022) A study on the maize streak virus epidemic model by using optimized linearization-based predictor-corrector method in Caputo sense. Chaos Solitons Fractals 158:112067

    Article  MathSciNet  Google Scholar 

  10. Odibat Z, Erturk V S, Kumar P, Ben Makhlouf A, Govindaraj V (2022) An implementation of the generalized differential transform scheme for simulating impulsive fractional differential equations. Math Prob Eng 2022

  11. Odibat Z, Erturk VS, Kumar P, Govindaraj V (2021) Dynamics of generalized Caputo type delay fractional differential equations using a modified Predictor-Corrector scheme. Phys Scr 96(12):125213

    Article  Google Scholar 

  12. Kumar P, Erturk V S, Kumar A (2021) A new technique to solve generalized Caputo type fractional differential equations with the example of computer virus model. J Math Extension 15:1–23

  13. Kumar P, Erturk V S, Murillo-Arcila M, Harley C (2022) Generalized forms of fractional Euler and Runge-Kutta methods using non-uniform grid. Int J Nonlinear Sci Numer Simul. https://doi.org/10.1515/ijnsns-2021-0278

  14. Mall S, Chakraverty S (2018) Artificial neural network approach for solving fractional order initial value problems. arXiv preprint arXiv:1810.04992

  15. Rostami F, Jafarian A (2018) A new artificial neural network structure for solving high-order linear fractional differential equations. Int J Comput Math 95(3):528–539

    Article  MathSciNet  Google Scholar 

  16. Pakdaman M, Ahmadian A, Effati S, Salahshour S, Baleanu D (2017) Solving differential equations of fractional order using an optimization technique based on training artificial neural network. Appl Math Comput 293:81–95

    MathSciNet  Google Scholar 

  17. Effati S, Pakdaman M (2013) Optimal control problem via neural networks. Neural Comput Appl 23(7):2093–2100

    Article  Google Scholar 

  18. Sabouri J, Effati S, Pakdaman M (2017) A neural network approach for solving a class of fractional optimal control problems. Neural Process Lett 45(1):59–74

    Article  Google Scholar 

  19. Gao F, Dong Y, Chi C (2021) Solving fractional differential equations by using triangle neural network. J Funct Spaces 2021

  20. Ibrahim RW (2013) The fractional differential polynomial neural network for approximation of functions. Entropy 15(10):4188–4198

    Article  MathSciNet  Google Scholar 

  21. Raja MAZ, Qureshi IM, Khan JA (2011) Swarm Intelligent optimized neural networks for solving fractional differential equations. Int J Innov Comput Inf Control 7(11):6301–6318

    Google Scholar 

  22. Almarashi A A (2012) Approximation solution of fractional partial differential equations by neural networks. Adv Num Anal 2012

  23. Chaharborj SS, Chaharborj SS, Mahmoudi Y (2017) Study of fractional order integro-differential equations by using Chebyshev neural network. J Math Stat 13(1):1–13

    Article  Google Scholar 

  24. McFall KS, Mahan JR (2009) Artificial neural network method for solution of boundary value problems with exact satisfaction of arbitrary boundary conditions. IEEE Trans Neural Networks 20(8):1221–1233

    Article  Google Scholar 

  25. Viera-Martin E, Gómez-Aguilar J F, Solís-Pérez J E, Hernández-Pérez J A, Escobar-Jiménez R F (2022) Artificial neural networks: a practical review of applications involving fractional calculus. Eur Phys J Special Topics 231(10):2059–2095

  26. Wang S, Teng Y, Perdikaris P (2021) Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J Sci Comput 43(5):A3055–A3081

    Article  MathSciNet  Google Scholar 

  27. Huang GB, Zhu QY, Siew CK (2004) Extreme learning machine: a new learning scheme of feedforward neural networks. In 2004 IEEE international joint conference on neural networks (IEEE Cat. No. 04CH37541) Vol. 2, pp 985–990. Ieee

  28. Wang J, Lu S, Wang SH, Zhang YD (2021) A review on extreme learning machine. Multimed Tools Appl 81:41611–41660

  29. Yang Y, Hou M, Luo J (2018) A novel improved extreme learning machine algorithm in solving ordinary differential equations by Legendre neural network methods. Adv Differ Equ 2018(1):1–24

    Article  MathSciNet  Google Scholar 

  30. Li S, Liu G, Xiao S (2022) Extreme learning machine with kernels for solving elliptic partial differential equations. Cognitive Comput 15:413–428

  31. Rathod N, Wankhade SB (2020) Improving extreme learning machine algorithm through optimization technique. In Advanced computing technologies and applications (pp 157–163). Springer, Singapore

  32. Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707

    Article  MathSciNet  Google Scholar 

  33. Schiassi E, Furfaro R, Leake C, De Florio M, Johnston H, Mortari D (2021) Extreme theory of functional connections: a fast physics-informed neural network method for solving ordinary and partial differential equations. Neurocomputing 457:334–356

    Article  Google Scholar 

  34. Kharazmi E, Zhang Z, Karniadakis GE (2019) VPINNs: variational physics-informed neural networks for solving partial differential equations. arXiv preprint arXiv:1912.00873

  35. Mertikopoulos P, Papadimitriou C, Piliouras G (2018) Cycles in adversarial regularized learning. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms (pp 2703–2717). Society for Industrial and Applied Mathematics

  36. Mortari D (2017) The theory of connections: connecting points. Mathematics 5(4):57

    Article  MathSciNet  Google Scholar 

  37. De Florio M, Schiassi E, Furfaro R (2022) Physics-informed neural networks and functional interpolation for stiff chemical kinetics. Chaos 32(6):063107

    Article  MathSciNet  Google Scholar 

  38. Mortari D (2022) Using the theory of functional connections to solve boundary value Geodesic problems. Math Comput Appl 27(4):64

    Google Scholar 

  39. Coskun UH, Sel B, Plaster B (2022) Magnetic field mapping of inaccessible regions using physics-informed neural networks. Scientific Reports 12(1):12858

  40. De Florio M, Schiassi E, Furfaro R, Ganapol BD, Mostacci D (2021) Solutions of Chandrasekhar’s basic problem in radiative transfer via theory of functional connections. J Quant Spectrosc Radiat Transfer 259:107384

    Article  Google Scholar 

  41. Schiassi E, D’Ambrosio A, Drozd K, Curti F, Furfaro R (2022) Physics-informed neural networks for optimal planar orbit transfers. J Spacecr Rocket 59(3):834–849

    Article  Google Scholar 

  42. Schiassi E, D’Ambrosio A, Scorsoglio A, Furfaro R, Curti F (2021) Class of optimal space guidance problems solved via indirect methods and physics-informed neural networks

  43. Dehghani M, Hubálovský Š, Trojovský P (2022) A new optimization algorithm based on average and subtraction of the best and worst members of the population for solving various optimization problems. PeerJ Comput Sci 8:e910

    Article  Google Scholar 

  44. Odibat Z, Shawagfeh N (2020) An optimized linearization-based predictor-corrector algorithm for the numerical simulation of nonlinear FDEs. Phys Scr 95(6):065202

    Article  Google Scholar 

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Puducherry, Karaikal, 609609, India

    Sivalingam S M & V. Govindaraj

  2. Institute for the Future of Knowledge, University of Johannesburg, PO Box 524, Auckland Park 2006, Johannesburg, South Africa

    Pushpendra Kumar

Authors
  1. Sivalingam S M
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pushpendra Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. Govindaraj
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

SMS:  conceptualization, visualization, software, resources, formal analysis, investigation, writing—original draft. PK:  conceptualization, investigation, resources, visualization, writing—review and editing. VG: supervision, formal analysis, writing—review and editing.

Corresponding author

Correspondence to Pushpendra Kumar.

Ethics declarations

Conflict of interest

This work does not have any conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

S M, S., Kumar, P. & Govindaraj, V. A novel optimization-based physics-informed neural network scheme for solving fractional differential equations. Engineering with Computers 40, 855–865 (2024). https://doi.org/10.1007/s00366-023-01830-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-023-01830-x

Keywords

Search

Navigation