1 Introduction

The importance of generating non-polluting energy comes at a critical time when global emissions continue to rise [1]. One of the methods of producing low-emission electricity is wind turbines which generate electricity by transferring the energy from the incoming freestream air to their generators through their blades. The blades act like wings on a plane by generating lift which causes them to rotate. The efficiency of a wind turbine is dependent on the amount of energy that a wind turbine can transfer from the freestream air to the generator [2]. One of the obstacles to increased efficiency is the drag caused by the blades as they rotate, especially near the tip of the blade [3]. Due to the rotational nature of wind turbines the tip of the blade has a higher velocity than the root of the blade, hence a higher contribution to drag. An aim of aerodynamicists, therefore, is to modify the tip of the blade to reduce drag.

Since the late nineteenth century, wingtip devices have been an area of active research for aerodynamicists and are now a common feature on most commercial airplanes [4]. These wing devices, or winglets as they are commonly known, are attachments at the end of wings whose primary function is to reduce a type of drag known as lift-induced drag, often referred to induced drag. The induced drag is a function of lift; the relationship is shown as

$$\begin{array}{*{20}c} {{\text{Cd}}_{i} \left( {{\text{Cl}}} \right) = \frac{{{\text{Cl}}^{2} }}{{e\pi {\text{AR}}}}} \\ \end{array} ,$$
(1)

in Eq. (1) [5] where \({\text{Cd}}_{i}\) is the coefficient of induced drag, \({\text{Cl}}\) is the coefficient of lift, \({\text{AR}}\) is the aspect ratio, and e is the Oswald efficiency factor. The aspect ratio is simply the ratio between the length of the blade and the chord, and the Oswald efficiency factor is a correction factor to account for deviations from ideal elliptical lift distribution profiles.

Both wings and blades generate lift due to a pressure difference between the upper and the lower surfaces surface of the wing. The upper surface will experience a lower pressure causing the blade to be pulled in that direction. The regions of air on the upper and lower surfaces of the blade remain separated until they re-join at the trailing edge. This holds for most parts of the blade except for the tip, where the higher pressure from the lower surface air wraps around the blade to the upper surface causing the air to rotate—even after the blade has passed through the air. The rotating air from the wind turbine blade is known as the vortex and the formation of these wingtip vortices can be seen in Fig. 1. It is a turbulent region of air, called wake, that can last for several minutes and can affect the performance of wings and blades. Large, long-lasting vortices are one reason why smaller planes tend to wait before taking off after a larger airplane. The wake can also negatively affect the performance of surrounding wind turbines. This is important to consider as many wind turbines are positioned close to each other in wind turbine farms. For the interested reader, Hansen’s book [6] provides a comprehensive overview of wind turbine aerodynamics.

Fig. 1
figure 1

A diagram of the formation of wingtip vortices in an idealised flow. These vortices are an indicator of the amount of induced drag caused by the wing

Full size image

Winglets are devices placed on wing tips which have been used in experimental setups and commercial purposes to reduce induced drag and wake size [4, 5]. However, there are some considerations which need to be accounted for while incorporating them on the end of a wing. The first is that they increase the surface area exposed to the freestream air which increases the overall skin friction drag of the wing. The second disadvantage is the introduction of complex geometry which leads to an increase in the wing’s profile drag. Adding an additional device on the end of the wing increases the overall weight and cost not only due to the device itself, but also by the additional internal structure required to support the winglet. This work focuses on the drag considerations though the other disadvantages are necessary for a complete analysis.

One of the most comprehensive studies on winglets was performed by engineers at NASA [4]. They explored a variety of measures to reduce induced drag on modern commercial airplanes and conducted tests at Mach 0.78, just below the cruising speed for those airplanes. An endplate was attached to the tip of a wing in various configurations to investigate the effects of adding a flow control device. The experimental results demonstrated a decrease in induced drag by 20% for the configuration that most closely matches what is seen on most commercial airplanes.

Though the use and research of winglets has primarily been on commercial airplanes, wind turbines blades provide unique challenges which may result in them having more to gain from winglets. In addition to the experimental studies which have been conducted using winglets on wind turbine blades [7, 8], there are two primary reasons why winglets could be particularly beneficial for wind turbines; the first of which is the focus of this paper:

  1. 1.

    Induced drag makes up a larger portion of drag in the operating speeds of a wind turbine blade as shown in Fig. 2. This means that winglets become more effective at lower speeds, especially when turbines are starting up.

  2. 2.

    Since offshore wind turbines are much larger than airplane wings, the proportional weight and non-lift induced drag increases generated by a winglet are significantly smaller for wind turbines compared to airplane wings.

Fig. 2
figure 2

The two main components of drag, induced and parasitic, plotted against freestream velocity for a given lift. Induced drag makes up a bigger portion of the total drag at lower freestream velocities which includes the velocity of the tip of the blade

Full size image

The induced drag is inversely proportional to the square of relative velocity while parasitic drag is proportional to the square of the velocity [9]. Therefore, induced drag makes up a greater proportion of the overall drag at a lower velocity. This is true for a given amount of lift as would be expected for wind turbines. Though induced drag increases with an increase in angle of attack, the rotational speed of the blades will decrease. At a lower relative velocity, the angle of attack of the blade will be higher but the blades will be spinning slower; at a higher velocity, the angle of attack will be lower, but the rotational speed of the blades will increase.

A proposed solution to reducing the induced drag and the wake is a patented ducted winglet [10]. By introducing a duct within the winglet, a section of the freestream air is channelled through the duct, then exhausted at the tip where it re-joins the freestream air. The original patent is based on the ducted winglet being used on a commercial airplane, though the inventor claims that it may be used in other applications, such as wind turbine blades. The aim of this design is to artificially extend the winglet, thereby extending the length of the blade and increasing the aspect ratio. From Eq. (1), this would theoretically lead to a lower coefficient of induced drag. The reduction of induced drag is the aim of the winglet, though it cannot be considered in isolation—other forms of drag must be included in the analysis as well. This leads to the following question: can the novel ducted winglet design lower induced drag compared to a non-ducted design without increasing its overall drag? The patent presents several claims to explain the reduction in drag resulting from the addition of a duct. In this work we will use computational fluid dynamics (CFD) to investigate the following claims:

Claim 1: Counter rotating flows occur inside the duct;

Claim 2: Counter rotating flows occur at the outlet of the duct;

Claim 3: There is a region of high pressure which directs the air;

Claim 4: There is a reduction of velocity of air as it enters the duct;

Claim 5: There is an aerofoil-shaped region of air created inside the duct which influences rotation;

Claim 6: There is a 15% improvement in the lift-to-drag ratio; and

Claim 7:There are non-symmetric velocity/pressure profiles within the duct.

The primary contribution of this paper is an understanding of the characteristics of a novel ducted winglet design and a reflection on how this compared to claims in the patent. The importance of this contribution is to hold to account the claims made in the patent using previously tested methods.

Others have tried to achieve a reduction in induced drag through other means of flow control. Notably, some have been with the use of ducts or duct-like designs. Aldheeb, Asrar [11] designed a porous wingtip with the goal of affecting the vortices. Pores that were perpendicular to the freestream flow decreased the size of vortices, although it also led to a reduction in the lift-to-drag ratio. In a similar experiment, Gunasekaran and Gerham [12] designed a wing with gaps parallel to the freestream air along the entirety of the wingspan. Their results were similar to the previous experiment as they also noticed a reduction in vortex size and a reduction in the lift-to-drag ratio. In a different approach to reducing the vortex size, Heyes and Smith [13] experimented with 6 wingtip geometries which generated contra-rotating vortices. In some cases, they managed to reduce the size of the vortex. Heyes and Smith noted a reduction in lift though there is no mention as to the effect on drag.

This work presents a CFD study in which an unmodified wind turbine blade tip is compared to a standard winglet and a novel ducted winglet. The method used to evaluate these three geometries follows, along with quantitative and flow field results. The claims made in the patent are compared to CFD results with similarities and differences discussed.

2 Methods and materials

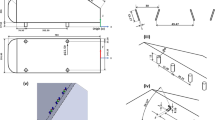
The winglet investigated in this work is a novel design based on patent schematics published in 2017 [10]. The design is unique in that it contains a duct which runs through the winglet. Freestream air enters near the bottom of the winglet, on the higher pressure side, and exits at the top of the winglet, on the low pressure side (Fig. 3).

Fig. 3
figure 3

A cross-section of the patented ducted winglet [10]

Full size image

The parametrization of the novel design was done in MatlabFootnote 1 and included the generation of text files with 3-dimensional coordinates. 6 elliptical inner profiles defined the shape of the duct while another 11 profiles defined the outer portion of the winglet. Each of the 6 inner duct profiles is defined by 3 parameters as shown in Fig. 5: the ellipse ratio

$$\begin{array}{*{20}c} {\frac{{x^{2} - h}}{{a^{2} }} + \frac{{y^{2} - k}}{{b^{2} }} = 1} \\ \end{array} ,$$
(2)

with variables shown in Fig. 4, the chord length, and its position relative to the leading edge. In total, 18 parameters defined the shape of the duct. The text files which contained the coordinates of each profile were imported into SolidWorks,Footnote 2 a computer-aided design program. A 3-dimensional design of the winglet was then created and prepared so that simulations could be run (Fig. 5).

Fig. 4
figure 4

The parameters of an ellipse, defined by Eq. (2)

Full size image
Fig. 5
figure 5

Profiles defining the outer and inner shapes of the novel ducted winglet

Full size image

An angle of attack sweep study is conducted from 1° to 8° with respect to the oncoming air for all three geometries (Fig. 6). To determine the effectiveness of the novel design, time-averaged lift and drag values were compared for all cases. Additionally, the lift-to-drag ratio is used to measure the relative changes in both variables to determine the effectiveness of the design. The reason behind this is that it measures the trade-off between lowering the drag and the reduced lift that is usually associated with decreased drag.

Fig. 6
figure 6

CFD wind turbine domain used for all three blade configurations; reference blade tip shown

Full size image

The size and duration of a vortex is an indirect measure of its induced drag. Lower induced drag coefficients are associated with smaller vortices. At this point it is important to remember the difference between causation and correlation. Trying to reduce the vortices in an attempt to reduce drag will not work. Effective winglets will reduce the induced drag and as a result from this, reduce vortex strength.

An indirect way to measure the amount of drag associated with induced drag is using Trefftz plane analysis [14]. It is a wake integration method that uses the magnitude of the vorticity at an arbitrary distance downstream from the blade. For the analysis in this paper, 1 m downstream was used. The results are valid as long as the distance behind the blade is consistent because the ranking would still be the same, however, the values would be different. The following equation

$$\begin{array}{*{20}c} {D = {\iint }v^{2} + w^{2} {\text{d}}S} \\ \end{array} ,$$
(3)

is used to determine the induced drag is given by integrating the horizontal, \(v\), and vertical, \(w\), velocity components with respect to the direction of the freestream velocity. The Trefftz plane analysis is conducted during post-processing, which is done using Ansys Ensight.Footnote 3 Result files from Ensight are generated and the integration is done in Matlab.

2.1 Computational model

The surface meshing, volume meshing, pre-processing and solving were all completed by in-house software called FLITE3D [15]. Developed for applications in the aviation industry, FLITE3D is an Reynolds-Averaged Navier–Stokes based CFD solver which has been used by industry on a number of projects, such as the Airbus A380 and Bloodhound LSR [16]. FLITE3D creates high-quality, unstructured hybrid triangular surface meshes and hexahedral volume meshes using the advancing-front method in the boundary layer region while the Delaunay method is used in the rest of the domain to generate tetrahedral elements. The solver portion of FLITE3D uses a cell-centred finite volume method and the Spalart–Allmaras turbulence model. Simulations were run using a pseudo-steady-state solver.

Simulations were run on a local HPC cluster. Each server has 2 × 20 Intel(R) Xeon(R) Gold 6230/2.10 GHz CPU cores for a total of 40 cores. Each simulation was run on 160 cores for 72 h; all simulations were run to the wall clock limit. The simulations with the highest element count were run for a total of 144 h.

The experiment compared three different geometries: an unmodified blade tip, a non-ducted winglet, and the novel ducted winglet which are presented in Fig. 7. The blade used for each simulation is taken from the IEA 15 MW offshore wind turbine as defined by the NREL [17]. The blades were simulated as static blades in much the same way an airplane wing would be simulated. This is possible to do if the frame of reference is taken at the blade. A simplification made in this work assumes that the velocity remains the same across the entire domain boundary. While this is not the case practically, the effects across the rest of the blade from a higher incoming freestream velocity remain constant for each geometry. In essence, the tip of the blade will be the only cause of differences in results.

Fig. 7
figure 7

Meshes of the three different geometries that were tested: A an unmodified blade tip, B a standard winglet, and C the novel ducted winglet

Full size image

3 Results

A mesh convergence study was performed for the first 5° to ensure that the simulation was properly capturing the phenomena regarding the novel ducted design. The mesh convergence included two refinement zones: one around the entire blade and another around the tip of the blade. Due to computational resource constraints, the mesh convergence study could not be extended further to show complete convergence. However, Fig. 8 shows that the consistent ranking between angles of attack can meet the ultimate goal of this paper by ranking the designs in appropriate order. Additionally, the difference in lift-to-drag ratio between the various angles remains approximately constant as the number of elements increases. This gives confidence that any results that stem from the following analysis will be ranked in correct order with approximately the correct magnitude of change in lift and drag values. Ranking is used in this work as all blades are subject to equal conditions and vary only in the design of the blade tip. Rather than using CFD to determine the specific pressures and velocities at certain regions of the ducted winglet, the relative ordering of the geometries can determine which of the three designs is the most effective given the imposed conditions.

Fig. 8
figure 8

Mesh convergence study conducted on the ducted winglet at 5 different angles of attack

Full size image

Across all 8 angles of attack, the unmodified reference blade had the highest lift while the novel ducted design had the lowest lift values. The standard winglet also had decreased lift across all angles of attack compared to the unmodified blade but slightly more than the ducted design. A summary of the results is tabulated including the percentage difference between the unmodified blade in Table 1 with the L/D ratio for the three geometries compared in Fig. 9.

Table 1 Computational parameters used for simulations
Full size table
Fig. 9
figure 9

The lift-to-drag ratio across 8 angles of attack for the three different geometries

Full size image

The drag values for the standard winglet are the lowest among all angles of attack. The ducted winglet has slightly higher values for drag than the standard winglet but still considerably lower than the unmodified blade (Fig. 10).

Fig. 10
figure 10

Non-dimensionalised drag values for the three geometries

Full size image

The lift-to-drag ratio is compared for all three blades, where a higher ratio is preferable as it demonstrates a more efficient design. This is because it can create the same amount of lift and incur a smaller drag penalty than a less efficient design. With respect to a wind turbine blade, a higher lift-to-drag ratio means that it could start rotating, and therefore generating electricity, at lower wind speeds. The standard, non-ducted winglet has the highest ratio among the three blades across all angles of attack. This is primarily due to its reduction in drag when compared to both the novel ducted design and the unmodified blade. The novel design ranks second best ahead of the unmodified blade.

The results from the lift-to-drag ratio demonstrates that the addition of a winglet increases overall efficiency through a relatively large reduction in drag while incurring a small penalty in lift. While the ducted version of the winglet also shows overall increased efficiency compared to an unmodified blade, the addition of a duct reduces efficiency when compared to a non-ducted winglet.

The ducted design was specifically designed for reducing induced drag so simply looking at the overall drag may not be indicative of its effect. The results from the Trefftz plane analysis are shown in Fig. 11. The novel design has a lower induced drag value than the standard winglet, demonstrating that the design does indeed lower the induced drag. However, as the overall drag is higher, it also demonstrates that it does so at the cost of other types of drag. The reasons for this are explored in the following section.

Fig. 11
figure 11

Normalised induced drag for the three geometries. Lower values indicate a lower drag

Full size image

So, does the novel ducted winglet design lower induced drag compared to a non-ducted design without increasing its overall drag? It does not appear to be the case as the non-ducted design consistently has lower drag values across all angles of attack. However, the novel ducted design does have lower induced drag across all angles of attack. In this section, we will explore why this is the case and what factors of the novel design contribute to increased overall drag but lower induced drag. Moreover, the claims made in the original patent are going to be compared to the results of the simulations. Comparisons are made as close as possible to the figures provided in the patent, though slight variation might exist due to a lack of specificity provided. The comparisons of the claims are made here to provide explanations based on the results from the independent CFD simulations conducted as part of this work (Tables 2, 3).

Table 2 Lift-to-drag ratios for the three different geometries
Full size table
Table 3 Coefficient of induced drag values for the three geometries tested for 8 angles of attack
Full size table

One of the reasons why the novel ducted design increases drag is due to the duct itself. The presence of the duct contributes to the blade’s overall form drag. As stated in the patent, the freestream velocity decreases as it enters the duct. This can be shown through the increasing pressure as air begins to enter the duct as demonstrated in Fig. 12. To decrease the velocity of the air, the winglet must exert a force on the air. As a result, the energy spent decreasing the velocity of the air directly impacts the drag, thereby leading to an increase in drag.

Fig. 12
figure 12

Coefficient of pressure plotted on the inside of the duct. A region of high pressure (1) develops at the rear of the duct inlet indicating a lower velocity

Full size image

Another reason the ducted design increases drag is increased surface area. The additional 0.84 m2 of surface area of the duct adds to the skin friction drag. However, the proportion of increased drag compared to is nearly negligible when compared to the 547 m2 of the entire blade.

Lastly, a small portion of interference drag is created as the air travels through the duct. Lower angles of attack, as shown in Fig. 13, create eddy currents within the duct which contribute to the interference drag. As the airflow travels through the duct more smoothly, the amount of interference drag decreases.

Fig. 13
figure 13

Velocity (m/s) streamlines showing the path that the air takes through the duct. A small region (1) of recirculating air is visible at the front of the duct near the midpoint

Full size image

The induced drag is measured by the magnitude of the vorticity of the air downstream of the blade. In the case of the novel ducted design, the vorticity is lower than that of the non-ducted design. The primary reason is the air that travels through the duct interrupts the outboard flow on the high pressure side of the blade that would otherwise continue to the low pressure side. As the air exits the duct, it acts as an artificial increase of the winglet itself. The reduction of induced drag therefore agrees with the equation for the induced drag coefficient, Eq. (1).

4 Discussion

A comparison between the claims made in the patent and the results from this study are presented here to better understand the drag characteristics of the ducted design. The patent outlines in detail specific areas which the inventor claims contribute to the decrease in induced drag. The following claims are going to be explored in this section: counter rotating flows occur inside the duct and at the outlet (Claim 1 and 2), a region of high pressure which directs the air (Claim 3), a reduction of velocity of air as it enters the duct (Claim 4), an aerofoil-shaped region of air created inside the duct which influences rotation (Claim 5), a 15% improvement to the lift-to-drag ratio (Claim 6), and that there are non-symmetric velocity/pressure profiles within the duct (Claim 7).

Claim 1 The patent claims that there are two regions of air in which air in one region rotates in the opposite direction to the other. The claim is accompanied by a figure in the patent, included here as Fig. 14a. According to the patent, Fig. 9a shows evidence that the presence of a high pressure region and a lower pressure region within the duct cause counter-rotating flows. However, the direction in which the flow is travelling within the duct is not apparent. Without any additional information, the only thing apparent from the figure is that velocity on the outboard edge of the winglet is lower than that on the inboard edge. From this it can also be assumed that the pressure on the on the outboard edge is higher than the inboard edge. A comparison between the patent and the result from this study (Fig. 14b) are shown. The CFD results from this study do not show the same dissymmetry in velocity.

Fig. 14
figure 14

A comparison of plane cut showing the velocity from a the patent [10] and b CFD results from this study

Full size image

To investigate this claim and to assess the direction of rotation within the duct, streamlines are superimposed in the duct during post-processing. Figure 13 shows that at 5° angle of attack, air does not rotate within the duct, either clockwise or counter clockwise as the patent indicates.

Claim 2 As a result of the flow within the duct, the patent also claims that the counter rotating regions of air will continue to rotate once the air has exited out of the duct. This claimed phenomenon is shown in Fig. 14a. Again, from the CFD results provided by the patent in Fig. 14b, it is not possible to determine this solely from the figure. The CFD results indicate that there is a region close to the exit that has a different velocity than the presumed freestream velocity around it. The analysis conducted in this paper shows the vorticity near the exit of the duct in Fig. 15b. The vorticity does not indicate two separate directions. Instead, it shows somewhat uniform vorticity near the exit.

Fig. 15
figure 15

A comparison between a how the patent [10] describes the exhaust of air and b flow field results with streamlines superimposed

Full size image

Claims 3, 4, and 5 The previous two analyses also help answer related claims. The claims—a region of high pressure inside the duct channels air towards the exit, and an aerofoil shape of air created inside the duct which influences rotation—can be answered using the figures already provided.

A region of high pressure does appear to exist within the duct, although there is no evidence that it is not the result of freestream air entering the duct as opposed to a design feature that aids in directing flow. Whether the region of high pressure is aerofoil shaped begins to be conjecture, however, as shown previously in Figs. 13 and 14b, it does not influence the rotation within the duct.

Claim 6 The other claims in the patent refrain from quantitative analysis of the novel winglet apart from the velocity decrease experienced by the air within the duct and the improvement to the lift-to-drag ratio. The velocity decrease is evident in Figs. 12 and 13, and scenario specific (ERJ145 airplane wing); as such a separate analysis is not provided. As for the lift-to-drag ratio improvement of 15%, this does not seem to be the case. At best, the ducted winglet provided a 1.8% improvement in the lift-to-drag ratio. Some reasons which may explain the difference between the quoted improvement and the improvement found during the CFD simulations are that the design used in this work is not an exact replica of the design in the patent, that the application area of a wind turbine is different to that of an airplane wing, and different freestream conditions.

Claims 7 Figure 14 compares a velocity cross-section inside the duct. The patent states that there is an asymmetrical region of pressure and velocity about the length of the duct. That does appear to be the case, but the phenomenon is not replicated in Fig. 14b. It is difficult to know what plane is used in Fig. 14a; it could be near the front, middle, or rear of the duct which could influence the velocity and pressure profiles.

To reiterate, the analysis of the claims provided by the patent are not provided as an attack on the validity of the design. Rather, they serve as an updated explanation for the phenomena seen in CFD simulations.

5 Conclusion, limitations, and future work

A novel ducted design for use on wind turbine blades was simulated using computational fluid dynamics and was compared to an unmodified blade and a standard winglet. According to the patent the aim of the design was to reduce the induced drag. While the novel design had a lower induced drag compared to the other two geometries, it had an overall drag that was higher than the standard winglet but still lower than an unmodified blade. The novel design was also more efficient than an unmodified blade when using lift-to-drag as an efficiency measure, though less efficient than the standard winglet. Another reason for its reduced efficiency was a reduction in lift, although this was expected as related work has yielded similar results. The reasons why the novel design did not perform as well as a standard winglet were discussed including the duct’s effect on other types of drag. The claims in the patent which describe the original design of the novel winglet were also investigated to determine their validity and were discussed. In general, the claims do not provide a detailed enough description for the reasons why the novel design reduces drag and omit the potential downsides to the design. Understanding the characteristics of the design is the primary contribution of this paper. Addressing the potential advantages and addressing drawbacks of the design are explored in the following section.

Four limitations of this study are discussed: the parametrised and generalised design, the simulation setup, the assumption that the design is suited for wind turbine blades, and the freestream conditions. Firstly, the choice to parameterise the design using ellipses stemmed from considerations for future work. Should the design show potential, its sensible to incorporate a means of optimising its shape. However, the design in this work does not match the patented design exactly, and thus leaves room for possible error. Considerable efforts were made to ensure that the parameterised design followed the intentions of the patent. Secondly, the simulation setup causes the entire blade to experience the same velocity across its entire span and not a varying velocity profile as would be expected on a rotating blade. As each geometry experienced the same conditions, the effects of this limitation are minute. Thirdly, the patent claims that the application of the design can be expanded to wind turbines and marine-specific applications. This statement was taken as true, although there is no guarantee that could be used in this field. Lastly, conditions such as air velocity and density experienced by airplanes varies much more than that of a wind turbine blade. It’s possible that the patented design was optimised for certain conditions that are not suitable for a wind turbine blade.

The work conducted in this paper gives rise to some interesting opportunities for future work. The first of which is an optimisation study to investigate if the additional drag incurred by the duct could be minimised or if the reduction in induced drag could be maximised. As the design has been proven to reduce the downstream vorticity, it would be worth investigating how the reduction in vorticity affects other wind turbines downstream.