Abstract
This paper proposes a framework for implementing viscoelastic constitutive model from the classical continuum mechanics (CCM) theory within non-ordinary state-based peridynamics (NOSBPD). The motivation stems from the inadequacy of CCM to model very complex material behaviours such as initiation and propagation of cracks and nonlocal behaviour due to size effects. The proposed formulation leverages on the constitutive correspondence between NOSBPD and CCM to incorporate a CCM viscoelastic constitutive model based on hereditary integral into NOSBPD. The combination of hereditary constitutive model and NOSBPD effectively makes this formulation a nonlocal time–space viscoelastic framework where temporal nonlocality is incorporated by a hereditary viscoelastic model which stipulates that the behaviour of a material at any point in time depends on both the present action and the complete history of previous actions on the material, and spatial nonlocality on the other hand is incorporated via the nonlocal mechanism provided by the NOSBPD. For model validation, three benchmark problems were solved using the proposed framework. Results obtained were compared to results from analytical solution and solutions from referenced literature. In addition, parametric study was conducted to determine the influence of nonlocality on numerical prediction. Conclusions drawn from the validation studies presented are that the proposed framework is able to predict viscoelastic responses that agree well with local macro models as well as nonlocal micromodels/nanomodels as reported in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Energy dissipative behaviour has been observed in many materials. A large class of these behaviours falls under a subcategory of inelastic material behaviour called viscoelastic response. A viscoelastic response is characterised by a combination of elastic (time independent) and viscous (time dependent) responses. Characterisation of viscoelastic material response in the framework of Classical Continuum Mechanics (CCM) has received and continue to receive extensive research interest within the theoretical and computational mechanics community. However, certain mathematical and physics-based limitations associated with the classical theory motivated the development of numerous continuum models [1,2,3,4] to overcome the limitations of the CCM. One of these models is Peridynamics (PD) which was proposed in [5] as a nonlocal reformulation of the CCM theory. Although itself, a continuum theory, PD circumvent the mathematical limitations of the classical theory by replacing the spatial derivatives present in the equation of motion of the CCM theory with integral operators. As a consequence, PD acquired the advantage of not requiring a continuous differentiable displacement field. Therefore, evolving discontinuity, such as the initiation and propagation of cracks, is treated as an inherent characteristic of the material and is thus modelled using the PD fundamental equation of motion without the need for additional assumptions or modifications. This advantage has motivated a growing interest in using PD to characterise materials with strong or evolving discontinuous response [6,7,8,9,10,11,12,13,14,15,16,17,18].
From a physics standpoint, the integral operator necessarily introduces nonlocality to the PD formulation. This nonlocal feature of PD makes it suitable as a modelling paradigm to study the physics of bodies in which the response at a point is influenced by response of material points located at some finite distance away. This has resulted in extensive research efforts to be spent in pushing the scope of application of PD in many frontiers of numerical characterisation of materials response where nonlocal response is envisaged. In a research [19], it was demonstrated that PD can accurately predict size effect in geometrically equivalent structures across a whole range of sizes. PD has also been employed to study other nonlocal physical processes such as metal machining process [20], diffusion and other transport phenomena [21,22,23]. Peridynamic frameworks have also been proposed for homogenisation of heterogeneous materials [24,25,26,27,28,29,30,31] as well as multiscale [32,33,34,35,36,37,38] and Multiphysics modelling [39,40,41,42].
Notwithstanding the growing research interests in exploiting peridynamics for different applications, relatively few research has been undertaken in the direction of developing models and material characterization in the framework of PD viscoelasticity. This is especially needed in emerging fields such as virtual reality simulation that aims to allow realistic visuals and haptic feedbacks for its users in the field of medical training as well as the use of viscoelastic materials as vibration dampers and acoustic absorbers in aerospace, automobile, marine transport, and engineering of nanodevices. The attainment of this goal will require the development of physics-based models of tissues, biomaterials, and polymers. It is known that these materials often exhibit viscoelastic response [43,44,45] when subjected to stimuli.
In addition, viscoelastic materials are known to exhibit complex behaviour such as variation in material properties with change in sample size [46, 47], a phenomena known as size/scale effect. Scale effect is a very important consideration in the field of miniaturisation engineering where viscoelastic nanomaterials are increasingly being used as candidate materials for development of nanodevices [48]. As the scale of observation becomes smaller, intermolecular interaction becomes too important to ignore [49]. This effectively introduces a notion of nonlocal interaction and hence an internal length scale in the analysis. This effectively invalidates the local hypothesis of the CCM [50], and emphasises the need to develop a nonlocal viscoelastic modelling framework that will incorporate size dependent length scale parameter.
Other complex phenomena encountered in the characterization of viscoelastic materials include initiation and propagation of cracks [51] and its dependence on speed of propagation [52] as well as dynamic crack induced pressure and shear waves [53]. These are a few of the motivating reasons that necessitate the development of PD viscoelasticity framework with capability to model continuous, discontinuous, and nonlocal material response. To this end, characterisation of viscoelastic materials in the framework of PD theory is beginning to gain attention. A Bond-based Peridynamic (BBPD) viscoelastic material model was proposed in [54]. To derive the integral representation of the nonlocal viscoelastic model, Fourier- and Laplace-transform were utilized. It was demonstrated through analytical and numerical solution of the viscoelastic model that the proposed formulation can predict viscoelastic response.
A thermodynamically consistent viscoelasticity model in the framework of Ordinary state-based peridynamics (OSBPD) was proposed in [55] that relies on the additive decomposition of the extension state into a volumetric and deviatoric components. The deviatoric extension state is further decomposed into elastic and back extension components. A key assumption in the formulation is that the volumetric response is assumed to be elastic while the deviatoric response is viscoelastic. The viscoelastic response was assumed to be governed by a combination of the standard linear solid and Maxwell model. The proposed framework was implemented to study the relaxation response of a single bond. In [56], an explicit time integration algorithm for this model was proposed. This OSBPD viscoelastic framework was extended in [57] to incorporate Prony series representation of the viscoelastic material property functions. This allows the possibility of fitting the Prony series with viscoelastic material functions such as the relaxation modulus and creep compliance data obtained from experiment. A viscoelastic characterisation of fracture in membranes was undertaken in [58]. A generalization of the OSBPD viscoelastic framework was proposed in [59] to account for viscoelastic response in both spherical and deviatoric response of materials.
A viscoelastic model based on a NOSBPD correspondence formulation called Bond-Associated Peridynamic [60] framework was proposed in [61]. The framework was utilised to simulate viscoelastic response in the interface region of two dissimilar materials. Other rate dependent formulations proposed in the framework of PD include viscoplasticity [62] and visco-hyperelasticity [63, 64].
The aim in this contribution is to propose a viscoelastic framework for Non-ordinary State-based Peridynamics (NOSBPD). The motivation is to leverage on the ability of the NOSBPD formulation to admit state-of-the-art constitutive models of the CCM theory through correspondence principle, thus allowing for viscoelastic modelling of generalised materials within the peridynamic framework.
This proposed formulation differs from the previously proposed method on several fronts. The first point of departure is that the previous formulations [54, 55, 57] were built on the framework of either BBPD or OSBPD. This poses restriction on the range of materials that can be modelled using these frameworks since BBPD can only admit materials with a Poisson’s ration of \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}\), while OSBPD is based on the assumption that the bond force between two interacting material points is parallel to the bond [65].
An advantage to be drawn from this formulation which is based on NOSBPD is that the NOSBPD is a generalisation of the BBPD and the OSBPD thus allowing for far reaching generalization in the scope of materials that can be modelled. Also, a particular formulation of the NOSBPD called correspondence model uses familiar quantities such as stress and strain based on the principle of constitutive correspondence. This allows the proposed framework to feed off from the state-of-the-art viscoelastic constitutive model from the CCM framework. Another point of departure between this proposed framework and the previously developed frameworks is that this proposed framework allows for both partial and total viscoelastic formulation to be implemented.
Although the formulation proposed in [61] share some similarities with this proposed framework in that they are both based on the general framework of NOSBPD correspondence model, the two formulation differs fundamentally in their kinematics. Whilst the method proposed in [61] uses a bond-associated method to compute deformation gradient, in this proposed framework, the nonlocal deformation gradient is computed using the method proposed in the original development of the NOSBPD [66]. When computing the nonlocal deformation gradient in the bond-associated method, only a fraction of the material points within the horizon of a material point are utilised. This can lead to inaccurate prediction of strain energy density hence the need for a correction factor to compensate for this inadequacy [60].
Another feature of this formulation that distinguishes it from the prior formulations is that it permits a more generalised viscoelastic implementation. This formulation allows partial viscoelastic formulation, unlike the prior formulations, where the assumption of bulk elastic response and shear viscoelastic response is imposed, as well as a total viscoelastic formulation where both bulk and deviatoric viscoelastic responses are accounted for.
In the reminder of this presentation, a concise review of the NOSBPD theory will be presented in 0 to be followed by a discussion on nonlocal kinematics relevant to the state-based formulation in 0. Constitutive correspondence principle linking constitutive models from CCM with the NOSBPD is presented in 0. Discussion on a state variable viscoelastic constitutive model is presented in 0 and implementation strategy for the proposed framework is discussed in 0. Results of numerical simulation to validate the proposed framework is presented in 1.0 and concluding remarks in 2.0.
2 State-based peridynamic theory
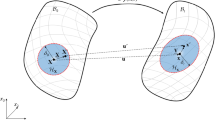
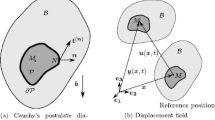
One of the foundational concepts in PD just as in CCM is the continuum hypothesis, which asserts that a body consists of an infinite number of particles, each of which shares the same physical characteristics as the bulk. A key distinction between the two is that while in CCM, a material point interacts only with its immediate neighbours, PD allows interaction over a finite distance. Consider a deformable body \(\mathcal{B}\) as shown in Fig. 1. A point P occupying the position \(\mathbf{x}\) in \(\mathcal{B}\) interacts with infinitely many other points located within a finite domain. If this domain is taken to be a ball of radius \(\delta >0\) centred at \(\mathbf{x}\), such that
then \({\mathcal{B}}_{\delta }\left(\mathbf{x}\right)\) is called the family of \(\mathbf{x}\) and contains all the material points Q occupying the position \(\mathbf{x}\mathbf{^{\prime}}\) that interacts with P (for the rest of this presentation, points P and Q will be identified by their position vectors \(\mathbf{x}\) and \({\mathbf{x}}^{\mathbf{^{\prime}}},\) respectively). The interaction between \(\mathbf{x}\) and \(\mathbf{x}\mathbf{^{\prime}}\) is referred to as a bond and the distance \({\varvec{\xi}}={\mathbf{x}}^{\mathrm{^{\prime}}}-\mathbf{x}\) in the reference or undeformed configuration is called the bond length. The family of bonds \({\mathcal{H}}_{\mathbf{x}}\) for point \(\mathbf{x}\) is thus given as
Let \({\varvec{u}}(\mathbf{x})\) and \({\varvec{u}}\left({\mathbf{x}}^{\mathbf{^{\prime}}}\right)\) be the respective displacement undergone by \(\mathbf{x}\) and \(\mathbf{x}\mathbf{^{\prime}}\) in the deformed configuration. Then the relative displacement between \(\mathbf{x}\) and \(\mathbf{x}\mathbf{^{\prime}}\) is given by: \({\varvec{\eta}}={\varvec{u}}\left({\mathbf{x}}^{\mathbf{^{\prime}}}\right)-{\varvec{u}}\left(\mathbf{x}\right)\). Consequently, the positions of \(\mathbf{x}\) and \(\mathbf{x}\mathbf{^{\prime}}\) in the deformed configuration are given as \(\mathbf{y}=\mathbf{x}+\boldsymbol{ }{\varvec{u}}\left(\mathbf{x}\right)\) and \(\mathbf{y}={\mathbf{x}}^{\mathbf{^{\prime}}}+\boldsymbol{ }{\varvec{u}}\left({\mathbf{x}}^{\mathbf{^{\prime}}}\right)\), respectively.
In the context of state-based PD [66], functions that are defined on bonds are called states. There are three (3) important states that are deserving of specific mention here. These are the reference position vector state, the deformation vector state, and the force vector state. For the point \(\mathbf{x}\), the reference position vector state \(\underset{\_}{\mathbf{X}}\) is a function that maps a bond vector in the family of \(\mathbf{x}\) in the undeformed configuration unto itself, that is
The deformation vector state is a function that operates on a bond vector in the undeformed configuration, whose value is the image of the bond vector in the deformed configuration. That is,
A force vector state \(\underset{\_}{\mathbf{T}}\) is a function that maps the deformation vector state to a force density vector for each bond vector in \({\mathcal{H}}_{\mathbf{x}}\) such that:
where \(\mathbf{t}\) is a force density at \(\mathbf{x}\) due to its interaction with \({\mathbf{x}}^{\mathbf{^{\prime}}}\). The equation that tracks the motion of point \(\mathbf{x}\) is given by the following integro-differential equation
where \({\varvec{b}}\left(\mathbf{x},t\right)\) is a body force density and \(t\) denotes time, and the angle brackets, \(\langle \bullet \rangle\) in (3–6) signify the vector on which the state operates.
3 Constitutive correspondence and nonlocal kinematics
As mentioned in Sect. 1 , the NOSBPD correspondence model utilizes the constitutive model of the CCM and thus allowing the familiar concepts of stress and strain tensors to be used in the framework of PD. To be able to leverage this capability, nonlocal kinematic quantities that parallel those in the CCM will be derived in the proceeding passage. Utilising the definition of the nonlocal gradient operator given in [67, 68], a Taylor series expansion of (4) about \(\xi =0\) will yield
where \({{\mathcal{G}}_{\omega }}_{\mathbf{x}}\) is the nonlocal gradient operator evaluated at \(\mathbf{x}\), \(\mathbf{I}\) is the second order isotropic tensor and \(\mathcal{O}\left({\left|{\varvec{\xi}}\right|}^{2}\right)\) represent terms of order higher than one. If small deformation assumption is made, then \(\mathcal{O}\left({\left|{\varvec{\xi}}\right|}^{2}\right)=0\) and (7) reduces to
The parenthesized term in the right hand side of (8) is the nonlocal deformation gradient [68]. If we denote the nonlocal deformation gradient as \(\mathbf{F}\), then (8) can be written as,
The nonlocal deformation gradient is given by [66]
where \(\mathbf{K}\) is a shape tensor defined as
A nonlocal strain tensor can be defined by considering the difference between the squares of bond length \(\xi =\left|{\varvec{\xi}}\right|=\left|{\mathbf{x}}^{\mathbf{^{\prime}}}-\mathbf{x}\right|\) in the undeformed configuration and \(\lambda =\left|{\varvec{\lambda}}\right|=\left|\mathbf{y}\left({\mathbf{x}}^{\mathbf{^{\prime}}}\right)-\mathbf{y}\left(\mathbf{x}\right)\right|\) in the deformation configuration as shown in Fig. 2. From (9), we can write
If a deformation or strain tensor \(\mathbf{E}\) is defined as
then (13) becomes
The tensor \(\mathbf{E}\) in (14) is the nonlocal equivalent of the Green–Lagrange strain tensor and \(\mathbf{F}\) is the nonlocal deformation gradient tensor defined in (10). Under the assumption of infinitesimal deformation, it has been shown in [68] that the nonlocal deformation gradient tensor (13) can be written as
where \({\varvec{\upvarepsilon}}\) is the infinitesimal strain tensor and \(\mathbf{I}\) is the second order isotropic tensor.
4 Correspondence model
For a given deformation tensor \(\mathbf{F}\), let \(\Phi \left(\bullet \right)\) be a function that maps \(\mathbf{F}\) to the corresponding strain energy density in CCM. Also, let \(W\) be the nonlocal PD strain energy density. It has been shown in [66] that constitutive correspondence between PD and CCM is achieved if for some choice of the deformation tensor \(\mathbf{F}\) given by (9) the PD strain energy density is equal to the strain energy density from CCM, that is,
The particular form of the PD force density vector state \(\underset{\_}{\mathbf{T}}\) is obtained by evaluating the Fréchet derivative of the strain energy function \(W\left(\underset{\_}{\mathbf{Y}}\right)\) with respect to \(\underset{\_}{\mathbf{Y}}\). This operation [66] yields the expression for the PD force density vector state as
where \(\underset{\_}{\omega }\) is a weight function and \(\mathbf{P}\) is the first Piola stress tensor. Under the assumption of small deformation, (17) is rewritten as
where \({\varvec{\sigma}}\) is the Cauchy stress tensor.
5 Viscoelastic constitutive model
The correspondence model (17) or (18) allow PD to admit a wide spectrum of constitutive models from the CCM framework. In this section, a linear viscoelastic model will be derived that is compatible with the PD correspondence model. Two equivalent approaches have generally been utilised to develop viscoelastic constitutive models. The first approach uses ordinary differential equations to establish the constitutive relation while the second establishes constitutive relation between stress and strain using integrals via Boltzmann superposition principle. The three basic mechanical models typically used to model linear viscoelastic response are the Maxwell, Kelvin, and the Standard Linear Solid (SLS) models.
In this work, we limit our focus to linear viscoelasticity based on the integral formulation. The integral formulation in one-dimension is often stated as
where \(E\) is the time dependent relaxation modulus and the variable of integration \(\tau\) is a time variable measured backward from the current time \(t\). Several mathematical representations of the relaxation modulus exist. A very popular representation among these is the Prony-Dirichlet series or Prony series for short. The Prony series consist of a finite sum of decaying exponential often expressed [69] as
It is worth noting that in (20), the extreme values of the relaxation modulus can easily be obtained as
where \(E(0)\) is the instantaneous Young’s modulus and \(E(\infty )\) is the long term or equilibrium Young’s modulus. Introducing (20) into (19)
where \({\sigma }_{0}\left(t\right)={E}_{0}\varepsilon \left(t\right)\) is the elastic contribution and
is referred to as the internal state variable and account for the time dependent contribution to the viscoelastic response. For this reason, this methodology can be considered to belong to a class of methodologies called internal variable methods in the literature. If the strain in the integral of (23) is substituted by \(\varepsilon \left(\uptau \right)={\sigma }_{0}\left(t\right)/{E}_{0}\), we obtain
where \({\gamma }_{j}\) is a normalised relaxation function given by \({\gamma }_{j}={E}_{j}/{E}_{0}\). To implement (22) in a numerical scheme such as in the framework of NOSBPD correspondence model will require a strategy for numerical integration of (23) or (24). This can be achieved using an algorithm [69] that discretises for example (24) in terms of a finite time interval. Let the deformation history be split into two periods \(0\le \tau \le {t}_{n}\) of known deformation and \({t}_{n}\le \tau \le {t}_{n+1}\) of unknown deformation, then the integral in (24) can accordingly be split and written as
If we make the simplifying assumption that over the time increment \(\Delta t\), \({\sigma }_{0}\) varies linearly with time, then
Introducing (26) into (25) yields
If we write \(A_{j} = \left( {1 - \exp \left( { - \frac{\Delta t}{{\tau_{j} }}} \right)} \right)/\left( {\frac{\Delta t}{{\tau_{j} }}} \right)\), then
Thus the stress at time \({t}_{n+1}\) is computed as
Observe that (29) is a recursive function that requires the variables \({h}_{j}^{n}\) and \({\varepsilon }^{n}\) from the previous times step to be able to compute the stress state at the current time step. A generalisation of (29) to higher dimension is achieved by rewriting the Prony series (20) in terms of tensor quantities (using Voigt notation) as:
where the transient relaxation modulus \({C}_{ij}(t)\) is a fourth order tensor. Consequently, each term in (30) is also a forth order tensor which in the context of viscoelastic materials such as polymers represents a particular mechanism by which the material responds to an applied load. The first term, \({C}_{i{j}_{o}}={C}_{ij}(t=\infty )\) is the equilibrium relaxation modulus which represents the elastic component of the material response. The component of the relaxation tensor \({C}_{i{j}_{m}}\) and the relaxation time parameter \({\tau }_{m}\) in the m\(\mathrm{th}\) term of the series characterises the viscous response. Introducing (30) into (19) would yield the generalised form of (29) as
where \({\varvec{\sigma}}\) and \({\varvec{\varepsilon}}\) are the vector representation of the second order stress and strain tensors respectively, and the fourth order tensors \({\underset{\_}{\mathbf{C}}}_{0}\) and \({\underset{\_}{\mathbf{C}}}_{j}\) are as defined in (30).
For practical and numerical consideration, it is sometimes necessary to make the assumption that the material behave elastically in dilatation and viscoelastically in its shear response. To this effect, the stress tensor is split into a spherical and deviatoric components and given by
where \(\mathbf{I}\) is a second order isotropic tensor, \({\sigma }_{m}\) and \(\widetilde{{\varvec{\sigma}}}\) are the mean stress and deviatoric stress, respectively. If the assumption of elastic bulk response is enforced, (32) is shown [69] to take the form
In this case, the procedure for the incremental determination of the state variable is applied only on the deviatoric component \(\widetilde{{\varvec{\sigma}}}\) of the stress tensor such that
where
6 Implementation strategy
The framework proposed in this contribution is capable of simulating both dynamic and static response of materials undergoing linear viscoelastic deformation. The numerical solution strategy adopted in this formulation consists of a nested spatial and time numerical integration procedures. The spatial integration procedure evaluates the total force acting on a material point at a given time while the time integration procedure tracks the position of material points with passage of time. To numerically implement the spatial integration, the meshfree method proposed in [70] is utilised. In this method, the equation of motion (6) is approximated by
where \(\rho_{i} : = \rho \left( {{\mathbf{x}}_{i} } \right)\), \({\ddot{\user2{u}}}_{{\varvec{i}}} = \frac{{\partial {\varvec{u}}_{i} }}{\partial t}\) with \({\varvec{u}}_{i} : = {\varvec{u}}\left( {{\varvec{x}}_{i} } \right)\) and \(N\) is the number of points in the horizon of node \(i\). The time integration procedure employs forward Euler method to compute the current values of accelerations, velocities, and positions of points. With this method, the explicit time integration of (36) yields the acceleration \({\ddot{{\varvec{u}}}}_{{\varvec{i}}}\), velocity \({\dot{{\varvec{u}}}}_{{\varvec{i}}}\) and displacement \({{\varvec{u}}}_{i}\) of a point \(i\) at current time \(t={t}^{n}\) as follows;
where \({\mathcal{L}}_{i}^{n}=\sum_{j=1}^{N}\left[\underset{\_}{\mathbf{T}}\left[{\mathbf{x}}_{i},t\right]\langle {\mathbf{x}}_{j}-{\mathbf{x}}_{i}\rangle -\underset{\_}{\mathbf{T}}\left[{\mathbf{x}}_{j},t\right]\langle {\mathbf{x}}_{i}-{\mathbf{x}}_{j}\rangle \right]{V}_{j}\). In the case of dynamic problems, the solution strategy is implemented as outlined above. However, for static problems, the numerical procedure is given some modifications. The modified computational scheme consists of integration over two time parameters, viz. a numerical time and a viscoelastic or material time. The numerical time is the time frame in which a steady-state solution is recovered from a dynamic problem by damping out the transient component. As the transient solution is damped out, the solution converges to the steady-state solution. In this approach, the quasi-static transient problem is first converted into a dynamic problem. Then fictitious inertia and damping forces are added to damp out the artificial dynamic motion. The method utilised in this work to attenuate the transient solution is called Adaptive Dynamic Relaxation (ADR) method which is an explicit iterative procedure that relies on mass proportional damping (see [71] for details).
7 Suppression of zero mode instability
Although the non-ordinary state-based peridynamic correspondence model offers a lot of advantages some of which have already been highlighted in Sect. 1 of this study, it suffers from a problem commonly referred to as the ‘zero-energy modes’ instability. This is known to cause oscillation in the deformation and stress field. While several techniques have been suggested to address this problem, including [20, 72,73,74,75,76,77], this study will utilise the method proposed in [73] for reason of simplicity to implement. This method supresses the zero-energy mode instability by introducing a supplementary artificial force density vector \({\underset{\_}{\mathbf{T}}}_{a}\left[{\varvec{x}},t\right]\langle {{\varvec{x}}}^{^{\prime}}-{\varvec{x}}\rangle\) on the bond \({{\varvec{x}}}^{^{\prime}}-{\varvec{x}}\) such that (18) becomes:
The artificial force density vector \({\underset{\_}{\mathbf{T}}}_{a}\left[{\varvec{x}},t\right]\langle {{\varvec{x}}}^{^{\prime}}-{\varvec{x}}\rangle\) in (38) is given by:
where \(\underset{\_}{\omega }\langle \left|{\varvec{\xi}}\right|\rangle\) is the weight function, \({\varvec{C}}\left({\varvec{\xi}}\right)=c\left({\varvec{\xi}}\otimes{\varvec{\xi}}\right)/{\left|{\varvec{\xi}}\right|}^{3}\) is the tensor-valued symmetric micromodulus function, \(c=18k/\pi {\delta }^{4}\) is the bond force constant in the BBPD, and \(\underset{\_}{{\varvec{z}}}\langle {\varvec{\xi}}\rangle =\underset{\_}{\mathbf{Y}}\langle {\varvec{\xi}}\rangle -\mathbf{F}{\varvec{\xi}}\).
8 Model verification
In this section, the NOSBPD viscoelastic framework proposed will be verified against results obtained from analytical solution and Finite Element Method (FEM), either based on results obtained using a commercial FEM software (ANSYS), or results from published works. To model the viscoelastic response using the proposed NOSBPD viscoelastic formulation, computer codes were developed in MATLAB to solve three benchmark problems including a bar subjected to tensile load representing 1-dimensional and a plate subjected to tensile load representing a 2-dimensional quasi-static transient problems as well as axial vibration in a bar representing transient dynamic problem.
The material properties utilized in the following numerical examples is adopted from Abaqus Benchmark Manual (version 6.11). The relaxation function of the material is represented by the Prony series
where \({k}_{1}=6.89\mathrm{MPa}\), \({k}_{2}=62.01\mathrm{MPa}\) and \(\tau =1.0\mathrm{sec}\). In this example, the bulk response is assumed to be elastic and the time independent bulk modulus \(K\) is \(689MPa\). From (40), the long-term Young’s modulus is \(E\left(\infty \right)={E}_{0}={k}_{1}\).
8.1 Viscoelastic bar subjected to constant axial load
Consider a bar having a length of \(1000\mathrm{ mm}\) and a square cross-section with dimensions \(10\mathrm{ mm}\times 10\mathrm{ mm}\). Let the bar be fixed at one end and a constant load of \(0.689\mathrm{ MPa}\) is suddenly applied at the other end. The solution strategy adopted is the complete viscoelastic formulation. The load is applied and held constant over a time period of \(50 s\). The time increment is taken to be \(\Delta t=0.0001 s\) which translates to a total time step of \(\mathrm{50,000}\). The displacement of points in the bar at initial and final times are presented in Fig. 3, while the displacement as well as the creep strain of the tip of the bar with respect to time are presented in Fig. 4.
Results presented in Fig. 3a, b respectively, shows that the instantaneous and long-term displacements predicted using the proposed framework agree well with analytical results. Results of creep strain presented in Fig. 4 also show good agreement with the analytical results.
8.2 Plate extension
This problem is a plane stress quasi-static transient analysis of a viscoelastic rectangular plate with dimensions \(1.0\mathrm{m}\times 1.0\mathrm{m}\) as shown in Fig. 5. The thickness, \(h\) of the plate is \(0.1\mathrm{ m}\). The left edge of the plate is subjected to a roller-type support. A load of \(1 \mathrm{MPa}\) is suddenly applied to the right edge of the plate and held constant for \(50\mathrm{ s}\) and then removed. The plate is then allowed to recover in a further 50 s thus bringing the total simulation time to \(100 \mathrm{s}\).
To implement the numerical simulation, the plate was discretised into \(10\times 10\) grid giving a total of \(100\) material points. To utilise the recursive function (31) to update the stress at any time \({t}_{n+1}\), a numerical algorithm based on ADR methodology is utilised. This numerical algorithm consists of a two-tier time integration solution strategy. The first-tier time integration computes the viscoelastic deformation of the plate over a finite time increment \(\Delta t\). This time increment would be denoted as the ‘material’ time. The material time increment used in this simulation is \(\Delta t=0.1\mathrm{ s}\). The simulation is done over a total material time of \(t=100\mathrm{s}\). As a quasi-static transient problem, the plate is assumed to attain equilibrium over every material time step. This allows the treatment of the plate at every material time step as a static problem. Hence the ADR time integration methodology is utilised in this tier of the solution strategy to find the steady-state solution of the problem over each material time increment. The time increment in the ADR time integration is specified as 1. The time frame in the ADR algorithm is denoted as ‘ADR time’. Results from this simulation are compared with results from FE implementation in ANSYS. The viscoelastic displacement of the loaded edge of the plate with time using this proposed formulation is shown in Fig. 6, alongside prediction from ANSYS. Also, the displacement field in both \(x\) and \(y\) directions corresponding to loading time \(t=50\mathrm{ s}\) (when the load is removed) and \(t=100\mathrm{ s}\) (at the end of simulation) are, respectively, shown in Figs. 7, 8.
As can be observed from Figs. 6, 7, 8, the prediction of the transient displacement of the loaded edge of the plate as well as the displacement field in the plate at times \(t=50 s\) and \(t=100 s\) using the proposed method agrees well with FE prediction using ANSYS, thus further reinforcing the validity of the proposed method to model time dependent behaviour of materials.
8.3 Axial vibration of a viscoelastic bar
In this section, the proposed NOSBPD viscoelastic formulation is applied to simulate the axial vibration of a viscoelastic bar. This example will be used as a probe to examine the suitability of the proposed framework in the viscoelastodynamic regime. The bar is clamped at one end and subjected to an initial sudden stretch at the other end for a short period of time after which the load is removed. The viscoelastic material property of the bar is defined by the Prony series coefficients given in Sect. 8. The density of the material is arbitrarily taken to be \(10000 \mathrm{Kg}/{\mathrm{m}}^{3}\). The bar has a length of \(1.0 m\) and a cross sectional area of \(1.0\times {10}^{-6} {\mathrm{m}}^{2}\). To implement this problem in the numerical scheme of the proposed formulation, the bar is discretised into \(1000\) material points, so that each material point has a size of \(\Delta x=1.0\times {10}^{-3} m\). A horizon size, \(\delta =3\Delta x\) is adopted. Numerical time integration solution technique [71] is utilised to track the position of material points with passage of time due to applied load. The numerical integration was implemented over a total simulation time of \(2.8065 s\) with a time interval, \(\Delta t=3.742\times {10}^{-5}\) s.
The transient displacement of two points located at \(x=0.4995\mathrm{ m}\) and \(x=0.9995\mathrm{ m}\) are shown in Fig. 9. For comparison, the response of the bar subjected to the same loading condition but with equilibrium material properties corresponding to time \(t=\infty\) was also computed using analytical solution method. The equilibrium material property yields elastic response of the material. It is observed from the figures that compared with the elastic response; the viscoelastic property progressively damps out the oscillation thereby creating a response that is asymptotic to the steady-state solution. This attenuating effect that viscoelastic properties have on vibration of a medium is called viscoelastic damping [78, 79]. Viscoelastic materials added to structural elements and devices to enhance their damping characteristics are called viscoelastic damping materials (VDM). Characterisation of static and dynamic response of VDM is an active field of research in many disciplines including automotive and aerospace industries.
Introduction of nonlocality into continuum models is known to introduce dispersion in wave propagation [80]. The horizon is the parameter that defines the degree of nonlocality in the NOSBPD theory, and just like other nonlocal continuum models, the degree of nonlocality also plays important role in the behaviour of peridynamic solution. To investigate the influence of horizon size on the dynamic response of viscoelastic materials, the current viscoelastodynamic problem is simulated using varying horizon sizes of \(\delta =3\Delta x\), \(10\Delta x\), \(15\Delta x\), and \(20\Delta x\). The result for this parametric study showing the trend of dispersion behaviour is presented in Fig. 10.
Numerical results presented in Fig. 10 indicate that the horizon influences the period of oscillation while the amplitude of vibration remains almost the same. This dispersive behaviour due to the introduction of nonlocal interaction has also been observed in a one-dimensional, viscoelastic bond-based peridynamic medium [81], as well as in the dynamic analysis of nanobeams [79, 82]. The ability to control the dispersive behaviour of viscoelastic materials through a nonlocal parameter is a very important strength of this proposed framework that promises to find application in engineering of nano materials and devices where size effects due to dimensional constraints for example, affects mechanisms of deformation such as dislocation motion. In such situation where size dependent response becomes an important consideration, the use of local models based on CCM becomes questionable as they do not admit intrinsic size dependence in their solution, and so nonlocal models are increasingly being utilised to characterise such materials and have been shown to better predict response of materials than local models based on CCM theory [83].
9 Conclusion
This paper presents a NOSBPD viscoelastic framework for simulation of materials exhibiting rate dependent behaviour. The proposed formulation leveraged on a constitutive correspondence principle to allow highly established viscoelastic models from CCM to be implemented in NOSBPD framework. Being a nonlocal theory, and endowed with the capability of modelling continuous and discontinuous material response using the same governing equation of motion without the need for modifications, a NOSBPD viscoelastic formulation promises to provide a computational framework with capacity to model viscoelastic materials in the presence of discontinuities such as initiation and propagation of cracks or nonlocal response due to scale effects as observed in small scale material characterisation.
To validate the proposed framework, three numerical problems representing 1-D and 2-D quasi-static transient and 1-D transient dynamic problems were solved. In the quasi-static regime, the proposed framework was utilised to characterise the response of a bar and a plate subjected to a constant tensile load. The viscoelastic transient response predicted by the proposed framework shows good agreement with results from analytical and FEM methods.
In the viscoelastodynamic regime, results of simulating the axial vibration of a bar also shows good agreement with results obtained using FEM. Parametric study indicated that the influence of nonlocality on the dispersion behaviour of the bar is limited to the period of oscillation and not so much influence is observed on the amplitude of vibration. Characterization of nonlocal behaviour is made possible because of the notion of horizon introduced by the NOSBPD framework as a material parameter.
Although one of the benefits to be derived in developing this framework is the effectiveness of PD to model materials with strong discontinuous behaviour such as the existence of cracks, discussion on the application of this framework to characterise materials with cracks is deferred to a future contribution.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Ren H, Zhuang X, Rabczuk T (2020) A higher order nonlocal operator method for solving partial differential equations. Comput Methods Appl Mech Eng 367:113132
Ren HL et al (2019) An explicit phase field method for brittle dynamic fracture. Comput Struct 217:45–56
Rabczuk T, Ren H, Zhuang X (2019) A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem. Comput Mater Continua 59(1):31–55
Zhuang X, Ren H, Rabczuk T (2021) Nonlocal operator method for dynamic brittle fracture based on an explicit phase field model. Eur J Mech A Solids 90:104380
Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209
Galadima YK et al (2022) Peridynamic computational homogenization theory for materials with evolving microstructure and damage. Eng Comput. https://doi.org/10.1007/s00366-022-01696-5
Basoglu MF et al (2019) A computational model of peridynamic theory for deflecting behavior of crack propagation with micro-cracks. Comput Mater Sci 162:33–46
Candaş A, Oterkus E, İmrak CE (2020) Dynamic crack propagation and its interaction with micro-cracks in an impact problem. J Eng Mater Technol. https://doi.org/10.1115/1.4047746
De Meo D, Russo L, Oterkus E (2017) Modeling of the onset, propagation, and interaction of multiple cracks generated from corrosion pits by using peridynamics. J Eng Mater Technol. https://doi.org/10.1115/1.4036443
Imachi M et al (2020) Dynamic crack arrest analysis by ordinary state-based peridynamics. Int J Fract 221(2):155–169
Kefal A et al (2019) Topology optimization of cracked structures using peridynamics. Contin Mech Thermodyn. https://doi.org/10.1007/s00161-019-00830-x
Liu X et al (2018) An ordinary state-based peridynamic model for the fracture of zigzag graphene sheets. Proc R Soci A 474(2217):20180019
Nguyen CT, Oterkus S (2019) Peridynamics formulation for beam structures to predict damage in offshore structures. Ocean Eng 173:244–267
Ozdemir M et al (2022) A comprehensive investigation on macro–micro crack interactions in functionally graded materials using ordinary-state based peridynamics. Compos Struct 287:115299
Ozdemir M et al (2020) Dynamic fracture analysis of functionally graded materials using ordinary state-based peridynamics. Compos Struct 244:112296
Vazic B et al (2017) Dynamic propagation of a macrocrack interacting with parallel small cracks. AIMS Mater Sci 4(1):118–136
Wang H, Oterkus E, Oterkus S (2018) Three-dimensional peridynamic model for predicting fracture evolution during the lithiation process. Energies 11:1461
Zhu N, De Meo D, Oterkus E (2016) Modelling of granular fracture in polycrystalline materials using ordinary state-based peridynamics. Materials 9:977
Hobbs M et al (2022) An examination of the size effect in quasi-brittle materials using a bond-based peridynamic model. Eng Struct 262:114207
Wu CT, Ren B (2015) A stabilized non-ordinary state-based peridynamics for the nonlocal ductile material failure analysis in metal machining process. Comput Methods Appl Mech Eng 291:197–215
Galadima YK, Oterkus E, Oterkus S (2022) Static condensation of peridynamic heat conduction model. Math Mech Solids. https://doi.org/10.1177/10812865221081160
Wang Y et al (2021) A Nonlocal fractional peridynamic diffusion model. Fractal Fract 5(3):76
Oterkus S, Fox J, Madenci E 2013 Simulation of electro-migration through peridynamics. In 2013 IEEE 63rd Electronic Components and Technology Conference.
Buryachenko VA (2019) Computational homogenization in linear elasticity of peristatic periodic structure composites. Math Mech Solids 24(8):2497–2525
Diyaroglu C, Madenci E, Phan N (2019) Peridynamic homogenization of microstructures with orthotropic constituents in a finite element framework. Compos Struct 227:111334
Madenci E, Barut A, Phan N (2018) Peridynamic unit cell homogenization for thermoelastic properties of heterogenous microstructures with defects. Compos Struct 188:104–115
Madenci E, Barut A, Phan ND 2017 Peridynamic unit cell homogenization, in 58th AIAA/ASCE/AHS/ASC structures, structural dynamics, and materials conference
Nayak S et al (2020) A peridynamics-based micromechanical modeling approach for random heterogeneous structural materials. Materials (Basel, Switzerland) 13(6):1298
Xia W et al (2019) Representative volume element homogenization of a composite material by using bond-based peridynamics. J Compos Biodegrad Polym. https://doi.org/10.12974/2311-8717.2019.07.7
Xia W, Oterkus E, Oterkus S (2021) Ordinary state-based peridynamic homogenization of periodic micro-structured materials. Theoret Appl Fract Mech 113:102960
Galadima YK, Oterkus E, Oterkus S (2020) Investigation of the effect of shape of inclusions on homogenized properties by using peridynamics. Procedia Struct Integr 28:1094–1105
Alali B, Lipton R (2012) Multiscale dynamics of heterogeneous media in the peridynamic formulation. J Elast 106(1):71–103
Galadima YK et al (2021) Chapter–17 multiscale modeling with peridynamics. In: Oterkus E, Oterkus S, Madenci E (eds) Peridynamic modeling, numerical techniques, and applications. Elsevier, Amsterdam, pp 371–386
Ren H et al (2016) Dual-horizon peridynamics. Int J Numer Meth Eng 108(12):1451–1476
Tong Q, Li S (2016) Multiscale coupling of molecular dynamics and peridynamics. J Mech Phys Solids 95:169–187
Galadima Y, Oterkus E, Oterkus S (2019) Two-dimensional implementation of the coarsening method for linear peridynamics. AIMS Mater Sci 6(2):252–275
Silling SA (2011) A coarsening method for linear peridynamics. Int J Multiscale Comput Eng 9(6):609-622
Galadima YK, Oterkus E, Oterkus S (2020) Model order reduction of linear peridynamic systems using static condensation. Mathe Mech Solids. https://doi.org/10.1177/1081286520937045
Sanfilippo D et al (2021) Combined peridynamics and discrete multiphysics to study the effects of air voids and freeze-thaw on the mechanical properties of asphalt. Materials (Basel) 14(7):1579
Wang X, Tong Q (2021) A multiphysics peridynamic model for simulation of fracture in si thin films during lithiation/delithiation cycles. Materials (Basel) 14(20):6081
Yan H, Sedighi M, Jivkov AP (2020) Peridynamics modelling of coupled water flow and chemical transport in unsaturated porous media. J Hydrol 591:125648
Vasenkov AV (2021) Multi-physics peridynamic modeling of damage processes in protective coatings. J Peridyn Nonlocal Model 3(2):167–183
Sasaki N (2012) Viscoelastic properties of biological materials viscoelasticity–from theory to biological applications. InTech, London, pp 99–122
Wu DT et al (2022) Viscoelastic biomaterials for tissue regeneration. Tissue Eng Part C Methods 28(7):289–300
Gutierrez-Lemini D (2014). In: Gutierrez-Lemini D (ed) Fundamental aspects of viscoelastic response in engineering viscoelasticity. Springer, Boston, US, pp 1–21
Buechner PM, Lakes RS (2003) Size effects in the elasticity and viscoelasticity of bone. Biomech Model Mechanobiol 1(4):295–301
Huntley JM (1880) Crack growth in viscoelastic media: effect of specimen size. Proc R Soc London 1990(430):525–539
Li C, Tian X, He T (2021) Nonlocal thermo-viscoelasticity and its application in size-dependent responses of bi-layered composite viscoelastic nanoplate under nonuniform temperature for vibration control. Mech Adv Mater Struct 28(17):1797–1811
Farajpour A, Ghayesh MH, Farokhi H (2018) A review on the mechanics of nanostructures. Int J Eng Sci 133:231–263
Pinnola FP et al (2022) Analytical solutions of viscoelastic nonlocal timoshenko beams. Mathematics 10(3):477
Mulla Y et al (2018) Crack initiation in viscoelastic materials. Phys Rev Lett 120(26):268002
Ciavarella M, Cricri G, McMeeking R (2021) A comparison of crack propagation theories in viscoelastic materials. Theoret Appl Fract Mech 116:103113
Gori M et al (2018) Pressure shock fronts formed by ultra-fast shear cracks in viscoelastic materials. Nat Commun 9(1):4754
Weckner O, Nik Mohamed NA (2013) Viscoelastic material models in peridynamics. Appl Mathe Comput 219(11):6039–6043
Mitchell JA. 2011. A non-local, ordinary-state-based viscoelasticity model for peridynamics. Sandia National Laboratories, United States. p. Medium: ED; p.28.
Speronello M (2015) Study of computational peridynamics, explicit and implicit time integration, viscoelastic material, in Scuola di Ingegneria. Università degli Studi di Padova, Università degli Studi di Padova
Madenci E, Oterkus S (2017) Ordinary state-based peridynamics for thermoviscoelastic deformation. Eng Fract Mech 175:31–45
Ozdemir M et al (2022) Fracture simulation of viscoelastic membranes by ordinary state-based peridynamics. Procedia Struct Integr 41:333–342
Delorme R et al (2017) Generalization of the ordinary state-based peridynamic model for isotropic linear viscoelasticity. Mech Time-Depend Mater 21(4):549–575
Chen H (2018) Bond-associated deformation gradients for peridynamic correspondence model. Mech Res Commun 90:34–41
Behera D, Roy P, Madenci E (2021) Peridynamic modeling of bonded-lap joints with viscoelastic adhesives in the presence of finite deformation. Comput Methods Appl Mech Eng 374:113584
Foster JT, Silling SA, Chen WW (2010) Viscoplasticity using peridynamics. Int J Numer Meth Eng 81(10):1242–1258
Huang Y et al (2022) Peridynamic model for visco-hyperelastic material deformation in different strain rates. Continuum Mech Thermodyn 34(4):977–1011
Madenci E, Roy P, Behera D (2022) Peridynamic Modeling of visco-hyperelastic deformation. Advances in peridynamics. Springer International Publishing, Cham, pp 123–144
Wu L et al (2019) A non-ordinary state-based peridynamic formulation for failure of concrete subjected to impacting loads. Comput Model Eng Sci 118(3):561–581
Silling SA et al (2007) Peridynamic states and constitutive modeling. J Elast 88(2):151–184
Du Q et al (2013) A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws. Math Models Methods Appl Sci 23(3):493–540
Galadima YK et al (2022) A computational homogenization framework for non-ordinary state-based peridynamics. Eng Comput. https://doi.org/10.1007/s00366-021-01582-6
Kaliske M, Rothert H (1997) Formulation and implementation of three-dimensional viscoelasticity at small and finite strains. Comput Mech 19(3):228–239
Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17):1526–1535
Madenci E, Oterkus E (2014) Peridynamic theory and its applications. Springer, New York, USA
Gu X, Madenci E, Zhang Q (2018) Revisit of non-ordinary state-based peridynamics. Eng Fract Mech 190:31–52
Li P, Hao ZM, Zhen WQ (2018) A stabilized non-ordinary state-based peridynamic model. Comput Methods Appl Mech Eng 339:262–280
Littlewood DJ 2010 Simulation of Dynamic Fracture Using Peridynamics, Finite Element Modeling, and Contact. ASME 2010 International Mechanical Engineering Congress and Exposition. ASME, Vancouver, British Columbia, Canada
Luo J, Sundararaghavan V (2018) Stress-point method for stabilizing zero-energy modes in non-ordinary state-based peridynamics. Int J Solids Struct 150:197–207
Silling SA (2017) Stability of peridynamic correspondence material models and their particle discretizations. Comput Methods Appl Mech Eng 322:42–57
Tupek MR, Radovitzky R (2014) An extended constitutive correspondence formulation of peridynamics based on nonlinear bond-strain measures. J Mech Phys Solids 65:82–92
Keramat A, Ahmadi A (2012) Axial wave propagation in viscoelastic bars using a new finite-element-based method. J Eng Math 77(1):105–117
Martin O (2019) Nonlocal effects on the dynamic analysis of a viscoelastic nanobeam using a fractional Zener model. Appl Math Model 73:637–650
Bažant ZP et al (2016) Wave dispersion and basic concepts of peridynamics compared to classical nonlocal damage models. J Appl Mec. https://doi.org/10.1115/1.4034319
Silling SA (2019) Attenuation of waves in a viscoelastic peridynamic medium. Math Mech Solids 24(11):3597–3613
Ansari R et al (2015) Free vibration of fractional viscoelastic Timoshenko nanobeams using the nonlocal elasticity theory. Phys E 74:318–327
Aydogdu M, Filiz S (2011) Modeling carbon nanotube-based mass sensors using axial vibration and nonlocal elasticity. Phys E 43(6):1229–1234
Acknowledgements
The first author is supported by the government of the federal republic of Nigeria through the Petroleum Technology Development Fund (PTDF). This work was supported by an Institutional Links Grant, ID 527426826, under the Egypt-Newton-Mosharafa Fund partnership. The grant is funded by the UK Department for Business, Energy and Industrial Strategy and Science, Technology and Innovation Funding Authority (STIFA)—Project No. 42717 (An Integrated Smart System of Ultrafiltration, Photocatalysis, Thermal Desalination for Wastewater Treatment) and delivered by the British Council.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Galadima, Y.K., Oterkus, S., Oterkus, E. et al. Modelling of viscoelastic materials using non-ordinary state-based peridynamics. Engineering with Computers 40, 527–540 (2024). https://doi.org/10.1007/s00366-023-01808-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-023-01808-9