1 Introduction

Traumatic brain injury (TBI), defined as an alteration in brain function, or other evidence of brain pathology, caused by an external force [1], is a leading cause of death and disability [2]. Up to 90% of cases are in the mild severity range (mTBI including concussion and sub-concussive impact [3, 4]) yet many patients report long-term impairments [5, 6]. The early and rapid detection of mTBI is critical for successful patient management, therapy and rehabilitation, but there is currently no reliable objective method for identifying those individuals who will suffer prolonged symptoms versus those likely to recover naturally.

A recent study identified that the type of mechanical impact in TBI determines the pattern of structural damage and neuropathological sequelae [7, 8] with finite element (FE) models as well as in vivo experiments. Two impacts with similar kinematic values (e.g. impact velocity and head movements) can be manifested differently, indicating the complexities involved [8]. But this also indicates that characterising the strain environment after head impact has the potential to provide clinically relevant information for TBI patients, to support diagnosis and prognosis.

Indeed, FE analysis has been used extensively in brain biomechanics, especially in neurotrauma. Since its first use in the 1970s as a simplified model that approximated the brain as a fluid-filled sphere [9, 10], the field has made great strides. Today’s state-of-the-art models include most of the major components in the brain with their corresponding material descriptions implemented with sophisticated constitutive models. The Wayne State University Brain Injury Model (WSUBIM), which represents a 50th percentile male human head, is capable of simulating direct and indirect impacts and has been validated against intercranial pressure [11] and brain relative motion data [12]. Mao et al. developed a head model as the Global Human Body Model Consortium (GHMBC) [13] which also represents a 50th percentile male human head and was validated against 35 different loading cases from various experimental data sets in the literature. Kleiven et al. have developed the “KHT” series of brain models since early 2000 [14, 15], which have been used in a number of different applications including the investigation of the relationship with kinematic sensor readings [16] and multiscale analysis [17, 18]. Ji and colleagues have also developed and validated a high-fidelity FE model of the brain from MRI scans of a concussed player [19, 20]. This model has been used extensively in a number of different applications such as brain network-based models [21] and estimating vascular strains [22]. We have also developed a subject-specific FE model of the brain from high-resolution MRI images of an American football player and combined it with a machine-learning based approach for rapid prediction of brain strains [23]. Another major injury mechanism of TBI is blast impact, which has also been actively analyzed with computational models. Of note is the study by Tayor et al. [24] who developed and validated a set of modelling tool for simulating blast loading to the human head.

Despite such advancements, two major limitations of previous studies need to be highlighted. First is that only a limited amount of experimental data is available for model validation. In fact, all of the above mentioned studies used the same previous experimental studies [11, 12] in validating their models, especially by comparing relative brain motion. However, considering the huge variations present in brain structure and morphology in any given population, it is not ideal to compare the performance of a model with experimental datasets when they are from two different subjects. Moreover, this has limited the use of FE models to predicting the absence or presence rather than predicting the location and/or extent of the injury. One way of mitigating this limitation is to use data from animal models of TBI for both FE model development and validation. FE models of animal brains for TBI exist in the literature for pig [25] and rat brain models [26], which provided high resolution experimental data from well-controlled TBI experiments performed either with controlled cortical impacts[26] or brain motion measurements[27, 28]. However, these experiments were either performed separately prior to the model generation or experimental data was used for some other purposes (e.g. histological analysis), providing only a means for indirect model validation.

Another limitation of current FE models in the literature is the difficulty of generating subject-specific models that reflect an individual subject’s unique geometry and material properties—in part due to the amount of preprocessing and manual work required for model generation. This has encouraged the development of machine-learning-based approaches where one can bypass expensive and time-consuming FE analysis [23, 29]. There are some studies in the literature that have used multiple subject-specific FE models in their analysis, but they used rather complex mesh-matching [30] or morphing algorithms [31] that depended heavily on in-house code which may not be easily replicated by others for studies with a large number of subjects. Some studies developed a high-fidelity multiscale model for predicting traumatic axonal injuries[25, 32], but they either used the generic 50th percentile model with diffusion tensor images (DTI) from a public dataset or CT scans from other subjects for model registration. Although these models have greatly improved the capability of FE models, their use in a large human dataset is still not feasible. Indeed, all previous studies with multiple subject-specific models have used homogeneous brain material descriptions that, therefore, do not consider subject-specific material properties. Hence, there remains a fundamental need for a robust and rapid subject-specific FE model generation method tailored for multi-subject analysis. Moreover, in recent years, advanced neuroimaging modalities such as diffusion tensor imaging (DTI) and susceptibility-weighted imaging (SWI) have shown potential for offering high-resolution brain images that could be used to characterize structural changes in the brain after head trauma [33,34,35]. However, uptake of this new information offered by advanced MRI to FE models has been hampered by the lack of a robust pipeline able to generate subject-specific FE models directly from MRI images.

The aim of this study to develop and validate an FE model of the sheep brain from advanced MRI images based on our TBI sheep experimental model. To the best of our knowledge, this is the first validated sheep brain FE model. Specifically, with our TBI sheep model, we were able to measure injury patterns pre- and post-impact with advanced MRI. We then used the pre-impact MRI images for model generation and performed the FE analysis with the same boundary condition as the TBI experiment for model validation. We hypothesize that subject-specific FE models will display a complex time-varying strain distribution pattern after impact that matches brain injury patterns displayed in the MRI, highlighting the need for subject-specific information from advanced MRI images in FE model generation and analysis.

2 Methods

A combined MRI and computational analysis pipeline was developed using our animal mTBI model. First, mTBI experiments were performed on our sheep TBI model. Advanced MRI scans including diffusion tensor images (DTI) were taken before and after the impact, and then used to analyse damage patterns with a specimen-specific FE model (Fig. 1).

Fig. 1
figure 1

Overall framework for MRI-based specimen-specific computational analysis of mTBI. Top shows the experimental procedure, the middle row shows the type of analysis performed with advanced MRI images and the bottom shows the FE model generated from the MRI and the cross-sectional view on the coronal and transverse planes

Full size image

2.1 Animal experiment

All animal experiments were approved by the University of Auckland’s Animal Ethics Committee and conducted in accordance with the New Zealand Animal Welfare Act 1999. Our ovine TBI model has been previously described [36]. Dry mixed breed Romney ewes (3 years old) were acclimated to a standard pellet diet with food and water supplied ad libitum for at least 1 week prior to the experiment. On the day of the experiment general anesthesia was induced by i.v. thiopental sodium (15 mg/kg) and maintained by (2–3%) isoflurane following intubation. After baseline MRI imaging, with anaesthesia maintained at all times, the animal was brought out of the MRI machine and placed in the sphinx position, with its head supported with a pillow to allow natural recoil movement. An acute impact that constituted a mild TBI was delivered Using a CASH® Special Concussion stunner (Accles & Shelvoke Ltd, UK) with a 1 grain cartridge which produces ~ 76 J of impact energy from a circular impactor (ø = 25 mm). This resulted in non-penetrating injury from a direct impact with unconstrained head motion comparable to previous ovine models of TBI [37, 38]. The stunner was positioned perpendicular to the area between the horn buds, centered above the midsagittal plane. This resulted in an impact to the superior frontal area of the cerebrum (Fig. 1). Post-impact, the animal was returned to the MRI machine for a second round of scanning, which was identical to the baseline sequence.

2.2 MR imaging

The MR scanning was performed using a 3 T Siemens (MAGNETOM Skyra, Erlangen, Germany), 32 channel head coil. Multiple MRI sequences were acquired, including T1 MPRAGE and diffusion MRI both of which were used in the FE model generation. Diffusion MRI data were acquired with the following imaging parameters: FOV = 17.4, matrix size: 128 × 128, 70 slices, voxel size = 1.4 × 1.4 × 1.4 mm, TR/TE/flip-angle = 12 s/91 ms/90°, 2 b values with b = 0 s/mm2, 64 with b = 2000s/mm2, scan time = 4:28 min. T1 MPRAGE data were acquired with the following parameters: FOV = 23 cm, matrix size: 256 × 256, 120 slices, voxel size = 0.9 × 0.9 × 0.9 mm, TR/TE/flip-angle = 2 s/3.5 ms/9°, scan time = 4:40 min. FLAIR images were also acquired with TR/TE/flip-angle = 5.5 s/95 ms/150°, inversion time = 1.91, matrix size: 256 × 256, 30 slices, voxel size = 0.6 × 0.6 × 3.3 mm, Echo Train length = 17.

2.3 Image analysis

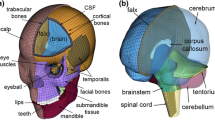
Images were analysed using FSL (FMRIB software library, http://fsl.fmrib.ox.ac.uk/fsl/, version 6.0). Due to the challenges in manually segmenting MRI images [39], we used an established automated methods. First the initial T1-W scan (Fig. 2A) was used to extract the brain using Brain Extraction Tool (BET) in FSL, which accurately segment MRI head images into brain and non-brain parts [40]. After the brain was extracted (Fig. 2B), we used a method called FAST (FMRIB’s Automated Segmentation Tool), which segments MR images of the brain into different tissue types such as white matter, grey matter or CSF, while performing correction for spatial intensity variation in the MR images (Fig. 2C). It is based on a hidden Markov random field model and an associated Expectation–Maximization algorithm [41] and has been quantitatively evaluated for its accuracy [42].

Fig. 2
figure 2

MRI processing and segmentation. A T1-W image of the sheep head B Extracted brain from T1-W image with BET, C Segmented brain tissues with FAST. Blue: Grey matter, Orange: white matter; Yellow CSF. All images are coronal images

Full size image

Diffusion images, acquired using spin-echo EPI sequence, were processed using FDT (FMRIB's Diffusion Toolbox). First, localized geometric distortion was removed with topup and eddy tools from FDT. Then diffusion tensor information at each voxel was obtained with DTIFIT for our further analysis. These diffusion parameters include radial diffusivity (RD), mean diffusivity (MD), fractional anisotropy (FA), and axial diffusivity (AD), and FA color-coded with principal eigenvector direction (color FA). Then, all this information is transferred to a text file using a custom Matlab script (V. R 2018, The Math Works, Inc., Columbia, MD). The resulting file contains the exact location of each voxel and all other structural (cerebellum, cerebrum, and brain stem, white matter, grey matter, CSF) as well as diffusion information (FA, MD, AD, RD, and color FA that represent the principal diffusion direction) and was used when assigning different material properties to individual elements in the FE model as described later (Fig. 3).

Fig. 3
figure 3

DTI images of the sheep brain. A FA map, B color FA map, C, D white matter fiber orientation distribution function overlaid on the voxels

Full size image

2.4 FE model generation and material property descriptions

A high-fidelity FE model of sheep TBI has been developed directly from MRI. First the MRI segmentations of the skull and the whole brain were exported as surface models. This was then turned into a high-resolution hexahedral mesh using an automated algorithm that uses the free-form deformation technique for matching the outer geometry of a solid mesh to a given cloud of datasets. Specifically, our method is made up of two steps: (1) generation of a template mesh from which subject-specific meshes can be generated and (2) free-form deformation (FFD) of the template mesh to deform the template mesh to subjects’ dataset from medical images such as CT or MRI [43]. FFD method involves embedding a mesh to be customized (called slave mesh) inside a wrapper mesh (called host mesh). The host mesh is deformed according to an objective function to minimize the distance between control points in the ‘least-square’ sense and pass the deformation to the slave mesh. The control points can be placed both on the host and the slave meshes. The objective function is then expressed as the following:

$$F\left( {u_{n} } \right) = \mathop \sum \limits_{d = 1}^{N} w_{d} \left\| {u\left( {\xi_{1d} ,\xi_{2d} } \right) - z_{d}^{2} } \right\| + F_{s} \left( {u_{n} } \right) ,$$
(1)

where \({z}_{d}\) are the geometric coordinates of data points d placed on the slave mesh, \({w}_{d}\) is a weight for each data point, \(u\left({\xi }_{1d},{\xi }_{2d}\right)\) are the corresponding mesh points from the host meshes which is obtained via interpolation with the basis function \({u}_{n}\). One unique feature that differentiates our approach to other FFD methods is the inclusion of a Sobolev smoothing term \({F}_{s}\left({u}_{n}\right)\) for additional control over the deformation of the host mesh given below:

$$F_{s} \left( {u_{n} } \right) = \iiint_{{0}}^{{1}} {\left\{ {\gamma _{1} \left\| {\frac{{\partial u}}{{\partial \xi _{1} }}} \right\|^{2} + \gamma _{2} \left\| {\frac{{\partial u}}{{\partial \xi _{2} }}} \right\|^{2} + \gamma _{3} \left\| {\frac{{\partial u}}{{\partial \xi _{3} }}} \right\|^{2} + \gamma _{4} \left\| {\frac{{\partial ^{2} u}}{{\partial \xi _{1}^{2} }}} \right\|^{2} + \gamma _{5} \left\| {\frac{{\partial ^{2} u}}{{\partial \xi _{2}^{2} }}} \right\|^{2} + \gamma _{6} \left\| {\frac{{\partial ^{2} u}}{{\partial \xi _{3}^{2} }}} \right\|^{2} + \gamma _{7} \left\| {\frac{{\partial ^{2} u}}{{\partial \xi _{1} \partial \xi _{2} }}} \right\|^{2} + \gamma _{8} \left\| {\frac{{\partial ^{2} u}}{{\partial \xi _{2} \partial \xi _{3} }}} \right\|^{2} + \gamma _{9} \left\| {\frac{{\partial ^{2} u}}{{\partial \xi _{3} \partial \xi _{1} }}} \right\|^{2} + \gamma _{{10}} \left\| {\frac{{\partial ^{3} u}}{{\partial \xi _{1} \partial \xi _{2} \partial \xi _{3} }}} \right\|^{2} } \right\}d\xi _{1} d\xi _{2} d\xi _{3} }$$
(2)

where \({\gamma }_{i} (i=1\cdots 3)\) are the three arc-lengths, \({\gamma }_{i} (i=4\cdots 6)\) are the three curvatures in the \({\xi }_{1,}{\xi }_{2,}{\xi }_{3}\) directions, respectively, and \({\gamma }_{i} (i=7\cdots 9)\) are the three surface area terms for faces \({(\xi }_{1-}{\xi }_{2})\), \({(\xi }_{2-}{\xi }_{3})\) and \({(\xi }_{3-}{\xi }_{1})\), while \({\gamma }_{10}\) is related to the volume, which ensures the shape of the original volume is not too distorted after fitting so that the customized mesh is not anatomically distorted. We have used this method extensively in the past in subject-specific FE model generation for various tissues and joints such as the Achilles tendon and the hip joint [44,45,46]. We applied this to the brain in this study. The number of elements for the template mesh was determined after mesh convergence analysis and the resulting total number of elements was 321,070 consisting of 343,874 nodes. This was then deformed using the FFD described above to generate a subject-specific model by deforming the template mesh to the segmented MR dataset.

We have also incorporated major tissue types in the brain model—the skull (both compact and spongy bones separately), dura mater, pia mater, cerebrospinal fluid and the brain tissue. The material properties used are given in Table 1.

Table 1 Different materials incorporated in our model
Full size table

The brain tissue was modelled using the hyper-viscoelastic fiber-reinforced anisotropic model using the formulation by Gasser, Ogden and Hozapfel (GOH) [48] to incorporate white mater structural anisotropy. This model has been used to describe the anisotropy of the brain by a number of previous works [49,50,51]. In this material formulation, the strain energy function W is defined as the following:

$$W = \frac{G}{2}\left( {\widetilde{{I_{1} }} - 3} \right) + K\left( {\frac{{J^{2} - 1}}{4} - \frac{1}{2}\ln \left( J \right)} \right) + \frac{{k_{1} }}{{k_{2} }}\left( {e^{{k_{2} \left\langle {\tilde{E}_{\alpha } } \right\rangle^{2} }} - 1} \right),$$
(3)

where W is the strain energy per unit volume, G is the shear modulus, K is the bulk modulus, J is the determinant of deformation gradient, \({k}_{1}\) and \({k}_{2}\) are the parameters related to the fiber stiffness. The last term in Eq. (1) was from the GOH [37] form with one fiber family, where:

$$\tilde{E}_{\alpha } = k\left( {\tilde{I}_{1} - 3} \right) + \left( {1 - 3k} \right)\left( {\tilde{I}_{4\alpha } - 1} \right),$$
(4)

which characterizes the deformation of the fibers with the fiber dispersion parameter k and the function \(\tilde{I}_{4\alpha }\) defined as the following:

$$\tilde{I}_{4\alpha } = \tilde{\user2{C}}:{\varvec{n}}_{{0{\varvec{\alpha}}}} \otimes {\varvec{n}}_{{0{\varvec{\alpha}}}} ,$$
(5)

where \(\widetilde{{\varvec{C}}}\) is the isochoric part of the right Cauchy-Green strain tensor and \({{\varvec{n}}}_{0\boldsymbol{\alpha }}\) is the fiber direction unit vector in the undeformed configuration. The viscoelastic behavior was incorporated with the following relaxation function:

$$G\left( t \right) = 1 + \mathop \sum \limits_{i = 1}^{N} g_{i} e^{{\left( {\frac{ - t}{{\tau_{i} }}} \right)}}$$
(6)

The fiber dispersion parameter in the GOH model has been linked with FA measures from diffusion MRI by Giordano and Klevin [50] using the following relationship:

$$FA = \frac{{\sqrt {\left( {\frac{1 - 2k}{k} - 1} \right)^{2} } }}{{\sqrt {\left( {\frac{{\left( {1 - 2k} \right)}}{k}} \right)^{2} + 2} }}.$$
(7)

We have used this relationship as well as the GOH material law to describe the anisotropy of the brain tissue and have linked it with the FA measurements from MRI (Table 2).

Table 2 FA ranges and corresponding k values for GOH material
Full size table

The viscoelastic behavior was modelled with a relaxation function that was added to the second Piola–Kirchhoff stress as the following:

$$S\left( t \right) = S^{\infty } + \mathop \smallint \limits_{ - \infty }^{t} G\left( {t - s} \right)\frac{{dS^{e} }}{ds}ds,$$
(8)

where S is the elastic stress derived from W in Eq. (1) and G is the relaxation function described with the following discrete relaxation spectrum:

$$G\left( t \right) = 1 + \mathop \sum \limits_{i = 1}^{N} \gamma_{i} {\text{exp}}( - t/\tau_{i} ) .$$
(9)

The viscoelastic parameters as well as other parameters for the GOH were obtained from Kleiven and Giordano [52].

Each element was automatically assigned with the material property that corresponds to the MRI voxel information using the in-house python code. This is based on the automatic material assignment algorithm that we developed for assigning bone materials to FE models from CT scans [53]. This has been successfully used in assigning different material information to different elements for various types of FE models in the past [23, 44, 46, 54, 55].

This works by searching for the closest voxel to the element of interest by aligning the FE model in the MRI coordinates. This way the correspondence between elements in the FE model and MRI voxels are established, allowing us to assign subject-specific material properties as well as geometry from the MRI scans of the subject (Fig. 4).

Fig. 4
figure 4

Material property assignments from T1-W and DTI images. Starting with brain segmentation from T1-W image, DTI map was obtained which was used to assign each element in the FE model with corresponding materials the FA values

Full size image

Dynamic simulation was performed with FEBio (www.febio.org) with the boundary condition that mimics the actual load application from the experiment described above. The contact between the brain and meninges layers was modelled with frictionless contact to accurately model the deformation and movements between these two tissues upon impact application.

Three different analyses were performed. First a fully subject-specific analysis was performed with the model that contains both subject-specific geometry and material properties. This was compared with the post-impact MRI scan for model validation. After that, the model was modified to examine (1) the importance of having subject-specific material properties; (2) the importance of incorporating sliding movements between the brain and the skull. The first was examined using a homogeneous material property commonly used in a majority of brain FE models [14, 30, 47]. The second was examined by modifying the contact constraints from frictionless to tied contact, which essentially eliminates sliding between the brain and skull.

3 Results

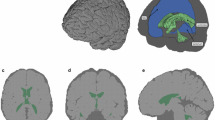
The post-impact MRI scans show two locations where brain changes occurred after mechanical impacts. Among the MRI sequences we tested, Fluid Attenuated Inversion Recovery (FLAIR) images showed the brain damage patterns most clearly (Fig. 5). The most prominent injury can be seen immediately underneath the area where the impact was delivered. Although it was not a penetrating impact, this area initially received the most energy which resulted in the contusion in the area. Another area of damage appeared diagonally opposite the location where the major damage occurred. This indicates that the movements and deformation from the initial impact also caused secondary movement and subsequent contusion in areas away from the location of the impact, resulting in contrecoup brain injury.

Fig. 5
figure 5

FLAIR images of pre- and post-impact. The views from the location of impact and its neighbouring regions are shown. The area of brain damages can be seen directly underneath of the impact location as well as the contrecoup location

Full size image

The size of the damage area was quantified using the ITK-SNAP’s segmentation tool [56], which is was measured to be 550.94mm3 when the coup and contrecoup injuries are combined. This is about 0.4% of the total cerebrum volume. The size and locations of damage sites are shown in 3D in Fig. 6.

Fig. 6
figure 6

Quantification of damages incurred from the mechanical insults

Full size image

Our specimen-specific FE model was able to predict the brain damage patterns shown by FLAIR MR images accurately. The initial peak strain appeared right underneath of the location of impact application. The peak strain then shifted towards the area where the contrecoup injury occurred, diagonally opposite to the area of the initial impact application. In particular, the incorporation of different tissue types in the brain (CSF, meninges and brain white and gray matter) as well as the FA dependent anisotropy incorporated with the GOH material description allowed a tissue specific strain distribution pattern that matched closely with the experimental results (Fig. 7).

Fig. 7
figure 7

FE simulation results matching the FLAIR image taken post-impact. The locations of high peak strains correspond to the areas in the brain where contusion occurred after the impact

Full size image

The strain distribution pattern displayed complex patterns where peak strain moved from the initial impact location down to the contrecoup area. Subsequently, the peak strain travelled towards the ventricular region of the brain, indicating that other regions of the brain, not shown in the MRI, might also have sustained damage (Fig. 8).

Fig. 8
figure 8

Detailed strain map after the head impact around the regions of the brain where the damage was predicted. The top row shows the coronal view while the bottom row shows the transverse view. The numbers in the column represent the distance away from the impact site in the anterior direction

Full size image

However, this pattern was only evident when the spatially varying GOH material was used. With the homogeneous Ogden material property often used in other brain FE models, the strain pattern was more diffusively dissipated from the locations of impact and failed to predict the contrecoup injury seen in the GOH model as well as in the MRI scans. Moreover, the overall strain magnitude was smaller than GOH model and more concentrated around the area of impact with a slower dissipation of strains during the simulation time (Fig. 9).

Fig. 9
figure 9

Simulation results with Ogden homogeneous material. The areas with high strains are concentrated around the impact area with much slower and smaller strain dissipation to the other areas

Full size image

When sliding between the brain and skull was not allowed, using a tied contact condition between the skull and the brain, the strain transfer pattern was more gradual and downwards from the superior part of the brain, rather than showing a peak underneath the impact location. This also predicted much less strain concentration on the contrecoup area (Fig. 10) indicating that the sliding movement between brain and skull plays an important role in the subsequent injury patterns.

Fig. 10
figure 10

Strain patterns when sliding between brain and the bone were not allowed. More direct transfer of strains from the site of impact can be seen

Full size image

4 Discussions

The aim of this study was to develop a new method to combine advanced MRI with subject-specific FE models to perform in-depth analysis of brain injury patterns after TBI. This was achieved using the advanced MRI images that we collected from our TBI sheep experiment [36] and developing a new method to generate subject-specific FE models of the brain directly from MRI scans. The animal was MRI scanned before and after impact delivery to measure changes in brain structures. FLAIR MRI scans showed contusion near the site of impact delivery, and to the countercoup region diagonally opposite to the impact delivery site. The FE model generated with pre-impact MRI scans predicted this pattern of damage well but also revealed high strain areas were also present in other regions of the brain. These results highlight the value of the FE model for a more in-depth analysis of the patterns of brain damage after head impact.

An interesting finding from our study was the importance of incorporating spatially varying subject-specific material descriptions in the FE analysis of TBI. We have used the material description introduced by Giordano and colleagues [52] where they established the relationship between the MRI DTI index (FA) with the material coefficient in the GOH model [48]. Using this relationship as well as our element material assignment technique, we were able to assign different material parameters for each element depending on the corresponding MRI DTI index. This way, our model captured the subject-specificity for both geometry and material properties, which turned out to be an important factor for accurate prediction of brain damage patterns after TBI. This was made possible by having an analysis framework that is fully based on MRI images of the animal. The geometry of the brain and skull were obtained from the segmented T1-W images, while the DTI images provided the FA values and directions, which allowed a spatially varying material descriptions specific to the subject to be incorporated.

The importance of having subject-specific information in FE analysis, especially in the case of tissue damage or injury have long been recognized [43, 44], yet it has not become as widespread in brain injury analysis due to the complexity of brain FE models. Ji and colleagues performed geometrically subject-specific FE analysis on concussed athletes using their MRI scans [30]. They used mesh-matching that combines an affine registration with B-spline nonrigid registration to deform the baseline model to the subjects’ MRI scans. However, subject-specific material properties as well as internal structures were not incorporated in these models. Li and colleagues developed an anatomically detailed subject-specific model of the brain [31]. They used a mesh-morphing technique for morphing the MRI scans, from which subject-specific models were generated. This allowed them to incorporate internal structures and their inter-subject variability. However, they also did not use spatially varying material descriptions, but rather used the homogenous from their previous study [14]. The method that we developed defer from these two previous studies. First, the mesh generation technique that we used is based on Free-Form Deformation [57], which we have used extensively in generating subject-specific models of various organs and tissues as a part of Physiome Project [58, 59]. This has recently been translated into an open-source python library, which we have used in our subject-specific model generation [60]. Second, our model uses heterogeneous material descriptions which obtained the spatially varying characteristics from the MRI scans. Based on our experience in using CT images for incorporating spatially varying bone density into FE models [53], we have developed a method that can identify MRI voxels that belong to each FE element and assign corresponding FA values to each element. This allowed us to have a completely subject-specific FE model of the brain – both in terms of geometry and material properties. One of the major strengths of our model is that it can be applied to any other subjects or species if we are given their MRI scans. Another strength is the fairly automated pipeline for model generation. Rather than using multiple different software tools, our pipeline is made up of our own custom python code based on a publicly available python library [60], which can be scripted for fast model generation in a study with a large number of subjects.

Our study also used a unique experimental dataset for TBI FE models. Currently available FE models in the literature all used the same experimental dataset for model validation [11, 12]. Although these datasets are instrumental in providing quantitative data for model validation in terms of brain motion and pressure, it is not ideal to compare the performance of a subject-specific FE model to a dataset collected from a different cadaveric head. Moreover, this restricted the use of the FE model to predicting the presence or absence of TBI and/or injury threshold rather than injury locations or patterns. Therefore, we have performed our own in vivo animal experiment with our sheep TBI model [36] including advanced MRI scanning pre- and post-impact. This allowed us to measure the changes in the brain structure by analysing pre- and post-impact MRI scans. Our scans display the changes in the brain, especially the signs of contusion in specific areas—sites of impact and countercoup injury. This provided a qualitative data for model validation in our study.

Animal models of TBI have been used in the past for FE analysis especially for the piglets [25] and rat brains [26] but none of them used pre- and post-impact MRI for model generation and validation at the same time. Moreover, there are benefits of using the adult sheep brain as a model of TBI including the comparable size to the human brain, their gyrencephalic brain structure and the presence of well-developed meninges [61].Considering that our pipeline can be easily customised and scaled to human brains, the benefits of using a large animal model for mTBI as well as their comparability to human brains gives us confidence that models generated from human MRI will have an equivalent high level of accuracy.

There are a number of limitations in our study. First is the use of human brain material properties in our model. Although we have characterized brain material properties from our experiment, we could not use this as this was based on a brain slicing technique that is different to the MRI voxels. As a result, we could not incorporate a specific sheep brain material property. This means that the strain magnitude predicted by the model cannot be used in establishing an injury threshold for sheep. However, the pattern that our model predicted showed good qualitative match with the post-impact MRI scans, giving us confidence about our model performance. Second limitation is that only qualitative validation was performed as we compared the strain pattern with post-impact MRI images. Future work will include more quantitative comparison between MRI images and model to determine the best MRI indices for damage prediction in human TBI. Finally, unlike other well-established automatic mesh generation method that generates all hex mesh with the clear boundaries between different materials in a single domain [62], we differentiate different materials by assigning each element with its corresponding material using the subject’s MR images. Although our approach can be numerically more efficient, if one needs to impose contact interfaces between different materials, our method cannot be used. This feature will be incorporated into our future studies.

In conclusion, we have developed a novel pipeline that combines FE analysis with MRI imaging for fully subject-specific analysis. We have applied this to our mTBI sheep model and developed a first validated sheep brain FE model. The developed pipeline is general enough to be applied to various different species including human brains. We will perform both human brain analysis as well as other animal analysis for comparative studies to characterize the injury mechanisms of mTBI.