Abstract
Peridynamic theory has been shown to possess the capabilities of describing phenomena that theories based on partial differential equations are not capable of describing. These phenomena include nonlocal interactions and presence of singularities in system responses. To exploit the capabilities offered by peridynamics in the homogenization of heterogenous media, a nonlocal computational homogenization theory based on peridynamic correspondence model (non-ordinary state-based peridynamics) is proposed. To set the development of the theory on a rigorous mathematical framework and to ensure consistency with the nonlocal nature of the peridynamic theory, a nonlocal vector calculus was used in the analysis of the nonlocal homogenization theory. The proposed theory is a two-scale micro–macro-homogenization strategy in which the constitutive relation at the macroscale is derived from explicit solution of a nonlocal volume constraint problem at the microscale. To justify the coupling between the two scales, nonlocal analogues of the stress and strain average theorems as well as the Hill–Mandel macrohomogeneity condition were derived. Validation of the proposed theory is achieved via numerical solution of Representative Volume Elements (RVE) from composite materials and comparing the results with those obtained by means of established methodologies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Understanding how materials behave has contributed tremendously to the development of modern technologies. Historically, the Cauchy continuum theory has been and continues to dominate as the tool used by scientists and engineers in studying the behaviour of materials. Central to the Cauchy continuum theory is the continuum hypothesis which presupposes that at an arbitrarily small scale (microscale), materials consist of a continuous distribution of infinitesimal particles that are idealised as point mass and each having physical properties such as mass, displacement and velocity which are volume averages over a finite-size domain defined in the microscale. The term microscale in this context should be understood to mean the scale at which the material is decomposed into continuum particles which does not necessarily have to be in the order of micrometres.
The state of the material at a point is governed by balance laws and interaction between the continuum particles is achieved through exchange of mass, momentum, and energy with immediate neighbours in accordance with Noll’s principle of local action. The composition, geometries, distribution, and properties of these particles along with the characteristics of heterogeneities such as cracks and voids constitute the material’s microstructure. The detail of this microstructure typically transcends many orders of magnitude. When developing a model to characterise these materials, a resolution threshold is selected below which information about the microstructure is ignored. If the selected level of resolution is not able to encapsulate important microstructural details, the model must be enriched to be able to capture the desired level of details.
A straightforward solution is the use of micromodels in which the resolution is refined until the model can explicitly resolve all important microstructural details. This solution strategy has been utilised to model microstructurally heterogeneous materials such as composites using numerical techniques such as the Finite-Element method [1,2,3,4], Finite-Difference Method [5,6,7,8], and meshless methods such as the Element-free Galerkin method [9,10,11,12] to name just a few. This method of enriching the model suffers from several drawbacks amongst which include the fact that the microstructural details that plays important role in the response of the material may exist over wide orders of magnitude and explicit resolution of the microstructure for some applications may require computational resources that is prohibitively expensive. Other more fundamental problems include the fact that the response of a material specimen in the framework of the classical continuum theory is independent of the size and shape of the specimen [13]. This is, however, not the case as several studies [14,15,16,17] have indicated that material behaviour changes as their characteristic size decreases, a phenomenon known as size or scale effect [18]. Other problems include the presence of discontinuity in material response for which the classical theory is not good at handling [19] and resolution of nonlocal effects such as the existence of long-range interaction [20].
A variety of enrichment methodologies have been developed over the years to overcome the challenges associated with the classical Cauchy continuum theory. A broad class of these methodologies is called the generalised continuum theories [21] or microcontinuum theories [22]. In developing these methodologies, the local action hypothesis is relaxed or eliminated, and interaction between continuum points located at finite distance apart is permitted thereby leading essentially to continuum models that are nonlocal. The nonlocality implied here should be understood in the sense used in [23] to encompass ‘weakly’ nonlocal and ‘strongly’ nonlocal models. In this sense, the weakly nonlocal models, though mathematically adhering to the principle of local action, account for nonlocality by enriching the constitutive model with the first or higher gradient of relevant state variables or thermodynamic forces [24]. A foremost contribution to the development of the generalised continuum models is the work of Voigt [25]. Later contributions would lead to the development of a range of nonlocal models. The weak generalised continuum theories can broadly be classified into those that retain the kinematics of the classical Cauchy theory but account for nonlocality by incorporating higher gradients of the classical kinematic variables in the definition of the strain energy and those with extended kinematics, with the strain energy in this case expressed as a function of the classical kinematic variables and their gradient in addition to the newly incorporated variables. Among theories in the first category, we can cite the couple stress theories [26,27,28] and the strain gradient theories [29,30,31,32]. Of those in the second category, we can cite the Cosserat theory [33], the micromorphic theories [34], micropolar theory [35,36,37] and the internal variable models [38,39,40,41].
In the strong nonlocal category of enrichment, belong the integral-type nonlocal models. The development of these class of nonlocal models can be traced to the works of Kunin [42], Kroner [43] and Eringen [44]. In contrast to the weak nonlocal models, the integral-type nonlocal models completely jettison with the notion of locality even in their mathematical formulation by substituting the gradients of relevant state variables with a weighted integral of these state variables. By doing so, these models posit that the state variables at a continuum point is influenced directly by the state variables of all other points in the body or at least some finite neighbourhood of the point under consideration. Subsequent development of the integral-type nonlocal continuum theories includes the introduction of Peridynamic continuum theory [45], the Nonlocal Operator Method (NOM) originally proposed in [46] and later extended in [47] as Higher Order Nonlocal Operator Method (HONOM) to eliminate the requirement of shape functions in obtaining partial derivatives and a Long-range cohesive interaction model proposed in [48,49,50].
Peridynamics is a reformulation of the classical elasticity theory with extended capabilities of modelling discontinuous system response and long-range force interaction. Since its introduction, theory continues to receive growing interest from researchers and have thus found application in solving a wide range of engineering problems [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70]. This is because it offers a theoretical and mathematical framework that allow for the modelling of systems with singularities without the need for modification of the governing equations. Discontinuous state variables are handled with the same equations as the continuous state variables. Another advantage offered by peridynamics is the introduction of an intrinsic length-scale parameter into the governing equation. This parameter allows the theory to be useful in modelling problems across a wide range of scales [71] and has been shown to correlate with the notion of an ‘effective distance’ introduced in [20] as a parameter that influences direction of crack in dynamic fracture.
Although peridynamics has been proven to overcome a lot of challenges associated with the classical Cauchy continuum theory, there are still problems for which resolution of relevant physics of the problem to obtain acceptable model fidelity require inordinate computational resources that is either prohibitively expensive or currently not available. The need to find a balance between acceptable model fidelity and lowering computational cost has motivated the development of a range of multiscale enrichment protocols for the peridynamic theory. The objective of these protocols is to enhance the capability of peridynamics in capturing and utilising information across spatial scales at acceptable computational cost. This objective is achieved in one of two approaches. The first approach is by developing a framework that allow the coupling of peridynamic theory with other theories of mechanics with the goal of leveraging on the strengths of the coupled modelling theories. This will fall under the purview of concurrent multiscale modelling. The second is achieved through frameworks that allow coupling of models at different length scale in the same part of a computational domain and are categorised as Hierarchical multiscale modelling.
A variety of concurrent multiscale modelling framework for peridynamics have been proposed. These approaches can broadly be categorised into monomodel and multimodel approaches. In the monomodel approach, peridynamics is used to model the entire computational domain. Multiscale capability is achieved by refining the grid appropriately to resolve details at different length scales. Development in this respect includes the adaptive grid refinement method proposed in [72,73,74]. Refinement of the grid requires changing the grid density and the horizon which in turn induces a change in the micromodulus function of the peridynamic model. This change is done relying on a scaling algorithm. A variable horizon method was proposed in [75] to solve the problem of ghost forces that is a consequence of using variable horizon by introducing the concept of partial stress and a splice technique. To resolve the problem of ghost forces without recourse to the partial stress and splice technique of [75], a dual horizon method [76] was proposed with extended capability of covering both bond-based peridynamics and state-based peridynamics. The dual horizon method was extended as Voronoi-based peridynamics in [77] for non-uniform discretization based on Voronoi diagrams.
The multimodel concurrent approaches are hybridization frameworks that focus primarily in developing coupling methodologies that allow peridynamics to be used concurrently with other modelling frameworks such as the classical continuum or atomistic modelling theories. The goal is to leverage on the advantages offered by each of the coupled models. These methods can broadly be classified as kinematic-based, force-based or energy-based coupling methods. In the kinematic-based methods [78,79,80,81], coupling is achieved by implementing a contact algorithm over the interface region that requires the satisfaction of a series of kinematical constraints. The force-based approaches [82,83,84,85,86,87,88] rely on the balance of force in the interface region to achieve coupling of the models. In some cases, nonlocal weight functions are used to account for the contributions from the models in the balance of force. In the energy-based approach, coupling relies on the principle of energy conservation in the interface region. Two notable subclasses of the energy-based approach have been proposed such as the morphing methods [89,90,91,92,93,94] and the Arlequin coupling method [95].
In the hierarchical multiscale subclass, efforts have been expended by several researchers that led to the development of different hierarchical methods. A class of the hierarchical methods that we will designate as Model Reduction techniques in the framework of peridynamics was first proposed in [96] as coarsening method. The key idea of the Model Reduction techniques is to be able to capture the behaviour high-fidelity models using fewer degrees of freedom. The reduction in the order of model is achieved by substituting a high-fidelity model with a surrogate model with fewer degrees of freedom. The coarsening method was extended in [97] for two-dimensional applications. A related method of model reduction based on static condensation of a high-fidelity peridynamic model was proposed in [98].
Another subclass of the hierarchical methodologies developed for peridynamics is the homogenization methods which encompasses several related methods. The earliest attempt at developing a homogenization framework for peridynamics appeared in [99, 100] in which a two-scale solution expansion of the peridynamic equation for a heterogeneous medium was proposed based on the concept of two-scale convergence. The framework is a three-step solution strategy of computing an average displacement field as a solution of a peridynamic macroscopic equation and computing micro-level displacement field from a solution of a microscopic equation. The displacement field of the heterogeneous medium is found by superimposition of the micro-displacement field unto the macro-field in a final step. Although the mathematical framework was developed, numerical validation for the method is yet to be done.
A class of mean-field homogenization methods that can be categorised as a generalisation of the self-consistent methods [101] of the classical theory to peridynamics were proposed in [102,103,104] by extending the effective field hypothesis of the classical elasticity of composites to the nonlocal peridynamic framework. The effective elastic properties of a heterogeneous medium are determined through the introduction of a stress polarisation tensor.
Among the homogenization methodologies exists a class designated as full-field (computational) homogenization techniques which achieve a much higher resolution of the microscopic fields than the mean-field methods. In several works [105,106,107], various computational homogenization methodologies have been proposed to evaluate effective properties of heterogenous medium in the bond-based peridynamic framework based on the description of the microgeometry of the heterogeneous medium by solving a well-defined microscale volume-constrained problem. An extension of the computational homogenization framework to Ordinary state-based peridynamics was proposed in [108].
The objective in this study is to develop a multiscale constitutive theory for non-ordinary state-based peridynamics (peridynamic correspondence model) in the framework of computational homogenization. The methodology will be set on a rigorous mathematical foundation in a manner that will account for the nonlocal nature of the peridynamic theory. To achieve these goals and for the sake of self-contained presentation, this paper will start off with a brief review of relevant results from a nonlocal vector calculus developed in [109]. This provides a mathematical framework that is consistent with the nonlocal nature of Peridynamics. Key results from the nonlocal vector calculus will be used as the building block to derive the nonlocal Peridynamic model in Sect. 3. Discussion on the discretization methodology for the peridynamic model adopted in this presentation is provided in Sect. 3.3. The development of a nonlocal computational homogenization for the peridynamic model is presented in Sect. 4 while numerical experiments to validate the proposed methodology is presented in Sect. 5. Concluding remarks and discussion on future research outlook is presented in Sect. 6.
2 Nonlocal vector calculus primer
In developing the nonlocal vector calculus, two types of functions and operators were defined in [109]. Let \(k,m\) and \(n\) be positive integers and let \({\varvec{x}}\) and \({{\varvec{x}}}^{\prime}\) be points in \({\mathbb{R}}^{n}\). For a given domain \(\Omega \subseteq {\mathbb{R}}^{n}\), functions or operators that maps \(\Omega\) into \({\mathbb{R}}^{m\times n}\) or \({\mathbb{R}}^{n}\) or \({\mathbb{R}}\) are called point functions or operators, respectively. On the other hand, functions, or operators from \(\Omega \times\Omega\) into \({\mathbb{R}}^{m\times n}\) or \({\mathbb{R}}^{n}\) or \({\mathbb{R}}\) are called two-point functions or operators, respectively. Point functions and two-point functions could be scalar, vector or tensor valued functions.
A very important concept to start with in this review is the nonlocal flux. Given a tensor two-point function \({\varvec{\psi}}:{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\), then the definition
is the nonlocal flux of \({\varvec{q}}\) from \({\Omega }_{1}\) into \({\Omega }_{2}\) where \({\int }_{{\Omega }_{2}}{\varvec{\psi}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\mathrm{d}{{\varvec{x}}}^{\prime}\) is identified as the nonlocal flux density into the region \({\Omega }_{2}\) from point \({\varvec{x}}\in {\Omega }_{1}\). It can be deduced from (1) that the nonlocal flux is not necessarily zero even if the intersection of the closures of \({\Omega }_{1}\) and \({\Omega }_{2}\) is an empty set. This is in stark contrast with the local flux which is zero if \({\overline{\Omega } }_{1}\cap {\overline{\Omega } }_{2}=\varnothing\). The nonlocal flux density is related to the intensive quantity \({\varvec{q}}\) through a constitutive relation. If \({\varvec{\psi}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\) is assumed to be antisymmetric, then the following statements are true:
-
1.
There is no self-interaction, i.e.
$${\int }_{\Omega }{\int }_{\Omega }{\varvec{\psi}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\mathrm{d}{\varvec{y}}\mathrm{d}{\varvec{x}}=0.$$(2) -
2.
The nonlocal action-reaction principle holds for \({\Omega }_{1},{\Omega }_{2}\subset\Omega\)
$${\int }_{{\Omega }_{1}}{\int }_{{\Omega }_{2}}{\varvec{\psi}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\mathrm{d}{{\varvec{x}}}^{\prime}\mathrm{d}{\varvec{x}}+{\int }_{{\Omega }_{2}}{\int }_{{\Omega }_{1}}{\varvec{\psi}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\mathrm{d}{{\varvec{x}}}^{\prime}\mathrm{d}{\varvec{x}}=0.$$(3)
The action-reaction principle given by (3) simply states that the flux from \({\Omega }_{1}\) into \({\Omega }_{2}\) is equal to the flux that exits \({\Omega }_{2}\) into \({\Omega }_{1}\).
2.1 Nonlocal divergence and gradient operators and their adjoint
Given the two-point function \({\varvec{v}} :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\) and the scalar two-point function\(u :{\mathbb{R}}^{n}\to {\mathbb{R}}\). Let \(\boldsymbol{\alpha }\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n} \to {\mathbb{R}}^{m}\) be an antisymmetric vector two-point function. The action of nonlocal divergence operator \(\mathcal{D}\) and its adjoint \({\mathcal{D}}^{*}\) on \({\varvec{v}}\) and \(u\), respectively, are defined as
and
where \(\mathcal{D}\left({\varvec{v}}\right)\left({\varvec{x}}\right) :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\) and \({\mathcal{D}}^{*}\left(u\right)\left({\varvec{x}},{{\varvec{x}}}^{\mathbf{^{\prime}}}\right) : {\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\times {\mathbb{R}}^{k}.\)
Given the scalar two-point function \(\eta \boldsymbol{ }:\boldsymbol{ }{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}\) and the vector point function \({\varvec{u}}\boldsymbol{ }:\boldsymbol{ }{\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\), for a given antisymmetric vector two-point function \({\varvec{\beta}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\), the action of the nonlocal gradient operator \(\mathcal{G}\) and its adjoint \({\mathcal{G}}^{*}\) on \(\eta\) and \({\varvec{u}}\), respectively, are defined as
and
where \(\mathcal{G}\left(\eta \right)\left({\varvec{x}}\right) :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\) and\({\mathcal{G}}^{*}\left({\varvec{u}}\right)\left({\varvec{x}},{{\varvec{x}}}^{\mathbf{^{\prime}}}\right) :{\mathbb{R}}^{n}\to {\mathbb{R}}\).
Observe that, unlike in local calculus which deals with point functions only, nonlocal calculus involves two kinds of functions: point and two-point functions. This, therefore, necessitates the definition of alternative forms of the nonlocal operators defined in (7) and (8). The alternative forms of the nonlocal divergence and gradient operators were given in [28] to be the pairs \(\mathcal{D},-{\mathcal{G}}^{*}\) and \(\mathcal{G},-{\mathcal{D}}^{*}\). For example, in the alternative pair \(\mathcal{D},-{\mathcal{G}}^{*}\), while \(\mathcal{D}\) operates on tensor two-point functions, \(-{\mathcal{G}}^{*}\) operates on tensor point functions. Similarly, for the pair \(\mathcal{G},-{\mathcal{D}}^{*}\), \(\mathcal{G}\) operates on vector two-point functions while \(-{\mathcal{D}}^{*}\) operates on vector point functions.
It is possible to apply the nonlocal divergence operator on a tensor function and the nonlocal gradient operator on a vector function. Let \(\boldsymbol{\alpha }\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) be an antisymmetric vector two-point function. Given the tensor two-point function \({\varvec{\Psi}}:{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{m\times k}\) and the vector two-point function \({\varvec{v}}:{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\), the nonlocal divergence is defined by its action on \({\varvec{\Psi}}\) as
where\(\mathcal{D}\left({\varvec{\Psi}}\right)\left({\varvec{x}}\right) :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{m\times k}\). The action of the nonlocal adjoint operator \({\mathcal{D}}^{*}\) on \({\varvec{v}}\) is given by
where \({\mathcal{D}}^{*}\left({\varvec{v}}\right)\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right) : {\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\times {\mathbb{R}}^{k}\). The nonlocal gradient of \({\varvec{v}}\) is given by
where \(\mathcal{G}\left({\varvec{v}}\right)\left({\varvec{x}}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{m\times k}\). The action of the nonlocal adjoint operator \({\mathcal{G}}^{*}\) on \({\varvec{\Psi}}\) is given by
2.2 Interaction kernels and domains
In (7) and (8), the two-point vector functions \(\boldsymbol{\alpha }\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\) and \({\varvec{\beta}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\) are also known as the interaction kernels. In the context of Peridynamics, these kernels are assumed to have a finite domain that does not map to zero. Given two points \({\varvec{x}},{{\varvec{x}}}^{\prime}\in {\mathbb{R}}^{n}\), and \(\delta \in {\mathbb{R}}^{+}\), let \({\mathcal{B}}_{\delta }({\varvec{x}})\) be a ball or radius \(\delta\) centred at \({\varvec{x}}\), then for example, the interaction kernel \(\boldsymbol{\alpha }({\varvec{x}},{{\varvec{x}}}^{\prime})\) is nonzero only if \({{\varvec{x}}}^{\prime}\in {\mathcal{B}}_{\delta }({\varvec{x}})\), i.e.
where \(\delta\) is the interaction radius also known as the horizon in the context of PD. Interaction kernels that satisfy (12) are called truncated kernels [110] or localised kernels [111]. Another key concept that is connected to the notion of truncated kernels is the interaction domain. Let \(\Omega \subset {\mathbb{R}}^{n}\) be a bounded open set. The interaction domain \({\Omega }_{I}\) consists of points outside of \(\Omega\) that interact with points in \(\Omega\). Given the truncated interaction kernel \(\boldsymbol{\alpha }({\varvec{x}},{{\varvec{x}}}^{\prime})\), an interaction domain \({\Omega }_{I}\) is defined as
The interaction subdomain contains all the points \({{\varvec{x}}}^{\prime}\) in the complement domain \({\mathbb{R}}^{n}\backslash\Omega\) that interact with points \({\varvec{x}}\) in \(\Omega\). Many geometrical relationships exist between \(\Omega\) and \({\Omega }_{I}\) [109]. A typical such relationship is shown in Fig. 1.
2.3 Nonlocal interaction operators
Given a domain \(\Omega\), let \({\Omega }_{I}\) be the interaction domain associated with \(\Omega\) as defined in Sect. 2.2. Corresponding to the nonlocal divergence operator \(\mathcal{D}\left({\varvec{v}}\right)\left({\varvec{x}}\right)\), a point interaction operator \(\mathcal{N}\left({\varvec{v}}\right): {\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}\) is defined as
Corresponding to the nonlocal gradient operator \(\left(\eta \right)\left({\varvec{x}}\right)\), a point interaction operator \(\mathcal{S}\left(\eta \right)\left({\varvec{x}}\right) :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{m\times k}\) is defined as
2.4 Nonlocal integral theorem
A very important outcome of the nonlocal operators developed in the proceeding subsections is statement of the nonlocal Gauss theorem. Recall from (2) that
Consider the right-hand side of (16). If the kernel function \(\boldsymbol{\alpha }\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)\) is antisymmetric and (2) holds, then:
From (18) and considering (3), it can be deduced that \({\int }_{{\Omega }_{I}}\mathcal{N}\left({\varvec{v}}\right)\left({\varvec{x}}\right)\mathrm{d}{\varvec{x}}\) in (17) represents the flux from \(\Omega\) into \({\Omega }_{I}\). Thus, (17) is the mathematical statement of the nonlocal Gauss theorem which postulates that the integral of the nonlocal divergence of \({\varvec{v}}\) over \(\Omega\) is equal to the total flux exiting \(\Omega\) into \({\Omega }_{I}\).
We next consider the nonlocal analogue of integration by parts expressions involving the nonlocal divergence and gradient operators. Given the point functions \(u\left({\varvec{x}}\right):{\mathbb{R}}^{n}\to {\mathbb{R}}\) and \({\varvec{v}}\left({\varvec{x}}\right):{\mathbb{R}}^{n}\to {\mathbb{R}}^{m},\)
2.5 Nonlocal weighted operators
Since the classical continuum theory is a local theory, the functions utilised are point functions. This is not the case with peridynamics which is a nonlocal theory, hence some of the functions utilised are point functions while some are two-point functions. The differential operators defined in Sect. 2.1 are operators that act on two-point functions. To complete the definition of the nonlocal operators, another class of operators need to be defined that act on point functions.
Given the point function \({\varvec{u}} :{\mathbb{R}}^{n}\to {\mathbb{R}}^{k}\) and the point function\(v :{\mathbb{R}}^{n}\to {\mathbb{R}}\), let \(\omega \left({\varvec{x}},{{\varvec{x}}}^{\prime}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{+}\) and let the operators \(\mathcal{D}\) and \(\mathcal{G}\) be as defined in Sect. 2.1, then the weighted nonlocal divergence operator acting on \({\varvec{u}}\) is defined as
The weighted nonlocal gradient operator acting on \(v\) is defined as
The extended application of the weighted nonlocal divergence and gradient operators on tensor and vector fields, respectively, follows as in (8) and (10). In addition, as is with the unweighted nonlocal operators, adjoint operators can also be defined for the weighted nonlocal operators. Let \({\mathcal{D}}^{*}\) and \({\mathcal{G}}^{*}\) be as defined in Sect. 2.1 and \(\omega :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}\) be a non-negative symmetric function known as the weight function, then the action of the adjoint operator \({\mathcal{D}}_{\omega }^{*}\) corresponding to the nonlocal weighted divergence operator on \(v\) is defined as
The action of the adjoint operator \({\mathcal{G}}^{*}\) corresponding to the nonlocal weighted gradient operator \({\mathcal{G}}_{\omega }^{*}\) on \({\varvec{v}}\) is defined as
The relationship established between \(\mathcal{D}\) and \(-{\mathcal{G}}^{*}\) and between \(\mathcal{G}\) and \(-{\mathcal{D}}^{*}\) allows us to, respectively, write (21) and (22) as
and
Equations (25) and (26) serve to define two forms to each of the weighted nonlocal divergence and gradient operators, respectively, and have been shown to be equal [109]. For example, from (25), the first form of the weighted nonlocal divergence is given by
and the second form is given by
2.6 Nonlocal differential operators for peridynamic application
Often, the governing equations in the classical continuum theory are expression of physical balance laws that are composed of partial differential operators. Although the peridynamic theory as a nonlocal model replaces the spatial derivatives with integral operators, it can be shown to have retained the structure of the balance law in the classical theory. This is achieved by introducing nonlocal analogues of the differential operators used in the local theory. The nonlocal operators presented in Sect. 2 will be used to derive application specific to nonlocal differential operators and the generalised notion of nonlocal derivative for application in peridynamics. Let \(\omega :{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}\) be a non-negative weight function of compact support in \({\mathcal{B}}_{\delta }({\varvec{x}})\subset {\mathbb{R}}^{n}\) where \({\mathcal{B}}_{\delta }\left({\varvec{x}}\right)\) is a ball of radius \(\delta >0\) centred at \({\varvec{x}}\). Let a shape tensor [112] \(\mathbf{K}:{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}^{n\times n}\) be defined as
where \({{\varvec{\xi}}}_{{\varvec{x}}{{\varvec{x}}}^{\prime}}={{\varvec{x}}}^{\prime}-{\varvec{x}}\) and\({{{\varvec{x}}}^{\prime}\in \mathcal{H}}_{x}=\left\{{{\varvec{x}}}^{\prime}\in {\mathbb{R}}^{n} :\left|{{\varvec{x}}}^{\prime}-{\varvec{x}}\right|\le \delta \right\}\). Let \(\boldsymbol{\alpha }\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)={\varvec{\beta}}\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)={{\varvec{\xi}}}_{{\varvec{x}}{{\varvec{x}}}^{\prime}}{\mathbf{K}}^{-1},\) then the nonlocal unweighted and weighted divergence and gradient operators from (4), (6), (25) and (26) are, respectively, given as
where (32) and (33) appeared in [113] are defined as the notions of nonlocal material divergence and gradient operators, respectively. From (28), the second form of the weighted nonlocal divergence operator is
3 Peridynamic model
Peridynamics is a nonlocal alternative to the classical continuum mechanics developed in [45]. The objective was to create a nonlocal continuum theory that is capable of modelling both continuous and discontinuous material response in a single framework. This was achieved by replacing the differential operators in the equilibrium equation of motion of the classical continuum theory with an integral operator. Given a bounded open domain \(\Omega \in {\mathbb{R}}^{n}\), in peridynamics, a continuum point \({\varvec{x}}\in\Omega\) interacts with infinitely many other points located within its domain of influence. If this domain of influence is assumed to be a ball \({\mathcal{B}}_{\delta }({\varvec{x}})\) of radius \(\delta >0\) centred at \({\varvec{x}}\), then \(\delta\) is called the horizon of \({\varvec{x}}\), such that
where \({\mathcal{B}}_{\delta }({\varvec{x}})\) is called the family of \({\varvec{x}}\). Interaction between two points \({\varvec{x}}\) and \({{\varvec{x}}}^{\prime}\) is called a bond and the distance \(|{\varvec{\xi}}|=|{{\varvec{x}}}^{\prime}-{\varvec{x}}|\) in the undeformed reference configuration is called the bond length. The relative displacement \({\varvec{\eta}}\) in the deformed configuration is given by \({\varvec{\eta}}={\varvec{u}}\left({{\varvec{x}}}^{\prime},{\varvec{t}}\right)-{\varvec{u}}({\varvec{x}},{\varvec{t}})\), where \({\varvec{u}}\left({{\varvec{x}}}^{\prime},{\varvec{t}}\right)\) and \({\varvec{u}}({\varvec{x}},{\varvec{t}})\) are the displacements of material points at \({{\varvec{x}}}^{\prime}\) and \({\varvec{x}},\) respectively, at time \(t\).
In the original development [45] that came to be known as the Bond-Based Peridynamics, the force in each bond is a central force and each bond is independent of all other bonds. This lack of dependence limits the value of Poisson’s ratio to 1/3 for 2D and 1/4 for 3D isotropic solids. To circumvent this limitation and obtain a more general material model, State Based Peridynamics was developed. To pursue the development of the state-based peridynamics, [112] introduced mathematical objects called states which are functions defined on bonds in \({\mathcal{B}}_{\delta }\left({\varvec{x}}\right)\). To define the domain \(\mathcal{H}\) of the state, let \(\delta >0\) be the horizon of a point \({\varvec{x}}\) in a body \(\mathfrak{B}\), then:
is the family of bonds for the point \({\varvec{x}}\). Equation (36) allows for a more precise definition of a state. Let \({\mathcal{L}}_{m}\) be the set of all tensors of order \(m\), then a state of order \(m\) associated with the point \({\varvec{x}}\) is a function \(\underset{\_}{\mathbf{A}}\langle \bullet \rangle :\mathcal{H}\to {\mathcal{L}}_{m}\). Angle brackets are used to indicate the bond acted upon by the state. A state that maps vectors in \(\mathcal{H}\) to a scalar is called a scalar state. Similarly, a state that maps vectors in \(\mathcal{H}\) to vectors is called a vector state. The set of all states of order \(m\) is denoted by \({A}_{m}\), thus if the set of all scalar states is denoted as \(\mathcal{S}\), then \(\mathcal{S}={A}_{1}\) and similarly if the set of all vector states is denoted as \(\mathcal{V}\), then \(\mathcal{V}={A}_{2}\). Let \(\underset{\_}{\omega }\langle {\varvec{\xi}}\rangle\) be an influence function obtained when the scalar state \(\underset{\_}{\omega }\in \mathcal{S}\) acts on \({\varvec{\xi}}\), then the tensor product of two vector states \(\underset{\_}{\mathbf{A}}\in \mathcal{V}\) and \(\underset{\_}{\mathbf{B}}\in \mathcal{V}\) is defined as
Perhaps the most important state in the peridynamic formulation is the vector state and there are three important vector states that are worth mentioning here: the reference position vector state, deformation state \(\underset{\_}{\mathbf{Y}}\) and the force vector state \(\underset{\_}{\mathbf{T}}\).
The reference position vector state \(\underset{\_}{\mathbf{X}}\) is a function whose value is the bond it acts on. It is defined as
The reference position vector state can be thought of as an identity vector state since it simply output the value of its argument. The deformation state \(\underset{\_}{\mathbf{Y}}\) is a function operating on each bond length \({\varvec{\xi}}={{\varvec{x}}}^{\prime}-{\varvec{x}}\) in the family of point \({\varvec{x}}\), whose value is the image of the bond in the deformed configuration:
where \({{\varvec{y}}}^{\prime}\left({{\varvec{x}}}^{\prime},t\right)\) and \({\varvec{y}}\left({\varvec{x}},t\right)\) are, respectively, the coordinates of the points \({{\varvec{x}}}^{\prime}\) and \({\varvec{x}}\) in the deformed configuration at time \(t\). The force state \(\underset{\_}{\mathbf{T}}\) is a function that is associated with each bond in the family of point \({\varvec{x}}\) with some force density vector such that
A very import tensor (already introduced in Sect. 2.6) in the formulation of the state-based peridynamics is the shape tensor \(\mathbf{K}\). This tensor can also be defined using the notion of states. Following from (37), the shape tensor \(\mathbf{K}\) is defined as
where \(\underset{\_}{\mathbf{X}}\) is as defined in (38). Although vector state and second-order tensors both map vectors to vectors, they are essentially different. For example, a state is in general nonlinear in its argument and is infinite dimensional. In contrast, a second-order tensor is linear function of its argument and has a dimension of 9. It was, however, demonstrated in [31] that given a second-order tensor \({\varvec{\Phi}}\), it is possible to obtain a vector state through an expansion operation defined as
where \(\underset{\_}{\upepsilon }\left({\varvec{\Phi}}\right)\langle {\varvec{\xi}}\rangle\) is the vector state expanded from \({\varvec{\Phi}}\). Conversely, given a vector state \(\underset{\_}{\mathbf{A}}\in \mathcal{V}\), a second-order tensor can be obtained by a reduction operation defined as
The governing equation of motion in PD can be formulated using the nonlocal vector calculus presented in Sect. 2 based on a statement of balance law which postulates the dependence of the rate of change in the content of an extensive quantity over a given domain on the rate at which the quantity is produced within the domain and a flux through the boundary of the domain.
Let the region occupied by a body \(\mathcal{B}\) be given by the open domain \(\Omega \subseteq {\mathbb{R}}^{n}\). Let \(\stackrel{\sim }{\Omega }\subseteq\Omega\) be an open subregion, then a quantitative statement of a balance law for \(\Omega\) can be stated as
where (13) postulates that \(\mathcal{A}\left(\stackrel{\sim }{\Omega },{\varvec{q}}\right)\) (the time rate of change of the intensive quantity \({\varvec{q}}\)) is equal to \(\mathcal{P}\left(\stackrel{\sim }{\Omega }\right)\) (the rate at which the quantity is produced within the subdomain by sources) minus \(\mathcal{F}\left(\stackrel{\sim }{\Omega },{\mathbb{R}}^{n}\backslash \stackrel{\sim }{\Omega };{\varvec{q}}\right)\) (the rate at which the intensive quantity exit the subdomain). Let the quantity \(({\varvec{q}})\) to be balanced is the momentum density so that \({\varvec{q}}=\rho \dot{{\varvec{u}}}\) where \(\dot{{\varvec{u}}}\) is the velocity of a point in \(\stackrel{\sim }{\Omega }\) and \(\rho\) is the density of the material. Let \({\varvec{b}}\) denotes the rate of production of \({\varvec{q}}\) in \(\stackrel{\sim }{\Omega }\), then:
To obtain an expression for the rate at which the flux of \({\varvec{q}}\) exits the subdomain \(\stackrel{\sim }{\Omega }\), let \({\stackrel{\sim }{\Omega }}_{I}\subset\Omega\) be the domain interacting with \(\stackrel{\sim }{\Omega }\) as defined in (13), then:
Applying the nonlocal Gauss theorem (17), then (46) can be written as
Thus, (44) becomes
From localization theorem, (48) can be written as
From (34), (49) can be written as
where (50) follows from the antisymmetric property of \({\varvec{\xi}}\). From (42), the integrand of the integration in (50) can be understood to be a vector obtained when a vector state \(\underset{\_}{\upepsilon }\left(\omega{\varvec{\Psi}}{{\varvec{K}}}^{-1}\right)\) is expanded from a second-order tensor \(\omega{\varvec{\Psi}}{{\varvec{K}}}^{-1}\) acting upon the bond \({{\varvec{\xi}}}_{{\varvec{x}}{{\varvec{x}}}^{\prime}}\) or \({{\varvec{\xi}}}_{{{\varvec{x}}}^{\prime}{\varvec{x}}}\) as the case maybe. If we write
and since \(\boldsymbol{\alpha }\left({\varvec{x}},{{\varvec{x}}}^{\prime}\right)=0\) whenever \({{\varvec{x}}}^{\prime}\notin {\mathcal{B}}_{\delta }\left({\varvec{x}}\right)\), then (50) can be written as
Equation (52) is the state-based peridynamic equation of motion. \(\underset{\_}{\mathbf{T}}\left[{\varvec{x}},{\varvec{t}}\right]\) and \(\underset{\_}{\mathbf{T}}\left[{{\varvec{x}}}^{\prime},{\varvec{t}}\right]\) are the force states at \({\varvec{x}}\) and \({{\varvec{x}}}^{\prime},\) respectively. When these states act upon the bonds \({{\varvec{\xi}}}_{{\varvec{x}}{{\varvec{x}}}^{\prime}}\) and \({{\varvec{\xi}}}_{{{\varvec{x}}}^{\prime}{\varvec{x}}},\) respectively, the results are bond force density vectors acting at points \({\varvec{x}}\) and \({{\varvec{x}}}^{\prime},\) respectively. Notice that we still do not know what the second-order tensor \({\varvec{\Psi}}\) represents. Its identity can be established from a constitutive material model that will relate the bond force density to the displacement. This will be the subject of Sect. 3.2.
3.1 Nonlocal kinematic quantities
In this section, the nonlocal differential operators in Sect. 2.6 will be used to derive the expression of relevant kinematic objects that are nonlocal analogue of their counterparts in the local theory.
3.1.1 Gradient of the displacement and deformation vector fields
An important quantity in the formulation of continuum mechanics is the gradient of the displacement vector. Let \({\varvec{u}}\left({\varvec{x}},t\right)\) be the displacement of a point \({\varvec{x}}\) at time \(t\). Then, from (33), the gradient of the displacement field at \({\varvec{x}}\) as a function of the undeformed bond is given as
Another key kinematic quantity that plays an important role in the development of the state-based peridynamic theory is the concept of the deformation tensor. In the nonlocal peridynamic setting, the deformation tensor, denoted as, F, is the finite-dimensional equivalent of the deformation state. Let \({\mathcal{L}}^{+}\) be the set of all second-order tensors with positive determinants. Let \({\Omega }_{0}\) and \({\Omega }_{t}\) be the reference and deformed configuration of a body \(\mathfrak{B}\) undergoing deformation. Let \({\varvec{x}}\) be the position of a material point in \({\Omega }_{0}\) and \({\varvec{y}}\) be its position in\({\Omega }_{t}\). Let \(\mathbf{F}\in {\mathcal{L}}^{+}\) exists such that the deformed image of the bond \({{\varvec{\xi}}}_{{\varvec{x}}{{\varvec{x}}}^{\prime}}\) is given by
Using (33), the nonlocal material gradient of the deformation as a function of the undeformed bond is evaluated as
Equation (55) is the definition of the nonlocal deformation gradient given in [112]. We can further write (55) as
where the second equality follows from the linearity of the integral operator. Notice that the nonlocal deformation gradient is devoid of any notion of the local derivative operator which would have required that the deformation field be continuously differentiable (at least in a weak sense for the case of Finite-Element Method). In its present form, the deformation gradient is still defined in the presence of singularities such as cracks.
3.1.2 Nonlocal strain tensor
We can define the notion of strain by comparing the length of a bond before and after deformation. Let \({\varvec{\xi}}={{\varvec{x}}}^{\prime}-{\varvec{x}}\) and \({\varvec{\lambda}}={\varvec{y}}\left({{\varvec{x}}}^{\prime}\right)-{\varvec{y}}\left({\varvec{x}}\right)\), then from (38) and (54), we have
If we define a deformation or strain matrix \(\mathbf{E}\) as
then (57) can be written as
where \(\mathbf{E}\) is the nonlocal analogue of the Green–Lagrange strain tensor and \(\mathbf{F}\) is the nonlocal deformation gradient defined in (55). Considering (56), (58) can be written as
Following from the assumption of infinitesimal deformation where the displacement gradient is small, that is \(\left|{{\mathcal{G}}_{\omega }}_{{\varvec{x}}}\left({\varvec{u}}\left({\varvec{x}}\right)\right)\right|\ll 1\), we may neglect the nonlinear term in the definition of the Green–Lagrange strain tensor \(\mathbf{E}\) so that (60) reduces to
where \({\varvec{\varepsilon}}\) is the infinitesimal strain tensor and \({\mathcal{G}}^{s}\) denotes a symmetric tensor operator.
3.2 Constitutive model
We will now focus our attention on (51) and (52) to establish the relationship between kinetic and kinematic quantities and ultimately establish the identity of the tensor \({\varvec{\Psi}}\). Various attempts have been made to develop constitutive models for the peridynamic theory [112, 114,115,116,117,118,119,120]. These material models can broadly be grouped into bond-based, ordinary state-based and non-ordinary state-based models. Let \(W\left(\underset{\_}{\mathbf{Y}}\right):\mathcal{V}\to {\mathbb{R}}\) be the peridynamic strain energy density, then generally, for an elastic material, the force density state can be expressed [112] as
where \(\nabla W\left(\underset{\_}{\mathbf{Y}}\right)\) is the Fréchet derivative of \(W\left(\underset{\_}{\mathbf{Y}}\right)\) with respect to \(\underset{\_}{\mathbf{Y}}\). A correspondence constitutive model proposed in [112] will be used in this study. This material model is based on the non-ordinary state-based framework that allows for the adaptation of the classical continuum model into peridynamics. A key motivation for this choice is to take advantage of decades of development and calibration of the classical model.
In the correspondence model, \(W\left(\underset{\_}{\mathbf{Y}}\right)\) is assumed to be equal to the strain energy density \(\Omega \left(\mathbf{F}\right):{\mathcal{L}}_{2}\to {\mathbb{R}}\) from the classical theory where the deformation gradient \(\mathbf{F}\) from the local theory is approximated by its nonlocal counterpart given by (55). So that (62) becomes
Evaluating the Fréchet derivative in (63) is shown [112] to result in the expression
where \({\varvec{P}}\) is the first Piola stress tensor. Comparing (64) to (42), it can be deduced that the force state \(\underset{\_}{\mathbf{T}}\) is a state expanded from the tensor \(\underset{\_}{\omega }\left(\left|{{\varvec{\xi}}}_{{\varvec{x}},{{\varvec{x}}}^{\prime}}\right|\right)\mathbf{P}{\mathbf{K}}^{-1}\), i.e.
Comparing (51) and (65) shows that
Thus, in compact notation, the state-based peridynamic balance of linear momentum can be written as
To complete the definition of the nonlocal problem, we need to apply appropriate constraints to certain region of the problem domain. To this end, let the interaction domain \({\Omega }_{I}={\Omega }_{c}\) be the constrained volume. Let \({\Omega }_{c}\) splits into two disjoint subdomains \({\Omega }_{cd}\) and \({\Omega }_{cn}\) such that \({\Omega }_{cd}\cap {\Omega }_{cn}=\varnothing\) and either of \({\Omega }_{cd}\) and \({\Omega }_{cn}\) could be an empty set. \({\Omega }_{cd}\) is the subdomain where Dirichlet boundary condition is applied and \({\Omega }_{cn}\) is the subdomain where Neumann boundary condition is applied. Analogous to the boundary value problem of the classical local theory, constraint on the solution \({\varvec{u}}\) of (49) over \(\Omega\) is applied as follows: a given function value \({{\varvec{g}}}_{d}\) is prescribed on the solution over \({\Omega }_{cd}\) such that
To prescribe the Neumann-type constraint, recall that in the classical boundary value problem, this involves prescribing a traction or flux density \({\varvec{\sigma}}\bullet {\varvec{n}}\) over the traction boundary. From (18) and the discussion that follows, the nonlocal flux density over \({\Omega }_{In}\) is given by \({\int }_{{\Omega }_{I}}{\mathcal{N}}_{\omega }\left(\mathbf{P}\right)\left({\varvec{x}}\right)d{\varvec{x}}\). Let \({{\varvec{g}}}_{n}\) be a given function value of the flux density over \({\Omega }_{cn}\), the Neumann constraint can be stated as
The presence of the second-order time derivative of the solution \({\varvec{u}}\) in (67) means in addition to the boundary constraints (68), (69), initial conditions also need to be specified. The initial condition involves prescribing the initial values of the solution and its first derivative. Let \({{\varvec{u}}}_{I}\) and \({\dot{{\varvec{u}}}}_{I}\) be the initial values of \({\varvec{u}}({\varvec{x}})\) and \(\dot{{\varvec{u}}}\left({\varvec{x}}\right),\) respectively, then
and
are the initial conditions. So that (67)–(71) gives the complete definition of the nonlocal problem:
Notice that the constraints (68) and (69) are prescribed over domains \({\Omega }_{cd}\) and \({\Omega }_{cn}\) that have positive volume in \({\mathbb{R}}^{n}\). This contrasts with the classical local theory where constraints are applied on domains that have zero volume. For this reason, (72) is referred to as initial volume constraint problem.
3.3 Discretization of the Peridynamic model
As can be seen from (72), the governing equation of motion in Peridynamics gives rise to a continuum model. To be amenable to computer implementation, different numerical approximation schemes have been proposed such as the meshfree method [121, 122], the collocation methods [123, 124] and methods based on finite-element mesh [125, 126]. Due to its simple implementation algorithm and relatively low computational cost, the meshfree method suggested in [121] is the most widely used [127] and is the preferred method in this work for these same reasons. In this approximation method, the discrete form of (52) is
where \({\rho }_{i}:=\rho ({{\varvec{x}}}_{i})\), \({\ddot{{\varvec{u}}}}_{{\varvec{i}}}=\frac{{\partial }^{2}{{\varvec{u}}}_{i}}{\partial {t}^{2}}\) with \({{\varvec{u}}}_{i}:={\varvec{u}}({{\varvec{x}}}_{i})\) and \(N\) is the number of nodes in the neighbourhood of node \(i\).
4 Peridynamic homogenization theory
The homogenization procedure developed in this work is a two-scale scheme: a microscopic scale represented by an RVE, and a macroscopic scale represented by a homogeneous effective medium. The constitutive law of the microscale model is assumed to be explicitly known at every point of the micro-domain while the constitutive law of the micromodel is not known everywhere. The objective is to retrieve a constitutive law of the macroscale substitute medium from a numerical solution of an initial volume constraint problem (IVCP) at the level of the underlying microstructure. In this multiscale framework, an RVE is assigned to each integration point of the macro-continuum. A peridynamic equilibrium solution of the RVE is sought using boundary condition generated by the macroscale deformation gradient. The solution of the RVE IVCP yields the microscale stress field which is then homogenised to produce macroscale stresses and associated material tangent tensor. The coupling of the micro- and macroscale is achieved through averaging relationships and the energetic equivalence statement of the Hill–Mandel micro-homogeneity condition.
4.1 Effective material constants
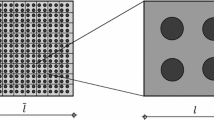
Consider a heterogeneous medium \({\mathfrak{B}}^{o}\) with characteristic size of heterogeneities to be \({l}_{\mathrm{hetro}}\). Momentarily, let this medium be replaced by a homogeneous ‘effective’ medium \({\mathfrak{B}}^{h}\). The original heterogeneous medium is the microscale, and the geometrical arrangement and material characteristics of the heterogeneities constitute the microstructure while the effective medium is the macroscale. Define a grid on \({\mathfrak{B}}^{h}\) and let each point \(\overline{{\varvec{x}} }\) on this grid be associated with a neighbourhood \({\Omega }_{s}\). Let \({\Omega }_{s}\) be bounded by a region \({\Omega }_{c}\) of positive volume in\({\mathbb{R}}^{n}\). Let a sample of \({\mathfrak{B}}^{h}\) occupying the regions \({\Omega }_{s}\) and \({\Omega }_{c}\) be denoted as \({\Omega }_{s}^{0}\) and \({\Omega }_{c}^{o}\), respectively. In addition, let a sample of \({\mathfrak{B}}^{o}\) occupying \({\Omega }_{s}\) be denoted as \({\Omega }_{s}^{o}\) as shown in Fig. 2.
Now, define a grid on \({\Omega }_{s}\) and let the position of points on this grid in the reference configuration be denoted as \({\varvec{x}}\). The grid associated with \(\overline{{\varvec{x}} }\) is called the macroscale and the grid associated with \({\varvec{x}}\) is the microscale. Let the characteristic lengths associated with the macroscale and the microscale be \({l}_{\mathrm{macro}}\) and \({l}_{\mathrm{micro}}\), respectively. The morphology and material properties of the constituents of \({\mathfrak{B}}^{o}\) in the microscale are called the microstructure of \({\mathfrak{B}}^{h}\). If \({\Omega }_{s}^{\mathrm{o}}\) exists such that
then \({\Omega }_{s}^{\mathrm{o}}\) is referred to as a Representative Volume Element (RVE) associated with the macro-point \(\overline{{\varvec{x}} }\) where (74) is the statement of the principle of separation of scale. This principle requires that the scale of the microstructure (or fluctuation of micro-field such as stress and strain) should be much smaller than the size of the RVE considered which in turn should be much smaller than the characteristic length scale of the macro-domain (or fluctuation of macro-field variables).
Let \({\mathfrak{B}}^{h}\) be subjected to an affine deformation at its boundary. This will produce a homogeneous strain \(\overline{{\varvec{\varepsilon}} }\) (for small deformation). This homogeneous strain will in turn generate a homogeneous stress field \(\overline{{\varvec{\sigma}} }\) everywhere in \({\mathfrak{B}}^{h}\). For simplicity, we will assume linear elastic material response in both scales, then the material model that relates \(\overline{{\varvec{\sigma}} }\) and \(\overline{{\varvec{\varepsilon}} }\) given by the generalised Hooke’s law:
is the effective or homogenised constitutive law, where \({\mathbb{C}}^{*}\) and \({\mathbb{S}}^{*}\) are the effective stiffness and compliance tensors, respectively. At the microscale, the constitutive relation in each phase of the microscale is given by
If the condition for the existence of the RVE is satisfied (henceforth, this condition will be assumed to be satisfied), then the microscopic deformation will be assumed to admit the following decomposition:
where \({{\varvec{u}}}^{\boldsymbol{*}}\left({\varvec{x}}\right)\) is the displacement fluctuation due to the presence of the microstructure and \({{\varvec{\varepsilon}}}^{\boldsymbol{*}}={\mathcal{G}}_{{\varvec{x}}}{{\varvec{u}}}^{\boldsymbol{*}}\left({\varvec{x}}\right)\).
4.2 Micro–macroscale transition
4.2.1 Average theorems
The transition of mechanical properties from the microscale to the macroscale is achieved using volume average relations. Let \(\psi\) be a quantity defined over a domain \(\Omega\). We denote the volume average of \(\psi\) over \(\Omega\) as
where \({V}_{\Omega }\) is the volume associated with \(\Omega\).
Theorem 4.1
Nonlocal average stress theorem. Let \(\mathfrak{B}\) be a heterogeneous body occupying the region \(\overline{\Omega }={\Omega }_{\mathrm{s}}\bigcup {\Omega }_{c}\) where \({\Omega }_{\mathrm{s}}\) is the region where solution is sought and \({\Omega }_{c}\) is the boundary volume. We denote the average stress and average strain over \({\Omega }_{s}\) as \(\langle {\varvec{\sigma}}\rangle\) and \(\langle {\varvec{\varepsilon}}\rangle\), respectively. Let \(\mathfrak{B}\) be in a state of static equilibrium when a constant stress tensor \(\overline{{\varvec{\upsigma}} }\) is applied on the boundary volume \({\Omega }_{c}\), then the volume average of the stress field in \({\Omega }_{\mathrm{s}}\) is equal to \(\overline{{\varvec{\upsigma}} }\), that is
Proof
From (67), static equilibrium of the RVE in the absence of body forces requires the divergence of the Cauchy stress tensor in the case of small deformation to vanish, that is
The Cauchy stress field in \({\Omega }_{s}\) can be written as
Taking the volume average of (81) and utilising (20) yields
Considering the relationship \({\mathcal{D}}_{\omega }=-{\mathcal{G}}_{\omega }^{*}\) and utilising (80), then (82) reduces to
Theorem 4.2
Nonlocal average strain theorem. Let \(\mathfrak{B}\) be as defined in Theorem 4.1. If \(\mathfrak{B}\) is subjected to applied displacement on the boundary volume \({\Omega }_{c}\) generated by a constant strain tensor \(\overline{{\varvec{\varepsilon}} }\) such that \({{\varvec{u}}}^{0}=\overline{{\varvec{\varepsilon}}}{\varvec{x} }\) for all \({\varvec{x}}\in {\Omega }_{c}\), then the average of the infinitesimal strain field \({\varvec{\varepsilon}}({\varvec{x}})\) (for all \({\varvec{x}}\in {\Omega }_{\mathrm{s}}\)) is equal to \(\overline{{\varvec{\varepsilon}} }\), that is
Proof
From (78), the volume average of the strain field over \(\Omega\) is given by
This implies that the volume average of the strain field is completely defined in terms of the strain at the boundary volume.
4.2.2 Macrohomogeneity condition
For the averaged fields \(\langle {\varvec{\sigma}}\rangle\) and \(\langle {\varvec{\varepsilon}}\rangle\) to be admissible variables in the macroscale constitutive relation, the so-called Hill–Mandel macrohomogeneity condition [128] must be satisfied. The macrohomogeneity condition provides the basis for the substitution of an initially heterogeneous medium with a homogeneous one. This is achieved by prescribing an energetic equivalence between the heterogenous medium and the homogeneous substitution medium. Let the strain energy density of the underlying classical continuum material be
then invoking the principle of constitutive correspondence allows us to write the strain energy of the peridynamic model as (85). The macrohomogeneity condition is stated as
In other words, the condition requires that the average strain energy of the heterogeneous medium be equal to the strain energy density of the homogeneous medium. The condition under which (86) is satisfied for a peridynamic continuum material under constitutive correspondence will be established through a nonlocal analogue of the Hill’s lemma.
Theorem 4.3
Nonlocal Hill’s lemma: Consider the body defined in Theorem 4.1. Let \({\sigma }_{ij}\) and \({\varepsilon }_{ij}\) be the stress and strain field in \(\mathfrak{B}\) under prescribed boundary traction or boundary displacement, then
is the nonlocal Hill’s lemma.
Proof
We can write the scalar product of the average of the stress and strain tensor as
Thus, we can rewrite (86) as
which proves (87). It is obvious from (87) that for the Hill–Mandel condition, (86) to be satisfied will require that
Thus, the satisfaction of the Hill–Mandel macrohomogeneity condition requires the integral in (89) to vanish.
4.2.3 RVE boundary volume constraints
In the classical continuum framework, the satisfaction of (89) is traditionally achieved in one of the following ways: (1) Voigt (or Taylor) assumption, (2) Reuss (or Sachs) assumption, (3) Homogeneous displacement, (4) Prescribed periodicity in displacement, (5) Homogeneous stress, and (6) Prescribed periodicity in traction. Methods 1–3 are categorised as deformation-driven approaches while methods 4–6 are categorised as stress-driven approaches. The task now is to establish the boundary requirements that will make the lemma (87) satisfy the Hill–Mandel condition in the nonlocal framework using the methods 1–6.
Voigt (Taylor) model
In this method [129], (89) is satisfied by assuming a homogeneous deformation of the form \({u}_{i}={x}_{j}{\overline{\varepsilon }}_{ij}\) in \(\overline{\Omega }\). This implies a constant strain field \({\varvec{\varepsilon}}\left({\varvec{x}}\right)=\overline{{\varvec{\varepsilon}} }\) in the RVE. Inserting this assumption into (75) yields
From (90), the implication of the Taylor (Reuss) assumption is that the homogenised or effective stiffness tensor is simply the volume average of the stiffness tensor of the constituents. It will also be noticed that utilising the Taylor assumption means, we can obtain the effective material properties without the need to solve the microscale peridynamic (RVE) problem.
Reuss model
In this model [130], (89) is verified by assuming a constant stress \({\varvec{\sigma}}\left({\varvec{x}}\right)=\overline{{\varvec{\sigma}} }\) in \(\overline{\Omega }\). If this assumption is inserted into (75) yields
thus meaning that the effective compliance tensor is simply the volume average of the compliance tensor of the constituents. As with the Voigt model, the utilisation of the Reuss assumption allows the determination of the effective properties without recourse to solving the microscopic peridynamic (RVE) model.
Constant traction boundary volume constraint (CTVBC)
One way of satisfying (89) is to prescribe appropriate traction on the boundary volume \({\Omega }_{c}\). A traditional way of achieving this in the classical continuum framework is by applying the so-called constant traction boundary condition. In the nonlocal framework, this is achieved by imposing on the boundary volume \({\Omega }_{c}\), a constant traction generated by constant stress field
Substituting (92) into (89) will vanish the boundary volume integral and, therefore, satisfying the Hill–Mandel condition (86).
Linear displacement boundary volume constraint (LDBVC)
This boundary condition is also referred to as homogeneous boundary condition in the literature. This boundary condition is achieved by applying appropriate displacement field to the boundary of the RVE that will varnish the gradient of the displacement terms of the integrand of the boundary volume integral (89). A traditional way of achieving this is to apply a linear displacement of the form
Inserting (93) into (89) yields
Thus, proving (93) satisfies the Hill–Mandel condition (86).
Periodic boundary volume constraint (PBVC)
This model is appropriate to model materials with periodic microstructure. The reference configuration of the RVE is assumed to be a geometric shape with even number of sides or faces for two- and three-dimensional problems, respectively. A square RVE is shown in Fig. 2 for two-dimensional problems, with each pair \(i\) of the RVE boundary region assumed to be equally sized subsets, that is, there should be a one-to-one correspondence between points in \({\Omega }_{i}^{+}\) and \({\Omega }_{i}^{-}\).
In this method, a displacement field of the form (77) is applied on the boundary region such that for each pair of boundary points \(({{\varvec{x}}}^{+}\in {\Omega }_{i}^{+},{{\varvec{x}}}^{-}\in {\Omega }_{i}^{-})\):
The difference in displacement between two corresponding boundary points \({{\varvec{x}}}^{+},{{\varvec{x}}}^{-}\) is then given by
To achieve static equilibrium of the RVE, an anti-periodic stress field is applied in the boundary domain such that
for each pair of points in \({\Omega }_{i}^{+}\) and \({\Omega }_{i}^{-}\).
Utilising (95) and (96), the Hill–Mandel condition is satisfied as follows:
4.2.4 Bounds for effective properties
Predictions from the Voigt and Reuss assumptions were shown in [131] to provide the upper and lower bounds for the effective material properties. That is,
where \({\mathbb{C}}^{*R}\), \({\mathbb{C}}^{*V}\) are the effective stiffness tensors due to Reuss and Voigt assumptions, respectively, and \({\mathbb{C}}^{*}\) is the effective stiffness due to any other method. As emphasised in [132], the corresponding entries of \({\mathbb{C}}^{*R}\), \({\mathbb{C}}^{*}\) and \({\mathbb{C}}^{*V}\) do not necessarily satisfy (97), however, the corresponding diagonal terms and eigenvalues are shown to satisfy (97). It can also be shown that the inequality (97) hold true in terms of elastic constants such as bulk and shear moduli. Consider a given strain tensor \({\varepsilon }_{kl}\) at a point, the stress \({\sigma }_{ij}\) acting at the point for a linear 2D isotropic media undergoing small deformation is given by (96) and the fourth-order isotropic tensor \({\mathbb{C}}_{ijkl}\) can be written as
where \(\kappa\) and \(\mu\) are the bulk and shear moduli, respectively. If we define two fourth-order isotropic tensors \({I}_{1}\) and \({I}_{2}\) as
then (98) can be written as
It can be shown from (100) that the compliance tensor can be written as
For the sake of brevity, we will adopt a symbolic notation that will allow us write (100) and (101) as
Given a two-phase composite having constituent material constants \({\kappa }_{0}\), \({\kappa }_{1}\), \({\mu }_{0}\) and \({\mu }_{1}\) and volume fractions \({c}_{0}\) and \({c}_{1}\) such that \({\kappa }_{1}>{\kappa }_{0}\) and \({\mu }_{1}>{\mu }_{0}\), then the volume average of the stiffness and compliance tensor can be written as
Utilising (102) and (103) in (97), it can easily be shown that
It follows from (104) that
and
where the left-hand sides of (105) and (106) give the Reuss lower bound while the right-hand sides give the Voigt upper bound, and \({\kappa }^{*}\) and \({\mu }^{*}\) and the 2D effective bulk and shear moduli. It is noted that the distance between the Reuss lower bound and the Voigt upper bound is large and often does not give much information, a tighter bound is achieved using the Hashin–Shtrikman bounds [133]:
and
4.3 Computational implementation of the PDCHT
To obtain the numerical solution of the RVE in the PDCHT framework, the RVE will be discretised following the procedure outlined in Sect. 3.3. Being a nonlocal problem, the RVE is subjected to appropriate volume constraints. In the numerical validation that follows in Sect. 5, the RVEs will be subjected to LDBVC and PBVC. Although computational algorithm to implement these boundary conditions in the framework of finite-element analysis is well established and discussed by many authors [134,135,136,137], however, implementing them in a nonlocal boundary value constraint problem such as the RVE in the PDCHT framework require special treatment. This is particularly the case with the PBVC. To implement the PBVC in the PDCHT framework, the displacement-driven approach to homogenization is utilised in this work and thus, to determine the effective elasticity tensor, the first of (75) is employed. Combining this with (79) and (84) allows us to write the expression for the effective elasticity tensor as
where the stress field \({\sigma }_{ij}\) in \({\Omega }_{s}\) is obtained using discretised peridynamic equation of motion (73) and \({\overline{\varepsilon }}_{kl}\) is the prescribed strain tensor on the boundary volume. For a two-dimensional problem, \({\mathbb{C}}_{ijkl}^{*}\) has six components. However, owing to its symmetric property, only three components are independent. Thus, to determine the components of \({\mathbb{C}}_{ijkl}^{*}\) for a two-dimensional problem requires the application of three loading conditions that results in deformation modes which render all but one of the three independent components of the strain tensor to zero. For the purpose of this implementation, these deformation modes are given as
where \(c\) is the magnitude of the prescribed strain tensor. These strains are then used to generate displacement in the boundary volume depending on the boundary condition used. In the case of LDBC, the displacement \({\varvec{u}}\) generated at every node \({{\varvec{x}}}_{i}\) in the boundary volume after discretization of the RVE follows from (93) as
where \({\alpha }_{i}\) and \({\beta }_{i}\) are the components of the coordinates of \({{\varvec{x}}}_{i}\) in the first and second reference direction, respectively. To implement the PBC, nodes in the boundary volume are broadly grouped into ‘facial’ nodes and ‘corner’ nodes. Thus, from Fig. 3, all nodes in boundary sub-volumes \({\Omega }_{1}^{-}\), \({\Omega }_{1}^{+}\), \({\Omega }_{2}^{-}\) and \({\Omega }_{2}^{+}\) are facial nodes while those in \({\Omega }_{3}^{-}\), \({\Omega }_{3}^{+}\), \({\Omega }_{4}^{-}\) and \({\Omega }_{4}^{+}\) are corner nodes. If we write (95) in expanded form for two-dimensional space, we have
for every pair of points in the i-th pair of two opposite parallel faces. Applying (101) to facial pairs \({\Omega }_{1}^{-}\), \({\Omega }_{1}^{+}\), \({\Omega }_{2}^{-}\) and \({\Omega }_{2}^{+}\) results in the following relative displacement boundary constraints:
With the group of equations in (102)-(a) associated with the pair \({\Omega }_{1}^{-}\), \({\Omega }_{1}^{+}\) and the group (102)-(b) associated with the pair \({\Omega }_{2}^{-}\) and \({\Omega }_{2}^{+}\), respectively, it will be noticed that each corner volume is shared by two facial volumes and applying (102) to nodes within these boundary volumes will lead to over constrained boundary. To eliminate this problem, the following translational periodicity is imposed at the corner boundary volumes: if we write \({\Omega }_{3}^{-}={\Omega }_{1}^{c}\), \({\Omega }_{3}^{+}={\Omega }_{2}^{c}\), \({\Omega }_{4}^{-}={\Omega }_{3}^{c}\) and \({\Omega }_{4}^{+}={\Omega }_{4}^{c}\), then volumes \({\Omega }_{1}^{c}\) and \({\Omega }_{2}^{c}\) are assumed to be images of \({\Omega }_{3}^{c}\) under horizontal and vertical translational symmetry, respectively, while \({\Omega }_{4}^{c}\) is the image of \({\Omega }_{3}^{c}\) under combined horizontal and vertical symmetry so that the following relative displacement constraints are imposed between nodes in the corner boundary volumes:
and
To eliminate translational rigid body motion of the RVE, nodes within the corner volume \({\Omega }_{3}^{c}\) are constrained. The determination of the effective elastic tensor in both problems proceeds under the assumption of small deformation and plane stress. This allows the use of infinitesimal strain tensor and Cauchy stress tensor directly in (64). Once the Cauchy stress field in the RVE is obtained, (98) is used to recover the effective elasticity tensor.
5 Validation of the homogenization scheme
Having established and justified the peridynamic correspondence homogenization theory (PDCHT) in Sect. 4, numerical examples are presented in this section to benchmark the scheme against the Reus–Voigt and Hashin–Shtrikman bounds discussed in Sect. 4.2.3. Prediction from the PDCHT would also be compared against predictions from other classical mean-field homogenization methods such as the Eshelby dilute estimate [138] and the Mori–Tanaka method [139]. In addition, the result from the PDCHT will be compared to result obtained from computational homogenization based on the Finite-Element Analysis. After validation of the PDCHT strategy, the framework will be used to predict the effective properties given elliptical inclusion to observe the influence of inclusion shape on the effective properties predicted by the method. All materials considered throughout this section are assumed to be two-phased consisting of a matrix phase and a stiffer fibre phase (inclusion). Properties associated with matrix will be denoted with the superscript \(\left(m\right)\) while those associated with the fibre phase will be denoted with superscript \(\left(f\right)\). Both matrix and fibre phases are assumed to be isotropic under isothermal linear elasticity.
To pursue the objectives of validating the proposed method, three numerical examples will be considered. Figure 4 shows the RVE configurations to be considered in this section, and the properties of the constituent materials for the RVEs to be considered in the numerical examples are given in Table 1.
5.1 Comparing the PDCHT results with bounding theorems and other established methods
In this example, effective properties predicted from the PDCHT will be compared against computational result from the bounding theorems of Reuss, Voigt and Hashin–Shtrikman, the mean-field methods of Eshelby and Mori–Tanaka as well as the full-field method based on the finite-element analysis as done by the authors. The material is assumed to be a glass in epoxy-matrix composite with properties given in Table 1 under a plane strain condition. The RVE geometry is assumed to consist of epoxy matrix with a circular glass fibre centrally placed as shown in Fig. 4a. The problem is solved over the range of all admissible fibre volume fractions 0–100%. Solutions will be sought considering LDBVC and PBVC. Results from the computations are presented as follows.
The predicted evolution of the effective elastic stiffness tensor and corresponding effective elastic constants from PDCHT, the bounding theorems and other established methods are presented in Figs. 5 and 6, respectively, for the case of LDBVC. Similar analysis with the same RVE subjected to PBVC is conducted and the results are presented in Figs. 7 and 8 representing the evolution of the effective stiffness tensor and elastic constants, respectively.
Prediction from PDCHT of the effective stiffness tensors presented in Figs. 5 and 7 lie within the Reuss–Voigt bound as well as the tighter Hashin–Shtrikman bound thus satisfying (97). Similar agreement with the bounding theorems is observed with prediction of the effective bulk and shear moduli as presented in Figs. 6 and 8 thus satisfying (105) and (106) for the Reuss–Voigt bounds and (107)–(108) for the Hashin–Shtrikman bounds. This is true for both the predictions under LDBVC and PBC. Another consequence of the bounding Eqs. (97), and (105)–(108) is that the elastic modulus from any proposed homogenization theory is predicted to lie within the Reuss–Voigt and Hashin–Shtrikman bound. The evolution of the effective elastic modulus obtained from the proposed theory indeed lies within these bounds as shown in Figs. 6c and 8c for LDBVC and PBVC, respectively.
The result of prediction from the PDCHT is also compared to predictions from the mean-field homogenization methods of Eshelby and Mori–Tanaka as well as a full-field computational method based on FEM solution of the RVE. The results from these methods are also presented in Figs. 5, 6, 7 and 8. The predictions from both the PDCHT and FEM comply with the bounding theorems and compared to predictions from the Mori–Tanaka method, the PDCHT prediction gives an upper estimate of the effective properties. It is worthy to note that the prediction in this example from the Mori–Tanaka method coincide with those from the Hashin–Shtrikman lower bound. This is the case in some situations and has been reported in the literature [González]. Predictions from the Eshelby dilute method agrees with results from the PDCHT only for very low fibre volume fraction. This is an expected trend as the dilute method is expected to give reasonable predictions only for very low (dilute) fibre volume fraction.
Since the fibre is assumed to be of circular cross-section, it can be shown that the maximum volume fraction that can be achieved with a perfectly circular fibre cross-section is \(78.54\%\). Beyond this volume fraction, the circular geometry of the fibre cross-section degenerates and thereby causes a change in the morphology of the RVE. This change in morphology is reflected in the results predicted from the PDCHT and FEM solutions of the RVE and expectedly not the bounding theorems as shown in Figs. 5, 6, 7 and 8. A comparison of the predicted effective elastic modulus obtained using both LDBVC and PBVC as shown in Fig. 9 shows that the prediction using the LDBVC provides an upper estimate of the two boundary conditions at least within the small deformation regime. This is a tested and proven result from the literature [132, 140, 141].
5.2 Comparing the PDCHT results with results from published works
The objective in this example is to compare predictions from the proposed PDCHT with experimental results from [142] and computational predictions from the following references: [105, 108, 143,144,145]. The RVE is assumed to be a square array of circular shaped boron fibre placed in the centre of aluminium matrix as shown in Fig. 4a. The properties of boron and aluminium are given in Table 1. The RVE volume-constrained problem is solved under the assumption of plane stress and PBVC.
Prediction of effective elastic properties of the composite system from the PDCHT is presented in Table 2 alongside results from some published references. Analysis of the results shows that the prediction from PDCHT provides the closest correlation to the experimental result from [142] in the estimate of the effective elastic and shear moduli. Compared to other computational methods, prediction of these moduli from the PDCHT gives the lower estimates. However, the effective Poisson’s ratio \({\nu }_{12}=0.185\) predicted by the PDCHT is markedly different from the experimental result but agree well with predictions from the FEM, OSBPDHT, FEM, PD UC and LTEHOT.
5.3 Effective properties of RVE with elliptical fibre inclusion
In this example, two RVEs, the first with circular and the second with elliptical fibre inclusions as shown in Fig. 4a and b, respectively, will be considered. Two composites will be considered. The first is a glass in aluminium-matrix composite and the second is a graphite in aluminium-matrix composite with material properties as given in Table 1. The stiffness ratio (or phase contrast) \(\varphi\) (\(\varphi :={E}_{\left(f\right)}/{E}_{\left(m\right)}\)) of the first material is \(1.07\) while that of the second material is \(3.44\). The objective in this example is to briefly demonstrate the capability of the PDCHT in capturing the effect of inclusion shape and phase contrast on the effective behaviour of materials using the LDBVC.
The evolution of the normalised effective elasticity modulus (effective stiffness ratio) \({\varphi }_{i}^{*}={E}_{i}^{*}/{E}_{i\left(m\right)}\) with respect to fibre volume fraction \({c}_{\left(f\right)}\) for RVEs with both circular and elliptical inclusion for the two materials alongside results from FEM simulation of the same problems are presented in Fig. 10. In Tables 3, 4, 5 and 6, the evolution of the elastic modulus in directions \(1\) and \(2\) as well as the percentage difference between predictions from PDCHT and FEM are presented.
From the result presented for predictions from both PDCHT and FEM, the effective material behaviour as represented by the evolution of the effective elastic modulus for the RVE with circular inclusion shows linear behaviour for low material phase contrast \(\left(\varphi =1.07\right)\) and weak nonlinear behaviour for higher material phase contrast \(\left(\varphi =3.44\right)\). In the case of RVE with elliptical inclusion, the result for lower material phase contrast shows linear behaviour while the effective material behaviour at higher material phase contrast shows strong nonlinear behaviour. The amplified nonlinearity is because the elliptical inclusion introduces an anisotropy in the microgeometry of the composite. In addition, the prediction of effective material properties for RVEs with circular inclusion from Tables 2 and 3 shows an isotropic effective material response while predictions for RVEs with elliptical inclusion shows an orthotropic effective material behaviour.
Comparing the results from the PDCHT and FEM, it is noted that at lower material phase contrast, the predicted effective behaviour from the two methods shows good agreement for both inclusion shapes especially at low material phase contrast. The maximum percentage difference in the estimated results from these methods is \(0.421\%\) for circular inclusion and \(0.45\%\) for elliptical inclusion. However, at higher material phase contrast \((\varphi =3.44)\), the maximum percentage difference raises to \(6.55\%\) for circular inclusion and \(9.2\%\) in the case of elliptical inclusion, with the predictions from the PDCHT yielding more nonlinear behaviour with increasing material phase contrast. This nonlinear effective material behaviour is an expected prediction and has been reported in literature [146]. In addition, the difference in result between the PDCHT and FEM predictions at high material phase contrast also did not come as a surprise because it has been reported in the literature [147, 148] that marked difference between different homogenization approaches at high stiffness ratio have been observed.
6 Conclusion
This paper presented a first-order homogenization theory in the framework of the non-ordinary state-based correspondence model. The development of the theory is set on a rigorous mathematical framework consistent with the nonlocal nature of the peridynamic theory. Using this homogenization theory, it is now possible to obtain microstructure informed properties of materials for use at the macroscale within the framework of peridynamic modelling. The proposed nonlocal homogenization theory is validated by solving benchmark problems and comparing the results with those obtained using the Reuss, Voigt and Hashin–Shtrikman bounding theorems, the mean-field methods of Eshelby and Mori–Tanaka as well as the finite-element method. These results are shown to comply with the bounding theorems as well as agree with results from the mean-field and full-field methods mentioned above.
Comparison of predictions from the proposed homogenization framework with results from the literature shows good agreement. Lastly, the PDCHT has been shown to be capable of capturing interesting material behaviour some of which have been reported in the literature such as the effect of change in the effective material property when the morphology of the RVE changes as illustrated in the first example. This effect was demonstrated more elaborately in the third example by comparing the prediction for RVEs with circular and elliptical shaped inclusion. The proposed method was also shown to be able to capture the effect of material phase contrast on the effective behaviour of the composite system.
The advantage of PDCHT theory over homogenization frameworks based on the classical continuum theory derives from the strengths of the peridynamic theory. This framework is, therefore, especially useful in circumstances involving evolution of the microstructure or problems in which nonlocal interaction plays important role in the overall response of the heterogenous media. Another advantage that can be leveraged with this development is that because the peridynamic correspondence model uses familiar quantities from the classical continuum theory, Once the effective material tangent is obtained, we are free to use either of peridynamic theory or the classical continuum theory to characterise the macroscopic response of the medium. Where the peridynamic theory is utilised at the macroscale, this result in a standard multigrid method we will call the PD2 method. In the case where the classical theory is utilised, this result in what is referred to in the literature as Heterogenous Multiscale Method (HMM) [149]. In this case, numerical schemes such as the finite-element method or the finite difference method can be utilised to solve the macro-model.
Since one of the greatest strengths of the peridynamic theory lies in its capability in handling strong discontinuity in the response field of a system, this homogenization theory will be applied to problems with evolving microstructure such as micro-crack coalescing and propagation in a future work.
References
Goda T, Váradi K, Friedrich K (2001) Fe micro-models to study contact states, stresses and failure mechanisms in a polymer composite subjected to a sliding steel asperity. Wear 251(1):1584–1590
Huang H, Talreja R (2006) Numerical simulation of matrix micro-cracking in short fiber reinforced polymer composites: initiation and propagation. Compos Sci Technol 66(15):2743–2757
Paik SH et al (2007) Computational material characterization of active fiber composite. J Intell Mater Syst Struct 18(1):19–28
Yuan MN et al (2012) Numerical analysis of the stress–strain distributions in the particle reinforced metal matrix composite SiC/6064Al. Mater Des 38:1–6
Al-Amery RIM, Roberts TM (1990) Nonlinear finite difference analysis of composite beams with partial interaction. Comput Struct 35(1):81–87
Nath SKD (2014) A finite difference solution of a simply supported beam of orthotropic composite materials using displacement potential formulation. Chin J Eng 2014:961503
Wennberg D et al (2014) Finite difference adaptation of the decomposition of layered composite structures on irregular grid. J Compos Mater 48(20):2427–2439
Zhu Z, Brown TG (2002) Full-vectorial finite-difference analysis of microstructured optical fibers. Opt Express 10(17):853–864
Belytschko T et al (1994) Element-free Galerkin methods. Int J Numer Methods Eng 37(2):229–256
Meng GW et al (2015) Enriched element-free Galerkin method for fracture analysis of functionally graded piezoelectric materials. Math Probl Eng 2015:638–783
Pekbey Y et al (2012) The meshless element free Galerkin method for buckling analysis of simply supported laminate composite plates. Adv Compos Lett 21(6):145–157
Rosca VE et al (2015) Element free Galerkin formulation for problems in composite micromechanics. Appl Mech Mater 809–810:896–901
Abali BE et al (2015) Strain gradient elasticity with geometric nonlinearities and its computational evaluation. Mech Adv Mater Mod Process 1(1):4
Chan WL et al (2012) Experimental studies of the size effect affected microscale plastic deformation in micro upsetting process. Mater Sci Eng A 534:374–383
Ma Q, Clarke DR (1995) Size dependent hardness of silver single crystals. J Mater Res 10(4):853–863
Poole WJ et al (1996) Micro-hardness of annealed and work-hardened copper polycrystals. Scripta Mater 34(4):559–564
Stölken JS, Evans AG (1998) A microbend test method for measuring the plasticity length scale. Acta Mater 46(14):5109–5115
Kandaz M, Dal H (2018) A comparative study of modified strain gradient theory and modified couple stress theory for gold microbeams. Arch Appl Mech 88(11):2051–2070
Hansbo A, Hansbo P (2004) A finite element method for the simulation of strong and weak discontinuities in solid mechanics. Comput Methods Appl Mech Eng 193(33):3523–3540
Ramulu M et al (1983) Further studies on dynamic crack branching. Exp Mech 23(4):431–437
Madeo A (2015) 1—General introductory aspects. In: Madeo A (ed) Generalized continuum mechanics and engineering applications. Elsevier, pp 1–18
Chen Y et al (2009) A generalized continuum theory and its relation to micromorphic theory. J Eng Mech 135(3):149–155
Jirásek M (2004) Nonlocal theories in continuum mechanics. Acta Polytechnica 44(5–6):17–34
Bažant ZP, Jirásek M (2002) Nonlocal integral formulations of plasticity and damage: survey of progress. J Eng Mech 128(11):1119–1149
Voigt W (1887) Theoretische studien über Elasticitätsyerhälnisse der Kristable. Abn der Königl, Ges., Wiss Göttingen 34:3–51
Toupin R (1962) Elastic materials with couple-stresses. Arch Ration Mech Anal 11(1):385–414
Mindlin RD, Tiersten HF (1962) Effects of couple-stresses in linear elasticity. Arch Ration Mech Anal 11(1):415–448
Koiter W (1964) Couple stresses in the theory of elasticity. I and II Proc K Ned Akad Wet. Philos Trans R Soc Lond Ser B 67:17–44
Mindlin RD, Eshel N (1968) On first strain-gradient theories in linear elasticity. Int J Solids Struct 4(1):109–124
Mindlin RD (1965) Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct 1(4):417–438
Fleck NA, Hutchinson JW (1997) Strain gradient plasticity. In: Hutchinson JW, Wu TY (eds) Advances in applied mechanics, vol 33. Elsevier, pp 295–361
Fleck NA, Hutchinson JW (2001) A reformulation of strain gradient plasticity. J Mech Phys Solids 49(10):2245–2271
Cosserat ECF (1909) Théorie des corps déformables. Librairie Scientifique A Hermann et Fils, Paris
Eringen AC, Suhubi ES (1964) Nonlinear theory of simple micro-elastic solids—I. Int J Eng Sci 2(2):189–203
Eringen AC (1966) Linear theory of micropolar elasticity. J Math Mech 15(6):909–923
Eringen AC (1966) Theory of micropolar fluids. J Math Mech 16(1):1–18
Eringen AC (1969) Micropolar fluids with stretch. Int J Eng Sci 7(1):115–127
Coleman BD, Gurtin ME (1967) Thermodynamics with internal state variables. J Chem Phys 47(2):597–613
Kestin J, Rice JR (1970) Paradoxes in the application of thermodynamics to strained solids. In: Stuart EB, Gal-Or B, Brainard AJ (eds) Critical Review of Thermodynamics. Mono Book Corp., Baltimore, pp 275–298
Lazopoulos KA, Ogden RW (1998) Nonlinear elasticity theory with discontinuous internal variables. Math Mech Solids 3(1):29–51
Madeo A (2015) 4—Remodeling of bone reconstructed with bio-resorbable materials. In: Madeo A (ed) Generalized continuum mechanics and engineering applications. Elsevier, pp 83–108
Kunin IA (1966) Theory of elasticity with spatial dispersion one-dimensional complex structure. J Appl Math Mech 30(5):1025–1034
Kröner E (1967) Elasticity theory of materials with long range cohesive forces. Int J Solids Struct 3(5):731–742
Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16
Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209
Ren H et al (2020) A nonlocal operator method for solving partial differential equations. Comput Methods Appl Mech Eng 358:112621
Ren H et al (2020) A higher order nonlocal operator method for solving partial differential equations. Comput Methods Appl Mech Eng 367:113132
Paola MD, Zingales M (2008) Long-range cohesive interactions of non-local continuum faced by fractional calculus. Int J Solids Struct 45(21):5642–5659
Di Paola M et al (2009) Physically-based approach to the mechanics of strong non-local linear elasticity theory. J Elast 97(2):103–130
Paola MD et al (2010) The mechanically-based approach to 3D non-local linear elasticity theory: long-range central interactions. Int J Solids Struct 47(18):2347–2358
Diyaroglu C, Oterkus S, Oterkus E, Madenci E (2017) Peridynamic modeling of diffusion by using finite-element analysis. IEEE Trans Compon Packag Manuf Technol 7(11):1823–1831
De Meo D, Oterkus E (2017) Finite element implementation of a peridynamic pitting corrosion damage model. Ocean Eng 135:76–83
Imachi M, Tanaka S, Bui TQ, Oterkus S, Oterkus E (2019) A computational approach based on ordinary state-based peridynamics with new transition bond for dynamic fracture analysis. Eng Fract Mech 206:359–374
Basoglu MF, Zerin Z, Kefal A, Oterkus E (2019) A computational model of peridynamic theory for deflecting behavior of crack propagation with micro-cracks. Comput Mater Sci 162:33–46
Zhu N, De Meo D, Oterkus E (2016) Modelling of granular fracture in polycrystalline materials using ordinary state-based peridynamics. Materials 9(12):977
Diyaroglu C, Oterkus S, Oterkus E, Madenci E, Han S, Hwang Y (2017) Peridynamic wetness approach for moisture concentration analysis in electronic packages. Microelectron Reliab 70:103–111
Imachi M, Tanaka S, Ozdemir M, Bui TQ, Oterkus S, Oterkus E (2020) Dynamic crack arrest analysis by ordinary state-based peridynamics. Int J Fract 221(2):155–169
Kefal A, Sohouli A, Oterkus E, Yildiz M, Suleman A (2019) Topology optimization of cracked structures using peridynamics. Contin Mech Thermodyn 31(6):1645–1672
Yang Z, Vazic B, Diyaroglu C, Oterkus E, Oterkus S (2020) A Kirchhoff plate formulation in a state-based peridynamic framework. Math Mech Solids 25(3):727–738
Vazic B, Wang H, Diyaroglu C, Oterkus S, Oterkus E (2017) Dynamic propagation of a macrocrack interacting with parallel small cracks. AIMS Mater Sci 4(1):118–136
Ozdemir M, Kefal A, Imachi M, Tanaka S, Oterkus E (2020) Dynamic fracture analysis of functionally graded materials using ordinary state-based peridynamics. Compos Struct 244:112296
Huang Y, Oterkus S, Hou H, Oterkus E, Wei Z, Zhang S (2019) Peridynamic model for visco-hyperelastic material deformation in different strain rates. Contin Mech Thermodyn 1–35
De Meo D, Russo L, Oterkus E (2017) Modeling of the onset, propagation, and interaction of multiple cracks generated from corrosion pits by using peridynamics. J Eng Mater Technol 139(4):041001
Vazic B, Oterkus E, Oterkus S (2020) Peridynamic model for a Mindlin plate resting on a Winkler elastic foundation. J Peridyn Nonlocal Model 2:229–242
Liu X, He X, Wang J, Sun L, Oterkus E (2018) An ordinary state-based peridynamic model for the fracture of zigzag graphene sheets. Proc R Soc A Math Phys Eng Sci 474(2217):20180019
Wang H, Oterkus E, Oterkus S (2018) Three-dimensional peridynamic model for predicting fracture evolution during the lithiation process. Energies 11(6):1461
Candaş A, Oterkus E, İmrak CE (2021) Dynamic crack propagation and its interaction with micro-cracks in an impact problem. J Eng Mater Technol 143(1):011003
Madenci E, Dorduncu M, Barut A, Phan N (2018) Weak form of peridynamics for nonlocal essential and natural boundary conditions. Comput Methods Appl Mech Eng 337:598–631
Nguyen CT, Oterkus S (2019) Peridynamics formulation for beam structures to predict damage in offshore structures. Ocean Eng 173:244–267
Oterkus S, Madenci E (2015) Peridynamics for antiplane shear and torsional deformations. J Mech Mater Struct 10(2):167–193
Javili A et al (2019) Peridynamics review. Math Mech Solids 24(11):3714–3739
Bobaru F et al (2009) Convergence, adaptive refinement, and scaling in 1D peridynamics. Int J Numer Meth Eng 77(6):852–877
Bobaru F, Ha YD (2011) Adaptive refinement and multiscale modeling in 2D peridynamics. Int J Multiscale Comput Eng 9(6):635–660
Dipasquale D et al (2014) Crack propagation with adaptive grid refinement in 2D peridynamics. Int J Fract 190(1):1–22
Silling S et al (2015) Variable horizon in a peridynamic medium. J Mech Mater Struct 10(5):591–612
Ren H et al (2016) Dual-horizon peridynamics. Int J Numer Meth Eng 108(12):1451–1476
Gu X et al (2017) Voronoi-based peridynamics and cracking analysis with adaptive refinement. Int J Numer Meth Eng 112(13):2087–2109
Macek RW, Silling SA (2007) Peridynamics via finite element analysis. Finite Elem Anal Des 43(15):1169–1178
Littlewood DJ (2010) Simulation of dynamic fracture using peridynamics, finite element modeling, and contact. In: ASME 2010 international mechanical engineering congress and exposition
Oterkus E et al (2012) Combined finite element and peridynamic analyses for predicting failure in a stiffened composite curved panel with a central slot. Compos Struct 94(3):839–850
Agwai A et al (2012) Drop-shock failure prediction in electronic packages by using peridynamic theory. IEEE Trans Compon Packag Manuf Technol 2(3):439–447
Badia S, Bochev P, Fish J, Gunzburger M, Lehoucq R, Nuggehally M, Parks M (2007) A force-based blending model for atomistic-to-continuum coupling. Int J Multiscale Comput Eng 5:387–406
Fish J et al (2007) Concurrent ATC coupling based on a blend of the continuum stress and the atomistic force. Comput Methods Appl Mech Eng 2007(196):4548–4560
Kilic B, Madenci E (2010) Coupling of peridynamic theory and the finite element method. J Mech Mater Struct 5:707–733
Liu W, Hong J-W (2012) A coupling approach of discretized peridynamics with finite element method. Comput Methods Appl Mech Eng 245–246:163–175
Seleson P et al (2013) A force-based coupling scheme for peridynamics and classical elasticity. Comput Mater Sci 66:34–49
Shojaei A et al (2016) A coupled meshless finite point/peridynamic method for 2D dynamic fracture analysis. Int J Mech Sci 119:419–431
Shojaei A, Zaccariotto M, Galvanetto U (2017) Coupling of 2D discretized peridynamics with a meshless method based on classical elasticity using switching of nodal behaviour. Eng Comput 34(5):1334–1366
Lubineau G et al (2012) A morphing strategy to couple non-local to local continuum mechanics. J Mech Phys Solids 60(6):1088–1102
Azdoud Y et al (2013) A Morphing framework to couple non-local and local anisotropic continua. Int J Solids Struct 50(9):1332–1341
Azdoud Y et al (2014) The morphing method as a flexible tool for adaptive local/non-local simulation of static fracture. Comput Mech 54(3):711–722
Han F et al (2016) A morphing approach to couple state-based peridynamics with classical continuum mechanics. Comput Methods Appl Mech Eng 301:336–358
Galvanetto U et al (2016) An effective way to couple FEM meshes and peridynamics grids for the solution of static equilibrium problems. Mech Res Commun 76:41–47
Han F et al (2016) Adaptive coupling between damage mechanics and peridynamics: a route for objective simulation of material degradation up to complete failure. J Mech Phys Solids 94:453–472
Han F, Lubineau G (2012) Coupling of nonlocal and local continuum models by the Arlequin approach. Int J Numer Meth Eng 89(6):671–685
Silling SA (2011) A coarsening method for linear peridynamics. Int J Multiscale Comput Eng 9(6):609–622
Galadima Y, Oterkus E, Oterkus S (2019) Two-dimensional implementation of the coarsening method for linear peridynamics. AIMS Mater Sci 6(2):252–275
Galadima YK, Oterkus E, Oterkus S (2020) Model order reduction of linear peridynamic systems using static condensation. Math Mech Solids 26:552–569
Alali, B. and R. P. Lipton. Multiscale Analysis of Heterogeneous Media in the Peridynamic Formulation. arXiv: Analysis of PDEs, 2010.
Alali B, Lipton R (2012) Multiscale dynamics of heterogeneous media in the peridynamic formulation. J Elast 106(1):71–103
Hollister SJ, Kikuchi N (1992) A comparison of homogenization and standard mechanics analyses for periodic porous composites. Comput Mech 10(2):73–95
Buryachenko VA (2014) Effective elastic modulus of heterogeneous peristatic bar of random structure. Int J Solids Struct 51(17):2940–2948
Buryachenko VA (2017) Effective properties of thermoperistatic random structure composites: some background principles. Math Mech Solids 22(6):1366–1386
Buryachenko VA (2020) Generalized Mori-Tanaka approach in micromechanics of peristatic random structure composites. J Peridyn Nonlocal Model 2(1):26–49
Madenci E et al (2018) Peridynamic unit cell homogenization for thermoelastic properties of heterogenous microstructures with defects. Compos Struct 188:104–115
Buryachenko VA (2019) Computational homogenization in linear elasticity of peristatic periodic structure composites. Math Mech Solids 24(8):2497–2525
Xia W et al (2019) Representative volume element homogenization of a composite material by using bond-based peridynamics. J Compos Biodegrad Polym 7:51–56
Xia W et al (2021) Ordinary state-based peridynamic homogenization of periodic micro-structured materials. Theor Appl Fract Mech 113:102960
Du Q et al (2013) A nonlocal vector calculus, nonlocal volume-constrained pproblems, and nonlocal balance laws. Math Models Methods Appl Sci 23(03):493–540
Vollmann C et al (2019) Nonlocal models with truncated interaction Kernels—analysis, finite element methods and shape optimization. Universität Trier
D’Elia M, Bochev P (2021) Formulation, analysis and computation of an optimization-based local-to-nonlocal coupling method. Results Appl Math 9:100129
Silling SA et al (2007) Peridynamic states and constitutive modeling. J Elast 88(2):151–184
Bergel GL, Li S (2016) The total and updated Lagrangian formulations of state-based peridynamics. Comput Mech 58(2):351–370
Aguiar AR, Fosdick R (2013) A constitutive model for a linearly elastic peridynamic body. Math Mech Solids 19(5):502–523
Mitchell J, Silling S, Littlewood D (2015) A position-aware linear solid constitutive model for peridynamics. J Mech Mater Struct 10(5):539–557
Prakash, N. and G.D. Seidel, A novel two-parameter linear elastic constitutive model for bond based peridynamics, in 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.
Roy Chowdhury S et al (2015) A micropolar peridynamic theory in linear elasticity. Int J Solids Struct 59:171–182
Song X, Khalili N (2019) A peridynamics model for strain localization analysis of geomaterials. Int J Numer Anal Meth Geomech 43(1):77–96
Tupek MR, Radovitzky R (2014) An extended constitutive correspondence formulation of peridynamics based on nonlinear bond-strain measures. J Mech Phys Solids 65:82–92
Zhou X-P, Tian D-L (2021) A novel linear elastic constitutive model for continuum-kinematics-inspired peridynamics. Comput Methods Appl Mech Eng 373:113479
Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17):1526–1535
Parks ML et al (2008) Implementing peridynamics within a molecular dynamics code. Comput Phys Commun 179(11):777–783
Wang H, Tian H (2014) A fast and faithful collocation method with efficient matrix assembly for a two-dimensional nonlocal diffusion model. Comput Methods Appl Mech Eng 273:19–36
Evangelatos GI, Spanos PD (2011) A collocation approach for spatial discretization of stochastic peridynamic modeling of fracture. J Mech Mater Struct 6(7–8):1171–1195
Chen X, Gunzburger M (2011) Continuous and discontinuous finite element methods for a peridynamics model of mechanics. Comput Methods Appl Mech Eng 200(9):1237–1250
Wang H, Tian H (2012) A fast Galerkin method with efficient matrix assembly and storage for a peridynamic model. J Comput Phys 231(23):7730–7738
Seleson P, Littlewood DJ (2016) Convergence studies in meshfree peridynamic simulations. Comput Math Appl 71(11):2432–2448
Hill R (1967) The essential structure of constitutive laws for metal composites and polycrystals. J Mech Phys Solids 15(2):79–95
Voigt W (1889) Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann Phys 274(12):573–587
Reuss A (1929) Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J Appl Math Mech Zeitschrift für Angewandte Mathematik und Mechanik 9(1):49–58
Hill R (1952) The elastic behaviour of a crystalline aggregate. Proc Phys Soc Sect A 65(5):349–354
Yu W (2016) An introduction to micromechanics. Appl Mech Mater 828:3–24
Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. J Mech Phys Solids 11(2):127–140
Tian W et al (2019) Periodic boundary condition and its numerical implementation algorithm for the evaluation of effective mechanical properties of the composites with complicated micro-structures. Compos B Eng 162:1–10
Otero F et al (2015) Numerical homogenization for composite materials analysis. Comparison with other micro mechanical formulations. Compos Struct 122:405–416
Smit RJM, Brekelmans WAM, Meijer HEH (1998) Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput Methods Appl Mech Eng 155(1):181–192
de Neto EAS, Feijóo RA (2010) Variational foundations of large strain multiscale solid constitutive models: kinematical formulation. Advanced computational materials modeling. Wiley, pp 341–378
Eshelby JD, Peierls RE (1957) The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond Ser A Math Phys Sci 241(1226):376–396
Mori T, Tanaka K (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall 21(5):571–574
Denisiewicz A et al (2021) Influence of boundary conditions on numerical homogenization of high performance concrete. Materials 14:1009
Loo EG, van der Meer FP (2020) Stress-controlled weakly periodic boundary conditions: axial stress under varying orientations. Int J Numer Methods Eng 121(19):4458–4470
Kenaga D et al (1987) The characterization of boron/aluminum composite in the nonlinear range as an orthotropic elastic-plastic material. J Compos Mater 21(6):516–531
Sun CT, Vaidya RS (1996) Prediction of composite properties from a representative volume element. Compos Sci Technol 56(2):171–179
Aboudi J et al (2001) Linear thermoelastic higher-order theory for periodic multiphase materials. J Appl Mech 68(5):697–707
Yu W, Tang T (2007) Variational asymptotic method for unit cell homogenization of periodically heterogeneous materials. Int J Solids Struct 44(11):3738–3755
Jöchen K (2013) Homogenization of the linear and non-linear mechanical behavior of polycrystals. KIT Scientific Publishing
Klusemann B, Svendsen B (2010) Homogenization methods for multi-phase elastic composites: comparisons and benchmarks. Tech Mech 30(4):374–386
Klusemann B et al (2012) Homogenization methods for multi-phase elastic composites with non-elliptical reinforcements: comparisons and benchmarks. Eur J Mech A Solids 34:21–37
Weinan E et al (2007) Heterogeneous multiscale methods: a review. Commun Comput Phys 2(3):367–450
Acknowledgements
The first author is supported by the government of the federal republic of Nigeria through the Petroleum Technology Development Fund (PTDF). This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-18-1-7004.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Galadima, Y.K., Xia, W., Oterkus, E. et al. A computational homogenization framework for non-ordinary state-based peridynamics. Engineering with Computers 39, 461–487 (2023). https://doi.org/10.1007/s00366-021-01582-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-021-01582-6