1 Introduction

A sandwich structured composite is an advanced type of composite materials usually fabricated by attaching two fairly thin but strong face sheets to a relatively thick lightweight core [1]. Using a first order shear deformation theory and Hamilton’s principle, Karroubi and Irani Rahaghi [2] performed a study on the free vibration of a three-layer rotating shell which consists of a functionally graded core and two piezoelectric face sheets. The emphasis of the current study is on the time-dependent deflection of a sandwich plate made of a porous plate whose materials functionally scattered along thickness and in-plane directions as a core solid with two similar homogenous faces.

In the few recent decades, more and more craftsmen have tried to seek for advanced materials which have more capacity to resist both different mechanical loadings and sever environmental conditions [3, 4]. This way, 2D-FG solids have attracted enormous attentions from both research and industrial divisions [5]. Scientists have showed that functionally graded materials with two directional dependent materials properties have more resistance against severe temperature variations compared to one-dimensional (1D) functionally graded materials (FGMs) [6,7,8]. Beferani et al. [9] analyzed the vibrational characteristics of functionally graded plates on Winkler and Pasternak foundations. Sheikholeslami and Saidi [10] showed the impacts of some factors such as the thickness ratio and elastic foundation parameters on the natural frequencies of thick functionally graded rectangular plates. Some years later, Chen et al. [11] explored the effects of several factors such as geometric features and material parameters on the vibrational behaviors of cylindrical 2D-FG shells. The vibrational and buckling performances of 2D-FG beams were analyzed by Nguyen and Lee [12]. Using the generalized differential quadrature method, Fariborz and Batra [13] studied the free vibration of curved beams with two directional material properties. Tang and Ding [14] used Euler–Berloni theory along with the von Kármán scheme for large deflections to investigate the effects of material gradients on the mechanical characteristics of 2D-FG beams under hygro-thermal loads. The nonlinear vibrational behaviors of pre- and post-buckled nonuniform bi-directional functionally graded microbeams under nonlinear thermal loading were investigated by Attia and Mohamed [15]. In another study, Saini and Lal [16] analyzed the free vibrational behavior of functionally graded moderately thick circular plates with two-dimensional material and temperature distribution.

During the fabrication of functionally graded materials, micro-voids can be created inside the FGMs. For instance, porosity formation can be a result of mixing some materials with different sintering temperature [17]. Wang et al. [18] investigated the thermal vibration of a cylindrical shell with structural defections dispersed monotonously or functionally through the thickness path. Zhou et al. [19] conducted a study on the vibrational and flutter behaviors of functionally graded plates containing porosities. Esmaeilzadeh and Kadkhodayan [20] used the kinetic dynamic relaxation technique combined with Newmark approach to undertake a numerical study on nonlinear dynamic behaviors of porous stiffened 2D-FG sheets. Following that, they [21] investigated the effects of porosity configurations on time-dependent behavior of bi-layer sandwich plates.

The numerical replicas of structures which rest on elastic foundations are frequently employed to duplicate numerous real models in industrial sectors. In several cases, an elastic medium can be assumed as simple instruments such as spring. Beferani and Saidi [22] used the third order shear deformation plate theory along with the Levy approach to investigate the buckling and vibrational behaviors of symmetrically laminated thick rectangular plates supported by elastic foundations. In another research, Gao et al. [23] presented the effects of some factors such as damping ratios and temperature changes on the dynamic performance of composite orthotropic plates resting on an elastic medium.

Structures subjected to moving loads can be seen in various applications such as trains on the track, airplanes passing floating airports, machine tools, etc. From a computational point of view, the travelling load is usually applied as a simple massless force or an oscillator or an inertial force. Numerous historical studies concerning the moving load problem exist in the open literatures [20, 24,25,26,27]. Simsek [28] conducted a study on nonlocal vibration of a single-walled carbon nanotube carrying a moving harmonic load. The nonlocal elasticity theory was used by Chang [29] and Nami and Janghorban [30], respectively, to study dynamic behaviors of double-walled nanotubes and nanoplates. Shahsavari and Janghorban [31] also investigated dynamic deflections and shearing responses of nanoplates under moving loads using the nonlocal theory. With the consideration of nano-system coefficients, Barati et al. [32] undertook a research on transient responses of nanobeams under inertia forces. Recently, stability of graphite sheets resting on elastic foundations and subjected to moving nanoparticles was investigated by Pirmoradian et al. [33].

Based on the comprehensive literature review conducted by the authors, on the basis of the FSDT, there is no numerical study on the nonlinear dynamic behaviors of sandwich rectangular plates with porous 2D-FG core mounted on elastic foundations and under the action of moving loads. In this study, a 2D-FG core is assumed to be defected with porosity inclusions uniformly or functionally distributed through its thickness. Hamilton’s principle in conjunction with von-Karman theory are used to derive the time-dependent equations, and then an amalgamation of kinetic dynamic relaxation method and Newmark implicit integration are employed for solving governing equations. Eventually, the influence of some key parameters including elastic foundations, material gradient properties, boundary constrains, and moving load on transient responses of the sandwich plate are precisely scrutinized. The result of this research work can be applied to bridging engineering and transportation divisions, where dynamic effects of the moving vehicles on bridge structures can play a significant role on their lifetime.

2 Theoretical modelling

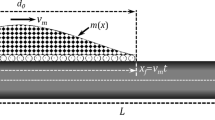
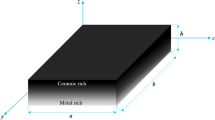
Consider a rectangular sandwich plate with length a, width b and thickness h (= hc + 2hf) along x, y and z directions, respectively, as shown in Fig. 1. This plate rests on an elastic foundation and is exposed to a moving load. Subscripts c and f denote the core layer and face surfaces, respectively.

Fig. 1
figure 1

Schematic of a sandwich plate resting on an elastic foundation under a moving load

Full size image

2.1 Bi-directional FG plate with geometrical imperfections

Figure 1 shows that the mixture of the 2D-FG core changes along both x and z directions. The upper surface of the plate, hc/2, is completely made out of material 3, then its mechanical properties vary to a composition of martial 1 and 2 at the bottom of the sheet. The plate’s mechanical properties change along axial direction at z = − hc/2, as well, from pure material 1 at x = 0 to unadulterated ceramic 2 at x = a.

The effective mechanical properties, P (x, z), of the 2D-FG core with even micro-void inclusions (Fig. 2a) based on the rule of mixtures can be measured by [20]

Fig. 2
figure 2

Two types of porosity distributions through the plate thickness

Full size image
$$\begin{aligned} P(x,z) & = P_{1} \left( {1 - \left( {\frac{z}{{h_{{\text{c}}} }} + \frac{1}{2}} \right)^{n} } \right)\left( {1 - \left( \frac{x}{a} \right)^{m} } \right) + P_{2} \left( {1 - \left( {\frac{z}{{h_{{\text{c}}} }} + \frac{1}{2}} \right)^{n} } \right)\left( \frac{x}{a} \right)^{m} + P_{3} \left( {1 - \left( {\frac{z}{{h_{c} }} + \frac{1}{2}} \right)^{n} } \right) \\ & \quad - \frac{\alpha }{2}(P_{1} + P_{2} + P_{3} ), \\ \end{aligned}$$
(1)

where P1, P2 and P3 are, respectively, mechanical properties (Young’s modulus (E), and mass density (ρ)) of materials 1, 2 and 3, and also positive parameters n and m are gradient indexes along z- and x-axes. In the case of the core with uneven porosities (Fig. 2b), the effective mechanical properties become [20]:

$$\begin{aligned} P(x,z) & = P_{1} \left( {1 - \left( {\frac{z}{{h_{{\text{c}}} }} + \frac{1}{2}} \right)^{n} } \right)\left( {1 - \left( \frac{x}{a} \right)^{m} } \right) + P_{2} \left( {1 - \left( {\frac{z}{{h_{{\text{c}}} }} + \frac{1}{2}} \right)^{n} } \right)\left( \frac{x}{a} \right)^{m} + P_{3} \left( {1 - \left( {\frac{z}{{h_{{\text{c}}} }} + \frac{1}{2}} \right)^{n} } \right) \\ & \quad - \frac{\alpha }{2}(P_{1} + P_{2} + P_{3} )\left( {1 - \frac{2|z|}{{h_{{\text{c}}} }}} \right), \\ \end{aligned}$$
(2)

where P (x, z) represents Young’s modulus (E), and mass density (ρ). Also, α denotes porosity fraction. The Poisson’s ratio (υ) is assumed to be constant.

2.2 Fundamental equations

Because the main aim of the current study is to investigate dynamic response of moderately thick sandwich plates, equivalent single layer theory of the first-order shear deformation is hired to describe the kinematics of deformation of the plate. The FSDT provides a sufficiently accurate description of global response for moderately thick layered structures with complex constitutive behavior [34]. Based on FSDT along with von-Karman nonlinearity, the stress–displacement relationships of face layers and a porous 2D-FGM core are written as follows:

$$\left\{ \begin{gathered} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{xy} \hfill \\ \sigma_{yz} \hfill \\ \sigma_{xz} \hfill \\ \end{gathered} \right\}_{{\text{c}}} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{11} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } \\ \end{array} } \right]_{{\text{c}}} \times \left\{ {\left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \\ {\frac{\partial v}{{\partial y}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \\ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}} \\ {\psi_{y} + \frac{\partial w}{{\partial y}}} \\ {\psi_{x} + \frac{\partial w}{{\partial x}}} \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\frac{{\partial \psi_{x} }}{\partial x}} \\ {\frac{{\partial \psi_{y} }}{\partial y}} \\ {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \\ 0 \\ 0 \\ \end{array} } \right\}} \right\}$$
(3a)
$$\begin{gathered} \hfill \\ \left\{ \begin{gathered} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{xy} \hfill \\ \sigma_{yz} \hfill \\ \sigma_{xz} \hfill \\ \end{gathered} \right\}_{{\text{f}}} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{11} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } \\ \end{array} } \right]_{{\text{f}}} \times \left\{ {\left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \\ {\frac{\partial v}{{\partial y}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \\ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}} \\ {\psi_{y} + \frac{\partial w}{{\partial y}}} \\ {\psi_{x} + \frac{\partial w}{{\partial x}}} \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\frac{{\partial \psi_{x} }}{\partial x}} \\ {\frac{{\partial \psi_{y} }}{\partial y}} \\ {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \\ 0 \\ 0 \\ \end{array} } \right\}} \right\}, \hfill \\ \end{gathered}$$
(3b)

in which u, v and w are, respectively, the displacements of the sandwich plate along x, y and z directions. Also \(\psi_{x}\) and \(\psi_{y}\) denote angular dislocations about y and x axes. The plane stress-reduced stiffness coefficients (Qij) of the ceramic’s layers (f) and porous 2D-FG core (c) are respectively defined as follows [21]:

$$\begin{gathered} {\text{Face}}:\left\{ \begin{gathered} Q_{11} = \frac{{E_{{\text{f}}} }}{{1 - \upsilon_{{\text{f}}}^{2} }} \hfill \\ Q_{12} = \frac{{\upsilon_{{\text{f}}} E_{{\text{f}}} }}{{1 - \upsilon_{{\text{f}}}^{2} }} \hfill \\ C_{44} = C_{55} = Q_{66} = G_{{\text{f}}} = \frac{{E_{{\text{f}}} }}{{2(1 + \upsilon_{{\text{f}}} )}} \hfill \\ \end{gathered} \right. \hfill \\ {\text{Core:}}\left\{ \begin{gathered} Q_{11} = \frac{{E_{{\text{c}}} (x,z)}}{{1 - \upsilon_{{\text{c}}}^{2} }} \hfill \\ Q_{12} = \frac{{\upsilon_{{\text{c}}} E_{{\text{c}}} (x,z)}}{{1 - \upsilon_{{\text{c}}}^{2} }} \hfill \\ C_{44} = C_{55} = Q_{66} = G_{{\text{c}}} (x,z) = \frac{{E_{{\text{c}}} (x,z)}}{{2(1 + \upsilon_{{\text{c}}} )}} \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered}$$
(4)

\(\upsilon_{{\text{f}}}\) and \(\upsilon_{{\text{c}}}\) are, respectively, the Poisson’s ratios of the face sheets and the core. The stress resultants and moments are defined as [35]:

$$\begin{aligned} \left( {N_{i} ,M_{i} } \right) & = \mathop \smallint \limits_{{h_{{\text{c}}} /2}}^{{h_{{\text{c}}} /2 + h_{{\text{f}}} }} \left( {\left( {1,z} \right)\sigma_{i} } \right)_{{\text{f}}} {\text{d}}z + \mathop \smallint \limits_{{ - h_{{\text{c}}} /2}}^{{h_{{\text{c}}} /2}} \left( {\left( {1,z} \right)\sigma_{i} } \right)_{{\text{c}}} {\text{d}}z + \mathop \smallint \limits_{{ - \left( {h_{{\text{c}}} /2 + h_{{\text{f}}} } \right)}}^{{ - h_{{\text{c}}} /2}} \left( {\left( {1,z} \right)\sigma_{i} } \right)_{{\text{f}}} {\text{d}}z,\quad \left( {i = xx,yy,xy} \right) \\ Q_{i} & = K^{2} \left( {\mathop \smallint \limits_{{h_{{\text{c}}} /2}}^{{h_{{\text{c}}} /2 + h_{{\text{f}}} }} \left( {\sigma_{iz} } \right)_{{\text{f}}} {\text{d}}z + \mathop \smallint \limits_{{ - h_{{\text{c}}} /2}}^{{h_{{\text{c}}} /2}} \left( {\sigma_{iz} } \right)_{{\text{c}}} {\text{d}}z + \mathop \smallint \limits_{{ - \left( {h_{{\text{c}}} /2 + h_{{\text{f}}} } \right)}}^{{ - h_{{\text{c}}} /2}} \left( {\sigma_{iz} } \right)_{{\text{f}}} {\text{d}}z} \right),\quad \left( {i = x,y} \right), \\ \end{aligned}$$
(5)

\(K^{2}\) represents the transverse shear correction constant and is set as 0.833.

To derive the fundamental equations, the Hamilton’s principle is used as,

$$\int\limits_{0}^{T} {(\delta T + \delta W - \delta K){\text{d}}t = 0} ,$$
(6)

where \(\delta T\) is the variation of strain energy and also \(\delta W\), and \(\delta K\) are, separately, the variation of applied work and kinetic energy of a mechanism. \(\delta T\) can be expressed in terms of stress and strain as:

$$\delta T = \iiint\limits_{V} {\delta t{\text{d}}V = \iiint\limits_{V} {\sigma_{ij} \delta }}\varepsilon_{ij} {\text{d}}V.$$
(7)

The variation of kinetic energy can be expressed by:

$$\delta K = \iiint\limits_{V} {\left( {\rho_{f} + \rho_{c} (x,z)} \right)\left( {(u + z\psi_{x} )\delta (\dot{u} + z\dot{\psi }_{x} ) + (v + z\psi_{y} )\delta (\dot{v} + z\dot{\psi }_{y} ) + \dot{w}\delta \dot{w}} \right)}{\text{d}}V.$$
(8)

Finally, the kinematic equation of sandwich plates subjected to a moving load (F) can be formulated as follows:

$$\begin{gathered} \left\{ \begin{gathered} \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_{0} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{2} \theta_{x} }}{{\partial t^{2} }}} \right), \hfill \\ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} = I_{0} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{2} \theta_{y} }}{{\partial t^{2} }}} \right), \hfill \\ \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + {\rm N}\left( w \right) - F\overline{\delta }\left( {x - x_{0} } \right) - K_{{\text{w}}} w + K_{{\text{s}}} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right), \hfill \\ \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} = I_{1} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{2} \theta_{x} }}{{\partial t^{2} }}} \right), \hfill \\ \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{yy} }}{\partial y} - Q_{y} = I_{1} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{2} \theta_{y} }}{{\partial t^{2} }}} \right). \hfill \\ \end{gathered} \right. \hfill \\ N{(}w{)} = N_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }}, \hfill \\ \end{gathered}$$
(9)

where N(w) depicts the nonlinear term, Kw is the Winkler foundation modulus, and Ks is the Pasternak shear foundation, and \(\overline{\delta }\) is the Dirac function specify the moving line force position with an assigned velocity along the x-axis, and;

$$I = \mathop \smallint \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2} + h_{{\text{f}}} }} \rho_{{\text{f}}} {(}z^{0} ,z^{1} ,z^{2} {\text{)d}}z + \mathop \smallint \limits_{{ - \frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} \rho_{{\text{c}}} \left( {x,z} \right){(}z^{0} ,z^{1} ,z^{2} {\text{)d}}z + \mathop \smallint \limits_{{ - \left( {\frac{{h_{{\text{c}}} }}{2} + h_{{\text{f}}} } \right)}}^{{ - \frac{{h_{{\text{c}}} }}{2}}} \rho_{{\text{f}}} {(}z^{0} ,z^{1} ,z^{2} {\text{)d}}z.$$
(10)

Three set of boundary constrains, namely simply supported boundary conditions, SCSC and clamped boundary condition and, are considered for the completion of the derived equations.

  1. (a)

    Fully simply supported boundary edge (SSSS)

    $$\left\{ \begin{gathered} x = 0,a \to u = v = w = \psi_{y} = M_{xx} = 0 \hfill \\ y = 0,b \to u = v = w = \psi_{x} = M_{yy} = 0 \hfill \\ \end{gathered} \right..$$
    (11)
  2. (b)

    Parallel edges are simply supported and clamped (SCSC)

    $$\left\{ \begin{gathered} x = 0,a \to u = v = w = \psi_{y} = M_{xx} = 0 \hfill \\ y = 0,b \to u = v = w = \psi_{x} = \psi_{y} = 0 \hfill \\ \end{gathered} \right..$$
    (12)
  3. (c)

    Fully clamped boundary edge (CCCC)

    $$\left\{ \begin{gathered} x = 0,a \to u = v = w = \psi_{x} = \psi_{y} = 0 \hfill \\ y = 0,b \to u = v = w = \psi_{x} = \psi_{y} = 0 \hfill \\ \end{gathered} \right..$$
    (13)

3 Numerical methods

The kinetic dynamic relaxation scheme accompanied by Newmark integral technique are recruited in the study for solving Eq. (9).

3.1 Newmark integration method

On the basis of Newmark approach, the first and second derivatives of x at the next time period, tj+1, are defined as:

$$\dot{\varvec{x}}_{{{\varvec{j}} + 1}} = \left( {\frac{\gamma }{{\beta \Delta t_{j} }}{(}{\varvec{x}}_{{\varvec{j + 1}}} - {\mathbf{x}}_{{\mathbf{j}}} {)} - \left( {\frac{\gamma }{\beta } - 1} \right)\dot{\varvec{x}}_{{\varvec{j}}} - \left( {\frac{\gamma }{2\beta } - 1} \right)\Delta t_{j} \ddot{\varvec{x}}_{{\varvec{j}}} } \right){,}$$
(14)
$$\ddot{x}_{j + 1} = \left( {\frac{1}{{\beta {(}\Delta t_{j} {)}^{2} }}{(}x_{j + 1} - x_{j} {)} - \frac{1}{{\beta \Delta t_{j} }}\dot{x}_{j} - \left( {\frac{1}{2\beta } - 1} \right)\ddot{x}_{j} } \right){,}$$
(15)

in which, x is the displacement field of the nanoplate (\({\mathbf{x}} = {\mathbf{u}},{\mathbf{v}},{\mathbf{w}},{{\varvec{\uppsi}}}_{x} ,{{\varvec{\uppsi}}}_{y}\)), Δt is real time interval, \(\gamma\) and \(\beta\) are Newmark’s coefficients. By substituting Eqs. (14) and (15) into Eq. (9), it gives:

$$\left[ {\overline{\varvec{K}}_{j + 1} } \right]{\varvec{x}}_{j + 1} = \{ \overline{\varvec{P}}_{j + 1} \} ,$$
(16)

in which \(\left[ {\overline{\varvec{K}}_{j + 1} } \right]\) is the corresponding stiffness matrix and \(\{ \overline{\varvec{P}}_{j + 1} \}\) represents corresponding load vector, defined as:

$$\left[ {\overline{\varvec{K}}_{j + 1} } \right] = \frac{1}{{\beta (\Delta t_{j} )^{2} }}\left[ {{\varvec{I}}_{j + 1} } \right] + \left[ {{\varvec{K}}_{{{\varvec{j}} + 1}} } \right]$$
(17)
$$\left\{ {{\overline{\mathbf{P}}}_{j + 1} } \right\} = \left\{ {{\mathbf{P}}\left( {{\text{t}}_{j + 1} } \right)} \right\} + \left\{ {\left[ {{\mathbf{I}}_{j + 1} } \right]\left[ {\frac{1}{{\beta (\Delta t_{j} )^{2} }}{\mathbf{x}}_{{\mathbf{j}}} + \frac{1}{{\beta \Delta t_{j} }}{\dot{\mathbf{x}}}_{{\mathbf{j}}} + \left( {\frac{1}{2\beta } - 1} \right){\mathbf{\ddot{x}}}_{j} } \right]} \right\},$$
(18)

where \(\left[ {{\mathbf{I}}_{j + 1} } \right]\) is the mass matrix and \(\left[ {{\varvec{K}}_{{{\varvec{j}} + 1}} } \right]\) represents the stiffness matrix. Also, {Pj+1} denotes the external work vector.

3.2 Kinetic dynamic relaxation technique

Equation (9) can be solved when it is transformed into fictitious dynamic space by artificial inertia matrix \(\left[ {\mathbf{\rm M}} \right]_{{{\text{DR}}}}\) as follows [36]:

$$\left[ {\varvec{M}} \right]_{{{\text{DR}}}}^{n} \left\{ {\varvec{a}} \right\}^{n} + \left[ {\overline{\varvec{K}}_{j + 1} } \right]^{n} {\varvec{x}}_{j + 1}^{n} = \left\{ {\overline{\varvec{P}}_{j + 1}^{n} } \right\}{,}$$
(19)

where \(\left\{ {\varvec{a}} \right\}^{n}\) and \(\left[ {\mathbf{M}} \right]_{{{\text{DR}}}}^{n}\) denote, respectively, the fictitious acceleration vector in nth iteration of the Kinetic DR [36] and diagonal artificial mass matrix. A proper fictitious mass can guarantee the convergence of K-DR technique. Such an artificial mass is defined in accordance with the Gershgörin theorem [37].

$${\varvec{m}}_{ii}^{{{\text{DOF}}}} \ge 0.5\left( {\tau^{n} } \right)^{2} \mathop \sum \limits_{p = 1}^{{{\text{DOF}}}} |{\varvec{k}}_{ip} |,\quad {\varvec{k}}_{ip} = \frac{{\partial \left\{ {[{\overline{\mathbf{K}}}]_{j + 1}^{n} x_{j + 1}^{n} } \right\}}}{\partial x},$$
(20)

in which \({\varvec{m}}_{ii}\) and DOF are, respectively, fictitious mass matrix elements and the number of degrees of freedom. Nodal velocity and dislocation vectors at the next fictitious time stage, \(\tau\), can be stated by:

$$\left\{ {\varvec{v}} \right\}^{{{\varvec{n}} + 1/2}} = {\varvec{v}}^{{{\varvec{n}} - 1/2}} + \frac{{\tau^{n} }}{{\left[ {\varvec{M}} \right]_{{{\text{DR}}}} }}\left\{ {\mathbf{R}} \right\}^{n} ,\left\{ {\mathbf{R}} \right\}^{n} = \left\{ {{\overline{\mathbf{P}}}_{j + 1}^{n} - \left[ {{\overline{\mathbf{K}}}_{j + 1} } \right]^{n} {\mathbf{x}}_{j + 1}^{n} } \right\}$$
(21)
$$\left\{ {\varvec{x}} \right\}^{{{\varvec{n}} + 1}} = \left\{ {\varvec{x}} \right\}^{{\varvec{n}}} + \tau^{n} \left\{ {\varvec{v}} \right\}^{{{\varvec{n}} + \frac{1}{2}}} .$$
(22)

Furthermore, the kinetic energy of system can be obtained by:

$${\text{KE}}^{n + 1} = \frac{1}{2}\sum\limits_{i = 1}^{{{\text{DOF}}}} {{\mathbf{m}}_{ii}^{n} } \left( {{\mathbf{v}}_{i}^{{n + \frac{1}{2}}} } \right)^{2} .$$
(23)

As the maximum value of kinetic energy is determined, the K-DR iteration is started again with another novel initial nodal displacement and velocity as follows [38]:

$$\left\{ {\mathbf{x}} \right\}^{{{\varvec{n}} - 1/2}} = \left\{ {\mathbf{x}} \right\}^{{\varvec{n}}} - \left( {\frac{3}{2}\tau^{n} } \right)\left\{ {\varvec{v}} \right\}^{{{\varvec{n}} + 1/2}} + \frac{{\left( {\tau^{n} } \right)^{2} }}{{2\left[ {\mathbf{M}} \right]_{{{\text{DR}}}}^{n} }}\left\{ {\mathbf{R}} \right\}^{n}$$
(24)
$$\left\{ {\mathbf{v}} \right\}^{{n + \frac{1}{2}}} = \frac{\tau }{{2[{\mathbf{M}}_{{{\text{DR}}}} ]^{n} }}\left\{ {\mathbf{R}} \right\}^{n} .$$
(25)

The satisfaction of two criteria (i.e. \(\left| {{\text{KE}}^{n + 1} } \right| \le 10^{ - 12}\) and \(\left| {\left\{ {{\mathbf{R}}^{n} } \right\}} \right| \le 10^{ - 9}\) ) leads to stopping the K-DR procedure. These steps are iterated for each time increment of implicit Newmark integration.

4 Numerical results

4.1 Comparison study

Case study 1 for the first case, the dynamic response of a 1D-FG plate under a uniform harmonic force, \(F(x,y,t) = 10\sin (2000t)\) is carried out with the current method, and the obtained results are compared with those reported by [39]. The following properties have been considered:

$$\left\{ \begin{gathered} a = b = 1,h/a = 0.2, \hfill \\ E_{1} = 70\;{\text{GPa}},\rho_{1} = 2702\,{\text{kg}}/{\text{m}}^{3} ,\upsilon_{1} = 0.3, \hfill \\ E_{2} = 200\;{\text{GPa}},\rho_{2} = 5700\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{2} = 0.3. \hfill \\ \end{gathered} \right.$$
(26)

Also \(\overline{w} = \frac{{100E_{1} h^{3} w}}{{12a^{4} (1 - v_{1}^{2} )F_{0} }}\) is defined as the non-dimensional deflection where \(F_{0}\) represents transverse load applied on the top surface of the plate. Figure 3 reveals a perfect match between the obtained results and those reported in [39].

Fig. 3
figure 3

Time dependent non-dimensional deflection at the center of a clamped square FG plate

Full size image

Case study 2 in the second example, the transverse displacements at the center of clamped and simply supported plates under action of a moving load are obtained by K-DR method. The parameters used in this example are:

$$\left\{ \begin{gathered} a = b = 1,{{\rho h} \mathord{\left/ {\vphantom {{\rho h} {D = 1,{F \mathord{\left/ {\vphantom {F {D = 1}}} \right. \kern-\nulldelimiterspace} {D = 1}}}}} \right. \kern-\nulldelimiterspace} {D = 1,{F \mathord{\left/ {\vphantom {F {D = 1}}} \right. \kern-\nulldelimiterspace} {D = 1}}}} \hfill \\ x_{0} = vt,y_{0} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \end{gathered} \right.$$
(27)

In this sample, the external load, F, moves on the mid-line of the plate along the x direction. The bending rigidity of the plate is denoted by D and t is the time needed for the load to travel on the plate. From Figs. 4 and 5, a close agreement can be seen between the present results and the reference [40].

Fig. 4
figure 4

Vertical displacement at the center of a clamped plate under a traveling force

Full size image
Fig. 5
figure 5

Vertical displacement at the center of a simply supported plate under a traveling force

Full size image

Case study 3 for checking the accuracy of the present formulation and numerical system, the effects variations of vertical (n) and axial (m) grading indexes on the non-dimensional central deflection of a CCCC bi-dimensional functionally graded plate under a moving load with the velocity of v are compared in Table 1. The plate has the following geometrical and mechanical features;

$$\begin{gathered} a = b = 1000\;{\text{mm}},h_{{\text{c}}} = 100\;{\text{mm}} \hfill \\ E_{1} = 116\;{\text{GPa}},\rho_{1} = 1200\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{1} = 0.3 \hfill \\ E_{2} = 200\;{\text{GPa}},\rho_{2} = 7850\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{2} = 0.3 \hfill \\ E_{3} = 380\;{\text{GPa}},\rho_{3} = 3960\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{3} = 0.18,F = 400\frac{kN}{m},x_{0} = vt. \hfill \\ \end{gathered}$$
(28)
Table 1 Influences of gradient indexes (n, m) on the magnitude of wmax/h
Full size table

From Table 1, it can be noticed that the current results are in perfect agreements with those of Ref. [20] which can confirm the accuracy of the methodology and solutions.

4.2 Parametric study

The influences of the elastic foundations, porous distributions, material gradient indexes and borderline constrains on dimensionless dynamic central deflection of the sandwich plates with imperfect 2D-FG core are investigated. To do this, a square-shaped three-layer plate with the following geometrical and mechanical properties is considered.

$$\begin{gathered} a = b = 1000\;{\text{mm}},h_{{\text{c}}} = 100\;{\text{mm}} \hfill \\ E_{1} = 116\;{\text{GPa}},\rho_{1} = 1200\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{1} = 0.3 \hfill \\ E_{2} = 200\;{\text{GPa}},\rho_{2} = 7850\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{2} = 0.3 \hfill \\ E_{3} = 380\;{\text{GPa}},\rho_{3} = 3960\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{3} = 0.3 \hfill \\ E_{{\text{f}}} = 200\;{\text{GPa}},\rho_{{\text{f}}} = 7850\;{\text{kg}}/{\text{m}}^{3} ,\upsilon_{{\text{f}}} = 0.3. \hfill \\ \end{gathered}$$
(29)

The upper surface of the plate is exposed to a line load travelling along the x axis with a constant velocity of v:

$$F = 400\frac{{{\text{kN}}}}{{\text{m}}},x_{0} = vt$$
(30)

The following dimensionless deflection is used to express results:

$$W = \frac{w(a/2,b/2)}{{h_{{\text{c}}} }} \times 1000.$$
(31)

Unless mentioned otherwise, hs, Ks and Kw are respectively 10 mm, 0.0 GPa m and 1.0 GPa/m, respectively.

Influence of the foundation stiffness on dimensionless central deflection of SSSS sandwich plates subjected to a moving load (v = 20 m/s) for two porous distributions with fraction of 0.2 and (n, m) = (1, 1) is considered and the resulted magnitudes are provided in Table 2. As depicted in Table 2, the elastic foundations can lead to a considerable decline of the dynamic dislocation in all cases. The plates with even porosity pattern have the largest dynamic deflection of − 1.55 when Kw = 0 and Ks = 0. The deflection of plates resting on an elastic foundation with even and uneven porous cores as well as Ks = 0.1 GPa m and Kw = 1.0 GPa/m t falls noticeably to − 1.13 and − 1.04, respectively.

Table 2 Effects of elastic foundations and porosity distributions on the supreme amount of deflection of the sandwich plate (SSSS)
Full size table

Figure 6 demonstrates how the material gradient factors (n, m) affect the transient vertical displacement of sandwich SSSS, SCSC and CCCC plates with even porous 2D-FG core \(\left( {\alpha = 0.2} \right)\) under a moving load with a velocity of 20 m/s. For all three sorts of boundary conditions, it is evident that with a rise in the quantity of material gradient indexes (n, m), a greater dynamic deflection will be seen since climbing these parameters result in decreasing the bending rigidity of the sandwich plate. It is also seen that the influence of the index (n) is much noticeable in comparison with the grading index (m) when the plate edges are SCSC and CCCC.

Fig. 6
figure 6

Effects of the material gradient indexes (n, m) on dynamic behavior of the uneven porous 2D-FG sandwich plate; a SSSS, b SCSC, c CCCC

Full size image

The non-dimensional central deflection of a SSSS sandwich plate subjected to a moving load (v = 20 m/s) is plotted in Fig. 7 for even and uneven porosity distributions, respectively. It is obvious from Fig. 7 that the dimensionless dynamic displacement of the plates increases with a growth in the values of porosity fractions. In comparison with the uneven distribution, the influence of the imperfection rise is much greater when the plate is defected with even porosity distribution, see Fig. 7a. In this case, the dynamic deflection increases to 0.22 and 0.36 unit by rising the porosity fraction of 0.2 and 0.4, respectively.

Fig. 7
figure 7

Impacts of the porosity coefficients on dynamic behavior of the SSSS sandwich plates; a even porosity distribution, b uneven porosity distribution (n = m = 1)

Full size image

Figures 8a–c, respectively, show non-dimensional transient deflection at the center versus different magnitudes of Ω (= hf/hc) for n = m = 1 with SSSS, SCSC and CCCC boundary conditions, respectively. It is presumed that v = 20 m/s, α = 0.2 and porosity distribution is even. From these figures, it is seen that the dynamic deflections decrease remarkably with a rise in the value of Ω for every edge constrain. The most significant decreases due to ceramic layers can be shown when Ω changes from 0 to 0.05. It is also seen from these figures that SSSS case offers greater effects on the reduction of dimensionless dynamic displacements in all face layer’s thicknesses. For instance, the face layer with depth ratio (Ω) of 0.1 condenses the vertical displacement of the SSSS plate with no face surfaces about 0.98 unit whereas it is 0.718 and 0.507 for the SCSC and CCCC plates, respectively.

Fig. 8
figure 8

Non-dimensional vertical displacement at the center of the 2D-FG sandwich plate with porosity distributed evenly through the thickness exposed to a moving load in various boundary constrains (α = 0.2, n = m = 1, v = 20 m/s); a SSSS, b SCSC, c CCCC

Full size image

5 Concluding remarks

The nonlinear transient behavior of sandwich plates with porous 2D-FG cores subjected to moving mechanical loads supported by the elastic foundations with SSSS, SCSC and CCCC boundary surroundings has been explored. Having governed by FSDT along with von Karman nonlinearity, the kinetic equations have been solved by implementing the kinetic dynamic relaxation method coupled with Newmark’s integration approach. In this investigation, two types of porosity distributions have been considered, and the effects of imperfection distributions and coefficients, parameters of elastic foundation and boundary conditions have been analyzed. From the numerical results, the following conclusions are noticeable:

  • Elastic foundations offer more reinforcing effects when plates have imperfections in the even pattern.

  • Transient responses of the plates increase with an increment in the magnitudes of porosity fractions; and compared to the structures with even micro-voids, the ones with uneven porosity have the lower bending deformation.

  • The dynamic characteristics of the structure are highly influenced by material properties parameters (n, m); and the longitudinal functionally graded factor (n) has a superior impact on CCCC than SSSS sheets.

  • The effect of face layer’s thickness on the dynamic response of SSSS plates is more noticeable compared to that of SCSC and CCCC plates. So, it can be said that the impact of the face layer’s thickness on the decrease of displacement growths by decreasing constrains on the plate edge surroundings.