Monte Carlo Tree Search as an intelligent search tool in structural design problems

Abstract

Monte Carlo Tree Search (MCTS) is a search technique that in the last decade emerged as a major breakthrough for Artificial Intelligence applications regarding board- and video-games. In 2016, AlphaGo, an MCTS-based software agent, outperformed the human world champion of the board game Go. This game was for long considered almost infeasible for machines, due to its immense search space and the need for a long-term strategy. Since this historical success, MCTS is considered as an effective new approach for many other scientific and technical problems. Interestingly, civil structural engineering, as a discipline, offers many tasks whose solution may benefit from intelligent search and in particular from adopting MCTS as a search tool. In this work, we show how MCTS can be adapted to search for suitable solutions of a structural engineering design problem. The problem consists of choosing the load-bearing elements in a reference reinforced concrete structure, so to achieve a set of specific dynamic characteristics. In the paper, we report the results obtained by applying both a plain and a hybrid version of single-agent MCTS. The hybrid approach consists of an integration of both MCTS and classic Genetic Algorithm (GA), the latter also serving as a term of comparison for the results. The study’s outcomes may open new perspectives for the adoption of MCTS as a design tool for civil engineers.

Introduction and state of the art

Modern structural engineering is a discipline that strongly relies on computationally intensive methods. On the one hand, procedural, rule-based work-tasks as calculating, drawing, and preparing technical reports are already largely automated and integrated in Building Information Modelling (BIM), also thanks to widespread commercial and scientific applications. On the other hand, for those tasks concerning higher-level skills—as choosing an effective load-bearing structural system, construction material or supporting the idea of automated design—there is plenty of space for research, especially within the fiercely expanding area of Artificial Intelligence (AI) [1]. The application of AI in structural engineering has the potential to improve the work efficiency of experienced engineers, to support effectively unexperienced technicians and to share and spread the knowledge within professional engineering teams. First successful attempts to use AI and computers for the generation of design concepts date back to the 1980s (e.g. [2, 3]). Since then, several projects focusing on various techniques as inductive learning (e.g. [4, 5]), deep learning and neural networks (e.g. [6,7,8,9]), constraint search (e.g. [10]), evolutionary computation and genetic algorithm (e.g. [11,12,13,14]), cellular automata (e.g. [15, 16]) or generative approaches (e.g. [17]) were carried out.

Looking at existing studies, we found that, while developing an intelligent tool to solve structural design tasks, limitations may arise with regards to, at least, three different aspects: (1) the lack of generality and portability of the selected methodologies; (2) the unavailability of sufficient training data; (3) a computational effort that grows too rapidly as problems’ complexity grows. Considering this, we believe that a successful approach to the problem of automated structural design should be (1) as portable as possible, (2) data independent, and (3) computationally efficient. Interestingly, in 2016, Silver et al. [18] showed that adopting the so-called Monte Carlo Tree Search (MCTS) algorithm [19]—with support of deep neural networks [20]—can represent a huge step forward in this sense. In particular, Silver et al. [18] demonstrated how computers can outperform humans on the complex board game Go [21]; such task was for long considered untreatable by machines, as the game has a search space of 10¹⁷² possible different configurations, and requires the development of a long-term game strategy. Since its inception, MCTS was indeed successfully implemented in many board games [22,23,24,25], protein folding problems [26], chemical design applications [27], planning and logistics [28, 29], and is currently intended as one of the best approaches in Artificial General Intelligence for games (AGI) [30]. Interestingly, as of 2021, only a small number of engineering-related applications of MCTS exist [31, 32].

As discussed in the next section, MCTS has the potential to be successfully applied to many different civil engineering problems, especially those concerning structural design. Indeed, on the one hand, the latter is characterised by rules and procedures that can easily be translated into code. On the other hand, complex design processes in engineering are often solved on the basis of experience and already known solutions from previous projects. In many cases, this leads to uneconomic structural solutions, as the limited view in combination with working time pressure prevents innovative and problem-oriented alternatives. The support of complex design processes in civil engineering may require evaluating a huge number of different solutions. Interestingly—as observed by Edelkamp et al. [29]—MCTS can deal not just with “deterministic, fully observable, discrete, static” environments, but also with “stochastic, partially observable, dynamic, continuous” environments. The development of structural design and structural safety procedures may benefit from this latter point.

In the following, first of all, we introduce MCTS. Secondly, we report the pseudocodes adopted for the considered application. As a third step, we describe the engineering problem we focused on, also providing insights about how to actually implement the methodology in the specific engineering context. Fourth, we describe a case study, so to provide the reader with numbers about MCTS’s performance as a search tool. Finally, we evaluate results and then discuss possible limitations, also taking Genetic Algorithm [33] as a term of comparison.

Methodology

Monte Carlo Tree Search

MCTS (e.g. [19, 34]) is a search technique that works on a tree data structure; from a single initial node (the root), other nodes are added that represent different instances of the search space S. The MCTS is aheuristic, i.e. it does not require task-dependent heuristics [35]: knowing the available actions at each step, and their corresponding outcomes (including stop conditions) is sufficient for it to run. Also, the algorithm is anytime, i.e. it can determine the next step to take within any time budget. Finally, it is selective, that means it can grow the search tree asymmetrically, favouring those branches that host the most promising moves [36]. MCTS is often used in board- and video-game environments [25, 30, 37,38,39], where a tree’s node may represent a player’s move, while the end of a match stops the expansion of the tree.

MCTS algorithm consists of four main steps, i.e. Selection, Expansion, Roll-out and Back-propagation (see Fig. 1—adapted from [35]). The steps are repeated iteratively until a stop condition emerges. During Selection, starting from the root, the tree is descended so as to find a not fully expanded node—n^*—for the sake of brevity, here referred to as a leaf. The path from the root to the leaf is determined by using a selection policy (e.g. [40]) that suggests the best promising moves. Then, from the selected leaf, a node is added to the tree (Expansion phase). The branch to be expanded can be selected randomly, while avoiding the repetition of already existing sibling nodes. As a third step, the roll-out (i.e. a simulation that continues until a terminal state is reached) is performed; during it, nodes are generated and temporarily incorporated into a solution, but not permanently added to the tree. Finally, the reward of the roll-out is back-propagated from the node selected for expansion (n^*), back to the tree’s root. In this way, the agent is informed about the quality of the search iteration it performed. In Fig. 2, we show MCTS’s pseudo-code, adapted to our study from existing literature (e.g. [30]), is shown. As a first research step, we adopted the algorithm’s basic formulation; other, more sophisticated approaches, such as SP-MCTS [41] may be considered in further research initiatives. In the present work, both the algorithmic and the engineering parts were coded from scratch, in Java.

Fig. 1

adapted from Chaslot et al.

A scheme of the Monte Carlo Tree Search algorithm—[35]

Fig. 2

MCTS’ pseudo-code adapted in the present study

The meaning of the parameters included in Fig. 2 are given in the following.

• PD, problem’s dimension. It is the number of single different moves the MCTS agent can take as a first step (i.e. the branching factor at root node).

• FG, fitness goal. It is a real number in the range [0, 1], representing the performance goals in terms of solution’s fitness.

• RL, roll-out length. It is the maximum number of moves to be played on the roll-out phase. We set it as a random integer between 1 and the number of moves actually possible at the considered step. Randomness is adopted as we want not all the roll-outs to end with the same number of played moves. The point is, in our non-adversarial (1-player) approach, there is no direct opponent that can terminate the descent of the tree by winning/losing/drawing the game; we wanted to avoid that roll-outs not reaching the performance goal (a stop condition) would finish with a saturated board, as this would have biased the search.

• move_available (n). It is a function that returns true if the tree can be expanded; it returns false otherwise.

• is_leaf (node). It is a function that, given a node, returns a Boolean value about it being or not being a leaf node.

• best_child (node). It is a function that, for any given node, returns its best performing child-node (or one of its best child-nodes, in case of an ex aequo). As shown between lines 7 and 9 of the pseudo-code of Fig. 2, the MCTS algorithm calls best_child function as soon as the tree descent reaches a node that is not a leaf.

• add_random_child_node (node). It is a function that, given a node, adds randomly one of the non-explored successor nodes.

• roll_out (node, int). It is a function that, from the given node and max number of moves, performs roll-out and returns the level of fitness performed.

• back_propagate (node, double). It is a function that takes as an input both a node and a value of fitness, and back-propagates the latter from the given node, back to the root of the tree.

The back-propagation consists of updating both the sum of rewards (expressed in terms of fitness value) and the number of simulations executed, for each node between the tree’s root and the node from which the last roll-out was launched. In the following algorithm’s iteration (if any), such parameters are used by the best_child function, to determine the most promising node so far. In particular, in this study, we follow the Upper Confidence Bound 1 applied to Trees (UTC) approach (see Formula 1), as suggested by Kocsis and Szepesvári [40] to balance both exploration and exploitation of the state under consideration:

$$\genfrac{}{}{0pt}{}{\mathrm{argmax}}{i}\genfrac{}{}{0pt}{}{\left\{\frac{{\Sigma r}_{i}}{{n}_{i}}+c\cdot \sqrt{\frac{\mathrm{ln}{N}_{i}}{{n}_{i}}}\right\}.}{}$$

(1)

The meaning of the literals of Formula 1 is the following: i is the index of the node, $\Sigma$ r_i is the sum of the rewards for child node i, n_i is the number of simulations conducted for child node i, N_i is the total number of simulations executed from the parent node of node i, c is the exploration parameter, empirically set. In our study we fine-tuned the value to 0.8.

While solving a search task, MCTS does not carry out a full simulation of the search space. On the contrary, the search tree usually grows in an asymmetric fashion.

Adapting the reference algorithm to the envisaged problem

In our study, we adapted the default MCTS methodology to the specific needs of the envisaged engineering problem, as follows. First of all, the search is intended at finding reinforced concrete (RC) structures that satisfy a given fitness goal in terms of specific engineering aspects. We intend a structure as made of a rigid slab (that incorporates rigid horizontal RC beams), supported by vertical RC bearing elements (columns and walls); the algorithm creates different design hypotheses (or trials) by changing (1) shape, (2) size, (3) number and (4) position of such elements. In this context, the root node represents an empty design, while any other node represents a trial RC structure with certain characteristics and corresponding fitness value. The tree is the data structure in which all nodes are organized. In Go-related applications of MCTS (e.g. [39]), adding one node to the tree means placing one stone on the game’s board. In our study, the addition of a node to the search tree represents the insertion of a unitary bearing element (i.e. the minimum amount of structural material that can be added, in the following also called design unit) to an existing hypothesis. In this way, the algorithm creates child-nodes from nodes; the existence of a logical edge between parent- and child-node makes it possible to link a trial structure’s performance to that of all its ancestors.

A node is called a leaf as long as child-nodes can be added to it (independently of its position within the tree). In the practical implementation of MCTS we propose, there is a limit to the maximum number of child-nodes (as discussed in Sect. 4). For what concerns tree descent, in this context it means going form the empty solution down to a leaf node, where a new trial structure can be added. As a trial structure (a node) is added to the tree, its potential as a possible intermediate step towards the final structural design is evaluated by executing a roll-out. This consists of adding (without including the corresponding nodes into the tree) a random amount of bearing elements to the above-mentioned trial and then testing the solution’s fitness. After this step, the performance of all the intermediate trial structures between the one from which roll-out started and the tree’s root is updated by back-propagation.

In two-player game applications, as presented by Silver et al. [39], before every move, each player performs one or more roll-outs (according to a search budget), to be able to identify the best next action. In general, the match’s outcome after a move cannot be controlled by the agent, as it is not known in advance which decision the opponent will take after it. For this reason, a high ratio of won games has to be discovered along the tree, and used to calculate chances of success for the moves to take. In our case study, there is no opponent for the agent; so (1) every path leading to a sufficiently performing solution corresponds to reaching the goal [41], and (2) any path of the search tree, in accordance with the budget of moves, is de facto possible. Considering this, and considering that we express performance as a decimal number in the range [0, 1], in order to provide feedback to the algorithm, we took the level of performance achieved at the end of a path as a proxy for r_i. The measure we adopted for performance is presented in Sect. 3.

Term of comparison

In this work, we consider a Genetic Algorithm (GA) [33, 42, 43] as a benchmark for the results obtained with MCTS. The GA-approach was chosen as it is largely widespread in multi-objective search problems [44]; also, it has some relevant features similar to MCTS. First of all, it does not need an analytical model of the system to be investigated, but rather just a list of admissible actions and corresponding consequences at each step. Second, it can start from zero knowledge about the quality of the solutions; in other words, no external data are needed to train the algorithm. Third, it can be interrupted at any time while running: stopping it before reaching the performance trigger would just affect the goodness of the obtained solution. Fourth, both MCTS and GA can explore a search space in an asymmetrical way. This is important for civil engineering applications, where the number of branches of technically possible solutions is extremely large, but most of them have to be disregarded as just tiny minority scores sufficiently well. As a parallel to Fig. 2, the pseudo-code of the GA algorithm we implemented (in Java) is given in Fig. 3.

Fig. 3

Genetic Algorithm’s pseudo-code—adapted from [33]

The meaning of the parameters listed in Fig. 3 is given in the following:

• FG, fitness goal. It is a real number within the range [0, 1], representing the performance goals in terms of solution’s fitness.

• PS, population size. It is the number of solutions that form each generation.

• NI, maximum number of iterations. It is the maximum number of generations that can be produced by the agent during the search.

• CR, crossover rate. It is the percentage of solutions selected for reproduction by means of crossover.

• MR, mutation rate. It is the percentage of solutions undergoing mutation. In a given solution, a mutation consists of losing and/or getting a number of cells between 1 and 5.

• IR, immigration rate. It is the percentage of brand-new solutions introduced at each generation.

Numerical values of the parameters are reported in Sect. 4.

The agents

In the following, we show two different agents based on Monte Carlo Tree Search: the first one (also called MCTS) is a direct implementation of a plain, 1-player version of the algorithm, as reported in Figs. 1 and 2. The second one, (so-called MCTS-GA), is a hybrid agent, that makes use of both MCTS and classic Genetic Algorithm, in two consecutive steps. This agent first uses MCTS to rapidly explore the solution space, starting from zero knowledge about the final solution, and looks for a sufficiently good, but still imperfect design hypothesis. As a further step, the agent makes use of a Genetic Algorithm to refine the imperfect design. In practical terms, MCTS-GA executes the pseudo-code showed in Fig. 2 as long as its best design hypothesis’ fitness is lower than a certain fraction of the fitness goal (FG). After reaching this partial target (that we tuned to 80% of FG), it stops the execution of MCTS, and starts running our implementation of the pseudo-code given in Fig. 3 (i.e. GA). In doing this, the Genetic Algorithm takes as first-generation PS (i.e. population size) copies of the best design hypothesis previously elaborated by MCTS. The whole search job ends as soon as the fitness level reaches the full value of FG.

Additionally—in order to have a reference for the achieved performance levels—we included two other agents (GA1 and GA2), these being two implementations of classic GA, with different values of controlling parameters (see Sect. 4).

Structural design tasks as search problems

When dealing with structural design tasks, engineers often have to explore a vast space of possible alternatives. But exploration comes at a cost, as developing one design instance requires (1) qualified workforce, (2) additional time to product delivery and (3) computational resources. In this sense, as long as a technical problem can be described analytically in a way the algorithm can handle, MCTS may result in being quite helpful, as it operates effectively in vast search spaces, with a limited number of instantiations [22].

Many structural engineering design problems could be treated just as search-problems with a vast solution space. We prove this, with an example. Let the work task consist of designing an earthquake-resistant u-storey reinforced concrete building, with v load-bearing elements at each storey. In this problem, the shape, size and positions of the bearing elements affect the dynamic response of the building and determine the seismic response to be considered in the calculations. We call w, the number of possible different cross-sections for a single load-bearing element at ground floor. We assume that, once the cross-section at floor i-1 has been selected, the number of possible alternatives for the element immediately on top of it (i.e. that at floor i) is immediately reduced—for consistency reasons—by a factor of x. Both variables are integers and at least equal to 1. As a consequence, for each set of t load-bearing elements on the same vertical line, the number of possible different solutions—y—is as given in Formula 2.

$$y=\prod_{k=0}^{u-1}\mathrm{max}\left\{\left\lfloor \frac{w}{{x}^{k}}\right\rfloor, 1\right\}.$$

(2)

The possible different combinations of vertical elements for the whole building is equal to z = y^v. As an example, with u = 6, v = 49, w = 36, x = 4, we get y = 648 and then z ≈ 5.85, the total number of combinations would be 10¹³⁷ (for sake of brevity we ignored the design options concerning the beams). With a machine capable of evaluating 100 × 10⁹ different structural models each second (that is far from true, as a structural calculation can take seconds to minutes to be completed), the full exploration of this search space would take 10¹¹⁸ years to be finished on a regular desktop machine.

Similar problems can be developed for steel and masonry buildings as well, this proving that search problems concern many different applications in practical structural engineering.

Definition of the considered structural problem

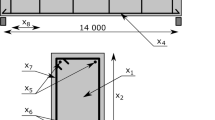
In this paper, we consider a simple reference design problem, to show how MCTS may be integrated among structural engineering design tools. The problem consists of a one-storey RC building with a rigid horizontal slab placed on both columns and shear walls as vertical load-bearing elements. Beams are considered as part of the slab. The task is to define number, shape, size and position of the load-bearing elements, so to achieve specific targets (θ) in terms of the dynamic behaviour of the structure. Targets are expressed in terms of (1) a selected main translational periods (T_X, T_Y) [45], and (2) maximum distance between the centre of mass (CM) and the centre of stiffness (CS) of the structure [45]. The problem can be simplified to a single degree of freedom (SDOF) as illustrated in Fig. 4, where (1) the mass m is obtained from both the slab’s and (half of the) vertical elements’ mass, while (2) stiffness values K_x and K_y depend (as an assumption) just on flexural deformability of the bearing elements. More in detail, horizontal stiffness in the direction i – K_i—is obtained as given in Formula 3 [46].

$${K}_{i}=\sum_{s=1}^{n}\frac{12 E{J}_{s,i}}{{h}_{s}^{3}},$$

(3)

where n is the number of RC bearing elements; E is concrete’s Young Module (assumed always equal to 30,000 MPa); J_s,i is the moment of inertia around the axis orthogonal to direction i; h_s is the height of the sth bearing element (always assumed equal to 3.0 m).

Fig. 4

SDOF system of the one-storey RC building

Once the story’s lateral stiffness in the direction i is known, the correspondent vibration period—T_i—can be calculated as given in Formula 4 [45].

$${T}_{i}=2\cdot \pi \sqrt{\frac{m}{{K}_{i}}}.$$

(4)

To resemble real-life projects’ requirements, while looking for suitable combinations of bearing elements, our agents have to observe rules. First of all, we assume that design units cannot be placed everywhere on the ground-floor; on the contrary—so to simulate real-life design limitations—positions exist where they are not allowed (see white-coloured 1-cells in Fig. 5); we call such limitations geometric constraints (γ). Second, we do assume that the building’s storey has a squared shape, with an assigned value of the distributed mass of η t/m² (these being design assumptions, υ). The set of target values θ, geometric constraints γ, and design assumptions υ forms a design task, δ.

Fig. 5

a Example of a design task in a 4-by-4 grid. b Insertion of a bearing element in a free cell of the task’s grid. c A 3D view of the inserted bearing element

Problem’s analytical description and assumptions

To be able to handle the problem analytically, we discretized the structural plan into a grid of identical squared cells; each cell hosts an integer value from the set {0, 1, 2}. Zeros (0) identify free positions, i.e. locations were a design unit can be placed; one (1) values stay for unavailable locations, i.e. cells not accessible to the agent for selection. As bearing elements are inserted, free positions are filled with the number two (2).

All the envisaged agents operate on the grid by changing one single cell at a time. MCTS can just add design units (in the expansion step)—see for example Fig. 5a–c—while GA can both add and remove them (using crossover and mutation). Every time a design unit is added or removed, the global geometry of the bearing elements changes and has to be re-computed. In addition, if any two cells come to have a side in common, they are considered as belonging to the same structural bearing element. On one hand, the insertion of a design unit in a certain position can lead to two, three or four different bearing entities (columns and/or walls) being unified into a new, larger structural element; on the other hand, the removal of a design unit may provoke disconnection and separation of one structural element in up to four new smaller and independent entities. Because of this, in our study, the agents’ search space is characterised by strong discontinuity and non-linearity. As an example, Fig. 6a–c show how the number of bearing elements and as a consequence the horizontal stiffness of the storey along the X-direction can change drastically in just one single step. In the code, a specific procedure to update the global geometry of the load-bearing elements in case of insertion or removal of a bearing units was developed and implemented. (In our study, as a work hypothesis, we set no limitations to the shape and size a bearing element can have, as long as (1) it is obtained by putting squared cells together, and (2) it is consistent with γ.)

Fig. 6

Example of discontinuity in the design process. a Two distinct plain walls along the Y-direction. b One single H-shaped structure. c 3D view of the H-shaped structure

In Fig. 7, we show an example of the MCTS’ four steps; it was obtained by adapting Fig. 1 to the specific search of our problem. In Fig. 7a, the tree is already partially developed; the root is not a leaf anymore, so the best_child() function is called to select the most promising branch. (In the figure, a light-grey triangle with a white circle on top represents a sub-tree we omitted for the sake of clarity.) In Fig. 7b, a leaf node is expanded with the addition of a new node. In Fig. 7c, a roll-out is performed, till a reward is generated. Finally, in Fig. 7d, the reward is back-propagated, by updating the values of total reward and number of simulations performed all along the path back to the tree’s root. After back-propagation (as suggested by the transparency of the node at the bottom of the tree in Fig. 7d), those nodes created within the roll-out are discarded.

Fig. 7

Visualisation of MCTS’ four steps as envisaged in the present study

Problem’s search space

In Silver et al. [18], the MCTS application for the board game Go had to consider a search space of the order of 10¹⁷² different configurations. In that study, the algorithm proved to work effectively, also due to its integration with Deep Neural Networks. In our work, as the first attempt at an application in the realm of structural engineering, we adopted some limitations. First of all, our search space’s maximum dimension (problem’s initial branching factor) is up to 2.239¹⁰². Such number is obtained by generating grids with a total of 340 zero-cells, and then letting the agent decide whether to place or not to place a design unit in each of them (the total dimension of the grids is always 20-by-20 cells). For each task we posed, many combinations could fit as an acceptable solution. In general, the more solutions exist for a design task, the easier for the agent to find them. Unfortunately, telling in advance how large this number is, is not trivial, also because design tasks δ may be very different from each other. The GA-based agents will serve as a term of comparison of design task’s complexity. As a second limitation, at this stage, we discarded any neural network as a support for the MCTS-agent, as well as nested algorithm’s architecture existing in the current literature [34].

Performance measures

For all the agents, performance has to be measured each time a new structural solution is generated. On the one hand, this happens at the end of any roll-out phase. On the other hand, it is needed as new items are included in the solutions pool. Formula 5 is applied to calculate the performance of the i-th solution, p_i.

$${p}_{i}=\mathrm{max}\left\{ \frac{ A+ B+\lambda \cdot \Gamma }{2+\lambda }, 0\right\},$$

(5)

where

$$A=1- \frac{\left|{T}_{x,i}{- T}_{x}^{*}\right|}{{T}_{x}^{*}},$$

(6)

$$B=1- \frac{\left|{T}_{y,i}{- T}_{y}^{*}\right|}{{T}_{y}^{*}},$$

(7)

T^*x is the target translational period in X-direction; T^*_y is the target translational period in Y-direction; T_x,i is the actual translational period in X-direction of the ith solution; T_y,i is the actual translational period in Y-direction of the ith solution; λ is a control parameter with values in {0, 1}; it is used for including or excluding the distance component from the performance assessment. Γ is the component explained in Formula 8;

$$\Gamma =\left\{\begin{array}{c}1- \frac{{d}_{i}-{d}^{*}}{{d}^{*}},\quad \mathrm{if} \,{ d}_{i}>{d}^{*}\\ 1,\quad \mathrm{if} \,{d}_{i}\le {d}^{*}\end{array}\right.,$$

(8)

d^* is the target distance between the structure’s centre of mass (CM) and centre of stiffness (CS); d_i is the actual distance between the structure’s centre of mass (CM) and centre of stiffness (CS).

In the tests, performance goals of both 95.0% and 97.5% are used; such high level of request forces the agents to look for solutions that satisfy more than one requirement at a time.

Case studies

To test the performance of the envisaged MCTS algorithm, and to compare it with the GA-approach, four different test families are executed, each one consisting, by assumption, of two hundred different design tasks. Reporting all the inputs and outputs of the tests is not possible; in Fig. 8 we show an example of the initial arrangement of the grid in a design task. In the Figure, light-grey cells represent locations where bearing elements are allowed, while pale-blue cells indicate geometric constraints. Features of the design task presented in Fig. 8 are reported in Table 1 (see test family number 2), while the solutions found by the four agents (and the corresponding numerical values of the design variables) are given in Sect. 5 (both in Fig. 9 and Table 3).

Fig. 8

Example of a design task δ in a 20-by-20 grid

Table 1 List of design tasks’ features considered for the case studies

Fig. 9

Example of the four agents’ solutions for a design task of test family #2. a MCTS’; b GA1’s; c GA2’s; d MCTS-GA’s

The tasks’ features (i.e. θ, γ, and υ) we selected for the case study were intended to make the search jobs both meaningful and feasible. First of all, the agents were expected to develop solutions by using structural elements whose dimensions are comparable to those of real buildings. Secondly, the target periods on the two directions X and Y were chosen different enough (see Table 1), so that a structural system of just squared pillars, with its symmetry of both translational mass and translational stiffness, will never represent an acceptable design solution. In other words, we made impossible for the agents to solve any design task by simply scattering a set of single design units on the grid. On the contrary, walls have to be introduced, so to differentiate the translational stiffness along with the two main directions (X and Y). At the same time, the existence of walls requires a progressive evolution of the design hypotheses as, in the grid we envisaged, they are quite unlikely to be obtained just by the initial random disposition of design units. (We allowed the generation of structures with RC-walls of any possible shape, i.e. also those unusual ones, commonly disregarded by engineers). Regarding feasibility, we limited the number of grid cells to 400; indeed, we adopted a grid of 20-by-20 squared cells (each one with a side of length 250 mm). Constraints were generated randomly—so to avoid biases in the design tasks—by rearranging 60 grid’s cells in rectangular shapes of different proportions. As a result, in any task, there are 340 zero (light-grey) cells where the agent can place design units (in other terms, the problem’s initial branching factor is 340). By taking a slab’s unitary mass η equal to 500 kg/m², and setting the target vectors θ as given in Table 1, we found four families of design problems that fit with our requirements. (In Table 1, performance goal refers to numerical values obtained by Formula 5.)

As the reader can see in Table 1, just two of the four test families include a non-zero λ. This means we considered the distance between the centre of mass and centre of gravity just half of the times.

For what concerns the Genetic Algorithm, as reported in Table 2, two different sets of values for the two main parameters CR and IR were adopted, so to have quite a wide spectrum for such approach. In the so-called GA1, we let the best 10% of the population survive and then generate, by crossover, 70% of the new pool of solutions. The remaining 20% is obtained by introducing brand new solutions (immigration). In GA2, on the contrary, 80% of a pool is obtained by immigration, while crossover represents just 10% of a pool. Both for GA1 and GA2, we set the chances of solutions developing mutations up to 20%, so to avoid the risk of search being stack in local optima. For each solution, we set the maximum number of design units that can undergo mutation to the value of 5 (such value was tuned by observing the GA-agents’ average performance on the assigned design tasks). In both cases, a population is made of 100 solutions.

Table 2 Parameters’ values for the two GA-agents

For the way the tests were set, GA represents quite an effective tool for solving a given task. Indeed, solutions are obtained by progressively adjusting cells on the board. As GA has the faculty of adding and removing design units (by using crossover and mutation), it can explore the search space without any need to look for moves in the future. On the contrary, MCTS can just add design units to the board and, if one of them has to be excluded from the final solution, the agent has to develop a new sub-branch of the search tree (that requiring more roll-outs).

Comparing results

The discussed methodology could be adopted for two main search targets in practical engineering applications. On the one hand, the discovery of convenient, otherwise inaccessible technical solutions; on the other hand, keeping computation-time to solution in line with conventional approaches. In this work, a first research step on the topic, we considered a relatively simple design task. For this reason, in the following we take just computation time as a key factor to show the methodology’s potential. In this regard, wanting to confront the results of MCTS and GA, we had to find a meaningful shared metric, as the two algorithms work on different data structures. On one hand, MCTS creates trees; on the other hand, GA generates pools of parallel solutions belonging to the same generation. In our study, each design hypothesis undergoes just one single calculation. (In MCTS, this happens every time a roll-out is executed; in GA, we have this at each fitness-evaluation step. In order not to overestimate the calculations needed for the GA-approach, we stopped evaluating a generation, as soon as one of its solutions overcomes the performance goal.)

In real life engineering, a single structure may require tens of analyses—whose duration is in the order of minutes—to be fully tested against code requirements; this is the case, for example, of modern pushover procedures [45] when conducted in compliance with current building codes’ standards (e.g. [47]). Computation time could be considered as a linear function of the number of hypotheses actually tested. In addition, when compared to structural calculations, auxiliary software modules concerning tree descent, back-propagation of performance, generation of new pools of solutions, or mutation, are negligible in terms of computational effort. For this reason, when comparing MCTS and GA, we took as a metric just the number of design hypotheses tested before a suitable solution is found, in the following referred to as H. In general, the larger the value of H, the more numerous the design hypotheses an agent needed to reach the performance goal in a design task. In other words, H represents the inverse of the effectiveness of an agent on an assigned search job.

In the tests, we did not provide our search agents with any initial knowledge about where to look for solutions; nonetheless, to limit the number of design hypotheses as much as possible and make the two agents based on MCTS actually competitive with GA, we had to add two basic heuristics: first, the maximum number of moves that can be taken from the root to a terminal state was assumed equal to 50. Second, the maximum number of child-nodes (at any step of the tree descent) was set equal to 4—this determines at which point a node stops being expandable (see Sect. 2 and Fig. 2). The first limit is obtained considering that no design task we posed requires more than 50 design units on the grid to be solved. The second restriction, whose numerical value was fine-tuned by trials, is intended to keep the search tree reasonably narrow, especially at first steps of tree expansion, i.e. at a stage when almost every choice can be considered acceptable by the agent, as there is limited or no feedback about the quality of the moves. Putting no limitations in the initial expansion would lead to a ramification of the search tree up to the branching factor, so compromising the agent’s performance in terms of tested design hypotheses. Also, we considered that, for the way the problem is posed, the performance of a whole design hypothesis is only limitedly dependent on the very first moves of the design agent.

The proposed limits do not represent a reasonable choice for every possible implementation of MCTS in structural engineering. On the contrary, for different design problems and with different performance metrics, they should be reconsidered.

Tests’ results are presented and discussed in the following section.

Results

In the analyses, we grouped tasks by families; each family consists of 200 comparable design tasks, i.e. problems we produced by using the same values for both design assumptions (υ) and target values (θ) (see Table 1), and by generating different combinations of same-dimension geometric constraints (γ). Each algorithm ran once per each task, i.e. 200 times per task family. Neither time limitations nor memory budget were set on the analyses.

To provide the reader with reference solutions, to be used in future studies, in Fig. 9 we report the four agents’ solutions for the design task of test family #2 already presented in Sect. 4; in light grey the area where bearing elements could be placed; in pale blue the geometric constraints; in black the bearing elements placed by the agent (i.e. the structural solution found). In Table 3 we show the parameters of the solutions found by the four agents in the example design task.

Table 3 Parameters and number of design hypotheses (H) of the solutions found by the four agents for the example design task

Looking at Table 3, it is clearly visible how MCTS-GA outperformed the other three agents in terms of number of design hypotheses (H) needed to reach target performance values (p_i). On the contrary, the MCTS-agent has the worst performance in this regard; nonetheless, the structural solution found by MCTS is more refined, as it is obtained with the smallest number of design units on the grid (also thanks to the presence of an “L-shaped” wall). This second design aspect is more related to the overall quality of the design. However, in the following, we will evaluate results just in terms of H, as comparing quality of solutions would require a much larger investigation, well beyond the scope of this first research step.

As a further step, we report an example of the performance pattern we obtained from the MCTS-agent: on the one hand, Fig. 10 shows numerical values obtained as per Formula 5 (i.e. agent’s overall performance). On the other hand, Fig. 11 presents values we obtained for overall performance’s components (Formulas 6, 7 and 8). On both cases, values were sampled every 10 design hypotheses.

Fig. 10

Example of sampled path for overall performance of the MCTS-agent

Fig. 11

Example of a sampled path of performance components A, B and Γ for the MCTS-agent (as per Formulas 6, 7 and 8)

From the figures, we notice two things. First, the values of performance oscillate quite till the end of the analyses. This depends (1) on the non-linearity of the problem and on the discontinuity of the search space (the addition on one design unit can dramatically change the performance), (2) on the random nature inherent in the methodology (that influences the rollout phase), and also (4) on the need for balancing exploration and exploitation (see the two terms included within the curly brackets of Formula 1) within the search. Because of the latter, as MCTS algorithm performs the search, it outputs design hypotheses that can have very different performance values, despite being released one after the other. Interestingly, in Fig. 10 the value of performance level is quite high since the very first steps of the search (i.e. it is greater than 80% after 10 samples, that means 100 design hypotheses). The choice we made of adopting a hybrid agent, that uses MCTS on the first part of a search job (rapidly exploring the search space), and then finalizes the design using GA is due to this experimental evidence we obtained.

Second, the numerical values the agent obtained from Formulas 6, 7 and 8 have different ranges. Among the sampled points, Γ is on average quite close to the value of 1.0; this depends both on the target distance range d^* we selected for the example (i.e. 1.0 m) and on the overall symmetric disposal of bearing elements, randomly added by the agent during the process. Some values of variable B are negative; this does not happen with values of A. The reason is that being the period target value in direction Y half than that in direction X (T^*_y = 0.0375 s, T^*_x = 0.0750 s), B’s positive codomain is half of A’s. As a consequence, the random process governing the agent’s search is more likely to produce negative values for variable B.

For what concerns overall tests’ results, in Table 4 we show how MCTS-GA outperformed all the other three approaches, in terms of a smaller amount of design hypotheses needed to solve an assigned task (H). (GA1 can be considered the best among the other three agents.)

Table 4 Relative number of times MCTS-GA outperformed MCTS, GA1 and GA2, respectively

In Table 5 we show essential statistics about variable H, for the four agents. While reporting results, we included the estimation of both mean (m_H) and standard deviation (s_H) of the variable; this makes possible for the reader to understand overall agents’ results on the four test families of 200 search jobs each. In addition, to extend the validity of results beyond the limits of the hundreds of design tasks here considered, in Table 5 we included lower and upper bounds (ξ_inf and ξ_sup) of the 95%-confidence interval of H (computed as per Formula 9). Such bounds make it possible to obtain intervals where real mean values of variable H (i.e. μ) have 95% probability to be (intervals are graphically reported in Fig. 12).

$${\xi }_{\mathrm{in}f}= m-1.96\frac{s}{\sqrt{n}} \le \mu \le m+1.96\frac{s}{\sqrt{n}} = {\xi }_{\mathrm{sup}},$$

(9)

where m is the average number of design hypotheses needed to reach the performance goal; s is the sample’s standard deviation, of variable H (i.e. of the number of design hypotheses needed to reach the performance goal); this is taken as an estimator of the actual standard deviation of the corresponding distribution, σ; n is the number of times the algorithm has run; μ is the average value of the real distribution, within the 95% confidence interval.

Table 5 Mean and standard deviation values of the number of design hypotheses needed (H) by the four agents

Fig. 12

Average values and 95%-confidence intervals of the number of design hypotheses tested before a suitable solution is found (H) for a given design task (δ); a test family #1; b test family #2; c test family #3; d test family #4

From data in Table 5, it clearly emerges how, for the proposed set of design problems, MCTS-GA always presents the lowest values for the mean of H. On the contrary, its standard deviation is not always the smallest (as GA1 has a smaller one in test families 3 and 4). Looking at the results data, we noticed this is due just to a limited number of tasks where MCTS-GA needed a relatively large number of design hypotheses.

Values of Table are graphically depicted in Fig. 12. From the figure, the reader can understand, at a glance, how MCTS-GA represents the best option for solving a task of any of the four families.

Data we reported in Fig. 12 could be disaggregated into single data points; an example, regarding test family 1, is given in Fig. 13. Unfortunately, from such kind of representation is not clearly emerging how well one agent is performing in comparison to others. So, to have a clearer picture of the whole performance of the four agents, in Fig. 14 we plotted again their values of H; this time, we sorted each set of data by value. In this way, correspondence between ordinates at the same abscissa is lost, but we get a more understandable information about how the MCTS-GA-agent resulted more efficient in producing results for each batch of tasks as a whole. Indeed, for the vast majority of the tasks, its ordinates clearly stay below those of the other three agents.

Fig. 13

taken from test family #1

Values of H for the four agents—example

Fig. 14

Number of design hypotheses needed to solve the task—H—sorted for each agent. a Test#1. b Test #2. c Test #3. d Test #4

Results we included on both tables and charts of this section clearly show that a plain, 1-player version of MCTS, for what concerns computation time, is far from being competitive in the problem we posed. On the contrary, an agent based on Genetic Algorithm, whose values of IR and CR are those of GA1 (see Table 1), performs very well. Nonetheless, a hybrid agent, obtained from both MCTS and GA, outperformed all the other approaches we considered.

Limitations

The here-discussed work is not free from limitations.

First of all, we assumed that it is possible to describe a real-life structural design problem by using a grid of squared cells, so to resemble a representation often used in board- and video-games. More complex engineering tasks (like designing a multi-storey building), may require different approaches (e.g. also considering imperfect knowledge) and more extensive simulations (e.g. a stack of grids to be operated in parallel). Despite the software we developed is far from being a ready-to-use tool, its algorithmic kernel will stay the same in future applications.

Second, we took as assumptions, that (1) design performance is deterministically obtainable once the structural model is given, and that (2) material properties are uniform everywhere. Introducing uncertainty and non-uniformity will enrich the search space dramatically.

Third, as an initial research step, we kept the maximum number of possible alternatives in the order of 2.239¹⁰². With the help of high-capability computational resources, such value may be enlarged in future studies.

Fourth, we computed horizontal stiffness as a function of the sole flexural deformability and we considered all the load bearing elements as liner elastic. This may affect the straightforward application of the developed code in practical design problems but is irrelevant for what we wanted to prove in terms of engineering problems’ searchability with MCTS. Future developments may reduce the distance to real-life implementations, by taking into consideration, for example, buildings’ non-linear structural response and/or performance-based design. Such further step will require, under the same algorithmic approach, a revision of both the here-discussed performance goals (e.g., by introducing terms as inelastic structural response or expected seismic consequences) and the correspondent performance measures (e.g. inelastic vibration periods, and expected annual losses respectively).

Fifth, real applications in structural engineering are more complex and have to consider specific architectural demands (e.g. position of the elevator shaft) and constructive rules (e.g. maximum spacing of load-bearing elements) which has to be translated into constraints. However, the principles to consider these restraints were illustrated and it can be expected that such constraints will reduce the number solutions and as a consequence the computational time.

Sixth, as a metric to evaluate solutions’ quality, we took into consideration the variable H (i.e. the number of design hypotheses an agent needed before reaching the performance target); at the same time, we ignored the complexity of the structural solutions proposed by the agents as a possible term of comparison. This happened as, for this first research step, we considered computation time a clearer metric than overall design quality.

Finally, in the study we considered (1) a plain version of MCTS, (2) a classic approach to the Genetic Algorithm, and (3) a combination of the two. This means that study’s results cannot be generalized to all the possible variants of the presented methodologies.

Conclusions

In civil structural engineering, design tasks exist that can be reduced to search problems. In this paper, we showed how the task of generating structural solutions with specific dynamic properties can be faced by adopting both MCTS and GA. On the one hand, the presented approach is effective, as it found acceptable solutions for the envisaged technical problems. On the other hand, it is efficient, as it outperformed the prominent GA technique in terms of necessary design hypotheses.

As a first step, we introduced the MCTS algorithm; then, we presented the pseudo-codes we implemented from scratch in language code Java. Secondly, we briefly showed how structural design problems can easily have an extremely vast search space. Third, we described a suitable problem for a single-storey RC building, which resembles design tasks engineers face in their work. The problem is characterised by both non-linearity and discontinuity. Then, we focused on a set of case studies, for each of which we run hundreds of instantiations using both Monte Carlo Tree Search and Genetic Algorithm. On the one hand, the pattern the plain MCTS-agent followed to reach solutions for the selected problems looked far from linear and continuous, also because the problem’s nature. On the other hand, such agent is capable of reaching a quite high value of performance very soon on the analyses. As a consequence, a hybrid agent, composed of an initial involvement of MCTS and later intervention of GA seems to be a successful strategy. Indeed, the results we obtained show that, with regard to computation time, plain MCTS is, by far, not the best option for the posed structural problem; nonetheless, a hybrid agent that implements MCTS and GA proved to be the most efficient tool. In our study, on average, it needed to take into consideration from 1.09 to 2.99 times less design hypotheses compared to GA, so to reach a performance point beyond the goal we set. Interestingly, this may result in extremely important in those cases—as real-life structural engineering—where simulation is time-consuming.

Our study is far from offering an exhaustive comparison between MCTS and GA. Nonetheless, it proved how, in some cases a hybrid implementation of both can provide efficient solutions to a structural engineering problem. In conclusion, this work has revealed that MCTS may become a very useful design tool for civil engineers, especially as a member of a toolbox of existing Artificial Intelligence techniques.

Future research will be aimed at reducing the limitations we discussed in the text (also implementing enhancements [41] beyond the plain, non-adversarial version of MCTS), and at expanding our reach in terms of engineering applications (i.e. including more complex and more realistic structures). In addition, other metrics rather than just number of tested design hypotheses (as for example design quality) may be introduced to expand the reach of this research work. Finally, other Monte Carlo search algorithms, as Nested Roll-out Policy Adaption (nRPA) [48] and Nested Monte Carlo Search (NMCS) [49] may represent a key to achieve further advancements in our research.