Abstract
To numerically approximate Borel probability measures by finite atomic measures, we study the spectral decomposition of discrepancy kernels when restricted to compact subsets of \(\mathbb {R}^d\). For restrictions to the Euclidean ball in odd dimensions, to the rotation group \(\textrm{SO}(3)\), and to the Grassmannian manifold \(\mathcal {G}_{2,4}\), we compute the kernels’ Fourier coefficients and determine their asymptotics. The \(L_2\)-discrepancy is then expressed in the Fourier domain that enables efficient numerical minimization based on the nonequispaced fast Fourier transform. For \(\textrm{SO}(3)\), the nonequispaced fast Fourier transform is publicly available, and, for \(\mathcal {G}_{2,4}\), the transform is derived here. We also provide numerical experiments for \(\textrm{SO}(3)\) and \(\mathcal {G}_{2,4}\).
Similar content being viewed by others
1 Introduction
Consider a Borel probability measure \(\mu :\mathscr {B}(\mathbb {R}^d)\rightarrow [0,1]\) on \(\mathbb {R}^d\), where \(\mathscr {B}(\mathbb {R}^d)\) denotes the Borel sigma algebra on \(\mathbb {R}^d\). For fixed \(n\in \mathbb {N}\), we aim to allocate a suitable n-point set \(\{x_1,\ldots ,x_n\}\subset \mathbb {R}^d\) such that the normalized atomic measure
approximates \(\mu \). Here, \(\delta _{x_j}:\mathscr {B}(\mathbb {R}^d)\rightarrow \{0,1\}\) denotes the point measure localized at \(x_j\). To quantify the \(L_2\)-discrepancy between \(\mu \) and \(\nu _n\), select a measure \(\beta \) on \(\mathscr {B}(\mathbb {R}^d)\) with \(\mu ,\delta _x\in L_2(\mathscr {B}(\mathbb {R}^d),\beta )\), for all \(x\in \mathbb {R}^d\), and consider
cf. [40, 42, 43], see Sect. 2 for explicit examplesFootnote 1. For fixed \(n\in \mathbb {N}\), we aim to minimize \(\mathscr {D}_{\beta }(\mu ,\nu _n)\) among all n-point sets \(\{x_1,\ldots ,x_n\}\subset \mathbb {R}^d\). The present manuscript is concerned with discretizations of (1.2) that facilitate numerical minimization.
The associated discrepancy kernel \(K_\beta :\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}\) is defined by
and we assume it is continuous. Fubini’s Theorem and \(\mu (B)=\int _{\mathbb {R}^d} \delta _x(B)\textrm{d}\mu (x)\) applied to
yield that (1.2) is identical to
If a compact set \(\mathbb {X}\subset \mathbb {R}^d\) is known in advance such that \(\text {supp}(\mu )\subset \mathbb {X}\), then we shall restrict the minimization to \(\{x_1,\ldots ,x_n\}\subset \mathbb {X}\), so that only the restricted kernel \(K_\beta |_{\mathbb {X}\times \mathbb {X}}\) matters. By endowing \(\mathbb {X}\) with a finite Borel measure \(\sigma _\mathbb {X}\) having full support, Mercer’s Theorem yields an orthonormal basis \(\{\phi _l\}_{l=0}^\infty \) for \(L_2(\mathbb {X},\sigma _\mathbb {X})\) and coefficients \((a_l)_{l=0}^\infty \) such that the spectral decomposition
holds with absolute and uniform convergence. We call \((a_l)_{l=0}^\infty \) the Fourier coefficients of the kernel \(K_\beta |_{\mathbb {X}\times \mathbb {X}}\). If \(\text {supp}(\mu ),\text {supp}(\nu _n)\subset \mathbb {X}\), then the Fourier expansion of the \(L_2\)-discrepancy (1.4) is
where the Fourier coefficients \(\hat{\mu }_l\) and \(\hat{\nu }_{n,l}\) of the measures \(\mu \) and \(\nu _n\), respectively, are well-defined if \(a_l\ne 0\). Truncation of the discretization (1.6) enables the use of the nonequispaced fast Fourier transform, thereby offering more efficient minimization of \(\mathscr {D}_\beta (\mu ,\nu _n)\), cf. [31, 33]. Thus, we aim to
A) compute \((a_l)_{l=0}^\infty \) and \((\phi _l)_{l=0}^\infty \) in the Fourier expansion (1.5) of \(K_\beta |_{\mathbb {X}\times \mathbb {X}}\).
The \(L_2\)-discrepancy \(\mathscr {D}_\beta (\mu ,\nu _n)\) also coincides with the worst case integration error
with respect to the reproducing kernel Hilbert space \(\mathscr {H}_\beta (\mathbb {X})\) generated by \(K_\beta |_{\mathbb {X}\times \mathbb {X}}\), cf. [12, 13, 30, 31]. To specify \(\mathscr {H}_\beta (\mathbb {X})\), we aim to
B) identify \(\mathscr {H}_\beta (\mathbb {X})\) with a classical function space.
Fourier decay properties generally quantify Sobolev smoothness. To accomplish (B), we aim to determine the asymptotics of \(K_\beta |_{\mathbb {X}\times \mathbb {X}}\)’s Fourier coefficients \((a_l)_{l=0}^\infty \) in (1.5).
For \(\mathbb {X}=\mathbb {S}^{d-1}\) and a particular choice of \(\beta \), the kernel \(K_{\beta }|_{\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}}\) essentially coincides with the Euclidean distance, see [12, 13]. The Fourier expansion is determined in [10], and the decay of the Fourier coefficients yields that \(K_{\beta }|_{\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}}\) reproduces the Sobolev space \(\mathscr {H}_\beta (\mathbb {S}^{d-1})=\mathbb {H}^{\frac{d}{2}}(\mathbb {S}^{d-1})\). For the sphere and the torus, the nonequispaced fast Fourier transform is available, and both (A) and (B) are discussed in [33, 34].
This manuscript is dedicated to derive analogous results for other compact sets \(\mathbb {X}\). We focus on the unit ball, the special orthogonal group, and the Grassmannian manifold,
We achieve goal (A) for \(\mathbb {X}=\mathbb {B}^d\) with odd d. Both goals, (A) and (B), are achieved for \(\textrm{SO}(3)\) and \(\mathcal {G}_{2,4}\). We also provide numerical experiments. For \(\textrm{SO}(3)\), the computations are based on the nonequispaced fast Fourier transform designed in [32, 44]. For \(\mathcal {G}_{2,4}\), we derive the nonequispaced fast Fourier transform by parametrization via the double covering \(\mathbb {S}^2\times \mathbb {S}^2\) and developing the respective transform there.
For \(\textrm{SO}(d)\) and \(\mathcal {G}_{k,d}\) with fixed k and d, in principle, one could still be able to compute the Fourier expansion in goal (A). However, one may be faced with rather complicated expressions. In our present computations for \(\textrm{SO}(3)\) and \(\mathcal {G}_{2,4}\), the structural relations to the unit sphere enabled the use of Chebychev and Legendre polynomials, which reduced the complexity. Nonetheless, we do accomplish (B) for the general cases \(\textrm{SO}(d)\) and \(\mathcal {G}_{k,d}\).
2 Two Introductory Examples
We first present a well-known elementary example on the interval [0, s], for which both aims A) and B) are achieved. Second, to support our perspective on discrepancy, we prove that the so-called Askey function is a discrepancy kernel of the form (1.3).
2.1 The Brownian Motion Kernel on [0, s]
Let \(\textrm{d}r\) be the Lebesgue measure on \([0,\infty )\). The mapping \( h:[0,\infty )\rightarrow \mathscr {B}(\mathbb {R})\) defined by \(r\mapsto [r,\infty ) \) induces the pushforward measure \(\beta :=h_*(\textrm{d}r)\) that induces the discrepancy
The associated discrepancy kernel \(K_\beta :\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}\) isFootnote 2
so that \(\mathscr {D}_\beta (\delta _x,\delta _y)=|x-y|\) for \(x,y\in [0,\infty )\). The restriction of the kernel \(K_\beta \) to \([0,s]\times [0,s]\) has the Fourier expansion
with respect to the Lebesgue measure \(\sigma _{[0,s]}\) on [0, s]. The reproducing kernel Hilbert space is
where the inner product between f and g is given by \(\langle f',g'\rangle _{L_2([0,s])}\), cf. [3, 22] and [43, Section 9.5.5]. Note that \(K_\beta |_{[0,1]\times [0,1]}\) is often called the Brownian motion kernel and \(\mathscr {H}_{\beta }([0,s])\) is continuously embedded into the Sobolev space \(\mathbb {H}^1([0,s])\).
2.2 Askey’s Function and Its Restrictions
Many positive definite kernels in the literature are of the form (1.3) and, hence, are discrepancy kernels. For odd d, Askey’s kernel function \((x,y)\mapsto (1-\Vert x-y\Vert )^{\frac{d+1}{2}}_+\) is positive definite, cf. [29]. In the following, we shall check that it is of the form (1.3).
Denote the Euclidean ball of radius s centered at \(z\in \mathbb {R}^d\) by
with the conventions \(\mathbb {B}^d_{s}:=\mathbb {B}^d_{s}(0)\) and \(\mathbb {B}^d:=\mathbb {B}^d_1\). Fix \(r>0\) and consider the discrepancy
where \(\textrm{vol}(\mathbb {B}^d_{\frac{r}{2}})=\frac{\pi ^{d/2}}{\Gamma (\frac{d}{2}+1)}(\frac{r}{2})^d\). The associated discrepancy kernel is
In order to additionally integrate over r, recall the (generalized) hypergeometric functions

where \(f_1,\ldots ,f_k,g_1,\ldots ,g_l,z\in \mathbb {R}\) and \((f)_n:=f\cdot (f+1)\cdots (f+n-1)\) denotes the Pochhammer symbol with \((f)_0:=1\). We consider \(G_d:[0,\infty )\rightarrow \mathbb {R}\) given by

Since d is odd, either \(\frac{d+1}{4}\) or \(\frac{d-1}{4}\) is a natural number, so that the series terminates and \(G_d\) is a polynomial in \(r^{2}\) on [0, 1]. By integration with respect to \(G_d\), we obtain the \(L_2\)-discrepancy and the associated discrepancy kernel
respectively. It turns out that \(K_d\) coincides with Askey’s function.
Theorem 2.1
Let d be odd. The discrepancy kernel \(K_d\) satisfies
The proof is presented in Appendix A. Provided that \(d\ge 3\), Askey’s kernel function reproduces the Sobolev space \(\mathbb {H}^{\frac{d+1}{2}}(\mathbb {R}^d)\) with an equivalent norm, see [49].
3 The Distance Kernel on \(\mathbb {S}^{d-1}\)
This section is dedicated to recall results on discrepancy kernels on the sphere \(\mathbb {S}^{d-1}\subset \mathbb {R}^d\), for \(d\ge 2\), from [12, 13, 31, 46] that shall guide our subsequent investigations.
Denote the geodesic ball of radius r centered at \(z\in \mathbb {S}^{d-1}\) by
where \(\textrm{dist}_{\mathbb {S}^{d-1}}(x,z)=\arccos (\langle x,z\rangle )\) is the geodesic distance on \(\mathbb {S}^{d-1}\). We define
and endow \([0,\pi ]\) with the weighted Lebesgue measure \(\sin (r){\mathrm d}r\), whereas \(\mathbb {S}^{d-1}\) carries the normalized, orthogonal invariant surface measure \(\sigma _{\mathbb {S}^{d-1}}\). The push-forward \(\beta _d:=h_*(\sin (r){\mathrm d}r \otimes \sigma _{\mathbb {S}^{d-1}})\) is a measure on \(\mathscr {B}(\mathbb {R}^d)\), so that the associated \(L_2\)-discrepancy is
The associated discrepancy kernel is
According to [12, 13, 31], see also [2], \(K_{\beta _d}\) satisfies
If either x or y is not contained in \(\mathbb {S}^{d-1}\), then \(K_{\beta _d}(x,y)=0\).
Choose \(\sigma _\mathbb {X}:=\sigma _{\mathbb {S}^{d-1}}\) for the decomposition (1.5) and let \(\{Y^m_{{l}} : l=1,\ldots ,Z(d,m)\}\subset L_2(\mathbb {S}^{d-1},\sigma _{\mathbb {S}^{d-1}})\) denote the set of orthonormal spherical harmonics of degree m on \(\mathbb {S}^{d-1}\), where \( Z(d,m)=\frac{2m+d-2}{d-2}\left( {\begin{array}{c}m+d-3\\ m\end{array}}\right) . \) For \(\tau >(d-1)/2\), the Sobolev space \(\mathbb {H}^\tau (\mathbb {S}^{d-1})\) is the reproducing kernel Hilbert space associated with the reproducing kernel
The coefficients in the Fourier expansion
satisfy \(|c_m|\sim m^{-d}\), cf. [12]. This is the same asymptotics as the coefficients in (3.3) for \(\tau =d/2\). Therefore, \(K_{\beta _d}|_{\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}}\) reproduces the Sobolev space \(\mathscr {H}_{\beta _d}(\mathbb {S}^{d-1})=\mathbb {H}^{\frac{d}{2}}(\mathbb {S}^{d-1})\) with an equivalent normFootnote 3.
In order to determine the Fourier coefficients of kernels on the sphere that are polynomial in \(\Vert x-y\Vert \), such as \(K_{\beta _d}|_{\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}}\), we require the Fourier coefficients of the monomial terms \( \Vert x-y\Vert ^p\). For any \(p\in \mathbb {N}\), the Fourier expansion
holds with coefficients determined by
Note that (3.5) is well-defined for the entire range \(p>-(d-1)\) and p is not required to be an integer. For \(p>0\), the following proposition is essentially due to [10], see also [12, 14]. Simple continuation arguments cover the full range of p, and the asymptotics \(\frac{\Gamma (-\frac{p}{2}+m)}{\Gamma (\frac{p}{2}+d-1+m)}=m^{-(p+d-1)}(1+o(1))\) are standard.
Proposition 3.1
( [10]) Suppose \(d\ge 2\). For any \(p >-(d-1)\), we have
In particular, if \(p\not \in 2\mathbb {N}\), then
and the series (3.4) terminates if \(p\in 2\mathbb {N}\).
For \(p\in 2\mathbb {N}\), the term \(\Gamma (-\frac{p}{2})\) is not well-defined and (3.6) is to be understood with the convention \(\frac{\Gamma (-\frac{p}{2}+m)}{\Gamma (-\frac{p}{2})}=(-\frac{p}{2})_m\). Hence, we observe \(a_m(p,\mathbb {S}^{d-1}) = 0\) for all \(m > p/2\) if \(p\in 2\mathbb {N}\).
It is noteworthy that the kernel \(K_{d,r}\) in (2.2) for \(d=3\) is a discrepancy kernel that does not generate a Sobolev space on \(\mathbb {R}^d\) but its restriction does. The proof of the following proposition is presented in Appendix B.
Proposition 3.2
Let \(r\ge 1\). The reproducing kernel Hilbert space of \(K_{3,r}\), given by (2.2) with \(d=3\), is continuously embedded into \(\mathbb {H}^{2}(\mathbb {R}^3)\), but the reverse embedding does not hold. In contrast, \(K_{3,r}|_{\mathbb {S}^{2}\times \mathbb {S}^{2}}\) reproduces \(\mathbb {H}^{\frac{3}{2}}(\mathbb {S}^{2})\) with an equivalent norm.
To provide numerical examples for \(d=3\), Proposition 3.1 provides the coefficients \((a_m)_{m=0}^\infty \) in the kernel expansion of \(K_{\beta _{3}}\),
For \(\text {supp}(\mu ),\text {supp}(\nu _n)\subset \mathbb {S}^2\), the \(L_2\)-discrepancy (1.6) for \(K_{\beta _{3}}\) with \(\mathbb {X}=\mathbb {S}^2\) becomes
where \(\hat{\mu }^m_{l}\) denotes the Fourier coefficient of \(\mu \) with respect to \(Y^m_{l}\), cf. (1.6). By truncating this series, the nonequispaced fast Fourier transform on \(\mathbb {S}^2\), cf. [33, 39, 41], enables efficient minimization of
among all n-point sets \(\{x_1,\ldots ,x_n\}\subset \mathbb {S}^2\) for fixed n. We are most interested in \(n\gg M\). See Figure 1 for a numerical experiment with \(M=8\) and \(n=50\).
The target measure \(\mu \) is supported on two circles on the sphere \(\mathbb {S}^2\) with weight ratio 9/1. Numerical minimization of (3.9) splits 50 points into 45 points equally distributed on one and 5 points on the other circle
4 Discrepancy Kernels on Compact Sets
Here we discuss discrepancy kernels that extend the kernels of the previous section in a natural way. For \(d\ge 1\), let us define the half-space
For fixed \(s>0\), we consider the mapping \( h:[-s,s]\times \mathbb {S}^{d-1}\rightarrow \mathscr {B}(\mathbb {R}^d)\) defined by \((r,z)\mapsto \Omega ^d_r(z) \) and endow \([-s,s]\) with the Lebesgue measure \({\mathrm d}r\). The push-forward measure \(\beta _{d,s}:=h_*({\mathrm d}r\otimes \sigma _{\mathbb {S}^{d-1}})\) leads to the associated \(L_2\)-discrepancy
The associated discrepancy kernel is
Since \(B^{\mathbb {S}^{d-1}}_r(z) = \Omega ^d_{\cos (r)}(z)\cap \mathbb {S}^{d-1}\), for \(r\in [0,\pi ]\) and \(z\in \mathbb {S}^{d-1}\), we deduce
with \(K_{\beta _d}\) as in (3.1). In contrast to \(K_{\beta _d}\), the kernel \(K_{\beta _{d,s}}\) is not identically zero outside of \(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}\) and makes also sense for \(d=1\).
Example 4.1
For \(d=1\), we have \(\mathbb {S}^0=\{\pm 1\}\), so that the half-spaces are \(\Omega ^1_r(1)=[r,\infty )\) and \(\Omega ^1_r(-1)=(-\infty ,-r]\). Direct calculation of (4.1) yields
where \(\textrm{H}\) is the Heaviside step function.
Proposition 4.2
The Fourier expansion of the kernel \(K_{\beta _{1,s}}|_{[-s,s]\times [-s,s]}\) with respect to the Lebesgue measure \(\sigma _{[-s,s]}\) on \([-s,s]\) is
Its reproducing kernel Hilbert space is
where the inner product between f and g is given by
Note that \(\mathscr {H}_{K_{\beta _{1,s}}}([-s,s])\) is continuously embedded into \(\mathbb {H}^1([-s,s])\). The proof of Proposition 4.2 is presented in Appendix C. It uses that, up to a constant, \(K_{\beta _{1,s}}|_{[-s,s]\times [-s,s]}\) is the Green’s function of the 1-dimensional harmonic equation \(\Delta u = f\) on \([-s,s]\) with the boundary conditions \(u'(s) = - u'(-s)\) and \(u(s) + u(-s) = -2u'(s)\).
It turns out that \(K_{\beta _{d,s}}\) has a simple form on \(\mathbb {B}^d_{s}\times \mathbb {B}^d_s\).
Theorem 4.3
For \(d\ge 1\), the discrepancy kernel \(K_{\beta _{d,s}}\) satisfies
The identity (4.2) for \(x,y\in \mathbb {S}^{d-1}\) with \(s=1\) has been established in [13], see also (3.2). Essentially, the same proof still works for the more general situation. Theorem 4.3 provides a simple form of \(K_{\beta _{d,s}}|_{\mathbb {X}\times \mathbb {X}}\) with \(\mathbb {X}= \mathbb {B}^d_{s}\), which may facilitate further computations. An immediate consequence is \(\mathscr {D}_{\beta _{d,s}}(\delta _x,\delta _y)=\frac{\Gamma (\frac{d}{2})}{\sqrt{\pi }\Gamma (\frac{d+1}{2})}\Vert x-y\Vert \), for \(x,y\in \mathbb {B}^d_{s}\).
5 The Euclidean Ball \(\mathbb {B}^d\)
This section is dedicated to derive the Fourier expansion of the discrepancy kernel \(K_{\beta _{d,1}}\) in (4.1) on \(\mathbb {B}^d\). Proposition 4.2 has covered \(d=1\), and we now derive the spectral decomposition of
for all odd d with odd \(p>1-d\) with respect to the Lebesgue measure \(\sigma _{\mathbb {B}^d}\) on \(\mathbb {B}^d\). The case \(d=3\) with \(p=-1\) is discussed in [37].
Let \(\{\mathcal {C}^{\alpha }_m: m\in \mathbb {N},\; \alpha >-1/2\}\) denote the family of Gegenbauer polynomials with the standard normalization
By \(\alpha =\frac{d}{2}-1\), the addition theorem for spherical harmonics yields
For \(m\in \mathbb {N}\), let us define the kernels \(\mathcal {K}^{d,p}_m:[0,1]\times [0,1]\rightarrow \mathbb {R}\),

For \(d\ge 3\) and arbitrary real \(p>1-d\), we deduce from [18] that
For \(x=0\) or \(y=0\), the right-hand side of (5.3) is well-defined by analytic continuation.
Using the addition formula (5.1) we obtain
The Fourier expansion of \({\mathcal {K}}_{m}^{d,p}\) with respect to the measure \(r^{d-1} \mathrm dr\) satisfies
where \(\int _{0}^{1} |\varphi _{m,j}^{d,p}(r)|^{2} r^{d-1}\mathrm dr = 1\). We consider
as well as the integral operator in Mercer’s theorem induced by \(K^{d,p}\),
so that direct computations yield
with the scaling \(\int _{{\mathbb {B}}^{d}}\left| \varphi _{m',j',l'}^{d,p}(x)\right| ^{2} \mathrm d x = \textrm{vol}({\mathbb {S}}^{d-1})\). This leads to the Fourier expansion
Thus, the original problem is reduced to the spectral decomposition of the sequence of kernels \(\mathcal {K}^{d,p}_m\), for \(m\in \mathbb {N}\). The kernel \(\mathcal {K}^{d,p}_m\) induces the integral operator
with eigenvalues \(\lambda ^{d,p}_{m,j}\) and eigenfunctions \(\varphi ^{d,p}_{m,j}\). We now specify these eigenvalues and eigenfunctions. In the following theorem, \(J_{\nu }\) denotes the Bessel function of the first kind of order \(\nu \) and \(\zeta _{k}:=\textrm{e}^{2\pi \textrm{i}/k}\) is the k-th root of unity.
Theorem 5.1
Suppose that both \(d\ge 3\) and \(p>1-d\) are odd and let \(m\in \mathbb {N}\). Then the following holds:
-
a)
Any eigenvalue \(\lambda \ne 0\) of \(T_m^{d,p}\) is in a one-to-one correspondence with
$$\begin{aligned} \omega = \big |\lambda ^{-1}2^{d+p-2}(d+2m-2)(-\tfrac{p}{2})_{\frac{d+p}{2}-1}(\tfrac{d+p}{2}-1)!\big |^{\frac{1}{d+p}} \end{aligned}$$(5.9)with \(\omega \) satisfying \(\det (A(\omega ))=0\), where
$$\begin{aligned} A(\omega ) = {\left\{ \begin{array}{ll} \left( \zeta _{d+p}^{-i\ell } J_{m+\frac{d}{2}-i-1}(\zeta _{d+p}^{\ell }\omega ) \right) _{i=1,\,\ell =0}^{\frac{d+p}{2},\,\frac{d+p}{2}-1}, &{} (-\tfrac{p}{2} )_{\frac{d+p}{2}-1} \lambda > 0,\\ \left( \zeta _{2(d+p)}^{-i(2\ell +1)}J_{m+\frac{d}{2}-i-1}(\zeta _{2(d+p)}^{2\ell +1}\omega ) \right) _{i=1,\,\ell =0}^{\frac{d+p}{2},\,\frac{d+p}{2}-1}, &{} (-\tfrac{p}{2} )_{\frac{d+p}{2}-1} \lambda < 0. \end{array}\right. }\nonumber \\ \end{aligned}$$(5.10) -
b)
The eigenfunctions are exactly
$$\begin{aligned} r\mapsto {\left\{ \begin{array}{ll} \sum _{\ell =1}^{\frac{d+p}{2}} c_\ell \,r^{1-\frac{d}{2}}J_{m+\frac{d}{2}-1}(\zeta ^{\ell -1}_{d+p}\omega r ), &{} (-\tfrac{p}{2} )_{\frac{d+p}{2}-1} \lambda > 0,\\ \sum _{\ell =1}^{\frac{d+p}{2}} c_\ell \,r^{1-\frac{d}{2}}J_{m+\frac{d}{2}-1}(\zeta ^{2\ell -1}_{2(d+p)}\omega r ), &{} (-\tfrac{p}{2} )_{\frac{d+p}{2}-1} \lambda < 0, \end{array}\right. } \end{aligned}$$where \(c\in \mathbb {R}^{\frac{d+p}{2}}\) is in the nullspace of \(A(\omega )\).
Remark 5.2
Computer experiments seem to indicate that the nullspace of \(A(\omega )\) is one-dimensional if \(\det (A(\omega ))=0\). In that case, the function
where \(A_{[1,\ell ]}(\omega )\) denotes the \((1,\ell )\) minor of \(A(\omega )\), spans the eigenspace associated with \(\lambda \).
Appendix D is dedicated to the proof of Theorem 5.1. The proof reveals strong ties with polyharmonic operators on the unit ball and higher order differential operators on the interval [0, 1]. We refer to [1] for structurally related spectral decompositions of polyharmonic operators on [0, 1] with homogeneous Neumann boundary conditions.
Corollary 5.3
(\(d=3\), \(p=1\)) The nonzero eigenvalues of \(T^{3,1}_m\), for \(m\in \mathbb {N}\setminus \{0\}\), are exactly \(\lambda =-\omega ^{-4}(4m+2)\), where \(\omega \) is a positive solution of the equation
The corresponding eigenspaces are 1-dimensional with the representative
The formulas in Corollary 5.3 are derived from Theorem 5.1. Since \(J_{m-\frac{1}{2}}(\textrm{i}\omega )\ne 0\), for all \(\omega \in \mathbb {R}\setminus \{0\}\), the eigenspaces are 1-dimensional and (5.12) is not the zero-function.
In view of (4.2) in Theorem 4.3 we are particularly interested in kernels of the form \(c-\Vert x-y\Vert \). In this case, the expansion holds with \(-\mathcal {K}^{d,1}_m\) for \(m\ge 1\) and \(c-\mathcal {K}^{d,1}_0\) for \(m=0\).
6 The Rotation Group \(\textrm{SO}(3)\)
In this section we derive the Fourier expansion of the discrepancy kernel on the special orthogonal group \(\textrm{SO}(3)\). The eigenfunctions turn out to be classical functions but the coefficients and their decay rates need to be determined. We also provide numerical experiments by using the nonequispaced fast Fourier transform on \(\textrm{SO}(3)\).
6.1 Fourier Expansion on \(\textrm{SO}(3)\)
By identifying \(\mathbb {R}^{d\times d}\) with \(\mathbb {R}^{d^2}\), Theorem 4.3 applies to subsets of \(\mathbb {R}^{d\times d}\) endowed with the trace inner product
and the induced Frobenius norm \(\Vert \cdot \Vert _{\textrm{F}}\) on \(\mathbb {R}^{d\times d}\). In this way, \(\textrm{SO}(3)\) is contained in \(\mathbb {B}^{9}_{\sqrt{3}}\), and it is natural to consider \({s}=\sqrt{3}\). We endow \(\textrm{SO}(3)\) with the normalized Haar measure \(\sigma _{\textrm{SO}(3)}\). Let \(\{\mathcal {D}^m_{k,l}:k,l=-m,\ldots ,m\}\) denote the orthonormal Wigner \(\mathcal {D}\)-functions on \(\textrm{SO}(3)\), which are closely related to the irreducible representations of \(\textrm{SO}(3)\) and provide an orthonormal basis for \(L_2(\textrm{SO}(3))\), cf. [48]. For \(p>0\), the Fourier expansion
holds and, analogous to (3.5), the coefficients are
We now compute these coefficients for the entire range \(p>-3\).
Proposition 6.1
For \(p > -3\), the coefficients (6.2) are
In particular, if \(p\not \in 2\mathbb {N}\), then
and the series (6.1) terminates if \(p\in 2\mathbb {N}\).
The proof is given in Appendix E. For \(p\in 2\mathbb {N}\), we again apply the convention \(\frac{\Gamma (-\frac{p}{2}+m)}{\Gamma (-\frac{p}{2})}=(-\frac{p}{2})_m\) in (6.3), so that \(a_m(p,\textrm{SO}(3))=0\) for all \(m>\frac{p}{2}\) if \(p\in 2\mathbb {N}\). Provided that \(\tau >3/2\), the Sobolev space \(\mathbb {H}^\tau (\textrm{SO}(3))\) is the reproducing kernel Hilbert space associated with the reproducing kernel
The choice \(p=1\) in Proposition 6.1 implies that the kernel \(K_{\beta _{9,s}}|_{\textrm{SO}(3)\times \textrm{SO}(3)}\) reproduces the Sobolev space \(\mathscr {H}_{K_{\beta _{9,s}}}(\textrm{SO}(3))=\mathbb {H}^{2}(\textrm{SO}(3))\) with an equivalent norm provided that \(s\ge \sqrt{3}\).
For \(d\ge 2\), we shall observe that \(K_{\beta _{d^2,\sqrt{d}}}|_{\textrm{SO}(d)\times \textrm{SO}(d)}\) reproduces the Sobolev space \(\mathbb {H}^{\tau }(\textrm{SO}(d))\), for \(\tau =\frac{d(d-1)+2}{4}\), with an equivalent norm. Indeed, Theorem 4.3 and Sect. 3 yield that \(K_{\beta _{d^2,\sqrt{d}}}|_{\mathbb {S}^{d^2-1}\times \mathbb {S}^{d^2-1}}\) reproduces \(\mathbb {H}^{\frac{d^2}{2}}(\mathbb {S}^{d^2-1})\) with equivalent norms. Rescaling implies that \(K_{\beta _{d^2,\sqrt{d}}}|_{\sqrt{d}\,\mathbb {S}^{d^2-1}\times \sqrt{d}\,\mathbb {S}^{d^2-1}}\) reproduces \(\mathbb {H}^{\frac{d^2}{2}}({\sqrt{d}\,}\mathbb {S}^{d^2-1})\). Since \(\textrm{SO}(d)\subset \sqrt{d}\,\mathbb {S}^{d^2-1}\), results on restricting kernels in [27] lead to \(\tau =\frac{d^2}{2}-\frac{1}{2}\left( (d^2-1)- \dim (\textrm{SO}(d))\right) \), where \(\dim (\textrm{SO}(d))=\frac{d(d-1)}{2}\).
6.2 Numerical Examples on \(\textrm{SO}(3)\)
Proposition 6.1 yields the coefficients of the kernel expansion
For \(\text {supp}(\mu ),\text {supp}(\nu _n)\subset \textrm{SO}(3)\), the \(L_2\)-discrepancy (1.6) for \(K_{\beta _{9,\sqrt{3}}}\) becomes
where \(\hat{\mu }^m_{k,l}\) denotes the Fourier coefficient of \(\mu \) with respect to \(\mathcal {D}^m_{k,l}\), cf. (1.6). We truncate the series (6.4) at \(M=8\) and minimize
among all n-point sets \(\{x_1,\ldots ,x_n\}\subset \textrm{SO}(3)\) for fixed \(n=30\). We efficiently solve the least squares minimization by using the nonequispaced fast Fourier transform on \(\textrm{SO}(3)\), cf. [32, 44]. Figure 2 shows the minimizing points mapped onto \(\mathbb {B}^3\).
We use the standard parametrization of \(\textrm{SO}(3)\) by \(\mathbb {S}^3\) via unit quaternions, which is then mapped into \(\mathbb {R}^3\) by stereographic projection and \(\mathbb {R}^3\) is parametrized by \(\mathbb {B}^3\) via \(x\mapsto \frac{x}{\Vert x\Vert }\tan (\frac{\pi }{2}\Vert x\Vert )\). The target measure \(\mu \) is supported on two disjoint parts with weight ratio 9/1 colored in darker blue by the cylindrical surface and the great circle. Numerical minimization of (6.5) splits 30 points in \(\textrm{SO}(3)\) into 27 points on the inner surface and 3 points on the great circle. We plotted 6 points on the great circle but antipodal points correspond to the same point in \(\textrm{SO}(3)\)
7 The Grassmannian \(\mathcal {G}_{2,4}\)
First, the Fourier expansion of the discrepancy kernel on \(\mathcal {G}_{2,4}\) is computed. To prepare for developing the nonequispaced fast Fourier transform on \(\mathcal {G}_{2,4}\), we then explicitly parametrize the Grassmannian \(\mathcal {G}_{2,4}\) by its double covering \(\mathbb {S}^2\times \mathbb {S}^2\). Next, we derive the nonequispaced fast Fourier transform on \(\mathbb {S}^2\times \mathbb {S}^2\) and provide numerical minimization experiments on \(\mathcal {G}_{2,4}\).
7.1 Fourier Expansion on \(\mathcal {G}_{2,4}\)
Theorem 4.3 also applies to the Grassmannian
with \(s=\sqrt{2}\) when \(\mathbb {R}^{4\times 4}\) is identified with \(\mathbb {R}^{16}\). To derive the Fourier expansion on \(\mathcal {G}_{2,4}\), we require some preparations. We shall use integer partitions \(\lambda =(\lambda _1,\lambda _2)\in \mathbb {N}^2\) with \(\lambda _1\ge \lambda _2\ge 0\). We also denote \(|\lambda |:=\lambda _1+\lambda _2\). The orthogonal group \(\textrm{O}(4)\) acts transitively on \(\mathcal {G}_{2,4}\) by conjugation and induces the irreducible decomposition
where \(\sigma _{\mathcal {G}_{2,4}}\) is the normalized orthogonally invariant measure on \(\mathcal {G}_{2,4}\) and \(H_{\lambda }(\mathcal {G}_{2,4})\) is equivalent to the irreducible representation \({\mathcal {H}}_{2\lambda }^{4}\) of \(\textrm{O}(4)\) with type \(2\lambda \), cf. [7, 35]. The normalized eigenfunctions of the Laplace–Beltrami operator on \(\mathcal {G}_{2,4}\) form an orthonormal basis for \(L_{2}(\mathcal {G}_{2,4})\), and each \(H_\lambda (\mathcal {G}_{2,4})\) is contained in the eigenspace \(E_{\alpha _\lambda }\) associated with the eigenvalue \(\alpha _\lambda = 4(\lambda _1^2+\lambda _2^2+\lambda _1)\), cf. [6,7,8, 23, 35, 45].
Let \(Q_\lambda \) be the reproducing kernel of \(H_\lambda (\mathcal {G}_{2,4})\). Any orthonormal basis \(\{\varphi _{\lambda ,l}\}_{l=1}^{\dim (\mathcal {H}^{4}_{2\lambda })}\) for \(H_{\lambda }(\mathcal {G}_{2,4})\) yields the spectral decomposition
The orthogonal decomposition (7.1) leads to the Fourier expansion
The coefficients \(a_\lambda (p,\mathcal {G}_{2,4})\) in (7.3) are
In order to determine \(a_\lambda (p,\mathcal {G}_{2,4}) \), we shall make use of the hypergeometric coefficients \( (f)_{(\lambda _1,\lambda _2)} := (f)_{\lambda _1} (f-\tfrac{1}{2})_{\lambda _2}\). Also recall the notation \(|\lambda |=\lambda _1+\lambda _2\) and \(\Vert \lambda \Vert =\sqrt{\lambda _1^2+\lambda _2^2}\).
Theorem 7.1
For \(p>-4\), we have

In particular, if \(p\not \in 2\mathbb {N}\), then
and the series (7.3) terminates if \(p\in 2\mathbb {N}\).
The proof of this theorem is contained in Section F.1 of Appendix F. If \(p\in 2\mathbb {N}\), then \( a_\lambda (p,\mathcal {G}_{2,4})=0\) for all \(|\lambda |>\frac{p}{2}\). For \(\tau >2\), the Sobolev space \(\mathbb {H}^\tau (\mathcal {G}_{2,4})\) is the reproducing kernel Hilbert space with associated reproducing kernel
cf. [11, 16]. Since the coefficients in (7.7) behave asymptotically as \(\Vert \lambda \Vert ^{-2\tau }\), the choice \(p=1\) in Theorem 7.1 implies that the kernel \(K_{\beta _{16,s}}|_{\mathcal {G}_{2,4}\times \mathcal {G}_{2,4}}\) reproduces the Sobolev space \(\mathscr {H}_{K_{\beta _{16,s}}}(\mathcal {G}_{2,4})=\mathbb {H}^{\frac{5}{2}}(\mathcal {G}_{2,4})\) with an equivalent norm provided that \(s\ge \sqrt{2}\).
Analogous to \(\textrm{SO}(d)\) at the end of Sect. 6.1, we deduce with [27] that, for \(d\ge 2\), \(K_{\beta _{d^2,\sqrt{k}}}|_{\mathcal {G}_{k,d}\times \mathcal {G}_{k,d}}\) reproduces the Sobolev space \(\mathbb {H}^{\frac{k(d-k)+1}{2}}(\mathcal {G}_{k,d})\) with an equivalent norm.
7.2 Parametrization of \(\mathcal {G}_{2,4}\) by 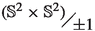
To derive the nonequispaced fast Fourier transform on \(\mathcal {G}_{2,4}\), we shall first explicitly construct the parametrization of \(\mathcal {G}_{2,4}\) by its double covering \(\mathbb {S}^2\times \mathbb {S}^2\). We denote the \(d\times d\)-identity matrix by \(I_d\), and the cross-product between two vectors \(x,y\in \mathbb {S}^2\) is denoted by \(x\times y\in \mathbb {R}^3\). The mapping \(\mathcal {P}:\mathbb {S}^2\times \mathbb {S}^2\rightarrow \mathcal {G}_{2,4}\) given by
is surjective and, for all \(x,y,u,v\in \mathbb {S}^2\),
see Section F.2 and Theorem F.4 of Appendix F. In order to specify the inverse map, note that  can be identified with \( \mathcal {M}(3):=\{xy^\top \in \mathbb {R}^{3\times 3} : x,y\in \mathbb {S}^2\}. \) We now define \(\mathcal {L}:\mathcal {G}_{2,4}\rightarrow \mathcal {M}(3)\),
can be identified with \( \mathcal {M}(3):=\{xy^\top \in \mathbb {R}^{3\times 3} : x,y\in \mathbb {S}^2\}. \) We now define \(\mathcal {L}:\mathcal {G}_{2,4}\rightarrow \mathcal {M}(3)\),
and direct computations lead to
The right-hand side determines x and y up to the ambiguity (7.9). Under the Frobenius norm, \(\mathcal {P}\) is distance preserving in the sense
The latter follows from (F.20) in Lemma F.6 in Section F.2 of Appendix F.
We shall now check how the spherical harmonics \(Y^m_l\) on \(\mathbb {S}^2\) relate to the eigenfunctions \(\varphi _{\lambda ,l}\in H_\lambda (\mathcal {G}_{2,4})\) of the Laplace–Beltrami operator on \(\mathcal {G}_{2,4}\), cf. (7.2). The functions \(Y_{k,l}^{m,n}:\mathcal {G}_{2,4}\rightarrow {\mathbb {C}}\) given by
are well-defined for \(m+n \in 2{\mathbb {N}}\), the latter taking into account the ambiguity (7.9).
Theorem 7.2
For \(m_\lambda :=(\lambda _1+\lambda _2)\) and \(n_\lambda :=(\lambda _1-\lambda _2)\), we have
The proof is presented at the end of Section F.2 of Appendix F. Note that the geodesic distance on \(\mathcal {G}_{2,4}\) is \(\textrm{dist}_{\mathcal {G}_{2,4}}(P,Q)=\sqrt{2}\sqrt{\theta _1^2+\theta _2^2}\), where \(\theta _1,\theta _2\in [0,\pi /2]\) are the principal angles determined by the two largest eigenvalues \(\cos ^2(\theta _1)\) and \(\cos ^2(\theta _2)\) of the matrix PQ. Aside from (7.12), \(\mathcal {P}\) is also distance-preserving with respect to the respective geodesic distances, i.e.,Footnote 4

This equality follows from (F.23) in Lemma F.6 in the appendix via further direct calculations.
The identity (7.14) provides explicit expressions for the orthonormal basis \(\{\varphi _{\lambda ,l}\}_{l=1}^{\dim (\mathcal {H}^{4}_{2\lambda })}\) of \(H_{\lambda }(\mathcal {G}_{2,4})\) that is used to construct the reproducing kernel \(Q_\lambda \) in (7.2). It also provides a fast Fourier transform on \(\mathcal {G}_{2,4}\) from the respective transform on \(\mathbb {S}^2\times \mathbb {S}^2\) that is developed in the subsequent section.
7.3 Nonequispaced Fast Fourier Transform on \(\mathcal {G}_{2,4}\)
The nonequispaced fast (spherical) Fourier transform on \(\mathbb {S}^2\) has been developed in [39, 41] under the acronym nfsft. Here, we shall derive the analogous transform on \(\mathbb {S}^2\times \mathbb {S}^2\), which induces the nonequispaced fast Fourier transform on \(\mathcal {G}_{2,4}\) via the mapping \(\mathcal {P}\) and (7.14) with (7.13).
For a given finite set of coefficients \(f^{m_1,m_2}_{k,l}\in \mathbb {C}\), \(m_1,m_2=0,\ldots ,M\), \(k=-m_1,\ldots ,m_1\), \(l=-m_2,\ldots ,m_2\), we aim to evaluate
at n scattered locations \((x_j,y_j)_{j=1}^n\subset \mathbb {S}^2\times \mathbb {S}^2\). Direct evaluation of (7.15) leads to \(O(n M^4)\) operations. We shall now derive an approximative algorithm that is more efficient for \(n\gg M\).
By following the ideas in [39, 41], switching to spherical coordinates reveals that (7.15) is a 4-dimensional trigonometric polynomial. This enables the use of the 4-dimensional nonequispaced fast Fourier transform nfft to significantly reduce the complexity. In spherical coordinates the spherical harmonics are trigonometric polynomials such that
where \(0\le \theta \le \pi \), \(0\le \varphi \le 2\pi \), and \(c^m_{k,k'}\in \mathbb {C}\) are suitable coefficients that we assume to be given or precomputed. Thus, for \( x = z(\theta _1,\varphi _1)\) and \(y=z(\theta _2,\varphi _2)\), there are coefficients \(b^{k,l}_{k',l'}\in \mathbb {C}\) such that
We check in Sect. 1 of Appendix F that the set of coefficients \(b^{k,l}_{k',l'}\) can be computed by \(O(M^5)\) operations provided that the numbers \(c^m_{k,k'}\) in (7.16) are given. The expression (7.17) can be evaluated at n scattered locations by the nonequispaced discrete Fourier transform ndft with \(O(n M^4)\) operations, cf. [39, 41]. An efficient approximative algorithm is the nonequispaced fast Fourier transform nfft that requires only \(O(M^4\log (M)+n|\log (\epsilon )|^4)\) operations with accuracy \(\epsilon \), see [39, 41] for details on accuracy. Thus, our algorithm for evaluating (7.15) at n scattered locations requires \(O(M^5+n|\log (\epsilon )|^4)\) operations. For \(n\gg M\), this is a significant reduction in complexity compared to the original \(O(nM^4)\) operations. We shall choose \(n\sim M^4\) in the subsequent section, so that the complexity is reduced from \(O(M^8)\) to \(O(M^5+M^4|\log (\epsilon )|^4)\) operations. For potential further reduction, we refer to Remark F.7 in the appendix.
7.4 Numerical example on \(\mathcal {G}_{2,4}\)
By Theorem 7.1, we can calculate the coefficients of the kernel expansion
The eigenfunctions \(\varphi _{\lambda ,l}\) are given by the tensor products of spherical harmonics in (7.13), cf. Theorem 7.2. For \(\text {supp}(\mu ),\text {supp}(\nu _n)\subset \mathcal {G}_{2,4}\), the \(L_2\)-discrepancy (1.6) of the kernel \(K_{\beta _{16,\sqrt{2}}}|_{\mathcal {G}_{2,4}\times \mathcal {G}_{2,4}}\) is
where \(\hat{\mu }_{\lambda ,l}\) is the Fourier coefficient of \(\mu \) with respect to \(\varphi _{\lambda ,l}\), cf. (1.6).
Let us consider \(\mu =\sigma _{\mathcal {G}_{2,4}}\). According to [11] (see also [15, 16]), the lower bound
holds for all n-point sets \(\{x_1,\ldots ,x_n\}\subset \mathcal {G}_{2,4}\). We truncate the series (7.18) and let \(\nu ^{M}_n=\frac{1}{n}\sum _{j=1}^n\delta _{x^M_j}\) denote a minimizer of
among all n-point sets \(\{x_1,\ldots ,x_n\}\subset \mathcal {G}_{2,4}\). A suitable choice \(n\sim M^4 \) leads to the optimal rate
cf. [11, 25]. Note that we can efficiently solve the least squares minimization (7.19) by using the nonequispaced fast Fourier transform on \(\mathcal {G}_{2,4}\) derived from the nonequispaced fast Fourier transform on \(\mathbb {S}^2\times \mathbb {S}^2\) of Sect. 7.3 and applying Theorem 7.2. Figure 3 shows logarithmic plots of the number of points versus the \(L_2\)-discrepancy. We observe a line with slope \(-5/4\) as predicted by (7.20).
Notes
If \(\beta \) is a pushforward measure, then the associated sigma algebra on \(\mathscr {B}(\mathbb {R}^d)\) is induced by the pushforward.
For \(r\in \mathbb {R}\), we use the notation \(r_+={\left\{ \begin{array}{ll} r,&{} r\ge 0,\\ 0,&{} \text {otherwise.} \end{array}\right. }\)
The kernel \(K_{\beta _d}|_{\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}}\) generates an inner product \(\langle \cdot ,\cdot \rangle _{K_{\beta _d}|_{\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}}}\) in \(\mathbb {H}^{\frac{d}{2}}(\mathbb {S}^{d-1})\), for which it is reproducing and the induced norm is equivalent to the standard norm in \(\mathbb {H}^{\frac{d}{2}}(\mathbb {S}^{d-1})\), which is induced by the standard kernel (3.3).
The geodesic distance on \(\mathbb {S}^2\) induces the geodesic distance on
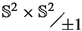 by
by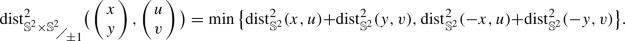
References
Adcock, B.: On the convergence of expansions in polyharmonic eigenfunctions. J. Approx. Theory 163(11), 1638–1674 (2011)
Alexander, R.: Generalized sums of distances. Pacific J. Math. 56(2), 297–304 (1975)
Alpay, D., Jorgensen, P.: Spectral theory for Gaussian processes: reproducing kernels, boundaries, and \(L^2\)-wavelet generators with fractional scales. Numer. Funct. Anal. Optim. 36(10), 1239–1285 (2015)
Ambrosio, L., Gigli, N., Savaré, G.: Gradient Flows in Metric Spaces and in the Space of Probability Measures. Birkhäuser Verlag, Basel (2005)
Aronszajn, N., Creese, T.M., Lipkin, L.J.: Polyharmonic Functions. Clarendon Press, Oxford (1983)
Bachoc, C.: Linear programming bounds for codes in Grassmannian spaces. IEEE Trans. Inf. Th. 52(5), 2111–2125 (2006)
Bachoc, C., Coulangeon, R., Nebe, G.: Designs in Grassmannian spaces and lattices. J. Algebr. Combin. 16, 5–19 (2002)
Bachoc, C., Bannai, E., Coulangeon, R.: Codes and designs in Grassmannian spaces. Discrete Math. 277, 15–28 (2004)
Baouendi, M., Goulaouic, C., Lipkin, L.: On the operator \(\Delta r^2+\mu (\partial /\partial r)r+\lambda \). J. Differ. Equ. 15, 499–509 (1974)
Baxter, B. J. C., Hubbert, S.: Radial basis functions for the sphere, in: Recent Progress in Multivariate Approximation International. Series Numerical Math, vol. 137, Birkhäuser, Basel, pp. 33–47 (2001)
Brandolini, L., Choirat, C., Colzani, L., Gigante, G., Seri, R., Travaglini, G.: Quadrature rules and distribution of points on manifolds. Annali della Scuola Normale Superiore di Pisa Classe di Scienze XIII 4, 889–923 (2014)
Brauchart, J.S., Dick, J.: A characterization of Sobolev spaces on the sphere and an extension of Stolarsky’s invariance principle to arbitrary smoothness. Constr. Approx. 38(3), 397–445 (2013)
Brauchart, J.S., Dick, J.: A simple proof of Stolarsky’s invariance principle. Proc. Am. Math. Soc. 141(6), 2085–2096 (2013)
Brauchart, J.S., Saff, E.B., Sloan, I.H., Womersley, R.S.: QMC designs: Optimal order quasi Monte Carlo integration schemes on the sphere. Math. Comp. 83, 2821–2851 (2014)
Breger, A., Ehler, M., Gräf, M.: Quasi Monte Carlo integration and kernel-based function approximation on Grassmannians, in: Frames and Other Bases in Abstract and Function Spaces: Novel Methods in Harmonic Analysis, vol. 1, Birkhäuser/Springer, pp. 333–353 (2017)
Breger, A., Ehler, M., Gräf, M.: Points on manifolds with asymptotically optimal covering radius. J. Complex. 48, 1–14 (2018)
Chauffert, N., Ciuciu, P., Kahn, J., Weiss, P.: A projection method on measures sets. Constr. Approx. 45(1), 83–111 (2017)
Cohl, H.S.: On a generalization of the generating function for Gegenbauer polynomials. Integral Transform. Spec. Funct. 24(10), 807–816 (2013)
Conway, J.H., Hardin, R.H., Sloane, N.J.A.: Packing lines, planes, etc.: packings in Grassmannian space. Exp. Math. 5, 139–159 (1996)
Davis, A.W.: Spherical functions on the Grassmann manifold and generalized Jacobi polynomials - Part 2. Lin. Alg. Appl. 289(1–3), 95–119 (1999)
de Gournay, F., Kahn, J., Lebrat, L., Weiss, P.: Optimal transport approximation of 2-dimensional measures. SIAM J. Imag. Sci. 12, 762–787 (2019)
Dick, J., Pillichshammer, F.: Discrepancy theory and quasi-Monte Carlo integration. In: Chen, W., Srivastav, A., Travaglini, G. (eds.) A Panorama of Discrepancy Theory. Springer, Cham (2017)
Ehler, M., Gräf, M.: Reproducing kernels for the irreducible components of polynomial spaces on unions of Grassmannians. Constr. Approx. 49(1), 29–58 (2018)
Erdélyi, A., Magnus, V., Oberhettinger, F., Tricomi, F.: Higher Transcendental Functions, vol. 1. McGraw-Hill, New York (1953)
Etayo, U., Marzo, J., Ortega-Cerdà, J.: Asymptotically optimal designs on compact algebraic manifolds. Monatsh. Math. 186, 235–248 (2018)
Fulton, W., Harris, J.: Representation Theory: A First Course. Springer, New York (1991)
Fuselier, E., Wright, G.B.: Scattered data interpolation on embedded submanifolds with restricted positive definite kernels: Sobolev error estimates. SIAM J. Numer. Anal. 50(3), 1753–1776 (2012)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, New York (2001)
Gneiting, T.: Radial positive definite functions generated by Euclid’s hat. J. Multi. Anal. 69, 88–119 (1999)
Gnewuch, M.: Weighted geometric discrepancies and numerical integration on reproducing Kernel Hilbert spaces. J. Complex. 28, 2–17 (2012)
Gräf, M.: Efficient Algorithms for the Computation of Optimal Quadrature Points on Riemannian Manifolds, Ph.D. thesis, TU Chemnitz, Universitätsverlag Chemnitz, (2013)
Gräf, M., Potts, D.: Sampling sets and quadrature formulae on the rotation group. Numer. Funct. Anal. Optim. 30, 665–688 (2009)
Gräf, M., Potts, D.: On the computation of spherical designs by a new optimization approach based on fast spherical Fourier transforms. Numer. Math. 119, 699–724 (2011)
Gräf, M., Potts, M., Steidl, G.: Quadrature errors, discrepancies and their relations to halftoning on the torus and the sphere. SIAM J. Sci. Comput. 34, A2760–A2791 (2012)
James, A.T., Constantine, A.G.: Generalized Jacobi polynomials as spherical functions of the Grassmann manifold. Proc. London Math. Soc. 29(3), 174–192 (1974)
John, F.: The fundamental solution of a linear elliptic differential equations with analytic coefficients. Commun. Pure Appl. Math. 3(3), 273–304 (1950)
Kal’menov, TSh., Suragan, D.: A boundary condition and spectral problems for the Newton potential. Oper. Theory Adv. Appl. 216, 187–210 (2011)
Kal’menov, T Sh., Suragan, D.: Boundary conditions for the volume potential for the polyharmonic equation. J. Differ. Equ. 48(4), 604–608 (2012)
Keiner, J., Kunis, S., Potts, D.: Using NFFT3—a software library for various non-equispaced fast Fourier transforms. ACM Trans. Math. Softw. 36, 1–30 (2009)
Kuipers, L., Niederreiter, H.: Uniform Distribution of Sequences. Wiley, Amsterdam (1974)
Kunis, S., Potts, D.: Fast spherical Fourier algorithms. J. Comput. Appl. Math. 161, 75–98 (2003)
Matoušek, J.: Geometric Discrepancy, Algorithms and Combinatorics. Springer, New York (2010)
Novak, E., Woźniakowski, H.: Tractability of Multivariate Problems. in: EMS Tracts in Mathematics. EMS Publishing House, Zürich, (2010)
Potts, D., Prestin, J., Vollrath, A.: A fast algorithm for non-equispaced Fourier transforms on the rotation group. Numer. Algorithms 52, 355–384 (2009)
Roy, A.: Bounds for codes and designs in complex subspaces. J. Algebr. Combin. 31(1), 1–32 (2010)
Skriganov, M.M.: Stolarsky’s invariance principle for projective spaces. J. Complex. 56, 101428 (2020)
Slater, L.J.: Generalized Hypergeometric Functions. Cambridge University Press, Cambridge (1966)
Varshalovich, D.A., Moskalev, A.N., Khersonskii, V.K.: Quantum Theory of Angular Momentum. World Scientific, Singapore (1988)
Wendland, H.: Scattered Data Approximation, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (2004)
Acknowledgements
ME and MG have been funded by the Vienna Science and Technology Fund (WWTF) through project VRG12-009. The research of CK has been partially supported by the Austrian Science Foundation (FWF) grant SFB F50 in the framework of the Special Research Program “Algorithmic and Enumerative Combinatorics”. ME would like to thank Christine Bachoc, Karlheinz Gröchenig, Andreas Klotz, and Gerald Teschl for helpful discussions.
Funding
Open access funding provided by Austrian Science Fund (FWF).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Edward B. Saff.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proofs for Section 2
Proof of Theorem 2.1
Let \(h_d:[0,\infty )\rightarrow \mathbb {R}\) denote Euclid’s hat function given by
where \(1_{\mathbb {B}^d_{1/2}}\) is the indicator function of \(\mathbb {B}^d_{1/2}\). For \(x,y\in \mathbb {R}^d\) and \(t=\Vert x-y\Vert \le 1\), we derive
where the last equality is due to partial integration. An explicit expression for \(h'_d\) is stated in [29, Equation (11)], so that we obtain

We now compare coefficients of powers of t with those of the polynomial \((1-t)^{\frac{d+1}{2}}\). In order to check the coefficient of \(t^{2l}\), we first observe

where the last equality makes use of Gauss’ Theorem for the hypergeometric series evaluated at 1 (cf. [47, Equation (1.7.6); Appendix (III.3)]). Direct computation yields
so that the coefficient of \(t^{2l}\) in \(K_{d}(x,y) \) is
Hence, the coefficients for even powers of t match. To check the coefficient of \(t^{2j+1}\), we first assume \(\frac{d-1}{4}\in \mathbb {N}\). The Pfaff–Saalschütz Theorem (cf. [47, Equation (2.3.1.3); Appendix (III.2)]) yields

Thus, the coefficient of \(t^{2j+1}\) in \(K_{d}(x,y)\) is nonzero if and only if \(j\le \frac{d-1}{4}\). Moreover, it is given by
Further computations using the duplication formula eventually lead to \(-\left( {\begin{array}{c}\frac{d+1}{2}\\ 2l+1\end{array}}\right) \). The case \(\frac{d+1}{4}\in \mathbb {N}\) is checked analogously. The observation \(K_d(x,y)=0\) for \(\Vert x-y\Vert >1\) concludes the proof. \(\square \)
Appendix B: Proofs for Section 3
Proof of Proposition 3.2
By expressing the \(\mathbb {R}^d\)-Fourier transform \(\widehat{1_{\mathbb {B}^d_{r}}}(\xi )\) in terms of the Bessel function of the first kind of order d/2 and using its asymptotics, we deduce
Due to the zeros of the Bessel function, the respective lower bound cannot hold. This implies the embedding claims for \(\mathbb {H}^{\frac{d+1}{2}}(\mathbb {R}^d)\), in particular, for \(d=3\).
To address the restricted kernel, we observe that the value \(\textrm{vol}(\mathbb {B}^d_{r/2})K_{d,r}(x,y)\) coincides with the \(\mathbb {R}^d\)-volume of the two intersecting balls \(\mathbb {B}^d_{r/2}(x)\cap \mathbb {B}^d_{r/2}(y)\). This volume has been explicitly computed in [31, Section 2.4.3]. For \(d=3\), we obtain
so that \(K_{3,r}|_{\mathbb {S}^{2}\times \mathbb {S}^{2}}\) is a polynomial of degree 3 in \(\Vert x-y\Vert \). Its Fourier coefficients \((a_m)_{m\in \mathbb {N}}\) are linear combinations of the Fourier coefficients of the monomial terms, so that (3.7) implies \(a_m\lesssim m^{-3}\).
We have checked that there are no cancelations in these linear combinations. Therefore, the asymptotics (3.7) also imply the associated bound from below, which leads to \(a_m \sim m^{-3}\). Thus, \(K_{3,r}|_{\mathbb {S}^{2}\times \mathbb {S}^{2}}\) reproduces the Sobolev space \(\mathbb {H}^{\frac{3}{2}}(\mathbb {S}^{2})\) with equivalent norms. \(\square \)
Appendix C: Proofs for Section 4
Proof of Proposition 4.2
Let us consider \(s=1\). The general case follows from rescaling. In order to determine the Fourier expansion of \(K_{\beta _{1,1}}|_{[-1,1]\times [-1,1]}\), we need to determine the eigenfunctions with respect to the positive eigenvalues of the integral operator
For \(\lambda >0\), the equation \(T\phi =\lambda \phi \) is equivalent to the associated Sturm–Liouville eigenvalue problem. Indeed, differentiating twice on both sides and carrying out a short calculation, we arrive at the second order homogeneous differential equation
with boundary conditions \( \phi '(1) = - \phi '(-1)\) and \(\phi (1) + \phi (-1) = -2\phi '(1). \) The general solution of (C.1) is \( \phi (x)=c_1\cos (\frac{x}{\sqrt{\lambda }})+c_2\sin (\frac{x}{\sqrt{\lambda }}). \) Direct calculations using the boundary conditions determine \(c_1,c_2\) and \(\lambda \), so that Mercer’s Theorem and normalization of the eigenfunctions provide the claimed Fourier expansion of the kernel.
Computations analogous to [43, Section 9.5.5] and [22] verify the claimed form of the reproducing kernel Hilbert space. \(\square \)
Appendix D: Proofs for Section 5
The two linearly independent eigenfunctions of the differential operator
on [0, 1] with respect to a possibly complex eigenvalue \(-\omega ^2\) are
where \(J_\nu \) and \(Y_\nu \) are the Bessel functions of first and second type, respectively.
Lemma D.1
For odd \(d\ge 3\), odd \(p>1-d\), and \(m\in \mathbb {N}\), any eigenfunction of \(T_m^{d,p}\) with eigenvalue \(\lambda \ne 0\) is a linear combination of \(\left\{ \mathcal {J}^{d,\omega _{\ell }}_{m}: \ell =1,\ldots ,\frac{d+p}{2}\right\} \), where
and
Proof of Lemma D.1
Up to a constant depending on d and p, \(K^{d,p}\) is the Green’s function of the polyharmonic equation \(\Delta ^{\frac{d+p}{2}}u=f\) on \(\mathbb {B}^d\) with certain nonlocal boundary conditions, cf. [38]. In particular and by specifying the constant, one deduces that any eigenfunction of \(T^{d,p}\) in (5.5) with eigenvalue \({\tilde{\lambda }}\ne 0\) is an eigenfunction of \(\Delta ^{\frac{d+p}{2}}\) with eigenvalue
The Laplacian in polar coordinates is \(\Delta = \partial ^2_r + \frac{d-1}{r}\partial _r + \frac{1}{r^2}\Delta _{{\mathbb {S}}^{d-1}}\). The decomposition (5.7) (see also (5.4)) yields \(\Delta ^{\frac{d+p}{2}}\varphi ^{d,p}_{m,j,l}=\big (D_{m}^{\frac{d+p}{2}} \varphi ^{d,p}_{m,j}\big )Y^m_l\) on \(\mathring{\mathbb {B}}^d\), where \(D_m\) is as in (D.1). Since \({\tilde{\lambda }} = \frac{(d-2)\textrm{vol}({\mathbb {S}}^{d-1})}{2m+d-2} \lambda \), any eigenfunction of \(T^{d,p}_m\) with eigenvalue \(\lambda \ne 0\) is an eigenfunction of \(D^{\frac{d+p}{2}}_m\) with eigenvalue
The linearly independent eigenfunctions of \(D_m^{\frac{d+p}{2}}\) with respect to any eigenvalue \(v \ne 0\) are
where
and we take
As an eigenfunction of a positive integer power of the Laplacian, \(\phi ^{d,p}_{m,j,l}\) is real analytic on \(\mathbb {B}^d\), cf. [5, 36]. Hence, the radial part \(\varphi ^{d,p}_{m,j,l}\) must be an analytic function on [0, 1] with even or odd parity for m even or odd, respectively, cf. [9]. The functions \(\mathcal {Y}^{d,\omega _{\ell }}_{m}\) do not have matching parity, which concludes the proof. \(\square \)
In order to identify the eigenvalues and the linear combination in Lemma D.1, we check how \(T_m^{d,p}\) in (5.8) acts on \(\mathcal {J}^{d,\omega }_{m}\).
Lemma D.2
For d and \(p>1-d\) odd, we have

Proof of Lemma D.2
The idea of the proof is to use the series expansion of the Bessel functions, apply the integral operator to each term, and eventually recover the right-hand side of (D.4). We shall provide the skeleton of the proof and omit some lengthy computations.
Let \(d \ge 1\), \(p \ge 1-d\) and \(r\ge s\). If \(d+p\) is even, direct computations yield
We obtain that \(( T_m^{d,2l-d} \mathcal {J}^{d,\omega }_{m})(r) \) equals
For \(\alpha > 0\), \(k \in {\mathbb {N}}_0\), \(\omega \in {\mathbb {C}}\) and \(r > 0\), integration of each term of the power series of the Bessel function eventually yields
which follows from direct computations and

for \(\alpha \in {\mathbb {R}}\), \(k \in {\mathbb {N}}_{0}\), and \(n \in {\mathbb {N}}\) with \(\alpha \not \in \{-(k+1),-k,\dots ,-n \}\). By applying (D.5) and (D.6), we can express \(( T_m^{d,2l-d} \mathcal {J}^{d,\omega }_{m})(r)\) as a sum of Bessel functions of various different orders. Straightforward but lengthy computations combined with the identity
eventually lead to the claimed equality (D.4).
In order to verify (D.7), according to the definition of the Bessel function \(J_\alpha (x)\), we have to show that the coefficient of \((x/2)^{\alpha +2m}\) on the right-hand side of (D.7) equals \((-1)^m/(m!\Gamma (m+\alpha +1))\), for \(m=0,1,\dots \). Let first \(m\ge l\). Then this coefficient \(R(\alpha ,m)\) equals

Both hypergeometric series can be evaluated by means of Gauss’ Theorem. Thus, we obtain
Now we reverse the order of summation in the second sum, i.e., we replace k by \(l-k\) there. Then both sums can be conveniently put together to yield

The hypergeometric function can be evaluated by means of the classical terminating very-well-poised \(_5F_4\)-summation (cf. [47, Equation (2.3.4.6); Appendix (III.13)]). After some simplification one arrives at the desired expression \((-1)^m/(m!\Gamma (m+\alpha +1))\).
If \(m<l\), then the first sum in (D.8) does not contribute anything because of the term \((m-l-1)!\) in the denominator. In the second sum, the summation over i may be started at \(i=l-m\), which can be evaluated by means of the binomial theorem. The result is zero except if \(k=l\). Again, in the end one obtains \((-1)^m/(m!\Gamma (m+\alpha +1))\).
\(\square \)
Proof of Theorem 5.1
We now combine Lemmas D.2 and D.1. Let the linear combination \( f=\sum _{\ell =1}^{\frac{d+p}{2}} c_\ell \mathcal {J}^{d,\omega _{\ell }}_{m} \) be an eigenfunction of \(T^{d,p}_m\) with eigenvalue \(\lambda \) and let \(\omega _{\ell }\) be as in (D.2). We obtain for any \(\ell = 1,\dots ,\frac{d+p}{2}\) that
and thus
where \(A(\omega )\) is as in (5.10), \(c=(c_{\ell })_{\ell =1,\dots ,\frac{d+p}{2}}\), and

For \(i=1,\dots ,\tfrac{d+p}{2}\), the hypergeometric functions in F are polynomials of exact degree \(d+p-2i\) and thus linearly independent. Hence, for \(c \ne 0\), the right-hand side of (D.9) vanishes if and only if \(A(\omega )\) is singular and c is in its nullspace. \(\square \)
Appendix E: Proofs for Section 6
Proof of Proposition 6.1
We shall derive the coefficients \(a_m(p,\textrm{SO}(3))\) from the family of spherical coefficients \(a_m(p,\mathbb {S}^1)\). The half-angle identity \(\sin (\frac{t}{2})=\sqrt{\frac{1-\cos (t)}{2}}\), for \(t\in [0,\pi ]\), implies
where \(s=\arccos (\langle x,y\rangle )\). For \(d=2\), the addition theorem yields
where \(\mathcal {T}_m\) are the Chebyshev polynomials of the first kind, i.e., \(\mathcal {T}_m\big (\cos (s)\big )=\cos (ms)\), for \(s\in [0,\pi ]\). The relation (3.4) for \(d=2\) with (E.1) and (E.2) leads to
We now switch to \(\textrm{SO}(3)\). For \(x,y\in \textrm{SO}(3)\), the relation
the choice \(s=\arccos (\frac{\textrm{trace}(x^\top y)-1}{2})\), and (E.3) imply
The Legendre polynomials satisfy \(\mathcal {T}_m = \frac{1}{2}(\mathcal {C}^1_{m}-\mathcal {C}^1_{m-2})\) with \(\mathcal {T}_0 = \mathcal {C}^1_0\) and \(\mathcal {C}^0_{-1} = 0\), for \(m \in {\mathbb {N}}\), so that we obtain
We derive (6.3) by calculating the differences \(2^{\frac{p}{2}}(a_{m}(p,\mathbb {S}^1) - a_{m+1}(p,\mathbb {S}^1))\) in (E.4) and applying the addition theorem of the orthonormal Wigner \(\mathcal {D}\)-functions,
see [48] for (E.5). Analytic continuation and well-known relations for the gamma function cover the remaining values of \(p > -3\).
Standard calculations yield \(\frac{\Gamma (m-\frac{p}{2})}{\Gamma (m+\frac{p}{2}+2)}=m^{-2-p}(1+o(1))\), which concludes the proof. \(\square \)
Appendix F: Proofs for Section 7
1.1 F.1. Proofs for Section 7.1
Proof of Theorem 7.1
Proof of (7.5): According to [20], \(Q_\lambda \) is explicitly given in terms of Legendre polynomials by
where \(c_\lambda :=\dim (\mathcal {H}^4_{2\lambda })=\left( 2-\delta _{0,\lambda _2}\right) \left( (2\lambda _1+1)^2-4\lambda ^2_2\right) \) and \(\theta _1\), \(\theta _2\) denote the principal angles between x and y and
In order to write the integral (7.4) in terms of the variables \(\xi _\pm \), we first observe
We set \(-q:=p/2\) as well as \(m:=\lambda _1+\lambda _2\) and \(n:=\lambda _1-\lambda _2\). According to [20], the measure \(\mu _{\mathcal {G}_{2,4}}\otimes \mu _{\mathcal {G}_{2,4}}\) in (7.4) turns into \(d\xi _{+}d\xi _{-}\) for the variables \(\xi _\pm \) on \(|\xi _{+}| \le \xi _{-} \le 1\), so that we obtain
Symmetry arguments yield
The series expansion of \((1-xy)^{-q}\) converges absolutely for \(q<2\), and the Legendre polynomials \(\mathcal {C}^{\frac{1}{2}}_m\) are orthogonal to the monomials \(x^k\) for \(k<m\) or \(m \not \equiv k \!\!\!\mod 2\). Therefore, the orthogonality relations yield
The use of the generating function and further calculations lead to
Application of (F.3) and \((q)_{m+2k}=(q)_m(m+q)_{2k}\) yields
By reordering and making use of \( n!\,(n+1)_{m-n+2k} = (m+2k)!\), which cancels the identical term in the denominator, we are led to
where the equality in the last line is due to the identities
The relation \((\tfrac{3}{2})_n (n+\tfrac{3}{2})_{\tfrac{m-n}{2}}=(\tfrac{3}{2})_{\tfrac{m+n}{2}}\) and our choices \(m=|\lambda |\), \(n=\lambda _1-\lambda _2\) yield \((\tfrac{m-n}{2})!(\tfrac{3}{2})_n (n+\tfrac{3}{2})_{\tfrac{m-n}{2}}=(\tfrac{3}{2})_{\lambda _1}\lambda _2!=(\tfrac{3}{2})_\lambda \), so that \(q=-p/2\) and the definition of the \({}_4F_3\) hypergeometric series conclude the proof of (7.5).
Proof of (7.6): The proof of the decay property for \(a_\lambda (p,\mathcal {G}_{2,4})\) requires some preparation and auxiliary results. For \(p\not \in 2\mathbb {N}\), direct calculations yield
In the following, we treat the case \(\lambda _1=an\) and \(\lambda _2= (1-a)n\) for \(n\in \mathbb {N}\) and \(n\rightarrow \infty \), with an arbitrary \(a\in [\frac{1}{2},1]\), so that \(|\lambda |=n\). Summarizing the proof of (7.6), we shall first verify that the summand in (F.4),
as a sequence in k, is unimodal, i.e., it first increases until it has reached its maximum and then decreases, see Lemma F.2. Second, approximation of S(n, k) for \(k\ge \varepsilon n^2\) with the help of Stirling’s formula, where \(\varepsilon >0\) but fixed, leads to an asymptotic formula for \(\sum _{k\ge \varepsilon n^2}S(n,k)\); see Lemma F.3. Third, we let \(\varepsilon \rightarrow 0\) to obtain the asymptotic behavior of the full sum \(\sum _{k\ge 0}S(n,k)\) for \(n\rightarrow \infty \); see (F.8). If the result is substituted in (F.4), the claimed decay in (7.6) follows immediately upon observing \(\Vert \lambda \Vert ^2=(2a^2-2a+1)n^2\).
To start with, we may consider S(n, k) as a function of real k.
Lemma F.1
Given \(n\in \mathbb {N}\), let \(k_0=k_0(n)\in (0,\infty )\) be such that \(\frac{\partial }{\partial k}S(n,k_0)=0\). Then
Lemma F.2
If n is large enough, S(n, k) has a unique — local and global — maximum for \(k\in [0,\infty )\).
Lemma F.3
Let \(\varepsilon >0\) be fixed and let \(A:=\frac{2a^2-2a+1}{p+6}\). Then
We postpone the proofs of Lemmas F.1, F.2, and F.3, and discuss their consequences first. If we let \(\varepsilon \rightarrow 0\) and substitute \(t=\frac{p+6}{2(1+x)}\) in the above integral, then the integral definition of the gamma function yields
Lemma F.3 and (F.7) provide the asymptotic lower bound on \(\sum _{k\ge 0}S(n,k)\) of the following two-sided claim:
To verify the asymptotic upper bound on \(\sum _{k\ge 0}S(n,k)\) in (F.8), we observe
which is due to Lemma F.2, saying that S(n, k) grows until its maximum at \(k=k_0\sim An^2\). By Lemma F.3 and letting \(\varepsilon \rightarrow 0\), we obtain the upper bound in (F.8). By taking into account the additional factor \(2^{-\frac{p}{2}-3}/\Gamma \big (-\frac{p}{2}\big )\) in (F.4) and the relation \(\Vert \lambda \Vert ^2=(2a^2-2a+1)n^2\), we observe that (F.8) provides our claim (7.6).
To complete the proof of (7.6) in Theorem 7.1, it remains to prove Lemmas F.1, F.2, and F.3.
Proof of Lemma F.1
The condition \(0=\frac{\partial }{\partial k}S(n,k_0)\) implies \(0=\frac{\partial }{\partial k}\big (\log S(n,k_0)\big )\). By using the digamma function \(\psi (z)\), the logarithmic derivative of (F.5) can be written as
For \(k=o(n)\), the above expression is certainly positive for large n, hence nonzero. If the order of magnitude of k is at least the one of n (in symbols, \(n=O(k)\)), then we may estimate the logarithmic derivative by
where the asymptotics \( \psi (x)=\log x-\frac{1}{2x}+O\big (x^{-2}\big )\), for \(x\rightarrow \infty \), cf. [24, Equation 1.18(7)]), were used. By applying the exponential function on both sides of \(\frac{\partial }{\partial k}\big (\log S(n,k_0)\big )=0\), together with the above estimation for \(\frac{\partial }{\partial k}\big (\log S(n,k)\big )\) we obtain
where
For \(k\sim cn\), we observe
so that we may assume that \(k_0\) is of larger asymptotic order of magnitude than n.
Define P(n, k) by
For k of larger asymptotic order of magnitude than n, the asymptotics of the digamma function implies that the error term \(O(n^{-1})\) in (F.9) and (F.10) may be replaced by \(O(k^{-2})\) and hence by \(o(k^{-1})\). The relations (F.10) and (F.11) lead to \(P(n,k_0)=o(k_0^3)\). Since direct computations yield
asymptotically leading terms in P(n, k) must cancel each other. We have already excluded \(k_0\sim cn\), so that we now consider \(k_0\sim cn^2\) for an appropriate constant c. The terms \(k^3\) and \(k^2n^2\) in P(n, k) must cancel each other, so that
The solution \(c=\frac{1}{p+6}(2a^2-2a+1)\) yields the leading term in (F.6). In order to derive the O(n) term in (F.6), we have to perform “bootstrap”, i.e., we substitute \(k_0=cn^2+k_1\) in (F.12) and apply analogous arguments to eventually conclude \(k_1=O(n)\). \(\square \)
Proof of Lemma F.2
We already saw in the previous proof that \(\frac{\partial }{\partial k}\log S(n,0)>0\), for sufficiently large n. Hence, \(\frac{\partial }{\partial k} S(n,0)>0\) holds, so that S(n, k) does not have a local maximum in \(k=0\). Convergence of the series (F.4) implies \(S(n,k)\rightarrow 0\) for integers \(k\rightarrow \infty \). Thus, for sufficiently large n, S(n, k) attains a local maximum at some \(k_0\in (0,\infty )\). Lemma F.1 implies \(k_0\sim \frac{1}{p+6}(2a^2-2a+1)n^2\). In order to investigate S(n, k) in a neighborhood of \(k_0\), we compute \(\frac{\partial ^2}{\partial s^2}\log S(n,k_0+s)\), which is
where \(k=k_0+s\) and \(\psi ^{(1)}(x)\) denotes the derivative of \(\psi (x)\). We claim that, for \(\vert s\vert =o( n^2)\) and sufficiently large n, we have \(\frac{\partial ^2}{\partial s^2}\log S(n,k_0+s)<0\). In order to establish this claim, we make use of \(\psi ^{(1)}(x)=\frac{1}{x}+\frac{1}{2x^2}+O(x^{-3})\), for \(x\rightarrow \infty \), cf. [24, Equations 1.16(9) and 1.18(9)]), to estimate the individual expressions in (F.13). Using \(k=k_0+s=k_0+o(n^2)= k_0+o( k_0)\), we obtain
where we have used \(\frac{1}{1+x}=1-x+x^2+O(x^3)\), for \(x\rightarrow 0\). We treat the other terms in (F.13) analogously. Note that \(k=k_0+o(n^2)\) also implies \( k= \frac{1}{p+6}(2a^2-2a+1)n^2+o(n^2)\), so that, by putting the individual estimates together, we arrive at
For sufficiently large n (and hence large \(k_0\)), this is evidently negative, as claimed. Thus, S(n, k) has a strict local maximum in \(k_0\).
Moreover, say there are \( k_0, k'_0\in (0,\infty )\), where S(n, k) has a local maximum, then Lemma F.1 implies that the magnitude of \(|k_0- k_0'|\) is of smaller order than \(n^2\). The above considerations imply \(k_0=k_0'\), which completes the proof. \(\square \)
To prove Lemma F.3, we shall approximate the summand S(n, k), given in (F.5), with the help of Stirling’s formula (F.14). It turns out that, under this approximation, the sum \(\sum _{k\ge 0}S(n,k)\) can then be interpreted as a Riemann integral.
Proof of Lemma F.3
Let \(k_0\) be the unique location of the maximum of S(n, k). We recall that Lemma F.1 yields \(k_0=An^2+O(n)\). We consider \(\log S(n,k)\), for \(k\ge \varepsilon n^2\), and write \(k=k_0+s\), so that \(s\ge -k_0+\varepsilon n^2\). Stirling’s formula
leads to the estimates
where we have factored out \(k_0+s\). By applying \(\log (1+x)=x-\frac{x^2}{2}+O(x^3)\), we obtain
Here, terms such as \(\frac{n^3}{(k_0+s)^2}\) or \(\frac{n}{k_0+s}\) are of the order \(O(n^ {-1})\) and can therefore be subsumed in the error term. Thus, we obtain
The reasoning for the \(O(\,.\,)\)-terms are based on our restriction to \(k_0+s\ge \varepsilon n^2\). However, the constants in these error terms do contain \(\varepsilon \).
For the other gamma functions in (F.5), we proceed similarly. If everything is put together, then we obtain
For the sum of the S(n, k), we have
By understanding, the sum over s is taken over those s, for which \(k_0+s\) is an integer. The error of the Riemann sum approximation
is of the order of magnitude \(O(k_0^{-1})\). This follows from the fact that the summand in the sum attains a unique local and global maximum — namely at \(s=0\) — and therefore the error is bounded above by \(k_0^{-1}\) times the absolute variation of the summand — which equals twice the maximum. Substitution of all this in (F.15) concludes the proof. \(\square \)
Our proof of (7.6) in Theorem 7.1 is now complete. \(\square \)
1.2 F.2. Proofs for Section 7.2
Recall that the action of \(\textrm{SO}(3)\times \textrm{SO}(3)\) on \(\mathbb {S}^2\times \mathbb {S}^2\) by left multiplication is transitive, and \(\textrm{SO}(4)\) acts transitively on \(\mathcal {G}_{2,4}\) by conjugation. For each \(O\in \textrm{SO}(4)\), there are \(a,b\in \mathbb {S}^3\) such that \(O=L_a R_b\), where the left and right isoclinic rotations are
For \(a\in \mathbb {S}^3\), the Euler–Rodrigues formula yields
We are looking for \(\mathcal {P}:\mathbb {S}^2\times \mathbb {S}^2\rightarrow \mathcal {G}_{2,4}\) satisfying
Theorem F.4
There are exactly two mappings \(\mathbb {S}^2\times \mathbb {S}^2\rightarrow \mathcal {G}_{2,4}\) satisfying (F.17). One is \(\mathcal {P}\) as in (7.8), and the other is \(I_4-\mathcal {P}\). In particular, \(\mathcal {P}\) is surjective and, for all \(x,y,u,v\in \mathbb {S}^2\),
Proof of Theorem F.4
The identity (F.17) for the specific choice of \(\mathcal {P}\) is verified by expanding both sides of the equality and comparing the polynomial expressions. We omit the straightforward but lengthy computation.
Since the conjugate action of \(\textrm{SO}(4)\) on \(\mathcal {G}_{2,4}\) is transitive, the identity (F.17) also implies surjectivity. Since left and right eigenspaces of \(\mathcal {L}(\mathcal {P}(x,y))\) in (7.10) and (7.11) are uniquely determined, we deduce that (F.18) holds.
Let us now address the uniqueness statement. For \(a:=(\alpha ,0,0)\), \(b:=(\beta ,0,0)\) with \(\alpha ,\beta \in \mathbb {S}^1\), we obtain the isoclinic rotations
where \(A_\alpha =\left( \begin{array}{cc}\alpha _1&{}-\alpha _2\\ \alpha _2&{}\alpha _1\end{array}\right) ,\;B_\beta = \left( \begin{array}{cc} \beta _1&{}-\beta _2\\ \beta _2&{}\beta _1 \end{array}\right) \in \textrm{SO}(2)\). Since \(S_ae_1=S_b e_1=e_1\), any mapping \(\tilde{\mathcal {P}}:\mathbb {S}^2\times \mathbb {S}^2\rightarrow \mathcal {G}_{2,4}\) satisfying (F.17) must obey
Let V denote the range of \(\tilde{\mathcal {P}}(e_1,e_2)\), which is a two-dimensional subspace of \(\mathbb {R}^4\). The relation (F.19) means that \(L_aR_b\) maps V into itself, i.e., \(L_aR_b V = V\). For all \(U_1,U_2\in \textrm{SO}(2)\), there are \(\alpha ,\beta \in \mathbb {S}^1\) such that
so that V must either coincide with \(\textrm{span}\{e_1,e_2\}\) or with \(\textrm{span}\{e_3,e_4\}\). Hence, \(\tilde{\mathcal {P}}(e_1,e_2)\) must coincide with either \(\textrm{diag}(1,1,0,0)\) or \(\textrm{diag}(0,0,1,1)\). It follows from (F.17) and \(\textrm{SO}(3)\) acting transitively on \(\mathbb {S}^2\) that in the first case \(\tilde{\mathcal {P}}=\mathcal {P}\) and in the latter \(\tilde{\mathcal {P}}=I_4-\mathcal {P}\).
\(\square \)
Remark F.5
The Grassmannian \(\mathcal {G}_{2,4}\) has been parametrized in [20] by means of angles but the explicit identity (F.17) that steers our present approach has not been considered there. Our parametrization is compatible with the one used in [19].
The following properties of \(\mathcal {P}\) are useful.
Lemma F.6
The probability measure \(\sigma _{\mathcal {G}_{2,4}}\), induced by the Haar measure on \(\textrm{O}(4)\), is the push-forward measure of \(\sigma _{{\mathbb {S}}^2}\otimes \sigma _{{\mathbb {S}}^2}\) under \(\mathcal {P}\), and we have, for all \(x,y,u,v\in \mathbb {S}^2\),
where \(\mathcal {I}_-:=\textrm{diag}(-1,1,1,1)\), and \(\theta _1\), \(\theta _2\) denote the principal angles between \(\mathcal {P}(x,y)\) and \(\mathcal {P}(u,v)\).
Note that the right-hand side of (F.23) is \(\pm \{\xi _+,\xi _-\}\) for \(\xi _+,\xi _-\) as in (F.2).
Proof of Lemma F.6
The product measure \(\sigma _{{\mathbb {S}}^2}\otimes \sigma _{{\mathbb {S}}^2}\) is \(\textrm{SO}(3)\times \textrm{SO}(3)\) invariant. According to (F.17), the pushforward measure of \(\sigma _{{\mathbb {S}}^2}\otimes \sigma _{{\mathbb {S}}^2}\) on \({\mathbb {S}}^2 \times {\mathbb {S}}^2\) under \(\mathcal {P}\) is \(\textrm{SO}(4)\) invariant, so that the uniqueness of the Haar measure implies the first claim of the lemma.
Each of the remaining claims is first proved for \(\mathcal {P}\) as defined in Proposition F.4 and then argued that it also holds for \(I_4-\mathcal {P}\). The identity (F.20) is easily observed for \(u,v=e_1\) first and then (F.17) yields the general case. According to
the identity (F.20) also holds for \(I_4-\mathcal {P}\). The statement (F.21) follows from expanding both sides of the equality and comparing polynomial expressions in x and y. If it holds for \(\mathcal {P}\), then it must also hold for \(I_4-\mathcal {P}\). One directly calculates (F.22).
In order to check (F.23), we first recognize that principal angles between \(I-\mathcal {P}(x,y)\) and \(I-\mathcal {P}(u,v)\) coincide with the ones between \(\mathcal {P}(x,y)\) and \(\mathcal {P}(u,v)\). By \(\xi _{\pm }\) as in (F.2) and as at the beginning of the proof of Theorem 7.1, we observe \(\textrm{trace}(\mathcal {P}(x,y)\mathcal {P}(u,v))=1+\xi _+\xi _-\). Hence, (F.20) leads to \( \xi _+\xi _- = \langle x,u\rangle \langle y,v\rangle . \) Theorem 7.2 implies that \(Q_\lambda \) in (7.2) satisfies
Comparison of this identity with (F.1) and few further calculations eventually lead to (F.23). \(\square \)
Proof of Theorem 7.2
The action of \(\textrm{SO}(3)\times \textrm{SO}(3)\) leads to the irreducible decomposition

The unit quaternions provide a group structure on \(\mathbb {S}^3\), so that the mapping \(a\mapsto S_a\) between  and \(\textrm{SO}(3)\) as well as \((a,b)\mapsto L_a R_b\) between
and \(\textrm{SO}(3)\) as well as \((a,b)\mapsto L_a R_b\) between  and \(\textrm{SO}(4)\) become group isomorphisms. Their combination induces a group isomorphism between \(\textrm{SO}(3)\times \textrm{SO}(3)\) and
and \(\textrm{SO}(4)\) become group isomorphisms. Their combination induces a group isomorphism between \(\textrm{SO}(3)\times \textrm{SO}(3)\) and  . Condition (F.17) requires that the respective actions on \(\mathbb {S}^2\times \mathbb {S}^2\) and \(\mathcal {G}_{2,4}\) commute with \(\mathcal {P}\). Hence, the induced pullback
. Condition (F.17) requires that the respective actions on \(\mathbb {S}^2\times \mathbb {S}^2\) and \(\mathcal {G}_{2,4}\) commute with \(\mathcal {P}\). Hence, the induced pullback

is an intertwining isomorphism. In particular, \(\mathcal {P}^*\) maps one irreducible subspace into the other. Thus, the irreducible decomposition of \(L_2(\mathcal {G}_{2,4})\) under the action of \(\textrm{SO}(4)\) is
In comparison to the irreducible decomposition of \(L_2(\mathcal {G}_{2,4})\) for the action of \(\textrm{SO}(4)\) in (F.24), the irreducible components \(H_\lambda (\mathcal {G}_{2,4})\) with respect to \(\textrm{O}(4)\) in (7.1) are usually larger.
Let us denote \( H^{m,n}:=\textrm{span}\{ Y_{k,l}^{m,n}: k = -m,\dots ,m,\; l=-n,\ldots ,n\}\). Property (F.21) yields that the irreducible subspaces of \(L_2(\mathcal {G}_{2,4})\) under the action of \(\textrm{O}(4)\) are
where \(m+n\in 2\mathbb {N}\) and \(m\ge n\), i.e.,
where \(m_\lambda =\lambda _1+\lambda _2\) and \(n_\lambda =\lambda _1-\lambda _2\).
By considering \(\mathcal {L}(P)=xy^\top \), \(\mathcal {L}(P)\cdot \mathcal {L}(P)^\top =xx^\top \), and \(\mathcal {L}(P)^\top \cdot \mathcal {L}(P)=yy^\top \), we observe that the homogeneous polynomials \( x_{i}y_{j}\) and \(x_{i}x_{j}\), \(y_{i}y_{j}\), for \(i,j = 1,\dots ,3, \) can be written as homogeneous polynomials in the matrix entries of \(P \in \mathcal {G}_{2,4}\) of degree 1 and 2, respectively. The monomial \(x^\alpha y^{\beta }\) with \(|\alpha |=m_\lambda \) and \(|\beta |=n_\lambda \) is composed of \(n_\lambda \) factors of the form \(x_iy_j\) and \((m_\lambda -n_\lambda )/2\) factors of the form \(x_{i}x_{j}\). Thus, \(x^\alpha y^{\beta }\) is a homogeneous polynomial of degree \(n_\lambda +2((m_\lambda -n_\lambda )/2) = m_\lambda \) in the matrix entries of P. We deduce
since the right-hand side of (F.25) are the polynomials of degree at most t in the matrix entries of \(P\in \mathcal {G}_{2,4}\), cf. [8]. By applying [26, Formulas (24.29) and (24.41)], we see that the dimension of \(H_{\lambda }(\mathcal {G}_{2,4})\) is
which matches \(\dim (V^{m_\lambda ,n_\lambda })\). Hence, there holds equality in (F.25). For fixed t, the dimensions in (F.26) are pairwise different, for all \(\lambda _1+\lambda _2=t\). An induction over t leads to \(H_{\lambda }(\mathcal {G}_{2,4})=V^{m_\lambda ,n_\lambda }\). \(\square \)
1.3 F.3. Proofs for Section 7.3
The relation (7.16) yields
where \(B_{k,l}(\theta _1,\theta _2)\) are given by
Hence, the coefficients from (7.17) satisfy
First evaluating the inner sum for \(k,l,l'=-M,\ldots ,M\) and \(m_1=\max (|k|,M-k'),\ldots ,M\), and afterwards the outer sum enables the computation of the coefficients \(b^{k,l}_{k',l'}\), for \(k,l,k',l'=-M,\ldots ,M\), in \(O(M^5)\) operations provided that the numbers \(c^{m}_{k,k'}\) in (7.16) are given.
Remark F.7
The complexity for evaluating the two sums in (F.27) can be further reduced to \(O(M^4\log ^2(M))\) by using a fast polynomial transform, cf. [39, 41]. In this way, the nonequispaced fast Fourier transform on \(\mathbb {S}^2\times \mathbb {S}^2\) takes \(O(M^4\log ^2(M)+n|\log (\epsilon )|^4)\) elementary operations. For \(n\sim M^4\), this implies the reduction of complexity from \(O(M^8)\) to \(O(M^4\log ^2(M)+M^4|\log (\epsilon )|^4)\) operations.
The adjoint nonequispaced fast Fourier transform is about computing
for given coefficients \((b_i)_{i=1}^M\subset \mathbb {C}\) and locations \((x_i,y_i)_{i=1}^M\subset \mathbb {S}^2\times \mathbb {S}^2\). Similar arguments as above and in Sect. 7.3 provide a fast evaluation of (F.28) by using the adjoint nonequispaced fast Fourier transform adjoint nfft, cf. [39, 41].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dick, J., Ehler, M., Gräf, M. et al. Spectral Decomposition of Discrepancy Kernels on the Euclidean Ball, the Special Orthogonal Group, and the Grassmannian Manifold. Constr Approx 57, 983–1026 (2023). https://doi.org/10.1007/s00365-023-09638-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00365-023-09638-0
Keywords
- Discrepancy kernels
- Spectral decompositions
- Euclidean ball
- Special orthogonal group
- Grassmannian manifold
- Nonequispaced fast Fourier transform







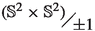

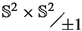 by
by