Abstract
We consider neural network approximation spaces that classify functions according to the rate at which they can be approximated (with error measured in \(L^p\)) by ReLU neural networks with an increasing number of coefficients, subject to bounds on the magnitude of the coefficients and the number of hidden layers. We prove embedding theorems between these spaces for different values of p. Furthermore, we derive sharp embeddings of these approximation spaces into Hölder spaces. We find that, analogous to the case of classical function spaces (such as Sobolev spaces, or Besov spaces) it is possible to trade “smoothness” (i.e., approximation rate) for increased integrability. Combined with our earlier results in Grohs and Voigtlaender (Proof of the theory-to-practice gap in deep learning via sampling complexity bounds for neural network approximation spaces, 2021. arXiv preprint arXiv:2104.02746), our embedding theorems imply a somewhat surprising fact related to “learning” functions from a given neural network space based on point samples: if accuracy is measured with respect to the uniform norm, then an optimal “learning” algorithm for reconstructing functions that are well approximable by ReLU neural networks is simply given by piecewise constant interpolation on a tensor product grid.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider approximation spaces associated to neural networks with ReLU activation function \(\varrho :{\mathbb {R}}\rightarrow {\mathbb {R}},\) \(\varrho (x) = \max \{0,x\}\) as introduced in our recent work [11]; see also Sect. 2. Roughly speaking, these spaces  are defined as follows: Given a depth-growth function \(\varvec{\ell }\!:\! {\mathbb {N}} \rightarrow {\mathbb {N}}_{\ge 2} \cup \{\infty \}\) and a coefficient growth function \({\varvec{c}}: {\mathbb {N}} \rightarrow {\mathbb {N}} \cup \{\infty \}\), the approximation space
are defined as follows: Given a depth-growth function \(\varvec{\ell }\!:\! {\mathbb {N}} \rightarrow {\mathbb {N}}_{\ge 2} \cup \{\infty \}\) and a coefficient growth function \({\varvec{c}}: {\mathbb {N}} \rightarrow {\mathbb {N}} \cup \{\infty \}\), the approximation space  consist of all functions that can be approximated up to error \({\mathcal {O}}(n^{-\alpha })\), with the error measured in the \(L^p([0,1]^d)\) (quasi)-norm for some \(p\in (0,\infty ]\), by neural networks with at most \(\varvec{\ell }(n)\) layers and n coefficients (non-zero weights) of size at most \({\varvec{c}}(n)\), \(n\in {\mathbb {N}}\). As shown in [11] these spaces can be equipped with a natural (quasi)-norm; see also Lemma 2.1 below. In most applications in machine learning, one is interested in “learning” such functions from a finite amount of samples. To render this problem well defined we would like the space
consist of all functions that can be approximated up to error \({\mathcal {O}}(n^{-\alpha })\), with the error measured in the \(L^p([0,1]^d)\) (quasi)-norm for some \(p\in (0,\infty ]\), by neural networks with at most \(\varvec{\ell }(n)\) layers and n coefficients (non-zero weights) of size at most \({\varvec{c}}(n)\), \(n\in {\mathbb {N}}\). As shown in [11] these spaces can be equipped with a natural (quasi)-norm; see also Lemma 2.1 below. In most applications in machine learning, one is interested in “learning” such functions from a finite amount of samples. To render this problem well defined we would like the space  to embed into \(C([0,1]^d)\). The question that we consider in this work is therefore to find conditions under which such an embedding holds true. More generally, we are interested in characterizing the existence of embeddings of the approximation spaces into the Hölder spaces \(C^{0,\beta }([0,1]^d)\) for \(\beta \in (0, 1]\). The existence of such embeddings is far from clear; for example, recent work [5,6,7, 9] shows that fractal and highly non-regular functions can be efficiently approximated by (increasingly deep) ReLU neural networks.
to embed into \(C([0,1]^d)\). The question that we consider in this work is therefore to find conditions under which such an embedding holds true. More generally, we are interested in characterizing the existence of embeddings of the approximation spaces into the Hölder spaces \(C^{0,\beta }([0,1]^d)\) for \(\beta \in (0, 1]\). The existence of such embeddings is far from clear; for example, recent work [5,6,7, 9] shows that fractal and highly non-regular functions can be efficiently approximated by (increasingly deep) ReLU neural networks.
The main contribution of this paper are sharp conditions for when the space  embeds into \(C([0,1]^d)\) or \(C^{0,\beta }([0,1]^d)\). These results in particular show that, similar to classical Sobolev spaces, one can trade smoothness for (improved) integrability in the context of neural network approximation, where “smoothness” of a function is understood as it being well approximable by neural networks.
embeds into \(C([0,1]^d)\) or \(C^{0,\beta }([0,1]^d)\). These results in particular show that, similar to classical Sobolev spaces, one can trade smoothness for (improved) integrability in the context of neural network approximation, where “smoothness” of a function is understood as it being well approximable by neural networks.
Building on these insights we consider the problem of finding optimal numerical algorithms for reconstructing arbitrary functions in  from finitely many point samples, where the reconstruction error is measured in the \(L^\infty ([0,1]^d)\) norm: As a corollary to our embedding theorems we establish the somewhat surprising fact that, irrespective of \(\alpha \), an optimal algorithm is given by piecewise constant interpolation with respect to a uniform tensor-product grid in \([0,1]^d\).
from finitely many point samples, where the reconstruction error is measured in the \(L^\infty ([0,1]^d)\) norm: As a corollary to our embedding theorems we establish the somewhat surprising fact that, irrespective of \(\alpha \), an optimal algorithm is given by piecewise constant interpolation with respect to a uniform tensor-product grid in \([0,1]^d\).
1.1 Description of Results
In the following sections we sketch our main results. To simplify the presentation, let us assume that the coefficient growth function \({\varvec{c}}\) satisfies the asymptotic growth \({\varvec{c}}\asymp n^\theta \cdot (\ln (2n))^{\kappa }\) for certain \(\theta \ge 0\) and \(\kappa \in {\mathbb {R}}\) (our general results hold for any coefficient growth function). Let
1.1.1 Embedding Results
Our first main theorem provides sharp embedding results into \(C([0,1]^d)\). A slight simplification of our main result reads as follows.
Theorem 1.1
Assume that \(\alpha > \frac{d}{p}\cdot \gamma ^*\). Then the embedding  holds. Assume that \(\alpha < \frac{d}{p}\cdot \gamma ^*\). Then the embedding
holds. Assume that \(\alpha < \frac{d}{p}\cdot \gamma ^*\). Then the embedding  does not hold.
does not hold.
Theorem 1.1 is a special case of Theorems 3.3 and 3.6 below that will be proven in Sect. 3.
We would like to draw attention to the striking similarity between Theorem 1.1 and the classical Sobolev embedding theorem for Sobolev spaces \(W^{\alpha ,p}\) which states that \(W^{\alpha ,p}([0,1]^d)\hookrightarrow C([0,1]^d)\) holds if \(\alpha > \frac{d}{p}\), but not if \(\alpha < \frac{d}{p}\). Just as in the case of classical Sobolev spaces we show that, also in the context of neural network approximation, it is possible to trade “smoothness” (i.e., approximation order) for (improved) integrability.
We also prove sharp embedding results into the Hölder spaces \(C^{0,\beta }([0,1]^d)\). A slight simplification of our main result reads as follows.
Theorem 1.2
Let \(\beta \in (0,1)\).
-
If \(\alpha > \frac{\beta + \frac{d}{p}}{1-\beta }\cdot \gamma ^*\), then the embedding
 holds.
holds. -
If \(\alpha < \frac{\beta + \frac{d}{p}}{1-\beta }\cdot \gamma ^*\), then the embedding
 does not hold.
does not hold.
Theorem 1.2 is a special case of Theorems 3.5 and 3.6 below that will be proven in Sect. 3.
Theorems 1.1 and 1.2 provide a complete characterization of the embedding properties of the neural network approximation spaces  away from the “critical” index \(\alpha = \frac{d}{p}\cdot \gamma ^*\) (embedding into \(C([0,1]^d)\)), respectively \(\alpha = \frac{\beta + \frac{d}{p}}{1-\beta }\cdot \gamma ^*\) (embedding into \(C^{0,\beta }([0,1]^d)\)). We leave the (probably subtle) question of what happens at the critical index open for future work.
away from the “critical” index \(\alpha = \frac{d}{p}\cdot \gamma ^*\) (embedding into \(C([0,1]^d)\)), respectively \(\alpha = \frac{\beta + \frac{d}{p}}{1-\beta }\cdot \gamma ^*\) (embedding into \(C^{0,\beta }([0,1]^d)\)). We leave the (probably subtle) question of what happens at the critical index open for future work.
1.1.2 Optimal Learning Algorithms
Our embedding theorems allow us to deduce an interesting and surprising result related to the algorithmic feasibility of a learning problem posed on neural network approximation spaces.
More precisely, we consider the problem of approximating a function in the unit ball

of the neural network approximation space  under the constraint that the approximating algorithm is only allowed to access point samples of the functions \(f \in U\). Formally, a (deterministic) algorithm
under the constraint that the approximating algorithm is only allowed to access point samples of the functions \(f \in U\). Formally, a (deterministic) algorithm  using m point samples is determined by a set of sample points \({\varvec{x}}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) and a map \(Q: {\mathbb {R}}^m \rightarrow L^\infty ([0,1]^d)\) such that
using m point samples is determined by a set of sample points \({\varvec{x}}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) and a map \(Q: {\mathbb {R}}^m \rightarrow L^\infty ([0,1]^d)\) such that

Note that A need not be an “algorithm” in the usual sense, i.e., implementable on a Turing machine. The set of all such “algorithms” is denoted  and we define the optimal order for (deterministically) uniformly approximating functions in
and we define the optimal order for (deterministically) uniformly approximating functions in  using point samples as the best possible convergence rate with respect to the number of samples:
using point samples as the best possible convergence rate with respect to the number of samples:

In a similar way one can define randomized (Monte Carlo) algorithms and consider the optimal order  for approximating functions in
for approximating functions in  using randomized algorithms based on point samples; see [11, Section 2.4.2]. In [11, Theorem 1.1] we showed (under the assumption \(\varvec{\ell }^*\ge 3\)) that
using randomized algorithms based on point samples; see [11, Section 2.4.2]. In [11, Theorem 1.1] we showed (under the assumption \(\varvec{\ell }^*\ge 3\)) that

We now describe a particularly simple algorithm that achieves this optimal rate. For \(m \in {\mathbb {N}}_{\ge 2^d}\), let \(n:= \lfloor m^{1/d}\rfloor - 1\) and let
be the piecewise constant interpolation of f on a tensor product grid with sidelength \(\frac{1}{n}\), where for \(\tau \in [0,1]^d\) the function \(\mathbb {1}_{\tau + \left[ 0,\frac{1}{n}\right) ^d}\) denotes the indicator function of the set \(\tau + \left[ 0,\frac{1}{n}\right) ^d\subset {\mathbb {R}}^d\). Since \((n+1)^d \le m\) it clearly holds that

We have the following theorem.
Theorem 1.3
Under the above assumptions on \(\varvec{\ell },{\varvec{c}}\), the piecewise constant interpolation operator \(A_m^{\mathrm {pw-const}}\) constitutes an optimal algorithm for reconstructing functions in  from point samples: we have
from point samples: we have

Proof
Equation (1.1) yields the best possible rate with respect to the number of samples. Without loss of generality we assume that \(\varvec{\ell }^*< \infty \) (otherwise there is nothing to show as the optimal rate is zero). We now show that all rates below the optimal rate \(\frac{1}{d} \cdot \frac{\alpha }{\gamma ^*+ \alpha }\) can be achieved by piecewise constant interpolation, which readily implies our theorem. To this end, let \(\lambda \in \bigl (0,\frac{1}{d} \cdot \frac{\alpha }{\gamma ^*+ \alpha }\bigr )\) be arbitrary and let \(\beta := d \cdot \lambda \in (0, \frac{\alpha }{\gamma ^*+ \alpha }) \subset (0,1)\). It is easy to check that \(\alpha > \frac{\beta }{1-\beta } \gamma ^*\). Hence, Theorem 1.2 (applied with \(p=\infty \)) implies the embedding  , yielding the existence of a constant \(C_1 > 0\) with
, yielding the existence of a constant \(C_1 > 0\) with

where \(U^\beta \) denotes the unit ball in \(C^{0,\beta }([0,1]^d)\). Therefore,

where the last inequality follows from the elementary fact that piecewise constant interpolation on the uniform tensor-product grid \(\{ \frac{0}{n}, \frac{1}{n},..., \frac{n}{n} \}^d\) achieves \(L^\infty \) error of \({\mathcal {O}}(n^{-\beta }) \subset {\mathcal {O}}(m^{-\beta / d}) \!=\! {\mathcal {O}}(m^{-\lambda })\) for functions \(f \in U^\beta \). Since \(\lambda <\frac{1}{d}\cdot \frac{\alpha }{\gamma ^*+ \alpha }\) was arbitrary, Equation (1.3) proves Equation (1.2) and thus our theorem. \(\square \)
Theorem 1.3 proves that, provided that the reconstruction error is measured in the \(L^\infty \) norm, the optimal “learning” algorithm for reconstructing functions that are well approximable by ReLU neural networks is simply given by piecewise constant interpolation on a tensor product grid, at least if no additional information about the target function is given. We consider it surprising that the optimal algorithm for this problem possesses such a simple and explicit representation.
We finally remark that we expect all our results to hold (in slightly modified form) if general bounded Lipschitz domains \(\Omega \subset {\mathbb {R}}^d\) are considered in place of the unit cube \([0,1]^d\).
1.2 Related Work
The study of approximation properties of neural networks has a long history, see for example the surveys [3, 7, 9, 12] and the references therein. Function spaces related to neural networks have been studied in several works. For example, [1, 4, 14] study so-called Barron-type spaces that arise in a certain sense as approximation spaces of shallow neural networks. The paper [2] develops a calculus on spaces of functions that can be approximated by neural networks without curse of dimension. Closest to our work are the papers [10, 11] which study functional analytic properties of neural network approximation spaces similar to the ones studied in the present paper. The paper [10] also considers embedding results between such spaces with different constraints on their underlying network architecture. However, none of the mentioned works considered embedding theorems of Sobolev type comparable to those in the present paper. An important reason for this is that the spaces considered in [10] do not restrict the magnitude of the weights of the approximating networks, so that essentially \({\varvec{c}}\equiv \infty \) in our terminology. The resulting approximation spaces then contain functions of very low smoothness.
1.3 Structure of the Paper
The structure of this paper is as follows. In Sect. 2 we provide a definition of the neural network approximation spaces considered in this paper and establish some of their basic properties. In Sect. 3 we prove our embedding theorems.
2 Definition of Neural Network Approximation Spaces
In this section, we review the mathematical definition of neural networks, then formally introduce the neural network approximation spaces  , and finally define the quantities \(\varvec{\ell }^*\) and \(\gamma ^*(\varvec{\ell },{\varvec{c}})\) that will turn out to be decisive for characterizing whether the embeddings
, and finally define the quantities \(\varvec{\ell }^*\) and \(\gamma ^*(\varvec{\ell },{\varvec{c}})\) that will turn out to be decisive for characterizing whether the embeddings  or
or  hold.
hold.
2.1 The Mathematical Formalization of Neural Networks
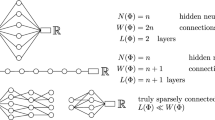
In our analysis, it will be helpful to distinguish between a neural network \(\Phi \) as a set of weights and the associated function \(R_\varrho \Phi \) computed by the network. Thus, we say that a neural network is a tuple \({\Phi = \big ( (A_1,b_1), \dots , (A_L,b_L) \big )}\), with \(A_\ell \in {\mathbb {R}}^{N_\ell \times N_{\ell -1}}\) and \(b_\ell \in {\mathbb {R}}^{N_\ell }\). We then say that \({{\varvec{a}}(\Phi ):= (N_0,\dots ,N_L) \in {\mathbb {N}}^{L+1}}\) is the architecture of \(\Phi \), \(L(\Phi ):= L\) is the number of layersFootnote 1 of \(\Phi \), and \({W(\Phi ):= \sum _{j=1}^L (\Vert A_j \Vert _{\ell ^0} + \Vert b_j \Vert _{\ell ^0})}\) denotes the number of (non-zero) weights of \(\Phi \). The notation \(\Vert A \Vert _{\ell ^0}\) used here denotes the number of non-zero entries of a matrix (or vector) A. Finally, we write \(d_{\textrm{in}}(\Phi ):= N_0\) and \(d_{\textrm{out}}(\Phi ):= N_L\) for the input and output dimension of \(\Phi \), and we set \(\Vert \Phi \Vert _{{{\mathcal {N}}}{{\mathcal {N}}}}:= \max _{j = 1,\dots ,L} \max \{ \Vert A_j \Vert _{\infty }, \Vert b_j \Vert _{\infty } \}\), where \({\Vert A \Vert _{\infty }:= \max _{i,j} |A_{i,j}|}\).
To define the function \(R_\varrho \Phi \) computed by \(\Phi \), we need to specify an activation function. In this paper, we will only consider the so-called rectified linear unit (ReLU) \({\varrho : {\mathbb {R}}\rightarrow {\mathbb {R}}, x \mapsto \max \{ 0, x \}}\), which we understand to act componentwise on \({\mathbb {R}}^n\), i.e., \(\varrho \bigl ( (x_1,\dots ,x_n)\bigr ) = \bigl (\varrho (x_1),\dots ,\varrho (x_n)\bigr )\). The function \(R_\varrho \Phi : {\mathbb {R}}^{N_0} \rightarrow {\mathbb {R}}^{N_L}\) computed by the network \(\Phi \) (its realization) is then given by
2.2 Neural Network Approximation Spaces
Approximation spaces [8] classify functions according to how well they can be approximated by a family \(\varvec{\Sigma } = (\Sigma _n)_{n \in {\mathbb {N}}}\) of certain “simple functions” of increasing complexity n, as \(n \rightarrow \infty \). Common examples consider the case where \(\Sigma _n\) is the set of polynomials of degree n, or the set of all linear combinations of n wavelets. The notion of neural network approximation spaces was originally introduced in [10], where \(\Sigma _n\) was taken to be a family of neural networks of increasing complexity. However, [10] does not impose any restrictions on the size of the individual network weights, which plays an important role in practice and which is important in determining the regularity of the function implemented by the network. Since the function spaces introduced in [10] ignore this quantity, the spaces defined there never embed into the Hölder-space \(C^{0,\beta }\) for any \(\beta > 0\).
For this reason, and following our previous work [11], we introduce a modified notion of neural network approximation spaces that also takes the size of the individual network weights into account. Precisely, given an input dimension \(d \in {\mathbb {N}}\) (which we will keep fixed throughout this paper) and non-decreasing functions \({\varvec{\ell }: {\mathbb {N}}\rightarrow {\mathbb {N}}_{\ge 2} \cup \{ \infty \}}\) and \({\varvec{c}}: {\mathbb {N}}\rightarrow {\mathbb {N}}\cup \{ \infty \}\) (called the depth-growth function and the coefficient growth function, respectively), we define

Then, given a measurable subset \(\Omega \subset {\mathbb {R}}^d\) as well as \(p \in (0,\infty ]\) and \(\alpha \in (0,\infty )\), for each measurable \(f: \Omega \rightarrow {\mathbb {R}}\), we define

where \(d_{p}(f, \Sigma ):= \inf _{g \in \Sigma } \Vert f - g \Vert _{L^p(\Omega )}\).
The remaining issue is that since the set  is in general neither closed under addition nor under multiplication with scalars,
is in general neither closed under addition nor under multiplication with scalars,  is not a (quasi)-norm. To resolve this issue, taking inspiration from the theory of Orlicz spaces (see e.g. [13, Theorem 3 in Section 3.2]), we define the neural network approximation space quasi-norm
is not a (quasi)-norm. To resolve this issue, taking inspiration from the theory of Orlicz spaces (see e.g. [13, Theorem 3 in Section 3.2]), we define the neural network approximation space quasi-norm  as
as

giving rise to the approximation space

The following lemma summarizes the main elementary properties of these spaces.
Lemma 2.1
Let \(\varnothing \ne \Omega \subset {\mathbb {R}}^d\) be measurable, let \(p \in (0,\infty ]\) and \(\alpha \in (0,\infty )\). Then, the approximation space  satisfies the following properties:
satisfies the following properties:
-
1.
 is a quasi-normed space. Precisely, given arbitrary measurable functions \(f,g: \Omega \rightarrow {\mathbb {R}}\), it holds that
is a quasi-normed space. Precisely, given arbitrary measurable functions \(f,g: \Omega \rightarrow {\mathbb {R}}\), it holds that  for \(C = C(\alpha ,p)\).
for \(C = C(\alpha ,p)\). -
2.
We have
 for \(c \in [-1,1]\).
for \(c \in [-1,1]\). -
3.
 if and only if
if and only if  .
. -
4.
 if and only if
if and only if  .
. -
5.
 .
.
Proof
For \(p\in [1,\infty ]\) this is precisely [11, Lemma 2.1]. The case \(p\in (0,1)\) can be proven in a completely analogous way and is left to the reader. \(\square \)
Remark 2.2
While we introduced the spaces  for general domains \(\Omega \), in what follows we will specialize to \(\Omega = [0,1]^d\). We expect, however, that all our results will remain true (up to minor modifications) for general bounded Lipschitz domains.
for general domains \(\Omega \), in what follows we will specialize to \(\Omega = [0,1]^d\). We expect, however, that all our results will remain true (up to minor modifications) for general bounded Lipschitz domains.
2.3 Quantities Characterizing the Complexity of the Network Architecture
To conveniently summarize those aspects of the growth behavior of the functions \(\varvec{\ell }\) and \({\varvec{c}}\) most relevant to us, we introduce three quantities that will turn out to be crucial for characterizing whether the embeddings  or
or  hold. First, we set
hold. First, we set
Furthermore, we define \(\gamma ^*(\varvec{\ell }, {\varvec{c}}), \gamma ^{\diamondsuit } (\varvec{\ell }, {\varvec{c}}) \in (0,\infty ]\) by
where we use the convention that \(\sup \varnothing = 0\) and \(\inf \varnothing = \infty \). As we now show, the quantities \(\gamma ^*\) and \(\gamma ^{\diamondsuit }\) actually coincide.
Lemma 2.3
We have \(\gamma ^*(\varvec{\ell },{\varvec{c}}) = \gamma ^{\diamondsuit }(\varvec{\ell },{\varvec{c}})\). Furthermore, if \(\varvec{\ell }^*= \infty \), then \(\gamma ^*(\varvec{\ell },{\varvec{c}}) = \gamma ^{\diamondsuit }(\varvec{\ell },{\varvec{c}}) = \infty \).
Proof
For brevity, write \(\gamma ^*:= \gamma ^*(\varvec{\ell },{\varvec{c}})\) and \(\gamma ^{\diamondsuit }:= \gamma ^{\diamondsuit } (\varvec{\ell },{\varvec{c}})\).
Case 1 (\(\varvec{\ell }^*= \infty \)): In this case, given any \(\gamma > 0\), one can choose an even \(L \in {\mathbb {N}}= {\mathbb {N}}_{\le \varvec{\ell }^*}\) satisfying \(L > 2 \gamma \). It is then easy to see \( \limsup _{n \rightarrow \infty } \frac{({\varvec{c}}(n))^L \cdot n^{\lfloor L/2 \rfloor }}{n^\gamma } \ge \limsup _{n \rightarrow \infty } 1 = 1 \in (0,\infty ]. \) By definition of \(\gamma ^*\), this implies \(\gamma ^*\ge \gamma \) for each \(\gamma > 0\), and hence \(\gamma ^*= \infty \).
Next, we show that \(\gamma ^{\diamondsuit } = \infty \) as well. To see this, assume towards a contradiction that \(\gamma ^{\diamondsuit } < \infty \). By definition of \(\gamma ^{\diamondsuit }\), this means that there exist \(\gamma \ge 0\) and \(C > 0\) satisfying
But choosing an even \(L \in {\mathbb {N}}\) satisfying \(L > 2 \gamma \), we have \(\lfloor L/2 \rfloor = L/2 > \gamma \), showing that the preceding displayed inequality cannot hold. This is the desired contradiction.
Case 2 (\(\varvec{\ell }^*< \infty \)): We first show \(\gamma ^*\le \gamma ^{\diamondsuit }\). In case of \(\gamma ^{\diamondsuit } = \infty \), this is trivial, so that we can assume \(\gamma ^{\diamondsuit } < \infty \). Let \(\gamma _0 \in [0,\infty )\) such that there exists \(C > 0\) satisfying \(({\varvec{c}}(n))^L \cdot n^{\lfloor L/2 \rfloor } \le C \cdot n^{\gamma _0}\) for all \(n \in {\mathbb {N}}\) and \(L \in {\mathbb {N}}_{\le \varvec{\ell }^*}\). Then, given any \(L \in {\mathbb {N}}_{\le \varvec{\ell }^*}\) and \(\gamma > \gamma _0\), we have
This easily implies \(\gamma ^*\le \gamma _0\). Since this holds for all \(\gamma _0\) as above, we see by definition of \(\gamma ^{\diamondsuit }\) that \(\gamma ^*\le \gamma ^{\diamondsuit }\).
We finally show that \(\gamma ^{\diamondsuit } \le \gamma ^*\). In case of \(\gamma ^*= \infty \), this is clear; hence, we can assume that \(\gamma ^*< \infty \). Let \(\gamma > \gamma ^*\) be arbitrary. Then
Thus, since convergent sequences are bounded, we see that \( ({\varvec{c}}(n))^{\varvec{\ell }^*} \cdot n^{\lfloor \varvec{\ell }^*/ 2 \rfloor } \le C \cdot n^\gamma \) for all \(n \in {\mathbb {N}}\) and a suitable \(C > 0\). Given any \(L \in {\mathbb {N}}_{\le \varvec{\ell }^*}\), we thus have \( ({\varvec{c}}(n))^L \cdot n^{\lfloor L/2 \rfloor } \le ({\varvec{c}}(n))^{\varvec{\ell }^*} \cdot n^{\lfloor \varvec{\ell }^*/ 2 \rfloor } \le C \cdot n^\gamma . \) By definition of \(\gamma ^{\diamondsuit }\), this implies \(\gamma ^{\diamondsuit } \le \gamma \). Since this holds for all \(\gamma > \gamma ^*\), we conclude \(\gamma ^{\diamondsuit } \le \gamma ^*\). \(\square \)
3 Sobolev-Type Embeddings for Neural Network Approximation Spaces
In this section, we establish a characterization of the embeddings  and
and  solely in terms of \(\gamma ^*(\varvec{\ell },{\varvec{c}})\) and the quantities \(d \in {\mathbb {N}}\), \(\beta \in (0,1)\), and \(p \in (0,\infty ]\). This is roughly similar to Sobolev embeddings, which allow one to “trade smoothness for increased integrability.”
solely in terms of \(\gamma ^*(\varvec{\ell },{\varvec{c}})\) and the quantities \(d \in {\mathbb {N}}\), \(\beta \in (0,1)\), and \(p \in (0,\infty ]\). This is roughly similar to Sobolev embeddings, which allow one to “trade smoothness for increased integrability.”
3.1 Sufficient Conditions for Embedding into \(C([0,1]^d)\)
In this subsection we establish sufficient conditions for an embedding  to hold. The following lemma—showing that functions with large (but finite) Lipschitz constant but small \(L^p\) norm have a controlled \(L^\infty \) norm—is an essential ingredient for the proof.
to hold. The following lemma—showing that functions with large (but finite) Lipschitz constant but small \(L^p\) norm have a controlled \(L^\infty \) norm—is an essential ingredient for the proof.
We first make precise the notion of Lipschitz constant that we use in what follows. Given \(d\in {\mathbb {N}}\) and a function \(f:[0,1]^d \rightarrow {\mathbb {R}}\) we define
Lemma 3.1
Let \(p \in (0,\infty )\) and \(d \in {\mathbb {N}}\). Then there exists a constant \(C = C(d,p) > 0\) such that for each \(0 < T \le 1\) and each \(f \in L^p([0,1]^d) \cap C^{0,1}([0,1]^d)\), we have
Proof
For brevity, set \(Q:= [0,1]^d\). Let \(f \in L^p([0,1]^d) \cap C^{0,1}([0,1]^d)\). Since Q is compact and f is continuous, there exists \(x_0 \in Q\) satisfying \(|f(x_0)| = \Vert f \Vert _{L^\infty }\). Set \(P:= Q \cap (x_0 + [-T,T]^d)\). For \(x \in P\), we have
Now, denoting the Lebesgue measure by \(\varvec{\lambda }\), taking the \(L^p(P)\) norm of the preceding estimate, and recalling that \(L^p\) is a (quasi)-Banach space, we obtain a constant \(C_1 = C_1(p) > 0\) satisfying
Next, [11, Lemma A.2] shows that \(\varvec{\lambda }(P) \ge 2^{-d} \, T^d\), so that we finally see
which easily implies the claim. \(\square \)
In order to derive a sufficient condition for the embedding  , we will use the following lemma that provides a bound for the Lipschitz constant of a function implemented by a neural network, in terms of the size (number of non-zero weights) of the network and of the magnitude of the individual network weights.
, we will use the following lemma that provides a bound for the Lipschitz constant of a function implemented by a neural network, in terms of the size (number of non-zero weights) of the network and of the magnitude of the individual network weights.
Lemma 3.2
([11, Lemma 4.1]) Let \(\varvec{\ell }: {\mathbb {N}}\rightarrow {\mathbb {N}}_{\ge 2} \cup \{ \infty \}\) and \({\varvec{c}}: {\mathbb {N}}\rightarrow [1,\infty ]\). Let \(n \in {\mathbb {N}}\) and assume that \(L:= \varvec{\ell }(n)\) and \(C:= {\varvec{c}}(n)\) are finite. Then each  satisfies
satisfies
Now, we can derive a sufficient condition for the embedding  . Below, in Sect. 3.3, we will see that this sufficient condition is essentially optimal.
. Below, in Sect. 3.3, we will see that this sufficient condition is essentially optimal.
Theorem 3.3
Let \(d \in {\mathbb {N}}\) and \(p \in (0,\infty )\), and suppose that \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) < \infty \). If \(\alpha > \frac{d}{p} \cdot \gamma ^{*}(\varvec{\ell },{\varvec{c}})\), then  . Furthermore, for each \(\gamma \in \bigl ( \gamma ^{*}(\varvec{\ell },{\varvec{c}}), \frac{p}{d} \, \alpha \bigr )\), we have the embedding
. Furthermore, for each \(\gamma \in \bigl ( \gamma ^{*}(\varvec{\ell },{\varvec{c}}), \frac{p}{d} \, \alpha \bigr )\), we have the embedding

Proof
As shown in Lemma 2.3, the assumption \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) < \infty \) ensures that \(L:= \varvec{\ell }^*< \infty \). Furthermore, since \( \gamma ^{\diamondsuit }(\varvec{\ell },{\varvec{c}}) = \gamma ^{*}(\varvec{\ell },{\varvec{c}}) < \frac{p}{d} \alpha \) we see by definition of \(\gamma ^{\diamondsuit }\) (see Eq. (2.2)) that there exist \(\gamma < \frac{p}{d} \alpha \) (arbitrarily close to \(\gamma ^{*}(\varvec{\ell },{\varvec{c}})\)) and \(C = C(\gamma ,\varvec{\ell },{\varvec{c}}) > 0\) satisfying \(({\varvec{c}}(n))^{L} \cdot n^{\lfloor L/2 \rfloor } \le C \cdot n^{\gamma }\) for all \(n \in {\mathbb {N}}\).
Let  . By Lemma 2.1, this implies
. By Lemma 2.1, this implies  , so that for each \(m \in {\mathbb {N}}\), we can choose
, so that for each \(m \in {\mathbb {N}}\), we can choose  satisfying \(\Vert f - F_m \Vert _{L^p} \le 2 \cdot 2^{-\alpha m}\). Since furthermore \(\Vert f \Vert _{L^p} \le 1\), this remains true for \(m = 0\) if we set \(F_0:= 0\). Note that there exists a constant \(C_1 = C_1(p) > 0\) satisfying
satisfying \(\Vert f - F_m \Vert _{L^p} \le 2 \cdot 2^{-\alpha m}\). Since furthermore \(\Vert f \Vert _{L^p} \le 1\), this remains true for \(m = 0\) if we set \(F_0:= 0\). Note that there exists a constant \(C_1 = C_1(p) > 0\) satisfying
Furthermore, note as a consequence of Lemma 3.2 and because of \(\varvec{\ell }(n) \le L\) for all \(n \in {\mathbb {N}}\) that
for a suitable constant \(C_2 = C_2(d,\gamma ,\varvec{\ell },{\varvec{c}}) > 0\).
Now, set \(\theta := \frac{p}{p+d} (\gamma + \alpha ) > 0\). Then, for each \(m \in {\mathbb {N}}\), we can apply Lemma 3.1 with \(T = T_m:= 2^{- m \theta } \in (0,1]\) to deduce for a suitable constant \(C_3 = C_3(d,p) > 0\) that
for a suitable constant \(C_4 = C_4(d,p,\gamma ,\varvec{\ell },{\varvec{c}}) > 0\) and \(\mu := \frac{p}{d+p} (\alpha - \frac{d}{p}\gamma ) > 0\). Therefore, we see for \(m_0 \in \mathbb {N}\) and \(M \ge m \ge m_0\) that
showing that \((F_m)_{m \in {\mathbb {N}}} \subset C([0,1]^d)\) is a Cauchy sequence. Since \(F_m \rightarrow f\) in \(L^p\), this implies (after possibly redefining f on a null-set) that \(f \in C([0,1]^d)\) and \(F_m \rightarrow f\) uniformly. Finally, we see
Since this holds for all  with
with  , we have shown
, we have shown  .
.
We complete the proof by showing  . By definition of \(\mu \) and since \(\gamma < \frac{p}{d}\alpha \) can be chosen arbitrarily close to \(\gamma ^{*}(\varvec{\ell },{\varvec{c}})\), this implies the second claim of the theorem. To see
. By definition of \(\mu \) and since \(\gamma < \frac{p}{d}\alpha \) can be chosen arbitrarily close to \(\gamma ^{*}(\varvec{\ell },{\varvec{c}})\), this implies the second claim of the theorem. To see  , note thanks to Equation (3.1) and because of \(F_m \rightarrow f\) uniformly that
, note thanks to Equation (3.1) and because of \(F_m \rightarrow f\) uniformly that
for a suitable constant \(C_6 = C_6(d,p,\gamma ,\alpha ,\varvec{\ell },{\varvec{c}})\).
Now, given any \(t \in {\mathbb {N}}_{\ge 2}\), choose \(m \in {\mathbb {N}}\) with \(2^m \le t \le 2^{m+1}\). Since  , we then see
, we then see  For \(t = 1\), we have
For \(t = 1\), we have  ; see Equation (3.2). Overall, setting \(C_7:= \max \{ 1, 2^\mu C_6, C_5 \}\) and recalling Lemma 2.1, we see
; see Equation (3.2). Overall, setting \(C_7:= \max \{ 1, 2^\mu C_6, C_5 \}\) and recalling Lemma 2.1, we see  and hence
and hence  , meaning
, meaning  . All in all, this shows that indeed
. All in all, this shows that indeed  . \(\square \)
. \(\square \)
3.2 Sufficient Conditions for Embedding into \(C^{0,\beta }([0,1]^d)\)
Our next goal is to prove a sufficient condition for the embedding  . We first introduce some notation. For \(d\in {\mathbb {N}}\), \(\beta \in (0,1]\) and \(f:[0,1]^d\rightarrow {\mathbb {R}}\) we define
. We first introduce some notation. For \(d\in {\mathbb {N}}\), \(\beta \in (0,1]\) and \(f:[0,1]^d\rightarrow {\mathbb {R}}\) we define
Then, the Hölder space \(C^{0,\beta }([0,1]^d)\) consists of all (necessarily continuous) functions \(f: [0,1]^d \rightarrow {\mathbb {R}}\) satisfying
It is well-known that \(C^{0,\beta }([0,1]^d)\) is a Banach space with this norm.
The proof of our sufficient embedding condition relies on the following analogue of Lemma 3.1.
Lemma 3.4
Let \(p \in (0,\infty ]\), \(\beta \in (0,1)\), and \(d \in {\mathbb {N}}\). Then there exists a constant \(C = C(d,p,\beta ) \!>\! 0\) such that for each \(0 < T \le 1\) and each \(f \in L^p([0,1]^d) \cap C^{0,1}([0,1]^d)\), we have
Proof
For \(x,y \in [0,1]^d\), we have \( |f(x) - f(y)|^{1-\beta } \le \big ( 2 \, \Vert f \Vert _{L^\infty } \big )^{1-\beta } \) and hence
and this easily implies \({\text {Lip}}_\beta (f) \le 2^{1-\beta } \cdot \Vert f \Vert _{L^\infty }^{1-\beta } \cdot ({\text {Lip}}(f))^\beta \).
Let us first consider the case \(p < \infty \). In this case, we combine the preceding bound with the estimate of \(\Vert f \Vert _{L^\infty }\) provided by Lemma 3.1 to obtain a constant \(C_1 = C_1(d,p) > 0\) satisfying
The second step used the elementary estimate \((a + b)^\theta \le a^\theta + b^\theta \) for \(\theta \in (0,1)\) and \(a,b \ge 0\).
The preceding estimate shows that it suffices to prove that
for a suitable constant \(C_2 = C_2(d,p,\beta ) > 0\). To prove the latter estimate, note for \(a, b > 0\) and \(\theta \in (0,1)\) that
thanks to the convexity of \(\exp \). The preceding estimate clearly remains valid if \(a = 0\) or \(b = 0\). Applying this with \(\theta = \beta \), \(a = T^{1-\beta } {\text {Lip}}(f)\), and \(b = T^{-\frac{d}{p}-\beta } \Vert f \Vert _{L^p}\), we thus obtain the needed estimate
This completes the proof in the case \(p < \infty \).
In case of \(p = \infty \), we combine the estimate from the beginning of the proof with Equation (3.3) to obtain
where the last step used that \(p = \infty \). \(\square \)
We now prove our sufficient criterion for the embedding  .
.
Theorem 3.5
Let \(d \in {\mathbb {N}}\), \(\beta \in (0,1)\), and \(p \in (0,\infty ]\), and suppose that \(\gamma ^*(\varvec{\ell },{\varvec{c}}) < \infty \). If
then  .
.
Remark
It is folklore knowledge that the modulus of continuity of a function is closely connected to how well the function can be uniformly approximated by Lipschitz functions. Precisely, for \(s > 0\), let
denote the modulus of continuity of a function \(f: [0,1]^d \rightarrow {\mathbb {R}}\). It is easy to see that if \(g: [0,1]^d \rightarrow {\mathbb {R}}\) satisfies \({\text {Lip}}(g) < \infty \), then \(\omega _f (t) \le 2 \, \Vert f - g \Vert _{L^\infty } + t {\text {Lip}}(g)\) for all \(t > 0\). In combination with Lemma 3.2 and the definition of the approximation space  , this observation can be used to obtain a simplified proof of Theorem 3.5 in the case \(p = \infty \).
, this observation can be used to obtain a simplified proof of Theorem 3.5 in the case \(p = \infty \).
However, for general \(p \in (0,\infty )\), the approximation error in the definition of the space  is measured in \(L^p\) instead of \(L^\infty \). Since we are not aware of a well-known connection between the modulus of continuity of a function and its \(L^p\)-approximability by Lipschitz functions, we therefore provide a proof of Theorem 3.5 from first principles.
is measured in \(L^p\) instead of \(L^\infty \). Since we are not aware of a well-known connection between the modulus of continuity of a function and its \(L^p\)-approximability by Lipschitz functions, we therefore provide a proof of Theorem 3.5 from first principles.
Proof
The assumption on \(\alpha \) implies in particular that \(\alpha > \frac{d}{p} \gamma ^*(\varvec{\ell },{\varvec{c}})\). Hence, Theorem 3.3 shows in case of \(p < \infty \) that  , and this embedding trivially holds if \(p = \infty \). Thus, it remains to show for
, and this embedding trivially holds if \(p = \infty \). Thus, it remains to show for  with
with  that \({\text {Lip}}_\beta (f) \lesssim 1\).
that \({\text {Lip}}_\beta (f) \lesssim 1\).
Let \(\nu := (\beta + \frac{d}{p}) / (1 - \beta )\). Recall from Lemma 2.3 and the assumptions of the present theorem that \( \gamma ^{\diamondsuit }(\varvec{\ell },{\varvec{c}}) = \gamma ^*(\varvec{\ell },{\varvec{c}})< \alpha / \nu < \infty \) and hence that \(L:= \varvec{\ell }^*\in {\mathbb {N}}\). By definition of \(\gamma ^{\diamondsuit }(\varvec{\ell },{\varvec{c}})\), we thus see that there exist \(\gamma > 0\) and \(C = C(\gamma ,\varvec{\ell },{\varvec{c}}) > 0\) satisfying \(\gamma < \alpha / \nu \) and \(({\varvec{c}}(n))^L \cdot n^{\lfloor L/2 \rfloor } \le C \cdot n^{\gamma }\) for all \(n \in {\mathbb {N}}\).
Let  with
with  . By Lemma 2.1, this implies
. By Lemma 2.1, this implies  , meaning that for each \(m \in {\mathbb {N}}\) we can choose
, meaning that for each \(m \in {\mathbb {N}}\) we can choose  satisfying \(\Vert f - F_m \Vert _{L^p} \le 2 \cdot 2^{-\alpha m}\). Since furthermore \(\Vert f \Vert _{L^p} \le 1\), this remains true for \(m = 0\) if we set \(F_0:= 0\). As in the proof of Theorem 3.3, we then obtain constants \(C_1 = C_1(p) > 0\) and \(C_2 = C_2(d,\gamma ,\varvec{\ell },{\varvec{c}}) > 0\) satisfying
satisfying \(\Vert f - F_m \Vert _{L^p} \le 2 \cdot 2^{-\alpha m}\). Since furthermore \(\Vert f \Vert _{L^p} \le 1\), this remains true for \(m = 0\) if we set \(F_0:= 0\). As in the proof of Theorem 3.3, we then obtain constants \(C_1 = C_1(p) > 0\) and \(C_2 = C_2(d,\gamma ,\varvec{\ell },{\varvec{c}}) > 0\) satisfying
Now, set \(\theta := (\alpha + \gamma )/(1 + \frac{d}{p})\). A direct computation shows that
Thus, applying Lemma 3.4 with \(T = 2^{-\theta m}\), we obtain a constant \(C_3 = C_3(d,p,\beta ) > 0\) satisfying
Next, note for \(g \in C^{0,\beta }([0,1]^d)\) and \(x,y \in [0,1]^d\) that
Taking the \(L^p\)-norm (with respect to y) of this estimate shows that
for a suitable constant \(C_5 = C_5(p) > 0\). Setting \(\sigma := \max \{ \mu , -\alpha \} < 0\) and applying the preceding estimate to \(g = F_{m+1} - F_m\), we see for a suitable constant \(C_6 = C_6(d,p,\beta ) > 0\) that \(\Vert F_{m+1} - F_m \Vert _{\sup } \le C_6 \cdot 2^{\sigma m}\) for all \(m \in {\mathbb {N}}_0\). Hence, the series \(F:= \sum _{m=0}^\infty (F_{m+1} - F_m)\) converges uniformly, so that we get \(F \in C^{0,\beta }([0,1]^d)\) with
Since \(\sum _{m=0}^N (F_{m+1} - F_m) = F_{N+1} \rightarrow f\) with convergence in \(L^p([0,1]^d)\) as \(N \rightarrow \infty \), we see that \(F = f\) almost everywhere, and hence (after changing f on a null-set) \(f \in C^{0,\beta }([0,1]^d)\) with \({\text {Lip}}_\beta (f) \le C_7\). As seen above, this completes the proof. \(\square \)
3.3 Necessary Conditions
In this section we complement our sufficient conditions by corresponding necessary conditions. Our main result reads as follows.
Theorem 3.6
Let \(p \in (0,\infty ]\), \(\beta \in (0,1]\), and \(d \in {\mathbb {N}}\). Then:
-
If \(p < \infty \) and \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) > \alpha / (d / p)\), then the embedding
 does not hold.
does not hold. -
If \(\gamma ^*(\varvec{\ell },{\varvec{c}}) > \frac{1-\beta }{\beta + \frac{d}{p}} \alpha \), then the embedding
 does not hold.
does not hold.
Remark
A combination of the preceding result with Theorem 3.3 provides a complete characterization of the embedding  , except in the case where \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) = \alpha / (d/p)\). This remaining case is more subtle and seems to depend on the precise growth of the function \({\varvec{c}}\).
, except in the case where \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) = \alpha / (d/p)\). This remaining case is more subtle and seems to depend on the precise growth of the function \({\varvec{c}}\).
Likewise, combining the preceding result with Theorem 3.5 provides a complete characterization of the embedding  , except in the “critical” case where \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) = \frac{1-\beta }{\beta + \frac{d}{p}} \, \alpha \).
, except in the “critical” case where \(\gamma ^{*}(\varvec{\ell },{\varvec{c}}) = \frac{1-\beta }{\beta + \frac{d}{p}} \, \alpha \).
Proof
The proof is divided into several steps, where the first two steps are concerned with constructing and analyzing a certain auxiliary function \(\zeta _{M'}\) which is then used to construct counterexamples to the considered embeddings.
Step 1: Given \(M' \ge 0\), define
In this step, we show for any \(n \in {\mathbb {N}}\), \(0 \le C \le {\varvec{c}}(n)\), \(L \in {\mathbb {N}}_{\ge 2}\) with \(L \le \varvec{\ell }(n)\) and any \(M' \ge 1\) and \(0 \le M \le C^L \, n^{\lfloor L/2 \rfloor }\) that

To prove this, set \(\mu := C^L \, n^{\lfloor L/2 \rfloor }\) and \(D:= C \cdot (1)\in {\mathbb {R}}^{1 \times 1}\), as well as
and finally
Note because of \(M' \ge 1\) that \( \Vert b_1 \Vert _{\infty }, \Vert A \Vert _{\infty }, \Vert B \Vert _{\infty }, \Vert D \Vert _{\infty }, \Vert A_1 \Vert _{\infty } \le C \le {\varvec{c}}(n) \le {\varvec{c}}( (L+d) n). \) Now, we distinguish two cases.
Case 1 (\(L \ge 2\) is even): In this case, define
Note that \(W(\Phi ) \le d n + n + n + \frac{L-2}{2} (n + n) \le (d+L) n\) and \(L(\Phi ) = L \le \varvec{\ell }(n) \le \varvec{\ell }( (d+L) n)\), showing that  . Because of \(A (\varrho (B x)) = C \sum _{j=1}^n \varrho (C x) = C^2 \, n \cdot \varrho (x)\) for \(x \in {\mathbb {R}}\) and because of
. Because of \(A (\varrho (B x)) = C \sum _{j=1}^n \varrho (C x) = C^2 \, n \cdot \varrho (x)\) for \(x \in {\mathbb {R}}\) and because of
for \(x \in {\mathbb {R}}^d\), it follows that \( R_\varrho \Phi = C^{L-2} \cdot n^{\frac{L-2}{2}} \cdot \frac{C^2 \, n}{M'} \cdot \zeta _{M'} = \frac{\mu }{M'} \cdot \zeta _{M'}. \) Since  and because of \(0 \le M \le \mu \), this proves Equation (3.4) in this case.
and because of \(0 \le M \le \mu \), this proves Equation (3.4) in this case.
Case 2 (\(L \ge 3\) is odd): In this case, define
Then \(W(\Phi ) \le d n + n + n + \frac{L-3}{2}(n + n) + 1 \le (d + L) n\) and \(L(\Phi ) = L \le \varvec{\ell }(n) \le \varvec{\ell }( (d+L) n)\), so that  . Using essentially the same arguments as in the previous case, we see \(R_\varrho \Phi = \frac{\mu }{M'} \cdot \zeta _{M'}\), which then implies that Equation (3.4) holds.
. Using essentially the same arguments as in the previous case, we see \(R_\varrho \Phi = \frac{\mu }{M'} \cdot \zeta _{M'}\), which then implies that Equation (3.4) holds.
Step 2: We show \(\big \Vert \zeta _{M'} \big \Vert _{L^p([0,1]^d)} \le (M')^{-d/p}\). To see this, note for \(x \in [0,1]^d\) that \(\sum _{i=1}^d x_i \ge 0\) and hence \(1 - M' \, \sum _{i=1}^d x_i \le 1\), showing that \(0 \le \zeta _{M'}(x) = \varrho \bigl (1 - M' \, \sum _{i=1}^d x_i\bigr ) \le \varrho (1) = 1\). Next, note that if \(0 \ne \zeta _{M'}(x) = \varrho \big ( 1 - M' \, \sum _{i=1}^d x_i \big )\), then \(1 - M' \, \sum _{i=1}^d x_i > 0\), which is only possible if \(x_j \le \sum _{i=1}^d x_i \le \frac{1}{M'}\) for all \(j \in \{ 1,\dots ,d \}\), that is, if \(x \in \frac{1}{M'} [0,1]^d\). Therefore, we see as claimed that
Step 3: In this step, we prove the first part of the theorem. By the assumptions of that part, we have \(p < \infty \) and \(\gamma ^*(\varvec{\ell },{\varvec{c}}) > \alpha / (d/p)\). By definition of \(\gamma ^*\), this implies that there exists \(\gamma > \alpha / (d/p)\) and some \(L \in {\mathbb {N}}_{\le \varvec{\ell }^*}\) satisfying
Since \(\varvec{\ell }^*\ge 2\), we can clearly assume that \(L \ge 2\). Choose a subsequence \((n_k)_{k \in {\mathbb {N}}}\) such that \(c_0 = \lim _{k \rightarrow \infty } ({\varvec{c}}(n_k))^L \cdot n_k^{\lfloor L/2 \rfloor - \gamma }\). Then, setting \(c:= \min \{ 1, c_0 / 2 \}\), there exists \(k_0 \in {\mathbb {N}}\) satisfying \(({\varvec{c}}(n_k))^L \cdot n_k^{\lfloor L/2 \rfloor } \ge c \cdot n_k^\gamma > 0\) and \(L \le \varvec{\ell }(n_k)\) for all \(k \in {\mathbb {N}}_{\ge k_0}\).
Choose \(\kappa \in (0,1]\) satisfying \(\kappa \le c\) and \(\kappa \cdot (d + L)^\alpha \le 1\). Furthermore, define
and choose \(k_1 \in {\mathbb {N}}\) satisfying \(n_k^\theta \le \kappa \cdot n_k^\beta \) for all \(k \ge k_1\).
We now claim for all \(k \ge \max \{ k_0, k_1 \}\) that if we set \(M:= \kappa \cdot n_k^\beta \) and \(M':= n_k^\theta \), then  . This will prove the claim, since \(\big \Vert \frac{M}{M'} \, \zeta _{M'} \big \Vert _{C([0,1]^d)} \ge \frac{M}{M'} \rightarrow \infty \) as \(k \rightarrow \infty \); here, we used that \(\zeta _{M'}(0) = 1\) and that \(\beta > \theta \).
. This will prove the claim, since \(\big \Vert \frac{M}{M'} \, \zeta _{M'} \big \Vert _{C([0,1]^d)} \ge \frac{M}{M'} \rightarrow \infty \) as \(k \rightarrow \infty \); here, we used that \(\zeta _{M'}(0) = 1\) and that \(\beta > \theta \).
To see that  , note that \(\beta \le \theta + \delta _2 = \gamma \) and hence
, note that \(\beta \le \theta + \delta _2 = \gamma \) and hence
so that \(M \le C^L \, n_k^{\lfloor \frac{L}{2} \rfloor }\) for a suitable \(0 \le C \le {\varvec{c}}(n_k)\). Thus, Equation (3.4) shows  . Now, for \(t \in {\mathbb {N}}\) there are two cases: If \(t \ge (d+L) \cdot n_k\), then
. Now, for \(t \in {\mathbb {N}}\) there are two cases: If \(t \ge (d+L) \cdot n_k\), then  . If otherwise \(t < (d+L) \cdot n_k\), then the estimate from Step 2 combined with our choice of M, \(M'\) and \(\kappa \) shows that
. If otherwise \(t < (d+L) \cdot n_k\), then the estimate from Step 2 combined with our choice of M, \(M'\) and \(\kappa \) shows that

Finally, we also have \( \Vert \frac{M}{M'} \, \zeta _{M'} \Vert _{L^p([0,1]^d)} \le \frac{M}{M'} \cdot (M')^{-d/p} \le \kappa \cdot n_k^{\beta - \theta - \theta \frac{d}{p}} \le n_k^{\theta + \delta _1 - \theta - \theta \frac{d}{p}} = n_k^{-\alpha } \le 1. \) Overall, this shows  , so that Lemma 2.1 shows
, so that Lemma 2.1 shows  as well. As seen above, this completes the proof of the first part of the theorem.
as well. As seen above, this completes the proof of the first part of the theorem.
Step 4: In this step, we prove the second part of the theorem. By the assumptions of that part, we have \( \gamma ^*(\varvec{\ell },{\varvec{c}}) > \alpha \frac{1 - \beta }{\beta + \frac{d}{p}} = \frac{\alpha }{\nu } \) for \(\nu := \frac{\beta + \frac{d}{p}}{1 - \beta }\). By definition of \(\gamma ^*\), we can thus choose \(\gamma > \frac{\alpha }{\nu }\) and \(L \in {\mathbb {N}}_{\le \varvec{\ell }^*}\) satisfying
Since \(\varvec{\ell }^*\ge 2\), we can clearly assume that \(L \ge 2\). Choose a subsequence \((n_k)_{k \in {\mathbb {N}}}\) such that \(c_0 = \lim _{k \rightarrow \infty } ({\varvec{c}}(n_k))^L \cdot n_k^{\lfloor L/2 \rfloor - \gamma }\). Then, setting \(c:= \min \{ 1, c_0 / 2 \}\), there exists \(k_0 \in {\mathbb {N}}\) satisfying \(({\varvec{c}}(n_k))^L \cdot n_k^{\lfloor L/2 \rfloor } \ge c \cdot n_k^\gamma > 0\) and \(L \le \varvec{\ell }(n_k)\) for all \(k \in {\mathbb {N}}_{\ge k_0}\).
Since \(\gamma > \frac{\alpha }{\nu } = \frac{1-\beta }{\beta + \frac{d}{p}} \alpha \), we have \(\frac{\alpha }{\beta + \frac{d}{p}} < \frac{\gamma }{1-\beta }\). Hence, we can choose \( \tau \in \bigl (\frac{\alpha }{\beta + \frac{d}{p}}, \frac{\gamma }{1-\beta }\bigr ) \subset (0,\infty ). \) Then \(\tau \cdot (1 - \beta ) < \gamma \) and furthermore
Hence, we can choose \( \theta \in \big ( \tau \cdot (1 - \beta ), \,\, \min \{ \gamma , \tau \cdot (1 + \frac{d}{p}) - \alpha \} \big ) \subset (0,\infty ). \)
Now, choose \(\kappa \in (0,1]\) such that \(\kappa \le c\) and \(\kappa \cdot (L + d)^\alpha \le 1\). Fix \(k \in {\mathbb {N}}_{\ge k_0}\) for the moment, and set \(M:= \kappa \cdot n_k^\theta \) and \(M':= n_k^\tau \ge 1\). Since \( ({\varvec{c}}(n_k))^L \cdot n_k^{\lfloor L/2 \rfloor } \ge c \cdot n_k^\gamma \ge \kappa \cdot n_k^\gamma , \) we can choose \(0 \le C \le {\varvec{c}}(n_k)\) satisfying \( C^L \cdot n_k^{\lfloor L/2 \rfloor } \ge \kappa \cdot n_k^\gamma \ge \kappa \cdot n_k^\theta = M. \) Then, Step 1 shows that  . Now, for \(t \in {\mathbb {N}}\) there are two cases: If \(t \ge (L + d) \cdot n_k\), then
. Now, for \(t \in {\mathbb {N}}\) there are two cases: If \(t \ge (L + d) \cdot n_k\), then  . If otherwise \(t < (L+d) \cdot n_k\), then the estimate from Step 2 combined with the bound \(\theta \le \tau \cdot (1 + \frac{d}{p}) - \alpha \) shows
. If otherwise \(t < (L+d) \cdot n_k\), then the estimate from Step 2 combined with the bound \(\theta \le \tau \cdot (1 + \frac{d}{p}) - \alpha \) shows

Furthermore, Step 2 also shows that
Overall, we see that  , so that Lemma 2.1 shows
, so that Lemma 2.1 shows  .
.
We now show that \(\Vert f \Vert _{C^{0,\beta }} \rightarrow \infty \) as \(k \rightarrow \infty \); since  , this will imply that the embedding
, this will imply that the embedding  does not hold. To see that \(\Vert f \Vert _{C^{0,\beta }} \rightarrow \infty \) as \(k \rightarrow \infty \), note that \(f(0) = \frac{M}{M'}\) and \(f(\frac{1}{M'},0,\dots ,0) = 0\). Hence,
does not hold. To see that \(\Vert f \Vert _{C^{0,\beta }} \rightarrow \infty \) as \(k \rightarrow \infty \), note that \(f(0) = \frac{M}{M'}\) and \(f(\frac{1}{M'},0,\dots ,0) = 0\). Hence,
since \(\theta > \tau \cdot (1 - \beta )\). \(\square \)
Notes
Note that the number of hidden layers is given by \(H = L-1\).
References
Barron, A.R.: Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 39(3), 930–945 (1993)
Beneventano, P., Cheridito, P., Jentzen, A., von Wurstemberger, P.: High-dimensional approximation spaces of artificial neural networks and applications to partial differential equations. arXiv preprint arXiv:2012.04326 (2020)
Berner, J., Grohs, P., Kutyniok, G., Petersen, P.: The modern mathematics of deep learning. In: Grohs, P., Kutyniok, G. (eds.) Mathematical Aspects of Deep Learning, pp. 1–111. Cambridge University Press, Cambridge (2022). https://doi.org/10.1017/9781009025096.002
Caragea, A., Petersen, P., Voigtlaender, F.: Neural network approximation and estimation of classifiers with classification boundary in a Barron class. arXiv preprint arXiv:2011.09363 (2020)
Daubechies, I., DeVore, R.A., Dym, N., Faigenbaum-Golovin, S., Kovalsky, S.Z., Lin, K.-C., Park, J., Petrova, G., Sober, B.: Neural network approximation of refinable functions. IEEE Trans. Inf. Theory 69(1), 482–495 (2023). https://doi.org/10.1109/TIT.2022.3199601
Daubechies, I., DeVore, R., Foucart, S., Hanin, B., Petrova, G.: Nonlinear approximation and (deep) \({\rm ReLU}\) networks. Construct. Approx. (2021). https://doi.org/10.1007/s00365-021-09548-z
DeVore, R., Hanin, B., Petrova, G.: Neural network approximation. Acta Numer. 30, 327–444 (2021)
DeVore, R.A., Lorentz, G.G.: Constructive Approximation. Grundlehren der Mathematischen Wissenschaften, vol. 303. Springer, Berlin (1993)
Elbrächter, D., Perekrestenko, D., Grohs, P., Bölcskei, H.: Deep neural network approximation theory. IEEE Trans. Inf. Theory 67(5), 2581–2623 (2021)
Gribonval, R., Kutyniok, G., Nielsen, M., Voigtlaender, F.: Approximation spaces of deep neural networks. Constr. Approx. (2021). https://doi.org/10.1007/s00365-021-09543-4
Grohs, P., Voigtlaender, F.: Proof of the theory-to-practice gap in deep learning via sampling complexity bounds for neural network approximation spaces. arXiv preprint arXiv:2104.02746 (2021)
Pinkus, A.: Approximation theory of the MLP model in neural networks. Acta Numer. 8, 143–195 (1999)
Rao, M.M., Ren, Z.D.: Theory of Orlicz Spaces. Monographs and Textbooks in Pure and Applied Mathematics, vol. 146. Marcel Dekker Inc, New York (1991)
Weinan, E., Ma, C., Wu, L.: Barron spaces and the compositional function spaces for neural network models. arXiv preprint arXiv:1906.08039 (2019)
Funding
Open access funding provided by University of Vienna.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Albert Cohen.
This paper is dedicated to Ron DeVore on the occasion of his 80th birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
F. Voigtlaender acknowledges support by the German Research Foundation (DFG) in the context of the Emmy Noether junior research group VO 2594/1–1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grohs, P., Voigtlaender, F. Sobolev-Type Embeddings for Neural Network Approximation Spaces. Constr Approx 57, 579–599 (2023). https://doi.org/10.1007/s00365-022-09598-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00365-022-09598-x



 holds.
holds. does not hold.
does not hold. is a quasi-normed space. Precisely, given arbitrary measurable functions
is a quasi-normed space. Precisely, given arbitrary measurable functions  for
for  for
for  if and only if
if and only if  .
. if and only if
if and only if  .
. .
. does not hold.
does not hold. does not hold.
does not hold.