Abstract
We study the spectral properties of bounded and unbounded Jacobi matrices whose entries are bounded operators on a complex Hilbert space. In particular, we formulate conditions assuring that the spectrum of the studied operators is continuous. Uniform asymptotics of generalized eigenvectors and conditions implying complete indeterminacy are also provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\mathcal {H}\) be a complex Hilbert space. Consider two sequences \(a = (a_n :n \ge 0)\) and \(b = (b_n :n \ge 0)\) of bounded linear operators on \(\mathcal {H}\) such that for every \(n \ge 0\), the operator \(a_n\) has a bounded inverse and \(b_n\) is self-adjoint. Then one defines the symmetric tridiagonal matrix by the formulaFootnote 1
The action of \(\mathcal {A}\) on any sequence of elements from \(\mathcal {H}\) is defined by the formal matrix multiplication. Let the operator A be the minimal operator associated with \(\mathcal {A}\). Specifically, by A we mean the closure in \(\ell ^2(\mathbb {N}; \mathcal {H})\) of the restriction of \(\mathcal {A}\) to the set of the sequences of finite support. Let us recall that
The operator A is called a block Jacobi matrix. It is self-adjoint provided the Carleman condition is satisfied, i.e.
where \(\left||{\cdot } \right||\) is the operator norm (see [2, Theorem VII-2.9]).
Block Jacobi matrices are related to such topics as: matrix orthogonal polynomials (see [8]), the matrix moment problem (see [13]), difference equations of finite order (see [10]), partial difference equations (see [2]), level dependent quasi-birth–death processes (see [9] and references therein). For further applications, we refer to [20, 25].
The theory of block Jacobi matrices is much less developed than the scalar ones, i.e., corresponding to \(\mathcal {H}= \mathbb {C}\). The aim of this paper is to provide extensions of results obtained in [26, 28] for \(\mathcal {H}= \mathbb {R}\) to the case of arbitrary \(\mathcal {H}\). It is of interest as we provide new results even for \(\mathcal {H}= \mathbb {C}^d\) with \(d \ge 1\), i.e., the most common (apart from \(\mathbb {R}\)) studied case.
Originally, we were interested in the unbounded case, i.e.,
But it seems that even the bounded case is not well understood (see [19, 23]). Therefore, we present a unified treatment of both bounded and unbounded cases. In the unbounded case, the formulation of our results is simpler.
In the proofs of the presented theorems we will use the following notion. A nonzero sequence \((u_n : n \ge 0)\) will be called a generalized eigenvector associated with \(z \in \mathbb {C}\) if it satisfies the recurrence relation
In Sect. 3, we show the correspondence between asymptotic behavior of generalized eigenvectors and the spectral properties of A.
The first main result of this article is Theorem 4, which generalizes the results obtained in [26] to the operator case. Its formulation involves an additional parameter sequence \(\alpha = (\alpha _n : n \ge 0)\). In Sect. 5, we present some of the possible choices of \(\alpha \). The following theorem is a special case of Theorem 4 (obtained for \(\alpha _n = a_n\)).
Theorem 1
Assume
andFootnote 2
-
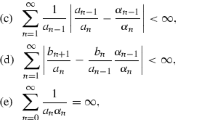
\((a) \quad \sum \limits _{n=1}^\infty \frac{\left||{[a_{n+1} a_{n+1}^* - a_n^* a_n]^-} \right||}{\left||{a_n} \right||^2} < \infty \),
-
\((b) \quad \sum \limits _{n=0}^\infty \frac{\left||{a_n b_{n+1} - b_n a_n} \right||}{\left||{a_n} \right||^2} < \infty \),
-
\((c) \quad \sum \limits _{n=0}^\infty \frac{1}{\left||{a_n} \right||^2} = \infty \).
Then the operator A is self-adjoint. Moreover,Footnote 3 \(\sigma (A) = \mathbb {R}\) and \(\sigma _{\text {p}}(A) = \emptyset \) provided
where C is invertible.
Before we formulate the next result, we need a definition. Given a positive integer N, we define the total N-variation \(\mathcal {V}_N\) of a sequence of vectors \(x = \big (x_n : n \ge 0 \big )\) from a vector space V by
Observe that if \((x_n : n \ge 0)\) has a finite total N-variation, then for each \(j \in \{0, \ldots , N-1\}\), a subsequence \((x_{k N + j} : k \ge 0)\) is a Cauchy sequence.
The following theorem is interesting even for \(N=1\). Since recently block periodic Jacobi matrices have obtained some attention (see [7, 19]), we formulate it for an arbitrary natural number N.
Theorem 2
Let \(N \ge 1\) be an integer. Assume
Let
-
\((a) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} - T_n} \right|| = 0\),
-
\((b) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} b_n - Q_n} \right|| = 0\),
-
\((c) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} a_{n-1}^* - R_n} \right|| = 0\),
-
\((d) \quad \lim \limits _{n \rightarrow \infty } \left\| \frac{a_n}{\left||{a_n} \right||} - C_n \right\| = 0\)
for N-periodic sequences \((T_n: n \ge 0)\), \((Q_n : n \ge 0)\), \((R_n : n \ge 0)\), and \((C_n : n \ge 0)\) with \(C_n\) invertible. Let \(\Lambda \) be the set of \(\lambda \in \mathbb {R}\) such thatFootnote 4
is a strictly positive or a strictly negative operator on \(\mathcal {H}\oplus \mathcal {H}\). Then for every compact set \(K \subset \Lambda \), there are positive constants \(c_1, c_2\) such that for every generalized eigenvector associated with \(\lambda \in K\) and every \(n \ge 1\),
When the Carleman condition is satisfied, the asymptotics (2) implies the similar conclusion as Theorem 1; i.e., \(\sigma _{\text {p}}(A) \cap \Lambda = \emptyset \) and \(\sigma (A) \supset \overline{\Lambda }\). In the scalar case, the subordination theory (see, e.g., [6]) implies that in fact the spectrum of A is purely absolutely continuous on \(\Lambda \). Unfortunately, a subordination theory for the nonscalar case has not been formulated (but there is some progress, see [5]). We expect that in our case the spectrum of A is, similarly to the scalar case, purely absolutely continuous of the maximal multiplicity on \(\Lambda \).
It is also of interest to obtain a characterization when the symmetric operator A is not self-adjoint (see, e.g., [12, 29]). The following theorem shows that in the setting of Theorem 2, the Carleman condition is also necessary to the self-adjointness of A.
Theorem 3
Let the assumptions of Theorem 2 be satisfied with \(\Lambda \ne \emptyset \). If (1) is not satisfied, then the conclusion of Theorem 2 holds for \(\Lambda = \mathbb {C}\). Consequently, for every \(z \in \mathbb {C}\),
Hence, we have the so-called complete indeterminate case. In particular, the symmetric operator A is not self-adjoint but it has self-adjoint extensions.
The estimate implied by Theorem 3 is useful even in the scalar case (see [3]).
The method of the proofs of the presented theorems is based on an extension of the techniques used in [26, 28]. In these articles, one examines the positivity or the convergence of sequences of quadratic forms on \(\mathbb {R}^2\) acting on the vector of two consecutive values of a generalized eigenvector u associated with \(\lambda \in \Lambda \subset \mathbb {R}\); i.e.,
for a suitably chosen sequence \((X_n(\lambda ) : n \ge 0)\), \(X_n(\lambda ) \in \mathcal {B}(\mathbb {R}^2)\). In trying to extend this method, one encounters several difficulties.
First of all, what is the right quadratic form for the operator case? One real number should control the norm of generalized eigenvectors, which, unlike the scalar case, need not be real. Moreover, the convergence (or at least positivity) should be easily expressible in terms of the recurrence relation. What additionally complicates the matter is the fact that in general the parameters \((a_n : n \ge 0)\) and \((b_n : n \ge 0)\), unlike the scalars, are not commuting with each other. The first one need not even be symmetric. Moreover, because of the fact that the Hilbert space \(\mathcal {H}\) can be arbitrary, we cannot assume that it is locally compact. This complicates the analysis of the proposed quadratic forms.
The second issue concerns the problem of how one can express quantitatively the rate of divergence or deviation from the positivity of the parameters. As simple examples of diagonal \(a_n\) and \(b_n\) show, the divergence of the norms is too coarse. The scaling from Theorem 2(d) seems to be a natural one. However, there are also different possibilities known in the literature (see [11]).
The article is organized as follows. In Sect. 2, we present basic notions needed in the rest of the article. In Sect. 3, we define generalized eigenvectors and prove the correspondence of their asymptotic behavior with the spectral properties of A. In Sect. 4, we prove Theorem 4. Next, in Sect. 5, we present its special cases. In particular, the choice of the parameter sequence \(\alpha _n \equiv \mathrm {Id}\) motivates us to define the notion of N-shifted Turán determinants in Sect. 6. Section 6 is devoted to the proof of Theorems 2 and 3. In Sect. 7, we present the situation when one can compute exact asymptotics of u. In the scalar case, it has applications to the so-called Christoffel functions. Finally, in Sect. 8, we present some examples illustrating the sharpness of the assumptions.
2 Preliminaries
In this section, we collect some basic notation and properties, which will be needed hereafter.
2.1 Operators
On the space of bounded operators, we consider only the norm topology. In particular, a sequence \((X_n : n \ge 0)\) converges to X provided
where \(\left||{\cdot } \right||\) is the operator norm.
For a sequence of operators \((X_n : n \ge 0)\) and \(n_0, n_1 \in \mathbb {N}\), we set
For any bounded operator X, we define its real part by
Direct computation shows that for any bounded operator Y, one has
and
Moreover,
For a number \(x \in \mathbb {R}\), we define its negative part by the formula
For a self-adjoint operator X, we define \(X^-\) by the spectral theorem.
For any bounded operator X, we define its absolute value by
2.2 Total Variation
Given a positive integer N, we define the total N-variation \(\mathcal {V}_N\) of a sequence of vectors \(x = (x_n : n \ge 0)\) from a vector space V by
Observe that if \((x_n : n \ge 0)\) has a finite total N-variation, then for each \(j \in \{0, \ldots , N-1\}\), a subsequence \((x_{k N + j} : k \ge 0)\) is a Cauchy sequence.
Proposition 1
If V is a normed algebra, then
Proof
Observe that
Hence,
Consequently,
Summing by n, the result follows. \(\square \)
3 Generalized Eigenvectors and the Transfer Matrix
For a number \(z \in \mathbb {C}\), a nonzero sequence \(u = (u_n :n \ge 0)\) will be called a generalized eigenvector provided that it satisfies
For each nonzero \(\alpha \in \mathcal {H}\oplus \mathcal {H}\), there is a unique generalized eigenvector u such thatFootnote 5 \((u_0, u_1)^t = \alpha \). If the recurrence relation (6) holds also for \(n = 0\), with the convention that \(a_{-1} = u_{-1} = 0\), then u is a formal eigenvector of the matrix A associated with z.
For each \((z \in \mathbb {C})\), we define the transfer matrix \(B_n(z)\) by
Then for any generalized eigenvector u corresponding to z, we have
It is easy to verify that
The rest of this section concerns relations between generalized eigenvectors and spectral properties of block Jacobi matrices.
The proof of [1, Lemma 2.1] implies that the adjoint operator to A can be described as the restriction of \(\mathcal {A}\) to \(\ell ^2(\mathbb {N}; \mathcal {H})\); i.e., \(A^* x = \mathcal {A}x\) for \(x \in {{\mathrm{Dom}}}(A^*)\), where
The following proposition is essential in examining properties of \(A^*\).
Proposition 2
Let \(z \in \mathbb {C}\). The sequence u satisfies \(\mathcal {A}u = z u\) if and only if
Proof
It immediately follows from the direct computations. \(\square \)
The following corollary describes some of the situations when we can describe the deficiency spaces of the operator A explicitly.
Corollary 1
Let \(z \in \mathbb {C}\). If every generalized eigenvector associated with z belongs to \(\ell ^2(\mathbb {N}; \mathcal {H})\), then
In particular, if (12) is satisfied for \(z = \pm i\), then the symmetric operator A is not self-adjoint, but it has self-adjoint extensions.
Proof
Observe that the space \(\ker [A^* - z \mathrm {Id}]\) is a Hilbert space. Indeed, since \(\ker [A^* - z \mathrm {Id}] = \mathrm {Im} \left[ {A - \overline{z} \mathrm {Id}} \right] ^\perp \) (see, e.g., [24, formula (7.1.45)]) it is a closed subspace of \(\ell ^2(\mathbb {N}; \mathcal {H})\).
Define the operator \(T : \ker [A^* - z \mathrm {Id}] \rightarrow \mathcal {H}\) by \(T u = u_0\). Then by (11), \(T u = 0\) implies \(u=0\); hence, T is injective. To prove the surjectivity, take \(u_0 \in \mathcal {H}\setminus \{ 0 \}\); then the sequence u defined by (11) is a generalized eigenvector associated with z. Therefore, it belongs to \(\ell ^2(\mathbb {N}; \mathcal {H})\). Hence, by (10), \(u \in {{\mathrm{Dom}}}(A^*)\), and consequently, T is surjective. Since the mapping T is a contraction, it is a bounded linear bijection. By the inverse mapping theorem, the operator T is a linear isomorphism.
The assertion about the self-adjoint extensions of A follows from von Neumann’s extension theorem (see, e.g., [24, Theorem 7.4.1]). \(\square \)
Remark 1
The proof of [21, Theorem 1] shows that the same conclusion holds if every generalized eigenvector associated with \(z=0\) belongs to \(\ell ^2(\mathbb {N}; \mathcal {H})\). As was pointed out in [4], the formulation of [21, Theorem 1] has a typo.
The following proposition is an adaptation of [26, Proposition 2.1]. We include it for the sake of self-containment.
Proposition 3
Let \(z \in \mathbb {C}\). If every generalized eigenvector u associated with z does not belong to \(\ell ^2(\mathbb {N}; \mathcal {H})\), then \(z \notin \sigma _{\text {p}}(A^*)\) and \(z \in \sigma (A^*)\).
Proof
Let \(u \ne 0\) be such that \(\mathcal {A}u = z u\). Then by Proposition 2, u is a generalized eigenvector associated with z. By assumption, \(u \notin \ell ^2(\mathbb {N}; \mathcal {H})\). Therefore, \(u \notin {{\mathrm{Dom}}}(A^*)\), and consequently, \(z \notin \sigma _{\text {p}}(A^*)\).
Observe that the vector u such that \((\mathcal {A}- z \mathrm {Id}) u = \delta _0 v\), where \(0 \ne v \in \mathcal {H}\), has to satisfy the following recurrence relation:
Hence u is a generalized eigenvector; thus \(u \notin \ell ^2(\mathbb {N}; \mathcal {H})\). Therefore, \(u \notin {{\mathrm{Dom}}}(A^*)\), and consequently, the operator \(A^* - z \mathrm {Id}\) is not surjective; i.e., \(z \in \sigma (A^*)\). \(\square \)
Remark 2
In the scalar case, if the assumptions of Proposition 3 are satisfied for \(z=0\), then the operator A is self-adjoint. We expect the same behavior for every \(\mathcal {H}\).
4 A Commutator Approach
The aim of this section is to prove the following theorem.
Theorem 4
Let A be a Jacobi matrix. Assume that there is a sequence \((\alpha _n : n \ge 0)\) of elements from \(\mathcal {B}(\mathcal {H})\) such that
-
\((a) \quad \sum \limits _{n=1}^\infty \frac{\big \Vert \mathrm{Re}[\alpha _{n+1} a_{n+1}^* - a_n^* a_{n-1}^{-1} \alpha _{n-1} a_n]^-\big \Vert }{\left||{\alpha _n a_n^*} \right||} < \infty \),
-
\((b) \quad \sum \limits _{n=1}^\infty \frac{\big \Vert a_{n-1}^{-1} \alpha _{n-1} a_n - \alpha _n\big \Vert }{\left||{\alpha _n a_n^*} \right||} < \infty \),
-
\((c)\quad \sum \limits _{n=1}^\infty \frac{\big \Vert \alpha _n b_{n+1} - b_n a_{n-1}^{-1} \alpha _{n-1} a_n\big \Vert }{\left||{\alpha _n a_n^*} \right||} < \infty \),
-
\((d)\quad \sum \limits _{n=1}^\infty \frac{1}{\left||{\alpha _n a_n^*} \right||} = \infty \).
Let \(\Lambda \) be the set of \(\lambda \in \mathbb {R}\) such that the following limit exists in the norm and defines a strictly positive operator on \(\mathcal {H}\oplus \mathcal {H}\):
Then \(\sigma _{\text {p}}(A^*) \cap \Lambda = \emptyset \) and \(\sigma (A^*) \supset \overline{\Lambda }\).
Given a sequence \((\alpha _n : n \ge 0)\) of elements from \(\mathcal {B}(\mathcal {H})\) and \(\lambda \in \mathbb {R}\), we define a sequence of binary quadratic forms \(Q^\lambda \) on \(\mathcal {H}\oplus \mathcal {H}\) by the formula
Moreover, we define the sequence of functions by the formula
where u is the generalized eigenvector corresponding to \(\lambda \) such that \((u_0, u_1)^t = \alpha \in \mathcal {H}\oplus \mathcal {H}\).
The first proposition provides a different representation of \(S_n\).
Proposition 4
An alternative formula for \(S_n\) is
Proof
By (8), one has
Then formula (9) implies
Hence, by formula (3),
which completes the proof. \(\square \)
The next proposition provides assumptions on the quadratic form under which it controls the norm of generalized eigenvectors.
Proposition 5
Let \(\Lambda \) be the set of \(\lambda \in \mathbb {R}\) such that the following limit exists in the operator norm and defines a strictly positive operator:
Then for every \(\lambda \in \Lambda \), there is an integer N and positive constants \(c_1, c_2\) such that for every generalized eigenvector u associated with \(\lambda \) and \(0 \ne \alpha \in \mathcal {H}\oplus \mathcal {H}\),
Proof
Fix \(\lambda \in \Lambda \). Let
where
Hence,
But from the definition of \(C(\lambda )\), we have
which are positive numbers. Therefore, there is N and \(c_1, c_2>0\) such that for every \(n \ge N\),
and the proof is complete. \(\square \)
The next corollary together with Proposition 3 suggest the method of proving that every \(\lambda \in \Lambda \) is not an eigenvalue of A but belongs to \(\sigma (A)\).
Corollary 2
Under the assumptions of Proposition 5, together with
if
then u does not belong to \(\ell ^2(\mathbb {N}; \mathcal {H})\).
Proof
By Proposition 5,
for a positive constant \(c_2\). Therefore, there exists a constant \(c>0\) such that
which cannot be summable. \(\square \)
The following lemma is the main algebraic part of the proof of Theorem 4.
Lemma 1
Let u be a generalized eigenvector associated with \(\lambda \in \mathbb {R}\) and \(\alpha \in \mathcal {H}\oplus \mathcal {H}\). Then
Proof
By Proposition 4 and formula (13), we have
for
Hence,
By the Schwarz inequality, the result follows. \(\square \)
We are ready to prove Theorem 4.
Proof of Theorem 4
By virtue of Corollary 2 and Proposition 3, it is enough to show that \(\liminf _n S_n(\alpha , \lambda ) > 0\) for every \(\lambda \in \Lambda \) and a nonzero \(\alpha \in \mathcal {H}\oplus \mathcal {H}\).
Fix \(\lambda \in \Lambda \) and a nonzero \(\alpha \in \mathcal {H}\oplus \mathcal {H}\). By Proposition 5, there exists N such that for every \(n \ge N\), \(S_n(\alpha , \lambda ) > 0\) holds. Let us define
Then
and consequently,
Hence,
implies \(\liminf _n S_n(\alpha , \lambda ) > 0\). By Proposition 5,
for some constant \(c>0\). Hence, by Lemma 1,
which is summable by assumptions (a), (b), and (c). This shows (14). The proof is complete. \(\square \)
5 Special Cases of Theorem 4
In this section, we show several choices of the sequence \((\alpha _n : n \ge 0)\). In this way, we show the flexibility of our approach. For the simplification of the condition for \(C(\lambda )\), we assume that the sequence \((a_n : n \ge 0)\) tends to infinity; i.e.,
This condition implies that \(C(\lambda )\) does not depend on \(\lambda \).
The first theorem is an extension of [18, Theorem 1.6] to the operator case. Since Sect. 6 is devoted to the proof of a far reaching extension of this result, we omit the details.
Theorem 5
Assume:
-
\((a) \quad \sum \limits _{n=1}^\infty \big \Vert a_{n+1}^* a_n^{-1} - a_n^* a_{n-1}^{-1}\big \Vert < \infty \),
-
\((b) \quad \sum \limits _{n=1}^\infty \big \Vert a_{n-1}^{-1} - a_n^{-1}\big \Vert < \infty \),
-
\((c) \quad \sum \limits _{n=1}^\infty \big \Vert b_{n+1} a_n^{-1} - b_n a_{n-1}^{-1}\big \Vert < \infty \),
-
\((d) \quad \sum \limits _{n=0}^\infty \frac{1}{\left||{a_n} \right||} = \infty \),
and \(C(\lambda )\) defined for \(\alpha _n \equiv \mathrm {Id}\) is a positive operator on \(\mathcal {H}\oplus \mathcal {H}\). Then the assumptions of Theorem 4 are satisfied.
We are ready to prove Theorem 1. Let us note that this result is a vector valued version of [26, Theorem 4.3]. In the scalar case, it has far-reaching applications (see [26, Section 5]).
Proof of Theorem 1
Take \(\alpha _n = a_n\). It is sufficient to show that \(\Lambda = \mathbb {R}\). We have
which is clearly positive for \(\lambda \in \mathbb {R}\). Hence, \(\Lambda = \mathbb {R}\). \(\square \)
To formulate the last example, we need a definition. Let
and
The following theorem is a vector valued version of [26, Theorem 4.3], and its proof is inspired by the techniques employed in the proof of [17, Theorem 3].
Theorem 6
Assume that for positive integers K, N and a non-negative summable sequence \(c_n\):
-
\((a) \quad \lim \limits _{n \rightarrow \infty } a_n^{-1} = 0\),
-
\((b) \quad (1 - c_n) \mathrm {Id}\le | (a_{n-1}^*)^{-1} a_n | \le \bigg ( 1 + \frac{1}{n} + \sum \limits _{j=1}^K \frac{1}{n g_j(n)} + c_n \bigg ) \mathrm {Id}\) for \(n > N\),
-
(c) the sequence \((b_n : n \ge 0)\) is bounded and \(\sum \limits _{n=0}^\infty \left||{a_n^{-1} b_n - b_{n+1} a_n^{-1} } \right|| < \infty \),
-
\((d) \quad \sum \limits _{n=1}^\infty \frac{||a_n^{-1} ||}{n} < \infty \).
Then the assumptions of Theorem 4 are satisfied with \(\Lambda = \mathbb {R}\).
Proof
We can assume that \(\log ^{(K)}(N) > 0\). Let
We have to compute the set \(\Lambda \) and check the assumptions (a), (b), (c) of Theorem 4.
Let us begin with the computation of \(\Lambda \). We have
which by the hypotheses (a) and (b) tends to
which is clearly a positive operator on \(\mathcal {H}\oplus \mathcal {H}\) for any \(\lambda \in \mathbb {R}\). Hence, \(\Lambda = \mathbb {R}\).
Let us show the assumption (a). We have
The above expression has been estimated in the proof of [26, Theorem 4.3].
Next, since
the hypothesis (c) implies that the assumption (b) will be satisfied if we show that the assumption (c) holds.
We have
where
By virtue of the hypothesis (d), the assumption (c) will be satisfied as long as
for a constant \(c>0\) and a non-negative summable sequence \((c_n' : n \ge 0)\). Because
and because of the non-negativity of \(T_n T_n^*\) and \(\left||{T_n T_n^*} \right|| = \left||{T_n} \right||^2\), the inequality (16) will be satisfied if
The spectral theorem applied to \(W_n^* W_n\) implies that the above inequality will be satisfied if
for every \(\lambda _n \in \sigma (W_n^* W_n)\), which by the hypothesis (b) corresponds to
But
and the above expression has been estimated in the proof of [26, Theorem 4.3]. This shows (17) and ends the proof. \(\square \)
6 Turán Determinants
Let us note that for \(\mathcal {H}= \mathbb {R}\), the expression \(S_n\) for \(\alpha _n \equiv \mathrm {Id}\) (see (13)) is known as the Turán determinant (see [14]). Hence, Theorem 5 motivates us to the following construction. Fix a positive integer N and a Jacobi matrix A. Let us define a sequence of quadratic forms \(Q^z\) on \(\mathcal {H}\oplus \mathcal {H}\) by the formula
where
Then we define the N-shifted Turán determinants by
where u is the generalized eigenvector corresponding to \(z \in \mathbb {C}\) such that \((u_0, u_1)^t = \alpha \in \mathcal {H}\oplus \mathcal {H}\).
The rest of this section is devoted to the analysis of the sequence \(S_n\). Since the proof of the uniform convergence of \(S_n\) is quite involved, we divide it into 3 subsections. The method used here is an adaptation of the techniques employed in [28].
6.1 Almost Uniform Nondegeneracy
Let \(\Lambda \) be a subset of \(\mathbb {C}\). In this section, we consider the family \(\{ Q^z : z \in \Lambda \}\) defined in (18).
We say that \(\{ Q^z : z \in \Lambda \}\) is uniformly nondegenerated on \(K \subset \Lambda \) if there are \(c \ge 1\) and \(M \ge 1\) such that for all \(v \in \mathcal {H}\oplus \mathcal {H}\), \(z \in K\), and \(n \ge M\),
We say that \(\{Q^z : z \in \Lambda \}\) is almost uniformly nondegenerated on \(\Lambda \) if it is uniformly nondegenerated on each compact subset of \(\Lambda \).
We begin with two simple auxiliary results that will be needed in the proof of the nondegeneracy of the considered quadratic forms.
Lemma 2
For every n and \(\lambda \in \mathbb {R}\), one has
Proof
Using (9) and (7), one can compute that both sides are equal to
and the result follows. \(\square \)
Proposition 6
Let N be an integer. Assume:
-
\((a) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} a_{n-1}^* - R_n} \right|| = 0\),
-
\((b) \quad \lim \limits _{n \rightarrow \infty } \left\| \frac{a_n}{\left||{a_n} \right||} - C_n \right\| = 0\),
for N-periodic sequences of invertible operators R and C. Then
In particular,
for a positive N-periodic sequence
Proof
We have
Hence,
and the result follows. \(\square \)
In the next proposition, we examine the limiting behavior of the considered quadratic forms.
Proposition 7
Let \(N \ge 1\) be an integer. Assume:
-
\((a) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} - T_n} \right|| = 0\),
-
\((b) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} b_n - Q_n} \right|| = 0\),
-
\((c) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n^{-1} a_{n-1}^* - R_n} \right|| = 0\),
-
\((d) \quad \lim \limits _{n \rightarrow \infty } \left\| \frac{a_n}{\left||{a_n} \right||} - C_n \right\| = 0\),
for N-periodic sequences T, Q, R, and C such that for every n, the operators \(R_n\) and \(C_n\) are invertible. Then on every compact subset of \(\mathbb {C}\), the sequence \((\left||{X_n(\cdot )} \right|| : n \ge 0)\) is uniformly bounded. Moreover,
uniformly on compact subsets of \(\mathbb {C}\), where
Proof
Let us define
We have
which tends to 0 uniformly on compact subsets of \(\mathbb {C}\). Consequently, since every function \(B_n(\cdot )\) is continuous, one has
uniformly on the compact subsets of \(\mathbb {C}\). In particular, this implies (20) and the uniform boundedness of \((\left||{X_n(\cdot )} \right|| : n \ge 0)\) on every compact subset of \(\mathbb {C}\). \(\square \)
Finally, in the last proposition, we formulate the conditions under which the sequence \(\{ Q^z : z \in \Lambda \}\) is almost uniformly nondegenerated.
Proposition 8
Let the assumptions of Proposition 7 be satisfied. If for every \(i \in \mathbb {N}\) and every \(z \in \Lambda \) there is \(\varepsilon (i, z) \in \{-1, 1\}\) such that
then \((Q^z : z \in \Lambda )\) is almost uniformly nondegenerated. Moreover, if \(\Lambda \subset \mathbb {R}\), then the same conclusion follows provided (21) holds only for \(i=0\).
Proof
By (20) and (21), we have that for every compact \(K \subset \Lambda \) there is a constant \(c>0\) such that for n sufficiently large and all \(z \in K\),
This implies the uniform nondegeneracy of \(\{ Q^z : z \in K \}\).
Consider \(\lambda \in \mathbb {R}\). According to Lemma 2, we have
Let \(n = kN+i\), and let us compute the limit of both sides as k tends to \(\infty \). By Propositions 6 and 7, we have
where
and the convergence is uniform on every compact subset of \(\mathbb {R}\). By (3), this implies that if for some \(\varepsilon (\lambda ) \in \{ -1, 1 \}\),
then for every \(j \in \{ 0, 1, \ldots , N-1 \}\),
The proof is complete. \(\square \)
6.2 Asymptotics of Generalized Eigenvectors
This section is devoted to showing the implications of the nondegeneracy of \((Q^z : z \in \Lambda )\) together with the positivity of \(|S_n|\) to the asymptotics of the generalized eigenvectors.
Theorem 7
Let the family \(\{Q^z : z \in K\}\) defined in (18) be uniformly nondegenerated on a compact set K. Suppose that there are \(c \ge 1\) and \(M' > 0\) such that for all \(\alpha \in \mathcal {H}\oplus \mathcal {H}\) such that \(\left||{\alpha } \right|| = 1\), \(z \in K\), and \(n \ge M\),
Then there is \(c \ge 1\) such that for all \(z \in K\), \(n \ge 1\), and for every generalized eigenvector u corresponding to z,
Proof
Let \(z \in K\), and let u be a generalized eigenvector corresponding to z such that \((u_0, u_1)^t = \alpha \), \(\left||{\alpha } \right|| = 1\). Since \(\{Q^z : z \in K \}\) is uniformly nondegenerated, there are \(c \ge 1\) and \(M \ge M'\) such that for all \(n \ge M\),
which together with (22) implies that there is \(c \ge 1\) such that for all \(n \ge M\),
For the general nonzero \(\alpha \), we use the fact that
and generalized eigenvectors depend linearly on the initial conditions. \(\square \)
Corollary 3
Suppose that the assumptions of Theorem 7 are satisfied. Let \(\Omega \subset \mathcal {H}\oplus \mathcal {H}\setminus \{ 0 \}\) be a bounded closed set, and let \(K \subset \Lambda \) be a compact set. Assume that for N-periodic sequence of self-adjoint operators \((D_n : n \ge 0)\),
uniformly on K and
uniformly on \(\Omega \times K\). Then
uniformly on \(\Omega \times K\).
Proof
Fix \(\varepsilon > 0\). By (23), there is M such that for all \(n \ge M\), \(z \in K\), and \(v \in \mathcal {H}\oplus \mathcal {H}\),
Hence,

uniformly on \(\Omega \times K\). By Theorem 7, there is a constant \(c' > 0\) such that
uniformly on \(\Omega \times K\). The proof is complete. \(\square \)
6.3 The Proof of the Convergence
In this section, we are going to prove that the sequence \((S_n : n \ge 0)\) is convergent, which leads to the proofs of Theorem 2 and 3.
Let us begin with the main algebraic part of the proof.
Lemma 3
Let u be a generalized eigenvector associated with \(z \in \mathbb {C}\) and \(\alpha \in \mathcal {H}\oplus \mathcal {H}\). Then
Proof
The formula (8) implies
Therefore, by the formulas (3) and (4),
where
By using \(E^{-1} = -E\), we can write
Hence,
Now we can compute
Therefore,
In particular, we can estimate
Therefore, by the last inequality together with (24), the Schwarz inequality, and (5), the result follows. \(\square \)
The main result of this section is the following theorem.
Theorem 8
Assume that for an integer \(N \ge 1\):
-
\((a) \quad \mathcal {V}_N \bigg ( a_n^{-1} : n \ge 0 \bigg ) + \mathcal {V}_N \bigg ( a_{n}^{-1} b_n : n \ge 0 \bigg ) + \mathcal {V}_N \bigg (a_{n}^{-1} a_{n-1}^* : n \ge 1 \bigg ) < \infty \);
-
\((b) \quad \frac{\left||{a_{n+1}} \right||}{\left||{a_n} \right||} < c_1\) for a constant \(c_1 > 0\) and all \(n \in \mathbb {N}\);
-
(c) the family defined in (18) \(\big \{Q^z : z \in K \big \}\) is uniformly nondegenerated on a compact connected set K.
Then there is \(c \ge 1\) such that for every \(n \ge 1\), for all \(z \in K \cap \mathbb {R}\), and for every generalized eigenvector u corresponding to z, we have
Moreover, if
then the same conclusion holds for \(z \in K\).
Proof
Let \(\Omega \subset \mathcal {H}\oplus \mathcal {H}\setminus \{ 0 \}\) be a connected bounded closed set. Let \(S_n\) be a sequence of functions defined by (19). In view of Theorem 7, it is enough to show that there are \(c \ge 1\) and \(M > 0\) such that
for all \(\alpha \in \Omega \), \(z \in K\), and \(n > M\). The study of the sequence \((S_n : n \ge 1)\) is motivated by the method developed in [28].
Given a generalized eigenvector corresponding to \(z \in K\) such that \((u_0, u_1)^t = \alpha \in \Omega \), we can easily see that for each \(n \ge 2\), \(u_n\), considered as a function of \(\alpha \) and z, is continuous on \(\Omega \times K\). As a consequence, the function \(S_n\) is continuous on \(\Omega \times K\). Since \(\{Q^z : z \in K\}\) is uniformly nondegenerated, there is \(M > 0\), such that for each \(n \ge M\), the function \(S_n\) has no zeros and has the same sign for all \(z \in K\) and \(\alpha \in \Omega \). Otherwise, by the connectedness of \(\Omega \times K\), there would be \(\alpha \in \Omega \) and \(z \in K\) such that \(S_n(\alpha , z) = 0\), which would contradict the nondegeneracy of \(Q_n^z\).
Next, we define a sequence of functions \((F_n : n \ge M)\) on \(\Omega \times K\) by setting
Then
First of all, let us show that
for a constant \(C>1\) independent of \(\alpha \) and z. If this is the case, then by (27) and the fact that each function \(F_n\) is continuous, to conclude (26) it is enough to show that the product
converges uniformly on \(\Omega \times K\) to a limit that is bounded away from 0, which will be satisfied if we prove that
Let us observe that by (19) and (5),
Moreover, by (8),
for
Hence,
For every i, the function \(z \mapsto \left||{B_i(z)} \right||\) is continuous on the compact set K. Hence, it is uniformly bounded. Furthermore, by the boundedness of \(\Omega \), one has that \(\left||{\alpha } \right||\) is bounded as well. This shows that the right-hand side of (33) is uniformly bounded on \(\Omega \times K\). Similarly,
is uniformly bounded. This implies that the right-hand side of (30) is uniformly bounded as well. Thus, the upper bound in the inequality (28) is proved. To prove the lower bound, let us see that the uniform nondegeneracy implies
for a constant \(c>0\) independent of \(\alpha \) and z. So by (31), it remains to show that \([Y(z)]^* Y(z)\) is a strictly positive operator uniformly with respect to \(z \in K\). It will be implied by the uniform bound on \(\left||{([Y(z)]^* Y(z))^{-1}} \right||\). According to (32),
and by (9), as in (33), the right-hand side of this inequality is uniformly bounded on K. Hence, by (31), there is a constant \(c'>0\) such that
Consequently, by the positive distance of \(\Omega \) to 0 and (34), we proved the remaining lower bound in (28).
It remains to prove (29). Let u be a generalized eigenvector corresponding to \(z \in K\) such that \((u_0, u_1)^t = \alpha \in \Omega \). In view of (a), each subsequence \((B_{kN+j}(z) : k \ge 1)\) is uniformly convergent, and consequently, the norms \(\Vert X_n(z) \Vert \) are uniformly bounded with respect to n and \(z \in K\). Moreover, since \(\{Q(z) : z \in K\}\) is uniformly nondegenerated,
for \(n \ge M\). Therefore, by Lemma 3,
for every \(\alpha \in \Omega \). Using (b), we can estimate
Thus, (a) and (25) imply (26). If condition (25) is not satisfied, consider \(K \cap \mathbb {R}\) instead K in the last inequality. The proof is complete. \(\square \)
The following corollary provides an estimate, which in the scalar case expresses the bound on the rate of the convergence of Turán determinants to the density of the spectral measure of A (see [27]). It follows from the standard proof of the convergence of infinite products of numbers.
Corollary 4
Under the hypothesis of Theorem 8, for every bounded and closed \(\Omega \subset \mathcal {H}\oplus \mathcal {H}\setminus \{ 0 \}\), the sequence of continuous functions \((S_n : n \ge 1)\) converges uniformly on \(\Omega \times (K \cap \mathbb {R})\) (or on \(\Omega \times K\) if (25) is satisfied) to the function g bounded away from 0. Moreover, by (35), there is a constant \(c>0\) such that for all \(m > 0\),
Finally, we are ready to prove Theorems 2 and 3.
Proof of Theorem 2
By Propositions 6 and 8, we have that the assumptions of Theorem 8 are satisfied. Therefore, the result follows from Theorem 7. \(\square \)
Proof of Theorem 3
Since every \(C_n\) is invertible, we have
Hence, for some \(c > 0\),
Consequently,
and (25) is satisfied. Moreover, this implies that \(T_n \equiv 0\), so, in the notation of Proposition 7, every \(\mathcal {F}^i(\cdot )\) is constant. Hence, Proposition 8 implies the almost uniform nondegeneracy of \(\{ Q^z : z \in \mathbb {R}\}\). Since \(\mathcal {F}^i(\cdot )\) is constant on \(\mathbb {C}\), Proposition 8 implies that \(\{ Q^z : z \in \mathbb {C}\}\) is almost uniformly nondegenerated as well. Thus, the assumptions of Theorem 8 are satisfied, and consequently, Theorem 7 implies the requested asymptotics. Finally, Corollary 1 finishes the proof. \(\square \)
7 Exact Asymptotics of Generalized Eigenvectors
The following theorem is a vector valued version of [27, Corollary 1].
Theorem 9
Let \(\Omega \subset \mathcal {H}\oplus \mathcal {H}\setminus \{ 0 \}\) be a bounded and closed set, and let \(K \subset \mathbb {R}\) (or \(K \subset \mathbb {C}\) whether the Carleman condition is not satisfied) be a compact set. Let N be an odd integer. Let the hypotheses of Theorem 2 be satisfied. Assume further that
Then \(C = C^*\), and
uniformly on \(\Omega \times K\), where
for \(S_n\) defined in (19).
Proof
We have
Hence,
Consequently,
Therefore, by Proposition 6, \(r \mathrm {Id}= C^{-1} C^*\) for \(r = \left||{C^{-1} C^*} \right||\). This implies that \(r C = C^*\). Taking norms, we obtain \(r=1\), and consequently, \(C = C^*\). Moreover, by Corollary 4, g is a continuous function on \(\Omega \times K\) that is bounded away from 0. Hence, by Corollary 3, the result follows. \(\square \)
In the scalar case, and under stronger assumptions, similar results were obtained in [16]. To obtain the complete information of the asymptotics, it is of interest to identify the function g. In the scalar case, g is related to the density of the spectral measure of A (see [27, Corollary 1]).
The following corollary is an extension of [27, Corollary 3] to the operator case. In the scalar case, it provides exact asymptotics of the so-called Christoffel functions, which have applications, e.g., in random matrix theory (see [22]) or signal processing (see [15]). We believe that in the operator case, it will also have some applications.
Corollary 5
Let the assumptions of Theorem 9 be satisfied. Assume further that
Then
uniformly on \(\Omega \times K\), where
for \(S_n\) defined in (19).
Proof
By the Stolz–Cesàro theorem (also known as L’Hôpital’s rule for sequences),
Theorem 9 implies that \(C=C^*\), and consequently, Proposition 6 shows that \(\left||{a_n} \right||/\left||{a_{n-1}} \right||\) tends to 1. Therefore, by Theorem 9, the result follows. \(\square \)
8 Examples
8.1 Examples of Theorem 4
In this section, we show examples of the special cases of Theorem 4 presented in Sect. 5, i.e., to Theorems 1 and 6. Since Theorem 5 is a weaker version of Theorem 2, the examples of it are postponed to the next section.
Example 1
Assume that X and Y are bounded noncommuting operators on \(\mathcal {H}\) such that X is invertible normal and Y is self-adjoint. Let
Write
i.e., the \(k\hbox {th}\) repetition of \(\tilde{x}_k\) and \(\tilde{y}_k\). We define in the block form,
Then for
the assumptions of Theorem 1 are satisfied.
Proof
We have
which by the monotonicity of \(x_n\) and normality of X is positive. Hence, the hypothesis (a) is satisfied.
Next, one has \(\left||{a_n} \right|| = x_n \left||{X} \right||\). Therefore, by
we obtain the hypothesis (c).
Finally,
and by the fact that \((x_{n+1}/x_n : n \ge 0)\) tends to 1, the hypothesis (b) will be satisfied if \((y_n/ x_n : n \ge 0)\) is summable. But
and the result follows. \(\square \)
Example 2
Let \(K \ge 1\) be an integer and M be such that \(\log ^{(K)}(M) > 0\) (see (15)). Assume that X and Y are bounded noncommuting self-adjoint operators on \(\mathcal {H}\) such that X is invertible. Let
for
Then the assumptions of Theorem 6 are satisfied.
Proof
The hypotheses (a) and (d) from Theorem 6 are straightforward.
Since X is self-adjoint,
Therefore, by [26, Example 4.5], the hypothesis (b) is satisfied.
It remains to show the hypothesis (c). We have
Since \((y_{n+1}/x_n : n \ge 0)\) tends to 1, it remains to show that \((y_n/x_n : n \ge 0)\) is summable. But
which by the Cauchy condensation test applied K times is summable. The proof is complete. \(\square \)
8.2 Examples of Theorems 2 and 3
The following Proposition provides a simple way of the construction of sequences satisfying the bounded variation condition of Theorem 2.
Proposition 9
Fix \(N \ge 1\) and a Hilbert space \(\mathcal {H}\). Let \((x_n : n \ge 0)\) and \((y_n : n \ge 0)\) be sequences of numbers such that \(x_n > 0\), \(b_n \in \mathbb {R}\), and
Let \((X_n : n \in \mathbb {Z})\) and \((Y_n : n \in \mathbb {Z})\) be N-periodic sequences of bounded operators on \(\mathcal {H}\) such that for every n, each \(X_n\) is invertible and each \(Y_n\) is self-adjoint. Let us define
Then
Proof
We have
Therefore, it is enough to apply Proposition 1. \(\square \)
The next proposition provides a convenient form of \(\mathcal {F}(\lambda )\) for \(N=1\).
Proposition 10
Assume;
-
\((a) \quad \lim \limits _{n \rightarrow \infty } \left||{a_n} \right|| = a \in (0, \infty ]\),
-
\((b) \quad \lim \limits _{n \rightarrow \infty } \frac{a_n}{\left||{a_n} \right||} = C\),
-
\((c) \quad \lim \limits _{n \rightarrow \infty } \frac{b_n}{\left||{a_n} \right||}= D\),
-
\((d) \quad \lim \limits _{n \rightarrow \infty } \frac{\left||{a_{n-1}} \right||}{\left||{a_n} \right||}= 1\).
Then, in the notation of Theorem 2,
Proof
Since
we have
Hence, the direct computation shows that \(\mathcal {F}(\lambda )\) has the requested form. \(\square \)
In the following example, we discuss the optimality of \(\Lambda \) in the case of constant coefficients.
Example 3
Let
Then the assumptions of Theorem 2 are satisfied with
Moreover, \(\Lambda \) is the maximal set where A has absolutely continuous spectrum of the multiplicity 2.
Proof
Let
Since \((a_n : n \ge 0)\) and \((b_n : n \ge 0)\) are constant, it is sufficient to show that matrix \(\mathcal {F}(\lambda )\) is positive definite for \(\lambda \in M_2\).
According to Proposition 10, we have
The determinants of its principal minors are equal to
Hence, the matrix \(\mathcal {F}(\lambda )\) is positively definite whether \(\lambda \in M_2\). Moreover, the determinant of the last minor is negative only for \(\lambda \in M_1\).
According to [30, Theorem 3], the matrix A is purely absolutely continuous on the closure of the set \(M_1 \cup M_2\). Moreover, the spectrum of A is of multiplicity 1 and 2 on \(M_1\) and \(M_2\), respectively. \(\square \)
In the next example, we consider the unbounded case for \(N=1\).
Example 4
Let
Let us assume that real sequences \((x_n: n \ge 0)\) and \((y_n: n \ge 0)\) such that \(x_n > 0\) and \(y_n \in \mathbb {R}\) for every n satisfy
and
For example: \(x_n = (n+1)^\alpha , y_n = q a_n\) for \(\alpha > 0\).
Then for
the assumptions of Theorem 2 are satisfied.
Proof
In view of Proposition 9, it is enough to show that \(\mathcal {F}\) is positive definite. In the notation of Proposition 10,
Hence, by Proposition 10,
The determinants of the principal minors of this matrix are equal to
Hence, this matrix is positive definite if and only if
\(\square \)
Notes
By \(X^*\) we denote the adjoint operator to X.
For a self-adjoint operator \(X \in \mathcal {B}(\mathcal {H})\), we define \(X^-\) by the spectral theorem.
By \(\sigma (A)\) we denote the spectrum of the operator A, whereas \(\sigma _{\text {p}}(A)\) is the set of its eigenvalues.
The real part of the operator X is defined by \(\mathrm {Re} \left[ {X} \right] = \frac{1}{2} (X + X^*)\).
We employ the following notation: \((v_1, v_2)^t = \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\).
References
Beckermann, B.: Complex Jacobi matrices. J. Comput. Appl. Math. 127(1–2), 17–65 (2001)
Berezanskiĭ, Y.: Expansions in Eigenfunctions of Selfadjoint Operators, vol. 17. American Mathematical Society, Providence (1968)
Berg, C., Szwarc, R.: On the order of indeterminate moment problems. Adv. Math. 250, 105–143 (2014)
Braeutigam, I.N., Mirzoev, K.A.: Deficiency numbers of operators generated by infinite Jacobi matrices. Dokl. Math. 93(2), 170–174 (2016)
Carvalho, S.L., Marchetti, D.H.U., Wreszinski, W.F.: Sparse block-Jacobi matrices with arbitrarily accurate Hausdorff dimension. J. Math. Anal. Appl. 368(1), 218–234 (2010)
Clark, S.L.: A spectral analysis for self-adjoint operators generated by a class of second order difference equations. J. Math. Anal. Appl. 197(1), 267–285 (1996)
Damanik, D., Lukic, M., Yessen, W.: Quantum dynamics of periodic and limit-periodic Jacobi and block Jacobi matrices with applications to some quantum many body problems. Commun. Math. Phys. 337(3), 1535–1561 (2015)
Damanik, D., Pushnitski, A., Simon, B.: The analytic theory of matrix orthogonal polynomials. Surv. Approx. Theory 4, 1–85 (2008)
Dette, H., Reuther, B., Studden, W., Zygmunt, M.: Matrix measures and random walks with a block tridiagonal transition matrix. SIAM J. Matrix Anal. A 29(1), 117–142 (2007)
Durán, A., Van Assche, W.: Orthogonal matrix polynomials and higher-order recurrence relations. Linear Algebra Appl. 219, 261–280 (1995)
Durán, A.J., Daneri, E.: Ratio asymptotics for orthogonal matrix polynomials with unbounded recurrence coefficients. J. Approx. Theory 110(1), 1–17 (2001)
Durán, A.J., Lopez-Rodriguez, P.: N-extremal matrices of measures for an indeterminate matrix moment problem. J. Funct. Anal. 174(2), 301–321 (2000)
Durán, A.J., López-Rodrıguez, P.: The matrix moment problem. In: Espanol, L., Varona, J.L. (eds.) Margarita Mathematica en memoria de José Javier Guadalupe, pp. 333–348. Universidad de La Rioja, La Rioja (2001)
Geronimo, J.S., Van Assche, W.: Approximating the weight function for orthogonal polynomials on several intervals. J. Approx. Theory 65(3), 341–371 (1991)
Ignjatović, A.: Chromatic derivatives, chromatic expansions and associated spaces. East J. Approx. 15(3), 263–302 (2009)
Ignjatović, A.: Asymptotic behaviour of some families of orthonormal polynomials and an associated Hilbert space. J. Approx. Theory 210, 41–79 (2016)
Janas, J.: Criteria for the absence of eigenvalues of Jacobi matrices with matrix entries. Acta Sci. Math. (Szeged) 80(1–2), 261–273 (2014)
Janas, J., Moszyński, M.: Alternative approaches to the absolute continuity of Jacobi matrices with monotonic weights. Integr. Equ. Oper. Theory 43(4), 397–416 (2002)
Janas, J., Naboko, S.: On the point spectrum of periodic Jacobi matrices with matrix entries: elementary approach. J. Differ. Equ. Appl. 21(11), 1103–1118 (2015)
Koelink, E.: Applications of spectral theory to special functions. arXiv:1612.07035
Kostyuchenko, A.G., Mirzoev, K.A.: Three-term recurrence relations with matrix coefficients. The completely indefinite case. Math. Notes 63(5), 624–630 (1998)
Lubinsky, D.S.: An update on local universality limits for correlation functions generated by unitary ensembles. SIGMA 12(78), 1–36 (2016)
Sahbani, J.: Spectral theory of a class of block Jacobi matrices and applications. J. Math. Anal. Appl. 438(1), 93–118 (2016)
Simon, B.: Operator Theory. A Comprehensive Course in Analysis, Part 4. American Mathematical Society, Providence (2015)
Sinap, A., Van Assche, W.: Orthogonal matrix polynomials and applications. J. Comput. Appl. Math. 66(1), 27–52 (1996)
Świderski, G.: Spectral properties of unbounded Jacobi matrices with almost monotonic weights. Constr. Approx. 44(1), 141–157 (2016)
Świderski, G.: Periodic perturbations of unbounded Jacobi matrices II: formulas for density. J. Approx. Theory 216, 67–85 (2017)
Świderski, G., Trojan, B.: Periodic perturbations of unbounded Jacobi matrices I: asymptotics of generalized eigenvectors. J. Approx. Theory 216, 38–66 (2017)
Zagorodnyuk, S.M.: The Nevanlinna-type parametrization for the operator Hamburger moment problem. J. Adv. Math. Stud. 10(2), 183–199 (2017)
Zygmunt, M.J.: Generalized Chebyshev polynomials and discrete Schrödinger operators. J. Phys. A Math. Gen. 34(48), 10613–10618 (2001)
Acknowledgements
I would like to thank Bartosz Trojan, Ryszard Szwarc, and an anonymous referee for helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Erik Koelink.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Świderski, G. Spectral Properties of Block Jacobi Matrices. Constr Approx 48, 301–335 (2018). https://doi.org/10.1007/s00365-018-9420-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00365-018-9420-z