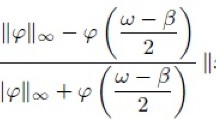Special Moduli of Continuity and the Constant in the Jackson–Stechkin Theorem

Abstract

We consider a special 2k-order modulus of continuity W _2k (f,h) of 2π-periodic continuous functions and prove an analog of the Bernstein–Nikolsky–Stechkin inequality for trigonometric polynomials in terms of W _2k . We simplify the main construction from the paper by Foucart et al. (Constr. Approx. 29(2), 157–179, 2009) and give new upper estimates of the Jackson–Stechkin constants. The inequality W _2k (f,h)≤3∥f∥_∞ and the Bernstein–Nikolsky–Stechkin type estimate imply the Jackson–Stechkin theorem with nearly optimal constant for approximation by periodic splines.

1 Introduction

The paper is devoted to the question of equivalence of two types of direct theorems in approximation theory:

• (a) the case of smooth functions (Favard estimates);

• (b) the case of arbitrary continuous functions (Jackson–Stechkin estimates).

We show that the Jackson–Stechkin inequality with the optimal constants follows from the Favard inequality (see the proof of Theorem 2 and (5.3)). The main tool in the proof of this statement is the function W _2k , measuring the smoothness of an integrable periodic function. Modulus W _2k is the special case of the generalized modulus of smoothness introduced by H. Shapiro [2, 15]. This characteristic is more delicate than the standard modulus of continuity of order 2k. The function W _2k allows us to obtain asymptotically sharp results for the approximation by Favard-type operators. For example, we obtain the Jackson–Stechkin inequality for the periodic splines with constants close to optimal.

The following two facts play a key role here:

• 1. Uniform (in k) boundedness of operators W _2k :

  $$W_{2k}(f,h)\le3\|f\|, \quad f\in C(\mathbb{T}),\ h>0. $$

• 2. The Bernstein–Nikolsky–Stechkin inequality in terms of W _2k .

The paper is organized as follows. In the second section, we introduce notation. In the third section, we consider the smooth characteristic W _2k and prove the uniform boundedness of W _2k (Lemma 1). The technical details of the proof can be found in the Appendix. Section 4 is devoted to the analog of the classical Bernstein–Nikolsky–Stechkin estimate in terms of W _2k (Theorem 1). The next important result in the paper is Theorem 2, which gives a simple and general proof of the Jackson–Stechkin theorem. We improve and simplify the main constructions from [9]. In the fifth section, we introduce Favard-type operators and show that Favard-type operators give Jackson–Stechkin theorems with almost optimal constants. That result is a consequence of the sharp inequality for the trigonometric approximation. We will show that to prove Jackson–Stechkin theorems with almost optimal constants, it is sufficient to obtain a Favard-type inequality (Theorem 3). Theorem 4 is devoted to approximation by periodic splines. Finally, we give in Theorems 5 and 6 the classical almost sharp variants of Theorems 1 and 3.

2 Notation

Let $\mathbb{I}$ denote either a one-dimensional torus $\mathbb{T}=[-\pi,\pi)=\mathbb{R}/(2\pi\mathbb{Z})$ or the real line $\mathbb{R}=(-\infty,\infty)$, and let $L(\mathbb{I})$ be the space of integrable functions $f:\mathbb{I}\rightarrow\mathbb{R}$ with the norm $\|f\|_{L(\mathbb{I})}=\int_{\mathbb{I}}|f(t)|\,dt$. The space of continuous 2π-periodic functions with the norm

$$\|f\|=\|f\|_{C(\mathbb{T})}=\max \bigl\{\bigl|f(t)\bigr|: t\in\mathbb{T} \bigr\} $$

is denoted by $C(\mathbb{T})$. In this paper, we are interested in the approximation of a real continuous function $f \in C (\mathbb{T})$ by trigonometric polynomials τ∈T _n of degree n:

$$\tau(x):= \sum_{j=-n}^n \alpha_j \exp (ijx), \quad\alpha_j = \overline{\alpha}_{-j}. $$

By ∗ we denote the convolution operation in $L(\mathbb{R})$ (see [16, Chap. 1, Sect. 1]):

$$ (f{\ast}g) (x)=\int_{\mathbb{R}}f(x-t)g(t)\,dt, $$

and by ⊛ the periodic convolution operation in $L(\mathbb{T})$ (see [10, Chap. 1, Sect. 1.5.4], [4, Chap. 3, Sect. 3.1]):

$$ (f{\circledast}g) (x)=\int_{\mathbb{T}}f(x-t)g(t)\,dt. $$

Let χ _h (x), h>0, be the characteristic function of the interval (−h/2,h/2) normalized in $L(\mathbb{R})$:

$$ \chi_{h}(x)= \begin{cases} 1/h, & x\in(-h/2,h/2), \\ 0, & x\notin(-h/2,h/2), \end{cases} \qquad \int_\mathbb{R}\chi_{h}(t)\,dt=1. $$

(2.1)

We will use the well-known periodization method (see [16, Chap. 7, Sect. 2, (2.1)]), which for a given $f\in{L(\mathbb{R})}$ provides the 2π-periodic function $\widetilde{f}$ from ${L(\mathbb{T})}$ by the formula

$$ \widetilde{f}(x)=\sum_{j\in\mathbb{Z}}f(x+2\pi j), $$

and (see the proof of Theorem 2.4 from [16, Chap. 7, Sect. 2])

$$ \|\widetilde{f}\|_{L(\mathbb{T})}\le\|{f} \|_{L(\mathbb{R})},\quad f\in{L(\mathbb{R})}. $$

(2.2)

For a nonnegative $f\in{L(\mathbb{R})}$, the inequality (2.2) changes to the equality

$$ \|\widetilde{f}\|_{L(\mathbb{T})}=\|{f} \|_{L(\mathbb{R})},\quad f\in{L(\mathbb{R})},\ f\ge0. $$

(2.3)

For example, the 2π-periodization of χ _h is given by the formula

$$\widetilde{\chi}_{h}(x)=\sum_{j\in\mathbb{Z}} \chi_{h}(x+2\pi j), $$

and (2.1), (2.3) imply that $\|\widetilde{\chi}_{h}\|_{L(\mathbb{T})}=1$ for each h>0. The Fourier series for $\widetilde{\chi}_{h}$ is

$$ \widetilde{\chi}_{h}(x) =\frac{1}{2\pi} \sum_{j\in\mathbb{Z}}\operatorname{sinc}({j}h/2)\exp(ijx) = \frac{1}{\pi} \Biggl[\frac{1}{2}+\sum_{j=1}^{\infty} \operatorname{sinc} ({j}h/2)\cos{j}x \Biggr], $$

(2.4)

where

$$ \operatorname{sinc}(x):=\frac{\sin x}{x}\quad\mbox{for }x \not =0, \qquad \operatorname{sinc}(0):=1. $$

Following [14, Chap. 3, Sect. 2, (III, 2; 96)], we write

$$\begin{aligned} f^{1*}(x)&:=f(x),\qquad f^{r*}(x):=\bigl(f*f^{(r-1)*} \bigr) (x) \quad\mbox{for } r=2,3,\ldots,\ f\in L(\mathbb{R}); \\ g^{{1\,\circledast}}(x)&:=g(x),\qquad g^{{r\,\circledast}}(x) := \bigl(g \circledast g^{{(r-1)\,\circledast}} \bigr) (x) \quad\mbox{for } r=2,3,\ldots,\ g \in L(\mathbb{T}), \end{aligned}$$

and consider the convolution squares

$$\begin{aligned} \phi_h(x) & := \chi_h^{2*}(x)= \begin{cases} \frac{1}{h} (1-\frac{|x|}{h} ), & x\in(-h,h), \\ 0, & x\notin(-h,h); \end{cases} \end{aligned}$$

(2.5)

$$\begin{aligned} \widetilde{\phi}_h(x) & := \widetilde{\chi}_h^{{2\,\circledast}}(x) =\frac{1}{2\pi}\sum _{j\in\mathbb{Z}}\operatorname{sinc}^2({j}h/2) \exp(ijx) =\sum_{j\in\mathbb{Z}}\phi_{h}(x+2\pi j). \end{aligned}$$

(2.6)

To prove equalities (2.6), it is sufficient to apply (2.4) and properties of periodic convolution (see [4, Part 3, Sect. 3.1]). Notably, the convolution f ⊛ g of the functions f,g from $L(\mathbb{T})$ belongs to $L(\mathbb{T})$, and for the Fourier coefficients of the convolution we have the following identity:

$$ \widehat{(f\,{\circledast}\,g)}_{j}={2\pi} \cdot\widehat{\varphi}_{j} \cdot \widehat{f}_{j} \quad \mbox{for all } j\in\mathbb{Z}, $$

where we use the standard notation for Fourier coefficients of $f\in{L(\mathbb{T})}$:

$$\widehat{f}_{j}:=\frac{1}{2\pi} \int_{{\mathbb{T}}}f(t)\exp(-ijt) \,dt,\quad j\in\mathbb{Z}. $$

The last equality in (2.6) follows from the general fact about periodization (see [16, Part 7, Sect. 2, Theorem 2.4, Corollary 2.6]).

Note that (2.3), (2.5), (2.6) imply that

$$ \|\phi_h\|_{L(\mathbb{R})}=\|\widetilde{ \phi}_h\|_{L(\mathbb{T})}=1 $$

(2.7)

for each h>0.

3 Special Modulus of Continuity

For fixed h>0 and $k\in\mathbb{N}$, consider the following operator from $C(\mathbb{T})$ to $C(\mathbb{T})$:

$$ W_{2k}(f,x,h):=(-1)^k \frac{1}{\binom{2k}{k}}\int_{\mathbb{R}} {\varDelta }_{t}^{2k}f(x) \phi_h(t)\,dt, $$

(3.1)

where

$${\varDelta }_t^{2k} f(x)=\sum_{j=-k}^k(-1)^{j+k} \binom{2k}{k+j}f(x+jt) $$

is a central difference of order 2k with the step t. The following representation is valid (cf. [9, Sect. 3]):

$$ W_{2k}(f,x,h)=f(x)-(f*\varLambda_{k,h})(x). $$

(3.2)

Here

$$ \varLambda_{k,h}(x)=2\sum_{j=1}^k (-1)^{j+1}a_j\phi_{jh}(x), $$

(3.3)

$$ a_j:=\frac{\binom{2k}{k-j}}{\binom{2k}{k}},\qquad \phi_{jh}(x)=\frac{1}{jh} \biggl(1-\frac{|x|}{jh} \biggr)_{+},\qquad u_+:=\max\{u,\,0\}. $$

(3.4)

For a 2π-periodic function $f\in{C(\mathbb{T})}$, this gives the following representation:

$$ W_{2k}(f,x,h)=f(x)-(f \circledast\widetilde{ \varLambda}_{k,h}) (x), $$

(3.5)

where

$$ \widetilde{\varLambda}_{k,h}(x) =\sum_{\ell\in\mathbb{Z}}{\varLambda}_{k,h}(x+2\pi\ell) =2\sum_{j=1}^k(-1)^{j+1}a_j \widetilde{\phi}_{jh}(x). $$

(3.6)

Note that for the positive numbers a _j =a _j (k), j=1,…,k, we have

$$ 2\sum_{j=1}^k (-1)^{j+1}a_j=1,\qquad 2\sum_{j=1}^k a_j=\frac{2^{2k}}{\binom{2k}{k}}-1\asymp\sqrt{k}. $$

(3.7)

The formulas (2.6), (3.6) and the first equality in (3.7) imply that

$$\int_{\mathbb{T}}\widetilde{\varLambda}_{k,h}(x)\,dx=1 \quad\mbox{for } k=1,2,3,\ldots. $$

We will show that

$$\|\widetilde{\varLambda}_{k,h}\|_{L(\mathbb{T})}<2\quad\mbox{for all} \ h>0\ \mbox{and}\ k\in\mathbb{N}. $$

For h>0 and $f\in{C}(\mathbb{T})$, let

$$\begin{aligned} W_{2k}(f,h) & :=\sup_{x\in\mathbb{T}}\bigl|f(x)-(f\circledast\widetilde{\varLambda }_{k,h}) (x)\bigr| =\bigl\|W_{2k}(f,\cdot,h)\bigr\|, \end{aligned}$$

(3.8)

$$\begin{aligned} W_{2k}^*(f,\delta)&:=\sup_{0<h\le\delta}W_{2k}(f,h). \end{aligned}$$

(3.9)

The definitions (3.8), (3.9), and (3.1) imply that

$$ W_{2k}(f,\delta)\le{W_{2k}^*(f,\delta)} \le\frac{1}{\binom{2k}{k}}\sup_{|t|\le\delta}\bigl\|{\varDelta }_{t}^{2k}f \bigr\| =:\frac{1}{\binom{2k}{k}}\,\omega_{2k}(f,\delta),\quad f\in{C}(\mathbb{T}), \ \delta>0 . $$

Lemma 1

If h>0, $k\in\mathbb{N}$ and $f \in {C}(\mathbb{T})$, then

$$W_{2k}(f, h) \le3\|f\|. $$

Proof

For every h>0 and $f\in{C}(\mathbb{T})$, we have (see (3.2)–(3.6))

$$ W_{2k}(f,x,h)=f(x)-(f \circledast\widetilde{ \varLambda }_{k,h}) (x)=f(x)-(f*\varLambda_{k,h}) (x), $$

(3.10)

where

$$\varLambda_{k,h}(x)=\frac{2}{{\binom{2k}{k}}} \sum_{j=1}^k(-1)^{j+1}{\binom{2k}{k-j}} \frac{1}{jh}\, \biggl(1-\frac{|x|}{jh} \biggr)_{+}. $$

First, consider the case k=1. In this case, we have (see (2.5), (2.6))

$$\begin{aligned} \varLambda_{1,h}(x) & =\phi_h(x)=\frac{1}{h} \biggl(1-\frac{|x|}{h} \biggr)_{+}, \\ \widetilde{\varLambda}_{1,h}(x) & =\widetilde{\phi}_h(x)=\sum_{j\in\mathbb {Z}}\phi_{h}(x+2\pi j) = \frac{1}{2\pi}\sum_{j\in\mathbb{Z}}\operatorname{sinc}^2({j}h/2) \exp(ijx). \end{aligned}$$

From this and from (2.7), we obtain

$$\begin{aligned} \|\widetilde{\varLambda}_{1,h}\|_{L(\mathbb{T})} &=\|\varLambda_{1,h}\|_{L(\mathbb{R})}=1, \\ W_{2}(f,h)&=\|f-f \circledast\widetilde{\varLambda}_{1,h}\|\le \bigl(1+\|\widetilde{\varLambda}_{1,h}\|_{L(\mathbb{T})} \bigr)\|f\|=2\|f\|, \\ W_{2}(f,h)&\le2\|f\|\quad\mbox{for}\ h>0. \end{aligned}$$

Hence, Lemma 1 in the case k=1 is proved.

Let $k\in\mathbb{N}$, k≥2. It is sufficient to consider the case h=1. In this case, Λ _k :=Λ _k,1 is an even, piecewise linear function (see Fig. 1) with vertices at the points (i,b _i,k ), i=−k,…,k, where

$$b_{-i,k}=b_{i,k}, \quad i=0,\dots, k-1,\qquad b_{-k,k}=b_{k,k}=0, $$

and

$$b_{i,k}=2{\binom{2k}{k}}^{-1}\sum _{j=i+1}^k\binom{2k}{k-j}(-1)^{j+1}\frac{1}{j} \biggl(1-\frac{i}{j} \biggr), \quad i=0,\dots,k-1. $$

Fig. 1

Function Λ ₃(x)

The inequalities (see Appendix, Lemma A)

$$ \begin{aligned} & (-1)^ib_{i,k}>0,\qquad |b_{i,k}|>|b_{i+1,k}|, \qquad \sum_{j=0}^{k}|b_{j,k}|<2, \quad i=0,\ldots,k-1, \end{aligned} $$

imply (see (3.8), (3.10), and (2.2)) that

$$\begin{aligned} W_{2k}(f,h) & =\|f-f \circledast\widetilde{\varLambda}_{k,h}\|\le \bigl(1+\|\widetilde{\varLambda}_{k,h}\|_{L(\mathbb{T})} \bigr)\|f\|, \\ \|\widetilde{\varLambda}_{k,h}\|_{L(\mathbb{T})} & \le \|{\varLambda}_{k,h}\| _{L(\mathbb{R})}= \int_{\mathbb{R}} \bigl|\varLambda_{k,h}(t)\bigr|\,dt<\sum_{j=0}^{k}|b_{j,k}|<2. \end{aligned}$$

Now Lemma 1 is completely proved. □

Remark 1

It is clear that the exact constant in Lemma 1 is equal to $1 + \|{\varLambda}_{k,1}\|_{L(\mathbb{R})}$. We have the following estimates of $n_{k}:=\|{\varLambda}_{k,1}\|_{L(\mathbb{R})}$ for small k≥2:

$$n_2=53/45 , \quad n_3 \approx1.26, \quad n_4 \approx1.31,\quad n_{10} \approx1.42,\quad n_{100} \approx1.58, \quad n_{500} \approx 1.63. $$

4 Bernstein–Nikolsky–Stechkin Inequality

The Bernstein–Nikolsky–Stechkin inequality [17] (see also [10, Theorem 3.5.3], [3, p. 131, (12.1)]) is the generalization of the classical Bernstein inequality for trigonometric polynomials

$$ \bigl\|{\tau^{(r)}}\bigr\|\le n^r\|\tau\|, \quad r\in \mathbb{N}, \ \tau\in T_{n}. $$

(4.1)

The Bernstein–Nikolsky–Stechkin inequality is given by

$$ \bigl\| \tau^{(r)} \bigr\| \le n^r \bigl(2\sin (nh/2) \bigr)^{-r}\bigl\|\varDelta _h^r\tau\bigr\|, \quad h \in(0, 2\pi/n), $$

(4.2)

where

$${\varDelta }_h^rf(x):=\sum_{j=0}^r(-1)^j\binom{r}{j}f(x+jh-rh/2). $$

Note that in the case r=1, h=π/n, the inequality (4.2) was proved by M. Riesz [12, §4] in 1914.

Let e _j (x):=exp(ijx), c _j (x):=cos(jx). It is easily seen that

$$W_{2k}(e_j,x,h)=\lambda_{h,k}(j)e_j(x), \qquad W_{2k}(c_j,x,h)= \lambda_{h,k}(j) c_j(x),\quad j\in\mathbb{Z}, $$

where

$$\lambda_{h,k}(j)=W_{2k}(c_j,h)= \frac{2^{2k}}{\binom{2k}{k}}\,\int_{{\mathbb{R}}} \biggl(\sin\frac{{j}u}{2} \biggr)^{2k}\,\phi_h(u)\,du. $$

Lemma 2

For α∈(1,2], we have the following inequality:

$$ W_{2k}(c_n, \alpha\pi/n) \ge \frac{4 (\alpha- 1)}{\alpha^2}. $$

(4.3)

For α=2, we have in (4.3) equality.

Proof

$$\begin{aligned} W_{2k}(c_n, \alpha\pi/n) & = 2 \, 2^{2k}{\binom{2k}{k}}^{-1} \int_0^{\pi \alpha/n} \sin^{2k} (nt/2) \frac{n}{\alpha\pi} \biggl( 1 - \frac{n}{\alpha\pi} t \biggr) \, dt \\ & = 2 \, 2^{2k}{\binom{2k}{k}}^{-1} \frac{2}{\alpha\pi} \int_0^{\pi \alpha/2} \sin^{2k}(u) \biggl(1 - \frac{2}{\pi\alpha} u \biggr) \, du \\ & = 2 \, 2^{2k}{\binom{2k}{k}}^{-1} \frac{2}{\alpha \pi} I. \end{aligned}$$

Set s:=πα/2. We have

$$\begin{aligned} I =& \int_0^{\pi/2} + \int_{\pi/2}^{s} = I_1 + I_2 \\ =& \int_0^{\pi/2} (\cos t)^{2k} \biggl( \frac{s+t-\pi/2}{s} \biggr) \, dt + \int_0^{s-\pi/2} ( \cos t)^{2k} \biggl( \frac{s-t-\pi/2}{s} \biggr) \, dt \\ =& \frac{1}{s} \int_{s-\pi/2}^{\pi/2} (\cos t)^{2k} t \, dt + \frac{s-\pi/2}{s} \biggl[ \int_0^{\pi/2} \cos^{2k}(t) \, dt + \int_0^{s- \pi/2}\cos^{2k} (t) \, dt \biggr] \\ =& \int_{s-\pi/2}^{\pi/2} (\cos t)^{2k} \biggl( \frac{t}{s} -\frac {s-\pi/2}{s} \biggr) \,dt + 2 \frac{s-\pi/2}{s} \int _0^{\pi/2} \cos^{2k}(t) \, dt \\ \ge& 2 \frac{s-\pi/2}{s} \int_0^{\pi/2} \cos^{2k}(t) \, dt = \frac{\alpha-1}{\alpha}2^{-2k} \, \binom{2k}{k} \pi. \end{aligned}$$

 □

The main result in this section is the following analog of the Bernstein–Nikolsky–Stechkin inequality.

Theorem 1

If τ∈T _n , $k,n\in\mathbb{N}$, then

$$ \bigl\|\tau^{(2k)}\bigr\|\le\frac{n^{2k}}{W_{2k}(c_n,h)}W_{2k}(\tau, h), \quad h \in(0,2\pi/n]. $$

(4.4)

In particular,

$$ \bigl\| {\tau^{(2k)}} \bigr\| \le \frac{\alpha^2}{4(\alpha-1)} n^{2k} W_{2k}(\tau,\alpha\pi/n) ,\quad \alpha\in(1,2]. $$

It is clear that Theorem 1 is sharp. We have the equality in (4.4) for τ=c _n .

Theorem 1 implies Bernstein’s inequality (4.1) for even derivatives. This follows from Lemma 3.

Lemma 3

If τ∈T _n , $k,n\in\mathbb{N}$, then

$$ \frac{W_{2k}(\tau, h)}{W_{2k}(c_n,h)} \le\|\tau\|, \quad h \in \bigl(0,\pi/(2n) \bigr). $$

Proof of Theorem 1

Theorem 1 follows from Lemmas 4, 5 below. Specifically, if

$$\tau(x)=\sum_{j=-n}^n\widehat{\tau}_je_j(x), $$

then

$$W_{2k}(\tau,x,h)=\sum_{j=-n}^n \lambda_{h,k}(j)\widehat{\tau}_je_j(x) $$

and

$$\bigl \vert \tau^{(2k)}(x)\bigr \vert =\Biggl \vert \sum_{j=-n}^n j^{2k}\widehat{\tau}_j e_j(x)\Biggr \vert = \Biggl|\sum_{\substack{j=-n\\ j\ne0}}^n j^{2k}\lambda_{h,k}^{-1}(j) \lambda_{h,k}(j)\widehat{\tau}_j\,e_j(x) \Biggr|. $$

Now Lemmas 4 and 5 imply that

$$\bigl\|\tau^{(2k)}\bigr\|\le n^{2k}{\lambda_{h,k}^{-1}(n)} \Biggl\|\sum_{j=-n}^n\lambda_{h,k}(j) \widehat{\tau}_je_j \Biggr\| =n^{2k}W^{-1}_{2k}(c_n,h) \bigl\|W_{2k}(\tau,\cdot,h)\bigr\|. $$

 □

Lemma 4

(cf. [19, p. 361])

Suppose that q(t) is a nonnegative, even, convex on [−n,n] function. Then for real $\tau(t)=\sum_{j=-n}^{n}\widehat{\tau}_{j}e_{j}(t)$, the following inequality is valid:

$$\Biggl\|\sum_{j=-n}^n q(j)\widehat{\tau}_je_j \Biggr\|\le{q(n)}\|\tau\|. $$

Lemma 5

Let $n,k\in\mathbb{N}$, h∈(0,2π/n]. Then the function $q(t):=t^{2k}\lambda^{-1}_{h,k}(t)$ satisfies the conditions of Lemma 4.

Proof

We have the following formula:

$$\lambda_{h,k}(j)= \frac{2^{2k}}{\binom{2k}{k}}\int_{{\mathbb{R}}} \biggl(\sin\frac{{j}u}{2} \biggr)^{2k}\phi_h(u)\,du, $$

where (see (2.5))

$${\phi_h}(u):=\chi_h^{2*}(u)\ge0, \quad {\phi}_h(-u) = {\phi}_h(u), \quad \int_{{\mathbb{R}}} {\phi}_h(u) =1,\quad \operatorname{supp} \phi_h(u)= [-h, h]. $$

The function t ^2k/sin^2k(tu/2) satisfies the conditions of Lemma 4. In other words,

$$\bigl(t^{2k}/{\sin^{2k}}(tu/2) \bigr)^{\prime\prime}_{tt} > 0, \qquad|u|<h\le2\pi /n,\quad t\in(0, n]. $$

We need to prove the inequality

$$ \biggl( \frac{ t^{2k}}{ \int_{{\mathbb{R}}}\sin^{2k} {(tu/2)}\phi _h(u)\,du} \biggr)^{\prime\prime}_{tt} >0. $$

(4.5)

Let

$$f(t):=t^{2k},\qquad g_u(t):=\sin^{2k}(tu/2). $$

Then the function

$$f(t)/g_u(t) $$

is convex on (0,n]. We are going to prove that for 0<h≤2π/n, the function

$$m_h(t):= \frac{t^{2k}}{\int_{{\mathbb{R}}}\sin^{2k}(tu/2)\phi_h(u)\,du} =\frac{f(t)}{\int_{\mathbb{R}}g_u(t)\,\phi_h(u)\,du} $$

is convex on (0,n].

The properties

$$f(t)/g_u(t)>0,\qquad \bigl(f(t)/g_u(t)\bigr)'_t= \bigl(f'(t)g_u(t)-f(t)g'_u(t)\bigr)/g_u^2(t)>0, $$

imply that

$$\begin{aligned} & m_h(t)= \frac{\int_{{\mathbb{R}}} f(t) {\phi_h}(u) \, du}{\int_{{\mathbb{R}}} g_u(t) {\phi_h}(u) \, du}>0 \quad\mbox{and} \\ & \frac{d}{dt}m_h(t)= \frac{\int_{{\mathbb{R}}} (f'(t)g_u(t)-f(t)g'_u(t) )\phi_h(u)\,du}{ (\int_{\mathbb{R}} g_s(t){\phi_h(s)}\,ds )^2}>0. \end{aligned}$$

The condition of positivity for the second derivative takes the following form:

$$\int_{\mathbb{R}}\int_{\mathbb{R}} { \bigl( \bigl(f''g_u-fg''_u \bigr)g_s-2g'_s\bigl(f'g_u-fg'_u \bigr) \bigr)}{\phi_h}(u){\phi _h}(s)\,du\,ds>0, \quad t\in(0,n]. $$

Consider the function

$$F(t,k,u,s):= \bigl(f''g_u - f g''_u\bigr)g_s -2g'_s\bigl(f'g_u - fg'_u\bigr) = F_1(t,k,u,s) \cdot F_2 (t,k,u,s), $$

where

$$\begin{aligned} F_1(t,k,u,s) & :=(k/2)t^{2k-2}\sin^{2k-2}(tu/2) \sin^{2k-2}(ts/2), \\ F_2(t,k,u,s)& :=\sin^2(ts/2) \bigl(4(2k-1) \sin^2(tu/2)+u^2 t^2-2ku^2 t^2\cos^2(tu/2) \bigr) \\ &\phantom{:=} {}+4kts\sin(ts/2)\cos(ts/2)\sin(tu/2) \bigl(tu\cos(tu/2)-2\sin(tu/2) \bigr). \end{aligned}$$

Let

$$u:=u_t=tu/2, \qquad s:=s_t = ts/2. $$

After the change of variable, we may assume that u,s∈(0,h], h∈(0,π].

Consider the case k≥2. First, reduce the value of F ₂ by omitting the positive quantity t ² u ²−4sin²(tu/2). Then, let

$$\begin{aligned} F_1(k,u,s) & :=\sin^{2k-2}(u) \sin^{2k-2}(s), \\ F_2(u,s)&:= \sin^2 s\bigl(\sin^2 u-u^2\cos^2u\bigr)+2s\sin s\sin {u}\cos s(u\cos u-\sin u). \end{aligned}$$

To get (4.5) for k≥2, it is sufficient to show that

$$ \int_{{\mathbb{R}}_+^2}F_1(k,u,s)F_2(u,s) \phi_h(u)\phi_h(s)\,du\,ds>0,\quad 0< h\le\pi. $$

(4.6)

It is sufficient to prove (4.6) for the symmetric function $F_{2}^{*}$ defined by

$$F_2^{*}(u,s):= F_2 (u,s) + F_2 (s,u) =2\sin s\sin u\varphi(s)\varphi(u)- \bigl(\sin s\varphi(u)-\sin u\varphi(s) \bigr)^2, $$

where

$$\varphi(u):=\sin u-u\cos u. $$

To prove (4.6), it is sufficient to prove positivity of the following one-dimensional integral:

$$\int_{\substack{s+u=a \\ s,u\in(0,h]}} \sin^{2k-2}(u)\sin^{2k-2}(s) F_2^*(u,s){\phi_h(u)\phi_h(s)}\, du>0, \quad 0<a<2h \le2 \pi. $$

The function φ(u)/sin(u) is increasing, and the function φ(a−u)/sin(a−u) is decreasing on the interval (max(0,a−π),a/2). Consequently, the function

$$\varPhi_a(u):=\frac{\varphi(u)}{\sin(u)}\cdot\frac{\sin(a-u)}{\varphi(a-u)} $$

is increasing on (max(0,a−π),a/2) from 0 to 1, and the function

$$F_2^*(u,a-u) =-{\sin^2}\, u\varphi^2(a-u) \bigl(\varPhi_a(u)-(2-\sqrt{3}) \bigr) \bigl(\varPhi_a(u)-(2+ \sqrt{3}) \bigr) $$

has exactly one zero on the interval (max(0,a−π),a/2). The functions $\sin(u) \sin(a-u)$, ϕ _h (u)ϕ _h (a−u) are increasing and positive on (max(0,a−π),a/2). These facts and the inequality $F_{2}^{*}(a/2,a/2)>0$ imply that it is sufficient to consider only the case k=2 and to prove that the following integral is positive:

$$\begin{aligned} I_h(a) :=&\int_{\substack{s+u=a \\ s,u\in(0,h]}}\sin^2(u)\sin ^2(s)F_2^*(u,s)\,du \\ =&2\int_{\max(0,a-h)}^{a/2}\sin^2(u) \sin^2(a-u)F_2^*(u,a-u)\,du>0,\quad 0<a<2h\le2\pi. \end{aligned}$$

Furthermore, it is sufficient to prove that I(a):=I _π (a)>0 (0<a<2π). The proof of this inequality can be found in the Appendix (see Sect. A.2), where a special simple case k=1 is also considered. □

In the proof of Lemma 3, we will use the following Lemma 6.

Lemma 6

Let $n,k\in\mathbb{N}$, h∈(0,π/(2n)). Then the function q(t):=λ _h,k (t) satisfies the conditions of Lemma 4.

Proof of Lemma 6

This follows from the formula

$$\biggl( \biggl( \sin\frac{{t}u}{2} \biggr)^{2k} \biggr)^{\prime\prime}_{tt} = \frac{1}{2} {\frac{ ( \sin ( tu/2 ) ) ^{2k}k{u} ^{2} ( 2k ( \cos ( tu/2 ) ) ^{2}-1 ) }{1 - ( \cos ( tu/2 ) ) ^{2}}} > 0, \quad 0 < t u < \pi/2. $$

 □

Proof of Lemma 3

Lemma 3 follows from Lemmas 4 and 6. For

$$\tau(x)=\sum_{j=-n}^n\widehat{\tau}_j e_j(x), $$

we have

$$W_{2k}(\tau,x,h)=\sum_{j=-n}^n \lambda_{h,k}(j)\widehat{\tau}_je_j(x), $$

and Lemmas 4 and 6 imply that

$$\Biggl\|\sum_{j=-n}^n\lambda_{h,k}(j) \widehat{\tau}_je_j \Biggr\| \le{\lambda_{h,k}(n)}\|\tau\|. $$

 □

5 Jackson–Stechkin Theorem

5.1 Jackson–Stechkin Inequality for Polynomial Approximation

In 1936, Jean Favard [6, 7] proved that the following Euler–MacLaurin formula for smooth 2π-periodic functions g with $\widehat{g}_{0}=0$:

$$ g(x)=\bigl(g^{(r)} \circledast B_r\bigr)(x), \qquad B_r(x):=\frac{1}{2\pi}\sum_{j\in\mathbb{Z},\ j\neq0}\frac{\exp (ijx)}{(ij)^r},\qquad i^2=-1, $$

(5.1)

gives a simple proof of the Bohr–Favard inequality (generalization of H. Bohr result [1], r=1). He used in [8] equality (5.1) to obtain a famous sharp inequality:

$$E_{n-1}(f):=\inf_{\tau\in T_{n-1}}\|f-\tau\|\le\frac{\mathcal{K}_r}{n^{r}}\bigl\|{ f^{(r)}} \bigr\|, \qquad \mathcal{K}_{r}:=\frac{4}{\pi}\sum_{j=-\infty}^\infty\frac{1}{(4j+1)^{r+1}}\le\frac{\pi}{2}. $$

In the present paper, the following “telescoping identity” by C. Neumann [11] (see also [13, p. 146], [14, (III,2;96)]) will be used. For every $f\in L(\mathbb{T})$ and m=2,3,… we have

$$ f=f-f\circledast\widetilde{\varLambda}_{k,h}+\sum _{j=1}^{m-1}\widetilde {\varLambda}^{j\,\circledast}_{k,h} \circledast (f-f\circledast\widetilde{\varLambda}_{k,h} ) +f\circledast \widetilde{\varLambda}^{m\,\circledast}_{k,h}. $$

(5.2)

This equality gives a simple proof with new almost optimal constants of the following Jackson–Stechkin type theorem (see [9]).

Theorem 2

Let $f\in C(\mathbb{T})$ and α>1, $k,n\in\mathbb{N}$. Then

$$E_{n-1}(f) \le \biggl(\sec\frac{\pi}{2\alpha} \biggr)W_{2k} \biggl(f,\frac{\alpha\pi}{n} \biggr) . $$

Proof

For arbitrary $f\in{C(\mathbb{T})}$, the representation (5.2) is valid. Using a subadditive property for E _n−1(f), we obtain

$$\begin{aligned} E_{n-1}(f) \le& E_{n-1}(f-f \circledast\widetilde{\varLambda}_{k,h}) +\sum _{j=1}^{m-1}E_{n-1} \bigl(\widetilde{ \varLambda}^{j\,\circledast}_{k,h} \circledast (f-f\circledast\widetilde{ \varLambda}_{k,h} ) \bigr) \\ &{} +E_{n-1} \bigl(f\circledast\widetilde{ \varLambda}^{m\,\circledast }_{k,h} \bigr) \\ \le&\|f-f\circledast\widetilde{\varLambda}_{k,h}\| +\sum _{j=1}^{m-1}E_{n-1}\bigl(\widetilde{ \varLambda}^{j\,\circledast }_{k,h}\bigr)_{L(\mathbb{T})} \|f-f\circledast \widetilde{\varLambda}_{k,h}\| \\ &{} +E_{n-1}\bigl(\widetilde{ \varLambda}^{m\,\circledast}_{k,h}\bigr)_{L(\mathbb{T})}\| f\| \\ =& \Biggl(1+\sum_{j=1}^{m-1}E_{n-1} \bigl(\widetilde{\varLambda}^{j\,\circledast }_{k,h}\bigr)_{L(\mathbb{T})} \Biggr) \|f-f\circledast\widetilde{\varLambda}_{k,h}\| +E_{n-1} \bigl(\widetilde{\varLambda}^{m\,\circledast}_{k,h}\bigr)_{L(\mathbb{T})}\| f \|, \end{aligned}$$

where

$$E_{n-1}(g)_{L(\mathbb{T})}:=\inf_{\tau\in T_{n-1}}\|g-\tau \|_{L(\mathbb{T})}. $$

So

$$E_{n-1}(f)\le \Biggl(1+\sum_{j=1}^{m-1}E_{n-1} \bigl(\widetilde{\varLambda}^{j\,\circledast }_{k,h}\bigr)_{L(\mathbb{T})} \Biggr) \|f-f\circledast\widetilde{\varLambda}_{k,h}\|+E_{n-1} \bigl(\widetilde{\varLambda }^{m\,\circledast}_{k,h}\bigr)_{L(\mathbb{T})}\|f \|. $$

Therefore, it is sufficient to estimate the best L-approximation of the smooth functions $\widetilde{\varLambda}_{k,h}^{j\,\circledast}$. This was done in [9]. Specifically, Lemma 4.2 from [9] contains the result, which reads (in our notation) as follows:

$$ E_{n-1}\bigl(\widetilde{\varLambda}_{k,h}^{j\,\circledast} \bigr)_{L(\mathbb{T})}= \sup_{g\in{T^{\perp}_{n-1}},\,g\not\equiv0}\frac{\|\widetilde{\varLambda }_{k,h}^{j\,\circledast}{\circledast}g\|}{\|g\|} =\sup _{g\in{T^{\perp}_{n-1}},\,g\not\equiv0}\frac{\|{\varLambda}_{k,h}^{j\, *}{*}g\|}{\|g\|}\le{\mathcal{K}}_{2j} \biggl( \frac{\mu\pi}{nh} \biggr)^{2j}, $$

(5.3)

where $T^{\perp}_{n-1}$ is the subspace of all functions from $C(\mathbb {T})$ that are orthogonal to T _n−1,

$$\mu^2:=\mu^2_{2k}:=\frac{8}{\pi^2}\sum_{\mathrm{odd}\,l}^{k}\frac{a_l}{l^2}<1, $$

and the numbers a _l =a _l (k), l=1,…,k, are defined by (3.4).

The inequality (5.3) implies that

$$E_{n-1}\bigl(\widetilde{\varLambda}_{k,h}^{j\,\circledast}\bigr)_{L(\mathbb{T})} \le{ \mathcal{K}}_{2j} \biggl(\frac{\pi\mu}{n h} \biggr)^{2j}={ \mathcal {K}}_{2j}\alpha^{-2j}\mu^{2j} <{ \mathcal{K}}_{2j}\alpha^{-2j}. $$

Since α>1 and ${\mathcal{K}}_{2j}\le{4/\pi}$, for $f\in {C(\mathbb{T})}$ we have the following:

$$E_{n-1}\bigl(\widetilde{\varLambda}^{j\,\circledast}_{k,h} \bigr)_{L(\mathbb{T})}\|f\| \le{\mathcal{K}}_{2j}\alpha^{-2j} \|f\|\to0\quad\mbox{for}\ j\to \infty, $$

and

$$ E_{n-1}(f) \le \Biggl(1+\sum_{j=1}^\infty{\mathcal{K}}_{2j}\alpha^{-2j}\mu ^{2j} \Biggr) W_{2k}(f,h) = \biggl(\sec\frac{\mu\pi}{2\alpha} \biggr)W_{2k} \biggl(f,\frac{\alpha\pi}{n} \biggr). $$

Here, we use the well-known expansion for the secant function (cf. [5, pp. 561–562, (6), (8)]). □

5.2 Favard-Type Operators

Consider a family $F:=\{F_{n,k}:\; n,k\in\mathbb{N}\}$ of operators

$$ F_{n,k}{:}\ C^{2k}(\mathbb{T})\mapsto{C( \mathbb{T})}, $$

with the properties

$$ \bigl\|g-F_{n,k}(g)\bigr\|\le C_F n^{-2k} \bigl\|{g^{(2k)}} \bigr\|, \quad g\in C^{2k}(\mathbb{T}), $$

where the constant 0<C _F <∞ does not depend on g, k, n. We will call F _n,k ∈F a Favard-type operator.

Theorem 3

Let $f\in{C(\mathbb{T})}$. If F _n,k is a Favard-type operator and τ _∗∈T _n−1 is the best uniform approximation of f, then

$$ \bigl\|f-F_{n,k}(\tau_*)\bigr\|\le \varOmega_\alpha(C_F) W_{2k} \biggl(f,\frac{\alpha\pi}{n} \biggr), \quad \alpha\in(1,2], $$

with

$$\varOmega_\alpha(C_F)= \sec\frac{\pi}{2\alpha} + \biggl(1+3\sec\frac{\pi}{2\alpha}\biggr) \frac{C_F \alpha^2}{4(\alpha-1)}. $$

Proof

Suppose that

$$E_{n-1}(f)=\|f-\tau_*\|,\qquad h_\alpha:=\frac{\alpha\pi}{n},\quad \alpha\in(1,2], $$

and let

$$M_{\alpha}:=\frac{C_F \alpha^2}{4(\alpha-1)}. $$

Theorem 1 and Lemma 1 imply that

$$\begin{aligned} \bigl\|\tau_*-F_{n,k}(\tau_*)\bigr\| &\le C_F n^{-2k}\bigl\|\tau_*^{(2k)}\bigr\| \le M_{\alpha}W_{2k}(\tau_*,h_\alpha) \\ &\le M_{\alpha} \bigl\{W_{2k}(f-\tau_*,h_\alpha)+W_{2k}(f,h_\alpha) \bigr\} \\ &\le M_{\alpha} \bigl\{3\|f-\tau_*\|+W_{2k}(f,h_\alpha) \bigr\}. \end{aligned} $$

Thus,

$$\bigl\|f-F_{n,k}(\tau_*)\bigr\|\le\|f-\tau_*\|+\bigl\|\tau_*-F_{n,k}(\tau_*)\bigr\| \le\varOmega_\alpha(C_F)W_{2k}(f, h_\alpha). $$

 □

5.3 Approximation by Periodic Splines

We say that $s\in\mathcal{S}\equiv\mathcal{S}_{2n,2k-1}$ if $s^{(2k-2)} \in C(\mathbb{T})$ and s ^(2k−2)(x)=s _j =const for x∈Δ _j :=[2πj/(2n),2π(j+1)/(2n)), j=0,…,2n−1.

The space $\mathcal{S}$ is the space of smooth periodic splines of degree 2k−1 with minimal defects (=1) on the uniform partition of $\mathbb{T}=\bigcup_{j=0}^{2n-1}\varDelta _{j}$. Define the operator of interpolation at the endpoints of Δ _j :

$$ { } I_{n,k}(g)\in\mathcal{S},\qquad I_{n,k}(g) (x_j)=g(x_j),\quad x_j=j\pi /n,\ j=0,1, \dots,2n-1. $$

V.M. Tihomirov [18] (see also [10, Theorem 5.2.6, p. 223]) proved that I _n,k is an operator of Favard type:

$$\bigl\|g-I_{n,k}(g)\bigr\|\le\mathcal{K}_{2k}n^{-2k} \bigl\|{g^{(2k)}}\bigr\| \le(4/{\pi}) {n^{-2k}} \bigl\|{g^{(2k)}}\bigr\|, \quad n,k\in\mathbb{N}. $$

Therefore, we obtain the following Jackson–Stechkin theorem for periodic splines.

Theorem 4

For $f\in{C(\mathbb{T})}$, α>1, $n,k\in\mathbb{N}$,

$$\bigl\|f-{I}_{n,k}(\tau_*)\bigr\|\le\varOmega_\alpha^*(4/\pi) W_{2k}^* \biggl(f,\frac{\alpha\pi}{n} \biggr), $$

where

$$\varOmega_\alpha^* ({4}/{\pi} ):= \begin{cases} \varOmega_\alpha ({4}/{\pi} ), & \alpha\in(1,2],\\ \varOmega_2 ({4}/{\pi} ), & \alpha\in(2,\infty). \end{cases} $$

5.4 Two Results for the Classical Modulus of Continuity ω _r

First, we improve the main result from [9] (see [9, Theorem 2.1]).

Theorem 5

For $f\in{C(\mathbb{T})}$, $n, r\in \mathbb{N}$, α>1,

$$E_{n-1}(f):=\inf_{\tau\in T_{n-1}}\|f-\tau\| \le\sec\bigl( \pi/(2\alpha)\bigr)\gamma_{r}^*\omega_r(f,\alpha\pi/n), $$

with

$$\gamma_r^*=\frac{1}{{r\choose\lfloor\frac{r}{2}\rfloor}}\asymp\frac {r^{1/2}}{2^r}. $$

In particular,

$$c_r\gamma_{r}^* \le \sup_{f\in C} \frac{E_{n-1}(f)}{\omega_{r}(f,\frac{2\pi}{n})} \le \sqrt{2} \gamma_{r}^*, $$

where

$$c_r = \left \{ \begin{array}{l@{\quad}l} 1 - \frac{1}{r+1}, & r = 2k-1; \\ 1, & r = 2k; \end{array} \right . \quad n>2r. $$

Proof

The proof follows from Theorem 1, keeping in mind the inequalities

$$W_{2k}(f,h)\le\gamma_{2k}^*\omega_{2k}(f, h),\quad \gamma_{2k}^*\omega_{2k}(f,h) \le\gamma_{2k-1}^* \omega_{2k-1}(f,h) $$

and the lower estimate from [9, Sect. 8, Theorem 8.2]. □

Now, let us rewrite Theorem 4 in standard form:

Theorem 6

For $f\in {C(\mathbb{T})}$, $n,k\in\mathbb{N}$, r∈{2k−1,2k}, α>1,

$$ { } E_{2n,2k-1}^S(f):=\inf_{s\in\mathcal{S}_{2n,2k-1}} \|f-s\| \le\varOmega_\alpha^* (4/\pi) \gamma_{r}^* \omega_r \biggl(f,\frac{\alpha\pi}{n} \biggr). $$

(5.4)

Note that Lemma 8.1 and Theorem 8.2 from [9] provide the lower estimate for the constants in (5.4) equal to $c_{r}\gamma_{r}^{*}$. Therefore, the estimate (5.4) is asymptotically sharp. For example, for α=2,

$$\biggl(1-\frac{1}{r+1} \biggr)\gamma_{r}^* \le \sup_{f\in{ C(\mathbb{T})}}\frac{E_{2n, 2k-1}^S (f)}{\omega_{r}(f,\frac{2\pi}{n})} \le 8.1 \gamma_{r}^*, \quad r\in\{2k-1,2k\}, \ 3r< 2n. $$

Appendix

1.1 A.1 Proof of Some Inequalities for Lemma 1

The estimates look simple enough, and one can check them by symbolic computations. The actual proof of these estimates is not as simple as it may seem at first glance.

Recall the notation:

$$ b_{i,k}={\frac{2}{\binom{2k}{k}}}\sum_{j=i+1}^k\binom{2k}{k-j} (-1)^{j+1} \frac{1}{j} \biggl(1-\frac{i}{j} \biggr),\quad i=0,\dots,k-1, \qquad b_{k,k}=0. $$

Define

$$ b_{i,\infty}:=2\sum_{j=i+1}^\infty(-1)^{j+1} \frac{1}{j} \biggl( 1- \frac{i}{j} \biggr). $$

Lemma A

Let $k\in\mathbb{N}$, k≥2. Then

$$\begin{aligned} & |b_{i,k}| =(-1)^i\,b_{i,k}<(-1)^i b_{i,k+1}<(-1)^i b_{i,\infty} \quad\textit{for}\ 0 \le{i}\le{k-1}, \end{aligned}$$

(A.1)

$$\begin{aligned} & |b_{i,k}| >|b_{i+1,k}|\quad\mbox{for}\ 0\le{i} \le{k-1}, \end{aligned}$$

(A.2)

$$\begin{aligned} & \sum_{i=0}^{\infty}|b_{i,\infty}|<2. \end{aligned}$$

(A.3)

Proof

Let 0≤δ≤1/2. Introduce an auxiliary notation

$$\begin{aligned} b_{i,k}(\delta) & :=\frac{2}{\binom{2k}{k}} \sum _{j=i+1}^k\binom{2k}{k-j}(-1)^{j+i+1} \frac{1}{j} \biggl(1-\frac {i+\delta}{j} \biggr), \quad i=0,\dots,k-1, \\ b_{i,\infty}(\delta)&:=2\sum_{j=i+1}^\infty(-1)^{j+i+1}\frac{1}{j} \biggl(1-\frac{i+\delta}{j} \biggr). \end{aligned}$$

It is clear that

$$ b_{i,k}(0)=(-1)^{i}b_{i,k}, \qquad b_{i,\infty}(0)=(-1)^{i}b_{i,\infty}. $$

(A.4)

We first show that for arbitrary $k\in\mathbb{N}$, we have inequalities

$$ 0<b_{i,k}(\delta)<b_{i,k+1}( \delta)<b_{i,\infty}(\delta)\quad\mbox{if}\ 0\le{i}\le{k-1},\ {0\le \delta\le{1}/{2}}. $$

(A.5)

By (A.4), these inequalities turn into (A.1) if δ=0. Further, we will show that (A.5) implies (A.2) if δ=1/2. In order to prove (A.5), let

$$ d_{i,k}(\delta):=\binom{2k}{k} \frac{b_{i,k}(\delta)}{2}=\sum_{j=i+1}^{k} (-1)^{j+i+1}\binom{2k}{k+j}\frac{1}{j} \biggl(1- \frac{i+\delta}{j} \biggr). $$

Observe that

$$\begin{aligned} \frac{\binom{2k+2}{k+1}}{\binom{2k}{k}} &= \frac{(2k+2)!}{(k+1)! (k+1)!} \frac{k! k!}{(2k)!} = \frac{(2k+1)(2k+2)}{(k+1)^2}=4-\frac{2}{k+1}, \\ \binom{2k+2}{k+1+j} &=\binom{2k}{k+j-1}+2\binom{2k}{k+j} + \binom{2k}{k+j+1}. \end{aligned}$$

Thus,

$$\begin{aligned} b_{i,k+1}(\delta)-b_{i,k}(\delta)&=\frac{2}{\binom{2k+2}{k+1}} \biggl\{d_{i,k+1}(\delta)- \biggl(4-\frac{2}{k+1} \biggr)d_{i,k}( \delta ) \biggr\}, \\ d_{i,k+1}(\delta)- \biggl(4-\frac{2}{k+1} \biggr)d_{i,k}( \delta) &=(-1)^{k+2+i}\frac{1}{k+1} \biggl(1-\frac{i+\delta}{k+1} \biggr) \\ &\quad {}+\sum_{j=i+1}^k(-1)^{i+j+1} \biggl \{\binom{2k}{k+j-1} \\ &\quad {} - \biggl(2-\frac{2}{k+1} \biggr)\binom{2k}{k+j} \\ &\quad {}+\binom{2k}{k+j+1} \biggr\} \frac{1}{j} \biggl(1-\frac{i+\delta}{j} \biggr). \end{aligned}$$

The following equality:

$$\begin{aligned} & \binom{2k}{k+j-1}- \biggl(2-\frac{2}{k+1} \biggr)\binom{2k}{k+j}+ \binom{2k}{k+j+1} \\ &\quad =\frac{{(2k+1)!}}{(k+j)! (k-j)!}\;\frac{2j^2}{{ \{(k+1)^2-j^2 \}}(k+1)} \\ &\quad =\frac{(2k+1)!\,j^2}{(k+j)!(k-j)!\,(k+1)^2} \biggl(\frac{1}{k+1-j}+\frac{1}{k+1+j} \biggr) \end{aligned}$$

is a key ingredient. It implies

$$\begin{aligned} & d_{i,k+1}(\delta)- \biggl(4-\frac{2}{k+1} \biggr)d_{i,k}( \delta) \\ &\quad = \frac{(2k+1)!}{(k+1)^2} \Biggl[\sum_{j=i+1}^k \frac{(-1)^{i+j+1}(j-i-\delta)}{(k+j)!(k-j)!} \biggl(\frac{1}{k+1-j}+\frac{1}{k+1+j} \biggr) \\ &\qquad {}+ \frac{(-1)^{k+i+2}(k+1-i-\delta)}{(2k+1)!} \Biggr]. \end{aligned}$$

Let the expression in the square brackets be denoted by A _i,k (δ). After simplification, it becomes

$$ A_{i,k}(\delta)=S_1(\delta)+S_2( \delta)+\frac{(-1)^{k+i+2}(k+1-i-\delta)}{(2k+1)!}, $$

where

$$S_1(\delta)=\sum_{j=i+1}^k \frac{(-1)^{i+j+1}(j-i-\delta )}{(k+j)!(k+1-j)!},\qquad S_2(\delta)=\sum _{j=i+1}^k\frac{(-1)^{i+j+1}(j-i-\delta)}{(k+j+1)!(k-j)!}. $$

By change of variables ν=j+1, j=ν−1 in S ₂(δ), we obtain

$$S_2(\delta)=-\sum_{\nu=i+2}^{k+1} \frac{(-1)^{i+\nu+1}(\nu-i-1-\delta )}{(k+\nu)!(k+1-\nu)!}. $$

Therefore,

$$\begin{aligned} A_{i,k}(\delta)& =\frac{1-\delta}{(k+i+1)!(k-i)!}+\sum_{j=i+2}^k \frac{(-1)^{i+j+1}(j-i-\delta)}{(k+j)!(k+1-j)!} \\ &\quad {}-\sum_{\nu=i+2}^{k}\frac{(-1)^{i+\nu+1}(\nu-i-1-\delta)}{(k+\nu )!(k+1-\nu)!} -\frac{(-1)^{i+k+2}(k-i-\delta)}{(2k+1)!} \\ &\quad {}+\frac{(-1)^{k+i+2}(k+1-i-\delta)}{(2k+1)!} \\ & =\frac{1-\delta}{(k+i+1)!(k-i)!}+\sum_{j=i+2}^k \frac{(-1)^{i+j+1}}{(k+j)!(k+1-j)!}+\frac{(-1)^{i+k+2}}{(2k+1)!}. \end{aligned}$$

Now

$$\begin{aligned} \begin{aligned} A_{i,k}(\delta)& =\frac{-\delta}{(k+i+1)!(k-i)!}+\sum_{j=i+1}^{k+1} \frac{(-1)^{i+j+1}}{(k+j)!(k+1-j)!} \\ &= A_{i,k}(0)-\frac{\delta}{(k+i+1)!(k-i)!}. \end{aligned} \end{aligned}$$

A nice formula for A _i,k (0) (see Lemma B below) yields

$$ A_{i,k}(\delta)=\frac{k(1-2\delta)+i+1-\delta}{(2k+1)(k+i+1)!(k-i)!}. $$

(A.6)

It follows from (A.6) that b _i,k+1(δ)−b _i,k (δ) is positive for δ≤1/2.

Let 0≤δ≤1/2, k=2^r, and r=n(i+1), n≥2. The estimates

$$\begin{aligned} \frac{1}{2} \bigl \vert b_{i,\infty}(\delta) - b_{i,k}(\delta) \bigr \vert & \le\Biggl \vert {\sum_{j=i+1}^{r}} (-1)^{j+i+1} \frac{1}{j} \biggl(1-\frac {i+\delta}{j} \biggr) \biggl( 1 - \frac{\binom{2k}{k-j}}{\binom{2k}{k}} \biggr)\Biggr \vert \\ &\quad {}+ \Biggl \vert \sum_{j=r+1}^{\infty} (-1)^{j+i+1} \frac{1}{j} \Biggr \vert + \Biggl \vert {\sum_{j=r+1}^{\infty}} (-1)^{j+i+1} \frac{1}{j} \ \frac {i+\delta}{j} \Biggr \vert \\ &\quad {}+ \Biggl \vert {\sum_{j=r+1}^{k}} (-1)^{j+i+1} \frac{1}{j} \frac{\binom {2k}{k-j}}{\binom{2k}{k}} \Biggr \vert \\ &\quad {}+ \Biggl \vert {\sum_{j=r+1}^{k}} (-1)^{j+i+1} \frac{1}{j} \frac{i+\delta}{j} \frac{\binom{2k}{k-j}}{\binom{2k}{k}} \Biggr \vert , \\ \binom{2k}{k-j} {\binom{2k}{k}}^{-1} & = \frac{k(k-1)\cdots (k-j+1)}{(k+1)(k+2) \cdots(k+j)}> \biggl(1-\frac{2j-1}{k+j} \biggr)^j >1-\frac{2j^2}{k} \end{aligned}$$

imply

$$\lim_{k\to\infty} b_{i,k}(\delta) = b_{i, \infty}( \delta). $$

The inequalities (A.5) are proved. It was mentioned above that (A.5) contains (A.1) as a particular case because

$$0<b_{i,k+1}(0)-b_{i,k}(0)=(-1)^i (b_{i,k+1}-b_{i,k} ) $$

and

$$0<\frac{2}{\binom{2(i+1)}{i+1}(i+1)^2}=(-1)^{i}b_{i,i+1}<\cdots <(-1)^{i}b_{i,\infty}. $$

Thus, (A.1) is proved. It is a principal inequality, which implies

$$\frac{|b_{i,\infty}|}{2}=\frac{(-1)^i b_{i,\infty}}{2} =:c_i\mbox{{=}}\sum _{j=i+1}^\infty(-1)^{i+j+1}\,\frac{1}{j} \biggl(1- \frac{i}{j} \biggr)>0 $$

and

$$c_i+c_{i+1}=\sum_{j=1}^\infty \frac{(-1)^{j+1}}{(j+i)^2}. $$

Now

$$\begin{aligned} \sum_{i=0}^\infty c_i & = (c_0 + c_1) + (c_2 + c_3) + \cdots+ (c_{2i}+ c_{2i+1})+ \cdots \\ & =\sum_{i=0}^\infty\sum _{j=1}^\infty(-1)^{j+1} \frac{1}{(j+2i)^2}= \sum_{j=1}^\infty(-1)^{j+1} \sum _{i=0}^\infty \frac{1}{(j+2i)^2}<1, \end{aligned}$$

and (A.3) follows. In order to derive (A.2), we note that the first inequality in (A.1) implies

$${b}_{i,k}(1/2)=\frac{|b_{i,k}|-|b_{i+1,k}|}{2} \quad\mbox{and}\quad {b}_{i,\infty}(1/2)=\frac{|b_{i,\infty}|-|b_{i+1,\infty}|}{2}. $$

From this and (A.5), we get (A.2). Lemma A is proved. □

Lemma B

$$A_{i,k}(0):=\sum_{j=i+1}^{k+1} \frac{(-1)^{i+j+1}}{(k+j)!(k+1-j)!}=\frac {k+i+1}{(k+i+1)!(k-i)!(2k+1)}. $$

Proof

We need to prove that

$$(k+i+1)!(k-i)!\sum_{j=i+1}^{k+1} \frac{(-1)^{i+j+1}}{(k+j)! (k+1-j)!}=1-\frac{k-i}{2k+1}. $$

An equivalent form is

$$\begin{aligned} & 1-\frac{k-i}{k+i+2}+\frac{(k-i)(k-i-1)}{(k+i+2)(k+i+3)}-\cdots+(-1)^{k-i} \frac{(k-i)!}{(k+i+2)\cdots{(k+k+1)}} \\ &\quad =1-\frac{(k-i)}{2k+1}. \end{aligned} $$

For $k\in\mathbb{N}$, i≤k−1, we have the equality

$$ \begin{aligned}[b] \frac{1}{2k+1} & =\frac{1}{k+i+2}-\frac{k-i-1}{(k+i+2)(k+i+3)}+ \cdots \\ &\quad {}+(-1)^{k-i-1}\frac{(k-i-1)!}{(k+i+2)\cdots(2k+1)}. \end{aligned} $$

(A.7)

One can prove (A.7) by induction on j=k−i−1 for fixed k:

$$\begin{aligned} & \frac{1}{k+i+2}-\frac{k-i-1}{k+i+2} \biggl(\frac{1}{k+i+3}+ \cdots+(-1)^{k-i-2} \frac{(k-i-2)!}{(k+i+3)\cdots(2k+1)} \biggr) \\ &\quad =\frac{1}{k+i+2}-\frac{k-i-1}{k+i+2} \biggl(\frac{1}{2k+1} \biggr)= \frac{1}{2k+1}. \end{aligned} $$

 □

1.2 A.2 Proof of Lemma 5. Computations

First, we consider the case k=1 in Lemma 5.

A.2.1

To prove inequality

$$ \biggl( \frac{ t^{2}}{ \int_{{\mathbb{R}}} \sin^{2}(tu/2) {\phi_h}(u)\, du} \biggr)^{\prime\prime}_{tt} = \biggl( \frac{t^2}{1-\sin^2(th/2)/(th/2)^2} \biggr)^{\prime\prime}_{tt}> 0, $$

it is sufficient to prove the convexity of the function

$$\frac{x^4}{x^2- \sin^2(x)} = \frac{x}{x+\sin x} \cdot\frac{x^3}{x - \sin x} $$

on the interval (0,π). The condition

$$\biggl(\frac{x}{x+\sin x} \biggr)^{\prime\prime}_{xx}>0 $$

is equivalent to the inequality

$$\varphi_1 (x):=\frac{3}{2} x+2x \cos x + \bigl(x^2-2 \bigr)\sin x + \frac{1}{2} x \cos2x -\sin2x >0. $$

We have φ ₁(0)=φ ₁(π)=0, and the inequality follows from the power expansions of the functions φ ₁(x), φ ₁(π−x) at 0:

$$\begin{aligned} \varphi_1(x) & > x^3 \biggl(\frac{2}{3} - \frac{1}{30} x^2 - \frac{11}{840} x^4 \biggr) >0, \quad x \in(0, 3\pi/4), \\ \varphi_1(\pi-x)& >x \biggl(\pi^2 - 2\pi x - \frac{\pi^2}{6} x^2 \biggr)>0, \quad x \in(0, \pi/4). \end{aligned}$$

The proof of the inequality

$$\biggl(\frac{x^3}{x-\sin x} \biggr)^{\prime\prime}_{xx}>0, \quad x \in(0, \pi), $$

is similar. We have

$$\begin{aligned} \varphi_2(x) & := 3 +\frac{7}{2} x^2 + 2 x^2 \cos x +\bigl(-6x - x^3\bigr) \sin x + \bigl(-3 + x^2/2\bigr) \cos2x \\ & \phantom{{}:={}} {}- 3x \sin2x >0, \end{aligned} $$

and

$$\varphi_2(x) > \frac{x^8}{360} \biggl(1 + \frac{x^2}{140} - \frac{29 x^4}{5040} \biggr) > 0, \quad x \in(0, \pi). $$

A.2.2

Below we will prove the following inequality:

$$I(a):= 2\int_{\max(0, a-\pi)}^{a/2} \sin^2(u) \sin^2(a-u) F_2^*(u,a-u) \, du >0, \quad 0<a< 2\pi, $$

where

$$\begin{aligned} & F_2^{*}(u,s)=2\sin(s)\varphi(s)\sin(u)\varphi(u)- \bigl( \sin(s)\varphi (u)-\sin(u)\varphi(s) \bigr)^2, \\ &\quad \varphi(u):= \sin u-u\cos u. \end{aligned} $$

We will show that I(a)>0 for 0<a<2π (see Fig. 2) by direct calculations. The proof will be divided into several steps.

• 1. For 0<a≤π, we obtain

  $$I(a)= \varphi_3(a) + \varphi_4(a), $$

  where

  $$\begin{aligned} \varphi_3(a) & := \frac{87}{256} a- \frac{1}{32}a^3+ \biggl(\frac{179}{576} a - \frac{1}{48} a^3 \biggr) \cos(2a)+ \biggl(-\frac{1145}{3456} + \frac{1}{8} a^2 \biggr)\sin(2a), \\ \varphi_4(a) & :=- \frac{19}{6144} a \cos(4a)+ \biggl( \frac{835}{221184}-\frac{1}{1536} a^2 \biggr)\sin(4a). \end{aligned}$$

  Consider the following cases.

  • 1.1. Suppose that $0<a \le\sqrt{15}/2$. The Taylor expansion of I(a) gives

    $$\begin{aligned} I(a) & = {\frac{1}{405405}} {a}^{13}-{\frac{4}{6081075}} {a}^{15}+{\frac{101}{1206079875}} {a}^{17} \\ &\quad {}-{\frac{248}{36395233875}}{a}^{19}+ \cdots. \end{aligned} $$

    It is easily seen that

    $$I(a)>\frac{a^{13}}{405405} \biggl( 1 -{\frac{4}{15}} {a}^2 \biggr) \ge 0, \quad a \in(0, \sqrt{15}/2]. $$

  • 1.2. In the case $\sqrt{15}/2 <a \le\pi$, the inequality I(a)>0 follows from the estimates:

    $$\begin{aligned} \varphi_3(a)& >0,\quad a \in[\sqrt{15}/2,3\pi/4); \qquad \varphi_3(a)>0.01, \quad a \in[3\pi/4, \pi); \\ \varphi_4(a)& >0, \quad a \in[\sqrt{15}/2,3\pi/4); \qquad \varphi_4(a)>-0.01, \quad a \in[3\pi/4,\pi). \end{aligned} $$

• 2. Now we turn to the case π<a<2π. Let us compute I ₁(b):=I(2π−b):

  $$\begin{aligned} I_1(b)& =\frac{1}{32} \bigl(3\pi+\bigl(87/8-3\pi^{2}\bigr)b-3\pi b^{2}+b^{3} \bigr) \\ &\quad {}+ \biggl(- \frac{\pi}{18} - \frac{\pi^{2}b}{8} + \frac{179b}{576} + \frac{\pi b^{2}}{8}- \frac{b^{3}}{48} \biggr) \cos(2b) \\ &\quad {}+ \biggl(\frac{\pi^{2}}{16} - \frac{1145}{3456} - \frac{11b\pi}{48} + \frac{b^{2}}{8} \biggr) \sin(2b) \\ &\quad {}+ \biggl( - \frac{11\pi}{288} - \frac{\pi^{2}b}{64} - \frac{19b}{6144} + \frac{\pi b^{2}}{64} \biggr)\cos(4b) \\ &\quad {} + \biggl(\frac{7\pi^{2}}{256} + \frac{835}{221184} - \frac{37b\pi}{768} - \frac{b^{2} }{1536} \biggr)\sin(4b). \end{aligned}$$

  We will show that I ₁(b)>0 for 0<b<π. Consider the following cases.

  • 2.1. Assume that 0<b<π/2. The following is a series expansion of I ₁(b):

    $$\begin{aligned} I_1(b) & =\frac{1}{105} \pi^2 b^7 - \frac{2}{315} \pi^2 b^9 + \frac{2}{945} \pi b^{10}+ \frac{29}{17325}\pi^2 b^{11} \\ &\quad {}- \frac{127}{155925} \pi b^{12}+ \biggl(\frac{1}{405405} - \frac{514}{2027025} \pi^2 \biggr) b^{13} + \cdots. \end{aligned}$$

    Under the above conditions on b, the omitted terms are positive. Therefore, it is sufficient to prove that polynomial p ₆(b):=I ₁(b)/b ⁷ is positive on (0,π/2). It is easy to check that derivative $p'_{6}(b)<0$, b∈(0,π/2) and that p ₆(π/2)>0.

  • 2.2. For π/2<b<3π/4, let I _1,1(c):=I ₁(c+π/2):

    $$\begin{aligned} I_{1,1}(c)&=\frac{135\,\pi}{512} - \frac{7 \pi^3 }{256} + \frac{87 c}{256} - \frac{3 \pi^2 c }{128} + \frac{3 \pi c^2}{64} - \frac{c^3}{32} \\ &\quad {}+ \biggl( - \frac{115 \pi}{1152} + \frac{13 \pi^3}{384} - \frac{179 c}{576} + \frac{\pi^2 c}{64} - \frac{3\pi c^2}{32} + \frac{c^3}{48} \biggr) \cos(2c) \\ &\quad {}+ \biggl( \frac{1145}{3456}+\frac{\pi^2}{48} + \frac{5 \pi c}{48} - \frac{c^2}{8} \biggr) \sin(2c) \\ &\quad {}+ \biggl(- \frac{1465 \pi}{36864} - \frac{\pi^3}{256} - \frac{19 c}{6144} + \frac{\pi c^2}{64} \biggr)\cos(4c) \\ &\quad {}+ \biggl(\frac{835}{221184}+\frac{19\pi^2}{6144}- \frac{25 \pi c}{512} - \frac{c^2}{1536} \biggr) \sin(4c). \end{aligned}$$

    To prove the estimate I _1,1(c)>0, we can take five terms in the power expansion of I _1,1:

    $$\begin{aligned} I_{1,1}(c) & > \frac{\pi^3}{384} + \frac{1525 \pi}{12288} + \biggl( \frac{71\pi^2}{1536} + \frac{19}{27} \biggr) c + \biggl(\frac{767 \pi}{1536} - \frac{7 \pi^3}{192} \biggr) c^2 \\ &\quad {}+ \biggl(-\frac{53 \pi^2}{576} - \frac{8}{81} \biggr) c^3+ \biggl(- \frac{53 \pi}{1152} - \frac{11 \pi^3}{576} \biggr) c^4 > 0, \\ &\qquad\ c \in (0,\pi/4). \end{aligned} $$

  • 2.3. In the case 3π/4≤a<π, we let I _1,2(d):=I ₁(π−d), and in the same way we obtain the inequality

    $$\begin{aligned} I_{1,2}(d) & > \biggl(\frac{11935\,\pi}{18432}-\frac{5\pi^3}{96} \biggr)+ \frac {35\pi^2 d}{384}+ \biggl(\frac{\pi^3}{24}-\frac{595\pi}{2304} \biggr)d^2 \\ &\quad {}-\frac{5\pi^2}{144} d^3 + \biggl( -\frac{35\pi}{1728} - \frac{\pi^3}{72} \biggr) d^4 -\frac{\pi^2 d^5}{72} > 0, \quad d \in(0,\pi/4]. \end{aligned} $$

Fig. 2

Functions I(a) and $\frac{10^{11}I(a)}{4a^{13}(2\pi -a)^{7}}> I(a)$, 0<a<2π