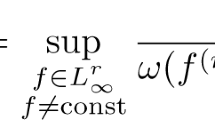For any \( \omega \) > 0, β \( \epsilon \) (0, 2\( \omega \)), and any measurable set B \( \epsilon \) I d := [0,d], μB = β, we obtain the following sharp inequality of the Remez type:
on the classes S φ (ω) of functions x with minimal period d(d ≥ 2ω) and a given sine-shaped 2\( \omega \)-periodic comparison function '. In particular, we prove sharp Remez-type inequalities on the Sobolev classes of differentiable periodic functions. We also obtain inequalities of the indicated type in the spaces of trigonometric polynomials and polynomial splines.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
E. Remes, “Sur une propriété extrémale des polynomes de Tchebychef,” Zap. Nauk.-Doslid. Inst. Mat. Mekh. Kharkov. Mat. Tov., Ser. 4, 13, Issue 1, 93–95 (1936).
M. I. Ganzburg, “On a Remez-type inequality for trigonometric polynomials,” J. Approxim. Theory, 164, 1233–1237 (2012).
E. Nursultanov and S. Tikhonov, “A sharp Remez inequality for trigonometric polynomials,” Constr. Approxim., 38, 101–132 (2013).
P. Borwein and T. Erdelyi, Polynomials and Polynomial Inequalities, Springer, New York (1995).
M. I. Ganzburg, “Polynomial inequalities on measurable sets and their applications,” Constr. Approxim., 17, 275–306 (2001).
B. Bojanov and N. Naidenov, “An extension of the Landau–Kolmogorov inequality. Solution of a problem of Erdos,” J. Anal. Math., 78, 263–280 (1999).
V. A. Kofanov, “Sharp upper bounds for the norms of functions and their derivatives in the classes of functions with given comparison function,” Ukr. Mat. Zh., 63, No. 7, 969–984 (2011); English translation: Ukr. Math. J., 63, No. 7, 1118–1135 (2011).
A. N. Kolmogorov, “On the inequalities between the upper bounds of successive derivatives on an infinite interval,” in: Selected Works, Mathematics and Mechanics [in Russian], Nauka, Moscow (1985), pp. 252–263.
A. A. Ligun, “Inequalities for upper bounds of functionals,” Anal. Math., 2, No. 1, 11–40 (1976).
N. P. Korneichuk, V. F. Babenko, V. A. Kofanov, and S. A. Pichugov, Inequalities for the Derivatives and Their Applications [in Russian], Naukova Dumka, Kiev (2003).
A. Zygmund, Trigonometric Series [Russian translation], Vol. 2, Mir, Moscow (1965).
A. P. Calderon and G. Klein, “On an extremum problem concerning trigonometrical polynomials,” Stud. Math., 12, 166–169 (1951).
L. V. Taikov, “One generalization of the Bernstein inequality,” Tr. Mat. Inst. Akad. Nauk SSSR, 78, 43–47 (1965).
V. M. Tikhomirov, “Widths of the sets in functional spaces and the theory of best approximations,” Usp. Mat. Nauk, 15, No. 3, 81–120 (1960).
A. A. Ligun, “Sharp inequalities for spline functions and the best quadrature formulas for some classes of functions,” Mat. Zametki, 19, No. 6, 913–926 (1976).
Author information
Authors and Affiliations
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 68, No. 2, pp. 227–240, February, 2016.
Rights and permissions
About this article
Cite this article
Kofanov, V.A. Sharp Remez-Type Inequalities for Differentiable Periodic Functions, Polynomials, and Splines. Ukr Math J 68, 253–268 (2016). https://doi.org/10.1007/s11253-016-1222-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-016-1222-5