Optimal subsampling design for polynomial regression in one covariate

Abstract

Improvements in technology lead to increasing availability of large data sets which makes the need for data reduction and informative subsamples ever more important. In this paper we construct D-optimal subsampling designs for polynomial regression in one covariate for invariant distributions of the covariate. We study quadratic regression more closely for specific distributions. In particular we make statements on the shape of the resulting optimal subsampling designs and the effect of the subsample size on the design. To illustrate the advantage of the optimal subsampling designs we examine the efficiency of uniform random subsampling.

1 Introduction

Data Reduction is a major challenge as technological advances have led to a massive increase in data collection to a point where traditional statistical methods fail or computing power can not keep up. In this case we speak of big data. We typically differentiate between the case where the number of covariates is much larger than the number of observations and the case where the massive amount of observations is the problem. The first case is well studied, most notably by Tibshirani (1996) introducing LASSO, which utilizes $\ell _{1}$ penalization to find sparse parameter vectors, thus fusing subset selection and ridge regression. The second case, often referred to as massive data, can be tackled in two ways. Firstly in a probabilistic fashion, creating random subsamples in a non-uniform manner. Prominent studies include Drineas et al. (2006), Mahoney (2011) and Ma et al. (2014). They present subsampling methods for linear regression models called algorithmic leveraging that sample according to probabilities based on the normalized statistical leverage scores of the covariate matrix. More recently Dereziński and Warmuth (2018) study volume sampling, where subdata is chosen proportional to the squared volume of the parallelepiped spanned by its observations. Conversely to these probabilistic methods one can select subdata by applying deterministic rules. Shi and Tang (2021) present such a method, that maximizes the minimal distance between two observations in the subdata. Wang et al. (2021) propose orthogonal subsampling inspired by orthogonal arrays. Most prominently, Wang et al. (2019) introduce the information-based optimal subdata selection (IBOSS) to tackle big data linear regression in a deterministic fashion based on D-optimality.

In this paper we study D-optimal subsampling designs for polynomial regression in one covariate, where the goal is to select a percentage $\alpha$ of the full data that maximizes the determinant of the information matrix. For the conventional study of approximate designs in this setting we refer to Gaffke and Heiligers (1996). Heiligers and Schneider (1992) consider specifically cubic regression on a ball. We consider D-optimal designs with measure $\alpha$ that are bounded from above by the distribution of the known covariate. Such directly bounded designs were first studied by Wynn (1977) and Fedorov (1989). Pronzato (2004) considers this setting using a form of the subsampling design standardized to one and bounded by $\alpha ^{-1}$ times the distribution of the covariates. More recently, Pronzato and Wang (2021) studies the same in the context of sequential subsampling. For the characterization of the optimal subsampling designs we make use of an equivalence theorem by Sahm and Schwabe (2001). This equivalence theorem enables us to construct such subsampling designs for various settings of the distributional assumptions on the covariate. Here we will only look at distributions of the covariate that are invariant to a sign change, i.e. symmetric about the vertical axis. We discuss the shape of D-optimal subsampling subsampling designs for polynomial regression of degree q first. We then study quadratic regression under several distributional assumptions more closely, after showing two examples for simple linear regression. In particular we take a look at the percentage of mass of the optimal subsampling design on the outer intervals compared to the inner one, which changes drastically given the distribution of the covariate, particularly for heavy-tailed distributions. In addition we examine the efficiency of uniform random subsampling to illustrate the advantage of the optimal subsampling designs. All numerical results are obtained by the Newton method implemented in the R package nleqslv by Hasselman (2018). All relevant R scripts are available on a GitHub repository https://github.com/TorstenReuter/polynomial_regression_in_one_covariate.

The rest of this paper is organized as follows. In Sect. 2 we specify the polynomial model. In Sect. 3 we introduce the concept of continuous subsampling designs and give characterizations for optimization. In Sects. 4 and 5 we present optimal subsampling designs in the case of linear and quadratic regression, respectively, for various classes of distributions of the covariate. Section 6 contains some efficiency considerations showing the strength of improvement of the performance of the optimal subsampling design compared to random subsampling. The paper concludes with a discussion in Sect. 7. Proofs are deferred to an Appendix.

2 Model specification

We consider the situation of pairs $(x_i,y_i)$ of data, where $y_i$ is the value of the response variable $Y_i$ and $x_i$ is the value of a single covariate $X_i$ for unit $i = 1,\dots ,n$, for very large numbers of units n. We assume that the dependence of the response on the covariate is given by a polynomial regression model

$$\begin{aligned} Y_{i} =\beta _0 + \beta _1 X_{i} + \beta _2 X_{i}^2 + \dots + \beta _q X_{i}^q + \varepsilon _{i} \end{aligned}$$

with independent, homoscedastic random errors $\varepsilon _i$ having zero mean (${\mathbb {E}}(\varepsilon _i)=0$, ${\text {Var}}(\varepsilon _i)=\sigma _\varepsilon ^2>0$). The largest exponent $q \ge 1$ denotes the degree of the polynomial regression, and $p=q+1$ is the number of regression parameters $\beta _0, \dots ,\beta _q$ to be estimated, where, for each $k= 1,\dots ,q$, the parameter $\beta _k$ is the coefficient for the kth monomial $x^k$, and $\beta _0$ denotes the intercept. For example, for $q=1$, we have ordinary linear regression, $Y_{i} =\beta _0 + \beta _1 X_{i} + \varepsilon _{i}$, with $p=2$ parameters $\beta _0$ (intercept) and $\beta _1$ (slope) and, for $q=2$, we have quadratic regression, $Y_{i} =\beta _0 + \beta _1 X_{i} + \beta _2 X_{i}^2 + \varepsilon _{i}$, with $p=3$ and an additional curvature parameter $\beta _2$. Further, we assume that the units of the covariate $X_i$ are identically distributed and that all $X_i$ and random errors $\varepsilon _{i^\prime }$ are independent.

For notational convenience, we write the polynomial regression as a general linear model

$$\begin{aligned} Y_{i} = \textbf{f}(X_{i})^{\top }\varvec{\beta }+ \varepsilon _{i} , \end{aligned}$$

where $\textbf{f}(x) = (1, x, \dots , x^{q})^{\top }$ is the p-dimensional vector of regression functions and $\varvec{\beta }= (\beta _0, \beta _1,\dots ,\beta _q)^\top$ is the p-dimensional vector of regression parameters.

3 Subsampling design

We are faced with the problem that the responses $Y_{i}$ are expensive or difficult to observe while the values $x_i$ of all units $X_i$ of the covariate are available. To overcome this problem, we consider the situation that the responses $Y_{i}$ will be observed only for a certain percentage $\alpha$ of the units ($0<\alpha <1$) and that these units will be selected on the basis of the knowledge of the values $x_{i}$ of the covariate for all units. As an alternative motivation, we can consider a situation where all pairs $(x_{i}, y_{i})$ are available but parameter estimation is computationally feasible only on a percentage $\alpha$ of the data. In either case we want to find the subsample of pairs $(x_{i}, y_{i})$ that yields the most precise estimation of the parameter vector $\varvec{\beta }$.

To obtain analytical results, the covariate $X_{i}$ is supposed to have a continuous distribution with density $f_{X}(x)$, and we assume that the distribution of the covariate is known. The aim is to find a subsample of this distribution that covers a percentage $\alpha$ of the distribution and that contains the most information. For this, we will consider continuous designs $\xi$ as measures of mass $\alpha$ on ${\mathbb {R}}$ with density $f_{\xi }(x)$ bounded by the density $f_X(x)$ of the covariate $X_i$ such that $\int f_{\xi }(x)\mathop {}\!\textrm{d}x = \alpha$ and $f_{\xi }(x) \le f_X(x)$ for all $x \in {\mathbb {R}}$. A subsample can then be generated according to such a continuous design by accepting units i with probability $f_\xi (x_i)/f_X(x_i)$.

For a continuous design $\xi$, the information matrix $\textbf{M}(\xi )$ is defined as $\textbf{M}(\xi ) = \int \textbf{f}(x)\textbf{f}(x)^\top f_\xi (x) \mathop {}\!\textrm{d}x$. In the present polynomial setup, $\textbf{M}(\xi ) = \left( m_{j + j^\prime }(\xi )\right) _{j = 0, \dots , q}^{j^\prime = 0, \dots , q}$, where $m_k = \int x^k f_\xi (x) \mathop {}\!\textrm{d}x$ is the kth moment associated with the design $\xi$. Thus, it has to be required that the distribution of $X_i$ has a finite moment ${\mathbb {E}}(X_i^{2q})$ of order 2q in order to guarantee that all entries in the information matrix $\textbf{M}(\xi )$ exist for all continuous designs $\xi$ for which the density $f_\xi (x)$ is bounded by $f_X(x)$.

The information matrix $\textbf{M}(\xi )$ measures the performance of the design $\xi$ in the sense that the covariance matrix of the least squares estimator ${{\hat{\varvec{\beta }}}}$ based on a subsample according to the design $\xi$ is proportional to the inverse $\textbf{M}(\xi )^{-1}$ of the information matrix $\textbf{M}(\xi )$ or, more precisely, $\sqrt{\alpha n}({{\hat{\varvec{\beta }}}}-\varvec{\beta })$ is normally distributed with mean zero and covariance matrix $\sigma _\varepsilon ^2\textbf{M}(\xi )^{-1}$, at least asymptotically. Note that for continuous designs $\xi$ the information matrix $\textbf{M}(\xi )$ is always of full rank and, hence, the inverse $\textbf{M}(\xi )^{-1}$ exists. Based on the relation to the covariance matrix, it is desirable to maximize the information matrix $\textbf{M}(\xi )$. However, as well-known in design optimization, maximization of the information matrix cannot be achieved uniformly with respect to the Loewner ordering of positive-definiteness. Thus, commonly, a design criterion which is a real valued functional of the information matrix $\textbf{M}(\xi )$ will be maximized, instead. We will focus here on the most popular design criterion in applications, the D-criterion, in its common form $\log (\det (\textbf{M}(\xi )))$ to be maximized. Maximization of the D-criterion can be interpreted in terms of the covariance matrix to be the same as minimizing the volume of the confidence ellipsoid for the whole parameter vector $\varvec{\beta }$ based on the least squares estimator or, equivalently, minimizing the volume of the acceptance region for a Wald test on the whole model. The subsampling design $\xi ^{*}$ that maximizes the D-criterion $\log (\det (\textbf{M}(\xi )))$ will be called D-optimal, and its density is denoted by $f_{\xi ^{*}}(x)$.

To obtain D-optimal subsampling designs, we will make use of standard techniques coming from constrained convex optimization and symmetrization. For convex optimization we employ the directional derivative

$$\begin{aligned} F_{D}(\xi , \eta ) = \lim _{\epsilon \rightarrow 0^+} \frac{1}{\epsilon } \left( \log (\det (\textbf{M}((1 - \epsilon ) \xi + \epsilon \eta ))) - \log (\det (\textbf{M}(\xi )))\right) \end{aligned}$$

of the D-criterion at a design $\xi$ with non-singular information matrix $\textbf{M}(\xi )$ in the direction of a design $\eta$, where we allow here $\eta$ to be a general design of mass $\alpha$ that has not necessarily a density bounded by $f_{X}(x)$. In particular, $\eta = \xi _x$ may be a one-point design which assigns all mass $\alpha$ to a single setting x in ${\mathbb {R}}$. Evaluating of the directional derivative yields $F_{D}(\xi , \eta ) = p - {\text {trace}}(\textbf{M}(\xi )^{-1}\textbf{M}(\eta ))$ (compare Silvey 1980, Example 3.8) which reduces to $F_{D}(\xi , \xi _x) = p - \alpha \textbf{f}(x)^\top \textbf{M}(\xi )^{-1} \textbf{f}(x)$ for a one-point design $\eta = \xi _x$. Equivalently, for one-point designs $\eta = \xi _x$, we may consider the sensitivity function $\psi (x, \xi ) = \alpha \textbf{f}(x)^\top \textbf{M}(\xi )^{-1} \textbf{f}(x)$ which incorporates the essential part of the directional derivative ($\psi (x, \xi ) = p - F_{D}(\xi , \xi _x)$). For the characterization of the D-optimal continuous subsampling design, the constrained equivalence theorem under Kuhn-Tucker conditions (see Sahm and Schwabe 2001, Corollary 1 (c)) can be reformulated in terms of the sensitivity function and applied to our case of polynomial regression.

Theorem 3.1

In polynomial regression of degree q with density $f_X(x)$ of the covariate $X_i$, the subsampling design $\xi ^*$ with support ${\mathcal {X}}^{*}$ is D-optimal if and only if there exist a threshold $s^*$ and settings $a_1> \dots > a_{2r}$ for some r ($1 \le r \le q$) such that

• (i) the D-optimal subsampling design $\xi ^{*}$ is given by

  $$\begin{aligned} f_{\xi ^{*}}(x) = \left\{ \begin{array}{ll} f_{X}(x) &{}\quad \text{ if } x \in {\mathcal {X}}^* \\ 0 &{}\quad \text{ otherwise } \end{array} \right. \, \end{aligned}$$

• (ii) $\psi (x, \xi ^*) \ge s^*$ for $x \in {\mathcal {X}}^*$, and

• (iii) $\psi (x, \xi ^*) < s^*$ for $x \not \in {\mathcal {X}}^*$,

where ${\mathcal {X}}^* = \bigcup _{k=0}^r {\mathcal {I}}_k$ and ${\mathcal {I}}_0 = [a_{1}, \infty )$, ${\mathcal {I}}_r = (-\infty , a_{2r}]$, and ${\mathcal {I}}_k = [a_{2k + 1}, a_{2k}]$, for $k = 1, \dots , r - 1$, are mutually disjoint intervals.

The density $f_{\xi ^*}(x) = f_X(x) \mathbbm {1}_{{\mathcal {X}}^*}(x) = \sum _{k=0}^r f_X(x) \mathbbm {1}_{{\mathcal {I}}_k}(x)$ of the D-optimal subsampling design $\xi ^*$ is concentrated on, at most, $q + 1$ intervals ${\mathcal {I}}_k$, where $\mathbbm {1}_{A}(x)$ denotes the indicator function on the set A, i.e., $\mathbbm {1}_A(x) = 1$ for $x \in A$, and $\mathbbm {1}_A(x) = 0$ otherwise. The density $f_{\xi ^*}(x)$ has a 0-1-property such that it is either equal to the density $f_X(x)$ of the covariate (on ${\mathcal {X}}^*$) or equal to 0 (on the complement of ${\mathcal {X}}^*$). Thus, the generation of a subsample according to the optimal continuous subsampling design $\xi ^*$ can be implemented easily by accepting all units i for which the value $x_i$ of the covariate is in ${\mathcal {X}}^*$ and rejecting all other units with $x_i \not \in {\mathcal {X}}^*$. The threshold $s^*$ can be interpreted as the $(1- \alpha )$-quantile of the distribution of the sensitivity function $\psi (X_i,\xi ^*)$ as a function of the random variable $X_i$ (see Pronzato and Wang 2021).

A further general concept to be used is equivariance. This can be employed to transform the D-optimal subsampling design simultaneously with a transformation of the distribution of the covariate. More precisely, the location-scale transformation $Z_i = \sigma X_i + \mu$ of the covariate and its distribution is conformable with the regression function $\textbf{f}(x)$ in polynomial regression, and the D-criterion is equivariant with respect to such transformations.

Theorem 3.2

Let $f_{\xi ^*}(x)$ be the density for a D-optimal subsampling design $\xi ^*$ for covariate $X_i$ with density $f_X(x)$. Then $f_{\zeta ^*}(z) = \frac{1}{\sigma } f_{\xi ^*}(\frac{z - \mu }{\sigma })$ is the density for a D-optimal subsampling design $\zeta ^*$ for covariate $Z_i = \sigma X_i + \mu$ with density $f_Z(z) = \frac{1}{\sigma } f_{X}(\frac{z - \mu }{\sigma })$.

As a consequence, also the optimal subsampling design $\zeta ^*$ is concentrated on, at most, $p = q + 1$ intervals, and its density $f_{\zeta ^*}(z)$ is either equal to the density $f_Z(z)$ of the covariate $Z_i$ (on ${\mathcal {Z}}^* = \sigma {\mathcal {X}}^* + \mu$) or it is equal to 0 (elsewhere) such that, also here, the optimal subsampling can be implemented quite easily.

A further reduction of the optimization problem can be achieved by utilizing symmetry properties. Therefore, we consider the transformation of sign change, $g(x) = -x$, and assume that the distribution of the covariate is symmetric, $f_X(-x) = f_X(x)$ for all x. For a continuous design $\xi$, the design $\xi ^g$ transformed by sign change has density $f_{\xi ^g}(x) = f_{\xi }(-x)$ and, thus, satisfies the boundedness condition $f_{\xi ^g}(x) \le f_X(x)$, when the distribution of $X_i$ is symmetric, and has the same value for the D-criterion as $\xi$, $\log (\det (\textbf{M}(\xi ^g))) = \log (\det (\textbf{M}(\xi )))$. By the concavity of the D-criterion, standard invariance arguments can be used as in Pukelsheim (1993, Chapter 13) and Heiligers and Schneider (1992). In particular, any continuous design $\xi$ is dominated by its symmetrization ${{\bar{\xi }}} = (\xi + \xi ^g)/2$ with density $f_{{\bar{\xi }}}(x) = (f_\xi (x) + f_\xi (-x))/2 \le f_X(x)$ such that $\log (\det (\textbf{M}({\bar{\xi }}))) \ge \log (\det (\textbf{M}(\xi )))$ (1993, Chapter 13.4). Hence, we can restrict the search for a D-optimal subsampling design to symmetric designs ${\bar{\xi }}$ with density $f_{{\bar{\xi }}}(-x) = f_{{\bar{\xi }}}(x)$ which are invariant with respect to sign change (${{\bar{\xi }}}^g = {\bar{\xi }}$). For these symmetric subsampling designs ${\bar{\xi }}$, the moments $m_{k}({\bar{\xi }})$ are zero for odd k and positive when k is even. Hence, the information matrix $\textbf{M}({\bar{\xi }})$ is an even checkerboard matrix (see Jones and Willms 2018) with positive entries $m_{j + j^\prime }({\bar{\xi }})$ for even index sums and entries equal to zero when the index sum is odd. The inverse $\textbf{M}({\bar{\xi }})^{-1}$ of the information matrix $\textbf{M}({\bar{\xi }})$ shares the structure of an even checkerboard matrix. Thus, the sensitivity function $\psi (x,{\bar{\xi }})$ is a polynomial with only terms of even order and is, hence, a symmetric function of x. This leads to a simplification of the representation of the optimal subsampling design in Theorem th:optspsdesignspsdegreespsq because the support ${\mathcal {X}}^*$ of the optimal subsampling design $\xi ^*$ will be symmetric, too.

Corollary 3.3

In polynomial regression of degree q with a symmetrically distributed covariate $X_{i}$ with density $f_X(x)$, the D-optimal subsampling design $\xi ^*$ with density $f_{\xi ^*}(x) = \sum _{k=0}^r f_X(x) \mathbbm {1}_{{\mathcal {I}}_k}(x)$ has symmetric boundaries $a_1, \dots , a_{2r}$ of the intervals ${\mathcal {I}}_0 = [a_{1}, \infty )]$, ${\mathcal {I}}_k = [a_{2k + 1}, a_{2k}]$, and ${\mathcal {I}}_r = (-\infty , a_{2r}]$, i. e. $a_{2r + 1 - k} = -a_k$ and, accordingly, ${\mathcal {I}}_{r - k} = -{\mathcal {I}}_k$.

This characterization of the optimal subsampling design $\xi ^*$ will be illustrated in the next two sections for ordinary linear regression ($q = 1$) and for quadratic regression ($q = 2$).

4 Optimal subsampling for linear regression

In the case of ordinary linear regression $Y_{i} =\beta _0 + \beta _1 X_{i} + \varepsilon _{i}$, we have

$$\begin{aligned} \textbf{M}(\xi ) = \begin{pmatrix} \alpha &{} m_1(\xi ) \\ m_1(\xi ) &{} m_2(\xi ) \end{pmatrix}, \end{aligned}$$

for the information matrix of any subsampling design $\xi$. The inverse $\textbf{M}(\xi )^{-1}$ of the information matrix is given by

$$\begin{aligned} \textbf{M}(\xi )^{-1} = \frac{1}{\alpha m_2(\xi ) - m_1(\xi )^2} \begin{pmatrix} m_2(\xi ) &{} -m_1(\xi ) \\ -m_1(\xi ) &{} \alpha \end{pmatrix}, \end{aligned}$$

and the sensitivity function

$$\begin{aligned} \psi (x, \xi ) = \frac{1}{\alpha m_2(\xi ) - m_1(\xi )^2} (m_2(\xi ) - 2 m_1(\xi ) x + \alpha x^2) \end{aligned}$$

(1)

is a polynomial of degree two in x. The D-optimal continuous subsampling design $\xi ^*$ has density $f_\xi (x) = f_X(x)$ for $x \le a_2$ and for $x \ge a_1$ while $f_\xi (x) = 0$ for $a_2< x < a_1$. The corresponding subsampling design then accepts those units i for which $x_i \le a_2$ or $x_i \ge a_1$, and rejects all units i for which $a_2< x_i < a_1$.

To obtain the D-optimal continuous subsampling design $\xi ^*$ by Theorem 3.1, the boundary points $a_1$ and $a_2$ have to be determined to solve the two non-linear equations

$$\begin{aligned} {\text {P}}(X_i \le a_2) + {\text {P}}(X_i \ge a_1) = \alpha \end{aligned}$$

(2)

and

$$\begin{aligned} \psi (a_2, \xi ^*) = \psi (a_1, \xi ^*) . \end{aligned}$$

By equation (1), the latter condition can be written as

$$\begin{aligned} \alpha a_2^2 - 2 m_1(\xi ^*) a_2 = \alpha a_1^2 - 2 m_1(\xi ^*) a_1 , \end{aligned}$$

which can be reformulated as

$$\begin{aligned} \alpha (a_1 + a_2) = 2 m_1(\xi ^*) . \end{aligned}$$

(3)

When the distribution of $X_i$ is symmetric, Corollary 3.3 provides symmetry $a_2 = -a_1$ of the boundary points. This is in agreement with condition (3) because $m_1(\xi ^*) = 0$ in the case of symmetry. Further, by the symmetry of the distribution, ${\text {P}}(X_i \le a_2) = {\text {P}}(X_i \ge a_1) = \alpha /2$, and $a_1$ has to be chosen as the $(1 - \alpha /2)$-quantile of the distribution of $X_i$ to obtain the D-optimal continuous subsampling design.

Example 4.1

(normal distribution) If the covariate $X_i$ comes from a standard normal distribution, then the optimal boundaries are the $(\alpha /2)$- and the $(1 - \alpha /2)$-quantile $\pm z_{1 - \alpha /2}$, and unit i is accepted when $|x_i| \ge z_{1 - \alpha /2}$.

For $X_i$ having a general normal distribution with mean $\mu$ and variance $\sigma ^2$, the optimal boundaries remain to be the $(\alpha /2)$- and $(1 - \alpha /2)$-quantile $a_2 = \mu - \sigma z_{1 - \alpha /2}$ and $a_1 = \mu + \sigma z_{1 - \alpha /2}$, respectively, by Theorem 3.2.

This approach applies accordingly to all distributions which are obtained by a location or scale transformation of a symmetric distribution: units will be accepted if their values of the covariate lie in the lower or upper $(\alpha /2)$-tail of the distribution. This procedure can be interpreted as a theoretical counterpart in one dimension of the IBOSS method proposed by Wang et al. (2019).

However, for an asymmetric distribution of the covariate $X_i$, the optimal proportions for sampling from the upper and lower tail may differ. By condition (7), there will be a proportion $\alpha _1$, $0 \le \alpha _1 \le \alpha$, for the upper tail and $\alpha _2 = \alpha - \alpha _1$ for the lower tail such that $a_1$ is the $(1 - \alpha _1)$-quantile and $a_2$ is the $\alpha _2$-quantile of the distribution of the covariate $X_i$, respectively. In view of condition (3), neither $\alpha _1$ nor $\alpha _2$ can be zero. Hence, the optimal subsampling design will have positive, but not necessarily equal mass at both tails. This will be illustrated in the next example.

Example 4.2

(exponential distribution) If the covariate $X_i$ comes from a standard exponential distribution with density $f_{X}(x) = e^{-x},\; x \ge 0$, we conclude from Theorem 3.1 that $f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{[0,b]\cup [a,\infty )}(x)$ with $a = a_1$ and $b = a_2$ when $a_2 \ge 0$. Otherwise, when $a_2 < 0$, the density $f_X(x)$ of the covariate $X_i$ vanishes on the left interval ${\mathcal {I}}_1 = (-\infty , a_2]$ because the support of the distribution of $X_i$ does not cover the whole range of ${\mathbb {R}}$. In that case, we may formally let $b = 0$. Then, we can calculate the entries of $\textbf{M}(\xi ^{*})$ as functions of a and b as

$$\begin{aligned} m_{1}(\xi ^{*})&= 1 + (a + 1)e^{-a} - (b + 1)e^{-b} \\ m_{2}(\xi ^{*})&= 2 + (a^2 + 2a + 2)e^{-a} - (b^2 + 2b + 2)e^{-b} \,. \end{aligned}$$

To obtain the optimal solutions for a and b in the case $a_2 \ge 0$, the two non-linear equations (2) and (3) have to be satisfied which become here $e^{-b} - e^{-a} = 1 - \alpha$ and $\alpha (a + b) = 2 m_1(\xi ^{*})$.

If $a_2 < 0$ would hold, the first condition reveals $a = - \log (\alpha )$ and, hence, $m_1(\xi ^{*}) = \alpha (a + 1)$. There, similar to the proof of Theorem 5.2 below, the second condition has to be relaxed to $\psi (a,\xi ^{*}) \ge \psi (0,\xi ^{*})$ which can be reformulated to $\alpha a \ge 2 m_1(\xi ^{*}) = 2\alpha (a + 1)$ and yields a contradiction. Thus, this case can be excluded, and $a_2$ has to be larger than 0 for all $\alpha$.

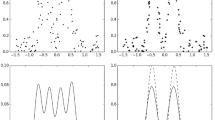
For selected values of $\alpha$, numerical results are presented in Table 1. Additionally to the optimal values for a and b, also the proportions ${\text {P}}(X_i \le b)$ and ${\text {P}}(X_i \ge a)$ are presented in Table 1 together with the percentage of mass allocated to the left interval [0, b]. In Fig. 1, the density $f_{\xi ^{*}}$ of the optimal subsampling design $\xi ^*$ and the corresponding sensitivity function $\psi (x,\xi ^*)$ are exhibited for $\alpha = 0.5$ and $\alpha = 0.3$. Vertical lines indicate the positions of the boundary points a and b, and the dotted horizontal line displays the threshold $s^*$.

Table 1 Numeric values for the boundary points a and b for selected values of the subsampling proportion $\alpha$ in the case of standard exponential $X_i$

Fig. 1

Density of the optimal subsampling design (solid line) and the standard exponential distribution (dashed line, upper panels), and sensitivity functions (lower panels) for subsampling proportions $\alpha = 0.5$ (left) and $\alpha = 0.3$ (right)

As could have been expected, less mass is assigned to the right tail of the right-skewed distribution because observations from the right tail are more influential and, thus, more observations seem to be required on the lighter left tail for compensation.

For $X_i$ having an exponential distribution with general intensity $\lambda > 0$ (scale $1/\lambda$), the optimal boundary points remain to be the same quantiles as in the standard exponential case, $a_1 = a/\lambda$ and $a_2 = b/\lambda$ associated with the proportion $\alpha$, by Theorem 3.2.

5 Optimal subsampling for quadratic regression

In the case of quadratic regression $Y_{i} =\beta _0 + \beta _1 X_{i} + \beta _2 X_{i}^2 + \varepsilon _{i}$ we have

$$\begin{aligned} \textbf{M}(\bar{\xi }) = \begin{pmatrix} \alpha &{} 0 &{} m_2(\bar{\xi }) \\ 0 &{} m_2(\bar{\xi }) &{} 0 \\ m_2(\bar{\xi }) &{} 0 &{} m_4(\bar{\xi }) \end{pmatrix}, \end{aligned}$$

(4)

for the information matrix of a symmetric subsampling design $\bar{\xi }$. The inverse $\textbf{M}(\bar{\xi })^{-1}$ of the information matrix is given by

$$\begin{aligned} \textbf{M}(\bar{\xi })^{-1} = \frac{1}{\alpha m_4(\bar{\xi }) - m_2(\bar{\xi })^2} \begin{pmatrix} m_4(\bar{\xi }) &{} 0 &{} -m_2(\bar{\xi }) \\ 0 &{} \alpha \frac{m_4(\bar{\xi })}{m_2(\bar{\xi })} - m_2(\bar{\xi }) &{} 0 \\ -m_2(\bar{\xi }) &{} 0 &{} \alpha \end{pmatrix}, \end{aligned}$$

and the sensitivity function

$$\begin{aligned} \psi (x, \bar{\xi }) = \frac{1}{\alpha m_4(\bar{\xi }) - m_2(\bar{\xi })^2} (m_4(\bar{\xi }) - 3 m_2(\bar{\xi }) x^2 + \alpha \frac{m_4(\bar{\xi })}{m_2(\bar{\xi })} x^2 + \alpha x^4) \end{aligned}$$

(5)

is a polynomial of degree four and is symmetric in x.

According to Corollary 3.3, the density $f_{\xi ^{*}}(x)$ of the D-optimal continuous subsampling design $\xi ^*$ has, at most, three intervals that are symmetrically placed around zero, where the density is equal to the bounding density $f_{X}(x)$, and $f_{\xi ^{*}}(x)$ is equal to zero elsewhere. Thus the density $f_{\xi ^{*}}(x)$ of the D-optimal subsampling design has the shape

$$\begin{aligned} f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{(-\infty ,-a]\cup [-b,b]\cup [a,\infty )}(x) , \end{aligned}$$

(6)

where $a > b \ge 0$. We formally allow $b = 0$ which means that $\psi (0,\xi ^*) \le s^{*} = \psi (a,\xi ^*)$ and that the density $f_{\xi ^*}(x)$ is concentrated on only two intervals, $f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{(-\infty ,-a]\cup [a,\infty )}(x)$. Although the information matrix will be non-singular even in the case of two intervals ($b=0)$, the optimal subsampling design will include a non-degenerate interior interval $[-b, b]$ in many cases, $b > 0$, as illustrated below in Examples 5.1 and 5.3. However, for a heavy-tailed distribution of the covariate $X_i$, the interior interval may vanish in the optimal subsampling design as shown in Example 5.5.

To obtain the D-optimal continuous subsampling design $\xi ^*$ by Corollary 3.3, the boundary points $a = a_1$ and $b = a_2 \ge 0$ have to be determined to solve the two non-linear equations

$$\begin{aligned} {\text {P}}(|X_i| \le b) + {\text {P}}(|X_i| \ge a) = \alpha \end{aligned}$$

(7)

and

$$\begin{aligned} \psi (b, \xi ^*) = \psi (a, \xi ^*) . \end{aligned}$$

(8)

By equation (5), the latter condition can be written as

$$\begin{aligned} \alpha m_2(\xi ^*) b^4 + \left( \alpha m_4(\xi ^*) - 3 m_2(\xi ^*)^2\right) b^2 = \alpha m_2(\xi ^*) a^4 + \left( \alpha m_4(\xi ^*) - 3 m_2(\xi ^*)^2\right) a^2 , \end{aligned}$$

which can be reformulated as

$$\begin{aligned} \alpha m_2(\xi ^*) (a^2 + b^2) = \alpha m_4(\xi ^*) - 3 m_2(\xi ^*)^2 . \end{aligned}$$

(9)

For finding the optimal solution, we use the Newton method implemented in the R package nleqslv by Hasselman (2018) to calculate numeric values for a and b based on equations (7) and (8) for various symmetric distributions.

The case $b = 0$ relates to the situation of only two intervals ($r = 1 < q$). There, condition (7) simplifies to $a = q_{1 - \alpha /2}$, where $q_{1 - \alpha /2}$ is the $(1 - \alpha /2)$-quantile of the distribution of the covariate $X_i$, and equation (8) has to be relaxed to $\psi (0, \xi ^*) \le \psi (a, \xi ^*)$, similar to the case $b = 0$ in Example 4.2.

Table 2 Numeric values for the boundary points a and b for selected values of the subsampling proportion $\alpha$ in the case of standard normal $X_i$

Example 5.1

(normal distribution) For the case that the covariate $X_i$ comes from a standard normal distribution, results are given in Table 2 for selected values of $\alpha$. Additionally to the optimal values for a and b, also the proportions ${\text {P}}(X_i \ge a) = {\text {P}}(X_i \le -a) = 1 - \Phi (a)$ and ${\text {P}}(-b \le X_i \le b) = 2\Phi (b) - 1$ are presented in Table 2 together with the percentage of mass $(2\Phi (b) - 1) / \alpha$ allocated to the interior interval $[-b, b]$. In Fig. 2, the density $f_{\xi ^{*}}$ of the optimal subsampling design $\xi ^*$ and the corresponding sensitivity function $\psi (x,\xi ^*)$ are exhibited for $\alpha = 0.5$ and $\alpha = 0.1$.

Fig. 2

Density of the optimal subsampling design (solid line) and the standard normal distribution (dashed line, upper panels), and sensitivity functions (lower panels) for subsampling proportions $\alpha = 0.5$ (left) and $\alpha = 0.1$ (right)

Vertical lines indicate the positions of the boundary points $-a$, $-b$, b, and a, respectively. In the subplots of the sensitivity function, the dotted horizontal line displays the threshold $s^*$. For other values of $\alpha$, the plots are looking similar.

The numerical results in Table 2 suggest that the interior interval $[-b, b]$ does not vanish for any $\alpha$ ($0< \alpha < 1$). This will be established in the following theorem.

Theorem 5.2

In quadratic regression with standard normal covariate $X_i$, for any subsampling proportion $\alpha \in (0,1)$, the D-optimal subsampling design $\xi ^{*}$ has density $f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{(-\infty , -a]\cup [-b, b]\cup [a, \infty )}(x)$ with $a> b > 0$.

For $X_i$ having a general normal distribution with mean $\mu$ and variance $\sigma ^2$, the optimal boundary points remain to be the same quantiles as in the standard normal case, $a_1, a_4 = \mu \pm \sigma a$ and $a_2, a_3 = \mu \pm \sigma b$, by Theorem 3.2.

Example 5.3

(uniform distribution) If the covariate $X_i$ is uniformly distributed on $[-1,1]$ with density $f_{X}(x) = \frac{1}{2}\mathbbm {1}_{[-1,1]}(x)$, we can obtain analytical results for the dependence of the subsampling design on the proportion $\alpha$ to be selected.

The distribution of $X_i$ is symmetric. By Corollary 3.3, the density of the D-optimal continuous subsampling design $\xi ^*$ has the shape

$$\begin{aligned} f_{\xi ^{*}}(x) = \frac{1}{2} \mathbbm {1}_{[-1,-a] \cup [-b,b] \cup [a,1]}(x) , \end{aligned}$$

(10)

where we formally allow $a = 1$ or $b = 0$ resulting in only one or two intervals of support. The relevant entries in the information matrix $\textbf{M}(\xi ^{*})$ are $m_2(\xi ^*) = \frac{1}{3}(1 - a^3 + b^3)$ and $m_4(\xi ^*) = \frac{1}{5}(1 - a^5 + b^5)$. If, in Corollary 3.3, the boundary points $a_1$ and $a_2$ satisfy $a_1 \le 1$ and $a_2 \ge 0$, then $a = a_1$ and $b = a_2$ are the solution of the two equations $a - b = 1 - \alpha$ and $\alpha m_2(\xi ^*) (a^2 + b^2) = \alpha m_4(\xi ^*) - 3 m_2(\xi ^*)^2$ arising from conditions (7) and (9). On the other hand, if there exist solutions a and b of these equations such that $0< b< a < 1$, then these are the boundary points in the representation (10), and the density of the optimal subsampling design is supported by three proper intervals. Solving the two equations results in

$$\begin{aligned} a(\alpha ) = \frac{1}{2}&(1 - \alpha ) + \Biggl ( \frac{1}{180(1 - \alpha )} \Bigl (45 - 15\alpha + 15\alpha ^2 -45\alpha ^3 + 20\alpha ^4 \nonumber \\&\quad - 4\alpha \sqrt{5} \sqrt{45 - 90\alpha + 90\alpha ^2 - 75\alpha ^3 + 57\alpha ^4 - 27\alpha ^5 + 5\alpha ^6} \, \Bigr ) \Biggr )^{1/2} \end{aligned}$$

(11)

and

$$\begin{aligned} b(\alpha ) = a(\alpha ) - (1 - \alpha ) \end{aligned}$$

(12)

for the dependence of a and b on $\alpha$. The values of a and b are plotted in Fig. 3.

Fig. 3

Boundary points a (dashed) and b (solid) of the D-optimal subsampling design in the case of uniform $X_{i}$ on $[-1,1]$ as functions of $\alpha$

There it can be seen that $0< a< b < 1$ for all $\alpha$ and that a and b both tend to $1/\sqrt{5}$ as $\alpha$ tends to 1. Similar to the case of the normal distribution, the resulting values and illustrations are given in Table 3 and Fig. 4. Note that the mass of the interior interval ${\text {P}}(-b \le X_i \le b)$ is equal to b itself as $X_{i}$ is uniformly distributed on $[-1,1]$.

Table 3 Values for the boundary points a and b for selected values of the subsampling proportion $\alpha$ in the case of uniform $X_i$ on $[-1, 1]$

Fig. 4

Density of the optimal subsampling design (solid line) and the uniform distribution on $[-1,1]$ (dashed line, upper panels), and sensitivity functions (lower panels) for subsampling proportions $\alpha = 0.5$ (left) and $\alpha = 0.1$ (right)

Also here, in Fig. 4, vertical lines indicate the positions of the boundary points $-a$, $-b$, b, and a, and the dotted horizontal line displays the threshold $s^*$. Moreover, the percentage of mass at the different intervals is displayed in Fig. 5.

Fig. 5

Percentage of mass on the support intervals [a, 1] (left) and $[-b,b]$ (right) of the D-optimal subsampling design in the case of uniform $X_{i}$ on $[-1,1]$ as a function of $\alpha$

The results in Table 3 and Fig. 5 suggest that the percentage of mass on all three intervals $[-1,-a]$, $[-b,b]$, and [a, 1] tend to 1/3 as $\alpha$ tends to 0. We establish this in the following theorem.

Theorem 5.4

In quadratic regression with covariate $X_i$ uniformly distributed on $[-1,1]$, let $\xi _{\alpha }^{*}$ be the optimal subsampling design for subsampling proportion $\alpha$, $0< \alpha < 1$, defined in equations (11) and (12). Then $\lim _{\alpha \rightarrow 0} \xi _{\alpha }^{*}([-b,b]) / \alpha = 1/3$.

It is worth-while mentioning that the percentages of mass displayed in Fig. 5 are not monotonic over the whole range of $\alpha \in (0,1)$, as, for example the percentage of mass at the interior interval $[-b, b]$ is increasing from 0.419666 at $b = 0.50$ to 0.448549 at $b = 0.92$ and then slightly decreasing back again to 0.447553 at $b = 0.99$.

Finally, it can be checked that, for all $\alpha$, the solutions satisfy $0< b< a < 1$ such that the optimal subsampling designs are supported on three proper intervals.

In the two preceding examples it could be noticed that the mass of observations is of comparable size for the three supporting intervals in the case of a normal and of a uniform distribution with light tails. This may be different in the case of a heavy-tailed distribution for the covariate $X_{i}$ as the t-distribution.

Example 5.5

(t-distribution) For the case that the covariate $X_i$ comes from a t-distribution with $\nu$ degrees of freedom, we observe a behavior which differs substantially from the normal case of Example 5.1. The interior interval typically has less mass than the outer intervals and may vanish for some values of $\alpha$. We show this in the case of the least possible number $\nu = 5$ of degrees of freedom to maintain an existing fourth moment, which appears in the information matrix of the D-optimal continuous subsampling design $\xi ^{*}$ while maximizing the dispersion.

Theorem 5.6

In quadratic regression with t-distributed covariate $X_i \sim t_{5}$ with five degrees of freedom, there is a critical value $\alpha ^* \approx 0.082065$ of the subsampling proportion $\alpha$ such that the D-optimal subsampling design $\xi ^{*}$ has

• (i) density $f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{(-\infty ,-a]\cup [-b,b]\cup [a,\infty )}(x)$ with $a> b > 0$ for $\alpha < \alpha ^*$.

• (ii) density $f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{(-\infty ,-t_{5,1-\alpha /2}]\cup [t_{5,1-\alpha /2},\infty )}(x)$, where $t_{5,1-\alpha /2}$ is the $(1 - \alpha /2)$-quantile of the $t_5$-distribution, for $\alpha \ge \alpha ^*$.

For illustration, numerical results are given in Table 4. The percentage of mass on the interior interval $[-b,b]$ is equal to zero for all larger values of $\alpha$ as stated in Theorem 5.6. The percentage of mass on $[-b,b]$ decreases with increasing subsampling proportion $\alpha$ before vanishing entirely.

Table 4 Values for the boundary points a and b for selected values of the subsampling proportion $\alpha$ in the case of $t_{5}$-distributed $X_i$

Further calculations provide that the critical value $\alpha ^{*}$, where a the D-optimal subsampling design switches from a three-interval support to a two-interval support, increases with the number of degrees $\nu$ of freedom of the t-distribution and converges to one when $\nu$ tends to infinity. This is in accordance with the results for the normal distribution in Example 5.1 as the t-distribution converges in distribution to a standard normal distribution for $\nu \rightarrow \infty$. We have given numeric values for the crossover points for selected degrees of freedom in Table 5, where $\nu = \infty$ relates to the normal distribution. The corresponding value $\alpha ^* = 1$ indicates that the D-optimal subsampling design is supported by three intervals for all $\alpha$ in this case.

Table 5 Values of the critical value $\alpha ^{*}$ for selected degrees of freedom $\nu$ of the t-distribution

6 Efficiency

To exhibit the gain in using a D-optimal subsampling design compared to random subsampling, we consider the performance of the uniform random subsampling design $\xi _{\alpha }$ of size $\alpha$, which has density $f_{\xi _{\alpha }}(x) = \alpha f_X(x)$, compared to the D-optimal subsampling design $\xi _{\alpha }^{*}$ with mass $\alpha$.

More precisely, the D-efficiency of any subsampling design $\xi$ with mass $\alpha$ is defined as

$$\begin{aligned} {{\,\textrm{eff}\,}}_{D,\alpha }(\xi ) = \left( \frac{\det (\textbf{M}(\xi ))}{\det (\textbf{M}(\xi _{\alpha }^{*}))}\right) ^{1/p}, \end{aligned}$$

where p is the dimension of the parameter vector $\varvec{\beta }$. For this definition the homogeneous version $(\det (\textbf{M}(\xi )))^{1/p}$ of the D-criterion is used which satisfies the homogeneity condition $(\det (\lambda \textbf{M}(\xi )))^{1/p} = \lambda (\det (\textbf{M}(\xi )))^{1/p}$ for all $\lambda > 0$ (see Pukelsheim 1993, Chapter 6.2).

For uniform random subsampling, the information matrix is given by $\textbf{M}(\xi _{\alpha }) = \alpha \textbf{M}(\xi _{1})$, where $\textbf{M}(\xi _{1})$ is the information matrix for the full sample with raw moments $m_k(\xi _{1}) = {\mathbb {E}}({\varvec{X}}_{i}^{k})$ as entries in the $(j,j^\prime )$th position, $j + j^\prime - 2 = k$. Thus, the D-efficiency ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha })$ of uniform random subsampling can be nicely interpreted: the sample size (mass) required to obtain the same precision (in terms of the D-criterion), as when the D-optimal subsampling design $\xi _{\alpha }^*$ of mass $\alpha$ is used, is equal to the inverse of the efficiency ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha })^{-1}$ times $\alpha$. For example, if the efficiency ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha })$ is equal to 0.5, then twice as many observations would be needed under uniform random sampling than for a D-optimal subsampling design of size $\alpha$. Of course, the full sample has higher information than any proper subsample such that, obviously, for uniform random subsampling, ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha }) \ge \alpha$ holds for all $\alpha$.

For the examples of Sects. 4 and 5, the efficiency of uniform random subsampling is given in Table 6 for selected values of $\alpha$

Table 6 Efficiency of uniform subsampling w.r.t. D-optimality for selected values of the subsampling proportion $\alpha$

and exhibited in Fig. 6 for the full range of $\alpha$ between 0 and 1 (solid lines).

Fig. 6

Efficiency of uniform random subsampling (solid line) and of an IBOSS-type subsampling design (dashed line) w.r.t. D-optimality

Here the determinant of the information matrix is determined as in the examples of Sects. 4 and 5 for the optimal subsampling designs $\xi _{\alpha }^{*}$ either numerically or by explicit formulas where available.

Both Table 6 and Fig. 6 indicate that the efficiency of uniform random subsampling is decreasing in all cases when the proportion $\alpha$ of subsampling gets smaller. In the case of quadratic regression with uniformly distributed covariate, the decrease is more or less linear with a minimum value of approximately 0.58 when $\alpha$ is small. In the other cases, where the distribution of the covariate is unbounded, the efficiency apparently decreases faster, when the proportion $\alpha$ is smaller than $10\%$, and tends to 0 for $\alpha \rightarrow 0$.

The latter property can be easily seen for linear regression and symmetric distributions: there, the efficiency ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha })$ of uniform random sampling is bounded from above by $c / q_{1 - \alpha /2}$, where $c = {\mathbb {E}}(X_i^2)^{1/2}$ is a constant and $q_{1 - \alpha /2}$ is the $(1 - \alpha /2)$-quantile of the distribution of the covariate. When the distribution is unbounded like the normal distribution, then these quantiles tend to infinity for $\alpha \rightarrow 0$ and, hence, the efficiency tends to 0. Similar results hold for quadratic regression and asymmetric distributions.

In any case, as can be seen from Table 6, the efficiency of uniform random subsampling is quite low for reasonable proportions $\alpha \le 0.1$ and, hence, the gain in using the D-optimal subsampling design is substantial.

By equivariance arguments as indicated above in the examples of Sects. 4 and 5, the present efficiency considerations carry over directly to a covariate having a general normal, exponential, or uniform distribution, respectively.

In the IBOSS approach by Wang et al. (2019), of the proportion $\alpha$ is taken from both tails of the data. The corresponding continuous subsampling design $\xi _{\alpha }^{\prime }$ would be to have two intervals $(-\infty , b]$ and $[a, \infty )$ and to choose the boundary points a and b to be the $(1 - \alpha /2)$- and $(\alpha /2)$-quantile of the distribution of the covariate, respectively. For linear regression, it can been seen from Corollary 3.3 that the subsampling design $\xi _{\alpha }^{\prime }$ is D-optimal when the distribution of the covariate is symmetric. As the IBOSS procedure does not use prior knowledge of the distribution, it would be tempting to investigate the efficiency of the corresponding continuous subsampling design $\xi _{\alpha }^{\prime }$ under asymmetric distributions. For the exponential distribution, this efficiency ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha }^{\prime })$ is added to the upper left panel in Fig. 6 by a dashed line. There the subsampling design $\xi _{\alpha }^{\prime }$ shows a remarkably high efficiency over the whole range of $\alpha$ with a minimum value 0.976 at $\alpha = 0.332$.

As an extension of IBOSS for quadratic regression, we may propose a procedure which takes proportions $\alpha /3$ from both tails of the data as well as from the center of the data. This procedure can be performed without any prior knowledge of the distribution of the covariate. The choice of the proportions $\alpha /3$ is motivated by the standard case D-optimal design on an interval where one third of the weight is allocated to each of the endpoints and to the midpoint of the interval, respectively. For a symmetric distribution, the corresponding continuous subsampling design $\xi _{\alpha }^{\prime \prime }$ can be defined by the boundary points a and b to be the $(1 - \alpha /3)$- and $(1/2 + \alpha /6)$-quantile of the distribution of the covariate, respectively. In the case of the uniform distribution, the subsampling design $\xi _{\alpha }^{\prime \prime }$ is the limiting D-optimal subsampling design for $\alpha \rightarrow 0$ by Theorem 5.4. In Fig. 6, the efficiency ${{\,\textrm{eff}\,}}_{D,\alpha }(\xi _{\alpha }^{\prime \prime })$ is shown by dashed lines for the whole range of $\alpha$ for the uniform distribution as well as for the normal and for the t- distribution in the case of quadratic regression. In all three cases, the subsampling design $\xi _{\alpha }^{\prime \prime }$ is highly efficient over the whole range of $\alpha$ with minimum values 0.994 at $\alpha = 0.079$ for the normal distribution, 0.989 at $\alpha = 0.565$ for the uniform distribution, and 0.978 at $\alpha = 0.245$ for the $t_{5}$-distribution, respectively. This is of particular interest for the $t_{5}$-distribution, where the interior interval of the D-optimal subsampling design $\xi _{\alpha }^{*}$ is considerably smaller than of the IBOSS-like subsampling design $\xi _{\alpha }^{\prime \prime }$ and even vanishes entirely for $\alpha > \alpha ^* \approx 0.08$. However, we only tested this extension of IBOSS for quadratic regression for symmetric distributions of the covariate. Further investigations for non-symmetric distributions is necessary.

7 Concluding remarks

In this paper we have considered a theoretical approach to evaluate subsampling designs under distributional assumptions on the covariate in the case of polynomial regression on a single explanatory variable. We first reformulated the constrained equivalence theorem under Kuhn-Tucker conditions in Sahm and Schwabe (2001) to characterize the D-optimal continuous subsampling design for general distributions of the covariate. For symmetric distributions of the covariate we concluded the following. The D-optimal subsampling design is equal to the bounding distribution in its support and the support of the optimal subsampling design will be the union of at most $q + 1$ intervals that are symmetrically placed around zero. Further we have found that in the case of quadratic regression the D-optimal subsampling design has three support intervals with positive mass for all $\alpha \in (0,1)$, whereas the interior interval vanishes for some $\alpha$ for a t-distributed covariate. In contrast to that, for linear regression, always two intervals are required at the tails of the distribution.

The main emphasis in this work was on D-optimal subsampling designs. But many of the results may be extended to other optimality criteria like A- and E-optimality from the Kiefer’s $\Phi _q$-class of optimality criteria, IMSE-optimality for predicting the mean response, or optimality criteria based on subsets or linear functionals of parameters.

The D-optimal subsampling designs show a high performance compared to uniform random subsampling. In particular, for small proportions, the efficiency of uniform random subsampling tends to zero when the distribution of the covariate is unbounded. This property is in accordance with the observation that estimation based on subsampling according to IBOSS is “consistent” in the sense that the mean squared error goes to zero with increasing population size even when the size of the subsample is fixed.

We propose a generalization of the IBOSS method to quadratic regression which does not require prior knowledge of the distribution of the covariate and which performs remarkably well compared to the optimal subsampling design. However, an extension to higher order polynomials does not seem to be obvious.

Appendix A: Proofs

Before proving Theorem 3.1, we establish two preparatory lemmas on properties of the sensitivity function $\psi (x, \xi )$ for a continuous subsampling design $\xi$ with density $f_{\xi }(x)$ and reformulate an equivalence theorem on constraint design optimality by Sahm and Schwabe (2001) for the present setting. The first lemma deals with the shape of the sensitivity function.

Lemma A.1

The sensitivity function $\psi (x, \xi )$ is a polynomial of degree 2q with positive leading term.

Proof of Lemma A.1

For a continuous subsampling design $\xi$ with density $f_\xi (x)$, the information matrix $\textbf{M}(\xi )$ and, hence, its inverse $\textbf{M}(\xi )^{-1}$ is positive definite. Thus the last diagonal element $m^{(pp)}$ of $\textbf{M}(\xi )^{-1}$ is positive and, as $\textbf{f}(x) = (1, x, \dots , x^q)^\top$, the sensitivity function $\psi (x, \xi ) = \textbf{f}(x)^{\top } \textbf{M}(\xi )^{-1} \textbf{f}(x)$ is a polynomial of degree 2q with coefficient $m^{(pp)} > 0$ of the leading term. $\square$

The second lemma reveals a distributional property of the sensitivity function considered as a function in the covariate $X_i$.

Lemma A.2

The random variable $\psi (X_i, \xi )$ has a continuous cumulative distribution function.

Proof of Lemma A.2

As the sensitivity function $\psi (x, \xi )$ is a non-constant polynomial by Lemma A.1, the equation $\psi (x, \xi ) = s$ has only finitely many roots $x_1, \dots , x_{\ell }$, $\ell \le 2q$, say, by the fundamental theorem of algebra. Hence, ${\text {P}}(\psi (X_i, \xi ) = s) = \sum _{k=1}^{\ell } {\text {P}}(X_i = x_k) = 0$ by the continuity of the distribution of $X_i$ which proves the continuity of the cumulative distribution function of $\psi (X_i, \xi )$. $\square$

With the continuity of the distribution of $\psi (X_i,\xi ^*)$ the following equivalence theorem can be obtained from Corollary 1(c) in Sahm and Schwabe (2001) for the present setting by transition from the directional derivative to the sensitivity function and considering ${\mathbb {R}}$ as the design region.

Theorem A.3

(Equivalence Theorem) The subsampling design $\xi ^*$ is D-optimal if and only if there exist a threshold $s^*$ and a subset ${\mathcal {X}}^*$ of ${\mathbb {R}}$ such that

• (i) the D-optimal subsampling design $\xi ^{*}$ is given by

  $$\begin{aligned} f_{\xi ^{*}}(x) = f_{X}(x) \mathbbm {1}_{{\mathcal {X}}^*}(x) \, \end{aligned}$$

• (ii) $\psi (x, \xi ^*) \ge s^*$ for $x \in {\mathcal {X}}^*$, and

• (iii) $\psi (x, \xi ^*) < s^*$ for $x \not \in {\mathcal {X}}^*$.

As ${\text {P}}(\psi (X_i, \xi ^*) \ge s^*) = {\text {P}}(X_i \in {\mathcal {X}}^*) = \int f_{\xi ^*}(x) \mathop {}\!\textrm{d}x = \alpha$, the threshold $s^*$ is the $(1 - \alpha )$-quantile of the distribution of $\psi (X_i, \xi ^*)$.

Proof of Theorem 3.1

By Lemma A.1 the sensitivity function $\psi (x, \xi )$ is a polynomial in x of degree 2q with positive leading term. Using the same argument as in the proof of Lemma A.2 we obtain that there are at most 2q roots of the equation $\psi (x, \xi ^*) = s^*$ and, hence, there are at most 2q sign changes in $\psi (x, \xi ^*) - s^*$. As $\psi (x, \xi ^*)$ is a polynomial of even degree, also the number of (proper) sign changes has to be even, and they occur at $a_1> \dots > a_{2r}$, say, $r \le q$. Moreover, for $0< \alpha < 1$, ${\mathcal {X}}^*$ is a proper subset of ${\mathbb {R}}$ and, thus, there must be at least one sign change, $r \ge 1$. Finally, as the leading coefficient of $\psi (x, \xi ^*)$ is positive, $\psi (x, \xi ^*)$ gets larger than $s^*$ for $x \rightarrow \pm \infty$ and, hence, the outmost intervals $[a_1, \infty )$ and $(- \infty , a_{2r}]$ are included in the support ${\mathcal {X}}^*$ of $\xi ^*$. By the interlacing property of intervals with positive and negative sign for $\psi (x, \xi ^*) - s^*$, the result follows from the conditions on the D-optimal subsampling design $\xi ^{*}$ in Theorem A.3. $\square$

Proof of Theorem 3.2

First note that for any $\mu$ and $\sigma >0$, the location-scale transformation $z = \sigma x + \mu$ is conformable with the regression function $\textbf{f}(x)$, i. e. there exists a non-singular matrix $\textbf{Q}$ such that $\textbf{f}(\sigma x + \mu ) = \textbf{Q}\textbf{f}(x)$ for all x. Then, for any design $\xi$ bounded by $f_{X}(x)$, the design $\zeta$ has density $f_{\zeta }(z) = \frac{1}{\sigma } f_{\xi }(\frac{z - \mu }{\sigma })$ bounded by $f_{Z}(z) = \frac{1}{\sigma } f_{X}(\frac{z - \mu }{\sigma })$. Hence, by the transformation theorem for measure integrals, it holds that

$$\begin{aligned} \textbf{M}(\zeta )&= \int \textbf{f}(z)\textbf{f}(z)^{\top } \zeta (\mathop {}\!\textrm{d}z) \\&= \int \textbf{f}(\sigma x + \mu )\textbf{f}(\sigma x + \mu )^{\top } \xi (\mathop {}\!\textrm{d}x) \\&= \int \textbf{Q} \textbf{f}(x)\textbf{f}(x)^{\top } \textbf{Q}^{\top }\xi (\mathop {}\!\textrm{d}x) \\&= \textbf{Q} \textbf{M}(\xi ) \textbf{Q}^{\top }. \end{aligned}$$

Therefore $\det (\textbf{M}(\zeta )) = \det (\textbf{Q})^{2} \det (\textbf{M}(\xi ))$. Thus $\xi ^{*}$ maximizes the D-criterion over the set of subsampling designs bounded by $f_{X}(x)$ if and only if $\zeta _{*}$ maximizes the D-criterion over the set of subsampling designs bounded by $f_{Z}(z)$. $\square$

Proof of Corollary 3.3

The checkerboard structure of the information matrix $\textbf{M}(\xi ^*)$ carries over to its inverse $\textbf{M}(\xi ^*)^{-1}$. Hence, the sensitivity function $\psi (x, \xi ^*)$ is an even polynomial, which has only non-zero coefficients for even powers of x, and is thus symmetric with respect to 0, i. e. $\psi (-x, \xi ^*) = \psi (x, \xi ^*)$. Accordingly, also the roots of $\psi (x, \xi ^*) =s^*$ are symmetric with respect to 0. $\square$

Proof of Theorem 5.2

In view of the shape (6) of the density and by Corollary 3.3, the tails are included in the optimal subsampling design such that $a < \infty$.

Next, we consider the symmetric design $\xi ^\prime$ which is supported only on the tails and which will be the optimal subsampling design when $b = 0$. This design has density $f_{\xi ^\prime }(x) = \mathbbm {1}_{(-\infty , -a] \cup [a, \infty )}(x) f_X(x)$ with $a = z_{1 - \alpha /2}$ for given $\alpha$. The information matrix $\textbf{M}(\xi ^\prime )$ is of the form (4) with relevant entries

$$\begin{aligned} m_2(\xi ^{\prime })&= \alpha + \sqrt{2/\pi } a \exp (-a^{2}/2), \\ m_4(\xi ^{\prime })&= 3 m_{2}(\xi ^{\prime }) + \sqrt{2/\pi } a^{3} \exp (-a^{2}/2) \, . \end{aligned}$$

For the sensitivity function (5), we have

$$\begin{aligned} \psi (0, \xi ^{\prime })&= \frac{\alpha m_{4}(\xi ^{\prime })}{\alpha m_{4}(\xi ^{\prime }) - m_{2}(\xi ^{\prime })^{2}} \end{aligned}$$

and

$$\begin{aligned} \psi (a, \xi ^{\prime })&= \frac{\alpha m_{4}(\xi ^{\prime })}{\alpha m_{4}(\xi ^{\prime }) - m_{2}(\xi ^{\prime })^{2}} - \frac{\alpha 2 m_{2}(\xi ^{\prime }) a^{2}}{\alpha m_{4}(\xi ^{\prime }) - m_{2}(\xi ^{\prime })^{2}} \\&\qquad \qquad + \frac{\alpha a^2}{m_{2}(\xi ^{\prime })} + \frac{\alpha ^2 a^{4}}{\alpha m_{4}(\xi ^{\prime }) - m_{2}(\xi ^{\prime })^{2}} \, . \end{aligned}$$

Let $c(\alpha ) = \psi (0, \xi ^{\prime }) - \psi (a, \xi ^{\prime })$ be the difference between the values of the sensitivity function at $x = 0$ and $x = a$, then

$$\begin{aligned} c(\alpha ) = \alpha a^{2}\left( \frac{2m_2(\xi ^{\prime })}{\alpha m_{4}(\xi ^{\prime }) - m_{2}(\xi ^{\prime })^{2}} - \frac{a^2\alpha }{\alpha m_{4}(\xi ^{\prime }) - m_{2}(\xi ^{\prime })^{2}} - \frac{1}{m_2(\xi ^{\prime })}\right) . \end{aligned}$$

(13)

$c(\alpha )$ is continuous in $\alpha$ and does not have any roots in (0, 1). Further, it can be checked that $c(0.1) > 0$, say. Thus $c(\alpha ) > 0$ which means that $\psi (0, \xi ^{\prime }) > \psi (a, \xi ^{\prime })$ for all $\alpha$. Hence, by Theorem A.3, the subsampling design $\xi ^{\prime }$ cannot be optimal and, as a consequence, the optimal subsampling design $\xi ^*$ has support on three proper intervals with $b > 0$ for all $\alpha$. $\square$

Proof of Theorem 5.4

Let

$$\begin{aligned} u(\alpha )&= 45 - 15\alpha + 15\alpha ^2 - 45\alpha ^3 + 20\alpha ^4 \\&\qquad \,\,- 4\sqrt{5}\sqrt{45\alpha ^2 - 90\alpha ^3 + 90\alpha ^4 - 75\alpha ^5 + 57\alpha ^6 - 27\alpha ^7 + 5\alpha ^8} \end{aligned}$$

and

$$\begin{aligned} v(\alpha )&= 180 (1 - \alpha ) \, . \end{aligned}$$

Then

$$\begin{aligned} b(\alpha ) = \Biggl ( \frac{u(\alpha )}{v(\alpha )} \Biggr )^{1/2} - \frac{1}{2} (1 - \alpha ) . \end{aligned}$$

We have $u(0) = 45$, $v(0) = 180$, and $b(\alpha )$ can be continuously extended to $b(0) = 0$ at $\alpha = 0$. The derivative of b is given by

$$\begin{aligned} b'(\alpha ) = \frac{1}{2} + \frac{1}{2} \frac{u'(\alpha )v(\alpha ) - u(\alpha )v'(\alpha )}{v(\alpha )^2} \sqrt{\frac{v(\alpha )}{u(\alpha )}} \, , \end{aligned}$$

(14)

where

$$\begin{aligned} u'(\alpha )&= -15 + 30\alpha - 135\alpha ^2 + 80\alpha ^3 - w(\alpha ), \end{aligned}$$

(15)

$$\begin{aligned} v'(\alpha )&= -180 , \end{aligned}$$

(16)

and

$$\begin{aligned} w(\alpha )&= 2 \sqrt{5} \frac{90 - 270\alpha + 360\alpha ^2 - 375\alpha ^3 + 342 \alpha ^4 - 189\alpha ^5 + 40\alpha ^6}{\sqrt{45 - 90\alpha + 90\alpha ^2 - 75\alpha ^3 + 57\alpha ^4 - 27\alpha ^5 + 5\alpha ^6}} . \end{aligned}$$

We have $v'(0) = -180$. To determine $u'(0)$ we note that $w(0) = 60$ and thus $u'(0) = -75$. Hence, also the derivative $b'(\alpha )$ can be continuously extended at $\alpha = 0$ and the value for $b'(0)$ can be obtained by plugging in the values of u(0), v(0), $u'(0)$, and $v'(0)$ into formula (14),

$$\begin{aligned} b'(0) = \frac{1}{2} + \frac{1}{2} \frac{-75 \cdot 180 + 45 \cdot 180}{180^2} \sqrt{\frac{180}{45}} = \frac{1}{3} \, . \end{aligned}$$

Finally, we note that $b(\alpha )/\alpha$ is the percentage of mass on the interior interval $[-b(\alpha ), b(\alpha )]$ and that $\lim _{\alpha \rightarrow 0} b(\alpha )/\alpha$ is the derivative $b'(0)$ of $b(\alpha )$ at $\alpha = 0$. Hence, the percentage of mass on the interior interval tends to $b'(0) = 1/3$ when the subsampling proportion $\alpha$ goes to 0. $\square$

Proof of Theorem 5.6

The proof will follow the idea of the proof of Theorem 5.2. For $\alpha \in (0, 1)$, we consider the symmetric design $\xi ^\prime$ which is supported only on the tails and which will be the optimal subsampling design when $b = 0$. This design has density $f_{\xi ^\prime }(x) = \mathbbm {1}_{(-\infty , -a] \cup [a, \infty )(x)} f_X(x)$ with $a = t_{5, 1 - \alpha /2}$. The relevant entries of the information matrix $\textbf{M}(\xi ^\prime )$ are

$$\begin{aligned} m_2(\xi ^{\prime })&= \frac{5}{3\pi } \left( \pi - \frac{2\sqrt{5}a(a^2 - 5)}{(a^2 + 5)^2} - 2 \arctan (a/\sqrt{5}) \right) , \\ m_4(\xi ^{\prime })&= \frac{25}{3\pi } \left( 3\pi + \frac{10\sqrt{5}a(a^2 +3)}{(a^2 + 5)^2} - 6 \arctan (a/\sqrt{5}) \right) . \end{aligned}$$

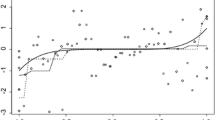
The sensitivity function $\psi (x, \xi ^\prime )$ and the difference $c(\alpha ) = \psi (0, \xi ^{\prime }) - \psi (a, \xi ^{\prime })$ between the values of the sensitivity function at $x = 0$ and $x = a$ are defined as for the normal distribution with the above moments $m_2(\xi ^{\prime })$ and $m_4(\xi ^{\prime })$ related to the t-distribution inserted. The function $c(\alpha )$ defined by (13) then looks as shown in Fig. 7.

Fig. 7

Difference $c(\alpha ) = \psi (0, \xi ^{\prime }) - \psi (a, \xi ^{\prime })$ (solid) for the case of a t-distributed covariate with 5 degrees of freedom

The vertical dotted line indicates the position of the critical value $\alpha ^{*} \approx 0.082065$, where the curve of the function $c(\alpha )$ intersects the horizontal dotted line indicating $c = 0$.

Thus for $\alpha < \alpha ^{*} \approx 0.082065$ we have $\psi (0,\xi ^{\prime }) > \psi (a,\xi ^{\prime })$ and the design $\xi ^\prime$ cannot be optimal by Theorem A.3. In this situation, an inner interval has to be included in the optimal subsampling design $\xi ^*$ with $b > 0$.

Conversely, for $\alpha \ge \alpha ^{*} \approx 0.082065$ we have that $\psi (0,\xi ^{\prime }) \le \psi (a,\xi ^{\prime })$. Hence, the design $\xi ^\prime$ is optimal by Theorem A.3, and no inner interval has to be added to the optimal subsampling design $\xi ^* = \xi ^\prime$ ($b = 0$). $\square$