Skip to main content
SpringerLink
Log in

Change point detection and estimation methods under gamma series of observations

  • Regular Article
  • Published:
Statistical Papers Aims and scope Submit manuscript

Abstract

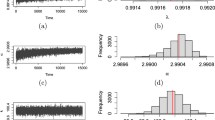
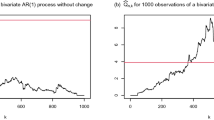
The aim of the article is to analyze inhomogeneous time series data caused by the presence of an unknown change point. We assume that the time series data are from a gamma distribution with an unknown time point of change in the scale and/or shape parameters. A complete change point methodology is proposed including change detection methodology based on the likelihood ratio statistic as well as estimation of the unknown change point by the method of maximum likelihood estimation (mle). Furthermore, we provide asymptotic distribution of the change point mle when a change occurs in the scale parameter of the gamma distribution. Extensive simulations have been conducted to show excellent agreement between the distribution of the change point under finite sample sizes and its asymptotic counterparts. The simulations are conducted under a change in the scale parameter as well as a change in both scale and shape parameters. A comparison analysis between known parameters and estimated parameters indicates that the error committed is negligible. Two examples, one from the financial market and another from climatology, are analyzed to adequately illustrate the proposed inferential methodology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Asmussen S (2003) Applied Probability and Queues. John Wiley, New York

    MATH  Google Scholar 

  • Bassiville, M., Nikiforov, I.V., 1998. Detection of Abrupt Changes: Theory and Application. Prentice-Hall, Inc.

  • Bai J (1995) Least absolute deviation estimation of a shift. Econmetr Th 11:403–436

    Article  MathSciNet  Google Scholar 

  • Bhattacharya GK, Johnson RA (1968) Non-parametric tests for shift at an unknown time point. Ann Math Stat 39:1731–1743

    Article  Google Scholar 

  • Borovkov AA (1999) Asymptotically optimal solutions in the change-point problem. Th Prob Its Appl 43:539–561

    Article  MathSciNet  Google Scholar 

  • Chen J, Gupta AK (2000) Parametric statistical change point analysis. Birkhäuser, New York

    Book  Google Scholar 

  • Csörgő M, Horváth L (1997) Limit theorems in change-point analysis. Wiley, New York

    MATH  Google Scholar 

  • Fotopoulos SB, Jandhyala VK, Khapalova E (2010) Exact asymptotic distribution of change-point MLE for change in the mean of Gaussian sequences. Ann Appl Stat 4:1081–1104

    Article  MathSciNet  Google Scholar 

  • Fotopoulos SB (2009) The geometric convergence rate of the classical change-point estimate. Stat Prob Lett 79:131–137

    Article  MathSciNet  Google Scholar 

  • Fotopoulos SB, Jandhyala VK (2001) Maximum likelihood estimation of a change point for exponentially distributed random variables. Stat Prob Lett 51:423–429

    Article  MathSciNet  Google Scholar 

  • Gombay E, Horvath L, Hušková M (1996) Estimators and tests for change in variance. Stat & Dec 14:145–159

    MathSciNet  MATH  Google Scholar 

  • Gombay E, Horvàth L (1996) On the Rate of Approximations for Maximum Likelihood Tests in Change-Point Models. J Mult Anal 56:120–152

    Article  MathSciNet  Google Scholar 

  • Gombay E, Horvath L (1990) Asymptotic distributions of maximum likelihood tests for change in the mean. Biometrika 77:411–414

    Article  MathSciNet  Google Scholar 

  • Haccou P, Meelis E, van de Geer S (1988) The likelihood ratio test for the change point problem for exponentially distributed random variables. Stoch Proc Appl 27:121–139

    Article  MathSciNet  Google Scholar 

  • Hinkley DV (1972) Time ordered classification. Biometrika 59:509–523

    Article  MathSciNet  Google Scholar 

  • Hinkley DV (1971) Inference about the change-point from cumulative sum tests. Biometrika 58:509–523

    Article  MathSciNet  Google Scholar 

  • Hinkley DV (1970) Inference about the change-point in a sequence of random variables. Biometrika 57:1–17

    Article  MathSciNet  Google Scholar 

  • James B, James KL, Siegmund D (1987) Tests for a change-point. Biometrika 74:71–83

    Article  MathSciNet  Google Scholar 

  • Jandhyala VK, Fotopoulos SB, MacNeill IB, Liu P (2013) Inference for single and multiple change-points in time-series. J Time Ser Anal 34:423–446

    Article  MathSciNet  Google Scholar 

  • Jandhyala VK, Fotopoulos SB (2001) Rate of convergence of the maximum likelihood estimate of a change-point. Sankhyă Ser A 63:277–285

    MathSciNet  MATH  Google Scholar 

  • Jandhyala VK, Fotopoulos SB (2000) A comparison of unconditional and conditional solutions to the maximum likelihood estimation of a change-point. Comp Stat Data Anal 34:315–334

    Article  Google Scholar 

  • Jandhyala VK, Fotopoulos SB (1999) Capturing the distributional behavior of the maximum likelihood estimator of a change-point. Biometrika 86:129–140

    Article  MathSciNet  Google Scholar 

  • Lundgren L (1993) Alternative Approaches to Evaluating the Impacts of Radionuclide Release Events: Chernobyl from the Swedish Perspective. Ambio 22:369–377

    Google Scholar 

  • Page ES (1955) A test for a change in a parameter occurring at an unknown point. Biometrika 42:523–526

    Article  MathSciNet  Google Scholar 

  • Page ES (1954) Continuous Inspection Schemes. Biometrika 41:100–115

    Article  MathSciNet  Google Scholar 

  • Persson C, Rodhe H, De Geer LE (1987) The Chernobyl Accident: A Meteorological Analysis of How Radionuclides Reached and Were Deposited in Sweden. Ambio 16:20–31

    Google Scholar 

  • Praagman J (1988) Efficiency of rank tests for the change-point problem. Ann Stat 16:198–217

    Article  MathSciNet  Google Scholar 

  • Siegmund, D., 1985. Sequential Analysis Tests and Confidence Intervals. Springer Series in Statistics.

  • Stoyan D, Daley DJ (1976) Comparison Methods for Queues and Other Stochastic Models. John Wiley, New York

    Google Scholar 

  • Veraverbeke N, Teugels JL (1975) The exponential rate of convergence of the distribution of the maximum of a random walk. J Appl Prob 12:279–288

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Finance and Management Science, Washington State University, Pullman, WA, 99164-4746, USA

    Stergios B. Fotopoulos

  2. Department of Information Systems and Business Analytics, Eastern Washington University, Cheney, USA

    Alex Paparas

  3. Department of Mathematics and Statistics, Washington State University, Pullman, WA, USA

    Venkata K. Jandhyala

Authors
  1. Stergios B. Fotopoulos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alex Paparas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Venkata K. Jandhyala
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stergios B. Fotopoulos.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fotopoulos, S.B., Paparas, A. & Jandhyala, V.K. Change point detection and estimation methods under gamma series of observations. Stat Papers 63, 723–754 (2022). https://doi.org/10.1007/s00362-021-01248-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00362-021-01248-x

Keywords

Search

Navigation