Abstract
We introduce semi-flexible majority rules for public good provision with private valuations. Such rules take the form of a two-stage, multiple-round voting mechanism where the output of the first stage is the default alternative for the second stage and the vote-share thresholds used in every round of binary voting (a) vary with the alternative on the table for a public-good level and (b) require a qualified majority for approving the alternative on the table by stopping the procedure. We show that these mechanisms implement the ex post utilitarian optimal public-good level, provided valuations can only be high or low. This public-good level is chosen after all potential socially optimal alternatives have been picked for a voting round. We explore ways to reduce the number of voting rounds and develop a compound mechanism when there are three or more valuation types.
Similar content being viewed by others
1 Introduction
A society has to choose the level of some public good, which is financed through uniform taxes. Individuals are heterogeneous regarding their preferred public-good level, and such preferences (and, thus, the individuals’ type) are private.Footnote 1 For this Bayesian setup, we introduce a family of voting mechanisms—called semi-flexible majority rules (SFMR), see below for more details—which implements the level of the public good that is optimal from an ex post perspective (end justice), provided individuals are of two types. Our family of mechanisms also satisfies desirable properties from a procedural viewpoint (procedural justice) and can be modified when individuals are of three or more types.
The starting point for our endeavor are so-called flexible majority rules (FMR), as surveyed in Gersbach (2017). FMR involve several voting rounds and work as follows: in every round, a binary vote takes place between the option to approve the proposal on the table—namely, a particular public-good level—and the option to stop the procedure with the last approved public-good level (or with the lowest feasible public-good level as a default option if no public-good level is approved). The successive proposals to be voted upon in this voting procedure are ordered increasingly from the lowest possible public-good level to the highest one. The vote-share thresholds needed to approve a given public-good level change with the proposal on the table. They increase from one vote to unanimity across the voting rounds in a way that mirrors the order in which the different public-good levels are voted upon. Equivalently, the vote-share thresholds needed to stop the procedure decrease from unanimity to one vote. Gersbach (2017) shows that FMR implement the ex post utilitarian optimum no matter the ex post citizens’ type distribution if citizens are of two types—those who want a low public-good level (low-type) and those who want a high public-good level (high-type). The voting procedure does so by granting a minority in every voting round either the right to approve a public-good level or the right to stop the procedure.
FMR are not without their drawbacks. As acknowledged in Gersbach (2017), “One particular feature [...] might be viewed as critical. It allows a minority to engineer a small change in the status quo.” Another problem with FMR is that a small minority may stop the procedure against the will of a large majority. Gersbach (2017) addresses these drawbacks by raising those vote-share thresholds used in FMR that are below the majority rule to at least half plus one of the votes. This is the method in some real-world procedures of successive voting rounds with varying vote-share thresholds.Footnote 2 However, this approach leads generically to second-best ex post utilitarian outcomes, even if individuals are of two types.
Our approach is different and aims at implementing the first-best ex post utilitarian outcome (whenever it is Bayesian incentive-compatible). We do this by introducing SFMR, which consist of two stages. The first stage is akin to FMR, so public-good levels are arranged in increasing order, with the vote-share thresholds needed for approving public-good levels varying from one vote to unanimity. When a vote-share threshold is not reached and the first stage ends, the mechanism does not stop but simply moves to the second stage, with the last approved public-good level being called the default (option). In the second stage, public-good levels are arranged in decreasing order and a majority of votes is required for choosing the level of the public good on the table by stopping the mechanism. The exact vote-share thresholds then depend on the default chosen in the first stage and are not arranged monotonically: they decrease for public-good levels higher than the default, and they increase for lower levels. In the basic description of SFMR, the lowest public-good level is considered to be the status quo and is chosen as the default if no first-stage threshold is attained, while the default is the final outcome of the mechanism if no second-stage threshold is attained.
For the analysis of the dynamic game underlying SFMR, we focus on perfect Bayesian equilibria in pure strategies. Moreover, to avoid implausible outcomes, agents iteratively eliminate weakly dominated strategies, moving backwards in the game tree. If individuals are of two types regarding public-good provision, we then show that SFMR implement the ex post utilitarian optimal public-good level—see Theorem 1. Hence, SFMR can replicate the outcome of FMR.Footnote 3
SFMR are a response, albeit only partial, to the drawbacks of FMR discussed above. By construction, SFMR (but not FMR) require a majority of votes to approve the public-good level on the table by stopping the procedure; we call this property majority approval. It can be seen as a desirable procedural feature. However, SFMR are still subject to the criticism that a minority can engineer a change in the status quo. Indeed, when the majority is of low type, no second-stage vote-share threshold is attained, and then the default approved in the first stage only by the minority of high type is the output of SFMR. This outcome can be avoided (a) on the equilibrium path if we modify the baseline setup so that each individual incurs a small, but positive cost in every voting round, and (b) on and off the equilibrium path if we modify SFMR so that the second stage is repeated until a vote-share threshold is attained. This means that (suitable extensions of) SFMR satisfy different versions of majority approval and that taken together, all these properties can address the tyranny of the minority that FMR exhibits more satisfactorily.
In contrast to FMR, with SFMR all public-good levels that are utilitarian optimal for some realization of the citizens’ valuations—called core alternatives—are picked on the equilibrium path for at least one voting round; we call this property inclusiveness. It can be seen as a procedural tenet in itself, since it guarantees that all core alternatives can be debated ahead of voting. Inclusiveness also means that every core alternative has a chance of being chosen. This feature can be particularly appealing when there is uncertainty about types at the individual level and/or the aggregate level, and it can lead to better outcomes compared to FMR. We illustrate these insights in a stylized extension of our baseline model.
The particular two-stage, multiple-round structure of SFMR enables this mechanism to deliver better outcomes than FMR also if the preferences of some citizens are not independent of the preferences of other citizens—i.e., if there are externalities at the preferences level—and if such preferences can be inferred from previous voting rounds. We illustrate this property of SFMR in another stylized extension of our baseline model, yet a comprehensive analysis of the subject is left for further research.
Two other contributions of our paper are worth highlighting. They apply to SFMR—our focus—but also to FMR (and, more generally, to other similar voting procedures implementing the ex post utilitarian optimum). First, we investigate how to reduce the number of voting rounds in equilibrium, which is of the order of the number of individuals. This number is small if our setup describes a (small) committee, say a few citizens acting as elected members of Parliament. With more individuals, one can (i) skip rounds according to some statistical information, e.g. if there is a correlation of preferences, or one can (ii) relax the utilitarian criterion and aim at approximating it with some margin of error.
Second, we also explore ways to move beyond two-type societies. With more than two types, we show that no Bayesian incentive-compatible mechanism can always implement the ex post utilitarian optimal solution. Yet, one can envision a number of mechanisms that elicit the citizens’ ex post type distribution and maximize ex post utilitarian welfare in certain cases, of which we explore one instance.
The paper is organized as follows: In Sect. 2 we review the papers that are most connected to our contribution. In Sect. 3 we set out the model and introduce our voting mechanism. In Sect. 4 we present our main result with two types of citizens. In Sect. 5 we discuss the case with three or more citizen types. Section 6 concludes. The proofs are in the Appendix.
2 Relation to the literature
Mechanisms based on fixed vote-share thresholds, e.g. the majority rule, have numerous advantages (Black 1948; May 1952; Maskin 1995; Moulin 2014). But they also have drawbacks (Arrow 1950; Gibbard 1973; Satterthwaite 1975; McKelvey 1976). For example, fixed majority rules cannot elicit the intensity of preferences, which makes the utilitarian optimum unattainable via such voting procedures (Green and Laffont 1977).
One can reconcile voting and ex post utilitarian welfare maximization by using flexible majority rules (FMR) (Bowen 1943; Gersbach 2017). Gershkov et al. (2017) prove that every unanimous and anonymous dominant-strategy incentive-compatible mechanism is outcome-equivalent to a successive procedure with decreasing thresholds in the form of FMR. We show that adding a confirmation stage to FMR does not change the outcome but makes the resulting procedure compatible with procedural concerns captured by majority approval—and, thus, by the majority rule.Footnote 4 According to Dahl (2008) and Sartori (1989), among others, the majority rule is a necessary procedural criterion of democracy.
There exist other mechanisms that make utilitarian welfare maximization compatible with voting, e.g. by using transfers (Ledyard and Palfrey 1994, 1999; Kwiek 2017).Footnote 5 Our mechanism renders utilitarian welfare maximization compatible with voting if there are two types but cannot generically achieve this if there are more types. The latter is in accord with the literature (see e.g. Gershkov et al. 2017) and occurs because intermediate types have incentives to misreport their valuations. Yet we offer one route how to extend the principles of our mechanism to the case of multiple types.
Our analysis connects our paper to other strands of the literature. First, Gersbach et al. (2021) show that it is beneficial for society to grant the initiative in proposal-making to the minority, with the majority having the opportunity to counter-propose. Our main finding complements this result. Instead of granting the first proposal, our setting enables a minority of the citizenry to have a say in setting the default that will be used in the final voting stage.
Second, when citizens are of two types, the problem which decision to adopt can be seen as a bargaining problem between two sets of agents, each corresponding to all citizens of the same type. There is an extensive body of literature on dynamic bargaining models where the outcome of one round is taken as a disagreement point for the next round (see e.g. Fershtman 1990; John and Raith 2001; Diskin et al. 2011; Grech and Tejada 2018). Our paper adds to this literature by studying a mechanism where both sets of agents jointly determine the disagreement point for the second stage.
3 Model
3.1 Setup
We consider a society of n individuals who decide about the level of a public good. We let \( n>2\) and assume that n is odd for ease of presentation.Footnote 6 Individuals are indexed by i, with \(i\in \{1,\ldots ,n\}\). Public-good levels are denoted by x or y, with \(x,y\in [0,\infty )\). The marginal cost of any unit of investment in the public good is \(c> 0\). Costs are distributed equally among individuals. There are two types of individuals, drawn from the type space \(\mathcal {T}=\{t^L,t^H\}\), where \(t ^L\) and \(t^H\) denote low type and high type, respectively (\(0<t^L < t^H\)). The type of individual i is denoted by \(t_i\), with \(t_i \in \mathcal {T}\). If an investment x is made, individual i derives utility from the public good equal to
with \(f(\cdot )\) being a real-valued function on \([0,+\infty )\) that is twice differentiable and satisfies \(f(0)=0\), \(f'(x)>0\), \(f''(x)<0\) for \(x>0\), \(\lim _{x\rightarrow 0^+}f'(x)=+\infty \), and \(\lim _{x\rightarrow \infty }f'(x)=0\). An example is \(f(x)=\sqrt{x}\). The first term, \(t_i\cdot f(x)\), is the benefit from the public-good level x, while the second term, \(\frac{c}{n}\cdot x\), is the per capita cost. Hence, from the implementation of any public-good level individuals of type \(t^H\) benefit more than individuals of type \(t^L\). According to Eq. (1), individual i’s utility is maximized at peak \(x_i:=x(t_i)>0\) defined by
Equation (1) defines a (strict) preference relation for citizen i, denoted by \(\succ _i\), over any finite set of public-good levels. This preference relation is single-peaked, with peak at \(x_i\), given the natural order according to which higher public-good levels are labeled with higher indices. Although equilibrium behavior for our mechanism is pinned down by \(\{\succ _i\}_{i=1}^{n}\), utilities \(\{v(\cdot ,t_i)_{i=1}^n\}\) are needed for the computation of utilitarian welfare.
Citizen types are privately drawn from a joint (prior) distribution that is common knowledge with the following property: for every \(k\in \{0,\ldots ,n\}\), the probability that there are exactly k individuals of the low type is positive. We do not specify the joint distribution as the properties of the mechanism that we consider do not depend on it.Footnote 7
Next, we determine the level of investment that maximizes utilitarian welfare. This investment level is denoted by \(x^{soc}\) and can be computed from Eq. (1) as follows:
It is convenient to introduce the notation \(t^{soc}=\frac{1}{n}\sum _{i=1}^n t_i\). The value \(t^{soc}\) can be interpreted as the socially optimal (virtual) type. Finally, for all \(j\in \{0,\ldots ,n\}\), we let \(y^j\) denote the public-good level defined by
which yields a unique solution for \(y^j\). That is, \(y^j\) is the preferred level of investment for a society with \(n-j\) individuals of type \(t^L\) and j individuals of type \(t^H\), as well as for a society consisting of n imaginary citizens of identical type \(\frac{n-j}{n} \cdot t^L+\frac{j}{n}\cdot t^H\). Since \(t^L<t^H\) and \(f'(\cdot )\) is decreasing, \(y^i<y^j\) if and only if \(i<j\). Then we define the set of alternatives
Set \(\mathcal {Y}\) consists of all the public-good levels that are utilitarian optimal for different combinations of individual types. Note that \(y^i>0\) for all \(i\in \{0,\ldots ,n\}\). Sometimes we refer to the elements of \(\mathcal {Y}\) as core alternatives—see Sect. 3.3. Unless specified otherwise, we assume that \(y^0\) is the status quo.
3.2 Semi-flexible majority rules
Next, we introduce Semi-Flexible Majority Voting Rules (SFMR). They are a family of mechanisms that consist of two stages. The first stage is akin to flexible majority rules (Gersbach 2017) and yields a default option \(\bar{x}\) for the second stage, where the final outcome is chosen. The sequence of events is as follows:
-
Stage 1
-
Round 1.1: A vote is held between (a) moving to Stage 2 with \(\bar{x}=y^0\) and (b) approving \(\bar{x}=y^1\) and moving to Round 1.2. At least one vote is required for the latter.
-
\(\vdots \)
-
Round \(1.(n-1)\): A vote is held between (a) moving to Stage 2 with \(\bar{x}=y^{n-2}\) and (b) approving \(\bar{x}=y^{n-1}\) and moving to Round 1.n. At least \(n-1\) votes are required for the latter.
-
Round 1.n: A vote is held between (a) moving to Stage 2 with \(\bar{x}=y^{n-1}\) and (b) approving \(\bar{x}=y^{n}\) and moving to Stage 2. Unanimity is required for the latter.
-
-
Stage 2 Let \(\bar{x}= y^k\), with \(k\in \{0,\ldots ,n\}\), be the outcome of Stage 1.
-
Round 2.1: A vote is held between (a) moving to Round 2.2 and (b) approving \(y^n\) as the final outcome and stopping the mechanism. Unanimity is required for the latter.
-
\(\vdots \)
-
Round \(2.(n-r+1)\) (with \(r\ge k\)): A vote is held between(a) moving to Round \(2.(n-r+2)\) and (b) approving \(y^{r}\) as the final outcome and stopping the mechanism. At least \(\max \left\{ r,\frac{n+1}{2}\right\} \) votes are required for the latter.Footnote 8
-
Round \(2.(n-r+1)\) (with \(r<k\)): A vote is held between (a) moving to Round \(2.(n-r+2)\) and (b) choosing \(y^{r}\) as the final outcome and stopping the mechanism. Unanimity is required for the latter.
-
\(\vdots \)
-
Round \(2.(n+2)\): If this round is reached, \(\bar{x}\) is chosen as the final outcome and the mechanism stops.
-
One can easily verify that all the public-good levels in \(\mathcal {Y}\) are the outcome of SFMR for certain voting behavior, so our mechanism satisfies onto-ness. Some further remarks are then in order. First, we assume that in every round all citizens vote simultaneously, and that the precise outcome of the vote is not made public. This means that what citizens see is whether they have moved to the next voting round within the same voting stage, whether they have moved to the next voting stage, or whether they have reached the end of the mechanism.Footnote 9
Second, in Stage 1, increasing thresholds have to be met to set higher levels of the public good as the default for Stage 2. This conveys the idea that higher levels of the public good as the default for subsequent voting necessarily require stronger support from the citizens. This property is illustrated by Fig. 1. Stage 1 corresponds to flexible majority rules as introduced in Gersbach (2017).
Stage 1—Number of votes (z) required to approve a public-good level and move to the next voting round. The mechanism starts with \(y^0\) as default public-good level and then considers a number of voting rounds where the public-good level \(y^r\) is on the table, with r starting at 1 and increasing one by one up to n
Third and last, in every voting round of Stage 2, a qualified majority of votes is required to approve an alternative from set \(\mathcal {Y}\) as the final outcome and to stop the mechanism. These thresholds depend on the outcome of Stage 1, viz. \(\bar{x}\) for some \(k\in \{0,\ldots ,n\}\). More specifically, the required threshold is minimal for \(\bar{x}\) and rises as the level of the public good deviates from \(\bar{x}\). For levels below \(\bar{x}\), in particular, unanimity is required. The specific vote-share thresholds for the different voting rounds of Stage 2 are shown in Fig. 2. Unlike in Stage 1, the thresholds in Stage 2 are not arranged monotonically.
Stage 2—Number of votes (z) required to approve a public-good level and stop the mechanism, with \(\bar{x}=y^k\) as the default set out in Stage 1. The mechanism starts with \(\bar{x}\) as default public-good level and then considers a number of voting rounds where the public-good level \(y^r\) is on the table, with r starting at n and declining one by one down to 1
3.3 Voting mechanisms: procedural justice and endstate justice
Our focus are SFMR, which are two-stage mechanisms with multiple binary voting rounds in each stage that take the outcome of the first stage as default for the second stage. To choose a public-good level, one could look more generally at voting mechanisms.Footnote 10 These can be defined as mechanisms with a (finite or infinite) number of stages and with multiple (finitely many) binary voting rounds in each stage, where the outcome of one stage—viz., some public-good level—is taken as default for the next stage. Moreover, there is an initial default, and in some voting rounds (not necessarily all) the mechanism can stop altogether.Footnote 11 Flexible majority rules (FMR) as surveyed in Gersbach (2017) are another instance of a voting mechanism, but there are many more, including some variations of SFMR that are defined in Sect. 4.3.
For now, we consider two properties of voting mechanisms. These properties specify procedural conditions that have no direct connection to outcomes. We follow Moulin (2008) and adopt the commonplace that “means matter as well as ends.” To the best of our knowledge, neither of these properties has received scholarly attention in the mechanism design approach to public good provision until now.
Majority approval: A majority of votes is required for the voting mechanism to approve the alternative on the table (viz. a public-good level) in some voting round by stopping the mechanism.Footnote 12
Majority support is essential for democracy. Giving too much decision power to a minority, no matter if this is only done nominally or effectively, may be recognized as a tyranny of such a minority. This could cast doubts on the legitimacy of the democratic decision-making scheme in question. Or it may be against the law. The legitimacy of decisions taken by voting mechanisms has long been the preoccupation of some philosophers and political scientists. Majority approval addresses some of these concerns formally. In Sect. 4.3, we discuss alternative versions of majority approval that capture such concerns from a different angle.
By definition, majority approval does not impose any requirement on vote-share thresholds for rounds where the mechanism cannot stop, as e.g. any first-stage voting round for SFMR. Not requiring a majority of votes for proposal-making is common in democracies.Footnote 13 It enables political action to be initiated by minorities. Majority approval also builds on this premise.
Inclusiveness (w.r.t. \(\pmb {\mathcal {Y}}\)): All alternatives from set \(\mathcal {Y}\) must be part of at least one voting round of the voting mechanism on the equilibrium path.Footnote 14
Recall that set \(\mathcal {Y}\), as defined in (4), contains all (core) alternatives that can be socially optimal from an ex ante perspective. Focusing on procedural aspects, inclusiveness is appealing for the following reasons. First, it ensures that citizens directly express their vote on all core alternatives. Second, inclusiveness therefore enables that all core alternatives are discussed ahead of voting. Thus, it can also be considered a property of deliberation. Third, suppose that the process through which individuals update their beliefs about the preferences of other citizens from the observation of voting outcomes is noisy. Consider those alternatives that citizens believe have a positive probability of being socially optimal from an interim perspective. Then, inclusiveness allows all such alternatives to be considered for a voting round.
Finally, as we show in Sect. 4.4, inclusiveness can also be an appealing property from an outcome perspective, at least in certain extensions of our baseline setup. More generally, the particular two-stage, multiple-round structure of SFMR enables these mechanisms to sometimes yield better outcomes than FMR. This is illustrated in Sect. 4.5.
4 Analysis
In this section we present our main result and provide a number of extensions.
4.1 Utilitarian welfare implementation
For our analysis, we consider perfect Bayesian equilibria in pure strategies and further assume that citizens eliminate weakly dominated strategies iteratively by moving backwards in the voting mechanism, and that this is common knowledge.Footnote 15 We obtain the following result:
Theorem 1
The outcome of Semi-Flexible Majority Rules (SFMR) is \(x^{soc}\).
Proof
See Appendix. \(\square \)
According to Theorem 1, SFMR implement the utilitarian social optimum ex post. Although uniqueness of beliefs is not guaranteed, all equilibria yield the same outcome.
For the intuition behind the above result, consider first Stage 2. For high-type citizens, approving the proposal on the table and stopping the mechanism weakly dominates voting to proceed to the next round in all rounds that consider public-good levels that are higher than, or equal to, the default \(\bar{x}\) set in Stage 1. In turn, for all rounds considering a lower public-good level than \(\bar{x}\), it is optimal for any citizen of the high type to vote to proceed to the next voting round. This is because unanimity is required for these rounds, and hence each high-type citizen knows that s/he can ensure that \(\bar{x}\) is eventually chosen if s/he always votes against stopping the mechanism and implementing a lower public-good level. As for low-type citizens, voting for the proposal on the table and stopping the mechanism is weakly dominated by voting to proceed to the next round in all rounds considering public-good levels that are higher than or equal to \(\bar{x}\), and it is also optimal for the remaining rounds (except the last one).
The most subtle decisions occur in the rounds considering a lower public-good level than \(\bar{x}\), in which unanimity is required to stop the mechanism: If a low-type citizen votes for the alternative on the table by stopping the mechanism, her/his vote might help to choose such a policy. If, on the contrary, s/he votes for the procedure to continue to the next round, the default determined in Stage 1 may be chosen if all remaining alternatives are subsequently rejected. Nevertheless, provided it is common knowledge that all citizens play no weakly dominated strategies in subsequent rounds and that high-type citizens hold correct beliefs about whether all agents are of the low type, each low-type citizen knows that her/his vote in these rounds is only pivotal when no citizen is of the high type (since unanimity is required to stop the mechanism in all such rounds and high-type individuals never vote to stop). In such a case, all low-type citizens ensure that the lowest public-good level is chosen by always voting to proceed to the next round until the last voting round of Stage 2 is reached.
Consider now Stage 1, assuming that citizens behave in Stage 2 as described above. It then turns out that the final outcome cannot be worse (better) for high-type (low-type) citizens as larger values of the default determined in Stage 1 are considered. This holds irrespective of the type composition of the electorate and the exact beliefs that the citizens have about it. Accordingly, voting to proceed to the next round in Stage 1 yields higher or equal utility for high-type individuals than choosing to stick to the last approved alternative and moving to Stage 2. For low-type individuals, the optimal voting decisions in Stage 1 are reversed.
4.2 Majority approval and inclusiveness
The next complementary result, which follows directly from the way SFMR is constructed and from the proof of Theorem 1, identifies further properties of this voting mechanism.
Corollary 1
SFMR satisfies majority approval and inclusiveness with respect to \(\mathcal {Y}\).
The appeal of majority approval and inclusiveness—and hence of SFMR—has been discussed in Sects. 3.3 and is further developed in Sects. 4.3–4.5. Majority approval is built into the mechanism, while inclusiveness depends on equilibrium behavior, and in particular on the individuals’ rationality. In our public-good provision setup, inclusiveness follows from the order in which the alternatives from set \(\mathcal {Y}\) are considered for binary voting: an ascending order in the first stage, and a descending order in the second stage.
In the proof of Theorem 1, we show that the alternative that maximizes utilitarian welfare, say \(y^k\in \mathcal {Y}\), is already chosen in the first stage of SFMR as default for the second stage, sometimes only with the explicit approval of a minority. It means that the second stage of SFMR serves as confirmation of the first stage, and hence of FMR. This property can be used as a theoretical justification for employing (much simpler and shorter) revelation mechanisms. Due to the way SFMR are constructed, alternatives \(y^1,\ldots ,y^k\in \mathcal {Y}\) are therefore considered for a round of binary voting in the first stage.
As for the second stage of SFMR, we distinguish two cases. On the one hand, when a minority of citizens are of the low type (i.e., when \(k\ge (n+1)/2\)), alternatives \(y^n,\ldots ,y^k\in \mathcal {Y}\) are considered for a round of binary voting in Stage 2. In the last round of SFMR on the equilibrium path, the mechanism stops with a majority of votes in favor of \(y^k\).
On the other hand, when a majority of citizens is of the low type (i.e., when \(k< (n+1)/2\)), \(y^n,\ldots ,y^0\in \mathcal {Y}\) are considered for a round of binary voting in Stage 2, and thus the second stage runs over all voting rounds. In all of these rounds, no alternative gathers the necessary votes to stop the mechanism, so the default chosen in the first stage is the outcome of SFMR. The fact that the first-stage default is only approved by a minority in such a stage does not contradict our formulation of majority approval, but it might be undesirable. It arises due to the rules of SFMR that regulate the scenario where no vote-share threshold is attained. However, there exist extensions of our setup and/or variations of our basic description of SFMR that do not feature this property. This is discussed next.
4.3 Two variants of majority approval
In our baseline setup, citizens do not discount payoffs that are attained at later voting rounds, and organizing a voting round does not lower the citizens’ utility. Under these assumptions, citizens do not care about how many rounds occur until a given outcome is reached.
What happens if either citizens discount future payoffs, albeit very little, or if the citizens’ utility decreases a bit every time a voting round takes place? If low-type agents are the majority and SFMR is run, the path described after Theorem 1 is no longer part of all equilibria if there is at least one agent of each type.Footnote 16 Indeed, at the round of the second stage where citizens must decide whether to proceed to another voting round in which a public-good level lower than the first-stage default \(\bar{x}\) could be chosen, namely Round \(2.(n-k+1)\), citizens already know the aggregate ex post type distribution. In particular, they know that there is at least one citizen of the high type. Hence, all citizens can anticipate that no threshold will be attained in the remaining rounds of the second stage, leading to implementation of \(\bar{x}\). Since this same outcome can be obtained if all citizens vote in favor of stopping the mechanism in Round \(2.(n-k+1)\), all citizens would prefer to do so to avoid the costs of having superfluous voting rounds. Following the logic of the proof of Theorem 1, one can verify that the latter will be part of one equilibrium, provided there is at least one citizen of each type.Footnote 17 Thus, SFMR satisfies the following property in at least one equilibrium:
De facto majority approval: A majority of votes is required for the voting mechanism to approve the alternative on the table (viz. a public-good level) in some voting round by stopping the mechanism. Moreover, the final outcome of the mechanism must be chosen on the equilibrium path by attaining a vote-share threshold that stops the mechanism and requires at least half of the votes plus one.
For finite voting mechanisms, one must specify the outcome if no threshold is attained. In the basic description of SFMR, \(y^0\) and \(\bar{x}\) are the defaults for Stage 1 and Stage 2, respectively. An alternative is the following: Stage 2 is repeated indefinitely (with \(\bar{x}\) chosen in Stage 1 as default) if no threshold is attained, which requires agents to discount payoffs attained at later voting rounds. Hence, \(\bar{x}\) cannot be implemented unless it gathers a majority of the votes, and this property must hold on and off the equilibrium path. As above, if high-type citizens are the minority and there is at least one of them, there is one equilibrium in which all citizens will unanimously vote to stop the mechanism in Round \(2.(n-k+1)\) the first time Stage 2 is run. Thus, SFMR satisfies the following property in at least one equilibrium:
De iure majority approval: A majority of votes is required for the voting mechanism to approve the alternative on the table (viz. a public-good level) in some voting round by stopping the mechanism. Moreover, the final outcome of the mechanism must be chosen by attaining a vote-share threshold that stops the mechanism and requires at least half of the votes plus one. Finally, the mechanism must end on the equilibrium path after a finite number of voting rounds.
Finally, we recall that Gersbach (2017) shows that the ex post utilitarian optimum is chosen by FMR in any equilibrium. This implies that FMR will neither satisfy de facto majority approval nor de iure majority approval. This could be used as a justification for employing SFMR (or variants) instead of FMR.
4.4 Inclusiveness from an outcome perspective
In practice, individuals may be uncertain about which alternative they prefer since there is uncertainty about the consequences of collective decisions. To illustrate this possibility briefly, suppose the simplest case in which there are two states of the world, u (unmixed) and m (mixed). At the onset, the priors about the state of the world, denoted by w, are \(P[w=u]=p\) and \(P[w=m]=1-p\), with p positive but arbitrarily small. If \(w=m\), the preferences of all individuals are given as in our baseline setup. By contrast, if \(w=u\), we assume that all individuals are of the low type. In each voting round, individuals receive a signal about the state of the world. The accuracy of these signals increases with the number of different core alternatives that have been put on the table so far, until the accuracy is perfect if and only if all core alternatives have been part of one voting round and the voting behavior has revealed the voters’ types. Since p is very small, FMR will lead to implementation of the public-good level that is optimal if \(w=m\). The reason is that deviations from the equilibrium supporting such an outcome involve potential individual gains that are arbitrarily small, while the potential individual losses are not arbitrary small.
The picture changes with SFMR. If \(w=m\), the outcome is the same as in our baseline setup, so the ex post utilitarian optimum is chosen. By contrast, if \(w=u\), SFMR leads to implementation of \(y^0\), which is also the ex post utilitarian optimum in such a state of the world. To see why this is the case, note that once the first-stage default, \(\bar{x}\), is the proposal on the table in the second stage (and, thus, all core alternatives have been on the table at least once for a round of voting), all individuals know the state of the world. If \(w=m\), the outcome will therefore be \(\bar{x}\). If \(w=u\), the outcome will be \(y^0\). Both results can be easily derived by mirroring the logic of the proof of Theorem 1. Finally, before \(\bar{x}\) is the proposal on the table in the second stage, all individuals behave as if the state of the world was m. As with FMR, this follows from the fact that deviating from the strategies supporting that outcome of Theorem 1 involves potential individual gains that are arbitrarily small, while the potential individual losses are not arbitrary small.
4.5 SFMR from an outcome perspective
As we have seen in the previous section, SFMR can be more appealing than FMR from an outcome perspective in an extension of our baseline setup. This is also the case if voting in the first stage offers valuable information for the second stage, due to the two-stage structure of SFMR. In Stage 1, each voter casts his/her ballot based solely on his/her individual preferences, without knowledge of the stance of all other voters on the issue. However, once the outcome of the first stage is known, voters can gain valuable insight into the voters’ profile and this may affect their preferences.
As an example, suppose that a small, low-income town proposes a public good package that includes the creation of parks, the renovations of homes and buildings, and improvements to infrastructure.Footnote 18 Initially, low-type citizens may oppose the plan due to potential tax hikes. However, after the first stage of voting, if the voter demographic reveals acceptance of the high level of the public good above a certain threshold, low-type citizens may be convinced to accept the high public-good level, as they are now aware of the long-term benefits of such renovations, e.g. increased tourism income, more business opportunities, improved education and healthcare, and a better quality of life, despite the short-term tax hike. Essentially, the presence of a sufficient number of high-type citizens exerts a positive externality on low-types.
Situations involving the above externalities can be captured by another extension of our baseline model. Let \(\mathcal {L}\subseteq \{1,\ldots ,n\}\) be the set of all low-type individuals and \(\mathcal {H}\subseteq \{1,\ldots ,n\}\) be the set of all high-type individuals. For some \(\hat{k}\in \{1,\ldots ,n\}\) and \(p\in (0,1)\), let also
Instead of being given by (1), the utility of individual i is now given by
Hence, if it turns out that the share of high types is sufficiently large, positive externalities might be created with probability p and the utility of all low-type citizens rises to the level of high-type citizens.
First, consider FMR. If p is below some threshold \(\bar{p} >0\) that depends on the parameters of the model, with positive probability the outcome does not correspond to the ex post utilitarian welfare optimum. To see this, it suffices to focus on the case where there are exactly \({\hat{k}}\) high-type individuals. Clearly, the voting process will reach alternative \(y^{\hat{k}}\), at which point individuals can only know that there are \(\hat{k}\) or more individuals of the high type. Now, none of the low-type individuals will vote to proceed to alternative \(y^{\hat{k}}\) and to mimic the behaviour of high-type individuals, since the potential individual gains are arbitrarily small and the potential individual losses are not arbitrary small. Hence, with FMR, the alternative \(y^{\hat{k}+1}\) will never be tried despite its positive probability of being socially preferred over \(y^{\hat{k}}\). Since with probability p the socially optimal alternative is \(y^{n}\), further, and potentially even more preferred, alternatives are not tested.
Second, consider SFMR. It is straightforward to show that the outcome will be the ex post socially optimal alternative. In Stage 1, all agents vote according to their preferences and would approve \(y^{1}\) until \(y^{\hat{k}}\) if, for instance, there are \({\hat{k}}\) high-type individuals. At this point, all individuals know that there are exactly \({\hat{k}}\) high-type individuals and they have observed whether positive externalities have been created and thus whether the process in Stage 1 continues or not. In Stage 2, the voting process starts with \(y^{n}\). If externalities are present, this alternative is socially optimal and is adopted by stopping the mechanism. If externalities are not present, the process continues and the default chosen in Stage 1 is implemented, which is also socially optimal.
4.6 Further discussions
Several further discussions of Theorem 1 shed light on its relevance and implications. Some of our insights apply beyond SFMR.
Fewer rounds
The large number of voting rounds—both on and off the equilibrium path—when SFMR is run is the consequence of the following: (i) the mechanism yields the ex post utilitarian optimum, (ii) the mechanism is detail-free, and (iii) the mechanism only considers rounds of binary voting, without any (explicit) proposal-making stage.
Nevertheless, one can reduce the number of voting rounds in certain cases if we relax some of the above features.Footnote 19 First, if the joint distribution of types has small support—e.g. because the preferences of different individuals are highly correlated—, all rounds can be skipped in which the alternative considered for voting cannot be a socially optimal alternative for some preference profile. On the other hand, an approximately socially optimal solution may suffice when the number of citizens is considerable. If n is large and the citizens’ types are i.i.d., in particular, the Central Limit Theorem guarantees that the socially optimal type is distributed approximately normally, with a mean \(\mu \) and a variance \(\sigma \) that could be estimated. Then one could add a criterion to our procedure to exclude the tails of the distribution and hence exclude the most extreme policies. For instance, for a given \(\alpha \ge 0\), the set
could be considered to run the mechanism instead of the entire set \(\mathcal {Y}\) as defined in (4). In such case, the maximal total number of rounds of the modified mechanism would be approximately equal to twice the cardinality of \(\mathcal {X}\). Parameter \(\alpha \) determines the (expected) loss of efficiency that such a mechanism would induce. The larger \(\alpha \), the lower the loss.
Second, one could consider an arbitrary finite subset \(\mathcal {Z}=\{z_1,z_2,\ldots \} \subseteq \mathcal {Y}\) consisting of a (small) number of provision levels of the public good, with \(z_k<z_l\) if and only if \(k<l\). One possibility is that \(\mathcal {Z}\) consists of public-good levels proposed by political parties, by regions within the same country, or by a popular initiative (in direct democracies). As before, one could then easily adapt SFMR to run only over the rounds corresponding to elements of \(\mathcal {Z}\), with the corresponding vote-share thresholds. While such variation of SFMR would not implement the utilitarian optimal solution in general, it would yield the element in \(\mathcal {Z}\) that is closest to the socially optimal level. This modified mechanism would satisfy majority approval and inclusiveness with respect to \(\mathcal {Z}\).Footnote 20
Less demanding majority thresholds
SFMR requires qualified majorities in Stage 2 for changes to the outcome of Stage 1, and unanimity, in particular, for public levels that are lower than the one specified in the default chosen therein. For a range of rounds, however, a whole family of qualified majority thresholds ensures utilitarian optimality, which includes the thresholds set out in Sect. 3. This is shown in the Appendix (see also Footnote 8). More specifically, given that \(y^k\) is the outcome of Stage 1, it suffices for the majority thresholds of Round 2.1 to Round \(2.(n+1-k)\) to be non-increasing, ranging from unanimity to a certain qualified majority (never lower than half plus one of the votes). This guarantees that high-type citizens cannot impose a public-good level that is higher than the socially optimal level. By contrast, the unanimity rule required in any voting round after Round \(2.(n+1-k)\) grants any individual the veto power to impose the default as the final outcome, which ensures optimality for any number of citizens of the low type.
The vote-share thresholds of Stage 2 can be lowered further when the possible number of high- or low-type individuals is bounded, and in particular when individual types are not drawn independently from each other. For instance, suppose that the number of high-type individuals has support \(\{0,\underline{n},\underline{n}+1,\ldots ,n\}\) for some \(\underline{n}\) with \(1<\underline{n}<n\). Then the unanimity thresholds that apply to public-good levels lower than the default can be lowered to \(\max \{n-\underline{n}+1,\frac{n+1}{2}\}\). The reason is that situations with only a few high-type individuals (below \(\underline{n}\)) cannot occur. In these circumstances, each high-type individual enjoys a de facto veto power enabling her/him to block the approval of any alternative that requires more than the support of \(n-\underline{n}\) citizens of the low type. Knowing this, low-type citizens also vote to proceed to the next round, since their vote only makes a difference if there are no citizens of the high type at all.Footnote 21
Two voting bodies
Some of the voting processes that are used in democracy entail two distinct stages, with the output of the first stage being taken as input for the second stage.Footnote 22 Semi-flexible majority rules have the same structure. Proceeding in two stages also allows separating the final decision-making phase from an initial phase of proposal-making, thereby making it possible for each stage to be subject to different desiderata.
What would be the outcome of SFMR if two different groups (with different aggregate preferences) participated in each stage of the mechanism? As it follows from the proof of Theorem 1, the first-stage group would choose the alternative maximizing the first group’s utilitarian welfare as default for the second stage. In Stage 2, however, the second group might end up choosing a different public-good level. Depending on the preferences of the two groups, this level could either maximize the first group’s utilitarian welfare or the second group’s utilitarian welfare, or neither. Regardless of the outcome, our mechanism would elicit the aggregate preferences of both groups, since all individuals would vote sincerely according to such preferences.
Conditioning on types
By construction, SFMR depends on the citizens’ utility function, since the elements of set \(\mathcal {Y}\) are calculated with the benefit function f. However, SFMR could be easily adapted to hinge on types rather than on policies if types are constant—though private—and the function f can take several forms. This would expand SFMR’s applicability to a wider range of problems.Footnote 23 For such a procedure to be implementable, it should be legal to base a democratic procedure for public-good provision on the aggregate type distribution, e.g. on the aggregate income distribution, rather than on the policies themselves.
Voting costs
In our baseline setup, citizens incur no voting costs. If voting is costless for citizens, abstaining in any round can be ruled out by sequential elimination of weakly dominated strategies. If voting were costly, citizens would like to vote only in those rounds where they are pivotal—if they want to vote at all. Yet, if the cost of voting in each round is small relative to the benefits from public good provision divided by the total number of rounds, our results would remain valid, as the well-known underdog effect would be avoided (see e.g. Börgers 2004).
Different default alternative
In our analysis of SFMR, we have proceeded on the assumption that the initial default alternative is \(y^0\), which coincides with the status quo (if there is one). It is the lowest level of public good that all societies accept. This situation could correspond to one-shot decisions on the provision of a certain public good such as building a high-speed train network of a given size from scratch, as then the status quo is zero by definition. In other cases, the decisions on public goods are recurrent, and the outcome of one decision becomes the status quo for the next decision. This is typically the case for expenditures on education—say, on public schools—or on defense. There are two ways in which SFMR could be used in such cases.
First, suppose that only increments on the public-good level can be approved. Then, our baseline model can simply be recast to assume that \(y^0\) is the status quo inherited from the previous execution of the mechanism. Second, suppose that the status-quo public-good level can be increased or decreased through SFMR. This can be captured by our baseline setup with the modification that if no threshold is attained in the first stage, the status quo inherited from the previous execution of the mechanism (viz., some \(y^k\), with \(k\in \{0,\ldots ,n\}\)) becomes the default for the second stage. With the description of SFMR, if all citizens are of the low type, they would have to vote for \(y^1\) as the default for the second stage to ensure that one threshold is met and \(y^k\) is chosen as default. Yet our proof of Theorem 1 shows that \(y^0\) would then be chosen in the second stage, and thus the ex post utilitarian optimum would also be attained in that case. Because flexible majority rules consist only of one round, they would not display this property when all individuals are of the low type.
Alternative rationality assumptions
The equilibrium notion we have used in our analysis requires that it is common knowledge that all citizens iteratively eliminate weakly dominated strategies by moving backwards in the game. Yet, Theorem 1 could also be obtained if citizens used cut-off strategies in Stage 2, according to which an individual can only change her/his vote (proceed or stop) at most once along the different voting rounds of a stage. Iterative elimination of weakly dominated strategies by moving backwards in the game can thus be seen as a foundation for such cut-off (behavioral) rules, in the case of two-stage, multiple-round voting mechanisms.Footnote 24
5 Multiple Types
In the previous section, we have assumed that individuals are of two types, low and high. In this section, we address the general case in which individuals can be of any finite number of types. First, we prove that for three or more types there is no Bayesian incentive-compatible mechanism that implements the ex post utilitarian optimum. Second, we explore one way to extend the application of SFMR when citizens can be of three or more types. The purpose of this second part is to show that it is possible to reconcile to some extent the principles behind SFMR if there are two types of agents with the impossibility result of the first part of this section.
5.1 A counter-example
With two types, SFMR implements the utilitarian optimal solution and elicits the information about how many individuals are of each type. Two noteworthy features occur when there are only two types of agents. First, there are as many different thresholds and different ratios of citizens of the two types as there are citizens in the population plus one. This makes it possible for the citizens to express the distribution of types through rounds of binary voting. Second, with two types, individuals have single-peaked preferences regarding public good provision with peaks at one of the two extremes of the set of alternatives \(\mathcal {Y}\), viz. \(y^0\) or \(y^n\).Footnote 25
The picture changes dramatically when individuals are of three or more types. To see this, we consider the following example: \(f(x)=\sqrt{x}\), \(c=1\), \(n=3\) and \(\mathcal {T} = \{t^L,t^M,t^H\}\), with \(t^L=1\), \(t^M=2\), and \(t^H=4\). The individual peaks for each type are
Using Eq. (3), the socially optimal level is equal to
where \(t_i\in \mathcal {T}\) is the type of individual \(i\in \{1,2,3\}\). Types are drawn i.i.d. from a probability distribution such that for any individual i,
where \(\varepsilon \) is strictly positive but arbitrarily small. Then consider the direct mechanism where individual \(i\in \{1,2,3\}\) reports \(\tilde{t}_i \in \mathcal {T}\) and the following public-good level is implemented:
This mechanism would be the only direct mechanism that implements the utilitarian optimum, provided that individuals report their types truthfully. Clearly, for individuals of types \(t^L\) and \(t^H\), it is weakly dominant to report their type truthfully. What about individuals of type \(t^M\)? By reporting their type truthfully and anticipating that the other two individuals are of type \(t^L\) with very high probability, they expect a payoff \(v^{truth}\), with
If individuals of type \(t^M\) report \(t^H\) instead, they expect a payoff \(v^{no truth}\), with
Hence, the direct mechanism is not Bayesian incentive-compatible, and by invoking the revelation principle, there is no mechanism that is Bayesian incentive-compatible and can implement the ex post utilitarian optimal solution \(x^{soc}\) in general.
5.2 A generalized voting mechanism
Next we show that with any finite number of types we can design a mechanism based on SFMR that implements the utilitarian optimal solution in some cases and that always elicits the information about how many citizens there are of each type. A similar line of reasoning could be applied to other voting mechanisms, in particular with FMR. Yet our focus on SFMR allows to see how majority approval and inclusiveness can be extended to multiple types.
Accordingly, suppose that there are \(T\ge 2\) possible types and let the type of individual i be denoted by \(t_i\), where \(t_i \in \mathcal {T}=\{t^1,\ldots ,t^T\}\) and \(0<t^1< \ldots <t^T\). The utilitarian optimal outcome is still given by Eq. (3). This means that any (voting) mechanism intending to implement such an outcome should involve the set of alternatives \(\mathcal {Y}\), where now
and \(n_l\) is the number of individuals of type \(t_l\). Then define the public-good level \(y^j_l\) for all \(l\in \{1,\ldots ,T-1\}\) and \(j\in \{0,\ldots ,n\}\) by
as well as the set
We note that \(y^j_l\) is the optimal public-good level when \(n-j\) individuals are of type \(t^l\) and j individuals are of type \(t^{l+1}\). By construction,
Sets \(\mathcal {Y}_1,\ldots ,\mathcal {Y}_{T-1}\) do not cover set \(\mathcal {Y}\), but there is a mapping from \(\mathcal {Y}\) to the set of type distributions such that every element of \(\mathcal {Y}\) can be written as a linear combination of the mapping of elements in \(\bigcup \limits _{l=1}^{T-1} \mathcal {Y}_l\). The optimal policy (i.e., the peak) for type \(t^1\) is
for type \(t^T\) is
while for type \(t^l\), with \(l\in \{2,\ldots ,T-2\}\), the optimal policy is
To construct our compound mechanism for multiple types, we introduce an initial communication stage, denoted by Stage 0. In this communication stage, citizens can express their preference as to which set of alternatives should be chosen for running SFMR—see set \(\mathcal {Z}\) below. To describe this communication stage, we introduce further notation.
Given citizen i’s preference relation \(\succ _i\) over the set of alternatives \(\mathcal {Y}\), define the preference relation \(\succ _i^T\) over the set (of sets)
as follows (with \(j,j'\in \{1,\ldots ,T-1\}\)):
In words, \(\mathcal {Y}_j \succ ^T_i \mathcal {Y}_{j'}\) if, for individual i of type \(t_i\), (a) no alternative in \(\mathcal {Y}_{j'}\) is better than an alternative in \(\mathcal {Y}_j\) and (b) there exists at least one alternative in \(\mathcal {Y}_j\) which is better than some alternative in \(\mathcal {Y}_{j'}\). Due to the way we constructed the elements of set \(\mathcal {Z}\), relation \(\succ ^T_i\) orders such elements completely. Moreover, from (7)–(9) it follows that \(\succ ^T_i\) is single-peaked (given the order \((\mathcal {Y}_1,\ldots ,\mathcal {Y}_{T-1})\)) with peak \(\mathcal {Y}_1\) if citizen i’s type is \(t^1\), peak \(\mathcal {Y}_{T-1}\) if citizen i’s type is \(t^T\), and peak(s) in \(\{\mathcal {Y}_{l-1},\mathcal {Y}_{l}\}\) if citizen i’s type is \(t^l\) (\(l\in \{2,\ldots ,T-2\})\).Footnote 26 If we assume that citizens play no weakly dominated strategies, it is clear that to decide which two elements of \(\mathcal {Z}\) should be chosen for SFMR to be run, citizen i chooses according to \(\succ _i^T\).
For citizen i, let \(\tau _i\in \mathcal {Z}\) denote his/her peak (or type) according to \(\succ _i^{T}\). Then consider
to be any (direct) mechanism, possibly non-deterministic, that assigns reported types \((\tau _i)_{i=1}^n\) (i.e., a vector of elements of \(\mathcal {Z}\)) to an element of \(\mathcal {Z}\). We assume that G is Pareto efficient, anonymous, and dominant-strategy incentive-compatible. By Moulin (1980), we know that such mechanisms exist, e.g. generalized median mechanisms.
Taking G as given, the G-generalized SFMR is a (non-deterministic) mechanism that specifies the following course of events:
-
Step 0: Apply G to \(\mathcal {Z}\). We let \(p_l=p_l(\tau '_1,\dots ,\tau '_n)\) denote the probability that \(\mathcal {Y}_l\), with
 , is the outcome of G when citizens send messages \((\tau '_i)_{i=1}^n\). The numbers \(p_1,\ldots ,p_{T-1}\ge 0\) satisfy \(\sum _{j=1}^{T-1}p_j=1\) and are not made public.
, is the outcome of G when citizens send messages \((\tau '_i)_{i=1}^n\). The numbers \(p_1,\ldots ,p_{T-1}\ge 0\) satisfy \(\sum _{j=1}^{T-1}p_j=1\) and are not made public. -
Step 1: Apply SFMR to \(\mathcal {Y}_1\), which yields as outcome an element \(y_1^{i_1}\in \mathcal {Y}_1\). Then define \(N^1\in \{0,\ldots ,n\}\) by \(N^1=n-i_1\).
-
\(\vdots \)
-
Step \(T-1\): Apply SFMR to \(\mathcal {Y}_{T-1}\), which yields as outcome an element \(y_{T-1}^{i_{T-1}}\in \mathcal {Y}_{T-1}\). Then define \(N^{T-1}\in \{0,\ldots ,n\}\) by \(N^{T-1}=n-i_{T-1}\).
-
Step T: The final outcome is the allocation \(y\in \mathcal {Y}\) chosen in accordance with the following rule:
$$\begin{aligned} y= {\left\{ \begin{array}{ll} y^{n-N^1}_1 &{} \text{ with } \text{ probability } p_1,\\ \ldots &{} \\ y^{n-N^{T-1}}_{T-1} &{} \text{ with } \text{ probability } p_{T-1}. \end{array}\right. } \end{aligned}$$
The G-generalized SFMR operates as follows. The (final) outcome is chosen randomly from one of the (potential) outcomes of \(T-1\) applications of SFMR, each of which considers a different set of alternatives. The weights according to which the non-deterministic mechanism chooses one particular application of SFMR are determined by the individuals themselves prior to running all SFMR applications, although they are not disclosed.
With most of the formal analysis in the Appendix, some remarks about the G-generalized SFMR are in order here.
Principles behind the G-generalized SFMR
The first observation is that the G-generalized SFMR captures to some extent the principles behind inclusiveness and approval. As for inclusiveness, all elements of \(\cup _{l=1}^{T-1}\mathcal {Y}_l\) are voted upon in at least one round of the corresponding application of SFMR. With multiple types set \(\mathcal {Y}\) can be extremely large, so focusing on \(\cup _{l=1}^{T-1}\mathcal {Y}_l\) might suffice. As for majority approval, each application of SFMR satisfies the property and the final outcome is the outcome of one of such applications. Hence, the concerns that majority approval tries to address are also dealt with to some extent by the G-generalized SFMR in the case of multiple types.
Any fairness and efficiency property of G carries over to the G-generalized SFMR. For instance, if G chooses the median generalized type (Moulin 1980), the G-generalized SFMR combines majoritarian concerns in a first step, and utilitarian concerns in a second step. From Moulin (1980), we know that generalized median mechanisms (i.e., the set of all strategy-proof voting mechanisms) can only implement order statistics such as the median but not the mean. Thus, with the G-generalized SFMR we offer a way of accommodating two principles—strategy-proofness and utilitarian welfare maximization—that are conflicting when there are three or more types.
Elicitation of types
For every application of SFMR, individuals report their preferences sincerely. This follows from (7)–(9) because (within each SFMR) individuals iteratively eliminate strategies that are weakly dominated, and, in particular, they never play strategies that are weakly dominated. Take \(\mathcal {Y}_1\), for example. Individuals of type \(t^1\) prefer the lowest possible public-good level (within \(\mathcal {Y}_1\)). Individuals of type \(t^2,\ldots ,t^T\) prefer the highest possible public-good level (within \(\mathcal {Y}_1\)). Because the outcome of SFMR running over \(\mathcal {Y}_1\) does not depend on any other application of SFMR, every individual who is not of type \(t^1\) votes as if s/he were of type \(t^2\). Analogous comments hold for the application of SFMR to sets \(\mathcal {Y}_2,\ldots ,\mathcal {Y}_{T-1}\). This means that if we let \(N^T=n\) and solve
then \(n_l\) is equal to the number of individuals of type \(t^l\), with \(l\in \{1,\ldots ,T\}\). Hence, the G-generalized SFMR elicits the information how many individuals there are of each type.Footnote 27
Outcome of the G-generalized SFMR
In general, \(x^{soc}\) is not implemented by the G-generalized SFMR (see the Appendix for a detailed account of the equilibria of the underlying game). Yet, the outcome of the G-generalized SFMR is an element of \(\cup _{l=1}^{T-1} \mathcal {Y}_l\).
Let us consider the case where agents are only of two types. We also assume that citizens receive sufficiently informative, yet noisy, public signals about the type distribution. This can be a good representation of societies that are polarized on some issue if the power to make proposals is in the hands of two organized groups. Let \(t^L,t^R\) (\(L,R\in \{1,\ldots ,T-1\}\)) be the two types that are present in the population, with \(L\le R-1\). For simplicity, we focus on the case where G selects the median (with probability one).
We start by considering the case where \(L=R-1\). Then, the utilitarian optimal solution belongs to \(\mathcal {Y}_L\). This outcome would be chosen by the G-generalized SFMR if there are more individuals of type \(t^L\) than of type \(t^R\). If there are more individuals of type \(t^R\) than of type \(t^L\), then \(y_{R}^0\in \mathcal {Y}_R\) would be chosen, which is itself close to the utilitarian optimum. Next, consider the general case, in which \(L\le R-1\). Then the utilitarian optimal solution belongs to set \(\cup _{l=L}^{R-1}\mathcal {Y}_{l}\). The outcome of the G-generalized SFMR would be \(y_{L}^j\in \mathcal {Y}_L\) (\(y_{R}^n\in \mathcal {Y}_{R-1}\)) if \(j>n-j\) (\(j<n-j\)), where j denotes the number of individuals of type \(t^L\).
Equation (1) implies that all citizens have concave utility in the public-good level, and hence that they are risk-averse. This means that if the probability that either type is the majority is close to 1/2, it would be in the best interest of both groups of individuals to run SFMR with only two types—\(t^L\) and \(t^R\)—instead of running the G-generalized SFMR over the entire set \(\mathcal {Z}\), which corresponds to types \(t ^1,\ldots ,t^T\). The former mechanism would implement the utilitarian optimal solution.
Finally, consider large populations. Then a social planner could randomly sample a (representative) subpopulation of individuals, who would then participate in the voting mechanism. The social planner would observe the actions taken by the individuals from the subpopulation when participating in the mechanism. S/he would also commit to transferring an amount of money to the participants that matches the utility these individuals would have gotten had the public-good level been implemented with the G-generalized SFMR, plus a sufficiently large fixed amount to ensure individual rationality in the augmented mechanism which includes the prior stage in which individuals can either accept or decline to be part of the sample. Then, with the information yielded by the mechanism, the social planner could implement a public-good level that approximates the utilitarian optimum for the entire population with arbitrarily high precision. It would suffice to sample sufficiently many individuals. With a very large population, the relative size of the sample would be negligible, and so would be the required transfers. These transfers could be financed by lump-sum taxes by the rest of the population.
The insight that large populations can approximate the utilitarian optimal solution when a voting procedure based on qualified majority rules is used is not new. Gershkov et al. (2017) show that the mean can be approximated by the right order statistic in large societies when types are continuous. Our approach, however, is different since we propose to build on the properties (i) that our voting mechanism elicits the preferences of a (representative) sample of participants and that (ii) by the law of large numbers the preferences of these voters will represent those of the entire population with arbitrarily high precision.
6 Conclusions
We presented a new (voting) mechanism that implements the utilitarian optimum in a standard problem of public-good provision when there are two types of citizens. Unlike other known mechanisms which use multiple-round voting with varying thresholds, we imposed the property that such thresholds require more than half of the votes to stop the mechanism and approve the public-good level on the table. This is a restriction often encountered in real settings. It reflects the majoritarian logic of democracy; we called this property majority approval and investigated several versions of this property. Our mechanism also displays the property that, on the equilibrium path, all potential socially optimal proposals are considered for voting at some point in time, which can foster deliberation. This property, which we have called inclusiveness, may also be desirable in real voting applications.
Our insights are also relevant from a purely positive perspective. It is known that reference points as default policies may have an impact on the outcome of voting procedures through various channels (see e.g. McKelvey 1976; Kahneman and Tversky 2013). We showed that the utilitarian optimal outcome can be attained when the reference point—i.e., the default—and the vote requirements for changing this reference point are chosen appropriately in an endogenous way by the population of individuals. This could be useful for the (optimal) design of thresholds for political action initiated by citizens, be it through signature gathering or through other means by which minorities can be granted the right to propose policies.
Finally, there are avenues for future research. For instance, one could characterize semi-flexible majority rules by using approval and inclusiveness together with other properties.
Notes
The features we impose on our problem of public good provision suffice for any alternative to be identified by a number, which is the assumption we need for our analysis. This means that our results carry over to other setups in which this magnitude is e.g. a tax levy or the minimum wage.
With two types, the output of the first stage—the default—is already the ex post utilitarian outcome. Hence, the second stage of SFMR serves as confirmation of FMR.
Hence, our results can be read as justifying the use of FMR or much simpler direct revelation mechanisms as shortcuts of SFMR.
We consider a mechanism with additional restrictions based on procedural considerations, so we depart from the standard mechanism design literature—see Bierbrauer and Sahm (2010) or Bierbrauer and Hellwig (2016) for recent papers where such considerations are central. Yet it is worth noting that the mechanism we suggest is incentive-compatible, anonymous, unanimous, and non-manipulable.
If n were even, we would need to specify what the outcome of any binary voting is when the threshold of some voting round is exactly n/2 and there are n/2 individuals voting in favor of one option and n/2 in favor of the other. Different rules for such decisions may yield different votes along the equilibrium path, but they all implement the utilitarian optimal solution.
The validity of Theorem 1 does not hinge on the assumption that the prior type distribution has full support, but proceeding with this assumption facilitates the analysis.
If we set \(h=n+1-r\), the majority threshold considered in Round h, with \(h\in \{1,\ldots ,n+1-k\}\), is \(f^k(h):=\max \left\{ n+1-h, (n+1)/2\right\} \). It turns out that for Theorem 1 to hold (see Sect. 4), it suffices to consider that \(\{f^k(\cdot )\}_{k=0}^n\) is a collection of non-increasing, onto functions \(f^k:\{1,\ldots ,n+1-k\}\rightarrow \{\max \{(n+1)/2,k\},\ldots ,n\}\) such that \(f^{k+1}(\cdot )\le f^k(\cdot )\). This is discussed in the Appendix.
Thus, SFMR guarantee privacy even for small groups of agents. Concerns about privacy in the context of voting, or more generally in the context of social choice, can be connected to concerns about freedom of choice (see e.g. Brandt and Sandholm 2005; Chevaleyre et al. 2007). Our results hold for more detailed disclosure policies.
We use the term voting as coined by Bierbrauer and Hellwig (2016), which means that “[...] the public good that is provided depends on the number of people preferring this level over the alternatives, without regard to the intensities of people’s preferences.”
Many democratic decision-making procedures are based on up-or-down (or binary) votes. Binary votes are simple and can prevent inefficiencies such as coordination failures.
We assume that no abstention occurs. Hence, absolute majority is equivalent to relative majority.
In Switzerland, 100,000 valid signatures are enough to propose a change to the Federal Constitution by triggering a popular vote in which the parliament can propose a counter-project instead of the status quo. A double majority (of votes and of cantons) is required to approve the change. See https://www.bk.admin.ch/bk/de/home/politische-rechte/volksinitiativen.html, retrieved on 29 October 2020.
Different possibilities for set \(\mathcal {Y}\), and thus for inclusiveness, are discussed in Sect. 4.6.
Iterative elimination means that, starting from the last voting round and moving backwards across voting rounds, all individuals eliminate iteratively all weakly dominated strategies for each voting round.
If all individuals are of the same type, the problem is trivial.
The proof of Theorem 1 remains valid for all rounds after Round \(2.(n-k+1)\). Now, all agents voting to stop at Round \(2.(n-k+1)\) yields \(\bar{x}\), but deviating also yields \(\bar{x}\), albeit possibly with some additional cost or discount. Hence, all agents voting to stop at Round \(2.(n-k+1)\) yields \(\bar{x}\), and each of them is best-responding to each other. Yet there might be other choices where they best-respond to each other. At Round \(2.(n-k+1)\), neither choice is weakly dominated. The analysis of any previous round remains the same.
This example is stylized and much more sophisticated examples could be considered.
This can be justified in several ways. For instance, drawing on the work on rational inattention by Sims (2003), one might want to limit the voting rounds as otherwise voters will abstain in many rounds. It can also be justified by administrative costs of organizing voting rounds.
Set \(\mathcal {Z}\) could also contain all public-good levels that maximize a given weighted utilitarian social function. Following the logic of the proof of Theorem 1, one can verify that the entire Pareto frontier could be traced out by running SFMR for all such social choice functions over \(\mathcal {Z}\). This means that variations of SFMR can produce outcomes in which some types have a particular weight in the collective decision.
Another example is a situation where the number of low-type individuals has support \(\{\overline{n}-1,\overline{n},\ldots ,n\}\) for some \(\overline{n}\) with \(1<\overline{n}<n\). In this case, the second-stage thresholds for the approval of public-good levels that are higher than the one prescribed by the default determined in Stage 1 can be lowered to \(\max \{n-\overline{n}+1,\frac{n+1}{2}\}\).
In direct democracies, citizens can make a proposal that is later amended, approved, or rejected by Parliament. For example, this is the case in Switzerland. In representative democracies, it is common for either the executive or one legislative chamber to make a first proposal that has to be either ratified or dismissed by a second legislative chamber (sometimes only one chamber is involved in the process). Such two-stage processes are used in countries such as the US, Germany, and Spain.
See Footnote 25.
Monotone (or cut-off) strategies have been used by Gershkov et al. (2017). They have also been justified by an iterative process of elimination of weakly dominated strategies. The subtleties, however, are different in our paper. One reason is that the last step of the procedure considered by Gershkov et al. (2017) consists of a vote between the last two exogenously given alternatives, while our procedure consists of a vote between the default determined endogenously in Stage 1, namely \(\bar{x} = y^k\), and the status quo, \(y^0\).
This property is independent of the actual values of \(t^L\) and \(t^H\). For Theorem 1 to hold, it suffices for low-type citizens to know they are of the low type and for high-type citizens to know they are of the high type. But they neither need to know \(t^L\) nor \(t^H\). Only the designer needs to know these values to determine the set of admissible alternatives. For Theorem 1 to hold, it is not necessary that the number of votes cast for each alternative in any voting round is made public either. It suffices to know the alternative that was set as default for Stage 2.
For type \(t^l\), with \(l\in \{2,\ldots ,T-2\}\), the peak depends on the values of \(t^1,\ldots ,t^T\) as well as on the beliefs held by the citizens.
One could also envision that this information is used by a social planner. It would suffice if citizens cannot foresee how this information is going to be used. Then they cannot inform their decisions in the G-generalized SFMR to manipulate the information collected by the social planner in their favor.
A mapping \(f:A\rightarrow B\) is onto if for all \(y\in B\) there is \(x\in A\) such that \(y=f(x)\).
Note that \(\underline{f}^k (h)\) and \(\overline{f}^k (h)\) are functions that assign integers (and their corresponding alternatives) to integers, so the convex hull refers only to functions of the same type.
We stress that in the main body of the paper, we have considered \(f^k(h)=\max \left\{ \frac{n+1}{2},n+1-h\right\} \).
For notational convenience, we have suppressed the dependence of \(r^*(k,j)\) on the function \(f^k(\cdot )\).
Similar statements can also be shown for values of k below \((n-1)/2\). Indeed, for \(k\in \{0,(n-1)/2\}\), we have \(f^k(n+1-k)=\max \{(n+1)/2,k\}=(n+1)/2\le j\). The first equality follows from Eq. (11) and the inequality is due to Inequality (14). This implies \(r^*(k,j)=\max \{r:f^k(n+1-r)\le j\}\ge k\). Using \(k=(n-1)/2\), in particular, we obtain \(r^*=r^*((n-1)/2,j)\ge (n-1)/2\).
This would contradict Bayesian update given i’s private signal about her/his own type.
References
Arrow KJ (1950) A difficulty in the concept of social welfare. J Polit Econ 58(4):328–346
Bierbrauer F, Sahm M (2010) Optimal democratic mechanisms for taxation and public good provision. J Public Econ 94(7–8):453–466
Bierbrauer FJ, Hellwig MF (2016) Robustly coalition-proof incentive mechanisms for public good provision are voting mechanisms and vice versa. Rev Econ Stud 83(4):1440–1464
Black D (1948) On the rationale of group decision-making. J Polit Econ 56(1):23–34
Börgers T (2004) Costly voting. Am Econ Rev 94(1):57–66
Bowen HR (1943) The interpretation of voting in the allocation of economic resources. Quart J Econ 58(1):27–48
Brandt F, Sandholm T (2005) Unconditional privacy in social choice. In: TARK, pp 207–218
Chevaleyre Y, Endriss U, Lang J, Maudet N (2007) A short introduction to computational social choice. In: International conference on current trends in theory and practice of computer science, pp 51–69, Springer, New York
Dahl RA (2008) Democracy and its critics. Yale University Press, Yale
Diskin A, Koppel M, Samet D (2011) Generalized Raiffa solutions. Games Econ Behav 73(2):452–458
Fershtman C (1990) The importance of the agenda in bargaining. Games Econ Behav 2(3):224–238
Gersbach H (2017) Flexible majority rules in democracyville: a guided tour. Math Soc Sci 85:37–43
Gersbach H, Imhof S, Tejada O (2021) Channeling the final say in politics: a simple mechanism. Econ Theor 71:151–183
Gershkov A, Moldovanu B, Shi X (2017) Optimal voting rules. Rev Econ Stud 84(2):688–717
Gibbard A (1973) Manipulation of voting schemes: a general result. Econometrica 41(4):587–601
Grech P, Tejada O (2018) Divide the dollar and conquer more: sequential bargaining and risk aversion. Int J Game Theory 47(4):1261–1286
Green J, Laffont J-J (1977) Characterization of satisfactory mechanisms for the revelation of preferences for public goods. Econometrica 45(2):427–438
John R, Raith MG (2001) Optimizing multi-stage negotiations. J Econ Behav Org 45(2):155–173
Kahneman D, Tversky A (2013) Prospect theory: an analysis of decision under risk. In: Handbook of the fundamentals of financial decision making: part I, pp 99–127. World Scientific
Kwiek M (2017) Efficient voting with penalties. Games Econ Behav 104:468–485
Ledyard JO, Palfrey TR (1994) Voting and lottery drafts as efficient public goods mechanisms. Rev Econ Stud 61(2):327–355
Ledyard JO, Palfrey TR (1999) A characterization of interim efficiency with public goods. Econometrica 67(2):435–448
Maskin E (1995) Majority Rule, Social Welfare Functions, and Games Forms (essays in honor of Amartya Sen), pp 100–109. Oxford University Press, Oxford, UK
May KO (1952) A set of independent necessary and sufficient conditions for simple majority decision. Econometrica 20(4):680–684
McKelvey RD (1976) Intransitivities in multidimensional voting models and some implications for agenda control. J Econ Theory 12(3):472–482
Moulin H (1980) On strategy-proofness and single peakedness. Public Choice 35(4):437–455
Moulin H (2008) Social choice. In: Weingast BR, Wittman D (eds) The Oxford handbook of political economy, vol 4. Oxford University Press, Oxford
Moulin H (2014) The strategy of social choice, vol 18. North Holland, Amsterdam
Sartori G (1989) The theory of democracy revisited. Part 1: the contemporary debate
Satterthwaite MA (1975) Strategy-proofness and Arrow’s conditions: existence and correspondence theorems for voting procedures and social welfare functions. J Econ Theory 10(2):187–217
Sims CA (2003) Implications of rational inattention. J Monet Econ 50(3):665–690
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Philip Grech, Matthew Jackson, Vincent Lohmann, and Hervé Moulin, as well as the participants of the 13th SING Conference in Paris, for valuable comments. We are also thankful to two anonymous reviewers for their suggestions how to sharpen the contribution of the paper. All errors are our own.
Oriol Tejada would like acknowledge financial support from the Spanish Ministry of Science and Innovation (grant no. PID2021-123747NA-100).
Appendix
Appendix
In this appendix, we do three things. First, in Sect. A.1, we introduce a family of voting mechanisms that includes SFMR, the voting mechanism analyzed in the main text of the paper. All our results apply to each element of this family of mechanisms. Second, in Sect. A.2, we provide the proof of Theorem 1, which is itself structured along several items, following the logic of backward induction. Third and last, in Sect. A.3, we provide the details needed in addition to the discussion of Sect. 5 for the proof of the result about the generalized SFMR.
1.1 A family of voting mechanisms based on semi-flexible majority rules
As discussed in Sect. 3—see Footnote 8—, the result of Theorem 1 not only holds for the voting mechanism described in this section, but also for a broader family of voting mechanisms (or voting procedures) containing the former as an instance. Each voting mechanism of this family is contingent on the choice of certain non-increasing sequences of majority thresholds to be applied to the first rounds of Stage 2, more specifically, to the rounds involving policies \(y^n\), \(y^{n-1}\),..., and \(y^k=\bar{x}\) (the default chosen in Stage 1) as defined in Sect. 3.2. Formally, for each \(k\in \{0,\ldots ,n\}\) let
and
While we interpret \(A^k\) as round indices (which, in turn, are associated with voting over particular alternatives), the elements of \(B^k\) are majority thresholds to be used for voting—see below. Note in particular that \(B^k=\{k,\ldots ,n\}\) if \(k\ge \frac{n+1}{2}\). For each \(k\in \{0,\ldots ,n\}\), with \(\bar{x}=y^k\) being the default chosen in Stage 1, let
be a function that is non-increasing and onto.Footnote 28 This means, in particular, that \(f^k(1)=n\) and
We further assume that
Every choice of \(\left\{ f^k(\cdot )\right\} _{k=0}^n\) then defines a voting mechanism. This generalizes the two-stage voting mechanism defined in Sect. 3 in that now, for Round 2.h, with \(h \in A^k= \{1,\ldots ,n+1-k \}\), the majority threshold required to adopt the proposal \(y^{n-h+1}\) on the table is \(f^k(h)\). For each \(k\in \{0,\ldots ,n\}\), we denote by \(\mathcal {F}^k\) the set of all functions satisfying the above properties.
First, if \(k\ge \frac{n+1}{2}\), there is only one possible element of \(\mathcal {F}^k\), namely
This is precisely the threshold function considered in the main body of the paper. Second, if \(k<\frac{n+1}{2}\), we have
Now define
and
Then note that
and
so
and
Because \(\underline{f}^k (h)\) and \(\overline{f}^k(h)\) are clearly non-decreasing in h, both functions therefore belong to \(\mathcal {F}^k\). In particular, \(\underline{f}^k(\cdot )\) is the threshold function considered in the main body of the paper. It is also straightforward to verify that for each \(f^k(\cdot ) \in \mathcal {F}^k\) and \(h\in A^k\),
The shape of the possible functions \(f^k(\cdot )\in \mathcal {F}^k\) is illustrated by Fig. 3 for the case where \(k<\frac{n+1}{2}\). It shows that \(\mathcal {F}^k\) is the convex hull of \(\underline{f}^k (\cdot )\) and \(\overline{f}^k (\cdot )\), which are the supremum and the infimum of the set of functions, respectively.Footnote 29
Generalized Stage 2—Number of votes (z) required to approve a policy, with \(\bar{x}=y^k\) the default set out in Stage 1. The mechanism starts with \(y^n\). Case \(k< \frac{n+1}{2}\) (with \(\hat{k} =\frac{n+1}{2}\) and \(\bar{k}= \frac{n-1}{2}+k\)). Functions \(\underline{f}^k(\cdot )\) and \(\overline{f}^k(\cdot )\) are depicted by dotted lines
For each default \(\bar{x}=y^k\) chosen in Stage 1, \(\mathcal {F}^k\) has been defined as the set of possible majority thresholds for voting rounds in Stage 2 where the proposal on the table specifies a public-good level higher than, or equal to, the one specified by the default chosen in Stage 1. This set is reminiscent of the class of decreasing thresholds considered by Gershkov et al. (2017). Indeed, when \(\bar{x} \) coincides with the status-quo, namely \(y^0\), our class of thresholds coincides with the subclass of thresholds considered by Gershkov et al. (2017) satisfying the additional property that no threshold can be below half plus one of the number of citizens. Such a class of thresholds can be rationalized from a mechanism-design viewpoint when the majority requirement is imposed beyond standard properties such as anonymity, unanimity, and incentive compatibility.
1.2 The proof of the main result
In this section we solve the game induced by any of the voting mechanisms described above, and, in particular, by the voting mechanism considered in the main body of the paper, viz. SFMR. We analyze the game backwards. We thus start with the analysis of Stage 2.
Proof of Theorem 1
First, we analyze Stage 2, then we analyze Stage 1. Finally we discuss the equilibria of the game.
Analysis of Stage 2
Let \(\bar{x} = y^k\) be the outcome of Stage 1, with \(k\in \left\{ 0,\ldots ,n\right\} \). We start by considering Round 2.h of Stage 2, with \(h\in \{n+1,\ldots ,1\}\). We next prove the following claim:
Claim 1
In any round 2.h, with \(h \in \{ n+1,\ldots ,1\}\),
- (i):
-
Any high-type citizen votes to implement the proposal on the table if \(h\in \{1,\ldots , n-k+1 \}\) (i.e., if we consider the initial rounds of Stage 2) or to proceed to the next round if \(h\in \{n-k+2,\dots , n+1\}\) (i.e., if we consider the last rounds of Stage 2).
- (ii):
-
Any low-type citizen votes to proceed to the next round in all rounds except the final round of Stage 2, i.e. except in Round \(2.(n+1)\).
To prove the above claim, we distinguish three cases.
Case I: \(h = n+1\)
The decision in Round \(2.(n+1)\) consists in choosing either \(y^{0}\) or \(\bar{x}=y^k\) as the final outcome. If \(k=0\), there is no real choice, and \(\bar{x}=y^0\) is adopted regardless of the citizens’ vote. Hence, let \(k>0\) and thus \( y^0 < \bar{x} \). In this case, unanimity is required for approval of \(y^{0}\). Then for any observed history of previous play, it is in any citizen’s best interest to vote for the alternative that yields higher utility, either \(y^{0}\) or \(\bar{x}\), because doing so makes a positive difference when the vote is pivotal—i.e., when all other citizens vote for \(y^0\)—and makes no difference otherwise. In other words, voting for the proposal on the table is weakly dominated for high-type citizens by voting to proceed to Round \(2.(n+2)\), while the weak-domination relation is reversed for low-type citizens. Hence, if citizens play no strategies that are weakly dominated, low-type citizens vote for \(y^0\) and high-type citizens vote to proceed to the last round, where \(\bar{x}\) is automatically adopted.
Case II: \(n-k+1< h < n+1\)
The decision in Round 2.h, with \(n-k+1< h < n+1\), consists in choosing between accepting \(y^{n-h+1}\) as the final outcome and proceeding to Round \(2.(h+1)\). Unanimity is required for \(y^{n-h+1}\) to be adopted. This implies that any individual has the (veto) power to ensure that the procedure continues to the next round and ultimately to Round \(2.(n+2)\), a round in which \(\bar{x}\) is adopted—if in all these rounds such a citizen votes in favor of this possibility.
Let us first consider an individual i of type \(t^H\). Such an individual votes to proceed to the next round until Round \(2.(n+2)\) is eventually reached. The reason is that s/he prefers \(\bar{x}=y^k\) over \(y^{n-h+1}\) (recall that \(n-k+1<h\)) and s/he anticipates that weakly dominated strategies (in particular, her/his own strategies) will be eliminated in future rounds. Indeed, consider Round 2.n as a base case for an induction argument. Then citizen i knows that in Round \(2.(n+1)\) s/he will vote to proceed to Round \(2.(n+2)\), as doing otherwise is weakly dominated for her/him. This has been proven in Case I above. Assume now that citizen i’s vote is pivotal in Round 2.n, i.e., all other citizens vote for the proposal on the table \(y^1\) (in all other cases, citizen i’s vote does not matter for the outcome). If citizen i votes for the proposal on the table, \(y^1\) is implemented. If, by contrast, citizen i votes to proceed to the next round, namely to Round \(2.(n+1)\), then \(\bar{x}\) will be implemented. Since individual i prefers alternative \(\bar{x}\) to alternative \(y^1\), s/he votes in Round 2.n to proceed to the next round.
For the above reasoning, we have used the following facts. First, it is common knowledge that agents recursively eliminate those strategies that are weakly dominated by moving backwards, and in particular that it is common knowledge that agents do not play weakly dominated strategies. Second, we have used the fact that citizen i knows that s/he himself/herself will take part in the binary voting of Round \(2.(n+1)\). This means, in particular, that s/he can form correct beliefs about whether all citizens are of the low type (s/he knows they are not). Then, iterating the above argument backwards from Round 2.n to Round \(2.(n-k+2)\), we obtain that for any observed history of previous play, any high-type citizen votes in favor of proceeding to the next round in all Rounds 2.h, with \(h\in \{n-k+2,\ldots ,n\}\). This results in adoption of \(\bar{x}\) regardless of the vote of the remaining citizens whenever there is at least one individual of the high type.
We now consider an individual of type \(t^L\). In Round 2.h, s/he faces a more subtle choice than a citizen of type \(t^H\). If s/he votes in favor of the alternative on the table, \(y^{n-h+1}\), her/his vote may theoretically help to guarantee that such a policy is chosen. If, by contrast, s/he votes for the procedure to continue to the next round, the risk s/he takes is that the default \(\bar{x}\) will eventually be chosen if all alternatives \(y^{n-h},\ldots ,y^0\) are subsequently rejected. Because s/he prefers alternative \(y^{n-h+1}\) to \(\bar{x}=y^k\) (recall that \(n-k+1<h\)), the choice is not obvious. Nevertheless, we next show that for an individual i of type \(t^L\), it is always optimal to vote to proceed to the next voting round.
We develop a further induction argument and consider Round 2.n as a base case. We focus on the situation where citizen i’s vote is pivotal, as her/his vote does not matter for outcomes otherwise. If s/he votes for the proposal on the table, alternative \(y^1\) is implemented. Instead, if s/he votes to proceed to the next round, namely to Round \(2.(n+1)\), then either \(y^0\) or \(\bar{x}\) will be implemented. Citizen i knows that the latter will occur if and only if there is at least one citizen who is of the high type. Moreover, since it is common knowledge that (high-type) citizens eliminate iteratively weakly dominated strategies, a high-type citizen votes in Round 2.n to proceed to the next round and hence citizen i’s vote is not pivotal in this round. That is, a necessary condition for i’s vote to be pivotal in Round 2.n is that all agents are of the low type. In this case, our previous analysis has shown that \(y^0\) is implemented in Round \(2.(n+1)\). This means that if, in Round 2.n, citizen i votes for the proposal on the table when all agents are of the low type, \(y^1\) is implemented. In contrast, if in this same case citizen i votes to proceed to the next round, namely to Round 2.n, alternative \(y^0\) is implemented. Since individual i prefers alternative \(y^0\) to alternative \(y^1\), s/he votes in Round 2.n to proceed to the next round.
For the above reasoning, we have used the fact that citizen i of type \(t^L\) knows that citizens of the high type can form correct beliefs about whether all agents are of the low type. Then, iterating the above argument backwards from Round 2.n to Round \(2.(n-k+2)\), we obtain that for any observed history of previous play leading to correct beliefs about whether all citizens are of the low type or not, any low-type citizen votes to proceed to the next round in all Rounds 2.h, with \(h\in \{n-k+2,\ldots ,n\}\). This results in the adoption of \(y^0\) if and only if all individuals are of the low type. If not, \(\bar{x}\) is implemented.
Case III: \(1\le h \le n-k+1\)
Again, the decision in Round 2.h, now with \(1\le h \le n-k+1\), consists in choosing \(y^{n-h+1}\) as the final outcome or proceeding to the next stage. (Note that \(r=n+1-h\) is the index used in Sect. 3 to describe policy \(y^r\).) This time, however, a majority of \(f^k(h)\) of votes is required for \(y^{n-h+1}\) to be adopted.Footnote 30 If such a majority does not materialize, the procedure continues, yielding some outcome \(y\in \mathcal {Y}\) satisfying the property that \(y\le y^{n-h+1}\), with \(y^{n-h+1}\ge \bar{x}=y^k\). Recall that \(n-k+1\ge h\). This means that if the procedure does not stop at Round 2.h, the outcome will leave high-type individuals worse off and low-type individuals better off (if \(h < n-k+1\)), or will leave high-type individuals weakly worse off and low-type individuals weakly better off (if \(h = n-k+1\)).
We distinguish two cases. First, assume that \(h < n-k+1\). Then, high-type individuals vote in favor of \(y^{n-h+1}\) and low-type individuals vote to proceed to the next round. The reason is that for any high-type citizen i, voting in favor of the proposal on the table weakly dominates voting to proceed to the next round. For this result to hold, no assumption about future voting behavior by other agents is needed. Similarly, for any low-type citizen, voting to proceed to the next round weakly dominates voting in favor of the proposal on the table. For this result to hold, the fact that agents will iteratively eliminate weakly dominated strategies in all future rounds and can form correct beliefs about whether all agents are of the high type does not matter. These two properties hold independently of the majority required in the voting round, viz. \(f^k(h)\).
Second, let us examine the case \(h = n-k+1\). Consider first a citizen i of type \(t^H\). If s/he votes for the proposal on the table, i.e. for \(y^k\), s/he may contribute to the adoption of such a proposal if her/his vote is pivotal (in any other case, her/his vote makes no difference for the outcome). If, on the other hand, citizen i’s vote is pivotal for the procedure to continue to the next round, s/he knows that s/he can ensure that \(\bar{x}=y^k\) will also be adopted in subsequent voting rounds thanks to her/his veto power. The latter requires that citizen i knows that s/he will vote in these subsequent rounds, and in particular that s/he can form correct beliefs about whether or not all citizens are of the low type. Yet, it is clear that, in Round \(2.(n-k+1)\), voting to proceed to the next round is weakly dominated for citizen i by voting for the proposal on the table, since doing so would produce an outcome \(y\le y^k=\bar{x}\). This holds independently of the fact that s/he can use her/his veto power in all subsequent rounds. Consider now a citizen of type \(t^L\). Reversely, voting to proceed to the next round produces an outcome \(y\le y^k=\bar{x}\), which is strictly preferred over \(y^k\) in the case where \(y< y^k\) (an outcome that is attainable for certain voting behavior). That is, for a low-type citizen, voting to proceed to the next round weakly dominates voting for the proposal on the table, \(y^k\). This holds independently of the majority required in the voting round, viz. \(f^k(n+1-k)=\max \{\frac{n+1}{2},k\}\). This completes the proof of Claim 1.
Having established the citizens’ behavior in all voting rounds of Stage 2, we now let k (with \(\bar{x} = y^k\)) vary from 0 to n and obtain the outcome of Stage 2 for different distributions of citizen types. More specifically, we next prove the following claim:
Claim 2
The outcome of Stage 2 for different distributions of citizen types as function of \(\bar{x}\) is given by the following table:
The numbers \(r^*(k,j)\) are defined in (15) below. To prove the above claim, we build on the insights provided in Cases I–III in the proof of Claim 1.
First, if \(j=0\), all citizens—who are of the low type—always vote to proceed to the next voting round, until Round \(2.(n+1)\) is reached, where all of them vote in favor of the proposal on the table, \(y^0\). Second, if \(0<j\le \frac{n-1}{2}\), all low-type citizens, who constitute a majority of the electorate, will block the approval of any proposal of Rounds 2.1 to \(2.(n+1-k)\). The reason is that a (qualified) majority is needed in all these rounds for the approval of the proposal on the table. However, since there is always at least one citizen of the high type, any such individual can guarantee that the default \(\bar{x}\) is eventually chosen. Third, if \(\frac{n+1}{2}\le j \le n \), a majority of the electorate is made up of citizens of the high type. If \(j=n\), in particular, all citizens, who are of type \(t^H\), vote for \(y^n\), and the procedure ends just after Round 2.1.
Accordingly, we are left with the constellation
Note that because there is always one citizen of type \(t^H\), the procedure yields some proposal y with the property that \(y\ge y^k=\bar{x}\). We distinguish two cases, depending on the default chosen in Stage 1, viz. \(\bar{x}\).
Case A: \(\frac{n+1}{2} \le k \le n\)
In this case, for \(h \in A^k=\{1,\ldots ,n+1-k\}\), we have \(f^k(h)=n+1-h\) as the majority threshold required for the approval of the proposal on the table of Round 2.h, namely \(y^{n+1-h}\). The reason is that for \(k\ge (n+1)/2\), the only non-increasing, onto function belonging to \(\mathcal {F}^k\) is \(f^k(h)=n+1-h\), since \(A^k\) and \(B^k\) have the same cardinality. Because in each of these rounds all individuals of the high type vote in favor of the proposal on the table and all individuals of the low type vote to proceed to the next voting round, the outcome of the procedure is \(\max \{y^{j},\bar{x}\}\), where \(\bar{x}=y^k\) is the default and j is the number of citizens of type \(t^H\). In particular, if \(\bar{x}=y^{j}\), the outcome is the default chosen in Stage 1.
Case B: \(0\le k \le \frac{n-1}{2}\)
For \(h\in A^k=\{1,\ldots ,n+1-k\}\), we again have \(f^k(h)\) as the majority threshold required for the approval of the proposal on the table of Round 2.h, namely \(y^{n+1-h}\). As in Case A, in each of these rounds all individuals of the high type vote in favor of the proposal on the table and all individuals of the low type vote to proceed to the next voting round. Accordingly, the final outcome of the procedure is \(\max \{y^{r^*(k,j)},\bar{x}\}\), where \(\bar{x}=y^k\) is the default, j is the number of citizens of type \(t^H\), andFootnote 31
That is, \(y^{r^*(k,j)}\) is the highest level of the public good that the j citizens of the high type can guarantee as an outcome throughout Rounds 2.1 to \(2.(n+1-k)\), given the default \(\bar{x}=y^k\) chosen in Stage 1. Using Eqs. (11) and (14), we obtain
It then follows that \(r^*(k,j)\) is well-defined and that \(r^*(k,j)\ge k\). Moreover, \(r^*(k,j)\) is non-decreasing in k, due to Eq. (12), and non-decreasing in j, by construction. We further note that also due to Eqs. (11) and (14), we have
This impliesFootnote 32
Trivially, Eq. (14) also implies that
We claim (and prove next) that
Indeed, we start noting that Eqs. (16) and (17) guarantee that \(n+1-r^*\) and \(n+1-j\) belong to the domain of function \(f^{(n-1)/2}(\cdot )\). For proving Inequality (18), we then note that
The above chain of inequalities can be explained as follows: The first inequality is due to Eq. (13). Note that Eq. (17) guarantees that \(n+1-j\) belongs to the domain of \(f^{(n-1)/2}(\cdot )\) and \(\underline{f}^{(n-1)/2}(\cdot )\). The first equality is a direct consequence of the definition of \(\underline{f}(\cdot )\). The second equality holds because \(j\ge \frac{n+1}{2}\). Lastly, the second inequality holds by definition of \(r^*=r^*\left( (n-1)/2,j\right) \). Since \(f^{(n-1)/2}(\cdot )\) is non-increasing, Inequality (18) follows from the above chain of inequalities.
To sum up, building on our entire analysis, we can arrange the outcome of Stage 2 for different default chosen in Stage 1 as was done in Table 1. This completes the proof of Claim 2. That is, as we are considering a larger value of \(\bar{x}\), the final outcome cannot be worse (or better) for high-type (low-type) citizens, whatever the type composition of the electorate. Note that together with the fact that \(f^k(\cdot )\) is non-increasing and onto, Eq. (18) is crucial for Table 1. Moreover, the outcome is strictly better (worse) in some cases. This completes the analysis of Stage 2.
Analysis of Stage 1
Next we consider the problem which actions are taken by the citizens in each Round 1.h of Stage 1, with \(h\in \{n,\ldots ,1\}\). Because agents eliminate weakly dominated strategies, we can focus our analysis on the case where a citizen’s vote is pivotal for the outcome of the voting round. Let us focus on high-type citizens first. From Table 1, it immediately follows that in Round 1.n, voting for \(y^n\) as default yields higher or equal utility than voting for \(y^{n-1}\), no matter the composition of the electorate, and hence regardless of the beliefs held by the citizens about such composition. As a matter of fact, unless a citizen of type \(t^H\) believes that all citizens are of the same type (\(t^L\) or \(t^H\)), voting to set \(\bar{x} = y^n\) as default yields higher utility than voting to set \(\bar{x} = y^{n-1}\). This means that in Round 1.n, for any citizen i of the high type, (a) it is always optimal to set \(\bar{x}=y^{n}\) and move to Stage 2, no matter the previous play of game, and (b) it is never optimal to set \(\bar{x}=y^{n-1}\) and move to Stage 2, unless citizen i believes that all agents are of the high type. Because i herself/himself is of the high type, s/he cannot believe that all agents are of the low type.Footnote 33 However, if the prior distribution of types has full support, i.e., the probability measure that assigns to every number \(k\in \{0,\ldots ,n\}\) the probability that there are k individuals of the low type at the beginning of the first voting round has full support, then at the beginning of Round \(1.(n-1)\), where only \(n-2\) binary voting rounds have taken place, no individual can be certain that all individuals are of the high type after having observed the play and updated their beliefs using Bayes’ rule.
At any prior round of Stage 1, in turn, voting to proceed to the next round yields higher or equal utility than voting to stick with the current default. This property holds no matter the composition of the electorate, and hence regardless of the beliefs held by the citizens about such composition. This means that for any citizen of the high type, voting to proceed to the next voting round in Stage 1 is optimal in any Round 1.h (with \(1\le h<n\)). To see whether there are other optimal choices for some given beliefs, we distinguish two cases depending on what the proposal on the table, \(y^{h-1}\), is. Recall that we are focusing on the case where the vote of a citizen i of the high type is pivotal for the outcome of the voting round. If \(\frac{n+1}{2}\le h-1 <n-1\), then voting to proceed to the next round yields higher utility than voting to stick with the current default unless citizen i believes that all citizens are of the high type. As before, if the prior distribution of types has full support, then at the beginning of Stage 1.h no individual can be certain that all individuals are of the high type, after having observed the play and updated their beliefs using Bayes’ rule. If \(0\le h-1<\frac{n+1}{2}\), voting to proceed to the next round yields higher utility than voting to stick with the current default unless (possibly) citizen i believes that the majority of the citizens are of the high type. However, if the prior distribution of types has full support, then at the beginning of Round 1.h, where only \(h-1\) binary voting rounds have taken place, no individual can be certain that a majority of the individuals are of the high type after having observed the play and updated their beliefs using Bayes’ rule.
For low-type individuals, the optimal decisions in Rounds 1.h (with \(1\le h\le n\)) are reversed. It is then important to point out that for the voting decision to hold as best responses for both citizen types, it is necessary for it to be common knowledge that in Stage 2 agents will iteratively eliminate weakly dominated strategies by moving backwards and that they will be able to form correct beliefs about whether all agents are of type \(t^L\).
It then follows that if citizens vote as described above, the elements of the off-diagonal of Table 1 are chosen in Stage 1. This yields the following table (recall that at least k votes are needed to set \(\bar{x}=y^k\)):
In short, combining the first-stage result with the second-stage result produces the outcome \(y^j\), where j is the number of high-type citizens.
Analysis of equilibria
We start by noting that if citizens vote in Stage 1 as described above, then at the end of this stage they reveal exactly how many citizens are of each type. This property is obtained from any initial type distribution (with full support) through Bayes’ rule because high-type individuals always vote to proceed to the next voting round, while low-type citizens always vote for the proposal on the table (with the exception of Round 1.n where high-type citizens vote for \(y^n\) and low-type citizens vote for \(y^{n-1}\)). Accordingly, \(\bar{x}=y^k\) if and only if k individuals are of the high type and \(n-k\) individuals are of the low type. This means that all citizens can form correct beliefs at the beginning of Stage 2 about how many citizens there are of each type, and in particular about whether all citizens are of type \(t^L\) (and that this is common knowledge). To sum up, any pair of strategies and beliefs is a perfect Bayesian equilibrium if they satisfy that
-
(i)
in any but the last voting round of Stage 1, all citizens of type \(t^L\) (type \(t^H\)) vote to (not to) set the proposal on the table as default for Stage 2,
-
(ii)
in the last voting round of Stage 1, all citizens of type \(t^L\) (type \(t^H\)) vote to set \(y^{n-1}\) (\(y^{n}\)) as default for Stage 2,
-
(iii)
in any voting round of Stage 2, all citizens of type \(t^L\) vote to proceed to the next round (except for the last round, namely for Round \(2.(n+1)\), where they vote for \(y^0\)),
-
(iv)
in any voting round of Stage 2, all citizens of type \(t^H\) vote in favor of the proposal of the table if and only if it prescribes a higher or equal public-good level than in the default \(\bar{x}\) determined in Stage 1,
-
(v)
the beliefs of all citizens at the end of Stage 1 are such that all citizens know the distribution of the types, and in particular whether all citizens are of the low type, and that this is common knowledge.
First, the actions taken at any voting round of Stage 2 are best responses given the beliefs and the strategies for the current and subsequent voting rounds of Stage 2 (if any). Second, the decisions taken at any voting round of Stage 1 are best responses (regardless of the exact beliefs of each individual at these nodes), given the strategies for the remaining voting rounds of Stage 1 and for all voting rounds of Stage 2. Third, as mentioned above, the beliefs at the end of Stage 1 can be computed through Bayes’ rule from the prior beliefs. Moreover, the resulting beliefs are consistent with the play along the rest of the equilibrium path. Accordingly, we have proved that the utilitarian optimal solution \(x^{soc}\) is an equilibrium outcome. Moreover, for any pair of strategy and beliefs satisfying the above conditions, citizens choose pure strategies that survive iterative elimination of weakly dominated strategies by moving backwards in the game, as is required by our equilibrium notion.
Are there other equilibria in the game underlying SFMR ? As we have shown above, if (v) holds, then in any perfect Bayesian equilibrium in which players eliminate iteratively weakly dominated strategies, (ii), (iii), and (iv) must, in turn, hold. Being independent of the beliefs in Stage 1, also (i) must hold. Therefore, if there are other equilibria, it must be the case that (v) does not hold. However, no citizen of the high type can hold wrong or non-conclusive beliefs about whether all citizens are of the low type at any node of the game, as this would contradict Bayesian updating.
To sum up, we obtain that the utilitarian optimal outcome \(x^{soc}\) is implemented uniquely by the mechanism. This completes the proof of Theorem 1.
\(\square \)
1.3 The case of multiple types
In this section, we complete the analysis of Sect. 5.2.
We start by noting that because we assume that individuals do not play strategies that are weakly dominated and eliminate such strategies iteratively, to find out what individuals do in Steps 1 to \(T-1\) in any equilibrium, we can apply the logic of the proof of Theorem 1 to each instance of SFMR. This is for three reasons: (i) once a particular instance of SFMR is chosen (randomly) through mechanism G in Step 0, the outcome is entirely determined by the actions chosen by the individuals in this application of SFMR; (ii) when participating in any instance of SFMR, individuals act as if this instance will be eventually chosen, since if it is not chosen their actions are irrelevant for payoffs; (iii) as discussed in Sect. 5.2, for each set \(\mathcal {Y}_l\), agents of types \(t^1,\ldots ,t^l\) behave as if they were of type \(t^l\), while all other individuals behave as if they were of type \(t^{l+1}\).
Analogously to Claim 1, we therefore obtain the following claim about Stage 2 for any Step \(\tau \) of the G-generalized SFMR:
Claim 3
In any round 2.h of Step \(\tau \) of the G-generalized SFMR, with \(\tau \in \{ 1,\ldots ,T-1 \}\) and \(h \in \{ n+1,\ldots ,1\}\),
- (i):
-
Any citizen of type \(t^l\), with \(l \in \{\tau +1,\ldots ,T\}\), votes to implement the proposal on the table if \(h\in \{1\ldots , n-k+1 \}\) (i.e., if we consider the initial rounds of Stage 2) or to proceed to the next round if \(h\in \{n-k+2,\ldots , n+1\}\) (i.e., if we consider the last rounds of Stage 2).
- (ii):
-
Any citizen of type \(t^l\), with \(l \in \{1,\ldots ,\tau \}\), votes to proceed to the next round in all rounds except the final voting round of Stage 2, i.e. except in Round \(2.(n+1)\).
As for the first stage of each of the instances of SFMR, one can proceed in a similar way and apply the counterpart of Claim 2 in the proof of Theorem 1 to each step, starting from the last step, and then using induction across all of them. As mentioned in Sect. 5, the latter combined with Claim 3 elicits the information how many individuals are of each type through the system of linear equations in (10).
Finally, we focus on Step 0. One can easily verify that for an agent of type \(t^1\), it is weakly dominated to report any \(\mathcal {Y}_l\ne \mathcal {Y}_1\) due to the properties of \(\succ _i^T\) and mechanism G. A symmetric reasoning shows that individuals of type \(t^T\) vote for \(\mathcal {Y}_{T-1}\). Take now \(l\in \{2,\ldots ,T-1\}\). A reasoning along the same lines shows that an individual of type \(t^l\) votes either for \(\mathcal {Y}_{l-1}\) or \(\mathcal {Y}_{l}\) but never for another set. The exact vote depends on the exact values of types \(t^{l-1}\), \(t^l\), and \(t^{l+1}\), and the beliefs the citizens have about the aggregate type distribution.
To sum up, recall that for any type \(l\in \{1,\ldots ,T\}\), we use \(n_l\) to denote the individuals who (report they) are of type \(t^l\). Then also recall from (10) that letting \(N^T= n\),
That is, for \(l\in \{1,\ldots ,T\)}, \(N^l\) denotes the number of individuals of types \(t^1,\ldots ,t^l\). Then we have shown the following:
-
1.
In Step 0,
-
any individual i of type \(t^1\) reports \(\tau '_i=\mathcal {Y}_1\),
-
any individual i of type \(t^l\) (with \(l\in \{2,\ldots ,T-1\}\)) reports either \(\tau '_i=\mathcal {Y}_{l-1}\) or \(\tau '_i=\mathcal {Y}_l\),
-
any individual i of type \(t^T\) reports \(\tau '_i=\mathcal {Y}_{T-1}\).
-
-
2.
The outcome of Step 1 is
-
\(y_1^{n-N^1}\) with probability \(p_1(\tau '_1,\ldots ,\tau '_n)\),
-
\(y_l^{n-N^l}\) (with \(l\in \{2,\ldots ,T-1\}\)) with probability \(p_{l}(\tau '_1,\ldots ,\tau '_n)\),
-
\(y_{T-1}^{n-N^{T-1}}\) with probability \(p_{T-1}(\tau '_1,\ldots ,\tau '_n)\).
-
-
3.
The numbers \(n_1,\ldots ,n_T\) reflect the actual shares in the population in terms of types.
\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gersbach, H., Tejada, O. Semi-flexible majority rules for public good provision. Soc Choice Welf (2024). https://doi.org/10.1007/s00355-024-01508-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00355-024-01508-3


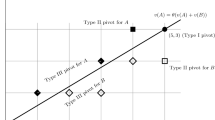



 , is the outcome of G when citizens send messages
, is the outcome of G when citizens send messages 