Abstract
This paper highlights the fact that different distributional aspects of ethnicity matter for conflict. We axiomatically derive a parametric class of indices of conflict potential obtained as the sum of each ethnic group’s relative power weighted by the probability of across group interactions. The power component of an extreme element of this class of indices is given by the Penrose–Banzhaf measure of relative power. This index combines in a non-linear way fractionalization, polarization and dominance. The empirical analysis verifies that it outperforms the existing indices of ethnic diversity in explaining ethnic conflict onset.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we provide a novel investigation of the relation between different distributional aspects of ethnicity and the occurrence of ethnic conflicts. The empirical evidence on the association between ethnic diversity and conflict is generally ambiguous. Still, there is no broad consensus on which distributional aspect of diversity is an important correlate with conflict. A strand of literature develops several theoretical models that investigate the relationship between diversity and conflict. Esteban and Ray (1999) derive from a rent-seeking model a relation between polarization and conflict. Along similar lines, Montalvo and Reynal-Querol (2005, 2008) motivate the use of discrete ethnic polarization as a correlate for conflict. Esteban and Ray (2011) propose a behavioral model according to which the equilibrium level of conflict can be approximately described by a weighted average of a Gini’s inequality index, the fractionalization index, and a specific polarization index from the class of indices axiomatically derived in Esteban and Ray (1994). Esteban et al. (2012) implement the above measures in an empirical exercise and confirm the predictions of the model. Caselli and Coleman (2013) provide a model of social distributive conflict in which ethnic boundaries are not fixed and immutable, and relate the incidence of ethnic conflict to groups’ relative size and to the share of expropriable resources in overall wealth. Recent developments in the field apply network theory to better understand the causal dynamics and the complex interdependencies at work at the onset and diffusion of conflict (Dorussen et al. 2016). Relying on the dyadic dimension of civil conflicts rather than on the distributional aspects of ethnicity, religion and/or income in a cross-country setting, several contributions have emphasized the role of rebel cooperation and competition on conflict dynamics (Metternich et al. 2013; Larson 2016; Zech and Gabbay 2016; Gade et al. 2019). Finally, a growing literature employs dynamic contest models to account for conflict persistence and spiral. Acemoglu and Wolitzky (2014), for instance, investigate occurrence of spirals of conflict over time in a dynamic matching model with overlapping generations. Baliga et al. (2011) study inter-state conflict by incorporating uncertainty about the opponent’s type. Meanwhile Fearon (2018) proposes a dynamic model based on military investments and mutual cooperation and shows that conflict will be avoided as long as investments in armaments are sufficiently high.
Even though in this paper we do not use any of these dynamic models, we implicitly allow for cooperation and interdependence between groups in a different setting and show that the probability of conflict outbreak can be related to fractionalization, polarization and dominance. In line with the existing economic literature, fractionalization takes into account how much a population is partitioned into many small groups, in fact, the common index of ethnic fractionalization coincides with the probability that two randomly selected individuals from the population do not belong to the same ethnic group. Indices of ethnic dominance instead focus on the interdependence between many minority groups and a dominant group that covers at least or about 50% of the population, while ethnic polarization places more attention on cases where two large ethnic groups are polarizing the distribution. These different distributive aspects of ethnic diversity have been considered as potentially relevant for the occurrence of ethnic conflict, namely through three sources of antagonism: the tensions between many small ethnic groups, their potential conflict with a dominant group or the possibility of conflict when the ethnic distribution is polarized between two large groups.
In this work we highlight the fact that the relative importance of these three aspects of diversity in the determination of conflict depends on the characteristics of the underlying population distribution across groups. We start from the basic specification of the Esteban and Ray’s (1994) [ER henceforth] model of social antagonism, and characterise a parameterized index of diversity, which we refer to as the P Index of Conflict Potential, that combines the groups’ effective power and the between-group interaction. Our approach departs from ER in three specific features. First, like in Montalvo and Reynal-Querol (2005), we define the distances between groups using a discrete rather than a continuous metric. Second, we assume that the power of a group depends not only on that group’s relative size but also on the relative sizes of all the other groups in the population. As a consequence, the power of a group is not necessarily proportional to its size. Third, we do not treat each group as an independent actor but we assume that groups can either act individually or form alliances with other groups in order to exploit potential increasing returns to coalition formation. These are reasonable assumptions since most conflicts include more than two opposed parties and belligerent powers often decide to cooperate in order to increase their capabilities (Lichbach 1995), counteract their rivals through minimum winning coalitions (Christia 2012), and increase their overall odds of victory by institutionalizing joint command and control of military operations (Akcinaroglu 2012). Between 1946 and 2008, for instance, 181 out of 345 rebel groups involved in civil conflicts around the world have started to cooperate with each other while fighting with the government (Akcinaroglu 2012). Moreover, what makes one group stronger or more efficient than another is not merely a function of its absolute power, rather it depends on its relative strength shaped by group characteristics (demographic size, military capacity or territorial control) and also by its potential interdependencies with other groups in the population.
We show that for some parameter values, the P index reduces to the existing diversity indices (fractionalization and discrete polarization). For high values of the parameter, the index is able to capture the presence of dominance, where all the power goes to the majoritarian group. The effective power component of the index in these cases approaches the Penrose (1946), Banzhaf (1965) and Shapley and Shubik (1954) measure of voting power in a simple majority game if applied to the distribution of the population shares of the different groups.
In general, the index emphasizes differently the overall effects of power and between group interactions according to the features of the underlying population distribution across groups. If the power component results more evenly distributed across groups, the interaction component becomes predominant and the index highlights fractionalization as the relevant aspect of diversity, while for unequal distributions of powers the emphasis is given to the combined effect of dominance and interaction.
We present an empirical exercise in which we test the performance of the derived indices of conflict potential against the commonly used distributional indices of ethnic diversity. Since our measures link the features of the population distribution across groups to the probability of conflict outbreak, we consider conflict onset rather than incidence as the dependent variable along the lines of the empirical specifications in Wimmer et al. (2009), Cederman and Girardin (2007) and Fearon (2003). Using the data on ethnic groupings from the Ethnic Power Relations data set (Wimmer et al. 2009) we show that, when compared to the existing and widely used indices of ethnic diversity, the index based on the Penrose–Banzhaf measure of relative power results in a strong and significant correlate of ethnic conflict onset even after inclusion of an additional set of regressors and under alternative model specifications. Our results highlight the fact that the different aspects of diversity should be combined in order to investigate their relation with conflict onset. The derived index provides a specification of the relative relevance of these aspects across different distributions.
The paper is organized as follows. In Sect. 2 we axiomatically derive the P index of conflict potential. Section 3 analyses the shape of the P index for different parameter values and population distributions, and explores the differences between the derived indices and the existing distributional measures using the data on ethnic distribution for a large set of countries. Section 4 presents our main empirical results and Sect. 5 concludes.
2 The model
2.1 The P index of conflict potential
Consider a population partitioned into \(n\ge 2\) non-overlapping groups. Let \(\pi _{i}\) be the relative population size of group i, where \(i=1,2,\ldots ,n\), and \(\Pi =(\pi _{1}, \pi _{2},\ldots ,\pi _{n})\) denote the vector of groups’ population shares. As in ER we conceptualize conflict potential as the sum of all effective antagonisms between individuals or groups in the society. The antagonism or alienation felt by one individual towards another is a function of the distance between them. Since, by assumption, individuals within each group are all alike, the strength of alienation at the group’s level is obtained as the sum of all individual alienations. The alienation becomes effective once it is translated into some form of organized action, such as political mobilization, protest or rebellion. The power of a group to translate the overall alienation into effective voicing depends on the degree of cohesiveness within the group, which in turn depends on the group’s relative size.
Here, we extend the ER approach and assume that the power of a group depends also on the relative sizes of all the groups listed in \(\Pi \). As in ER, we specify a function \(\Phi \) that combines the group’s power, that depends on \( \pi _{i}\) and \(\Pi \), with the alienation felt towards other groups. Following Montalvo and Reynal-Querol (2005), we define the distance \(D_{ij}\) between individuals belonging to two groups i and j, using a discrete metric, i.e.,
As pointed out in Montalvo and Reynal-Querol (2005), when the population is partitioned according to some categorical attribute like ethnicity, language or religion, identifying groups according to the so-called “belong—does not belong to” criterion is less controversial than defining the distances between them simply because it reduces significantly the measurement error. Moreover, as argued by social institutionalists, the salience of collective identities (i.e., distances) may be fluid and context dependent.Footnote 1 The potential for conflict in a society then derives from the interaction between power and alienation, aggregated over all pairwise comparisons:
We assume that \(\Phi (\pi _{i}, \Pi , 0)=0\) and let \(\Phi (\pi _{i}, \Pi , 1):=K\phi ^{n}(\pi _{i}, \Pi )\) for some constant \(K>0\). We add a superscript n to \(\phi \) to distinguish between distributions characterised by a different number of groups. Since \(\sum \pi _{i}=1\), the index defined in (1) can be written as:
and will be called the P Index of Conflict Potential. The function \(\phi ^{n}(\pi _{i},\Pi )\) for \(i=1,2,\ldots ,n\), will be referred to as the effective power associated with group i. The \(P(\Pi )\) index, hence, is obtained as a combined effect of two different elements, namely the groups’ effective power and the between group interactions, \(\pi _{i}(1-\pi _{i})\), measuring the probability of randomly selecting an individual from group i that interacts with an individual from another group. The sum of these components gives the probability that two individuals randomly selected from a population belong to different groups. Special cases of (2) are the Reynal-Querol (2002) and Montalvo and Reynal-Querol (2005) discrete polarization index, \(RQ=4\sum \pi _{i}^{2}(1-\pi _{i})\), where each group’s power is equal to its relative population size, and the fractionalization index, \(FRAC=\sum \pi _{i}(1-\pi _{i})\), which derives from (2) when each group’s power is constant and equal to 1.
The most interesting specification of the P Index in (2) is obtained when each group’s effective power is neither constant nor proportional to the group relative size but may also depend on the distribution of the relative sizes of the other groups. Here we assume that groups are allowed to form coalitions that generate bipartitions of the population, and that the effective power of each group depends on all the potential contributions of that group to the worth of all the coalitions that it can theoretically belong to. With only two groups, the power of both groups is 1/2 when their sizes are equal, and is non-decreasing in each group size. The extreme case is the one where the power of the bigger group is 1, while the power of the smaller one equals 0. Applying this latter rule to any bipartition of the population when the number of groups is larger than two, the marginal contribution of any group to the worth of a coalition equals 1 whenever the sum of the relative sizes of all the groups forming the coalition exceeds 1/2 and becomes smaller than 1/2 if that particular group leaves the coalition. It equals 1/2 if either the contribution of a group allows the coalition to reach 50% of the population or if without the group the coalition covers exactly 50% of the population. While the marginal contribution to the worth of a coalition is 0 in all other cases. The relative weight of the sum of marginal contributions of any group to all possible coalitions with respect to the sum of the contributions of all the groups in the population, represents then a measure of that group’s effective power. In this particular case, where extreme relevance is given to inequality between the bipartitions, the effective power coincides with the relative Penrose–Banzhaf index of voting power in a simple majority game. The associated index corresponds to the extreme element of the parametric family \(P_{\infty }^{n}\) that will be discussed in detail in the following sections.
Some real-life examples, based on the data on ethnic distributions and conflict onset that we will present in Sect. 4, may help to illustrate similarities and differences in the behaviour of the \(P_{\infty }^{n}\) index, FRAC and RQ.Footnote 2 For instance, when comparing countries like Kuwait where the ethnic group distribution is (0.49, 0.29, 0.22) and Mauritania with distribution (0.43, 0.41, 0.16), the change in terms of fragmentation (FRAC) and of the \(P_{\infty }^{n}\) index are proportional. This is because, given that no group reaches the majority of the population, with three groups the effective power of all groups is identical and therefore the \(P_{\infty }^{n}\) index results proportional to the interaction component measured by FRAC. In terms of polarization, however, the Mauritania’s distribution shows a slight increase in the RQ index because of the existence of two groups covering similarly high proportions of population. A more substantial difference in the behaviour of the three indices appears when the comparisons are made with Iraq with distribution (0.64, 0.19, 0.17). The population distribution in Mauritania is more polarized compared to Iraq, and it also results more fragmented. The \(P_{\infty }^{n}\) index, on the other hand, ranks the two countries differently from RQ and FRAC, assigning to Iraq a significantly higher value with respect to Mauritania. Yet, in the time range considered in our analysis (1946–2005), Mauritania actually did not experience any ethnic conflict while Iraq has suffered from three distinct violent conflict episodes (in 1961, 1982 and 2004). The different behaviour of the P index compared to RQ and FRAC is due to the fact that a majoritarian group emerges in Iraq thereby shifting the power to this group and then making the index proportional to the interaction of this group and the remaining population. A similar argument holds for the comparisons with Mozambique whose ethnic distribution resembles the one of Iraq and that has experienced one ethnic conflict in the time period considered.
We can derive examples that follow an analogous pattern also for countries with four ethnic groups. For instance, when comparing Gabon with ethnic distribution (0.41, 0.38, 0.13, 0.08) to Benin with (0.40, 0.22, 0.18, 0.18), we can see that in both countries no group is majoritarian. Nevertheless, for the computation of the \(P_{\infty }^{n}\) index, the larger group in Benin exhibits a higher effective power because it is determinant in reaching the majority of the population in all coalitions involving two groups, which is not the case in Gabon where the larger group reaches 49% of the population in coalition with the smaller group. For this reason, the increase in fragmentation recorded in Benin because of a less unequal distribution of population shares is also in line with the increase in the value of the \(P_{\infty }^{n}\) index while polarization is higher in Gabon whose distribution is characterized by two groups with similarly large population shares.
In analogy with the case of three groups, a better alignment of the \(P_{\infty }^{n}\) index with conflict onset with respect to FRAC can be observed when comparing Benin and Bolivia. While Bolivia has experienced a violent social arrest in 1952 prior to the revolution, Benin did not go under any inter-ethnic conflict. The presence of a dominant group in Bolivia, covering 61% of the population leads to an increase of the \(P_{\infty }^{n}\) index compared to Gabon and Benin, while FRAC decreases. Here the \(P_{\infty }^{n}\) index appears more in line with the RQ index that also exhibits a sharp increase because the distribution becomes more polarized given the presence of two large groups while the other two groups cover very low shares of population. Comparison of Bolivia with the ethnic distribution of Sri Lanka shows a reduction in all indices because of the increased share of population (71%) covered by the dominant group.
2.2 Axiomatic derivation of the effective power function
Let \(N:=\{1,2,\ldots ,n\}\) denote the set of all groups. The set of all vectors \( \Pi \) is in the n dimensional unit simplex \(\Delta ^{n}\). The effective power \(\phi ^{n}(\pi _{i},\Pi )\) of group \(i\in N\) with relative population size \(\pi _{i},\) given \(\Pi ,\) is defined as:Footnote 3
and satisfies the next properties.
Axiom 1
(Normalization (N))
For all \( \pi _{i}\in (0,1)\), \(\Pi \in \Delta ^{n}\), and \(n\ge 2\)
with \(\phi ^{n}(0,\Pi )=0\) and \(\phi ^{n}(1,\Pi )=1\).
Normalization requires that the powers of all groups sum to 1, and implies that the effective power of each group is bounded in the interval [0, 1].
Axiom 2
(Monotonicity (M))
For all \( \pi _{i}\in (0,1)\), \(\Pi \in \Delta ^{n}\), and \(n\ge 2\), then
The Monotonicity axiom implies that the effective power of a larger group cannot be lower than the effective power of a smaller group. This property implies the Symmetry of \(\phi ^{n}\) which requires that, if two groups are of equal size, then their effective power has to be the same. The reverse, however, is not necessarily true: the effective power could still be equal for groups of different relative size. Monotonicity in combination with Normalization implies that if all groups have identical relative size, each one of them has an effective power equal to 1/n. This result will provide a reference point for all the indices that we will obtain from the axiomatization. In fact, a common feature of these indices is that they all exhibit the same value for distributions where all the groups are of equal size. Moreover, this value will be proportional to the fractionalization index divided by n.
We now introduce two crucial assumptions: (i) groups can either act individually or through a coalition, and (ii) if any two or more groups form a coalition, the remaining groups belong to the “opponent” block. So we consider only bipartitions of the population.
What is the rationale behind these two assumptions? Suppose that there are 3 groups involved in a contest with only one strategic endowment, namely human resources. A relatively smaller group that is interested in winning the contest may find profitable to join the forces with some other group in order to contrast the adversary, even at the cost of the future division of power within the winning block. Consequently, a group that is large enough to ensure the victory alone will act as an independent actor. Hence, one block or coalition may be formed in order to contrast or challenge the other block. Skaperdas (1998), Tan and Wang (2010) and Esteban and Sakovics (2003) show that in a three groups contest, parties will have an incentive to form a coalition against the third if the formation of the alliance generates synergies that enhance the winning probability of the coalition. Skaperdas (1998) and Christia (2012) argue that this tendency is not only theoretical but also frequent in many real life situations and provide an example of the “... on and off alliance of the Bosnian and Croat forces against the more (strategically) well endowed Serb forces in Bosnia during the recent past ...” (Skaperdas 1998, pg. 27). Along similar lines, a close cooperation between the Eritrea People’s Liberation Front (EPLF) and the Tigray People’s Liberation Front (TPLF) during the Ethiopia’s civil war led to a victory against the authoritarian rule of the Mengistu government (DERG). These two rebel groups had different ideological and territorial objectives but at the same time they recognized the benefit, in terms of material and tactical capability, from joining the forces through an alliance. Another example relates to the two rival Kurdish groups, Patriotic Union of Kurdistan (PUK), and Kurdistan Democratic Party (KDPI) who started to collaborate in mid-1980s against the Ba’ath regime in Iraq, conversely the brief alliance between two Chadian groups, Forces of the North (FAN) and Popular Armed Forces (FAP) broke down in 1979 turning the two groups into bitter enemies.
A further motivation underlying the assumption on bipartitions is the following. According to the theory of alliance formation in a multi-group context (Riker 1962; Axelrod 1970; Christia 2012), when forming a coalition, alliance partners expect more benefit (in terms of odds of winning) from joining the forces against third parties than from a conflict against each other. One of the basic mechanisms underlying this theory assumes that coalitions’ relative power depends on the sum of their relative population size, military power and/or territorial control capacity. The relative power in turn determines the probability of winning, the smaller the difference between the coalitions’ relative power, the more similar the odds of winning the contest. The complexity of the model increases with the number of groups and potential coalitions. Since smaller relative power differentials translate into lower relative odds of winning, even with more than two potential alliances, coalitions will have an incentive to join the forces and form supra-coalitions, i.e., coalitions of coalitions, collapsing the coalition structure to a bipartition scheme (Christia 2012).
Here we do not model any endogenous mechanism of coalition formation nor we are interested in which coalition is more likely to form. The probability distribution over coalitions, hence, is assumed to be symmetric. Symmetry is a plausible assumption in our case since we do not have or use information about the differences among groups and we use a discrete metric to define these distances.Footnote 4 Considering only the bipartitions of the population, we rule out the possibility that more groups run on their own against the rest. However, we do not rule out any coalition between two or more groups. As previous examples clearly show, this assumption is not unrealistic, since in many situations that involve coalition formations in conflicts, even unmatchable parties often coordinate their interests in order to contrast the opponent, even when they are aware that the coalition is temporary (Esteban and Sakovics 2003). As we will show later, even under these simplifying assumptions the distribution of the effective power between groups will depend on the characteristics of the population distribution across them. This important feature of the effective power function will make the P index substantially different (both theoretically and empirically) from the existing distributional diversity indices based on the assumption of groups as independent actors.Footnote 5
In order to characterise the effective power for any arbitrary number of groups we first consider the simpler case of a distribution with only two groups. The results that we obtain will then be used to generalize the analysis for any arbitrary number of groups.
Consider a population divided into two different groups (\(n=2\)) with population shares \(\pi \) and \(1-\pi \). Denoting with \(\phi ^{2}(\pi )\) and \( \phi ^{2}(1-\pi )\) the effective power of the groups, we define the relative effective power between them as:Footnote 6
Thus, the relative effective power between groups is a function \(r(\cdot )\) of the groups relative population size \(\rho \) that coincides with the population shares odds ratio. From Monotonicity it follows that whenever \(\pi =1/2\), hence \(\rho =1\), the groups will equally share the power, that is, \(r(1)=1\).Footnote 7 The relative effective power is supposed to satisfy the following property:
Axiom 3
(Two groups relative power homogeneity (2GRPH)) Given \(\Pi \) and \(\Pi ^{^{\prime }}\), let \(\rho , \rho ^{^{\prime }}\le 1 (i.e., \pi ,\pi ^{^{\prime }}\le 1/2).\) If \(r(\rho ),r(\rho ^{^{\prime }})\ne 0\) then:
In order to interpret the 2GRPH axiom, suppose that we start from a population distribution \(\Pi \) in which, for instance, the size of the smaller group is 40% of that of the larger group (i.e., \(\rho =0.4\) ). Now imagine that a portion of the population from the second group migrates in a neighboring country such that the size of the smaller group is now 80% of that of the larger group (i.e., \(\rho =0.8\)). Thus \( \rho \) has doubled (i.e., \(\lambda =2\)). Such a variation in the relative population size may affect the relative effective power between the two groups. Now imagine a similar situation where \(\rho \) doubles but the relative size of one group moves from 30 to 60%. The 2GRPH axiom requires that the variation in the relative effective power is the same in both cases. In other words, no matter from where we start with respect to the relative size \(\rho \), the variation in the relative effective power is always the same as long as the change in \(\rho \) is of the same proportion across the two distributions.
We can now state the first result proved in the Appendix.
Lemma 2.1
Let \(n=2\), the effective power of a group with population share \(\pi \) satisfies Axioms N, M and 2GRPH if and only if \(\phi ^{2}(\pi )=\phi _{\alpha }^{2}(\pi )\) for \(\alpha \in \mathfrak {R}_{+}\cup \infty \) where
This functional form for the effective power is similar to the ratio form contest success function commonly used in the rent-seeking literature (Tullock 1980 with \(\alpha =1\), Skaperdas 1996, 1998; Nitzan 1991). However, the axiomatization of the effective power function differs from those in the literature.Footnote 8 The coefficient \(\alpha \) represents the elasticity of the relative effective power with respect to the relative population size. When \( \alpha =0\) the relative effective power equals 1, for \(\alpha =1\) each group’s power equals its population share, while for \(\alpha \rightarrow \infty \) the majoritarian group holds the absolute power. We will call such group with \(\pi >1/2\) dominant.
Consider now \(n>2\). Groups are allowed to form coalitions that generate the bipartitions of the population. A coalition is defined as any subset of the set N of all groups (including the empty set). In particular the grand coalition contains all the groups; an individual coalition contains only one group; and the empty coalition contains no group. Since we assume that groups can either act individually or form alliances or blocks with other groups, any measure of their effective power should take this possibility into account. This means that a measure of effective power has to consider all the potential contributions of a group to all the coalitions that it can possibly belong to.
Denote with \(C_{i}\) the set of all coalitions c that include group i. This set contains both the grand coalition and the \(i^{\prime }s\) individual coalition. The power of any coalition c is obtained by Lemma 2.1 as \( \phi ^{2}(\sum _{j\in c}\pi _{j})\), where the power of an empty coalition is 0 and the power of the grand coalition is 1.
We next define the marginal contribution of group i to the power of any coalition \(c\in C_{i}\) as (Shapley 1953):
The sum of the marginal contributions of group i over all coalitions in \(C_{i}\) is:
The effective power of any group i will be a function of \(M_{i}\) but it will also depend on the marginal contributions of the other groups \(M_{-i}\). However, as stated in the next axioms, what counts for the relative effective power between any two groups i and j is the ratio between some transformation of the sum of their marginal contributions.
Axiom 4
(Relative effective power (REP))
For any \(i,j\in N\), \(i\ne j\) and \(n\ge 2\); \(\exists ~g:\mathfrak {R}_{+}\rightarrow \mathfrak {R}_{+}\), such that for \(\phi ^{n}(\pi _{j},\Pi )>0\) we have
The REP axiom states that the relative effective power between any two groups \(i,j\in N\) depends on their sum of marginal contributions to all the coalitions that they can theoretically belong to. No matter how many groups there are in the population or how the marginal contributions are distributed among them, the relative effective power between any two groups will be determined exclusively by a ratio of a transformation \( g(\cdot )\) of their own Ms. The exclusive role of M in the determination of the relative effective power implies that the strength of one group with respect to another within the same distribution will be determined only by the relative importance they have in terms of the value they add to the coalitions they belong to. Since the same transformation function applies to marginal contributions of all the groups in the population, when two groups have the same M, this is the case also for their effective powers. The property leaves open the possibility that two groups covering different population shares may also be endowed by the same effective power. This could be the case because the \(g(\cdot )\) transformation may attach the same value to different M or because groups with different population shares exhibit the same value of M. The REP axiom considers comparisons across groups made within the same ethnic distribution, for this reason the transformation \(g(\cdot )\) may depend also on the distribution.
The relationship between the ratio of marginal contributions and the relative effective power is clarified by the following axiom where comparisons are extended to groups belonging to different distributions.
Axiom 5
(n groups relative power invariance (nGRPI))
Given two distributions, \(\Pi \) and \(\Pi ^{^{\prime }}\) with the same number of groups \(n\ge 2,\) if \(\phi ^{n}(\pi _{j},\Pi )>0\) and \( \phi ^{n}(\pi _{j}^{^{\prime }},\Pi ^{^{\prime }} )>0\) then
According to nGRPI if we compare two population distributions with the same number of groups, and if the ratio between the marginal contributions between any two groups from both distributions is the same, then their relative effective power has to be the same too. That is, the relative effective power is invariant with respect to the distribution of the groups population shares for groups with the same sum of marginal contributions. This axiom emphasizes the fact that the relative effective power between two groups i and j may depend also on the distribution of the other groups. However, this effect arises only if the distribution of the groups affects the ratios of the aggregate marginal contributions, \(M_{i}\) and \(M_{j}\).
Next theorem, proved in the Appendix, provides a role for the sum \( M_{i}^{\alpha }\) of the marginal contribution to all coalitions of group i obtained as in (5) making use in (4) of the functional form \(\phi _{\alpha }^{2}\) derived in Lemma 2.1. Thus,
Theorem 2.2
The effective power of group i satisfies Axioms N, M, 2GRPH, REP and nGRPI if and only if:
Group i’s effective power, hence, is defined as the relative sum of the marginal contributions of this group to all possible coalitions, valued according to \(\phi _{\alpha }^{2}\). Given (6), the effective power of a group can be a function of the relative size of all the groups in the population. For \(n>2\) and \(\alpha \notin \{0,1\}\), the effective power of any group i depends on both \(\pi _{i}\) and \(\Pi _{-i}\). As a consequence, the effective power of a group with a fixed population share \(\pi _{i}\) may vary significantly across different population distributions in response to the variation of the relative size of the other groups \(\Pi _{-i}\).
The previous result suggests that the effective power is not necessarily proportional to the groups’ relative size. This is in line with the literature on voting power.Footnote 9 For instance, when \(\alpha \rightarrow \infty \), the group \( i^{\prime }s\) effective power, \(\phi _{\infty }^{n}(\pi _{i},\Pi )\), coincides with its relative Penrose–Banzhaf index of voting power in a simple majority game (Felsenthal and Machover 1998).Footnote 10
As we will highlight in next section a transformation of the fractionalization index and of the RQ ethnic polarization index are special cases of the parametric family of the P index of conflict potential whose effective power functions are characterized in Theorem 2.2. Bossert et al. (2011) have provided a characterization of a generalization of the fractionalization index where differences between ethnic groups may not necessarily be binary, while Chakravarty and Maharaj (2011) have provided alternative characterizations of the ethnic polarization index. Both contributions differ from the current work because they assume some form of additivity for the aggregate index, as a result the contribution of the distribution of each ethnic group to the overall index is not affected by the distribution of the other ethnic groups. This is the case for the P index only for some parameter values that make it proportional to the fractionalization index or lead to the ethnic polarization indices but in general \(\phi _{\alpha }^{n}(\pi _{i},\Pi )\) may depend on \(\Pi \) and not only on \(\pi _{i}.\) Other contributions like Desmet et al. (2009) take into account the interaction between many peripheral/minoritarian groups and a central/majoritarian group. In this contribution also the distance (non necessarily binary) between groups is relevant. In an analogous manner, when distances are binary, the P index for \(\alpha \rightarrow \infty \) enphasizes the dominance component when the larger group exceed 50% of the population. To conclude, as pointed out the effective power function \(\phi _{\alpha }^{2}(\pi _{i},\Pi )\) for \(n=2\) relates to the ratio form contest success function even though, as argued the derivation is different. The generalization to \(\phi _{\alpha }^{n}(\pi _{i},\Pi )\) however, considers properties defined over the distribution of the aggregate marginal contributions of each group to all bipartitions of the population, instead of being defined over the distribution of the population shares of each group. The consistency between these properties that are set for a generic \(n\ge 2\) and those valid for \(n=2\) that lead to \( \phi _{\alpha }^{2}(\pi _{i},\Pi )\) is verified in the first part of the necessity part of the proof of Theorem 2.2. One may want to consider alternative specifications for the effective power function \(\phi ^{n}(\pi _{i},\Pi )\) in the spirit of the n groups contest functions of Skaperdas (1996) or their generalizations in Chakravarty and Maharaj (2014). In analogy with the derivation in Lemma 2.1, it could be possible to derive a functional form for \(\phi ^{n}(\pi _{i},\Pi )=f(\pi _{i})/\sum _{j}f(\pi _{j}) \) for non-decreasing \(f(\cdot ).\) In this case the relative power of group i w.r.t. group j depends only on \(\pi _{i}\) and \(\pi _{j}\) but not on the distribution of the other groups. This is not in general the case for the P index if \(n>3\). In fact for the P index this relative comparison depends on the ratio of the aggregate of the marginal contributions of the two groups to the power of each bipartition of the population. In our case these values could depend also on the distribution of all the other groups.
3 Properties of the P index of conflict potential
With the effective power function specified in (6), the P index of conflict potential becomes:
We set \(K=4\) so that the index ranges between 0 and 1.Footnote 11
Within the index formulation, the relative importance of groups’ power and between groups’ interaction depends on the features of the population distribution across groups, and crucially on the parameter \( \alpha \).
In the next subsection we analyse the properties of the P index for different values of the coefficient \(\alpha \) and for different population distributions. We show that for the case of two groups the parameter \(\alpha \) plays no role and the P index reduces to the RQ index of discrete polarization which is twice the fractionalization index. When the population is partitioned into more than two groups, the shape of the index depends on the choice of the parameter \(\alpha \).
3.1 The role of the coefficient \(\alpha \)
In what follows we consider the P index for \(\alpha =0\), \(\alpha =1\) and \(\alpha \rightarrow \infty \).
Case 1. When \(\alpha =0\), the effective power of each group is constant and equals 1/n. The P index becomes:
This is not exactly the fractionalization index because it is scaled by 4/n. The fractionalization index is shaped only by the interaction component and is defined as the probability that two individuals randomly selected from a population belong to different groups. For \( P_{0}^{n}(\Pi )\) the interaction component is combined with the effective power assigned to each group, which is decreasing in n. For a given n, the \(P_{0}^{n}\) index and the fractionalization index provide the same ranking. However, they significantly differ over distributions with different n. This aspect can be made evident when all the groups have the same size. In this particular case, \(P_{0}^{n}\) and FRAC move in opposite directions as n increases. In fact, when the relative size of each group is 1/n, the \(P^{n}_{0}\) index becomes \(4 \frac{1}{n} \frac{n-1}{n}\) while \( FRAC=\frac{n-1}{n}\).Footnote 12
Despite its very simple structure, the \(P^{n}_{0}\) index exhibits some interesting properties. In terms of the possible relation with conflict potential it is indeed quite difficult to relate an increased probability of across group interaction to the increased conflict vulnerability. As n increases the probability of interaction increases but this may not necessarily lead to conflict because groups become smaller, hence their chances to mobilize efficiently may decrease. There are two forces at play that should be taken into account: increased interaction versus reduced power. The index of fractionalization alone does not take both these aspects into account. For the \(P^{n}_{0}\) index, on the other hand, as n increases the contribution of interaction increases but it is rescaled by the power component, which decreases at a higher rate. With n equally sized groups, the maximum of conflict potential is reached for two groups, as happens with the discrete polarization index.
Case 2. When \(\alpha =1\), the effective power of each group equals its relative population size. In fact, \(\phi _{1}^{2}(\pi )=\pi \) and the marginal contribution of group i to the power of any coalition \(c\in C_{i}\) as in (4) is therefore \(m_{i}(c)=\pi _{i}\) for any c. Considering that the number of all possible coalitions that can include group i is \(2^{n-1}\) (that is the cardinality of the power set of the set of all the other \(n-1\) groups), it follows that according to (5) \(M_{i}^{1}=\pi _{i}\cdot 2^{n-1}\) for any group i. Then by substituting into (6) it follows that \(\phi _{1}^{n}(\pi _{i},\Pi )=\pi _{i}\) for all i. In this case the P index reduces to the RQ index of discrete polarization:
The larger is a group, the proportionally higher is its effective power to translate alienation into effective voicing.
For \(\alpha =0\) and \(\alpha =1\), hence, a group i’s effective power depends only on n and \(\pi _{i}\). In both cases \(\Pi _{-i}\) plays no role. The features of \(\Pi _{-i}\) become crucial for all the other values of \(\alpha \) and in particular for \(\alpha \rightarrow \infty \).
Case 3. As \(\alpha \rightarrow \infty \), the effective power converges to the relative Penrose–Banzhaf Index of voting power in a simple majority game. Effective power of group i is a function of both \(\pi _{i}\) and \(\Pi _{-i}\). If we denote by \(\pi ^{*}\) the relative size of the largest group in the population and with \(\gamma _{i}\) the relative Penrose–Banzhaf Index of voting power associated with group i, the \(P_{\infty }^{n}\) index can be written as:
where \(\theta _{n}= n/(2^{n-1}+n-2)\).
When one group is dominant, i.e., its relative size exceeds 1/2, the potential of conflict is determined only by that group’s relative size. In this case the P index coincides with the interaction component associated with this group. As the relative size of a dominant group approaches 1/2 the value of the index converges to 1. Similarly, when the size of a dominant group increases, the overall interaction decreases, and the index moves downward.Footnote 13 When no group has absolute majority the contribution of each group to the overall conflict potential is given by the product between their relative Penrose–Banzhaf index of voting power and their interaction component. Finally, with one group covering exactly one half of the population, the index is a convex combination between its maximum value 1 and \(P_{0}^{n}(\Pi )\).Footnote 14
3.2 P index for two and three groups
In the case of two groups the interaction component of each group is symmetric. As a result the P index is proportional to FRAC irrespective of \(\alpha \):
Thus, the simplest way to analyse the implications of different choices of \( \alpha \) is to consider the case with three groups. With \(n=3\) all the indices can be expressed as a function of the relative size of two groups (since \(\sum \pi _{i}=1\)). For expositional purposes, we fix the size of one group (here \(\pi _{2}\)) to 1/3 because we want to compare alternative population distributions with the uniform distribution, and we express the indices in terms of \(\pi _{1}\).
When all the groups have the same size, the P index yields the same value \(4\frac{n-1}{n^{2}}\) for any \(\alpha \). The P index with \(\alpha =1\) (i.e., the RQ index) is invariant to population transfers between groups when the relative size of one group is set to 1/3. The shape of \(P_{0}^{3}\) is identical to the shape of the fractionalization index that is quadratic and concave with respect to \(\pi _{1}\) with the maximum for \( \pi _{1}=1/3\).
For \(\alpha \) different from 0 and 1 the index becomes non-monotonic in \( \pi _{1}\) for \(\pi _{1}>1/3\). As \(\alpha \) approaches infinity, the shape of the index becomes particularly interesting. With \(n=3\), \(\pi _{2}=1/3\) and \( \alpha \rightarrow \infty \), the P index is:
where \(\pi _{1}\ge 1/3\) denotes the population share of the larger group.
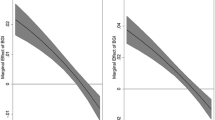
Figure 1 shows the \(P^{3}\) index for \(\alpha =0\) (dashed curve), \(\alpha =1\) (dot-dashed line) and \(\alpha >1\) (solid curves) expressed in terms of \( \pi _{1}\).Footnote 15 In the limit as \(\alpha \) approaches infinity, the \(P^{3}\) index assumes a particular shape characterised by a discontinuity at \(\pi _{1}=1/2\) (solid curve in the right hand-side of the figure).
Starting from a uniform distribution, i.e., when \(\pi _{1}=1/3\), the \(P_{\infty }^{3}\) index follows the shape of the fractionalization index. As \( \pi _{1}\) increases, the population becomes less fragmented and the index decreases. When the relative size of group 1 reaches 1/2, the index “jumps” to 8/9, the constant value obtained for \(\alpha =1\). Once \(\pi _{1}\) exceeds 1/2, the index reaches almost 1 and then decreases. The \(P_{\infty }^{3}\) index reaches its maximum when the relative size of one group becomes scarcely higher than 1/2 because in that case this group gains the absolute power and the “opposition” is powerless. This fact is in line with the notion of dominance of one group over the other(s).Footnote 16 It is worth noting here that the \(P_{\infty }^{3}\) index combines dominance (and, hence power) and interaction. It follows that, as the size of the dominant group increases, the probability of interaction decreases and so also the potential of conflict. As a result for a very large dominant group the index tends to 0. With no dominance, i.e., if the relative size of all groups is lower than 1/2, the conflict potential is entirely determined by the interaction component—the shape of \(P_{\infty }^{3}\) follows the shape of the fractionalization index.
3.3 \(P_{\infty }\) index for more than two groups
For any arbitrary number of groups, the value of the \(P_{\infty }^{n}\) index in the presence of dominance coincides solely with the interaction component of the dominant group. In the absence of dominance the index is either proportional to fractionalization or to a combination of fractionalization and the interaction component of either the largest or the smallest group as long as the number of groups in the population is not too large.
Consider for instance population distributions with \(6>n\ge 3\) such that \( \pi _{1}>\pi _{2}>\cdots >\pi _{n}\) and \(\pi _{1}<1/2\). For \(n=3\) the \( P_{\infty }^{3} \) index is given by the formulation in (11), thus if \( \pi _{1}<1/2\) it coincides with \(P_{0}^{3}\) and is proportional to fractionalization.Footnote 17
For \(n=4\) and population distributions characterised by \(\pi _{1}+\pi _{4}<1/2\) , the groups’ effective power \(\phi _{\infty }^{4}\) distribution is (1/3, 1/3, 1/3, 0), and for a given \(\pi _{4}\), the value of the \(P_{\infty }^{4}\) index is entirely determined by the interaction component. When the population becomes more fragmented, the interaction increases and the \(P_{\infty }^{4}\) index follows the shape of \(P_{0}^{4}\). Similarly, for all those distributions where \( \pi _{1}+\pi _{4}>1/2\), the groups’ effective power is then constant and its distribution is given by (1/2, 1/6, 1/6, 1/6). Also in these cases, now for a given \(\pi _{1}\), the \(P_{\infty }^{4}\) index results linearly correlated with the \(P_{0}^{4}\) index.Footnote 18 Thus, in the absence of dominance, when \(n=4\), the \( P_{\infty }^{4}\) index combines fractionalization with the interaction component either of the largest group or of the smallest one, or of both.
With \(n=5\), the \(P_{\infty }^{5}\) index coincides with \(P_{0}^{5}\) when \( \pi _{1}+\pi _{2}<1/2\), and for a given \(\pi _{1}\) is linearly related to \( P_{0}^{5}\) when \(\pi _{1}+\pi _{5}>1/2\). In fact, in the former case, all the groups in the population have the same effective power \(\phi _{\infty }^{5}\) of 1/5, while in the latter case the groups’ effective power distribution is constant and given by (7/11, 1/11, 1/11, 1/11, 1/11), which makes the \(P_{\infty }^{5}\) index linearly correlated with the \(P_{0}^{5}\) index for a given value of \(\pi _{1}\) .Footnote 19
As the number of groups increases, even a very small variation in the groups’ relative size may significantly alter their relative power. As a consequence, the correlation between the \(P_{\infty }^{n}\) index and fractionalization becomes less clear. For instance, when \(n=6\), starting from a distribution with a very low dispersion of population across groups, and increasing the relative size of the largest group, the population becomes less fragmented and the \(P_{0}^{6}\) index decreases. However, the relative power shifts towards the larger groups and the \(P_{\infty }^{6}\) index moves in the opposite direction with respect to the \(P_{0}^{6}\) index.
4 Empirical relevance of the P index of conflict potential
In this section we investigate the relationship between the P index and conflict behaviour. The measures of conflict potential relate the features of the population distribution across groups to the probability of conflict onset rather than to the incidence or intensity of a conflict. Our empirical exercise hence relies on a logistic model specified in Wimmer et al. (2009) and Cederman and Girardin (2007) that focuses on the onset of ethnic conflicts in the time range from 1946 to 2005. Ethnic conflict onset is a binary variable that takes the value of 1 in the first year of a conflict and 0 otherwise. The data on ethnic distributions and main explanatory and control variables come from the Ethnic Power Relations (Version 3.01) data set [EPR3 henceforth] which extends and improves the original Version 1.0 of the Ethnic Power Relations data set (Wimmer et al. 2009) [WCM henceforth].Footnote 20 As for the ethnic groups coding, the EPR3 data set has several advantages with respect to other data sources commonly used in the empirical literature such as the Minority at Risk data set (Gurr 1993, 2000), the Atlas Narodov Mira (1964) data set and the Fearon (2003) data set. First, it identifies all politically relevant ethnic groups and records changes in politically relevant categories over time. Second, the coding of ethnic groups does not limit the possibilities to any existing ethnic group list. Third, the EPR3 data set assesses formal and informal degrees of political participation and exclusion along ethnic lines.Footnote 21 As a robustness check, however, we also test the empirical performance of the P index using the Fearon’s (2003) groupings.
Regarding the conflict data, EPR3 extends the Armed Conflict Data Set [ACD henceforth] by coding each conflict for whether rebel organizations pursued ethno-nationalist aims and recruited along ethnic lines.Footnote 22 We consider ethnic conflicts for several reasons. First, the majority of the conflicts after the Second World War were ethnic in nature. Second, there is a substantial difference in the nature and the determinants of ethnic and non-ethnic conflicts (Sambanis 2001, 2004). There is no reason to believe that ethnic diversity is an important determinant of non ethnic conflicts, such as revolutions or any other form of anti-governmental protest. Third, ethnic conflicts are closely related to cultural and political identity—in ethnically heterogeneous societies political mobilization occurs mostly along ethnic lines.
The list of explanatory and control variables considered in our empirical analysis is the one commonly used in conflict researchFootnote 23 (Fearon and Laitin 2003; Collier and Hoeffler 2004; Montalvo and Reynal-Querol 2005; Sambanis 2001; Hegre and Sambanis 2006; Wimmer et al. 2009), it includes: GDP per Capita, Population Size, Oil Production per Capita, Mountainous Terrain, Noncontiguous Territory and New State, Democracy and Anocracy, Instability (regime change). In order to take into account the political dimension of ethnic conflicts, we follow WCM and consider three ethnic politics variables: the share of the population excluded from central government, the number of power sharing partners, and the percentage of years spent under imperial rule between 1816 and independence. We control for possible time trends by including the number of peace years since the outbreak of the previous conflict, a cubic spline function on peace years, and regional dummies.Footnote 24 In order to account for the variation in within-region ethnic conflict onset due to factors that are region-specific over time, we also construct a regional time trend dummy variables.Footnote 25
Together with the indices of fractionalization, discrete polarization, and several dominance dummies, we calculate the P index of conflict potential for different values of the parameter \(\alpha \) using the groups’ relative shares calculated in relation to total population. Given a particular structure of the effective power function and the related computational complexities, in order to calculate the P index for \( \alpha \ge 2\), we consider all the countries with no more than 6 ethnic groups as well as all those countries for which the number of groups was reduced to 6 according to the following criteria: the sum of the population sizes of all the groups ranked below the sixth largest group could not exceed 8% of the total population, and the relative population size of the biggest excluded group could not be larger than 5%. In such a way we consider 21 out of 27 countries originally characterised by more than 6 ethnic groups. The average (median) size of the largest eliminated group is 2% (2%), while the average (median) number of eliminated groups across countries is 2.612 (2). The average (median) sum of the size of the eliminated groups, on the other hand, is 3.3% (3%). The remaining 6 countriesFootnote 26 were excluded from the analysis since they don’t meet one or both the above mentioned criteria. Regarding the P index for \(\alpha =1\) and \( \alpha \rightarrow \infty \), as well as the fractionalization index, for our main empirical specifications we consider the original data set with no group or country excluded, containing 146 countries for which complete ethnic grouping is available.
4.1 Comparison between indices: a first insight into the data
In the previous section we have shown how the choice of the parameter \( \alpha \) and the features of the population distribution across groups determine the shape of the P index. As a first step in the assessment of the empirical validity of our indices, we analyse graphically the relationship between the P index for different values of \(\alpha \) using the data on ethnic distribution from the Ethnic Power Relations data set (Wimmer et al. 2009).
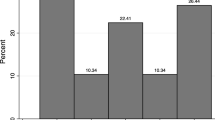
Figure 2 shows the relationship between \(P_{0}^{n}\), \(P_{4}^{n}\), \( P_{10}^{n} \) and \(P_{\infty }^{n}\), versus \(P_{1}^{n}\) (RQ polarization index). As \(\alpha \) increases, the correlation between RQ and the P index decreases, especially for high values of the indices. For instance, the correlation between RQ and P for \(RQ\in [0.7, 0.9]\) is 0.5 in the case of \(\alpha =4\), is 0.27 for \( \alpha =10\) and boils down to 0.19 for \(\alpha \rightarrow \infty \).
In order to analyse the relationship between the probability of conflict outbreak and different distributional aspects of ethnicity, we preliminarily verify how the indices correlate with conflict outcomes. Figure 3 shows \( P_{\infty }^{n}\) versus RQ with the labels for the frequency of ethnic conflict onsets [EC] in the time range from 1946 and 2005. The horizontal and the vertical lines represent respectively the mean values of \( P_{\infty }^{n}\) (0.5809) and RQ (0.5408).Footnote 27 The two indices differ most when they are both larger than their respective means. This range of values is associated with 76% of all conflict episodes as shown in detail in the right-hand side frame of Fig. 3.
In the next section we test the empirical performance of the derived indices and we show that the predictive power of \(P_{\infty }^{n}\) is significantly higher than the predictive power of the other indices of ethnic diversity in the explanation of ethnic conflict onset.
4.2 Explaining ethnic conflict onset
The empirical evidence on the association between ethnic diversity and conflict is very heterogeneous. Applying the fractionalization index, Sambanis (2001, 2004) and Hegre and Sambanis (2006) find a positive and statistically robust association between ethnic fractionalization and ethnic conflict and argue that as a country becomes ethnically more fragmented, the risk of conflict increases. Collier (2001) and Collier and Hoeffler (2004) show that the interaction between ethno-linguistic and religious fractionalization (which they term as “social fractionalization”) is negatively correlated with the likelihood of conflict because ethnic diversity makes rebellion harder since rebel cohesion becomes more costly. The mitigating effects of social fractionalization on conflict, however, disappear in the presence of ethnic dominance: with one ethnic group covering between 45 and 90% of the overall population, the risk of conflict is almost doubled. On the other side, Fearon and Laitin (2003) and Fearon et al. (2007) find no significant effect of ethnic and religious fractionalization on the likelihood of civil conflict outbreak.
Another important strand of literature pioneered by the International Conflict Research group emphasizes the role of political and economic exclusion and competition along ethnic lines in shaping the probability of conflict onset (see, for instance, Wucherpfennig et al. 2011; Cederman et al. 2013; Cederman and Wucherpfennig 2017; Bormann et al. 2019). These contributions highlight high degrees of ethnic exclusion and segmentation as a key motivation for rebellion, and dismiss grievances exacerbated by high ethnic fragmentation and/or polarization as irrelevant (Cederman and Girardin 2007; Wimmer et al. 2009; Cederman et al. 2013).
Several other scholars have argued that the relationship between ethnic diversity and conflict is not monotonic and suggest, in line with Horowitz (1985), that highly homogeneous and highly heterogeneous societies are less conflict prone with respect to societies divided into few prominent ethnic groups. Following this logic, Montalvo and Reynal-Querol (2005) apply their index of discrete ethnic polarization and find a positive and statistically significant association between ethnic polarization and the incidence of conflict.Footnote 28 Schneider and Wiesehomeier (2010), on the other hand, find that the relationship between ethnic polarization and conflict is ambiguous and depends on whether it is considered civil war incidence or civil war onset as a dependent variable while Collier and Hoeffler (2004) find no statistically significant relationship between ethnic polarization and the risk of conflict outbreak.
From an empirical point of view, hence, the relationship between ethnic diversity and conflict is quite ambiguous and still no broad consensus is reached on which distributional aspect of diversity is an important correlate to conflict onset. The particular feature of the P index of conflict potential that combines different aspects of diversity depending on the characteristics of the underlying population distribution across groups, may make a difference. We empirically validate our index in the context of the Cederman and Girardin’s (2007) and Wimmer, Cederman and Min’s (2009) model of ethnic conflict onset, using the data on ethnic distributions and main explanatory and control variables from the EPR3 data set.
In order to assess the relative performance of the P index with respect to different \(\alpha \), we first estimate our models of ethnic conflict onset using the reduced sample of countries. We then reestimate our models using the entire sample with no group or country excluded from the analysis, and consider the P index with the best performance in terms of the statistical significance and the goodness of fit. Table 1 presents the results of our estimations based on the reduced sample of countries.Footnote 29
Regarding the parameter \(\alpha \), only the coefficients associated with the P index with \(\alpha \ge 4\) are significantly different from zero. The magnitude and the significance of the coefficient associated with the index increases with \(\alpha \) and reaches its maximum for \( \alpha \rightarrow \infty \). Similarly, the goodness of fit measured by the Pseudo \( R^{2}\) is also increasing in \(\alpha \). Indeed, by comparing the outcome of various estimations based on \(P_{\alpha }^{n}\), it results that the highest value of the Pseudo \(R^{2}\) is obtained for \(\alpha \rightarrow \infty \).Footnote 30 The results remain robust even when we consider only countries with no more than 6 groups without relying on sample selection criteria described so far.
Table 2 reports the estimation results related to the entire set of countries with no group/country excluded from the analysis. Together with the RQ and the fractionalization index, we consider only the P index with \(\alpha \rightarrow \infty \) since it yields the best fit with respect to any other value of \(\alpha \) (Table 1). The estimated coefficients in Models 1–3 show that among the three distributional indices of ethnic diversity, only the P index with \(\alpha \rightarrow \infty \) is significantly different from zero. The level of GDP per capita is negatively correlated with the probability of conflict outbreak while the size of the population and a dummy for the first two years of independence, are positively related to ethnic conflict onset. This is in line with Doyle and Sambanis (2000), Fearon and Laitin (2003), Collier (2001); Collier and Hoeffler (2004), and Wimmer et al. (2009), among others. In contrast to Fearon and Laitin’s (2003) insurgency model, previous regime change, oil production per capita, and mountainous terrain receive limited support here. Although the coefficients associated with democracy and anocracy have the expected sign they do not reach a significance at the 0.05 level. The regional time trends are all insignificant except the one for the East-European countries (Balkans and the former Soviet Union) that experienced several ethnic conflicts at the beginning of the 1990s after the fall of communism. In line with Wimmer et al. (2009), the degree of ethnic exclusion and centre segmentation (number of ethnic groups in power) are significant with the expected sign in all model specifications, except in model 3 where the centre segmentation variable is not statistically different from zero at the 0.05 level.
Finally, in Models 5 and 6 we check the relative strength of \(P_{\infty }^{n}\) versus RQ and fractionalization. The coefficients on ethnic polarization and fractionalization are not significantly different from zero in combination with \(P_{\infty }^{n}\) which remains positive and statistically significant. More interestingly, since the coefficient on \( P_{\infty }^{n}\) and the goodness of fit of the model that includes both \( P_{\infty }^{n}\) and fractionalization are very similar to those in Model 3, we can conclude that fractionalization does not add much information to the model. This does not mean that ethnic fractionalization is never important but it simply means that the \(P_{\infty }^{n}\) index is able to “extract” the impact of the interaction between groups on the probability of conflict outbreak. The features of ethnic distribution as measured with the \( P_{\infty }^{n}\) index are, hence, an important correlate of ethnic conflict outbreak, even after controlling for several economic, structural and geographical characteristic, as well as for political exclusion and competition along ethnic lines.
Since the \(P_{\infty }^{n}\) index combines interaction and dominance, Table 3 checks its relative strength with respect to several dominance dummy variables commonly used in the empirical literature together with the fractionalization index.
Model 1 shows that the Collier and Hoeffler’s dominance dummy (defined as 1 if the relative size of the biggest group in the population is between 45% and 90%) is significantly different from zero with the expected sign. The RQ polarization index is not significant when we control for dominance (Model 2). This evidence is in line with Collier and Hoeffler (2004). Only the \(P_{\infty }^{n}\) index and the fractionalization index remain significant in combination with dominance (at the 0.09 and 0.01 level respectively). Similar results are obtained with the Schneider and Wiesehomeier’s (2008) ethnic dominance dummy (defined as 1 if the relative size of the biggest group in the population is between 60 and 90%) (Models 5–8). When combined with a “pure” dominance (i.e., defined as 1 if the relative size of the biggest group in the population is larger than 50%), the \(P_{\infty }^{n}\) and the fractionalization index result significant at the 0.01 level.Footnote 31
In addition to the Collier and Hoeffler’s and the Schneider and Wiesehomeier’s ethnic dominance dummies, Montalvo and Reynal-Querol (2005) propose another indicator of conflict potential, namely the size of the largest ethnic minority. From Table 4 we see that the coefficient on this variable is not significantly different from zero in any model specification, while the \(P_{\infty }^{n}\) index remains highly significant even in the presence of this variable.
Finally, Table 5 considers intermediate intensity conflicts only (Models 1–3) and the \(P_{\infty }^{n}\) index calculated by using the Fearon’s (2003) classification of ethnic groups (Models 4–5).Footnote 32 The \(P_{\infty }^{n}\) index remains highly significant in the model for intermediate intensity conflicts, as well as for Fearon’s (2003) ethnic grouping.
Given the fact that ethnic conflict is a rare event and that the standard logistic regression can underestimate the probability of such events, we also perform a rare event logit estimation (King and Zeng 2001). The results are similar to those obtained by using the traditional logistic model. Collier and Hoeffler (2004), Sambanis (2001) and Wimmer et al. (2009) report similar findings. In addition, we also check whether the results are driven by particular geographical regions that might be considered more or less conflict prone by eliminating one region at a time in our baseline regression models. The results do not change significantly and the relevance of the \(P_{\infty }^{n}\) index is unaltered. In addition to the clustering on country, we also control for the non-independence of observation over countries and over time. We do not find any substantial difference in the results. The test of the correlation coefficient is never significant which means that country—year observations are independent. The sign and level of significance of other covariates to ethnic conflict are similar to those obtained with the standard logistic and the rare event logistic estimation method. For the sake of space we do not report the estimation coefficients from these additional robustness checks.Footnote 33
5 Concluding remarks
In this paper we show how the relative importance of fractionalization, polarization and dominance in the determination of conflict potential may depend on the characteristics of the underlying population distribution across groups. We axiomatically derive a parameterized class of indices of conflict potential that combines the groups power and between-groups interaction. Conflict potential is obtained as a weighted sum of the effects of across-group interaction and their relative effective power. Under some population distributions the power component dominates the interaction component and generates effects similar to the presence of an extreme form of dominance where the size of one group is scarcely higher than one half of the population. When the interaction component dominates the power component, the main driver of conflict is fractionalization while for the intermediate case, what matters is the combination between the two. It is not important how large a group is but rather how decisive it can be in a hypothetical competition between all the groups in the population. A group can be powerless even when its size is not negligible, which is in line with the literature on voting power in simple majority games.
Our measures could differ from the existing diversity indices. We show that when we apply our indices to the empirical analyses of the correlates of ethnic conflict onset, this difference is not only theoretical but also empirical. The extreme member of our class of indices, the \(P_{\infty }^{n}\) index, outperforms the existing indices of ethnic diversity and it is the only distributional index that is significantly correlated to the likelihood of ethnic conflict onset. This evidence is robust to the inclusion of an additional set of regressors, time and regional controls as well as to the alternative estimation methods.
Notes
Political institutional settings, for instance, may deepen and institutionalise ethnic divisions (Horowitz 1985, Chandra 2004). Majoritarian institutions or institutions that cross-cut the ethnic group boundaries might weaken ethnic identity, while institutions based on distinctions between ethnic groups might increase ethnic salience. In a similar fashion, Bochsler (2010) suggests that electoral systems and territorial autonomy may influence the efficiency of ethnic minorities to mobilize, with proportional representations or majoritarian systems combined with territorial concentration of ethnic minorities increasing ethnic salience. Wimmer (2002) emphasizes the role of weak central states and networks of civil society while Rokkan et al. (1999) ascribes responsibility for ethnic tensions to centralized state structures in combination with cultural or economic heterogeneity and asymmetric federalism.
The details of the comparisons in the examples are reported in Table 6 in Appendix I.
For ease of exposition here we consider \(\Pi \in \Delta ^{n}\) even though for a given \(\pi _{i}\) only a subset of \(\Delta ^{n}\) is consistent with having one element associated with group i equal to \(\pi _{i}\), we also include the extreme values \(\pi _{i}\in \{0,1\}\) within the domain.
In general, the probability distribution over coalitions could also be asymmetric. For instance, if we were to attach to each individual with a clear ethnic or religious marker the level of income, wealth or some other indicator based on political or ideological scale, we could define the probability of any coalition in terms of the similarity between the groups’ income, wealth or ideological attributes. By employing network analysis on tactical cooperation among Syrian rebels, Gade et al. (2019), for instance, define distances between groups in terms of differences in their political ideology (nationalists, separatists or religious fanatics).
For instance, the RQ index and the fractionalization index assume that there is no interaction between groups.
In order to guarantee that \(r(\rho )\) is well defined, the denominator of the function should not be equal to 0. Because of the properties considered in this paper the function \(\phi ^{2}\) will be specified over comparisons where \(r(\rho )\) is defined. This aspect is clarified in the proof of Lemma 2.1.
Given a functional form for \(\phi ^{2},\) then \(r(\rho )\) derives directly by recalling that \(\pi =\rho /(1+\rho )\) and thus \(r(\rho ):=\frac{\phi ^{2}(\rho /(1+\rho ))}{\phi ^{2}(1/(1+\rho ))}\).
In his famous critique of the practice of assigning voting weights proportional to the number of citizens in different legislative bodies (“one man, one vote” requirement), Banzhaf (1965, p. 318) argues that the number of votes is not even a rough measure of the voting power of the individual legislator.
A simple majority game is a voting game in which an actor (or a coalition of actors) wins if the number of votes s/he possesses exceeds 50% of the total number of votes. In this case s/he is attributed the value of 1 and 0 otherwise. The Penrose–Banzhaf Index of voting power measures the ability of an actor to influence the outcome of voting in a collectivity and is defined as the relative number of times s/he can switch a coalition from losing to winning relative to the total number of swings of all the other actors. In our case, according to \(\phi _{\infty }^{2}(\pi )\) in Lemma 2.1, in addition it is considered that the power of a coalition covering exactly 50% of the population is 1/2. It is important to stress, however, that standard voting power indices do not take into account the voters’ preferences which may bias the real power of political actors. Indeed, Garrett and Tsebelis (1999) point out that agents are likely to form coalitions and align their votes according to their ideological orientation. As a consequence, only voters in a spatial proximity on the ideological scale will vote together forming connected coalitions. Moreover, voters with similar preferences often form a-priori blocks or coalitions before the actual voting takes place which, given the non-additive property of standard voting power indices, increases their power (Malawski 2004).
When \(K=4\), for any \(\alpha \ne 0\), the supremum of the index is 1 for any n. If \(\alpha =0\), the supremum is 1 if \(n=2\) and decreases as n increases.
It follows that as n increases \(P_{0}^{n}\) converges to 0 while FRAC increases and converges to 1.
When \(\pi ^{*}>1/2\) the \(P_{\infty }\) index is equivalent to the RQ index with only two groups (which is proportional to the fractionalization index) and measures the degree of bi-polarization, with the majoritarian group at one extreme and the “opponent” block at the other.
In fact, in this case for the larger group, say group 1, s.t. \(\pi _{1}=1/2,\) we have that its marginal contribution, computed making use of \(\phi _{\infty }^{2}\) in (4), to the power of the grand coalition of the whole population and when the group is considered alone is 1/2, while it equals 1 for all the other coalitions. Thus, considering that there are \( 2^{n-1}\) coalitions involving a group, we have \(M_{1}^{\infty }=2^{n-1}-1.\) For any of the other \(n-1\) groups the marginal contribution to the power of the coalition with group 1 and of the coalition with all the other groups is 1/2, while for all the other coalitions the marginal contribution is 0. It then follows that \(M_{i}^{\infty }=1\) for \(i=2,3,\ldots ,n.\) As a result from \( \phi _{\infty }^{n}(\pi _{i},\Pi )\) in (6) we obtain \(\phi _{\infty }^{n}(\pi _{i},\Pi )=1/(2^{n-1}+n-2)\) for \(i=2,3,\ldots ,n\) and \(\phi _{\infty }^{n}(\pi _{1},\Pi )=(2^{n-1}-1)/(2^{n-1}+n-2).\) Substituting into the definition of \(P_{\infty }^{n}(\Pi )\) and readjusting gives \(P_{\infty }^{n}(\Pi )=4\pi _{1}(1-\pi _{1})(2^{n-1}-2)/(2^{n-1}+n-2)+4/(2^{n-1}+n-2)\cdot \sum _{i}\pi _{i}(1-\pi _{i}).\) Recalling that \(\pi _{1}=1/2,\) that \(\theta _{n}=n/(2^{n-1}+n-2)\) and that \(P_{0}^{n}(\Pi )=\frac{4}{n}\sum _{i}\pi _{i}(1-\pi _{i})\), the formula simplifies to \(P_{\infty }^{n}(\Pi )=(1-\theta _{n})+\theta _{n}P_{0}^{n}(\Pi ).\)
The graph is symmetric by construction around \(\pi _{1}=1/3.\)
For instance, Collier and Hoeffler (2004) reason in terms of minority exploitation in ethnically heterogeneous societies, and claim that when the size of the predominant group is scarcely higher than 1/2, the potential to exploit the minority is highest and, hence its “frustration” is maximal. Since the minority in this case does not have access to legal channels for achieving political change, use of arms or some other kind of conflict technology is regarded a plausible alternative strategy.
With three groups, when \(\alpha \rightarrow \infty \), if the larger group is not dominant, the relative Penrose–Banzhaf index of power of each group is 1/3 irrespective of their relative sizes.
The \(P_{\infty }^{4}\) index in this case coincides with \(-\frac{1}{3} \cdot 4\pi _{4}(1-\pi _{4})+\frac{4}{3}P_{0}^{4}\) for distributions characterised by \(\pi _{1}+\pi _{4}<1/2\), and with \(\frac{1}{3} \cdot 4\pi _{1}(1-\pi _{1})+\frac{ 2}{3} P_{0}^{4}\) for distributions where \(\pi _{1}+\pi _{4}>1/2\). While for all distributions where \(\pi _{1}+\pi _{4}=1/2\), the \(P_{\infty }^{4}\) index is \(\frac{1}{6}\cdot 4\pi _{1}(1-\pi _{1})+P_{0}^{4}-\frac{1}{6}\cdot 4\pi _{4}(1-\pi _{4}).\)
The \(P_{\infty }^{5}\) index in the latter case is given by \(\frac{6}{11}\cdot 4\pi _{1}(1-\pi _{1})+\frac{5}{11}P_{0}^{5}.\)
The version 3.01 of the Ethnic Power Relations data set improves the previous coding of much of Latin America, Central Asia, Eastern Europe, and many other countries. See: http://www.epr.ucla.edu/. At date, an updated version of the EPR dataset is available containing information on all politically relevant ethnic groups and their access to state power in every country of the world from 1946 to 2017.
The list of politically relevant ethnic categories, in some cases, was changing from one sub-period to another, either because certain categories ceased to be or became relevant for the first time, or because higher or lower level of ethnic differentiation became salient (WCM, p. 326). The coders were asked not to exclude groups based only on their relative population size, since even small groups can be significant at the national or regional level. An ethnic category is politically relevant if is represented by at least one significant political actor or if the members of the groups are “[...] systematically and intentionally discriminated against in the domain of public politics [...]” (WCM, p. 325). By “significant” political actor it is meant a political organization (not necessarily a party), that is active in the national political arena. One group is discriminated against if there is an intentional political exclusion of the entire ethnic community from decision making, either at the national or at the regional level.
The ACD data set includes intermediate and high intensity conflicts. The definition of a conflict depends on the “battle death threshold”, i.e., the number of killed people in a year. The ACD data set considers all conflict with at least 25 battle deaths a year (where high intensity conflicts are those with more than 1000 battle deaths a year). The authors identify as ethnic “[...] the aims of achieving ethno-national self-determination, a more favourable ethnic balance of power in government, ethno-regional autonomy, the end of ethnic and racial discrimination, language and other cultural rights [...]” (WCM, p. 326). All other wars are defined as non-ethnic.
The illustration of the explanatory variables is given in the Appendix.
The world is divided in 6 geographical regions: Asia, Sub-Saharan Africa, Latin America, East Europe, North Africa and Middle East, and Western.
The regional time trend dummy variables are defined as: \( RegTrend=RegDummy+RegDummy*Year.\)
The list of countries not considered in the reduced sample contains: Russia, Democratic Republic of Congo, India, China, Namibia and Sudan.
The mean value of \(P_{\infty }^{n}\) in conflict and peace episodes is 0.74 and 0.57 respectively, while for the RQ index the mean values associated with conflict and peace episodes are respectively 0.65 and 0.54.
Collier and Hoeffler (1998) obtain a similar result by considering the square of ethnic fractionalization.
In all model specifications we correct for error correlation over time for a given country by calculating cluster—robust standard errors. For the sake of space we do not show time controls variables and regional dummies in the regression results tables.
Similarly, the Akaike (AIC) and the Bayesian Information Criterion (BIC) criterion suggest that the model with the best fit is the one that includes the \(P_{\infty }^{n}\) index. We have also calculated the Somers’ D statistic which provides an estimate of the rank correlation of the observed binary response variable (ethnic war onset) and the predicted probabilities. Since it can be used as an alternative indicator of model fit, we compared its value for the P index with different \(\alpha \). The results are in line with the previous conclusions based on the Pseudo \(R^{2}\) and on the other informational criteria.
The estimation of this latter model is available upon request.
Models 4 and 5 do not consider the ethnic politics variable since the share of the excluded population and the number of included ethnic groups are defined over the EPR grouping.
All the additional regression tables are available upon request.
References
Acemoglu D, Wolitzky A (2014) Cycles of conflict: an economic model. Am Econ Rev 104(4):1350–67
Akcinaroglu S (2012) Rebel interdependencies and civil war outcomes. J Confl Resolut 56(5):879–903
Axelrod RM (1970) Conflict of interest: a theory of divergent goals with application to politics. Markham publishing company, Chicago
Baliga S, Lucca DO, Sjöström T (2011) Domestic political survival and international conflict: is democracy good for peace? Rev Econ Stud 78(2):458–486
Banzhaf JF (1965) Weighting voting doesn’t work: a mathematical analysis. Rutgers Law Rev 19:317–343
Bochsler D (2010) Territory and electoral rules in post-communist democracies. Palgrave Macmillan, Basingstoke
Bormann NC, Cederman LE, Gates S, Graham BAT, Hug S, Strøm KW, Wucherpfennig J (2019) Power sharing: institutions, behavior, and peace. Am J Polit Sci 63(1):84–100
Bossert W, D’Ambrosio C, La Ferrara E (2011) A generalized index of fractionalization. Economica 78(312):723–750
Caselli F, Coleman WJ II (2013) On the theory of ethnic conflict. J Eur Econ Assoc 11:161–192
Cederman LE, Girardin L (2007) Beyond fractionalization: mapping ethnicity onto nationalist insurgencies. Am Polit Sci Rev 101:173–185
Cederman LE, Wucherpfennig J (2017) Inequalities between ethnic groups, conflict, and political organizations. Ethnopolitics 16(1):21–27
Cederman LE, Wimmer A, Min B (2010) Why do ethnic groups rebel? New data and analysis. World Polit 62(1):87–119
Cederman LE, Gleditsch KS, Buhaug H (2013) Inequality, grievances, and civil war. Cambridge University Press, New York
Chakravarty SR, Maharaj B (2014) New contest success functions. Working papers 340, ECINEQ, Society for the Study of Economic Inequality
Chakravarty SR, Maharaj B (2011) Measuring ethnic polarization. Soc Choice Welf 37(3):431–452
Chandra K (2004) Why ethnic parties succeed: patronage and ethnic head counts in India. Cambridge studies in comparative politics. Cambridge University Press, Cambridge
Christia F (2012) Alliance formation in civil wars. Cambridge University Press, Cambridge
Collier P (2001) Implications of ethnic diversity. Econ Policy 16(32):127–166
Collier P, Hoeffler A (1998) On economic causes of civil war. Oxf Econ Pap 50(4):563–573
Collier P, Hoeffler A (2004) Greed and grievance in civil war. Oxf Econ Pap 56(4):563–595
Desmet K, Weber S, Ortuõ Ortín I (2009) Linguistic diversity and redistribution. J Eur Econ Assoc 7(6):1291–1318
Dorussen H, Gartzke EA, Westerwinter O (2016) Networked international politics: complex interdependence and the diffusion of conflict and peace. J Peace Res 53(3):283–291
Doyle MW, Sambanis N (2000) International peacebuilding: a theoretical and quantitative analysis. Am Polit Sci Rev 94(4):779–801
Eichhorn W (1978) Functional equations in economics. Applied mathematics and computation. Addison-Wesley Publishing Company, Advanced Book Program, Boston
Esteban J (2003) Olson vs. Coase: coalitional worth in conflict. Theory Decis 55(4):339–357
Esteban J, Ray D (1994) On the measurement of polarization. Econometrica 62(4):819–851
Esteban J, Ray D (1999) Conflict and distribution. J Econ Theory 87(2):379–415
Esteban J, Ray D (2011) Linking conflict to inequality and polarization. Am Econ Rev 101(4):1345–74
Esteban J, Mayoral L, Ray D (2012) Ethnicity and conflict: an empirical study. Am Econ Rev 102(4):1310–1342
Fearon JD (2003) Ethnic and cultural diversity by country. J Econ Growth 8:195–222
Fearon JD (2018) Cooperation, conflict, and the costs of anarchy. Int Org 72(3):523–559
Fearon J, Laitin D (2003) Ethnicity, insurgency, and civil war. Am Polit Sci Rev 97:75–90
Fearon J, Kasara K, Laitin D (2007) Ethnic minority rule and civil war onset. Am Polit Sci Rev 101:187–193
Felsenthal DS, Machover M (1998) The measurement of voting power: theory and practice, problems and paradoxes. Edward Elgar, Cheltenham
Gade EK, Gabbay M, Hafez MM, Kelly Z (2019) Networks of cooperation: rebel alliances in fragmented civil wars. J Confl Resolut 63(9):2071–2097
Garrett G, Tsebelis G (1999) Why resist the temptation to apply power indices to the European Union? J Theor Polit 11(3):291–308
Gurr TR (1993) Minorities at risk: a global view of ethnopolitical conflicts. US Institute of Peace Press, Washington DC
Gurr TR (2000) Peoples versus states: minorities at risk in the new century. US Institute of Peace Press, Washington DC
Hegre H, Sambanis N (2006) Sensitivity analysis of empirical results on civil war onset. J Confl Resolut 50(4):508
Horowitz DL (1985) Ethnic groups in conflict. University of California Press, Berkeley
King G, Zeng L (2001) Logistic regression in rare events data. Polit Anal 9:137–163
Larson JM (2016) Interethnic conflict and the potential dangers of cross-group ties. J Peace Res 53(3):459–471
Lichbach MI (1995) The rebel’s dilemma. University of Michigan Press, Ann Arbor
Malawski M (2004) “Counting’’ power indices for games with a priori unions. Springer, US, Boston, pp 125–140
Metternich NW, Dorff C, Gallop M, Weschle S, Ward MD (2013) Antigovernment networks in civil conflicts: how network structures affect conflictual behavior. Am J Polit Sci 57(4):892–911
Montalvo JG, Reynal-Querol M (2005) Ethnic polarization, potential conflict and civil wars. Am Econ Rev 95(3):796–816
Montalvo JG, Reynal-Querol M (2008) Discrete polarisation with an application to the determinants of genocides. Econ J 118(533):1835–1865
Nitzan S (1991) Collective rent dissipation. Econ J 101(409):1522–1534
Penrose LS (1946) The elementary statistics of majority voting. J R Stat Soc 109:53–57
Reynal-Querol M (2002) Ethnicity, political systems, and civil wars. J Confl Resolut 46(1):29–54
Riker WH (1962) The theory of political coalitions. Yale University Press, London
Rokkan S, Flora P, Kuhnle S, Flora PSP, Urwin DW (1999) State formation, nation-building, and mass politics in Europe: the theory of Stein Rokkan: based on his collected works. Comparative European politics. Oxford University Press, Oxford
Sambanis N (2001) Do ethnic and nonethnic civil wars have the same causes? A theoretical and empirical inquiry (part 1). J Confl Resolut 45(3):259–282
Sambanis N (2004) What is civil war? Conceptual and empirical complexities of an operational definition. J Confl Resolut 48(6):814–858
Schneider G, Wiesehomeier N (2008) Rules that matter: political institutions and the diversity—conflict nexus. J Peace Res 45(2):183–203
Schneider G, Wiesehomeier N (2010) Diversity, conflict and growth: theory and evidence. Diversity 2(9):1097–1117
Shapley LS (1953) A value for n-person games. Contribution to the Theory of Games. Annals of Mathematics Studies, 2:28
Shapley LS, Shubik M (1954) A method for evaluating the distribution of power in a committee system. Am Polit Sci Rev 48:787–792
Skaperdas S (1996) Contest success functions. Econ Theor 7(2):283–290
Skaperdas S (1998) On the formation of alliances in conflict and contests. Public Choice 96(1–2):25–42
Tan G, Wang R (2010) Coalition formation in the presence of continuing conflict. Int J Game Theory 39(1):273–299
Tullock G (1980) Efficient rent seeking. In: Buchanan J, Tollison R and Tullock G (eds) Toward a theory of rent seeking society. Texas A and M University Press, College Station, pp 97–112
Wimmer A (2002) Nationalist exclusion and ethnic conflict: shadows of modernity. Cambridge University Press, Cambridge
Wimmer A, Min B (2006) From empire to nation-state: explaining wars in the modern world, 1816-2001. Am Sociol Rev 71(6):867–897
Wimmer A, Cederman LE, Min B (2009) Ethnic politics and armed conflict: a configurational analysis of a new global data set. Am Sociol Rev 74(2):316–337
Wucherpfennig J, Weidmann NB, Girardin L, Cederman LE, Wimmer A (2011) Politically relevant ethnic groups across space and time: introducing the GeoEPR dataset. Confl Manag Peace Sci 28(5):423–437
Zech ST, Gabbay M (2016) Social network analysis in the study of terrorism and insurgency: from organization to politics. Int Stud Rev 18(2):214–243
Funding
Open access funding provided by Università degli Studi di Verona within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We are grateful for comments and suggestions received on an earlier version of the paper presented at the International Economic Association World Congress (2014), Jan Tinbergen European Peace Science Conference (2014), European Econometric Society Meeting (2013), and Meeting of the Society for the Study of Economic Inequality (2013). The current version of the paper has substantially benefited from comments and suggestions by an editor and anonymous referees of the journal.
Appendices
Appendix I
See Table 6.
Proof of Lemma 2.1
Sufficiency part. Note that the obtained specification for \(\phi _{\alpha }^{2}(\pi )\) satisfies the axioms considered.
Necessity part. Consider axiom 2GRPH, requiring that \( \frac{r(\lambda \rho )}{r(\rho )}=\frac{r(\lambda \rho ^{^{\prime }})}{ r(\rho ^{^{\prime }})}\) for all \(\rho ,\rho ^{^{\prime }}\le 1,\) and \( \lambda >0\) such that \(\lambda \rho ,\lambda \rho ^{^{\prime }}\le 1\) with \( r(\rho ),r(\rho ^{^{\prime }})\ne 0.\) Note that because of the restrictions in 2GRPH, requiring that \(\pi \le 1/2 \), in combination with Normalization and Monotonicity one obtains that \( \phi ^{2}(1-\pi )=1-\phi ^{2}(\pi )\ge \phi ^{2}(\pi ).\) As a result \(\phi ^{2}(\pi )\le 1/2,\) that is \(\phi ^{2}(1-\pi )\ge 1/2\) that guarantees that \(r(\rho )\) is defined and that \(r(\rho )\in (0,1].\)
We first investigate the implications arising from this axiom combined with all the other axioms, when \(r(\rho ),r(\rho ^{^{\prime }})\ne 0,\) then we will move to the case where there exists \(\rho \) s.t. \(r(\rho )=0.\)
Recall first that if Monotonicity holds then \(\phi ^{2}(\pi )\le \phi ^{2}(\pi ^{\prime })\) if \(\pi <\pi ^{\prime },\) while if Normalization holds then \(\phi ^{2}(1-\pi )=1-\phi ^{2}(\pi )\). Therefore, if \(\pi <\pi ^{\prime }\) then \(\frac{\phi ^{2}(\pi )}{\phi ^{2}(1-\pi )}\le \frac{\phi ^{2}(\pi ^{\prime })}{\phi ^{2}(1-\pi ^{\prime })}.\) Thus, by construction \(r(\rho )\le r(\rho ^{\prime })\) if \(\rho <\rho ^{\prime },\) i.e., \(r(\rho )\) is non-decreasing. Note, moreover, that if 2GRPH holds then if \(r(\rho )=r(\rho ^{\prime })\) for some \(\rho <\rho ^{\prime }\) in some interval of (0, 1] then, given that we can set \(\rho ^{\prime }=\lambda \rho \), the condition \(\frac{r(\lambda \rho )}{r(\rho )}\) becomes \(\frac{r(\rho ^{\prime })}{r(\rho )}=1\) that holds in the interval and therefore, as \(\lambda \) varies, holds also for all the other values \(\rho ^{\prime }\ne \rho \) in the interval. As a result either \(r(\rho )\) is constant and different from 0 for all \(\rho \le 1\) or it is strictly increasing, that is \(r(\rho )<r(\rho ^{\prime })\) if \(\rho <\rho ^{\prime }.\) We focus first on the latter case.
If \(r(\rho ),r(\rho ^{^{\prime }})\ne 0\) then assume that 2GRPH holds. Let \( \rho _{0}:=\lambda \rho \in (0,1)\), that is \(\lambda =\rho _{0}/\rho \). It follows that \(r(\lambda \rho )=r(\rho _{0})\) and \(r(\lambda \rho ^{\prime })=r(\rho ^{^{\prime }}\cdot \rho _{0}/\rho ),\) thus 2GRPH requires that:
for some function \(g(\cdot ).\) Note that if we set \(\lambda <1\) (we will discuss the implication of \(\lambda >1\) afterwards) then \(\rho _{0}/\rho <1, \) it then follows that \(r(\rho _{0})=g(\rho _{0}/\rho )\cdot r(\rho )\) for all \(\rho _{0},\rho <1\) and \(\rho _{0}/\rho <1.\) This functional equation therefore holds also if we swap \(\rho _{0}/\rho \) with \(\rho \) on its r.h.s. , and we obtain \(r(\rho _{0})=g(\rho )\cdot r(\rho _{0}/\rho )\) for all \( \rho _{0},\rho <1\) and \(\rho _{0}/\rho <1.\) As a result it holds that:
for all \(\rho _{0},\rho <1\) and \(\rho _{0}/\rho <1.\) Note that we have assumed that \(r(\rho )>0\) for all \(\rho ,\) and therefore also \(r(\rho _{0})>0 \) and \(r(\rho _{0}/\rho )>0,\) which implies that \(g(\rho )>0.\) We can then rewrite:
for all \(\rho _{0},\rho <1\) and \(\rho _{0}/\rho <1,\) which is equivalent to set \(g(\rho )=k\cdot r(\rho )\) for some \(k>0.\) By substituting into (A.1) we obtain:
If we consider the function \(\sigma (\rho ):=k\cdot r(\rho )\) we have:
for all \(\rho _{0},\rho <1\) and \(\rho _{0}/\rho <1.\) The obtained equation is the (multiplicative) Cauchy functional equation specified for a domain where \(\rho \in (0,1)\) and for \(\sigma (\rho )\) strictly increasing. Note that the problem can be set equivalently to the one where the domain is on the strictly positive real line \(\mathfrak {R}_{++}\) by simply setting \(\sigma (\rho ):=s(x)\) where \(\rho =x/(1+x).\) The general solution for the restricted domain and for monotonic function is in Eichhorn (1978) [see Theorem 1.9.13 and Remark 1.9.23]. It leads to:
Moreover, the case analysed earlier where \(r(\rho )>0\) is constant can be summarized by the solution where \(\alpha =0.\)
In fact, by substituting for \(\sigma (\rho ):=k\cdot r(\rho )\) with \(k>0\) one obtains that:
for all \(\rho \in (0,1)\) where \(\beta =1/k.\) Note that this solution implies that 2GRPH holds also for all \(\lambda >1.\) Moreover, according to 2GRPH the functional equation should hold also for \(\rho =1\) and therefore its solution extends from \(\rho \in (0,1)\) to \(\rho \in (0,1].\)
Before analysing the implications for the solution arising from other axioms we go back to the case where there exist \(\rho \) s.t. \(r(\rho )=0.\) In this case 2GRPH does not hold. However, we have just derived that for some \(\rho \) where the function \(r(\rho )\) is not equal to 0, the solution (A.2) should hold. It follows that either \(r(\rho )=0\) for all \(\rho \in (0,1)\) or (A.2) holds. The former case can be embedded into (A.2) by extending the admissible values for \(\beta \) considering also \(\beta =0\) in (A.2).
We now move to consider the implications of the remaining axioms. Consider first the solution (A.2) for \(r(\rho )>0\) extended to hold for \(\rho \in (0,1].\) Recall that by Normalization \(\phi ^{2}(1-\pi )=1-\phi ^{2}(\pi )\). Then by definition:
where \(\pi \le 1/2,\) that is \(\phi ^{2}(\pi )=\beta \cdot \frac{\pi ^{\alpha }}{(1-\pi )^{\alpha }}\left[ 1-\phi ^{2}(\pi )\right] \) giving:
for all \(\alpha \ge 0,\) \(\beta >0,\) where \(\pi \le 1/2.\) Note that by Monotonicity \(\phi ^{2}(\pi )\le \phi ^{2}(1/2)=1/2,\) where the latter equality is obtained by Symmetry and Normalization. It follows that \(\phi ^{2}(1/2)=\frac{\beta }{\beta +1}=1/2\) requires that \(\beta =1,\) which gives the desired result for \(\phi _{\alpha }^{2}\) in Lemma 2.1. The values for \( \phi ^{2}(\pi )\) for \(\pi >1/2\) are obtained by setting \(\phi ^{2}(\pi )=1-\phi ^{2}(1-\pi )\) where \(1-\pi <1/2.\) To obtain \(\phi _{\infty }^{2}\) consider the solution for \(r(\rho )=0\) for all \(\rho \in (0,1),\) that is \( \phi ^{2}(\pi )=0\) for \(\pi <1/2.\) Combine this solution with the condition \( \phi ^{2}(1/2)=1/2\) and derive \(\phi ^{2}(\pi )\) for \(\pi >1/2\) by setting \( \phi ^{2}(\pi )=1-\phi ^{2}(1-\pi )\) where \(1-\pi <1/2,\) that is \(\phi ^{2}(\pi )=1\) for \(\pi >1/2.\qquad \blacksquare\)
Proof of Theorem 2.2
Sufficiency part. Note that the obtained specification for \(\phi _{\alpha }^{n}\) satisfies the axioms considered.
Necessity part. Consider axiom REP. We first check the restrictions that make it consistent with the specification of \(\phi ^{2}\) obtained in Lemma 2.1 applying 2GRPH, we will then extend the analysis to the case where \(n>2.\)
For \(n=2,\) the axiom REP requires that \(\frac{\phi ^{2}(\pi )}{\phi ^{2}(1-\pi )}=\frac{g(M_{i})}{g(M_{j})}\) for some function \(g:\mathfrak {R}_{+}\rightarrow \mathfrak {R}_{+}\) if \(\phi ^{2}(1-\pi )>0,\) where \(M_{i}\) is associated with the group with the population share \(\pi \) and \(M_{j}\) is associated with the other group with share \(1-\pi \). Note that by definition \( M_{i}=1-\phi ^{2}(1-\pi )+\phi ^{2}(\pi ),\) and \(M_{j}=1-\phi ^{2}(\pi )+\phi ^{2}(1-\pi ).\) Recalling that by Normalization \(\phi ^{2}(\pi )+\phi ^{2}(1-\pi )=1,\) one obtains that \(M_{i}=2\phi ^{2}(\pi ),\) and \(M_{j}=2\phi ^{2}(1-\pi ).\) Thus REP requires that:
for all \(\pi \in (0,1).\)
By letting \(f(x):=g(2x)\) and recalling that \(\phi ^{2}(1-\pi )=1-\phi ^{2}(\pi )\) one obtains, when \(\phi ^{2}(\pi )>0\), that
for all \(\phi ^{2}\in (0,1),\) where \(\phi ^{2}\) for short denotes \(\phi ^{2}(\pi ).\) Recall that \(\phi ^{2}=1/2\) if \(\pi =1/2.\)
The above functional equation is then consistent with setting \(\frac{f(\phi ^{2})}{\phi ^{2}}=h(\phi ^{2})\) if \(\phi ^{2}\le 1/2,\) with \( h(1/2)=2f(1/2), \) for some function \(h:(0,1]\rightarrow \mathfrak {R}_{+},\) and \( \frac{f(\phi ^{2})}{\phi ^{2}}=h(1-\phi ^{2})\) for \(\phi ^{2}>1/2.\)
It then follows that \(g(2\phi ^{2})=f(\phi ^{2})\) for all values of the domain of \(g(\cdot )\) in (0, 2) with:
Note that the domain of \(g(\cdot )\) is \(\mathfrak {R}_{+}\) while the above condition provides a restriction only for the domain interval (0, 2). More generally \( g(\cdot )\) may depend on the distribution \(\Pi _{-i,-j}\) of all the population groups except i and j and thus it can be written as related to a function \(h(\cdot )\) that could depend on \(\Pi _{-i,-j}\) if \(n>2.\) We denote such function as \(h_{\Pi }(\cdot ).\)
Thus for \(M\in (0,2)\) one obtains that \(g(M)=h_{\Pi }(M/2)\cdot M/2\) for \( M\le 1,\) and \(g(M)=h_{\Pi }(2-M/2)\cdot M/2\) for \(M>1.\)
It follows that for the case where \(M\in (0,2)\) with \(M_{j}>1\) and \(M_{i}<1\) , according to REP it holds \(\frac{\phi ^{n}(\pi _{i},\Pi )}{\phi ^{n}(\pi _{j},\Pi )}=\frac{g(M_{i})}{g(M_{j})}=\frac{h_{\Pi }(M_{i}/2)\cdot M_{i}}{ h_{\Pi }(2-M_{j}/2)\cdot M_{j}}.\)
By applying nGRPI one obtains also that:
where \(H(M_{i}/M_{j})\) does not depend on \(\Pi .\)
By combining this condition with the previous restrictions one obtains that this is the case only if \(h_{\Pi }(\cdot )=c>0.\)
That is, if \(M_{j},M_{i}\in (0,2)\) then \(\frac{\phi ^{n}(\pi _{i},\Pi )}{ \phi ^{n}(\pi _{j},\Pi )}=\frac{M_{i}}{M_{j}}.\) However, note that this is not a general condition that holds for all \(\frac{\phi ^{n}(\pi _{i},\Pi )}{ \phi ^{n}(\pi _{j},\Pi )},\) in fact this holds only if \(M_{j},M_{i}\in (0,2). \) That is, this is the case whenever \(\pi _{i},\) \(\pi _{j}\) are sufficiently small.
However, the derived proportionality of \(\frac{\phi ^{n}(\pi _{i},\Pi )}{ \phi ^{n}(\pi _{j},\Pi )}\) holds for a given ratio \(\frac{M_{i}}{M_{j}},\) but for appropriate choices of \(\pi _{i}\) and \(\pi _{j}\) when \(n\ge 3\) one can guarantee that \(M_{j},M_{i}\in (0,2)\) and that \(\frac{M_{i}}{M_{j}}\) can reach any positive value.
Thus we obtain that:
for all \(M_{j},M_{i},\) \(i,j\in N,\) all \(n\ge 2,\) and all \(\Pi \) (that are consistent with \(\pi _{i},\pi _{j}\)).
The specification of the two axioms, nGRPI and REP, lead to different restrictions on the final functional form, thereby showing their independence.
The desired result is then obtained by imposing the Normalization axiom. In fact, condition (A.3) implies that in the more general case \(\phi ^{n}(\pi _{i},\Pi )=M_{i}\cdot w(M)\) where M denotes the distribution of all aggregated marginal contributions of each group, and \(w(\cdot )\) is a generic function, identical for all groups (that may also depend on \(\Pi )\).
If this is the case then, by Normalization, \(\sum _{j}\phi ^{n}(\pi _{j},\Pi )=\sum _{j}M_{j}\cdot w(M)=w(M)\cdot \sum _{j}M_{j}=1\) thus, \( w(M)=1/\sum _{j}M_{j},\) thereby leading to:
where the \(M_{i}\) components are obtained making use of the function \(\phi ^{2}\) in Lemma 2.1.
To conclude we are left to consider the case where \(\phi ^{n}=0\) for some group j. In order to obtain this result it should be that \(M_{j}=0.\) If this is not the case then there exists a group j whose \(\phi ^{n}\) is 0 irrespective of the value of \(M_{j}.\) Note however that \(M_{j}\) is non-decreasing w.r.t. \(\pi _{j},\) and thus by Monotonicity we should have that \(\phi ^{n}\) is 0 also for all groups i whose size is below \(\pi _{j} \) or whose \(M_{i}\) is lower than \(M_{j}.\) But according to REP what is relevant is the ratio \(\frac{M_{i}}{M_{j}}\) so, taking two groups of which one has \(M_{i}>0\) but \(\phi _{i}^{n}=0\) with \(\frac{M_{i}}{M_{j}}\ne 0\) and \(\phi _{j}^{n}>0\), one can consider groups distribution such that \(\frac{ M_{i}}{M_{j}}\) is appropriately set at a desired positive value and therefore for all pairs i, j then \(\frac{M_{i}^{^{\prime }}}{ M_{j}^{^{\prime }}}<\frac{M_{i}}{M_{j}}\Rightarrow \frac{\phi ^{n}(\pi _{i}^{^{\prime }},\Pi ^{\prime })}{\phi ^{n}(\pi _{j}^{^{\prime }},\Pi ^{\prime })}\le \frac{\phi ^{n}(\pi _{i},\Pi )}{\phi ^{n}(\pi _{j},\Pi )} =0, \) thereby leading to a situation where all groups except the largest one in all possible distributions have \(\phi ^{n}=0.\) This, however, is not consistent with the Normalization axiom. It then follows that \(\phi _{i}^{n}=0\) only if \(M_{i}=0,\) making the result consistent with (A.4). \( \blacksquare \)
Appendix II: Explanatory and control variables
GDP per capita The GDP per capita data come from Cederman et al. (2010) and originates from Penn World Table 6.2. The data are in constant 2000 US Dollars.
Population size In order to account for the size of the country, we include the natural logarithm of the first lag of the population at a given year.
Oil production per capita The data for oil production per capita (in barells) come from Wimmer and Min (2006) and Cederman et al.’s (2010) data sets.
Mountainous terrain, noncontiguous territory and new state The data on mountains terrain are taken from the A.J. Gerrard’s project on mountains environment. Countries with the territory holding at least 10,000 people that are separated from the land area containing the capital city either by land or by 100 kilometres of water are coded as “Noncontiguous”. A dummy variable for “New State” is coded as 1 for the first two years of independence.
Democracy and autocracy In order to characterise the political system we use the Polity IV data set (PIV). The PIV is based on a 21-point scale: “autocracies” (− 10 to − 6), “anocracies” (regimes that are nor autocratic nor democratic) (− 5 to + 5), and “democracies” (+ 6 to + 10).
Instability By instability we intend the “previous regime change”. The regime change is defined as any change in the Polity Score of at least 3 points over the prior three years. The data are taken from the EPR3 data set and are based on PIV.
Share of the excluded population In order to account for the degree of exclusion along ethnic lines, we include the natural logarithm of the share of the population excluded from central government.
Number of power sharing partners We include the number of power sharing groups represented by ethnic elites at the central government. This variable is termed as the degree of centre segmentation.
Past imperial history This variable is given by the percentage of years spent under imperial rule between 1816 and independence. The data come from Wimmer and Min (2006).
Largest minority The relative size of the largest minority in the population. The data come from EPR3.
Ethnic diversity indices Regarding the P index of conflict potential, we consider three different values for the coefficient \( \alpha \), namely \(\alpha =1\) (actually the RQ discrete polarization index), \(\alpha =2\) and \(\alpha \rightarrow \infty \). We also construct the Collier and Hoeffler’s (2004) and Schneider and Wiesehomeier’s (2008) ethnic dominance dummy variables as well as the fractionalization index.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kovacic, M., Zoli, C. Ethnic distribution, effective power and conflict. Soc Choice Welf 57, 257–299 (2021). https://doi.org/10.1007/s00355-021-01317-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-021-01317-y