Abstract
We study the transfer of a resource from a group of suppliers to a group of demanders through links in a network. The analysis is relevant to situations where institutional constraints bar the use of the price mechanism: the allocation of workloads under fixed salaries, a commodity under disequilibrium prices, etc. In these contexts suppliers and demanders naturally have single-peaked preferences. We evaluate transfer rules on the basis of the “replacement principle” (Thomson, J Econ Theory 76(1):145–168 1997; Moulin, Q J Econ 102:769–783 1987), the requirement that a change in an agent’s preferences affects all other agents in the same direction in terms of welfare. We find that the only Pareto-efficient, participation-compatible, replication-invariant, and envy-free rule satisfying an appropriate formulation of the replacement principle is the “egalitarian rule” introduced by Bochet et al. (Theor Econ 7:395–423 2012).

Similar content being viewed by others
Notes
Strategy-proofness is the requirement on an allocation rule that agents never gain by misreporting their preferences.
See, for instance, Chun (2006); Dagan (1996); Moulin (1999), and Thomson (1994a, (1994b, (1995b, (1997). The prominence of the uniform rule is even confirmed in studies dropping the Pareto-efficiency criterion: see Sönmez (1994) and Kesten (2006). The uniform rule has also been extended to the problem of reallocating a commodity among agents with single-peaked preferences by Thomson (1995a), Klaus et al (1998), and Kıbrıs and Küçükşenel (2009).
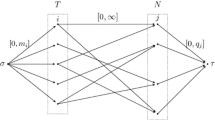
The basic mathematical notation is as follows: If \(\{X_i\}_{i\in I}\) is a family of sets indexed by \(I, X^I\) denotes the Cartesian product of the these sets taken over \(I, \times _{i\in I}X_i\). For each \(x\in X^I\) and each \(J\subseteq I\), we denote by \(x_J\) the projection of x onto \(X^J\). For each pair \(x,y\in \mathbb {R}^I, x\ge y\) whenever, for each \(i\in I, x_i\ge y_i\).
More precisely, \(\Gamma (i;A)=\{j\in N: ij\in G(A)\}\). Note that in general \(\Gamma (i;A)\subseteq A_i\) and that the inclusion may be strict since \(A_i\) is a subset of \(\mathbb {S}\cup \mathbb {B}\), not necessarily of N. Moreover, links in G(A) are formed bilaterally.
BIMS formulate this property but it does not appear in their characterization of the egalitarian rule. The equal treatment of equals condition they do use has a similar interpretation. Note that equal treatment of equals is not implied by this property (see Proposition 5 in BIMS).
In graph theory, a closely related concept is that of the “deficiency” of a vertex subset in a graph. See Lovász and Plummer (1986).
A symmetric description of \(P^*(R,A)|_{S_-}\) in terms of a sub-modular function is also possible.
As usual \(\mathbf {e}_i\) denotes the ith standard basis vector, the vector with a one in the ith coordinate and zeros elsewhere.
To see this, let \(N\in \mathcal {N}, (R,A)\in \mathcal {E}^N\), and let \(\varphi \) denote a link monotonic rule. Then, by link-monotonicity, \(\varphi _i(R,A){R_i} \varphi _i(R, \varnothing , A_{-i})\). However, by feasibility, \(\varphi _i(R, \varnothing , A_{-i})=0\) because agent i is not adjacent to any agent in \(G(\varnothing , A_{-i})\). Thus, \(\varphi _i(R,A){R_i} 0\) and \(\varphi \) satisfies voluntary praticipation.
See BIM (proof of Lemma 2) and the closely related result in BIMS (Lemma 2).
Convexity follows from the Efficiency and Feasibiltiy Lemmas. From these we deduce that \(P(\hat{R}, \hat{A})\) can be described as the intersection of closed half-spaces in \(\mathbb {R}_+^{\hat{N}}\) and is hence convex. Since \(\{z\in \mathbb {R}_+^{\hat{N}}:z\le p(\hat{R})\}\) is convex so is the intersection.
Note that \(\sum _{B_-} z_j=f(B_-)\) and, for each \(i\in B_-, \sum _{B_-{\setminus } i} z_j\le f(B_-{\setminus } i)\). Thus, because f is non-decreasing, \(z_i\ge f(B_-)-f(B_-{\setminus } i)\ge 0\).
References
Bochet O, İlkılıç R, Moulin H (2013) Egalitarianism under earmark constraints. J Econ Theory 148:535–562
Bochet O, İlkılıç R, Moulin H, Sethuraman J (2012) Balancing supply and demand under bilateral constraints. Theor Econ 7:395–423
Bogomolnaia A, Moulin H (2004) Random matching under dichotomous preferences. Econometrica 72(1):257–279
Ching S (1994) An alternative characterization of the uniform rule. Soc Choice Welf 11(2):131–136
Chun Y (2006) The separability principle in economies with single-peaked preferences. Soc Choice Welf 26(2):239–253
Dagan N (1996) A note on Thomson’s characterization of the uniform rule. J Econ Theory 69(1):255–261
De Frutos A, Massó J (1995) More on the uniform allocation rule: equality and consistency. WP 288.95 UAB, 1995
Dutta B, Ray D (1989) A concept of egalitarianism under participation constraints. Econometrica 57(3):615–635
Foley D (1967) Resource allocation and the public sector. Yale Economic Essays 7
Fujishige S (2005) Submodular functions and optimization, vol 58. Annals of Discrete Mathematics. Elsevier
Gibbard A (1985) Manipulation of voting schemes: a general result. Econometrica 41(4):587–601
Goswami M, Mitra M, Sen A (2013) Strategy-proofness and pareto-efficiency in quasi-linear exchange economies. Theor Econ
Hardy G, Littlewood J, Polya G (1929) Some simple inequalities satisfied by convex functions. Messenger Math 58
Hurwicz L (1972) On informationally decentralized systems. In: McGuire C, Radner R (eds) Decision and organization. North-Holland, pp 297–336
Kesten O (2006) More on the uniform rule: characterizations without Pareto-optimality. Math Soc Sci 51:192–200
Kıbrıs O, Küçükşenel S (2009) Uniform trade rules for uncleared markets. Soc Choice Welf 32:101–121
Klaus B, Peters H, Strocken T (1998) Strategy-proof division with single-peaked preferences and individual endowments. Soc Choice Welf 15
Lovász L, Plummer M (1986) Matching theory. North Holland
Moulin H (1987) The pure compensation problem: egalitarianism versus laissez-fairism. Q J Econ 102:769–783
Moulin H (1999) Rationing a commodity along fixed paths. J Econ Theory 84(1):41–72
Roth A, Sönmez T, Ünver U (2005) Pairwise kidney exchange. J Econ Theory 125:151–188
Satterthwaite M (1975) Strategy-proofness and Arrow’s conditions: existence and correspondence theorems for voting procedures and social welfare theorems. J Econ Theory 10:187–217
Schmeidler D (1979) A bibliographical note on a theorem by Hardy, Littlewood, and Polya. J Econ Theory 59(20):125–128
Schrijver A (2003) Combinatorial optimiazation. Springer, Berlin
Serizawa S (2002) Inefficiency of strategy-proof rules for pure exchange economies. J Econ Theory 106(2):219–241
Sönmez T (1994) Consistency, monotonicity, and the uniform rule. Econ Lett 46:229–235
Sprumont Y (1991) The division problem with single-peaked preferences. Econometrica 59(2):509–519
Thomson W (1994a) Consistent solutions to the problem of fair division when preferences are single-peaked. J Econ Theory 63(2):219–245
Thomson W (1994b) Resource-monotonic solutions to the problem of fair division when preferences are single-peaked. Soc Choice Welf 11:205–223
Thomson W (1995a) Axiomatic analysis of generalized economies with single-peaked preferences. Revised (2009)
Thomson W (1995b) Population-monotonic solutions to the problem of fair division when preferences are single-peaked. Econ Theory 5(2):229–246
Thomson W (1997) The replacement principle in economies with single-peaked preferences. J Econ Theory 76(1):145–168
Thomson W (1999) Welfare-domination and preference-replacement: a survey and open questions. Soc Choice Welf 16:373–394
Thomson W (2011) Handbook of Social Choice and Welfare. In: Arrow K, Sen A, Suzumura K (eds) Fair allocation rules. Elsevier, USA, pp 393–506
Zhou L (1991) Inefficiency of strategy-proof allocation mechanisms in pure exchange economies. Soc Choice Welf 8:247–254
Author information
Authors and Affiliations
Corresponding author
Additional information
First version: December 3rd, 2010. I thank William Thomson for extensive discussions and support. The feedback of an associate editor and two referees significantly improved this paper. I am especially thankful to one of the referees for detailed comments on the proofs and for suggesting explicitly mentioning some of the results now contained in Corollary 1. I gratefully acknowledge the insightful comments of Vikram Manjunath, Hervé Moulin, and Jay Sethuraman. All errors are my own.
A Appendix
A Appendix
1.1 A.1 Lemmas
This section gathers results used in proving Lemma 4 and that the egalitarian rules are replication-invariant and replacement-dominant.
For each \(N\equiv B\cup S\), each \(e\equiv (R,A) \in \mathcal {E}^N\), and each \(I\subseteq B\) (each \(I\subseteq S\)), let
Then, the cells partition \(\mathbb {P}(e)\) are defined by:Footnote 14
Remark 1
For each \(N\equiv B\cup S\) and each \(e\equiv (R,A) \in \mathcal {E}^N\),
That is, \(B_-^e\) is contained in every maximizer of \(\delta (J ; e)\) over \(J\subseteq B\) and is itself a maximizer. Similarly, \(S_-^e\) is contained in every maximizer of \(\delta (J ; e)\) over \(J\subseteq S\) and is itself a maximizer.
The first result describes the relationship between the decomposition of an economy described in Lemma 2 and that of its duplicate economy.
Lemma 6
(Replication) For each \(N\in \mathcal {N}\), each \(e\equiv (R,A)\in \mathcal {E}^N\), and each \(k\in \{1, \dots , |N|\}\),
Proof
Let \(N\equiv B\cup S\in \mathcal {E}^N, e\equiv (R,A)\in \mathcal {E}^N\), and \(\hat{e}\equiv 2* e\). Let \(\hat{N}=\hat{B}\cup \hat{S}\) consist of all the agents involved in economy \(\hat{e}\) (the agents in N and their clones). All the cells of \(\mathbb {P}(e)\) and \(\mathbb {P}(\hat{e})\) are defined in terms of \(B_-^e, S_-^e\) and \(B_-^{\hat{e}}, S_-^{\hat{e}}\), respectively. Thus, it suffices to show that \(i\in B_-^{e}\Leftrightarrow i,i^*\in B_-^{\hat{e}}\) and that \(i\in S_-^{e}\Leftrightarrow i,i^*\in S_-^{\hat{e}}\).
Let \(B'\equiv B_-^{\hat{e}}\cap B\) and \(B''\equiv B_-^e\cup \{i^*: i \in B_-^e\}\). Note that \(i\in B_-^{e}\Leftrightarrow i,i^*\in B_-^{\hat{e}}\) is equivalent to \(B'=B_-^e\) which is what we now prove. By Remark 1, \(\delta (B_-^e ;e)\ge \delta (B' ;e)\). Thus, if \(\delta (B_-^e ;e)>\delta (B' ;e)\),
This contradicts the fact that \(B_-^{\hat{e}}\) maximizes \(\delta (\cdot ; \hat{e})\) over the subsets of \(\hat{B}\) (Remark 1). Thus, \(\delta (B_-^e ;e)= \delta (B' ;e)\) and \(B'\) is a maximizer of \(\delta (\cdot ; e)\) over the subsets of B. Since \(B_-^e\) is inclusion-minimal across these maximizers, \(B_-^e\subseteq B'\). By Remark 1, \(\delta (B_-^{\hat{e}}; \hat{e})\ge \delta (B''; \hat{e})\). Thus, if \(\delta (B_-^{\hat{e}}; \hat{e})> \delta (B''; \hat{e})\),
This contradicts the fact that \(B_-^{{e}}\) maximizes \(\delta (\cdot ; e)\) over the subsets of B (Remark 1). Thus, \(\delta (B_-^{\hat{e}} ;\hat{e})= \delta (B'' ;\hat{e})\) and \(B''\) is a maximizer of \(\delta (\cdot ,\hat{e})\) over the subsets of \(\hat{B}\). Since \(B_-^{\hat{e}}\) is inclusion-minimal across these maximizers, \(B_-^{\hat{e}}\subseteq B''\). Thus, \(B'=B_-^{\hat{e}}\cap B\subseteq B'' \cap B=B_-^e\). Altogether, \(B'=B_-^e\), as desired. A symmetric argument shows that \(S_-^e\cup \{i^*: i \in S_-^e\}=S_-^{\hat{e}}\). \(\square \)
Lemma 7
Let \(\varphi \) be an efficient rule satisfying replacement-dominance. Let \(N\in \mathcal {N}, e\equiv (R,A)\in \mathcal {E}^N\), and \(i\in N\). Let \(R'_i \in \mathcal {R}\) be such that \(\mathbb {P}(R, A)=\mathbb {P}(R_i', R_{-i},A)\). Let \((K,L)\in \{(B_-^e, S_+^e), (S_-^e,B_+^e )\}, x\equiv \varphi (R,A)\) and \(x'\equiv \varphi (R_i', R_{-i},A)\).
Proof
We will prove Statement (i); the proof of Statement (ii) is symmetric. Let all notation be as in the statement of Lemma 7. Let \((K, L)=(B_-^e, S_+^e), i\in K\), and suppose that \(x_i'\ge x_i\). By replacement-dominance, either
By the Efficiency Lemma,
Suppose that (1a) holds. Then, by single-peakedness, (2) implies the desired result:
Suppose instead from here on that (1b) holds. Then, by single-peakedness, (2) implies
By the Efficiency Lemma, \(x'_{B_-^e\cup S_+^e},x_{B_-^e\cup S_+^e}\in Z(A_{B_-^e\cup S_+^e})\). Thus,
Case 1 \(x_i'=x_i\). By (4), \(\sum _{B_-^e}x_j'\ge \sum _{B_-^e}x_j\) and \(\sum _{S_+^e}x_j'\le \sum _{S_+^e}x_j\). Thus, by (5), \(\sum _{B_-^e}x_j=\sum _{B_-^e}x_j'\) and \(\sum _{S_+^e}x_j=\sum _{S_+^e}x_j'\). Thus, by (4), \(x'_{B_-^e\cup S_+^e}=x_{B_-^e\cup S_+^e}\). Similarly, \(x'_{B_+^e\cup S_-^e}=x_{B_+^e\cup S_-^e}\).
Case 2 \(x_i'>x_i\). Then, by (5),
Suppose that (6a) holds. By (2), \(x_j'<x_j\le p(R_j)\) which contradicts (4). Suppose that (6b) holds instead. By (2), \(x_j'>x_j\ge p(R_j)\) which again contradicts (4). These contradictions imply that we indeed have (3) which is the desired result.
The case in which \((K,L)=(S_-^e, B_+^e)\) is symmetric (exchanging the roles of buyers and sellers). \(\square \)
Proof of Lemma 4
Let \(\varphi \) denote a rule satisfying weak no-envy, efficiency, replacement-dominance, and replication-invariance. Let \(N\in \mathcal {N}, e\equiv (R,A)\in \mathcal {E}^N\), and \(x\equiv \varphi (R,A)\). Let \(i\in N\) and \(R_i'\in \mathcal {R}\) be such that \(p(R_i)=p(R_i')\). Let \(x'\equiv \varphi (R_i', R_{-i},A)\). We first show that \(x'=x\).
Let \(\hat{e}\equiv (\hat{R},\hat{A})\) denote the duplicate economy of e and let \(\hat{N}\) denote the agents involved in economy \(\hat{e}\) (the agents in N and their clones). Let \(\hat{x}\equiv 2*x\) and \(y\equiv \varphi (R_i', \hat{R}_{-i}, \hat{A})\). Let \(i^*\in \hat{N}\) denote i’s clone in \(\hat{N}{\setminus } N\) so that \(\hat{R}_i=\hat{R}_{i^*}\) and \(\hat{A}_i=\hat{A}_{i^*}\). Suppose that \(y_i\ne y_{i^*}\). Then, by weak no-envy, either \(y_i\ne p(R_i')=p(\hat{R}_i)\) or \(y_{i^*}\ne p(\hat{R}_{i*})\), or both. By the Replication Lemma, i and \(i^*\) are in the same cell of partition \(\mathbb {P}(\hat{R}, \hat{A})\). By the Decomposition Lemma, since \(p(R_i')=p(\hat{R}_i), \mathbb {P}(\hat{R}, \hat{A})=\mathbb {P}(R_i', \hat{R}_{-i}, \hat{A})\) (the decomposition depends on the peaks of a preference profile). Thus, i and \(i^*\) are in the same cell of partition \(\mathbb {P}(R_i', \hat{R}_{-i}, \hat{A})\) as well. Thus, by the Efficiency Lemma,
By single-peakedness, either \(y_{i^*} {P_i'} y_i\) or \(y_{i} {\hat{P}_{i^*}} y_{i^*}\). However, \(\hat{A}_i=\hat{A}_{i^*}\). This contradicts weak no-envy. Thus, \(y_i=y_{i^*}\). By Lemma 7, \(y=\hat{x}\).
Let \(R_{i^*}'\in \mathcal {R}\) be such that \(R_{i^*}'=R_i'\). Let \(y'\equiv \varphi (R_i', R_{i^*}',\hat{R}_{\hat{N}{\setminus } \{i, i^*\}}, \hat{A})\). Suppose that \(y_i'\ne y_{i^*}'\). Then, either \(y_i'\ne p(R_i')\) or \(y_{i^*}'\ne p(R_{i*}')\), or both. By the Decomposition Lemma, since \(p(R_{i^*}')=p(\hat{R}_{i^*}), \mathbb {P}(\hat{R}, \hat{A})=\mathbb {P}(R_i', \hat{R}_{-i}, \hat{A})=\mathbb {P}(R_i', R_{i^*}',\hat{R}_{\hat{N}{\setminus } \{i, i^*\}}, \hat{A})\). Thus, i and \(i^*\) are in the same cell of partition \(\mathbb {P}(R_i', R_{i^*}',\hat{R}_{\hat{N}{\setminus } \{i, i^*\}}, \hat{A})\). Thus, by the Efficiency Lemma,
By single-peakedness, either \(y_{i^*}' {P_i'} y_i'\) or \(y_{i}' {P_{i^*}'} y_{i^*}'\). However, \(\hat{A}_i=\hat{A}_{i^*}\). This contradicts weak no-envy. Thus, \(y_i'=y_{i^*}'\). By Lemma 7, \(y'=y=\hat{x}\). Thus, by replication-invariance, \(x'=x\).
Generally, let \( \tilde{R}\in \mathcal {R}^N\) be such that \(p(R)=p(\tilde{R})\). Labeling N so that \(N= \{1,2, \dots , n\}\) and repeating the argument above n-times we obtain,
\(\square \)
Proof of Lemma 5
Let \(\varphi \) denote a rule satisfying efficiency and cross-monotonicity, \(N\equiv B\cup S\in \mathcal {N}, (R,A)\in \mathcal {E}^N, K\in \{B,S\}, i\in K\), and \(R_i'\in \mathcal {R}\) be such that \(p(R_i)= p(R_i')\). Let \(S_-, S_0, S_+, B_-, B_0, B_+\) denote the cells of partition \(\mathbb {P}(R,A)\) and \(x\equiv \varphi (R,A)\) and \(y\equiv \varphi (R_i', R_{-i}, A)\). Note that \(\mathbb {P}(R,A)= \mathbb {P}(R_i', R_{-i}, A)\) since the profile of peaks is unchanged. Thus, by the Efficiency Lemma,
Since \(p(R_i)\le p(R_i')\), by cross-monotonicity, [for each \(j\in N{\setminus } K, y_j{R_j}x_j\)] and [for each \(j\in K{\setminus } \{i\}, x_j {R_j} y_j\)]. Since \(p(R_i)\ge p(R_i')\), by cross-monotonicity, [for each \(j\in N{\setminus } K, x_j{R_j}y_j\)] and [for each \(j\in K{\setminus } \{i\}, y_j {R_j} x_j\)]. Thus, each agent \(j\in N{\setminus } \{i\}\) is indifferent between \(x_j\) and \(y_j\). Thus, by (7), for each \(j\in N{\setminus } \{i\}, x_j=y_j\). Thus, since the sum of seller assignments equals the sum of buyer assignments, \(\sum _K x_j=\sum _{N{\setminus } K} x_j= \sum _{N{\setminus } K} y_j, x_i=y_i\). Thus, \(x=y\).
Generally, let \( \tilde{R}\in \mathcal {R}^N\) be such that \(p(R)=p(\tilde{R})\). Labeling N so that \(N= \{1,2, \dots , n\}\) and repeating the argument above n-times we obtain,
\(\square \)
1.2 A.2 Proof of Proposition 1
BIMS establish that the egalitarian rule is link monotonic, efficient, and that it satisfies volutnary participation and no-envy.
To show that the egalitarian rule is peaks-only observe that, by the Efficiency Lemma, the set of efficient allocations for two economies, \((R, A),(R', A')\in \mathcal {E}^N\) such that \(p(R)=p(R')\) and \(A=A'\), is the same, \(P(R,A)=P(R',A')\). Thus, the Lorenz-dominant allocation in \(P(R,A)\cap \{z\in \mathbb {R}_+^N: z\le p(R)\}\) is the same as that in \(P(R',A')\cap \{z\in \mathbb {R}_+^N: z\le p(R')\}\). Thus, \(E(R,A)=E(R',A)\).
It remains to show that the egalitarian rule is replication-invariant.
Claim 1
The egalitarian rule is replication-invariant.
Proof
Let \(N\in \mathcal {N}\) and \(e\equiv (R,A)\in \mathcal {E}^N\). Let \( \hat{R}\equiv 2*R, \hat{A}\equiv 2*A\), and \( \hat{e}\equiv (\hat{R},\hat{A})\). Let \(\hat{N}\) denote the agents involved in economy \(\hat{e}\) (the agents in N and their clones). Let \(x\equiv E(e)\) and \(\hat{x}\equiv E(\hat{e})\). It suffices to verify that \(\hat{x}=2*x\).
By the Efficiency Lemma, all agents in \(B_0^{\hat{e}}\cup S_0^{\hat{e}}\cup B_+^{\hat{e}}\cup S_+^{\hat{e}}\), receive at least their peak at \(\hat{x}\). By the definition of the egalitarian rule, \(\hat{x}\) does not exceed any agent’s peak. Thus, for each \(i\in B_0^{\hat{e}}\cup S_0^{\hat{e}}\cup B_+^{\hat{e}}\cup S_+^{\hat{e}}, \hat{x}_i=p(\hat{R}_i)\). Similarly, for each \(i \in B_0^{e}\cup S_0^{e}\cup B_+^{e}\cup S_+^{e}, x_i=p(R_i)=p(\hat{R}_i)\). Thus,
It remains to prove that, for each \(i\in B_-^{\hat{e}}\cup S_-^{\hat{e}}, \hat{x}_i=(2*x)_i\).
Step 1 For each \(i\in B_-^{\hat{e}}\cup S_-^{\hat{e}}, \hat{x}_i=\hat{x}_{i^*}\) where \(i^*\) denotes i’s clone.
Otherwise, there is a pair \(i, i^*\in B_-^{\hat{e}}\) (or \(i, i^*\in S_-^{\hat{e}}\)) with \(\hat{x}_i\ne \hat{x}_{i^*}\). Without loss of generality, \(\hat{x}_i< \hat{x}_{i^*}\). By the Efficiency Lemma, \(\hat{x}_i< \hat{x}_{i^*}\le p(\hat{R}_i)=p(\hat{R}_{i^*})\). Then, because i and \(i^*\) are symmetric (same preferences and potential transfer partners) in \(\hat{e}\), the allocation obtained by permuting the assignments of i and \(i^*\) and leaving all other agents assignments unaltered is in \(P(\hat{R}, \hat{A})\cap \{z\in \mathbb {R}_+^{\hat{N}}:z\le p(\hat{R})\}\), a convex set.Footnote 15 By convexity, this set contains a z such that, for each \(j\in \hat{N}{\setminus } \{i, i^*\}, z_j=\hat{x}_j\) and \(z_i= \frac{\hat{x}_i+\hat{x}_{i^*}}{2}= z_{i^*}\). Then, z Lorenz-dominates \(\hat{x}\). This contradicts the fact that \(\hat{x}\) is the Lorenz-dominant element. Thus, for each \(i\in B_-^{\hat{e}}\cup S_-^{\hat{e}}, \hat{x}_i=\hat{x}_{i^*}\).
Step 2 \(\hat{x}_{N}\in P(R, A)\cap \{z\in \mathbb {R}_+^{N}:z\le p(R)\}\).
For each \(J\subseteq B_-^e\) let \(J^*\equiv \{j^*\in \hat{N}: j^* \text { is the clone of } j\in J\}\). By the Replication Lemma \(J^*\subseteq B_-^{\hat{e}}\). By the Efficiency Lemma, \(\hat{x}_{ B_-^{\hat{e}}\cup S_+^{\hat{e}} }\in Z(\hat{A}_{ B_-^{\hat{e}}\cup S_+^{\hat{e}} })\). Thus, by the Feasibility Lemma and Step 1,
Thus, for each \(J\subseteq B_-^e, \sum _J\hat{x}_i \le \sum _{\Gamma (J; A_{ B_-^e\cup S_+^e } )} p(R_i)\) and \(\sum _{B_-^{e}}\hat{x}_i=\sum _{S_+^{e}}\hat{x}_i.\) By the Feasibility Lemma, \(\hat{x}_{B_-^e\cup S_+^e}\in Z(A_{B_-^e\cup S_+^e})\). Similarly, \(\hat{x}_{B_+^e\cup S_-^e}\in Z(A_{B_+^e\cup S_-^e})\), and by (8) and the Efficiency Lemma, \(\hat{x}_{B_0^e\cup S_0^e}\in Z(A_{B_0^e\cup S_0^e})\). Thus, by (8) and the fact that \(\hat{x}_N\le p(\hat{R})|_N=p(R)\) we have \(\hat{x}_{N}\in P(R, A)\cap \{z\in \mathbb {R}_+^{N}:z\le p(R)\}\).
Step 3 \(\hat{x}=2* x\).
Recall that \(N^*\equiv \hat{N}{\setminus } N\) and that, for each \(i\in N\) and her clone \(i^*\in N^*, A_i=\hat{A}_i=\hat{A}_{i^*}\). Thus, \((2*x)_N=x\in Z(A)\) implies \((2*x)_{N^*} \in Z(\hat{A}_{N^*})\). Thus, because \(Z(\hat{A}_{N})\times Z(\hat{A}_{N^*})\subseteq Z(\hat{A}), 2*x\in Z(\hat{A})\). Moreover, by Lemma 6 (8), and \(2*x\le p(\hat{R}), 2* x\in P(\hat{R}, \hat{A})\cap \{z\in \mathbb {R}_+^{\hat{N}}:z\le p(\hat{R})\}\). Thus, since \(\hat{x}\) is the egalitarian allocation at \((\hat{R},\hat{A})\), it Lorenz-dominates \(2*x\). However, by the definition of \(2*x\) and by Step 1, for each \(i\in N\) and corresponding clone \(i^*, (2*x)_i=(2*x)_{i^*}\) and \(\hat{x}_i=\hat{x}_{i^*}\). Thus, \(\hat{x}_N\) Lorenz-dominates x. On the other hand, since x is the egalitarian allocation for (R, A), by Step 2, x Lorenz-dominates \(\hat{x}_N\). Since there is only one Lorenz-dominant allocation in \(P(R, A)\cap \{z\in \mathbb {R}_+^{N}:z\le p(R)\}, x\) and \(\hat{x}_N\) coincide. Thus, by Step 1 again, \(2*x\) and \(\hat{x}\) coincide.
1.3 A.3 Proof of Proposition 2
We will use the fact that the egalitarian rule is cross-monotonic (Bochet et al. 2012) to prove that it is replacement-dominant. Let \(N\equiv B\cup S\in \mathcal {N}, A\in \mathcal {A}^N, R\in \mathcal {R}^N\) and \(i\in N\). Let \(R'\in \mathcal {R}^N\) be such that, for each \(j\in N{\setminus } \{i\}, R_j'=R_j\) and suppose, in accordance with the hypothesis of replacement-dominance, the partitions \(\mathbb {P}(R,A)\) and \(\mathbb {P}(R',A)\) coincide. Denote the common cells of these partitions by \(S_-,S_+,S_0,B_-,B_+,B_0\). and let \(x\equiv E(R,A)\) and \(y\equiv E(R',A)\). The egalitarian rule recommends efficient allocations under which no agent’s assignment exceeds her peak. Thus, by the Efficiency Lemma, for each \(j \in S_+\cup S_0 \cup B_+ \cup B_0, x_j=p(R_j)\) and \(y_j=p(R_j')\). Since the egalitarian rule is peaks-only, if \(p(R_i)=p(R_i')\), then \(x=y\) and replacement-dominance is satisfied. If instead \(p(R_i)\ne p(R_i'), i\notin B_0\cup S_0\): by the Efficiency Lemma, \(\sum _{B_0} p(R_i)=\sum _{S_0} p(R_i)\) and \(\sum _{B_0} p(R_i')=\sum _{S_0} p(R_i')\) and these conditions could not hold if \(p(R_i)\ne p(R_i')\). Thus,
Suppose that \(p(R_i)<p(R_i')\) and \(i\in S\). By cross-monotonicity, for each \(j\in B, y_j {R_j} x_j\) and, for each \(j\in S{\setminus } \{i\}, x_j {R_j} y_j\). Thus, since \(x\le p(R)\) and \(y\le p(R'), x_B\le y_B\) and, \(x_{S{\setminus } \{i\}}\ge y_{S{\setminus } \{i\}}\).
-
If \(i\in S_-\), by (9), \(y_{S_+} = p(R_{S_+})= x_{S_+}\). By the Efficiency Lemma, the coordinates of \(y_{B_-}\) and \( x_{B_-}\) thus add up to \(\sum _{S_+} p(R_j)\). Thus, since \(x_{B_-}\le y_{B_-}, y_{B_-}= x_{B_-}\). Thus x and y coincide on \(N{\setminus } S_-\). Thus, for each \(j\in N{\setminus } \{i\}, x_j {R_j} y_j\).
-
If \(i\in S_+\), by (9, \(y_{B_+} = p(R_{B_+})= x_{B_+}\). By the Efficiency Lemma, the coordinates of \(y_{S_-}\) and \( x_{S_-}\) thus add up to \(\sum _{B_+} p(R_j)\). Thus, since \(x_{S_-}\ge y_{S_-}, y_{S_-}= x_{S_-}\). Thus x and y coincide on \(N{\setminus } B_-\). Thus, for each \(j\in N{\setminus } \{i\}, y_j {R_j} x_j\).
If instead \(p(R_i)>p(R_i')\) and \(i\in S\), similar arguments establish that each agent other than i is affected in the same direction welfare-wise. The arguments establishing this when \(i\in B\) are symmetric. \(\square \)
1.4 A.4 Proof of Step 3 in Theorem 2
We first prove that \(\mathcal {B}(f)=P^*(R,A)|_{B_-}\). Let \(w\in \mathcal {B}(f)\). Then, for each \(I\subseteq B_-, \sum _I w_i\le f(I)\le \sum _{\Gamma ( I; A_{B_-\cup S_+})}p_i\) and, for each \(i\in B_-, w_i\le f(\{i\})\le p_i\). Additionally, by the definition of \(B_-\) in the beginning of Section 1, \(f(B_-)=\sum _{\Gamma (B_-; A_{B_-\cup S_+})}p_i=\sum _{S_+}p_i\). Thus, \(\sum _{B_-}w_i =\sum _{S_+}p_i\). Thus, by the Feasibility and Efficiency Lemmas, \(w\in P^*(R,A)|_{B_-}\). Conversely, let \(w\in P^*(R,A)|_{B_-}\). By the Feasibility Lemma,
Additionally, because \(w\le p_{B_-}\), for each \(I\subseteq B_-, \sum _I w_i \le \sum _I p_i\). Thus, for each pair J, K such that \(J\subseteq K\subseteq B_-, \sum _J w_i \le \sum _{\Gamma ( J; A_{B_-\cup S_+})}p_i\) and \(\sum _{K{\setminus } J} w_i\le \sum _{K{\setminus } J}p_i\). Thus, \(\sum _K w_i=\sum _J w_i+\sum _{K{\setminus } J} w_i \le \sum _{\Gamma ( J; A_{B_-\cup S_+})}p_i+ \sum _{K{\setminus } J}p_i\). Thus, for each \(K\subseteq B_-, \sum _K w_i\le f(K)\) and, as remarked above, \(\sum _{S_+}p_i=f(B_-)\). Thus, \(w\in \mathcal {B}(f)\).
We now prove that f is sub-modular. Let \(I_1,I_2 \subseteq B_-\). Let \(J_1\subseteq I_1\) and \(J_2\subseteq I_2\) attain the minima in the definition of f, for \(I_1\) and \(I_2\), respectively. Then, by the sub-modularity of the mapping \(I\mapsto \sum _{\Gamma (I;A_{B_-\cup S_+})}p_i\) and the definition of f,
Since \(I_1,I_2 \subseteq B_-\) were chosen arbitrarily, f is sub-modular.
We now prove that f is non-decreasing. Let \(I_1\subseteq I_2 \subseteq B_-\). Let \(J_1\subseteq I_1\) and \(J_2\subseteq I_2\) attain the minima in the definition of f, for \(I_1\) and \(I_2\), respectively. Then,
where the first inequality follows from the definition of \(J_1\), and the second one from the fact that \(\Gamma ([J_2\cap I_1];A_{B_-\cup S_+})\subseteq \Gamma (J_2;A_{B_-\cup S_+})\) and \(I_1{\setminus } [J_2\cap I_1]\subseteq I_2{\setminus } J_2\). Thus, \(f(I_1)\le f(I_2)\) and f is non-decreasing. Note that \(f(\varnothing )=0\) is immediate from the definition of f.
We now prove that \(\mathcal {B}(f)\) is compact and convex. First note that, for each \(z\in \mathcal {B}(f)\) and each \(i\in B_-, z_i\ge 0\).Footnote 16 Moreover, since p is a profile of non-negative finite real numbers, for each \(I\subseteq B_-, f(I)<\infty \). Thus, \(\mathcal {B}(f)\) is bounded. Since \(\mathcal {B}(f)\) is defined as the intersection of finitely many closed half spaces (weak inequalities) it is convex and closed. Since \(\mathcal {B} (f)\) is closed and bounded, it is compact.
1.5 A.5 Independence of the axioms
For simplicity, we establish the independence of the axioms in our theorems for economies where each seller is linked to each buyer. We refer to such economies as connected. The main results in Thomson (1994b, (1995b) on the standard division problem with single-peaked preferences are obtained under the assumption that, for each agent, there is a finite assignment indifferent to 0. If \(R_i\in \mathcal {R}\) satisfies this restriction, \(\pmb {d(R_i)}\equiv \max \{d\in \mathbb {R}_+: d {R_i} 0 \}\) is well defined and finite. For simplicity, we will work under this restriction throughout this section. Note that all of our results hold under this restriction since we never relied on preferences not satisfying it in our analysis.
We will use the uniform rule for the standard division problem with single-peaked preferences to construct a family of rules illustrating the independence of the axioms. For each finite set of buyers or sellers K and each \(R_K\equiv (R_i)_{i\in K}\in \mathcal {R}^K\), define:
\(\pmb {U(R_K,m)}\in \mathbb {R}_+^K\) where \(m \in \mathbb {R}_+\) and, for each \(i\in K\),
where \(\lambda \in \mathbb {R}_+\) is such that \(\sum _{i\in K} U_i(R,m)=m\).
\(\pmb {\sigma (R_K)}\equiv \sum _{i\in K} p(R_i)\).
Let f denote a function mapping preference profiles into a non-negative real numbers. The rule associated with f, denoted by \(\pmb {E^f}\), is such that, for each \(N\equiv B\cup S\in \mathcal {N}\), each connected \((R,A)\in \mathcal {E}^N\), and each \(i\in N\),
Lemma 8
Rule \(E^f\) satisfies efficiency and no-envy in connected economies.
Proof
Let f denote a function mapping preference profiles into a non-negative real numbers. Let \(N\equiv B\cup S\in \mathcal {N}, (R,A)\in \mathcal {E}^N\) be connected, and \(x\equiv E^f(R,A)\). By definition, if \( m \equiv \text {median}\{\sigma (R_B),\sigma (R_S), f(R)\}\),
Thus, x is feasible at A. Without loss of generality, suppose that \(\sigma (R_B)\ge \sigma (R_S)\). Since all sellers are linked to all buyers and conversely, (R, A) is in buyer-surplus; additionally, \( \sigma (R_B) \ge m \ge \sigma (R_S)\) which implies that,
Thus, by Lemmas 2 and 3, \(x \in P(R,A)\), establishing that \(E^f\) recommends feasible and efficient allocations. Note that \(x_B\) is the allocation recommended by the uniform rule for the standard division problem with single-preferences when the preference profile is \(R_B\) and the amount to allocate is m; since the uniform rule satisfies no-envy in that setting (Sprumont 1991), for each \(\{i,j\}\subseteq B, x_i {R_i} x_j\). Similarly, for each \(\{i,j\}\subseteq S, x_i {R_i} x_j\). Thus, \(E^f\) satisfies no-envy. \(\square \)
For each \(N\equiv B\cup S\in \mathcal {N}\) and each connected \((R,A)\in \mathcal {E}^N\), define the following rules:
-
\(\pmb {\varphi ^1}\) is such that, for each \(i\in N, \varphi _i^1(R,A)=0\).
-
\(\pmb {\varphi ^2}\) is such that:
-
(i)
if \(\min \{\sigma (R_B), \sigma (R_S)\}=0\), then, for each \(i\in N, \varphi _i^2(R,A)=0\);
-
(ii)
if \(\min \{\sigma (R_B), \sigma (R_S)\}>0\), then,
$$\begin{aligned} \varphi _i^2(R,A)&= \left\{ \begin{array}{ll} p(R_i)\frac{\min \{\sigma (R_B),\sigma (R_S)\}}{\sigma (R_S)} &{}\quad \text {if}\, i\in S\\ p(R_i)\frac{\min \{\sigma (R_B),\sigma (R_S)\}}{\sigma (R_B)} &{}\quad \text {if}\, i\in B \end{array} \right. . \end{aligned}$$
-
(i)
-
\(\pmb {\varphi ^3}=E^f\) where
$$\begin{aligned} f(R) = \left\{ \begin{array}{ll} |S| \cdot \min _{i\in S} d(R_i) &{}\quad \text {if }\, \sigma (R_S)< \sigma (R_B)\\ |B| \cdot \min _{i\in B}d(R_i) &{}\quad \text {otherwise } \end{array} \right. . \end{aligned}$$ -
\(\pmb {\varphi ^4}=E^f\) where
$$\begin{aligned} f(R) = \left\{ \begin{array}{ll} d(R_i) &{}\quad \text {if } \exists i\in S \text { s.t. } S=\{i\} \text { and } \sigma (R_S)<\sigma (R_B)\\ 0 &{}\quad \text {otherwise} \end{array} \right. . \end{aligned}$$ -
\(\pmb {\varphi ^5}=E^f\) where \(f(R) =\sigma (R_S)\).
Table 1 summarizes the axioms satisfied and not satisfied by these rules.
Proposition 3
(i) Rules \(\varphi ^2, \varphi ^3, \varphi ^4\), and \(\varphi ^5\) satisfy efficiency, \(\varphi ^1\) does not. (ii) Rules \(\varphi ^1, \varphi ^3, \varphi ^4\), and \(\varphi ^5\) satisfy no-envy, \(\varphi ^2\) does not. (iii) Rules \(\varphi ^1, \varphi ^2, \varphi ^4\), and \(\varphi ^5\) satisfy replacement-dominance, \(\varphi ^3\) does not. (iv) Rules \(\varphi ^1, \varphi ^2, \varphi ^3\), and \(\varphi ^5\) satisfy replication invariance, \(\varphi ^4\) does not. (v) Rules \(\varphi ^1, \varphi ^2, \varphi ^3\), and \(\varphi ^4\) satisfy voluntary trade, \(\varphi ^5\) does not. (vi) Rules \(\varphi ^1, \varphi ^2\), and \(\varphi ^5\) satisfy peaks-only, \(\varphi ^3\) and \(\varphi ^4\) do not.
Proof
-
(i)
By Lemma 8, rules \(\varphi ^3, \varphi ^4\), and \(\varphi ^5\) satisfy efficiency. To see that \(\varphi ^2\) does so as well, let \(N\equiv B\cup S\in \mathcal {N}, (R,A)\in \mathcal {E}^N\), and \(x\equiv \varphi ^2(R,A)\). Without loss of generality, assume that \(\sigma (R_S)\le \sigma (R_B)\). Thus, \(\sum _B x_i=\sigma (R_S)=\sum _S x_i\). Thus, since, for each \(i\in S, x_i\le p(R_i), x_i=p(R_i)\). Since, for each \(i\in B, x_i\le p(R_i)\), an allocation Pareto-improving upon x would require reallocating the amount \(\sigma (R_S)\) among the buyers; however, reallocating would entail reducing the assignment of a buyer, making her worse off.
-
(ii)
By Lemma 8, rules \( \varphi ^3, \varphi ^4\), and \(\varphi ^5\) satisfy no-envy. Since, for each economy and each agent, \(\varphi ^1\) recommends the same assignment, this rule satisfies no-envy as well. To see that \(\varphi ^2\) does not, let \(B=\{i,j\}, S=\{k,l\}\), and \(e_1\equiv (R,A)\in \mathcal {E}^{B\cup S}\) be such that \(p(R_i)=4, p(R_j)=2, p(R_k)=p(R_l)=1\), and \(x\equiv \varphi ^2(R,A)\). Then, \(x_i=\frac{4}{3}, x_j=\frac{2}{3}\), and \(x_k=1=x_l\). Thus, \(x_i{P_j} x_j\) while the allocation y such that \(y_i=1=y_j\), and \(y_k=1=y_l\) is also feasible, in violation of no-envy.
-
(iii)
Since \(\varphi ^1\) recommends the same allocation for each economy, it satisfies replacement-dominance. We now establish that rules \( \varphi ^2\) and \(\varphi ^5\) do so as well. Let \(N\equiv B\cup S\in \mathcal {N}, (R,A)\in \mathcal {E}^N, i\in N\), and \(R'\in \mathcal {R}^N\) be such that, for each \(j\in N{\setminus } \{i\}, R_j=R_j'\). Suppose that \(\mathbb {P}(R,A)=\mathbb {P}(R',A)\) so that replacement-dominance applies.
If \(\sigma (R_B)\ge \sigma (R_S)\), then \(\mathbb {P}(R,A)=\mathbb {P}(R',A)\) implies that \(\sigma (R_B')\ge \sigma (R_S')\). We now establish that each agent other than i is affected in the same direction welfare-wise under rules \(\varphi ^2\) and \(\varphi ^5\) when the preferences of i change from \(R_i\) to \(R_i'\):
-
If \(j\in S{\setminus } \{i\}, \varphi ^2_j(R,A)=p(R_j)=p(R_j')=\varphi ^2_j(R',A)\). Thus, each \(j\in S{\setminus } \{i\}\) is indifferent between the assignment she receives in (R, A) and \((R',A)\). For each \(j\in B{\setminus } \{i\}, \varphi ^2_j(R,A)=\frac{\sigma (R_S)}{\sigma (R_B)} p(R_j)\) and \(\varphi ^2_j(R',A)=\frac{\sigma (R_S')}{\sigma (R_B')} p(R_j)\). Thus, if \(\frac{\sigma (R_S)}{\sigma (R_B)}\le {(\ge )} \frac{\sigma (R_S')}{\sigma (R_B')}\), each \(j\in B{\setminus } \{i\}\) is at least (at most) as well-off. Thus, all agents other than i are at least (at most) as well-off.
-
If \(j\in S{\setminus } \{i\}, \varphi ^5_j(R,A)=p(R_j)=p(R_j')=\varphi ^5_j(R',A)\). Thus, each \(j\in S{\setminus } \{i\}\) is indifferent between the assignment she receives in (R, A) and \((R',A)\). If \(i\in S\) the amount transferred from sellers to buyers changes from \(\sigma (R_S)\) to \(\sigma (R_S')\). By the properties of the uniform rule (one-sided resource-monotonicity in Thomson 1994b), \(\sigma (R_S)\le {(\ge )} \sigma (R_S')\) implies each buyer’s assignment increases (decreases) or remains constant while being bounded above by her peak as was the case before the preference change, thus making each buyer at least (at most) as well-off. If \(i\in B\) the amount transferred from sellers to buyers remains constant. By the properties of the uniform rule (one-sided welfare domination under preference replacement in Thomson 1997), \(p(R_i) \ge {(\le )} p(R_i')\) implies that, for each buyer other that i, her assignment (decreases) or remains constant while being bounded above by her peak as was the case before the preference change. This makes each buyer other than i at least (at most) as well-off.
Thus, all agents other than i are at least (at most) as well-off.
If \(\sigma (R_B)<\sigma (R_S)\), similar arguments establish that each agent other than i is affected in the same direction welfare-wise under rules \(\varphi ^2\) and \(\varphi ^5\) in response to the preference change. These rules thus satisfy replacement-dominance.
We now prove that \(\varphi ^4\) satisfies replacement-dominance. Note that, if \(|S|\ge 2, \varphi ^4\) coincides with the egalitarian rule since \(E=E^f\) when \(f=0\). Thus, \(\varphi ^4\) satisfies replacement-dominance in economies where \(|S|\ge 2\).
Thus, it remains to consider the case where S is a singleton: let \(N\equiv B\cup S\in \mathcal {N}\) where S is the singleton \(\{k\}, (R,A)\in \mathcal {E}^N, i\in N\), and \(R'\in \mathcal {R}^N\) be such that, for each \(j\in N{\setminus } \{i\}, R_j=R_j'\). Suppose that \(\mathbb {P}(R,A)=\mathbb {P}(R',A)\) so that replacement-dominance applies. We now determine how the welfare of agents other than i is affected in going from \(\varphi ^4(R,A)\) to \(\varphi ^4(R',A)\).
-
Case 1 \(\sigma (R_S)\ge \sigma (R_B)\). Then \(\mathbb {P}(R,A)=\mathbb {P}(R',A)\) implies \(\sigma (R_S') \ge \sigma (R_B')\) and \(f(R)=0=f(R')\). Thus, under preference profile R, the amount transferred from the seller to the buyers is \(\sigma (R_B)\), while, under preference profile \(R'\), the amount is \(\sigma (R_B')\). Case 1.1 \(i=k\). Then, \(R_B=R_B'\) and \(\sigma (R_B)=\sigma (R_B')\). Thus, under both preference profiles, the amount transferred to buyers is the sum of their peaks and each buyer’s assignment is equal to her peak. This makes each buyer equally well-off under both preference profiles. Case 1.2 \(i\in B\). The amount transferred from the seller to the buyers goes from \(\sigma (R_B)\) to \(\sigma (R_B')\). By the properties of the uniform rule (one-sided welfare domination under preference replacement in Thomson 1997), for each buyer other that i, her assignment increases (decreases) or remains constant while being bounded below by her peak, thus making each buyer other than i at least (at most) as well-off.
-
Case 2 \(\sigma (R_S)<\sigma (R_B)\). Then, \(\mathbb {P}(R,A)=\mathbb {P}(R',A)\) implies \(\sigma (R_S')<\sigma (R_B')\). The amount transferred from the seller to the buyers goes from \(\min \{\sigma (R_B), d(R_k)\}\) to \(\min \{\sigma (R_B'), d(R_k')\}\). Case 2.1 \(i=k\). Then, \(\sigma (R_B)=\sigma (R_B')\). Thus, if \(d(R_k)\le {(\ge )} d(R_k')\), the amount transferred by the seller is at least (at most) as large. By the properties of the uniform rule (one-sided resource-monotonicity in Thomson 1994b), each buyer’s assignment increases (decreases) or remains constant while being bounded above by her peak, thus making each buyer at least (at most) as well-off. Case 2.2 \(i\in B\). Then, \(d(R_k)=d(R_k')\). Case 2.2.1 \(\min \{\sigma (R_B), d(R_k)\}=d(R_k)=\min \{\sigma (R_B'), d(R_k)\}\) so the amount transferred from seller k to buyers is constant. If \(p(R_i')\ge {(\le )} p(R_i)\), by the properties of the uniform rule (one-sided welfare domination under preference replacement in Thomson 1997), for each buyer other that i, her assignment decreases (increases) or remains constant while being bounded above by her peak, thus making each buyer other than i at most (at least) as well-off going from \(\varphi ^4(R,A)\) to \(\varphi ^4(R', A)\) while the assignment of seller k remains unchanged at \(d(R_k)\). Case 2.2.2 \(\min \{\sigma (R_B), d(R_k)\}=\sigma (R_B) , \min \{\sigma (R_B'), d(R_k)\}=\sigma (R_B')\). Then, for each \(j\in B{\setminus } \{i\}, \varphi ^4_j(R,A)=p(R_j)=\varphi ^4_j(R',A)\) and seller k may be made better or worse off. Case 2.2.3 \(\min \{\sigma (R_B), d(R_k)\}=d(R_k), \min \{\sigma (R_B'), d(R_k)\}=\sigma (R_B')\). Then, \(p(R_k)\le \sigma (R_B')\le \sigma (R_B)\) so k is at least as well-off and, for each \(j\in B{\setminus } \{i\}, \varphi ^4_j(R',A)=p(R_j)\) so each buyer other than i is made at least as well-off. Case 2.2.4 \(\min \{\sigma (R_B), d(R_k)\}=\sigma (R_B), \min \{\sigma (R_B'), d(R_k)\}=d(R_k)\). Then, \(p(R_k)\le \sigma (R_B)\le \sigma (R_B')\) so k is at most as as well-off and, for each \(j\in B{\setminus } \{i\}, \varphi ^4_j(R,A)=p(R_j)\) so each buyer other than i is made at most as well-off.
Thus, in all of the above cases, each agent other than i is affected in the same direction welfare-wise, as required by replacement-dominance.
We now prove that \(\varphi ^3\) does not satisfy replacement-dominance. Consider the economy \(e_1\) introduced in part (ii) of this proof and again let \(x\equiv \varphi ^3(e_1)\). Assume additionally that \(d(R_k)=d(R_l)=2\). Then, since the sum of the peaks of the buyers (6) is greater than the sum of the peaks of the sellers (2) and \(f(R) = |S| \cdot d(R_k) =4\), the amount transferred from sellers to buyers is 4. Then, \(x_i=x_j=x_k=x_l=2\). Consider an economy \(e_2\) identical to \(e_1\) with the exception that seller k now has a preference relation \(R_k'\) with \(p(R_k')=1\) as before but with \(d(R_k')=1.5\) and let \(y\equiv \varphi ^3(e_2)\). Then, since the sum of the peaks of the buyers (6) is greater than the sum of the peaks of the sellers (2) and \(f(R_k', R_{\{i,j,l\}}) =|S|\cdot d(R_k') =3\), the amount transferred from sellers to buyers is 3. Then, \(y_i=y_j=y_k=y_l=1.5\). Thus, i and j are worse off while l is better off, in violation of replacement-dominance.
-
(iv)
It is clear that rules \(\varphi ^1, \varphi ^2, \varphi ^3\), and \(\varphi ^5\) satisfy replication invariance. To see that \(\varphi ^4\) does not, let \(B=\{i\}, S=\{j\}\), and \( (R,A)\in \mathcal {E}^{B\cup S}\) be such that \(p(R_i)=4, p(R_j)=1, d(R_j)=3\), and \(x\equiv \varphi ^2(R,A)\). Then, since the sum of the peaks of the buyers (4) is greater than the sum of the peaks of the sellers (1) and \(f(R)=d(R_j)=3\), the amount transferred from sellers to buyers is 3. Then, \(x_i=3\) and \(x_j=3\). Since the duplicate of (R, A) involves two sellers and \(\varphi ^4\) coincides with the egalitarian rule in this case, \(\varphi ^2(2*R,2*A)=E(2*R,2*A)\equiv y\) where \(y_i=1=y_{i^*}\) and \(y_j=1=y_{j^*}\). Thus, \(2*x\ne y\).
-
(v)
Note that, under rules \(\varphi ^1\) and \(\varphi ^2\), each agents’ assignment is bounded above by her peak. In this range, agents’ welfare is increasing above that of receiving 0. Thus, these rules satisfy voluntary participation.
We now prove that \(\varphi ^3\) satisfies voluntary participation. Let \(N\equiv B\cup S\in \mathcal {N}, (R,A)\in \mathcal {E}^{N}\), and \(x\equiv \varphi ^3(R,A)\). Since \(\varphi ^3\) treats buyers and sellers symmetrically, assume without loss of generality that \(\sigma (R_S)\le \sigma ( R_B)\). If \(\sigma (R_S)=\sigma ( R_B)\), each agent is assigned her peak which is welfare-wise superior to receiving 0. Suppose instead that \(\sigma (R_S)< \sigma ( R_B)\). Then, the amount transferred from sellers to buyers is
$$\begin{aligned} m=\text {median}\{\sigma (R_S), \sigma ( R_B),|S| d \}\quad \text { where }d\equiv \min _{i\in S} d(R_i), \end{aligned}$$(10)for each \(i\in B, x_i\le p(R_i)\), and, for each \(i\in S, x_i\ge p(R_i)\). Thus, by single-peakedness, each buyer’s assignment under x is at least as desirable as 0. It remains to show that the same is true for sellers. By definition, for each \(i\in S, x_i=U_i(R_S, m)=\max \{\lambda , p(R_i)\}\) where \(\lambda \in \mathbb {R}_+\) is such that \(\sum _S\max \{\lambda , p(R_i)\}=m\). Thus, letting \(S'\equiv \{i\in S:p(R_i)> \lambda \}\), for each \(i\in S', x_i=p(R_i)\), and, for each \(i\in S{\setminus } S', x_i=\lambda \). If \(m=\sigma (R_S)\), then each seller receives her peak assignment and we are done so suppose instead that \(m \ne \sigma (R_S)\). By (10), this in turn requires \(m=\min \{\sigma (R_B),|S|d\}>\sigma (R_S)\).
-
Case 1 \(S'\) is empty. Then, for each \(i\in S, x_i=\lambda =\frac{m}{|S|}\le \frac{|S|d}{|S|}=d\le d(R_i)\).
-
Case 2 \(S'\) is non-empty. Then, \(S{\setminus } S'\) is also non-empty. Since m is the total amount transferred by sellers to buyers, defining \(p\equiv \frac{\sum _{S'} p(R_i)}{|S'|}\) to be the average assignment received by sellers in \(S'\) and recalling that \(\lambda \) is the assignment received by sellers in \(S{\setminus } S'\), we have that \(m=|S'| p + |S{\setminus } S'|\lambda \) or, rearranging, \(\lambda = \frac{m -|S'|p}{|S{\setminus } S'|}\). Since, \(p(R_i)>\lambda \) for each \(i\in S'\), we have \(p>\lambda \). Now, \(m=|S'| p + |S{\setminus } S'|\lambda \) and \(p>\lambda \) imply that \(p>\frac{m}{|S|}\). Thus, since \(m=\min \{\sigma (R_B),|S|d\}, \lambda = \frac{m -|S'|p}{|S{\setminus } S'|} < \frac{m-|S'|\frac{m}{|S|}}{|S{\setminus } S'|} =\frac{m}{|S|}\le \frac{|S|d}{|S|}=d. \) Thus, for each \(i\in S{\setminus } S', x_i=\lambda < d\le d(R_i)\), and, for each \(i\in S', x_i=p(R_i)\).
In both cases above, by single-peakedness, each agent’s assignment under x is at least as desirable as 0. Thus, \(\varphi ^3\) satisfies voluntary participation.
We now prove that \(\varphi ^4\) satisfies voluntary participation. In economies with more than one seller, \(\varphi ^4\) coincides with the egalitarian rule which satisfies voluntary participation. Thus, it suffices to establish that each agent finds her assignment to be at least as desirable as 0 when the set of sellers contains exactly one seller. Let \(N\equiv B\cup S\in \mathcal {N}\) be such that S consists of a single seller denoted by \(i, (R,A)\in \mathcal {E}^{N}\), and \(x\equiv \varphi ^4(R,A)\). If \(\sigma (R_S)<\sigma (R_B)\), the amount transferred from the seller to the buyers is \(m\equiv \text {median}\{\sigma (R_S),\sigma (R_B),d(R_i)\}=\min \{\sigma (R_B),d(R_i)\}\) and, by definition, \(x_i=m\le d(R_i)\) and, for each \(j\in B, x_j\le p(R_j)\). If \(\sigma (R_S)\ge \sigma (R_B)\), the amount transferred from the seller to the buyers is \(m\equiv \text {median}\{\sigma (R_S),\sigma (R_B),0\}=\sigma (R_B)\) and, by definition, \(x_i=m=\sigma (R_B)\le \sigma (R_S)=d(R_i)\) and, for each \(j\in B, x_j=p(R_j)\). In both cases, by single-peakedness, each agent’s assignment under x is at least as desirable as 0. Thus, \(\varphi ^4\) satisfies voluntary participation.
To see that \(\varphi ^5\) does not satisfy voluntary participation, consider an economy where each buyer has a peak of 0 and there is at least one seller with a strictly positive peak. Under \(\varphi ^5\), this seller is awarded her peak. Since the sum of sellers’ assignments is equal to the sum of buyers’, there is a buyer who is assigned a positive amount. This makes her worse off than receiving 0.
-
(vi)
The only preference information rules \(\varphi ^1, \varphi ^2\), and \(\varphi ^5\) rely on is the profile of peaks. Thus, for any two preference profiles with the same peaks, these rules recommend the same allocation. These rules are thus peaks-only. Rules \(\varphi ^3\) and \(\varphi ^4\) are not since they are sensitive to further preference information.
Rights and permissions
About this article
Cite this article
Flores-Szwagrzak, K. The replacement principle in networked economies with single-peaked preferences. Soc Choice Welf 47, 763–789 (2016). https://doi.org/10.1007/s00355-016-0991-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-016-0991-y