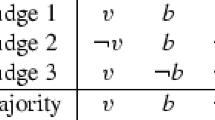Abstract
We characterize a rule for aggregating binary evaluations—equivalently, dichotomous weak orders—similar in spirit to the Borda rule from the preference aggregation literature. The binary evaluation framework was introduced as a general approach to aggregation by Wilson (J Econ Theory 10:89–99, 1975). In this setting we characterize the “mean rule,” which we derive from properties similar to those Young (J Econ Theory 9:43–52, 1974) used in his characterization of the Borda rule. Complementing our axiomatic approach is a derivation of the mean rule using vector decomposition methods that have their origins in Zwicker (Math Soc Sci 22:187–227, 1991). Additional normative appeal is provided by a form of tension minimization that characterizes the mean rule and suggests contexts wherein its application may be appropriate. Finally, we derive the mean rule from an approach to judgment aggregation recently proposed by Dietrich (Soc Choice Welf 42:873–911, 2014).







Similar content being viewed by others
Notes
Technically, such an evaluation is an ordered bipartition in the form of an ordered pair (H, L). That is, the unordered pair \(\{H,L\}\) bipartitions the set S of students, while the ordering of the pair (H, L) identifies which piece of the bipartition is the “Higher” piece. We use the term “bipartition” in this paper to always mean an ordered bipartition and we assume that both pieces of the bipartition are non-empty. Note that the same information as (H, L) would be conveyed by providing H alone (with the understanding that \(L=S\setminus H\)). A binary evaluation is thus formally equivalent to an approval voting ballot. A binary evaluation can also be identified with a dichotomous weak order relation, and we take this approach in Sect. 5.
We can write this majority evaluation as \((+1,+1,+1,+1)\) to denote that students 1, 2, 3 and 4 respectively are all in H. In this way, evaluations can be regarded as vectors. Note that the majority method satisfies an “independence” property in that the collective decision on a student is independent of the teachers’ evaluations of the other students. Significantly, the mean rule that we present in this paper does not satisfy this property.
In our model, if a student has a number of H evaluations equal to the mean then we take it that there are multiple solutions which are in an intuitive sense “tied”.
We are grateful to Nicolas Houy for proposing the first example of this kind.
In a planned sequel to this paper (Social Dichotomy Functions) we show that a measure of external displacement, related to total tension, is also optimized by “cutting” at the mean in this way, with no need to impose a monotonicity condition.
These ideas are developed in Saari (1994).
Approval Voting implicitly produces a partition into “winners” and “losers”, but this will not be tension-minimizing in general. As we can see from Table 1, the outcome under approval voting is \(H=\{s_{2}\}\) and \(L=\{s_{1},s_{3},s_{4}\}\) with the winner being \(s_{2}\).
Using a similar model, Brams et al. (1998) consider the “paradox of multiple elections” where voters vote yes/no on a sequence of propositions on a referendum. Generalizations of the binary evaluations model can be found in Dokow and Holzman (2010b) and in the literature on combinatorial domains (chapter 8 of Xia 2011 is an introduction).
Nonetheless, this notational convention has two substantive implications. First, it allows certain types of ties while forbidding others. For example, the two-way tie \(\{(+1,-1,+1,+1),(+1,-1,-1-1)\}\) is disallowed, as it does not arise as the set of all feasible evaluations that agree with some vector in \(\{-1,0,+1\}^{4}\). The effect is to eliminate variants of the mean rule that agree with it except that they yield some forbidden ties. Such variants might otherwise satisfy the four characterizing axioms of Theorem 7 ...“might” because in the absence of the convention, the consistency axiom must be reformulated (which can be done in more than one way). Still, it seems worth considering whether some altered version of the Theorem 7 axioms selects the mean rule uniquely from among these variants, without any assistance from our feasible outcome convention; this seems plausible, as the tension minimization characterization does select the mean rule uniquely.
Note, as well, that the feasible outcomes \(y=(+1,+1,0)\) and \(y^\prime = (+1,+1,-1)\) give rise to the same single feasible evaluation \((+1,+1,-1)\) (because \((+1,+1,+1)\) is not feasible). Thus, two rules that are formally distinct only for this reason (one outputs y at some profile for which the other outputs \(y^\prime \)) should actually be considered the same rule. This happens only for outcomes having a single 0 with all other coordinates equal, so one could alternately address the issue simply by further restricting the definition of feasible outcome so as to exclude such vectors.
Note that Young’s paper characterized the Borda rule as a social choice function. A characterization of the Borda rule as a social welfare function can be found in Nitzan and Rubinstein (1981). An alternative characterization of the mean rule based on principles from approval voting can be found in Duddy and Piggins (2013).
A weighted tournament, in the language of social choice.
Consider the set X of alternatives to be evaluated (identified, in Sect. 2, with the index set \(\{1,2,\dots ,k\}\)). Recall that a linear order on X is a binary relation \(\ge \) that is reflexive, transitive, complete (or total), and is also anti-symmetric—satisfying for all \(x,y\in X\) that whenever \(x\ge y\) and \(y\ge x\) both hold, \(x=y\). Weak order relations relax this last requirement, allowing both \(x\ge y\) and \(y\ge x\) to hold with \(x \ne y\), and writing \(x\sim y\) in this situation; \(\sim \) is thus an equivalence relation, with the equivalence classes known as I-classes (I for “indifference,” arising from the interpretation of \(\ge \) as “weakly preferred to”). A weak order can be thought of as a linear order of I-classes, and a dichotomous weak order \(X_H > X_L\) is one containing exactly two distinct I-classes, which we call \(X_{H}\) and \(X_{L}\), with \(x\ge y\) holding if and only if \(x\in X_{H}\), or \(y\in X_{L}\) (or both). The weak order corresponding to a binary evaluation places each alternative evaluated as \(+1\) into \(X_{H}\) and each evaluated \(-1\) into \(X_{L}\).
Each linear order ballot awards \(m-1\) points to its top-ranked alternative, \(m-2\) to its second-ranked, etc. One separately sums the points awarded to each alternative x by all ballots, and the resulting Borda scores determine the outcome ranking of alternatives. We discuss how to score indifferences (arising in weak order ballots) after Lemma 9.
Any vector of evenly spaced weights \((w,w-d,w-2d,w-3d,\dots )\) for \(d>0\) yields the same Borda SWF as the standard vector.
There are arguments for using this averaging method with any vector of Borda weights (see fn. 19) but for Lemma 9 we require the symmetric version.
Suppose we fix the m nodes, the \(j=\frac{(m)(m-1)}{2}\) edges, and the edge directions of a network. Then any single labeling of edges (with real numbers) corresponds to a vector of length j, and the space of all such labeling is thus identified with the Euclidean vector space \(\mathfrak {R}^{j}\). The sum \(\mathbf {v}+\mathbf {w}\) (of two edge labelings) assigns to each edge the sum of the labels separately assigned to that edge by \(\mathbf {v}\) and \(\mathbf {w}\), while scalar multiplication of \(\mathbf {v}\) by s simply multiplies each of \(\mathbf {v}\)’s edge labels by s. The set of cycles, then, is the linear span of the basic cycles, and forms the cycle subspace \(\mathbf {V}_{cycle}\)—a linear subspace of \(\mathfrak {R}^{j}\).
The inner product \(\mathbf {v}\cdot \mathbf {w}\) of two edge labelings is found by multiplying all pairs of corresponding edge labels, and then adding these products, and provides a notion of orthogonality.
This decomposition is not unique; the basic cycles are not linearly independent.
The cocycle subspace \(\mathbf {V}_{cocycle}\) is the linear span of the basic cocycles in \(\mathfrak {R}^{j}\); see fn. 21.
Once again the decomposition is not unique.
Thus subspaces \(\mathbf {V}_{cycle}\) and \(\mathbf {V}_{cocycle}\) are orthogonal complements in \(\mathfrak {R}^j\) and for each \(\mathbf {v}\in \mathfrak {R}^j\), the components \(\mathbf {v}_{cycle}\), \(\mathbf {v}_{coycle}\) may be obtained via orthogonal projection of \(\mathbf {v}\) onto the corresponding subspaces.
The last point can be established by induction on m: one assumes existence, for m alternatives, of a set \(S_{cycle}\) of \(\frac{(m-1)(m-2)}{2}\) linearly independent length-3 cycles and a set \(S_{cocycle}\) of \(m-1\) linearly independent cocycles. Note that these cardinalities add to \(\frac{(m)(m-1)}{2}\). One then shows that with the addition of one new alternative one can construct at least one more cocycle, which maintains linear independence of \(S_{cocycle}\) when added in, expanding \(|S_{cocycle}|\) to m, and can construct at least \(m-1\) more length-3 cycles, which maintain linear independence of \(S_{cycle}\) when added in, expanding \(|S_{cycle}|\) to \(\frac{(m-1)(m-2)}{2}+(m-1)=\frac{(m)(m-1)}{2}\), as desired.
With non-symmetric vectors of scoring weights, one cannot fully recover the scores from their scaled differences (corresponding to \(\mathbf {v}_{cocycle}\) edge labels), as the vector of scores also encodes the number n of voters, while from \(\mathbf {v}_{cocycle}\) it is not possible to recover n.
We are using “large enough” as a loose metaphor here—the precise version (Zwicker 1991) does not use a single numerical measure of size.
In a sense, then, it is thus doubly true that the mean rule depends only on \(\mathbf {v}_{cocycle}\). First, the Borda mean rule discards \(\mathbf {v}_{cycle}\), using only \(\mathbf {v}_{cocycle}\). Second, for the mean rule \(\mathbf {v}_{cycle}\) need not even be discarded. We say “in a sense” because the second argument is subtly incomplete—it fails to rule out the possibility that the mean rule relies on profile information not present in the net preference flow. In fact, the vector \(\{ y( P)_x \}_{x \in X}\) used as input for the mean rule incorporates some information about the total number of voters wiped out (by taking differences, in Eq. 3 below) when it is converted to net preferences.
To keep things short, we’ve suppressed all mention of ties in the remainder of this section. The modifications needed to take them into account are straightforward.
Perhaps by showing each exploits that information in the only reasonable way for its context.
In this example, the set of applicants is partitioned into a “invited to interview” set and a “not invited to interview set”.
Another approach would be to determine t before the votes are cast, and then require each panelist to vote for exactly t candidates. The t candidates with the greatest total number of votes are chosen for interview. See Peters et al. (2012).
References
Bogomolnaia A, Moulin H, Stong R (2005) Collective choice under dichotomous preferences. J Econ Theory 122:165–184
Brams S, Kilgour DM, Zwicker WS (1998) The paradox of multiple elections. Soc Choice Welf 15:211–236
Croom F (1978) Basic concepts of algebraic topology. Springer, New York
Dietrich F (2014) Scoring rules for judgment aggregation. Soc Choice Welf 42:873–911
Dietrich F, List C (2007) Arrow’s theorem in judgment aggregation. Soc Choice Welf 29:19–33
Dokow E, Holzman R (2010a) Aggregation of binary evaluations. J Econ Theory 145:495–511
Dokow E, Holzman R (2010b) Aggregation of non-binary evaluations. Adv Appl Math 45:487–504
Duddy C, Piggins A (2013) Collective approval. Math Soc Sci 65:190–194
Fishburn PC (1977) Condorcet social choice functions. SIAM J Appl Math 33(3):469–489
Harary F (1958) Graph theory and electric networks. IRE Trans Circuit Theory CT-6:95-109
Kasher A, Rubinstein A (1997) On the question “who is a J?”: a social choice approach. Logique et Analyse 160:385–395
Kornhauser LA, Sager LG (1993) The one and the many: adjudication in collegial courts. Calif Law Rev 81:1–59
List C (2008) Which worlds are possible? Judgment aggregation problem. J Philos Logic 37:57–65
List C, Pettit P (2002) Aggregating sets of judgments: an impossibility result. Econ Philos 18:89–110
List C, Polak B (2010) Introduction to judgment aggregation. J Econ Theory 145:441–466
Maniquet F, Mongin P (2015) Approval voting and Arrow’s impossibility theorem. Soc Choice Welf 44:519–532
Nehring K, Puppe C (2010) Abstract Arrowian aggregation. J Econ Theory 145:467–494
Nitzan S, Rubinstein A (1981) A further characterization of the Borda ranking method. Public Choice 36:153–158
Peters H, Roy S, Storcken T (2012) On the manipulability of approval voting and related scoring rules. Soc Choice Welf 39:399–429
Rubinstein A, Fishburn PC (1986) Algebraic aggregation theory. J Econ Theory 38:63–77
Saari DG (1994) Geometry of voting. Springer, Berlin
Saari DG (1995) Basic geometry of voting. Springer, Berlin
Saari DG (2001a) Decisions and elections: explaining the unexpected. Cambridge University Press, Cambridge
Saari DG (2001b) Chaotic elections: a mathematician looks at voting. American Mathematical Society, Providence
Saari DG (2008) Disposing dictators, demystifying voting paradoxes: social choice analysis. Cambridge University Press, Cambridge
Wilson R (1975) On the theory of aggregation. J Econ Theory 10:89–99
Xia L (2011) Computational voting theory: game-theoretic and combinatorial aspects, Ph.D Dissertation. Computer Science Department, Duke University, Durham. http://www.cs.rpi.edu/~xial/
Young HP (1974) An axiomatization of Borda’s rule. J Econ Theory 9:43–52
Zwicker WS (1991) The voters’ paradox, spin, and the Borda count. Math Soc Sci 22:187–227
Author information
Authors and Affiliations
Corresponding author
Additional information
Financial support from the Spanish Ministry of Economy and Competitiveness through MEC/FEDER grant ECO2013-44483-P, and the Irish Research Council co-funding from the European Commission, is gratefully acknowledged. Conal Duddy conducted this research while visiting the Centre for Philosophy of Natural and Social Science at the London School of Economics. He is grateful for their hospitality. Thanks to Felix Brandt, Franz Dietrich, Nicolas Houy, Vincent Merlin, Marcus Pivato and the participants at PET 13 for their helpful comments. This joint project began after we attended a workshop on New Developments in Judgement Aggregation and Voting Theory, held in Freudenstadt, September 2011. The workshop was organised by Clemens Puppe and Klaus Nehring. We are extremely grateful to them for organizing this workshop, and for providing financial support. Finally, we would like to thank the Managing Editor, the Associate Editor and a referee, for their helpful comments on an earlier version of this paper.
Rights and permissions
About this article
Cite this article
Duddy, C., Piggins, A. & Zwicker, W.S. Aggregation of binary evaluations: a Borda-like approach. Soc Choice Welf 46, 301–333 (2016). https://doi.org/10.1007/s00355-015-0914-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-015-0914-3