Abstract
Card-based cryptography is a variant of multi-party computation using physical cards like playing cards. There are two models on card-based cryptography, called public and private models. The public model assumes that all operations are executed publicly, while the private model allows the players private operations called private permutations (PP, for short). Much of the existing card-based protocols were developed under the public model. Under the public model, 2n cards are necessary for every protocol with n-bit input since at least two cards are required to express a bit. In this paper, we propose n-bit input protocols with fewer than 2n cards by utilizing PP, which shows the power of PP. In particular, we show that a protocol for (n-bit input) threshold function can be realized with only \(n+1\) cards by reducing the threshold function to the majority voting. Toward this end, we first offer that two-bit input protocols for logic gates can be realized with fewer than four cards. Furthermore, we construct a new protocol for three-input majority voting with only four cards by observing the relationship between AND/OR operations. This protocol can be easily extended to more participants, and to the protocol for threshold functions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Background and Motivation
It is known that multi-party computation can be realized by a deck of physical cards [2], referred to as card-based cryptography. Card-based cryptography realizes secure computation with simple manual operations, such as permuting and reversing cards, which are used in ordinary card games. Hence, it attracts attention from the viewpoint of education because it is easier to understand and implement than general cryptographic protocols. In this paper, we handle card-based cryptography that is constructed with two types of cards, \(\boxed {\clubsuit }\) and \(\boxed {\heartsuit }\).
Much of the existing protocols in card-based cryptography assume a model that all operations are performed in a public area, such as on a table. We call such a model public. In the public model, using face-back cards is the only way to express a player’s input value privately. Since two cards are required for the arbitrary representation of a Boolean value, 2n cards are necessary to construct an n-bit input protocol.
On the other hand, Marcedone et al. [3] and Nakai et al. [6, 8] independently proposed a new operating model that allows private permutations (PP), which is an operation to permute cards privately, such as by hiding the cards on her/his back. We call this model private. In particular, Marcedone et al. [3] proposed two-bit input AND protocol with three cards, i.e., less than the lower bound of the number of cards in the public model, by utilizing PP.Footnote 1 This result implies that PP has the power to break the lower bound in the public model. However, it is not obvious whether PP can break the lower bound other than the AND protocol.
Our Contributions and Ideas
In this paper, we propose several protocols with fewer number of cards than the lower bound of the public model by utilizing PPs. We summarize our contributions in Table 1. We first propose the following two-bit input protocols with less than four cards by utilizing PP:
-
three-card OR (in "Three-Card OR Protocol"), and
-
two-card XOR (in "Two-Card XOR Protocol").
Our three-card OR protocol has the symmetric form of the thee-card AND protocol proposed by Marcedone et al. [3]. The symmetric form enables us to unify these protocols to a protocol that realize simultaneously AND and OR operations with four cards. As we can see in the following idea, this simultaneous realization enables us to implement a three-input majority voting protocol that determines which of 0 and 1 is more dominant with three-bit values as inputs while keeping the input values privately.
Idea of three-input majority voting protocol Our main idea of the three-input majority voting protocol is to utilize the simultaneous realization of AND and OR operations. Observing the relations for \(a,b \in \{0,1\}\),
it seems that \(a \wedge b\) and \(a \vee b\) can be interpreted as the interim result of the majority voting between two players, called Alice and Bob. Here, we consider the strategy that \(a \wedge b\) and \(a \vee b\) are given to the third player, called Carol who holds \(c \in \{0,1\}\). As we can see in the following simple relations, the desired value to learn the majority voting result is different whether \(a \wedge b\) or \(a \vee b\) depending on c from the following:
From (1) to (4), Carol should choose \(a \wedge b\) if \(c=0\) and \(a \vee b\) if \(c=1\) to determine the three-input majority voting. We note that Carol does not use any card to input c since she plays only the role of selecting \(a \wedge b\) or \(a \vee b\). Thus, we can obtain a protocol for the three-input majority voting without adding any cards from the simultaneous AND and OR protocol, i.e., we can construct it using only four cards.Footnote 2
We show that our three-input majority voting protocol can be extended for more participants, i.e., it can be generalized to an n-input majority voting. We propose an efficient protocol for the (t, n)-threshold function based on the n-input majority voting protocol. Our (t, n)-threshold function protocol requires only \(n+1\) cards; nevertheless, at least 2n cards are required in the public model.
Organization
The remaining part of this paper is organized as follows: in the next section, we introduce operations used in this paper and explain the public and private models. In the third section, we describe the three-card AND protocol [3] and propose two-card XOR and three-card OR protocols. In the fourth section, we first show how to obtain AND and OR results with four cards simultaneously, and we propose a three-input majority voting protocol based on this protocol. Furthermore, we show that the three-input majority voting protocol can be extended to a threshold function protocol in the fifth section, which is the main difference from the earlier version [7]. We conclude this paper in the last section.
Operating Models in Card-Based Cryptography
This paper uses two kinds of cards, \(\boxed {\clubsuit }\) and \(\boxed {\heartsuit }\) . We assume that the same type of cards are indistinguishable and the backs of all cards are the same, which are represented as \(\boxed {?}\) . We do not use card orientation information such as  .
.
Public Model
Much of previous works in card-based cryptography adopt the public model that assumes all operations to be performed publicly. In the public model, the following operations are used:
-
Permutation permuting card order publicly.
-
Reverse turning over a card publicly.
-
Shuffle probabilistic permutation performed in public.
Efficiency is evaluated by the number of cards and the number of shuffles. In particular, the shuffle is a crucial operation to ensure privacy while making all operations public. The shuffle is a probabilistic permutation performed in public, and we assume that the result cannot be identified by all players, including the player who performed the operation. Many of the shuffles used in card-based cryptography do not completely randomize the order in the deck of cards but are defined as randomly selecting a permutation from a subset of all permutations. One of the shuffles is a random bisection cut [5]. We describe the procedure below.
For a positive integer v, suppose that there is a sequence of 2v face-down cards. Denote the left and right halves by \(\mathbf {u}_0\) and \(\mathbf {u}_1\), respectively. Namely, we define

Then, a player repeats the operation of interchanging \(\mathbf {u}_0\) and \(\mathbf {u}_1\) in a public area until all the players (including the player him/herself) cannot identify the order. Depicting this using figures, one of either

is selected with a probability 1/2, and all the players cannot distinguish the two cases. In other words, when the result is \((\mathbf {u}_r, \mathbf {u}_{1-r})\), no player can identify the random value \(r \in \{0,1\}\).
In this public model, since we do not use oriental information of cards, two cards are necessary to express a bit, such as \(0 \mapsto \boxed {\clubsuit }\boxed {\heartsuit }\) and \(1 \mapsto \boxed {\clubsuit }\boxed {\heartsuit }\) . Hence, only we can do to conceal an input is using a pair of face-down cards \(\boxed {?}\boxed {?}\) . The expression of a bit using two face-down cards is called commitment. The committed-format protocol has the advantage that it can be executed without parties knowing their own input values. On the other hand, all our proposed protocols assume that parties know the value of their own input.
Private Model
Marcedone et al. [3] and Nakai et al. [6, 8] independently proposed a new operating model that allows players to use private operations. This paper adopts the private model, where we use the following operationsFootnote 3:
-
(Public) permutation: permuting card order publicly.
-
Private permutation (PP) permuting card order privately.
-
Reverse turning over a card publicly.
-
Communication handing over cards to another player.
Efficiency is evaluated by the number of cards, the number of PPs, and communications.
When comparing the efficiencies between protocols based on public and private models, we interpret shuffles in the public model as two PPs and one communication in the private model. For instance, the following procedure in the private model simulates the effect of a random bisection cut [5] in the public model.
For a positive integer v, suppose that Alice holds 2v face-down cards.
-
1.
Alice determines \(r_A \in \{0,1\}\) with a probability of 1/2, and privately swaps the card order \(r_A\) times.
-
2.
Alice sends the result \((\mathbf {u}_{r_A},\mathbf {u}_{1-r_A})\) to Bob.
-
3.
Bob determines \(r_B \in \{0,1\}\) with a probability of 1/2, and privately swaps the card order \(r_B\) times.
As a result of the above operations, the card order becomes \((\mathbf {u}_{r_A \oplus r_B},\mathbf {u}_{1-r_A \oplus r_B})\). Then, no player can tell the value of \(r_A \oplus r_B\) since \(r_A\) (resp. \(r_B\)) is kept secret for Bob (resp. Alice). Thus, we obtain the same result of a random bisection cut.
A shuffle can be realized by combining two PPs and one communication. Thus, we can convert a protocol based on the public model to one based on the private model by converting each shuffle to two PPs and one communication. When we compare the efficiency between the two models, a protocol based on the public model is converted to the private model.
In the private model, it is possible to express inputs with PP itself instead of using the commitment. This observation enables us to construct an n-bit protocol with less than 2n cards. In Sect. 3.1, we introduce three-card AND protocol [3] that succeeds in reducing the number of cards by the technique of expressing an input with PP.
In the public model, players’ malicious behaviors need not be considered since all operations are monitored by players. On the other hand, PP enables players’ malicious behaviors.Footnote 4 Our protocols suppose the semi-honest model, which assumes all players follow the protocols.
Proposed Protocols for Logic Gates
Starting from the three-card AND protocol [3], this section proposes three-card OR and 2-card XOR protocols, which break the lower bound of the number of cards in the public model. In this section, let a and b be binary inputs of Alice and Bob, respectively.
Basic Idea: Inputs by Utilizing PPs
In the Epilogue in [3] (Solution B), the three-card AND protocol is proposed as shown in Protocol 1.Footnote 5 See step 2) in Protocol 1. Bob does not use the commitment to express his input, but he represents his input by PP. He uses only one card to input, and the protocol is realized with fewer than four cards, which is the lower bound of the public model. Namely, Protocol 1 succeeds in breaking the lower bound by utilizing PP to express inputs.
Security Proof of three-card AND protocol: We present a brief overview of the security proof for Protocol 1, which will be useful to understand the security of the protocols proposed hereafter.
Table 2 shows the card order at the end of step 2) and the output of the protocol. Subscripts of \(\clubsuit \) and \(\heartsuit \) indicate the player who had the card originally.Footnote 6 Since we compute AND, the player who inputs 1 can uniquely determine the other player’s input at the end of the protocol. Meanwhile, for the player who inputs 0, no information must leak out to him/her. When Alice inputs \(a=0\) (\(\clubsuit \)), the output is either \(\clubsuit _\mathrm {Alice}\) or \(\clubsuit _\mathrm {Bob}\), which is opened by Bob and is indistinguishable from Alice. When Bob inputs \(b=0\), he places his \(\clubsuit _\mathrm {Bob}\) on the left, and he simply shows this card to Alice. Hence, he obtains no information on Alice’s input.
It is clear that no information is obtained by the players other than Alice and Bob (if such players exist) because the only information they can get is the output. \(\square \)
Three-Card OR Protocol
Since Marcedone et al. [3] only concentrated on the construction of card-based AND protocols, no protocol was shown for the other logic gates using PP. Hereafter, we show card-based protocols for computing OR and XOR based on PPs, which are realized with three and two cards, respectively.
To construct card-based OR protocols, we should recall De Morgan’s law: \(a \vee b = \lnot (\lnot a \wedge \lnot b)\). The card-based OR protocol can be obtained from this identity by negating Alice’s input, Bob’s input, and the output. Specifically, when Alice inputs \(a=0\), she should use \(\heartsuit \) (otherwise \(\clubsuit \)), and when Bob inputs \(b=0\), he should place \(\clubsuit \) to the right of the card he received. Finally, the output should be negated. Then, we have Protocol 2, where the different parts from Protocol 1 are underlined.
The relationships among the inputs, the card order at the end of step 2), and the output are shown in Table 3. The security proof is not necessary since this protocol is essentially the same as Protocol 1.



Two-Card XOR Protocol
The proposed 2-card XOR protocol is shown in Protocol 3. In this protocol, PPs are used in steps 1) and 2). The relationships among the inputs, the pair of cards at the end of step 2), and the output are shown in Table 4.
Security of Two-card XOR Protocol: For Alice and Bob, they have no information to be kept secret because, if the value of XOR and one of the two inputs are given, the other input is uniquely determined. Furthermore, no information except for the output is known to the players other than Alice and Bob.
It is clear that no information is obtained by the players other than Alice and Bob (if such players exist) because they can get only the output. \(\square \)
Three-Input Majority Voting Protocol with Four Cards
Based on the observations on the AND and the OR protocols in the previous section, we propose a three-input majority voting protocol that uses only four cards. Consider the scenario where Alice, Bob, and Carol have binary values a, b, and c, respectively. They want to know the result of majority voting without revealing their individual inputs.
Formally, we want to compute the following function \(\mathsf {maj}(a,b,c)\in \{0,1\}\) securely:
Idea Behind Our Three-Input Majority Voting Protocol
Suppose that Alice, Bob, and Carol vote a, b, and c, respectively, in this order. We focus on the Carol’s vote \(c \in \{0,1\}\).
In the case of \(c=0\), the following equivalences hold:
This relationship implies that \(a \wedge b\) is the result of the majority voting when \(c=0\).
Meanwhile, in the case of \(c=1\), we have the following equivalences:
Hence, \(a \vee b\) is the result of the majority voting when \(c=1\).
Summarizing, we have
From this relationship, we obtain the following strategy for realizing the three-input majority voting: (1) Alice and Bob make two face-down cards representing \(a \wedge b\) and \(a \vee b\), (2) they send the cards to Carol, and (3) Carol picks up one of the received cards according to her input using PP.Footnote 7 For realizing (1), we construct a four-card AND/OR protocol that computes AND and OR simultaneously by unifying Protocols 1 and 2.
Unifying AND and OR Operations
Since the three-card AND and OR protocols in Protocols 1 and 2, respectively, are essentially the same based on the De Morgan’s law, and hence, they have a symmetric form. From this observation, we design a unified AND/OR protocol where \(a\wedge b\) and \(a \vee b\) result in the left and right cards, respectively, for inputs \(a,b\in \{0,1\}\).
Modification of Three-Card OR Protocol
To obtain the unified protocol, the formats of the outputs of Protocols 1 and 2 must be the same. Then, we exchange \(\clubsuit \) and \(\heartsuit \) in Protocol 2. Moreover, we swap the left and right cards in the step 2) of Protocol 2 to make \(a \vee b\) place on the right. Then, we obtain Protocol 4 from Protocol 2. The relationships among the inputs, the pair of cards at the end of step 2), and the output are shown in Table 5.
Four-Card AND/OR Protocol
Observe that the right card and the left card are discarded at the end of the protocol in both Protocols 1 and 4, respectively. We also observe that Bob has \(\clubsuit \) and \(\heartsuit \) at step 1) in both Protocols 1 and 4, respectively. From these observations, we can unify Protocols 1 and 4 by letting Bob have \(\clubsuit \) and \(\heartsuit \) in the initial setup. Then, we can implement the results of AND and OR simultaneously in one card-based protocol, as shown in Protocol 5.
We show in the next subsection that the four-card AND/OR protocol is useful in calculating the three-input majority voting with only four cards.
Three-Input Majority Voting Protocol with Four Cards
Based on the four-card AND/OR protocol, it is easy to obtain the majority voting protocol. First, Alice and Bob jointly compute \(a \wedge b\) and \(a \vee b\) simultaneously without opening the result. Then, Carol chooses either \(a \wedge b\) or \(a \vee b\) depending on \(c=0\) or \(c=1\), respectively, behind her back. See Protocol 6 for the detail. Table 6 shows the pair of cards at the end of step 2) and the output.
Note that the third player, Carol, has no card throughout the protocol for her input since her role is to choose \(a \wedge b\) or \(a \vee b\). Thus, our protocol for the three-input majority voting does not require any additional cards from the four-card AND/OR protocol.



Card-Based Threshold Function Protocol
In this section, we propose a protocol for the threshold functions by generalizing our three-input majority voting protocol. Let \(x_1, x_2,\dots ,x_n\) be Boolean inputs of n players \(P_1, P_2, \dots , P_n\), respectively. Then, our (t, n)-threshold function protocol aims to compute the following function without revealing inputs.
Before describing our threshold function protocol, we extend Protocol 6 to an n-input majority voting protocol. The idea of this extension is useful to construct a threshold function protocol.
Extention to n-Input Majority Voting Protocol
We first show that Protocol 6 can be extended to an n-input majority voting protocol. Here, we define the function for n-input majority voting as follows:Footnote 8
Idea of Extension
To obtain an n-input majority voting protocol, we provide another look at Protocol 6. Recall that Alice and Bob express their inputs by placing cards, whereas Carol does not. Carol inputs her vote by selecting either the left or right card from the cards she receives.
Table 7 summarizes the relation between the cards she receives and she outputs (depending on her input). In Protocol 6, Carol’s operation was “selecting an output card,” but we interpret it as “removing cards” as opposed to Alice and Bob for generalization. Specifically, we interpret Carol’s behavior as removing the right card if \(c=0\) and removing the left card if \(c=1\).
For generalizing the discussion above, suppose that \(m \in \mathbb {N}\) players place m cards according to their inputs. Then, it is natural to remove \(m-1\) cards depending on their inputs to remain one card that expresses the output. Hence, we assume that the number n of players is odd and consider the protocol in which \((n+1)/2\) players place cards and \((n-1)/2\) players remove the cards. We will discuss the protocol when n is even in Sect. 5.1 later.
Case 1: n is Odd
Noticing that n is odd, we divide n players into \((n+1)/2\) and \((n-1)/2\) players, which we call the first and the second halves, respectively.
The first half of players \(P_i \, (1\le i \le (n+1)/2 )\) performs the following operations with PP, like Alice and Bob.
-
If \(x_i=0\), then \(P_i\) places face-down \(\clubsuit \) on the leftmost of the received cards, and sends the cards after processing to \(P_{i+1}\).
-
If \(x_i=1\), then \(P_i\) places face-down \(\heartsuit \) on the rightmost of the received cards, and sends the cards after processing to \(P_{i+1}\).
On the other hand, the second half of players \(P_j\,((n+1)/2 < j \le n)\) performs the following operations with PP, like Carol.
-
If \(x_j=0\), then \(P_j\) removes the rightmost card of the received cards, and sends the cards to \(P_{j+1}\).
-
If \(x_j=1\), then \(P_j\) removes the leftmost card of the received cards, and sends the cards to \(P_{j+1}\).
Finally, \(P_n\) opens the remaining card as the output.
For instance, in the case where \(n=5\), we can obtain Table 8 by applying this protocol. This is an extension of Table 7, and we can see that the output is correct.
This protocol achieves n-input majority voting if n is odd. We show that correctness and security are satisfied in this case.
Correctness: Let \(\alpha \) and \(\beta \) be the numbers of players who input 0 among the first half players and the second half players, respectively. Then, the card order received by \(P_{(n+1)/2 + 1}\), who is the first player in the second half players, is as follows:

We consider the case where \(\alpha + \beta \) is less than \((n+1)/2\) or not.
-
\(\alpha + \beta <(n+1)/2\)
In this case, it holds that \(\beta < (n+1)/2 - \alpha \). Namely, the number of players \(\beta \) that remove the rightmost card is less than \((n+1)/2\,- \alpha \). Furthermore, one card is remained in the end since n is odd. Therefore, the final remaining card is \(\heartsuit \) representing 1, which is the correct result, as shown as follows:
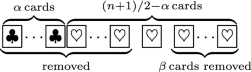
It is confirmed that output is correct.
-
\(\alpha + \beta \ge (n+1)/2\)
The number of players \(\beta \) to remove the rightmost card is \((n+1)/2\,- \alpha \) or more. Furthermore, one card is remained in the end since n is odd. Therefore, the final remaining card is \(\clubsuit \) representing 0, which is the correct result, as shown below.

It is confirmed that the correct output can be obtained.
\(\square \)
Security: It is trivial that no information beyond the output leaks since only the output card is opened and players’ operations are hidden by the assumption of PP. \(\square \)
Case 2: n is Even
If we apply the protocol described in Sect. 5.1 directly to the case where n is even, the protocol does not work because no card remains at the end of the protocol.
To remove this obstacle, we use the following equivalence relation:
This relation suggests using a dummy player \(P'_1\) who always inputs 1 for \((n+1)\)-input majority voting for computing n-input majority voting.
Note that \(P'_1\) is sufficient to have \(\heartsuit \) only since the dummy player always inputs 1. Hence, our majority voting protocol can be realized with \(n+1\) cards in this case. We also note that we should choose the dummy player from the first half of the players, i.e., from the players who use cards for the inputs. If we choose the dummy player from the second half of players, i.e., from the players who do not use cards for the inputs, the protocol needs \(n+2\) cards since all the first half players, i.e., \((n+2)/2\) players, have to hold two cards for the input. This is why we assign the dummy player to \(P_1\).
Card-Based (t, n)-Threshold Function Protocol
The idea to construct the threshold function protocol is similar to the n-input majority voting protocol when n is even. In this case, we use the following equivalence relation:
Thanks to this equivalence, we can realize the threshold function protocol by selecting an integer d such that \(f_{(t+d,n+d)}\) can be regarded as a majority voting function with \(n+d\) inputs. Then, \(n+d\) should be odd, and \(2(t+d)-1=n+d\) must hold, which yields \(d=n-2t+1\). Then, \(f_{(t,n)}\) can be computed by the protocol for \(f_{(n-t+1,2n-2t+1)}\) \(= \mathsf {maj}_{2n-2t+1}\). Note that \(d=n-2t+1\) is the number of dummy players in the first half. Hence, \(d \ge 0\), i.e., \(t \le \lceil n/2 \rceil \) must hold. We can assume \( t \le \lceil n/2 \rceil \) without loss of generality since inputs 0 and 1 can be reversed if \(t > \lceil n/2 \rceil \).Footnote 9 .
In summary, in computing \(f_{(t,n)}\), we construct a protocol for \(f_{(n-t+1,2n-2t+1)}\) \(= \mathsf {maj}_{2n-2t+1}\) with \(n-2t+1\) dummy players who input 1. The specific procedure is shown in Protocol 7. This protocol is constructed with t \(\clubsuit \,\)s and \(n-t+1\) \(\heartsuit \,\)s, i.e., \(n+1\) cards are used in total.
Conclusion
In this paper, we showed that PP has the power to break the lower bound of the number of cards in the public model. Actually, we proposed several protocols in the private model with fewer cards than the lower bound 2n, where n is the total bit length of inputs. In particular, we proposed a threshold function protocol with only \(n+1\) cards, which is the main result of this paper. It was not known that PP could break the lower bound except for the protocol for computing AND [3].
In the public model, the players must use a pair of face-down cards, called commitment, to input. Our main idea to break the lower bound was using PPs to input instead of commitment. The players can input without using cards by deciding the permutation depending on their input.
This idea helped us construct (two-bit input) OR and XOR protocols with three and two cards, respectively. The OR protocol was based on the AND protocol [3]. Furthermore, we showed that AND and OR operations could be simultaneously realized with four cards, i.e., we could simultaneously obtain two cards expressing \(a \wedge b\) and \(a \vee b\) given \(a, b \in \{0,1\}\). Based on this, we proposed a protocol for three-input majority voting with four cards. The three-input majority voting protocol can be extended to an n-input majority voting protocol with \(n+1\) cards.
By fixing inputs of dummy players, a threshold function protocol can be realized by computing a majority voting. We showed that a protocol for \(f_{(t,n)}\) could be realized by executing a protocol for \(\mathsf {maj}_{2n-2t+1}\) with \(n-2t+1\) dummy players who input 1.

Notes
After the earlier version of this paper [7] was published, it was proposed how to realize three-input majority voting with only three cards [16]. In addition, in [17], it was shown that three-input majority could be achieved with six cards using a private selection instead of the private permutation.
Slightly modified for later discussion, but essentially the same as the protocol in [3].
Hereafter, we remove the frame of cards for simplicity.
More formally, Carol privately makes \((a \wedge b, a \vee b)\) if \(c=0\) and \((a \vee b, a \wedge b)\) otherwise using PP. The left card is the picked out card in the procedure (3).
Note that the output is 1 if n is even and the numbers of inputs of 0 and 1 is the same.
The other way to realize the protocol when \(t > \lceil n/2 \rceil \) is to fix the dummy input to 0.
References
Abe, Y., Iwamoto, M., Ohata, K.: How to detect malicious behaviors in a card-based majority voting protocol with three inputs. In: 2020 International Symposium on Information Theory and Its Applications (ISITA), pp. 377–381 (2020)
den Boer, B.: More efficient match-making and satisfiability: the five card trick. In: Advances in Cryptology—EUROCRYPT ’89, Workshop on the Theory and Application of of Cryptographic Techniques, Houthalen, Belgium, April 10–13, 1989, Proceedings, pp. 208–217 (1989)
Marcedone, A., Wen, Z., Shi, E.: Secure dating with four or fewer cards. Cryptology ePrint Archive, Report 2015/1031 (2015). https://eprint.iacr.org/2015/1031
Mizuki, T., Kumamoto, M., Sone, H.: The five-card trick can be done with four cards. In: Advances in Cryptology—ASIACRYPT 2012—18th International Conference on the Theory and Application of Cryptology and Information Security, Beijing, China, December 2–6, 2012. Proceedings, pp. 598–606 (2012)
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Frontiers in Algorithmics, Third International Workshop, FAW 2009, Hefei, China, June 20–23, 2009. Proceedings, pp. 358–369 (2009)
Nakai, T., Misawa, Y., Tokushige, Y., Iwamoto, M., Ohta, K.: How to solve millionaires’ problem with two kinds of cards. New Gener. Comput. 39, 73–96 (2021)
Nakai, T., Shirouchi, S., Iwamoto, M., Ohta, K.: Four cards are sufficient for a card-based three-input voting protocol utilizing private permutations. In: Information Theoretic Security—10th International Conference, ICITS 2017, Hong Kong, China, November 29–December 2, 2017, Proceedings, pp. 153–165 (2017)
Nakai, T., Tokushige, Y., Misawa, Y., Iwamoto, M., Ohta, K.: Efficient card-based cryptographic protocols for millionaires’ problem utilizing private permutations. In: Cryptology and Network Security—15th International Conference, CANS 2016, Milan, Italy, November 14–16, 2016, Proceedings, pp. 500–517 (2016)
Nishida, T., Hayashi, Y., Mizuki, T., Sone, H.: Card-based protocols for any Boolean function. In: Theory and Applications of Models of Computation—12th Annual Conference, TAMC 2015, Singapore, May 18–20, 2015, Proceedings, pp. 110–121 (2015)
Ono, H., Manabe, Y.: Efficient card-based cryptographic protocols for the millionaires’ problem using private input operations. In: 2018 13th Asia Joint Conference on Information Security (AsiaJCIS), pp. 23–28 (2018)
Ono, H., Manabe, Y.: Card-based cryptographic protocols with the minimum number of cards using private operations. In: Zincir-Heywood, N., Bonfante, G., Debbabi, M., Garcia-Alfaro, J. (eds.) Foundations and Practice of Security, pp. 193–207. Springer International Publishing, Cham (2019)
Ono, H., Manabe, Y.: Card-based cryptographic logical computations using private operations. New Gener. Comput. 39, 10 (2020)
Ono, H., Manabe, Y.: Minimum round card-based cryptographic protocols using private operations. Cryptography 5(3), 17 (2021)
Shimizu, Y., Kishi, Y., Sasaki, T., Fujioka, A.: Card-based cryptographic protocols with private operations which can prevent malicious behaviors. In: IEICE Technical Report ISEC2017-113, pp. 129–135 (2018) (in Japanese)
Toyoda, K., Miyahara, D., Mizuki, T., Sone, H.: Secure computation of three-input majority function using six cards. In: Computer Security Symposium (CSS), pp. 4D1–4 (2020)
Watanabe, Y., Kuroki, Y., Suzuki, S., Koga, Y., Iwamoto, M., Ohta, K.: Card-based majority voting protocols with three inputs using three cards. In: 2018 International Symposium on Information Theory and Its Applications (ISITA), pp. 218–222 (2018)
Yasunaga, K.: Practical card-based protocol for three-input majority. In: Communications and Computer Sciences, advpub, IEICE Transactions on Fundamentals of Electronics (2020)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A preliminary version of this article appears in proceedings of International Conference on Information Theoretic Security (ICITS 2017) [7].
This work was supported by JSPS KAKENHI Grant numbers JP21H03395, JP20J21248, JP18K19780, and JP18H05289.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Nakai, T., Shirouchi, S., Tokushige, Y. et al. Secure Computation for Threshold Functions with Physical Cards: Power of Private Permutations. New Gener. Comput. 40, 95–113 (2022). https://doi.org/10.1007/s00354-022-00153-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00354-022-00153-7






