1 Introduction

Mayle (1991) and Denton (1993) emphasise the importance and complexity of laminar-turbulent transition in aerothermal design. Entropy generation and heat transfer are highly sensitive to boundary layer state, but the ability to predict transition computationally remains limited (Dick and Kubacki 2017). As designs move to lower Reynolds numbers, such as with small engine cores, the uncertainty in boundary layer state leads to uncertainty in performance, while in sub-scale testing incorrect boundary layer state on a component can entirely change the conclusions of an experimental campaign, particularly when investigating operating envelopes limited by boundary layer separation. There is, therefore, a need for tools that de-risk designs and experiments by quickly diagnosing boundary layer state.

A range of measurement methods are available to meet this need. At the low end of complexity and cost is oil flow visualisation. Changes in the boundary layer are seen from critical lines in the oil. Single oil flow experiments can be performed quickly assuming a suitable oil mixture is available but sweeping through operating conditions requires significant time to clean and re-apply oil, and the nonzero thickness of the oil makes it intrusive, possibly causing early transition. At the high end of complexity and cost are hot-film gauges. Boundary layer state changes are detected from changes in skin friction measured by discrete gauges. While capable of time-resolved measurements of unsteady effects, hot-films give low spatial resolution compared to full-field methods, are time consuming to instrument with and are limited to surfaces with low curvature, making quick design changes impractical.

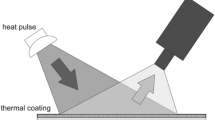
Infrared thermography (IR) offers simple, fast and non-intrusive visualisation of boundary layer state by measuring the changes in surface temperature that occur across flow features such as transition, separation and shock–boundary layer interaction as a result of changes in heat transfer coefficient and recovery temperature. An example IR visualisation is shown in Fig. 1. As with all thermograms shown in this paper, lighter colours indicate higher temperatures. The quantitative value of temperature is not important for the visualisation. The surface in Fig. 1 is heated internally, so the higher heat transfer coefficient in turbulent regions results in a lower surface temperature. Modern IR cameras are capable of measuring full-field surface temperatures with no additional instrumentation or surface preparation, but the use of IR is relatively uncommon in the literature compared to other techniques. This paper aims to encourage the adoption of IR as a diagnostic tool by demonstrating routes for optimisation and pointing out pitfalls to avoid in its use.

Fig. 1
figure 1

IR visualisation of laminar-turbulent transition of a flow over a heated surface

Full size image

Alternatives to IR for visualising surface temperatures are temperature-sensitive paints (TSPs) and thermochromic liquid crystals (TLCs) which change colour in the visible spectrum. The benefit of TSPs and TLCs is that visible light cameras with very high spatial resolution (>4000\(\times\)6000 pixels) are relatively cheap, whereas high-end IR cameras are limited to below 1000\(\times\)1000 pixels for 10–100 times the price and may also require expensive specialised windows. The advantages of IR are its speed and sensitivity. The temperature sensitivity of IR cameras is typically 10–50 mK compared to over 100 mK for TSPs and TLCs (Tropea et al. 2007). TSPs and TLCs need controlled illumination and inherently require applying a foreign substance to the surface which can affect the boundary layer. IR requires a surface with high emissivity, which most polymers already provide so no additional painting is needed.

IR measurements of boundary layers have been demonstrated by several authors in a range of flows. Key to successful IR visualisation is the use of an insulator on the surface of a test piece to maintain a temperature difference between boundary layer states. Without this insulation, a conductive surface destroys the temperature non-uniformity that IR measures. The magnitude of this non-uniformity relative to an IR camera’s noise floor is the signal-to-noise ratio (SNR) of the measurement. Most authors (Crawford et al. 2015; Joseph et al. 2016; Zuccher and Saric 2008) describe the use of an insulator but give no explanation of the choice. A recent study by Lalande et al. (2023) used a numerical boundary layer solver to demonstrate good practices in experimental design for generating a temperature gradient. In the work presented here a generalised low-order model is developed to show that there are routes for maximising SNR by choosing a suitable insulator for the flow being studied.

IR visualisations can be enhanced with image processing. Wynnychuk and Yarusevych (2020) and Ricci and Montelpare (2009) examined the first and second derivatives, respectively, of temperature on the surface of an aerofoil to capture separation points. Crawford et al. (2015) applied an image filter and de-warp, Dollinger et al. (2018) used temporal standard deviation and Fourier coefficients and Gleichauf et al. (2021) applied principle component analysis on up to 10,000 images. In rotating experiments IR is severely limited by noise due to the need for short integration times to reduce motion blur. To minimise this effect Gazzini et al. (2017) combined images with two integration times using a filtering algorithm. Von Hoesslin et al. (2020) used a transient temperature decline technique and Raffel et al. (2015) combined image de-rotation using a mirror with a differential method that compares images at slightly different aerofoil incidences. Each of these processing methods are capable of enhancing the measured signal; however, they all fundamentally benefit from a thermal design that increases the temperature difference between flow regimes, which is the focus of the following work.

This paper is split into three parts. First, a theoretical analysis sets up a 1D model considering two distinct boundary layer states. In this paper a high-speed flow is taken to be one where the recovery temperature difference and passive heat transfer are enough to detect changes in boundary layer state with IR. A low-speed flow is any other case where an active heat flux is needed to produce a wall temperature difference through changes in heat transfer coefficient. The boundary between the two depends on the minimum required SNR. The 1D model is used to investigate both regimes, showing that a maximum SNR exists at low speeds, while at high speeds there is a region in which SNR drops to zero due to an interplay between recovery temperature and heat transfer coefficient. The rest of the paper presents experimental validation of the model in low-speed and high-speed flows individually, with each section accompanied by a case study showing the application of IR in experiments where previously held fully turbulent assumptions are inappropriate and a diagnosis of boundary layer state is needed to correctly interpret results.

2 Theoretical analysis

Fig. 2
figure 2

Generalised layout of the 1D heat transfer model showing two disctinct boundary layer states

Full size image
Fig. 3
figure 3

Measured recovery factor on a zero-pressure-gradient flat plate for \(Pr = 0.72\). Data from Eckert and Weise (1942)

Full size image

This section of the paper presents a 1D heat transfer model of two distinct boundary layer states to determine the wall temperature in each regime and the effects of thermal parameters on IR visualisation. The overall layout of the model is shown in Fig. 2. The surface is a thermally insulating layer with thickness d and thermal conductivity \(\lambda\), below which is a thermally conductive substrate at a uniform temperature \(T_\text {sub}\). The fluid has free stream stagnation and static temperatures \(T_{0,\infty }\) and \(T_\infty\), respectively. Illustrative temperature profiles between the flow and substrate are shown. The temperature profile through the boundary layer may take one of several forms depending on the physics of the flow and thermal boundary conditions. The boundary layer has heat transfer coefficient h and a recovery temperature given by

$$\begin{aligned} T_\text {rec} = \left( 1+r\frac{\gamma -1}{2} M_\infty ^2\right) T_\infty \end{aligned}$$
(1)

where r is the recovery factor, \(M_\infty\) is the free stream Mach number and \(\gamma\) is the ratio of specific heats. The recovery factor arises due to conduction in the fluid, which prevents the fluid from reaching the stagnation temperature at the wall. The magnitude of this effect depends on the Prandtl number. In a zero-pressure-gradient flat plate flow, r can be shown, analytically, to be \(Pr^{1/2}\) for a laminar boundary layer and approximately \(Pr^{1/3}\) for a turbulent boundary layer (Shapiro 1954). Figure 3 shows that experimental data agree with theory, although there is some spread, and, importantly, that r varies significantly within the transitional regime.

The difference in recovery factors and heat transfer coefficients between laminar and turbulent boundary layers results in a wall temperature difference between the two:

$$\begin{aligned} \varDelta T_\text {lam-turb} = \left| T_\text {w,lam}-T_\text {w,turb}\right| \end{aligned}$$
(2)

If the surface is adiabatic then \(\varDelta T_\text {lam-turb}\) is the recovery temperature difference given by

$$\begin{aligned} \begin{aligned} \varDelta T_\text {lam-turb}&= T_\text {rec,turb}-T_\text {rec,lam}\\&= (r_\text {turb}-r_\text {lam}) \frac{\gamma -1}{2} M_\infty ^2T_\infty \\&\approx 0.01M_\infty ^2T_\infty \text {\hspace{2mm} (in air)} \end{aligned} \end{aligned}$$
(3)

With \(\varDelta T_\text {lam-turb}\), the SNR is given by

$$\begin{aligned} \text {SNR} = \frac{\varDelta T_\text {lam-turb}}{\text {NETD}} \end{aligned}$$
(4)

where NETD is the noise-equivalent temperature difference of the IR camera, a measure of its sensitivity that depends on the spectral range and integration time. An SNR of 10 or more is desirable for a clear visualisation. Equation 3 shows that the high-speed regime requires high Mach numbers and depends on the temperature of the flow.

In a steady, 1D analysis, heat flux through the insulator and boundary layer is given by

$$\begin{aligned} \dot{q} = \frac{\lambda }{d}(T_\text {sub}-T_\text {w}) = h(T_\text {w}-T_\text {rec}) \end{aligned}$$
(5)

The Biot number is the ratio of the thermal resistances of the insulator and boundary layer

$$\begin{aligned} Bi = \frac{hd}{\lambda } \end{aligned}$$
(6)

Insulator properties are constant, however the heat transfer coefficient changes when the boundary layer state changes, giving \(Bi_\text {lam}\) and \(Bi_\text {turb}\). Rearranging Eq. 5 for either boundary layer state gives the wall temperature as

$$\begin{aligned} T_\text {w} = T_\text {sub} - \frac{Bi}{Bi+1}(T_\text {sub}-T_\text {rec}) \end{aligned}$$
(7)

The following analysis considers the effect of changing the thermal resistance of the insulator, \(d/\lambda\), on \(\varDelta T_\text {lam-turb}\).

2.1 Low-speed flows

Fig. 4
figure 4

Demonstration of the effect of insulator Biot number on laminar-turbulent temperature difference in a low-speed flow heated by the surface

Full size image

In a low-speed flow where \(M_\infty \rightarrow 0\), the difference between static, stagnation and recovery temperature is negligible. In this case, IR visualisation requires an active heat flux to generate \(\varDelta T_\text {lam-turb}\) from the difference in heat transfer coefficients. The magnitude of \(\varDelta T_\text {lam-turb}\) depends on the balance of the thermal resistances between the boundary layer and insulator.

This balance is visualised qualitatively in Fig. 4. For \(d/\lambda \rightarrow 0\), i.e. a thin and/or high conductivity insulator, \(Bi\rightarrow 0\) and the thermal resistance of the boundary layer dominates. The laminar and turbulent wall temperatures approach the substrate temperature and \(\varDelta T_\text {lam-turb}\rightarrow 0\). For \(d/\lambda \rightarrow \infty\), i.e. a thick and/or low conductivity insulator, \(Bi\rightarrow \infty\) and the thermal resistance of the insulator dominates. The laminar and turbulent wall temperatures approach the stagnation temperature and \(\varDelta T_\text {lam-turb}\rightarrow 0\). In between these states there exists an optimal Biot number that balances the thermal resistance of the insulator and boundary layer, maximising \(\varDelta T_\text {lam-turb}\) and therefore maximising SNR.

With \(T_\text {rec}=T_{0,\infty }\), the normalised laminar-turbulent temperature difference found with Eq. 7 is

$$\begin{aligned} \frac{\varDelta T_\text {lam-turb}}{T_\text {sub}-T_{0,\infty }} = \frac{Bi_\text {turb}}{Bi_\text {turb}+1}-\frac{Bi_\text {lam}}{Bi_\text {lam}+1} \end{aligned}$$
(8)

Differentiating with respect to \(d/\lambda\) gives the optimal laminar Biot number that maximises \(\varDelta T_\text {lam-turb}\) as

$$\begin{aligned} Bi_\text {lam,optimal} = \left( \frac{h_\text {turb}}{h_\text {lam}}\right) ^{-1/2} \end{aligned}$$
(9)

where \(h_\text {turb}/h_\text {lam}\) is the ratio of heat transfer coefficients at transition. This ratio is specific to the flow but, from correlations for laminar and turbulent flows, usually takes values between 1.5 and 4 depending on features such as roughness, free stream turbulence and the presence of separation bubbles.

Fig. 5
figure 5

Analytic variation in \(\varDelta T_\text {lam-turb}\) with insulator Biot number for a low-speed flow with active heat flux. The dashed line indicates the locus of the maxima given by Eq. 9

Full size image

Figure 5 shows curves of Eq. 8. The locus of the optimum given by Eq. 9 lies around Biot numbers of 0.5-1, demonstrating that maximum SNR is achieved by balancing the thermal resistances of the insulator and boundary layer. The peak in \(\varDelta T_\text {lam-turb}\) is relatively flat in the direction of increasing Biot number but drops off sharply at low Biot numbers. This shows that experiments can use much thicker insulators than necessary without significant loss of SNR, allowing a single design to be used across a range of operating conditions. The risk is that an insulator that is slightly too thin or conductive, perhaps due to uncertainty in the conductivity of the material or in the true heat transfer coefficients, can catastrophically reduce SNR and ruin the visualisation.

2.2 High-speed flows

Fig. 6
figure 6

Demonstration of the effect of insulator Biot number on laminar-turbulent temperature difference in a high-speed flow heated by the surface

Full size image

In a high-subsonic flow, the difference in recovery temperature between laminar and turbulent boundary layers is great enough that it can be measured and used for visualisation. This is a passive method where the substrate temperature is not actively controlled but instead depends on the thermal boundary conditions of the experiment. In draw-down or blow-down high-speed facilities, the inlet stagnation temperature of the flow is often close to the initial temperature of the test piece, which is then cooled by the high-speed flow. In rotating facilities, or facilities with active control of temperature for Reynolds number matching, the inlet relative stagnation temperature may be significantly higher or lower such that the test piece is heated or cooled beyond the recovery temperature.

If the flow heats the test piece then \(\varDelta T_\text {lam-turb}\) behaves similarly to the result shown for low-speed flow in Fig. 5, except that the recovery temperature difference increases \(\varDelta T_\text {lam-turb}\). If the test piece is cooled by the flow then a qualitatively different result arises due to an interplay between heat transfer and recovery temperature differences. This interplay is visualised in Fig. 6. For \(d/\lambda \rightarrow 0\), \(Bi\rightarrow 0\) and, as in a low-speed flow, the conductivity of the surface means that laminar and turbulent wall temperatures approach the substrate temperature and \(\varDelta T_\text {lam-turb}\rightarrow 0\). For \(d/\lambda \rightarrow \infty\), \(Bi\rightarrow \infty\) and the surface approaches an adiabatic state. Unlike in low-speed flows, the recovery temperature difference means that \(\varDelta T_\text {lam-turb}\) approaches a finite value given by Eq. 3. In between these states are two possibilities. The lower heat transfer coefficient in a laminar boundary layer acts to make the laminar region hotter than the turbulent region, but the recovery temperature acts to make the laminar region cooler. At a relatively low Biot number \(<1\), the effect of heat transfer wins, resulting in an IR visualisation that shows laminar regions at a higher temperature. Between this state and the limiting case of an adiabatic wall, there must be a crossover where the two boundary layer states have equal surface temperatures and the SNR is zero.

Fig. 7
figure 7

Analytic variation in \(\varDelta T_\text {lam-turb}\) with insulator Biot number for a high-speed flow without active heat flux

Full size image

Applying Eq. 7 with \(T_\text {sub} = T_{0,\infty }\) at a fixed Mach number of 0.88 gives curves of \(\varDelta T_\text {lam-turb}\) shown in Fig. 7. It can be seen that the effects visualised in Fig. 6 appear in the quantitative results. At low Biot numbers, \(\varDelta T_\text {lam-turb}\) shows a peak in a region where \(T_\text {w,lam}>T_\text {w,turb}\). \(\varDelta T_\text {lam-turb}\) then drops to zero before rising again with \(T_\text {w,lam}<T_\text {w,turb}\). The Biot number at which \(T_\text {w,lam}>T_\text {w,turb}=0\) is seen to depend on the heat transfer coefficient ratio. It is also a function of the difference in \(T_\text {rec,lam}\) and \(T_\text {rec,turb}\) (Mach number) and the difference in \(T_\text {sub}\) and \(T_{0,\infty }\). A flow that acts to heat the surface behaves similarly to curves shown in Fig. 5, only with an asymptote at the recovery temperature difference. A flow where \(T_\text {sub}\gg T_{0,\infty }\) stretches the curves in Fig. 7 to the right, resulting in a broader peak in \(\varDelta T_\text {lam-turb}\) where \(T_\text {w,lam}>T_\text {w,turb}\).

The analysis underlying Fig. 7 assumes that the substrate remains at a fixed temperature, however without active control the substrate temperature will vary until a thermal equilibrium is reached. Early after turning on the wind tunnel the temperature on the surface is dominated by heat transfer. As the surface approaches the recovery temperature, the heat flux decreases and the final temperature distribution is closer to the recovery temperature than the constant \(T_\text {sub}\) assumption predicts. For a test piece being cooled by the high-speed flow this is analogous to moving from left to right on Fig. 7, visualised as \(T_\text {sub}\) moving from right to left in Fig. 6. Initially, \(T_\text {w,lam}>T_\text {w,turb}\) before the temperature equalises and then approaches the recovery temperature with \(T_\text {w,lam}<T_\text {w,turb}\). This inversion behaviour was observed computationally and experimentally by Lalande et al. (2023). In their study, Lalande et al. consider changes to fluid temperature and heat flux between two equilibrium states during an otherwise steady experiment. In a transient facility with short run times, the test piece would be initially isothermal and may never reach equilibrium, resulting in a different temperature profile development that can cause problems for IR visualisation as significant portions of the run may be in the low SNR regime. Additionally, the model used by Lalande et al. produces a pronounced drop before the expected rise in temperature at the transition point due to an interaction between the modelled convective and radiative heat transfer. Lalande et al. show some experimental evidence for this feature but it is not observed in the current work.

3 Low-speed experimental validation

This section presents experimental work undertaken to validate the 1D theory in a low-speed flow with active heating. IR visualisation is applied to transitional boundary layers on a low Reynolds number aerofoil to demonstrate that an optimum Biot number exists that maximises SNR. A case study is presented on the application of IR in low-speed testing.

3.1 Experimental design and methodology

To validate the 1D theory, the experimental set-up should generate realistic transitional boundary layers. A 300-mm chord, 430-mm span 2D NACA 0018 aerofoil is chosen. The aerofoil is placed in a working section with a cross-section of 458 mm \(\times\) 688 mm and connected to a low-speed (\(M_\infty <0.1\)) wind tunnel. At Reynolds numbers from 0.5–4.5 × 105 and incidences of ±15° the NACA 0018 displays a range of bypass and separation bubble transition mechanisms (Gerakopulos et al. 2010) that can be studied with IR. Whether transition is attached or separated is unimportant to the 1D model, which only requires two boundary layer states with a sharp change in heat transfer coefficient.

Details of the NACA 0018 test piece are shown in Fig. 8. The aerofoil is constructed from two aluminium parts that act as heat spreaders and form the substrate. One part has the NACA 0018 profile machined into its surface while the other has eight steps along its span. An ABS-like stereolithography-printed polymer shell interlocks with the steps, acting as the insulator and increasing in thickness along the span from 2 mm to 6 mm. Insulation is also added to the aluminium side with 0.1 mm thick layers of black polymer film. This variation in insulator thickness allows a range of Biot numbers to be tested on the same flow. The aerofoil surface is painted matt black to increase emissivity. The emissivity of the dull grey polymer insulator is already high (\(\approx 0.92\), where 1.0 is an ideal black body), so painting can be neglected if it significantly changes the surface quality.

Fig. 8
figure 8

NACA 0018 test piece

Full size image

The aerofoil is heated internally with 240 V silicone heater mats on the inner surface delivering up to 400 W and surrounded by insulating foam. The heaters are controlled with pulse-width modulation through a feedback loop to hold the aluminium at a fixed temperature. Data is collected with \(T_\text {sub} - T_{0,\infty } = {15\,\mathrm{\text {K}}}\pm {0.5\,\mathrm{\text {K}}}\). Seven K-type thermocouples are embedded in the aluminium for temperature measurement. The thermocouples are spread throughout the test piece to monitor the uniformity of heating. Steady-state temperatures across the span and chord are measured within 0.75 K of each other, which means that a non-uniformity correction such as that applied by Wynnychuk and Yarusevych (2020) is not required. The polymer side of the aerofoil has 51 surface pressure tappings, with diameter of 0.1 % of chord, drilled along the chord to compare pressure profiles with IR measurements. Pressure tappings in the tunnel wall and an inlet pitot-static system and thermocouple are used for flow velocity measurement.

A FLIR A615 IR camera is used for visualising the surface temperature on the aerofoil. The A615 is a relatively inexpensive industrial automation IR camera with a resolution of 640\(\times\)480 pixels, a spectral range of 7.5–14 \(\upmu\)m and an NETD of 50 mK. A 25° field-of-view lens is used for a full view of the aerofoil through a window in the tunnel floor made from a low-density polyethylene film, which has a transmissivity greater than 0.9 in the spectral range of interest (Gulmine et al. 2002). The camera is calibrated using a heated virtual black body to allow quantitative temperature measurement, however a qualitative IR visualisation does not require rigorous calibration procedures.

An example IR measurement of the aerofoil surface is shown in Fig. 9. Data is extracted from a single IR thermogram, with no averaging, from each run by taking a trace down the centre of each insulator thickness section. The four traces shown in Fig. 9 are taken from the central four thickness sections, as shown in Fig. 8. As the insulator thickness increases the surface temperature drops due to the increased thermal resistance between the heater and flow. Along the surface the temperature initially rises, corresponding to a thickening of the laminar boundary layer and drop in heat transfer coefficient. Between 20 and 30 % chord, the temperature drops sharply as the boundary layer transitions to turbulent and heat transfer increases. The start and end of transition are taken to be the maximum and minimum temperature points, respectively, with the temperature difference between these points used as \(\varDelta T_\text {lam-turb}\).

Fig. 9
figure 9

IR thermogram and temperature traces showing the temperature drop at transition on the aerofoil surface at \(Re = {}{3\times10^{5}}{}\) and 6° incidence. Trace locations shown in Fig. 8

Full size image

3.2 Results

To validate the predictions of the 1D model the aerofoil is tested over a range of incidences and Reynolds numbers, generating different of values for \(h_\text {turb}/h_\text {lam}\). Exact values of \(h_\text {turb}\) and \(h_\text {lam}\) are unknown. The theory in Sect. 2.1 shows that over the expected range for \(h_\text {turb}/h_\text {lam}\) of 1.5 to 4 the SNR and optimal insulator thickness vary by 50 %. The relative insensitivity of the SNR and optimal Biot number to the value of \(h_\text {turb}/h_\text {lam}\) means that correlations can be used in experimental design. In this study Reynolds analogy is applied following the method of Lalande et al. (2023), with skin friction calculations from XFOIL (Drela 1989) used to estimate heat transfer coefficients.

Figure 10 shows experimental values of \(\varDelta T_\text {lam-turb}\) for three values of \(h_\text {turb}/h_\text {lam}\). Analytic curves in the form of Eq. 8 are fit to the data. The agreement between the theory and experiment is excellent and is reflected across all operating conditions tested. Experimental results demonstrate the key points of the theory. It is possible to use a relatively thin insulating layer to generate the maximum possible \(\varDelta T_\text {lam-turb}\), however SNR drops off sharply at lower Biot numbers. The peak in \(\varDelta T_\text {lam-turb}\) is wide in the direction of increasing Biot number, so testing can be performed with relatively thick insulators without significant loss of SNR.

Fig. 10
figure 10

Comparison of 1D theory and experimental measurements of \(\varDelta T_\text {lam-turb}\)

Full size image

Comparing the data in Fig. 10 to the curves shown in Fig. 5 reveals some differences between experiment and theory. The main difficulty in comparing measurements to theory is uncertainty in the Biot number and heat transfer coefficient ratio, which arises due to use of Reynolds analogy and uncertainty in the thermal conductivity of the stereolithography-printed polymer insulator. Values of Biot number in Fig. 10 are therefore 50 % lower than those given by the theory. Measured values of \(\varDelta T_\text {lam-turb}\) are also as much as 40 % below those predicted. This is attributed to the effects of 2D conduction, which acts to reduce \(\varDelta T_\text {lam-turb}\) as heat flows chord-wise from laminar to turbulent regions, as seen in the calculations of Lalande et al. (2023).

Equation 8 shows that SNR is directly proportional to substrate temperature. IR avoids intrusive physical instrumentation and surface treatment, however a heated surface in air can destabilise the boundary layer and advance transition (Schlichting and Gersten 2016). To check that heating is not affecting the flow in this experiment, surface pressure profiles on the aerofoil with and without heating are compared in Fig. 11, along with IR thermograms from the heated cases. \(T_\text {sub}/T_{0,\infty } = 1.09\) corresponds to maximum safe heating for the polymer insulator, ten times the level required for usable visualisation. Kinks in the profiles indicate transition locations, with the profile for \(Re={}{1\times10^{5}}{}\) showing a large laminar separation bubble (LSB) between 20 % and 40 % chord. The LSB can be seen in IR from the stretch of uniformly high temperature. Boundary layer state changes seen in IR align with the features in the pressure profile and no measurable change due to heating can be seen in the profiles at either Reynolds number, demonstrating that the level of heating required for IR visualisation in this experiment is non-intrusive.

Fig. 11
figure 11

Suction surface pressure profiles for heated and unheated aerofoils at 8° incidence, with corresponding IR thermograms shown above

Full size image
Fig. 12
figure 12

IR visualisation of boundary layer state changes on the suction surface of the NACA 0018 aerofoil, with corresponding pressure profiles shown on the right

Full size image

In this experiment, it is found that a 3.5 mm thick insulator is close to optimal across the range of flows tested. With this set-up, high-quality measurements of boundary layer state over a wide operating range of the aerofoil can be done quickly with no additional instrumentation. Shown in Fig. 12 are thermograms and pressure profiles from the NACA 0018 over a range of incidence angles and Reynolds numbers. The movement of transition in both cases is clear to see, and in Fig. 12a the aerofoil can be seen to stall at the lowest Reynolds number. IR measurements agree closely with the measured pressure profiles. With automated control of tunnel speed and incidence, the aerofoil can be characterised over any range of incidence and Reynolds number automatically and in a short space of time, with each sweep shown in Fig. 12 taking less than 5 min. The same results with oil flow visualisation or a discrete probe would likely take many days. With the design in Fig. 8, a generic heater shape can be used and the outer profile of the insulator swapped to any desired aerofoil, allowing fast testing of a whole family of aerofoils.

3.3 Case study

The low-speed validation study has demonstrated how understanding the thermal characteristics of an experiment allows for high-quality visualisations to be achieved with minimal effort. In this part of the paper, a case study is presented on the use of IR in a low-speed flow for fast diagnosis of an unknown boundary layer state.

The application in this example is a distributed propulsor aerofoil being studied at the Whittle Laboratory based on the computational study by Hawkswell et al. (2022). A NACA 43018 aerofoil with a Fowler flap is used with a set of propulsors mounted along the leading edge. An example configuration is shown in Fig. 13a. Lift and drag measurements for the aerofoil with and without different propulsor-nacelle configurations are compared to determine an optimal configuration. The full-scale aerofoil operates at a \(Re=3\times10^6\), however testing is limited to \(Re=0.2\times10^6\). At this reduced Reynolds number an LSB forms on the surface of the aerofoil when propulsors are not attached. When attached, the additional mixing from the propulsor flow prevents the formation of the LSB. The LSB does not form at the full-scale Reynolds number due to earlier transition, so the effect of propulsors on lift and drag is unrealistically large at low Reynolds numbers.

Fig. 13
figure 13

Diagnosis of an unknown boundary layer state in a low Reynolds number test

Full size image

A boundary layer trip is needed to close the LSB while minimising parasitic drag. A method of visualising boundary layer state helps to identify such a trip. Two fast solutions were available: oil flow visualisation and IR thermography using the FLIR A615 camera. The aerofoil is not designed for use with IR; however, as it is of polymer construction, it is well suited to the method. Installing a heater is not necessary just for diagnosis, so a transient temperature change is generated by heating the aerofoil surface with a hot air gun or cooling it with a vortex cooler, resulting in wall–fluid temperature differences of approximately 10 K.

Oil flow visualisation is compared to IR in Fig. 13b. The LSB is captured by both methods, with the oil pooling up where the IR shows a high-temperature band as a result of the low heat transfer in the bubble. The major advantages of IR in this example are its speed and non-intrusiveness. Oil must be cleaned and reapplied between each operating point. The IR set-up takes less than 30 min and the thermal mass of the aerofoil means that a full sweep of incidence is possible without reheating. In testing the oil is seen to change the topology of the LSB as the nonzero thickness of the film causes early transition, while the IR has been shown to have minimal impact on the flow.

Polymer beads are used to generate a minimal trip that closes the LSB. Strips of different bead sizes are placed close to the leading edge to find the critical size. Figure 14 shows an IR visualisation of the effect of different bead sizes at one Reynolds number. Bead size is non-dimensionalised as a Reynolds number using the local boundary layer edge velocity. At \(Re_\text {bead} = 200-300\) the roughness has no effect on the formation of the LSB. The IR visualisation shows that \({\rm{Re}}_\text {bead} = 400\) is the critical value that trips the boundary layer enough to close the LSB, while \(Re_\text {bead} = 500\) produces a stronger trip that adds parasitic drag. The chosen beads are shown in Fig. 13a where they are placed along the leading edge of the main aerofoil and the flap.

Fig. 14
figure 14

IR visualisation showing critical roughness size needed to close the LSB on the aerofoil surface

Full size image

4 High-speed experimental validation

This section presents experimental work undertaken to validate the 1D theory in a high-speed flow where no active heating is needed and passive surface temperature differences are used for visualisation. IR visualisation is applied to high-subsonic and transonic transitional flows to demonstrate that SNR can fall to zero in certain steady-state and transient measurements. A second case study is presented demonstrating the use of IR in a transonic experiment with an unknown boundary layer state.

4.1 Experimental design and methodology

Fig. 15
figure 15

High-speed validation rig

Full size image

As with the low-speed validation work, the experimental set-up must generate laminar and turbulent boundary layers for visualisation with IR. The high-speed rig is shown in Fig. 15. The tunnel is a draw-down configuration with an atmospheric inlet and an outlet connected to a water ring vacuum pump. An aerofoil-like test piece sits in a 45 mm \(\times\) 45 mm working section. Bleed flow is extracted from the inlet to the working section and at the leading edge of the test piece. A pressure margin is provided by a throat at the bleed return down-stream of the working section, and the amount of bleed is controlled by ball valves. Peak surface Mach numbers (\(M_\text {peak}\)) from 0.7 to 1.2 are generated on the test piece with Reynolds numbers of 7–9.5 × 105.

Two test pieces are used: one machined from polycarbonate and one from aluminium 6082 alloy. The geometry and resulting flow is identical for each material. The low thermal conductivity of polycarbonate means that the surface temperature is approximately the recovery temperature, representing the limit of infinite Biot number. The thermal conductivity of aluminium 6082 is approximately 1000 times greater than polycarbonate, allowing for the assumption of a uniform substrate temperature. Size limitations in the high-speed rig make using multiple insulator thicknesses on the same test piece impractical. Instead the insulator thickness is increased by adding 0.1 mm thick layers of black polymer film to the aluminium surface. Up to twenty layers are added to increase Biot number from zero.

A concern when adding thickness to the test piece surface is that it may change the flow. To monitor this, the side wall of the working section has fifteen 0.3 mm diameter surface pressure tappings clustered around the test piece. The bleed valves are adjusted to ensure that the Mach number profile is matched for each run. A pitot probe measures stagnation pressure down-stream of the test piece and fast-response K-type thermocouples measure flow temperature at the inlet and working section, as well as the temperatures of the side wall, IR window and test piece.

A FLIR SC7300LW IR camera is used for visualising the high-speed test piece. The SC7300LW is a high-performance cooled IR camera with a resolution of 320\(\times\)256 pixels, a spectral range of 7.7 \(\upmu\)m-9.3 \(\upmu\)m and an NETD of 14 mK at an integration time of 320 \(\upmu\)s. A zinc sulphide window provides optical access to the test piece. This rig was developed by Hulhoven et al. (2024) for heat transfer measurements and has been extensively calibrated to account for radiosity from the side walls and window. Heater meshes in the inlet allow for up to 30 kW of power to be transferred to the flow, producing temperature changes of up to 90 K. Pre-heating the test piece before switching off the heater allows for transient changes in the visualisation to be investigated. Transient measurements are taken at a frame rate of 200 Hz. Semi-infinite heat transfer theory predicts the time for the polycarbonate surface to rise by 10 % of the overall temperature difference to be at least 0.1 s, so a frame time of 0.005 s fully resolves the thermal transient.

The atmospheric inlet of the high-speed rig means that Reynolds and Mach numbers are coupled, so collecting comparable data over a range of Reynolds numbers is difficult. To compare boundary layer states, one side of the leading edge is roughened with sand paper to trip the boundary layer. As the insulator thickness is uniform, a span-wise slice represents a comparison between two heat transfer coefficients with the same insulator and Mach number, as is assumed in the 1D model, and different ratios of heat transfer coefficients are found at different chord-wise positions.

An example visualisation is shown in Fig. 16. The test piece is allowed to reach thermal equilibrium with the flow before measurements are taken. The rough region at the leading edge can be seen to trip the boundary layer, resulting in a higher temperature on one side. The laminar side transitions further down-stream, eventually reaching equilibrium at the same temperature as the turbulent side. Recovery factors calculated from the measured temperatures and expected Mach number profile agree well with the theoretical values.

Fig. 16
figure 16

IR thermogram and temperature traces from the polycarbonate test piece at \(M_\text {peak} = 0.88\)

Full size image

4.2 Results

Figure 17 shows experimental values of \(\varDelta T_\text {lam-turb}\) for two points on the surface of the aluminium test piece where \(M\approx 0.8-0.85\). As in low-speed experiments, values of \(h_\text {turb}\) and \(h_\text {lam}\) are estimated with Reynolds analogy using skin friction coefficients from CFD calculations. Analytic curves are fitted to the data. Also shown in Fig. 17, the dashed lines indicate the values of \(\varDelta T_\text {lam-turb}\) measured at the same points on the polycarbonate test piece, which is approximately the recovery temperature difference.

Fig. 17
figure 17

Comparison of 1D theory and experimental measurements of \(\varDelta T_\text {lam-turb}\) at two streamwise locations on the aluminium test piece surface

Full size image

Experimental results once again validate the key features of the 1D model. At high Biot numbers, \(\varDelta T_\text {lam-turb}\) approaches the recovery temperature difference, which limits the maximum value of SNR achievable in a given flow with a passive method. At low Biot numbers, there is a peak in \(\varDelta T_\text {lam-turb}\), which drops to zero as Biot number increases. This is a heat transfer dominated regime in which the SNR remains low even as insulation is added to the surface. The extent of this regime is greater for a higher values of \(h_\text {turb}/h_\text {lam}\) as heat transfer has a stronger effect. When compared to Fig. 7, the heat transfer dominated regime is smaller in experiments due to the effect of the test piece being at thermal equilibrium with the flow. The substrate is cooled to below the stagnation temperature, reducing heat flux through the surface and amplifying the recovery temperature effect.

Transient tunnels, such as the Cambridge supersonic tunnel (Sabnis et al. 2023), the Oxford turbine research facility (Hilditch et al. 1994) and the von Karman Institute compression tube facility (Paniagua et al. 2013), are common in high-speed testing, so it is important to understand thermal effects in them when using IR. In this experiment thermal transients are investigated by pre-heating the flow and allowing the test piece to thermally soak. The heaters are switched off and the temperature development of the surface recorded in IR. Surface temperatures are rescaled to be initially uniform, mimicking conditions in a transient facility where the flow goes from zero to peak velocity in a short space of time.

Results from transient measurements are shown in Fig. 18. These results are for the aluminium test piece with a peak Mach number of 0.88 and 1 mm of insulation. Three temperature histories are shown: chord-wise profiles from the laminar half of the test piece in Fig. 18a, span-wise at 25 % chord in Fig. 18b and the development of \(\varDelta T_\text {lam-turb}\) at 25 % chord in Fig. 18c. The span-wise profiles in Fig. 18b demonstrate the effect described in Sect. 2.2. The initially uniform surface is cooled faster on the turbulent side, resulting in an IR visualisation that shows laminar regions at higher temperatures. After a few seconds the turbulent region approaches its equilibrium temperature, however as the laminar side has a lower recovery temperature it continues to cool. Temperatures eventually level out, giving an SNR of close to zero until the laminar region reaches its equilibrium point. Figure 18c compares this temporal development to a theoretical variation of \(\varDelta T_\text {lam-turb}\) with \(Bi^2\). The Biot number is squared to compare Fourier numbers, which is proportional to time divided by thickness squared. It can be seen that, as hypothesised in Sect. 2.2, the transient change in \(\varDelta T_\text {lam-turb}\) is equivalent to increasing Biot number up until the transient temperatures settle in to their steady-state value. This analogy demonstrates that increasing the insulation on a surface, and therefore increasing Biot number, results in a surface that responds faster to temperature changes.

Fig. 18
figure 18

Transient changes in temperature

Full size image

The chord-wise profiles in Fig. 18a demonstrate the impact of transient changes on a more realistic transitional temperature profile. In this case the effects of heat transfer coefficient, recovery factor and Mach number are coupled. Close to the leading edge the Mach number is highest and the boundary layer is laminar and thin, resulting in a high heat transfer coefficient and low recovery temperature. Beyond 45 % chord the Mach number is lowest and the boundary layer is thickened and fully turbulent, resulting in high heat transfer coefficients and high recovery temperatures. In between is a region of laminar and transitional boundary layer with high Mach numbers, resulting in relatively low heat transfer coefficients and recovery temperatures. This difference along the chord results in a slight dip forming between 10 % and 30 % chord as the test piece cools. It is not until several seconds have passed that the transitional temperature profile emerges. Such behaviour is highly problematic in a short duration facility. Avoiding this thermal regime by designing for high Biot numbers allows the surface to react quickly to the flow and reflect the recovery temperature differences.

A major benefit of IR in high-speed flows is its ability to visualise shock–boundary layer interaction (SBLI). The drop in Mach number through a shock results in a sharp increase in recovery temperature. In a turbulent SBLI the sudden thickening of the boundary layer due to the adverse pressure gradient at the shock tends to decrease the heat transfer coefficient, with a pronounced dip at the shock and an increase to an equilibrium level down-stream. In a laminar SBLI a \(\lambda\) shock structure is common where a separation is formed by the front leg that transitions and results in a non-equilibrium turbulent boundary layer down-stream. Details of the effect of boundary layer state in SBLIs are given by Davidson and Babinsky (2018). These changes in recovery temperature and heat transfer coefficient can be analysed with the 1D model in the same way as transition, and similar thermal design features benefit the visualisation of SBLI.

Fig. 19
figure 19

IR visualisation of shock–boundary layer interaction at \(M_\text {peak}=1.11\) with laminar (top) and turbulent (bottom) pre-shock–boundary layer states

Full size image
Fig. 20
figure 20

IR visualisation of shock–boundary layer interaction with different pre-shock boundary layer states and Mach numbers. The top half of each pair is turbulent pre-shock, the bottom is laminar

Full size image

Figure 19 shows IR visualisations of SBLI on the polycarbonate test piece. Unlike in the previous results where half of the test piece is tripped, these visualisations have the same boundary layer state across the full span. The difference between laminar and turbulent interactions can be seen clearly in the surface temperature profiles. The turbulent side shows a narrow peak in temperature at the shock that quickly relaxes to an equilibrium temperature that is higher than pre-shock. At this particular Mach number the laminar SBLI shows a different shock structure. Two distinct temperature peaks appear, followed by a sharp drop and rise in surface temperature. Without detailed measurements it is difficult to make conclusive statements about this structure, which may be the \(\lambda\) structure typical of laminar SBLIs, however the near-sonic Mach number and curved surface also suggest that the double shock structure found by Ackeret et al. (1947). A sweep of Mach number shown in Fig. 20 shows how the shock position and structure varies with Mach number. The laminar double shock can be seen at \(M_\text {peak} = 1.11\) and \(M_\text {peak} = 1.26\), but not at \(M_\text {peak} = 1.21\). As with the low-speed examples in Fig. 12, this is data that would require hours or days of instrumentation and testing with other methods, but with IR measurements can be taken in minutes to generate a full picture of the flow over the test piece.

4.3 Case study

The high-speed validation study demonstrates how to avoid potential failure modes of a passive IR visualisation from steady-state and transient thermal effects. The utility of IR for visualising both transition and SBLI has been shown in a controlled experiment. This part of the paper presents a second case study on the use of IR for fast diagnosis of an unknown boundary layer state in high-speed testing.

The application in this example is an engine nacelle being studied in a transient blow-down transonic wind tunnel at the University of Cambridge. Details of the study, rig and experimental procedure are given by Sabnis et al. (2023). In off-design conditions the stagnation point on the nacelle moves inside the intake, resulting in strong flow acceleration around the lip. At an inlet Mach number of 0.65, flow accelerates to Mach 1.4 on the outer part of the nacelle before the supersonic patch is terminated by a normal shock. The resulting SBLI can cause flow separation which has the potential for adverse interactions with the airframe.

Fig. 21
figure 21

Effect of surface roughness on the boundary layer state into the shock–boundary layer interaction on the nacelle rig

Full size image

As in the low-speed case study, the problem with sub-scale testing is a mismatch in Reynolds number. The experiment runs at a Reynolds number relative to the nacelle lip thickness of 1.2 × 106 while the full-scale nacelle operates at 3.7 × 106. This means that, where the SBLI is fully turbulent at full-scale, in experiments the SBLI might be laminar or transitional resulting in down-stream boundary layer development that does not reflect the full-scale behaviour. Initial investigations with Schlieren imaging, oil flow visualisation and pressure-sensitive paint proved inconclusive for determining boundary layer state. The full-field, non-intrusive nature of IR visualisation makes it well suited to such a problem. The nacelle is 3D printed as a shell of low conductivity polymer, putting it at a high Biot number that results in a fast surface response during transient tunnel runs and allows for clear visualisation of recovery temperature.

The FLIR SC7300LW set to an integration time of 320 \(\upmu\)s and a frame rate of 200 Hz is used for IR visualisation. Previous work with IR in the blow-down tunnel by Coschignano et al. (2019) meant that a suitable IR window and camera mount is available, allowing for camera set-up in less than an hour. The FLIR A615 was also tested and found to be sensitive enough for visualisation in the experiment. The A615 has double the resolution of the SC7300LW, however the A615’s low frame rate and difficulty focusing using the available optics make the SC7300LW the preferred camera here. IR thermograms are processed with a high-pass filter to remove span-wise non-uniformities that arise from the experimental set-up.

The as-printed nacelle has a roughness height Reynolds number relative to inlet conditions of approximately 400. Three tests are run to determine the effect of this roughness on the boundary layer state into the shock: one using the unpolished nacelle, one after polishing to a roughness height Reynolds number of approximately 50 and one with black paint applied to the polished surface for oil flow visualisation. IR visualisations of the transonic flow around the nacelle lip for each test are shown in Fig. 21 and reveal the effect of surface roughness on the SBLI. The smooth case shows a structure characteristic of a laminar SBLI with a temperature spike at the shock followed by a low-temperature region that recovers to an equilibrium turbulent boundary layer down-stream. The rough case shows a turbulent SBLI with a sharp temperature rise at the shock and no significant drop in temperature down-stream. In between these two is the painted case. The IR visualisation shows a mix of laminar and turbulent flow into the shock. Higher temperature regions show turbulent wedges, particularly around mid-span where there is a line of surface pressure tappings. This visualisation is particularly useful in identifying the laminar and turbulent SBLIs in the other two cases as the two regimes can be compared side-by-side. The mix of laminar and turbulent flow is caused by asperities in the paint producing turbulent streaks in the boundary layer around the lip. These observations are consistent with the effects seen by Coschignano et al. (2019) in their study of a similar transonic lip.

Fig. 22
figure 22

Transient changes to the visualisation of turbulent wedges on the nacelle

Full size image

The sharp change in boundary layer state and Mach number at a shock means that transient effects do not tend to result in an equalising of surface temperature between the two regimes as shown in Fig. 18. Problems, however, can arise in the transitional boundary layer found on the painted test piece. The mix of laminar and turbulent flow at the same Mach number means differences in heat transfer coefficient and recovery factor can hide the turbulent wedges that form. This is shown in Fig. 22 where three IR visualisations are shown from different points in a run. The high-speed flow around the lip tends to cool the surface as the inlet stagnation temperature is close to ambient. After 1 s the high heat transfer coefficient in the turbulent wedges has cooled the surface faster, making the wedges appear darker in IR compared to the lighter laminar region. As the run progresses the wedges approach their equilibrium temperature while the laminar region continues to cool. After 5 s the turbulent wedges up-stream of the shock appear to fade away as the temperatures equalise. The effect of the wedges on the SBLI can still be seen from the high-temperature streaks at the shock, however it would not be obvious what is causing these streaks from this visualisation alone. Towards the end of the run, which lasts for 20 s, the surface temperatures approach equilibrium and the turbulent wedges are at their higher recovery temperature compared to the cooler laminar boundary layer around them.

5 Conclusions

Infrared thermography is a fast, simple and non-intrusive method for visualising boundary layer behaviour in experiments. Methods for improving the signal-to-noise ratio of IR visualisations in low and high-speed flows have been investigated in this paper. A 1D heat transfer model has demonstrated that when an active heat flux is imposed on a low-speed flow there is an optimum Biot number, corresponding to an optimum level of insulation for a given flow, that maximises the SNR between regions with different heat transfer coefficients such as laminar-turbulent transition. The 1D model also demonstrates that in a high-speed flow, where recovery temperature differences allow for visualisation with only passive effects, there is an interplay between heat transfer and recovery temperature which results in SNR dropping to zero at some Biot number. Avoiding this region is critical to ensure high-quality visualisations.

Experimental work has validated the 1D modelling in both flow regimes. In low-speed flows the optimum Biot number that maximises SNR is shown to exist. SNR drops off sharply at low Biot numbers but remains high for Biot numbers greater than the optimal value. The heat flux needed for visualisation is shown to be non-intrusive with no change in transition location over a range of Reynolds numbers. In high-speed flows the interplay between heat transfer and recovery temperature is seen, with low Biot numbers resulting in laminar regions of the flow taking a higher surface temperature despite their lower recovery temperature. This interplay is also demonstrated in transient measurements where the SNR varies through a run. The thermal design of experiments in both regimes must be considered in order to maximise visualisation quality.

Two case studies are presented that demonstrate the utility of well-conditioned IR measurements in testing scenarios where uncertainty in boundary layer state hinders progress. An LSB on a low-speed distributed propulsor aerofoil and an SBLI on a transonic nacelle are visualised. In both cases IR is shown to be advantageous compared to other visualisation methods as it is non-intrusive and capable of giving a full-field visualisation in a short space of time.