1 Introduction

Shock wave boundary-layer interactions (SBLIs) are ubiquitous in most practical transonic and supersonic flows. The most obvious example occurs on the surface of transonic aircraft wings. In particular, during cruise conditions, the low pressure region on the suction side of the wing is terminated by a normal shock, which impinges on the boundary layer (B-L) at the wall.

In recent times, pressing environmental concerns are leading the charge towards new aerodynamic design guidelines to improve overall efficiency and reduce CO\(_2\) emissions (Anon 2011). Owing to their reduced skin friction, laminar boundary layers are a desirable way to achieve tangible drag reduction benefits over external aerodynamic surfaces. However, the consequences of an interaction between a shock wave and a laminar boundary layer are somewhat unclear as literature is rather scarce and has historically focussed on the more commonly observed turbulent counterpart (Atkin and Squire 1992; Délery 1985; Gadd 1962). Nonetheless, laminar boundary layers are generally more prone to separation even for weak shocks, which is of particular concern for most practical applications.

In literature, for a laminar SBLI, both free interaction theory, developed by Chapman et al (1958), and findings by Stewartson (1951), suggest that the pressure rise across a normal shock required to separate a laminar boundary layer is considerably smaller than in the turbulent case. These analytical findings are supported by early experimental investigations of a transonic bump flow by Ackeret et al (1947). In particular, for a weak normal shock impinging on a laminar boundary layer they observed an interaction topology similar to separated turbulent cases at higher Mach numbers. However, the observed spatial extent of the interaction was considerably larger for laminar interactions: the \(\lambda \) structure, which characterises separated normal (transonic) SBLIs, originated at a greater upstream distance. A similar flow topology, defined by very thin, elongated separation and a large interaction length, was reported by Liepmann (1946). These early studies, however, lacked a detailed characterisation of the downstream recovery of the boundary layer. More recent investigations by Davidson and Babinsky (2018) of a flat plate transonic SBLI addressed this. Somewhat surprisingly, they found the laminar separation to have little effect on the recovery of the boundary-layer downstream. In particular, the boundary-layer thickness and integral parameters downstream of the laminar SBLI showed no significant difference compared to a fully turbulent counterpart, achieved using tripping mechanisms. This behaviour is attributed to the incredibly small pressure rise required to separate the laminar flow. The resulting oblique wave corresponds to minimal flow deflection, which in turns yields a very thin separation bubble, as depicted schematically in Fig. 1. Before reaching the shock, the boundary-layer transitions to turbulence, and is now capable of withstanding the large adverse pressure gradients associated with the shock. It is noted that they could not resolve the velocity profile of the upstream boundary layer and its transition (Davidson and Babinsky 2018).

Fig. 1
figure 1

Laminar SBLI mechanism proposed by Davidson and Babinsky (2018)

Full size image

Recent investigations (Diop et al. 2019; Giepman et al. 2018) of supersonic interactions on flat plates also found transition to occur via thin regions of separated flow.

With the exception of the seminal work by Ackeret et al. (1947), the vast majority of the literature herein reported involved flows over flat surfaces in the absence of pressure gradients other than those imposed by the shock wave. However, this is not the case in many practical application such as engine inlets and on transonic wings, where the shock impinges on a curved surface and significant adverse pressure gradients downstream of the interaction are common. The current study addresses this by investigating the effect of varying the boundary layer state ahead of a normal shock located above a curved surface. To assert the state of incoming boundary layer, non invasive infra-red thermography is employed. A particular focus of this study is the effect of \(\text {Re}\) on the SBLI topology and on the subsequent recovery of the boundary layer; in particular, the B-L state downstream of the interaction is assessed using a combination of infra-red and high resolution Laser Doppler Anemometry (LDA). To achieve the intended \(\text {Re}\) range, two set-ups are employed. These are defined by the same geometry but at different scales. In particular the lower end of the Reynolds number range is covered using a 55%-scaled model.

2 Experimental configuration

2.1 Blow-down wind tunnel and working sections

Fig. 2
figure 2

Blow-down wind tunnel assembly depicting the settling chamber on the left and the two working sections used herein. Flow is exhausted via a variable area second throat to allow control of the entry Mach number

Full size image

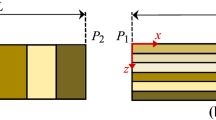
The experiments were performed in a transonic blow-down wind-tunnel. The assembly is schematically depicted in Fig. 2. The wind-tunnel is powered by two 50 kW compressors, which charge 24 large air receivers. The flow is then fed from these receivers into the settling chamber, where it is passed through a number of flow straighteners and turbulence grids before a 18:1 contraction. The entry Mach number is varied by adjusting the area of the second throat, where the flow is choked by means of an aerofoil (see RHS of Fig. 2).

Reynolds number is defined using an approximate measure of the B-L growing length x. The latter is the length between the model leading edge and the inviscid shock location (this measure is preferred to the ’true’ growing length as the stagnation point varies slightly across the range investigated). To achieve the Reynolds number range reported in Table 1:

  • the total pressure is varied;

  • two working sections of different sizes are used.

In the current configuration, \(P_0\) can be varied from an upper limit of 273 kPa down to 156 kPa.

Both working sections are depicted in Fig. 2. These are characterised by an aerofoil-like model, which divides the working section in two channels, bounded by curved solid walls. For the current investigation, the chord line is at an angle of \(\alpha =23^{\circ }\) from the horizontal. This first working section (originally designed to investigate transonic inlet flow) covers the range \(0.80\times 10^6\le \text {Re}_x\le 1.09\times 10^6\). The second working section, on the other hand, is a scaled version of the original one designed to replicate the same flow-field. The scale factor is 0.55, allowing investigation of \(0.44\times 10^6\le \text {Re}_x\le 0.77\times 10^6\).

The free-stream Mach number at the entry plane (as labelled in Fig. 2) is M\(_\infty =0.435\).

While progressively reducing the Reynolds number from the highest possible value \(\text {Re}_x=1.09\times 10^6\), which defines the experiment baseline, the entry Mach number, the shock position and strength are kept constant. More generally, the boundary layer growing length x and the pressure distribution is kept constant. The shock wave is held in the same location across the range tested using a plug to change the shock position in the lower channel as highlighted in Fig. 2. The latter allows a fine control (\(\varDelta \dot{m_l}<0.1\%\dot{m}\)) of the mass flow discharged via the lower passage and consequently of the position of the stagnation point and of the shock wave on the upper surface. The operating conditions that result in the flow-field herein described, and the Reynolds number range, are summarised in Table 1.

Table 1 Inflow conditions for the reference scenario
Full size table

2.2 Interaction surface definition

Fig. 3
figure 3

Geometry definition of the model area of interest, growing length x indicated in red. Coordinate s is defined as arc length along the surface

Full size image

A depiction of the model is given in Fig. 3. The front part of the model is designed using a modified super ellipse profile as used by Lin et al (1992) and Schrader et al (2010), amongst many, for flat plate boundary layers investigations. Mathematically, a modified super ellipse is defined as:

$$\begin{aligned} \left( \frac{x-a}{a}\right) ^m+\left( \frac{y}{b}\right) ^n=1 \end{aligned}$$
(1)

with

$$\begin{aligned} m{(x)}=2+\left( \frac{x}{a}\right) ^2, \end{aligned}$$
(2)

where a and b are the major and minor axis of the ellipse, respectively, controlling the position and the size of the ellipse co-vertex. Figure 3 depicts the coordinate system (originating at the model leading edge) and illustrates how the parameters defined in Eq. 1 relate to the model geometry. The current profile is defined by an aspect ratio \(\text {AR}=a/b=2.75\) and a value of \(n=2\). The boundary layer growing length x, defined earlier as the distance between the leading edge and the shock wave, is highlighted in red in Fig. 3.

This type of ellipse results in a continuous reduction in curvature from the leading edge to the model thickest point. Downstream of this, the geometry was tailored to provide a continuous diffusion up to the measurement point indicated in Fig. 3. At the reference incidence of \(\alpha =23^{\circ }\), the maximum divergence of the stream-tube ahead of this measurement plane, as a result of the combined diffuser-upper wall geometry, is \(\approx -1.1^{\circ }\). Downstream of the measurement plane, a second degree polynomial is used to define a generic geometry up to the trailing edge.

The surface of the model is painted with matt black paint, which result in a mean roughness height \(R_a\approx 1.6\ \upmu \)m for the full-scale model and \(R_a\approx 1.2\ \upmu \)m for the reduced scale one.

2.3 Experimental methods and uncertainties

Table 2 Summary of experimental uncertainties
Full size table

A Schlieren technique is used to visualize the flow-field. The images were captured at a rate of 6400 fps. The camera resolution is 1024 \(\times \) 1024 pixels and a horizontal knife edge is used.

Surface pressure measurements are taken in the centre-span using tappings. These are connected to a differential pressure transducer via tubing. The cavity is approximately 0.5 mm in diameter, which according to Meier (1977) can result in an over-prediction of static pressure by ~ 0.5–1.0%. A number of these pressure readings are used to calibrate pressure sensitive paint (PSP). According to Gregory et al (2007), a minimum of five different known pressure values are usually sufficient to minimise error. In the current investigation, the maximum deviation between the paint and surface tap values is found to be \(\le \) 2%.

Flow velocities in the tunnel centre-span are measured using a two component Laser Doppler Anemometry (LDA) system. This is used in a forward scatter configuration. The ellipsoidal working volume has a maximum diameter of 130 \( \upmu \) m. Paraffin particles, with a diameter of approximately 0.5\(\upmu \)m (Colliss 2014), are used to seed the flow. The laser emitting head and receiving optics are mounted on a three-axis traverse. The typical measurement accuracy, as stated by the manufacturer, is ± 0.1% of \(U_\text {max}\) (\(\sim \) 580 m/s) (Shakal and Troolin 2013). In addition the emitting head is oriented at an angle \(\eta \) = 8.5\(^{\circ }\) from the horizontal. A component of the span-wise velocity, w, therefore, affects the measurement of vertical velocity component. On the symmetry plane, where measurement are taken, w is expected to be at least one order of magnitude lower than v. As a consequence of this and of the small angle, the error in v is expected to be only 1%. The stream-wise velocity component u is unaffected by \(\eta \). The other common source of uncertainty is related to velocity bias. Here, this error is accounted for using the residence time weighting as suggested by Buchhave et al (1978).

Velocity measurements are used to estimate the incompressible boundary layer integral properties. These are preferred to their compressible counterpart as the latter are a strong function of Mach number, and thus unsuitable as a universal comparison measure. Estimating \(\delta ^*_i\) and \(\theta _i\) relies on integrating the velocity profile from the wall to the boundary layer edge. However, the measurement probe is of finite size and measuring any closer than 0.2 mm from the wall is infeasible. Furthermore, numerically integrating over discrete data points can yield significant error. To address these shortcomings, an analytical boundary layer profile is fitted to the data points before integration.

For this purpose, two models are used: the first was developed by Sun and Childs (1973) and the second by Musker (1979). The former builds on the classical linear combination of the law of the wall and Coles’ wake function (Coles 1956) and is valid down to \(y^+\approx 100\). For the buffer and viscous layers, the relationship proposed by Musker (1979) is used to obtain a complete solution for \(0\le y \le \delta \). The incompressible integral parameters are then calculated by simple numerical integration. A comprehensive investigation of the validity of this method has been performed by Titchener et al (2015). The main sources of errors were found to be the resolution of discrete data points and misalignment of the wall position. In particular, a minimum of twenty discrete measurements inside the boundary layer is required to yield an error \(\le 5\%\). This condition holds for a wide range of shape factors and is generally satisfied in this investigation.

Wall offset was found to cause a significant error in integral parameters (Titchener et al. 2015). A small misalignment of \(\varDelta y/\delta \) of the order of 0.01 yields an error exceeding 5%. For the thinnest boundary layer in this study, measured at the downstream location and defined by a thickness \(\delta \approx 2.6\) mm, the wall location is accurate within \(\varDelta y/\delta \le 0.007\). This places the outer error boundary to \(\epsilon \le 3\%\).

Total temperature is measured using two K-type thermocouples installed in the centre of the settling chamber. The accuracy of the thermocouples has been estimated, using a Fluke 5609 platinum resistance thermometer (PRT) probe rated at \(\pm\, 0.012\) K, to be \(\pm\, 0.2\) K.

The infra-red camera used to determine recovery temperature over the model is a liquid nitrogen cooled FLIR SC7300 with an integration time of 160 micro seconds and frame rate of 200 fps. The window used is manufactured from Zinc Sulphide (multi-spectral grade). The paint, camera and window system were calibrated in-situ using a copper block embedded with the aforementioned PRT. The copper block was chilled to below ambient and allowed to warm up slowly during a period of approximately 2 h to encompass the range of temperatures seen on the surface during a typical run. The emissivity of the paint was measured by comparison against a virtual black body in a copper block with the same thermometer. The background irradiation was modelled as that of a black body emitting at the ambient temperature as measured using the plenum thermocouples. The maximum difference between the temperature measured using the camera and the PRT is \(\pm \, 0.5\) K. Wall temperature from IR is used to estimate the recovery factor r. This is defined as:

$$\begin{aligned} r=\frac{ {T}_\text {aw}-{T}_\text {e}}{{T}_{0 \text {e}}-{T}_\text {e}} \approx f(Pr), \end{aligned}$$
(3)

Where T\(_\text {e}\) is the free-stream temperature at the measurement point (measured using isentropic relations); T\(_{0 \text {e}}\) the total temperature and, assuming an adiabatic wall, T\(_\text {aw}\) is the temperature at the wall as measured using the IR camera. Given the short run time of approximately 20 s, the adiabatic wall assumption does not strictly hold; however, for the sole purpose of obtaining an estimate of the recovery factor (which approaches a plateau during the run), this is deemed acceptable. The Prandtl number is taken as \(\text {Pr}=\) 0.71 (White 2006).

Experimental errors are summarised in Table 2.

3 Baseline: \(\text {Re}_x=1.09\times 10^6\)

Fig. 4
figure 4

a Schlieren photograph of the flow field; b surface pressure along the lip, from PSP; c surface pressure distribution averaged across the central 30% of the model width, from PSP. Centre-span tap values superimposed. \(\text {Re}_x=1.09\times 10^6\)

Full size image

Figure 4a shows a Schlieren image of the flow-field for the conditions summarised in Table 1. Surface pressure measurements are depicted in Fig. 4b, c.

The flow stagnates on the outer surfaceFootnote 1 of the model and is accelerated to supersonic speed around the leading edge. The resulting supersonic region corresponds to the brighter area visible on the left side of the Schlieren image and to the low pressure peak observed in Fig. 4b, c. This pocket of supersonic flow is terminated by a normal shock-wave, visible as a dark line in the Schlieren photograph. Ahead of the pressure rise associated with the shock wave, located at a stream-wise location (along the model surface from the leading edge) s/\(x\approx 0.9\), some degree of isentropic compression is observed. Downstream of the shock, the pressure gradients are adverse as the flow diffuses and the boundary layer can be seen to grow along the surface. The substantial pressure jump (see Fig. 4c) is generally expected to result in flow separation regardless of the boundary layer health and nature (Babinsky and Harvey 2011). Looking more closely at the interaction region, a bifurcation of the shock-foot into a \(\lambda \) structure, symptomatic of shock-induced separation, could not be observed. This would suggest, that the separation is likely too small to be resolved by the Schlieren technique. However, the presence of flow separation at this \(\text {Re}\) was confirmed by surface oil flow visualisation in a previous study (Coschignano et al. 2019).

Eleven wall-normal velocity profile measurements in the interaction region are used to characterise the SBLI. The resulting Mach number contours are shown in Fig. 5. Due to the small thickness of the boundary layer upstream of the normal shock, just three discrete velocity measurement could be obtained within the incoming boundary layer. Determining the velocity profile has, therefore, not been possible and only an estimate of its thickness immediately upstream of the interaction, \(\delta _1\), could be obtained; this is used to scale spatial coordinates in Fig 5. The shock foot smearing onset coincides with a thickening of the boundary layer at approximately 3\(\delta _{{1}}\) upstream of the inviscid M\(\approx \)1.4 shock location. This upstream influence exceeds the generally accepted value for an attached turbulent SBLI, which corroborates the assumption that there is a small amount of flow separation. Negative velocities were not measured, however, as LDA could not resolve the region \(y\le 0.2\delta _{{1}}\).

Fig. 5
figure 5

a Schlieren detail; b Mach number contours. \(\text {Re}_x=1.09\times 10^6\)

Full size image
Fig. 6
figure 6

a Surface temperature T, normalised by total temperature \(T^{0}\), obtained by IR at time t = 0.66 (total run time \(t_{\mathrm{t}}\approx \) 20 s); b Absolute surface temperature development during the wind-tunnel operation at the highlighted locations. Total temperature in the settling chamber shown in black; c Recovery factor at the highlighted locations. \(\text {Re}_x\,=\,1.09\times 10^6\)

Full size image

The state of the incoming boundary layer is yet to be determined.

Looking at the Schlieren image and at the small interaction length, it would appear that the shock wave interacts with a turbulent boundary layer. In fact, the flow appears qualitatively similar to other turbulent SBLIs reported in literature (Ackeret et al. 1947; Babinsky and Harvey 2011; Davidson and Babinsky 2018; Délery 1985; Gadd 1962). To assert the upstream boundary layer state, infra-red thermography is employed. Processed IR images and temperature (T) traces at selected points along the lip surface are shown in Fig. 6. Upstream of the shock, the most obvious features are two large turbulent wedges, characterised by a higher temperature compared to the surroundings. The presence of these wedges vastly facilitates the interpretation of the results and suggests that the boundary layer is, in fact, predominantly laminar across the model span. Furthermore, Fig. 6c demonstrates good agreement between the measured recovery factor and the theoretical laminar value \(r\) \(\ =\text {Pr}^{1/2}\), found in classical textbooks for flat plates in the absence of stream-wise pressure gradients (Schlichting 1979; White 2006). This appears to hold despite the presence of a curved surface and consequent pressure gradients. The recovery factor inside the wedge is measured to be \(r\) \( \ \approx 0.86\), somewhat in between the expected laminar (\(\text {Pr}^{1/2}\)) and turbulent (\(\text {Pr}^{1/3}\)) values.

Progressing downstream, shortly ahead of the normal shock (labelled in Fig. 6a), the surface temperature displays a progressive increase across the whole span. This is associated with the transition onset of the laminar boundary layer to a turbulent state. It is unclear whether this transition occurs via conventional mechanisms (e.g., T–S waves), or as a result of the shear layer separating due to the shock pressure rise, as suggested by Davidson and Babinsky (2018). The latter mechanism is generally accompanied by the presence of an oblique compression wave upstream of the main SBLI. This is not seen in the Schlieren image. As a result, it appears that the boundary layer transition upstream of the shock is independent from the SBLI and it is more likely to be due to the onset of conventional instabilities coinciding with the temperature rise reported.

Regardless of the transition mechanism, based on the absence of an oblique shock in the Schlieren, and the surface temperature increase ahead of the shock (observed in Fig. 6), the boundary layer is believed to be mostly turbulent by the time it reaches the M\(\approx \)1.4 normal shock-wave. Progressing further downstream, into the diffusing section of the model, the high surface temperature suggests the boundary layer to be fully turbulent. The measured recovery factor near the edge of the field of view (marked in magenta) agrees reasonably well with turbulent flat plate theoretical value, as shown in Fig. 6c. Velocity measurements presented in Fig. 9, taken \(\approx 70\delta _{{1}}\) downstream of the interactionFootnote 2, indicate a boundary layer shape factor \(H\) \(_i\)=1.327. This is typical for a healthy turbulent boundary layer; the other B–L parameters at this location are listed in Table 3, normalised by the growing length x.

Table 3 Boundary layer parameters \(\sim 70\delta _1\) downstream of the normal shock; \(\text {Re}_x=1.09\times 10^6\)
Full size table

4 Decreasing Reynolds number

Fig. 7
figure 7

Schlieren snapshots of the interaction region as the Reynolds number is decreased. Images 4–8 were obtained in the scaled facility. Note prominent front leg ahead of the main normal shock in bottom right corner

Full size image
Fig. 8
figure 8

Surface temperature, normalised by total temperature, obtained by IR, for decreasing Reynolds number

Full size image

Schlieren photographs of the flow-field as Reynolds number is progressively decreased from its baseline value are shown in Fig. 7. Infra-red thermography images are given in Fig. 8. For \(\text {Re}_x\le 0.77\times 10^6\), the reduced scale facility is used.

Looking at Schlieren and IR images, over the full-scale model the interaction remains qualitatively similar. As \(\text {Re}\) is progressively decreased to a value of \(0.80\times 10^6\), the large turbulent wedges disappear and the flow appears entirely laminar across the span. The onset of temperature rise does not appear to be affected by \(\text {Re}\).

As the \(\text {Re}\) is marginally decreased to \(\text {Re}=0.77\times 10^6\), using the smaller facility, Schlieren photographs show a broadly similar interaction topology. Interestingly, infra-red images show the flow to be predominantly turbulent as the span is dominated by ‘hot’ wedges. Despite the small change in \(\text {Re}\), the change not only is significant, but also counter-intuitive as turbulent flow appears to have increased with decreasing \(\text {Re}\). This could be a consequence of both models being painted using the same paint, thus the relative effect of surface roughness is expected to be greater for the much thinner boundary layer developing over the small scale rig.

Reducing the stagnation pressure further, similarly to what is observed over the full-scale model, the upstream flow becomes progressively less turbulent as wedges disappear. Looking at the Schlieren images, as total pressure is reduced, a distinct oblique wave becomes progressively more visible upstream of the shock, which is most evident at the lowest Reynolds number \(\text {Re}=0.44\times 10^6\). This interaction topology, characterised by a shallow front shock leg and a large interaction length, is qualitatively similar to the laminar SBLIs reported by Ackeret et al. (1947) and Davidson and Babinsky (2018).

At this low end of the \(\text {Re}\) range, infra-red thermography confirms the shock wave to be interacting with a laminar boundary layer across the entire span. The sharp rise in surface temperature in Fig. 8, indicating flow transition, is consistent with the stream-wise origin of the oblique wave just described. Although separation could not be confirmed with either measurement technique, this wave is thought to be caused by the boundary-layer separation. In particular, the angle of the oblique wave, measured from the Schlieren image (and thus prone to large uncertainty), is around \(\beta _s\approx 48^{\circ }\), which corresponds to a flow deflection \(\theta _s\approx 4^{\circ }\) and a pressure ratio of around 1.2, vastly exceeding that found sufficient to separate a laminar boundary layer (Ackeret et al. 1947; Stewartson 1951). Thus, the presence and angle of the wave, alongside the corresponding sharp temperature increase, would indicate separation to be present. However, as this cannot be proven with certainty, some degree of caution is necessary. Furthermore, it is not possible to assert with certainty whether the potentially separated free-shear layer reattaches before the shock; however, the high-temperature region immediately upstream of the shock might be symptomatic of large turbulence production typical of reattachment (Délery 1985).

Reynolds number has not been found to have any significant influence on the onset of temperature rise as no meaningful variation across the \(\text {Re}\) range is observed.

Fig. 9
figure 9

a Location of measurement plane; b surface pressure to ensure shock position across experiments and facilities; c wall normal velocity measurements, normalised by x; d normalised boundary layer fitted velocity profiles

Full size image
Fig. 10
figure 10

Variation of incompressible boundary layer parameters \(\approx 70\delta _0\) downstream of the normal shock with \(\text {Re}\). \(\blacktriangle \): full-scale facility; \(\blacktriangledown \): small scale facility; predominantly turbulent inflow BL. \(\beta \) is the scaling factor

Full size image

Boundary layer measurements at \(\approx 70\delta _{{1}}\) are shown in Fig. 9c, while Fig. 9d shows the fitted velocity profiles normalised by the boundary layer edge velocity and the respective thickness \(\delta \). Figure 10, on the other hand, shows the variation of incompressible boundary layer parameters relative to the reference high \(\text {Re}\) case discussed in Sect. 3. At a glance, across the whole Reynolds number range considered, regardless of the state of the inflow boundary layer, this appears to recover to a healthy turbulent equilibrium one. In particular, as inferred from Fig. 10, all boundary layers have shape factor values \(H\)\(_i\le 1.38\) in all cases decreasing as \(\text {Re}\) increases. An analogous trend is observed for the thickness \(\delta \) and the two integral parameters \(\theta _i\) and \(\delta ^*_i\), also presented in logarithmic plots in Fig. 10 normalised by the baseline values. Two main conclusion can be drawn:

  • Reynolds number does have a measurable effect on the boundary layer parameters with an overall healthier and thinner boundary layer observed at higher \(\text {Re}\). This is somewhat expected. Downstream of the shock, the recovery of the boundary layer following the SBLI is hindered by the presence of a continuous adverse pressure gradient. Therefore, it appears logical that a progressively more inertia-dominated flow (high \(\text {Re}\)), will result in a better recovery to a healthy velocity profile and its growth would be less than at lower Reynolds number.

  • In Fig. 10, those flow fields characterised by predominantly turbulent inflow ahead of the normal shock are highlighted in magenta. It is noted, despite some scatter, how these points lie on the same general trend-line alongside those other flow-fields defined by predominately or entirely laminar boundary layer ahead of the SBLI. Therefore, it would appear that the boundary layer nature upstream of a normal shock does not have any major effect on the subsequent downstream recovery to a healthy velocity profile. Most importantly, somewhat contrary to the belief that laminar separations would be large enough to influence the global flow-field, it was shown how, in those instances, where a laminar separation is believed to be occurring, this is very small. Across this separated region, the flow is expected to transition ahead of the main normal shock, and capable of withstanding the large shock pressure gradient without detrimental consequences downstream and resulting in a very benign interaction. Despite the presence of a curved surface and, more importantly, the adverse effect of additional pressure gradients, this conclusion is consistent to the findings by Davidson and Babinsky (2018) for a flat plate. As a result, it would appear that a laminar B-L interacting with a normal shock wave might not be so detrimental even in most practical applications, where some degree of curvature is present. In particular, given the relatively high \(\text {Re}\) experienced in applications such as transonic aircraft wings, the boundary layer transitions very quickly and the SBLI can accommodate a transitional flow without any large-scale penalty. A more pronounced effect could be expected for \(\text {Re}\) values so small that the boundary layer remains laminar across the first shock-induced separation and ahead of the main shock. Achieving these low \(\text {Re}\) values is beyond the capabilities of the Cambridge facility.

5 Conclusions

The effect of decreasing Reynolds number on the boundary layer development downstream of a normal shock impinging on a curved surface has been investigated. Across the \(\text {Re}\) range considered in this study (\(0.44\times 10^6\le \text {Re}_x\le 1.09\times 10^6\)), the nature of the inflow boundary layer upstream of the SBLI was found to vary considerably. At the reference \(\text {Re}_x=1.09\times 10^6\), infra-red images reveal the flow upstream of the normal shock to be predominantly laminar. Transition to turbulence appears to occur a short distance upstream of the M = 1.4 normal shock. The transition mechanism is still unclear but believed to be due to conventional instabilities. Nonetheless, it appears that the flow is turbulent in nature across the whole span immediately ahead of the normal shock impingement point. Overall, no large scale separation or unsteady shock motion is seen and the boundary layer quickly recovers its healthy velocity profile despite the presence of adverse pressure gradients downstream of the shock. As the Reynolds number is decreased the inflow boundary layer becomes progressively more laminar. Decreasing \(\text {Re}\) further in the small scale facility, a fully turbulent inflow is observed at first. This is currently attributed to relatively rougher surface of the small scale model. As \(\text {Re}\) is decreased further, the boundary layer becomes fully laminar across the entire span. Downstream of the normal shock, the boundary layer recovers a healthy velocity profile across the whole range considered. As \(\text {Re}\) is decreased, the downstream boundary layer is progressively thicker. This is to be expected as the BL growth rate in adverse pressure gradients is an inverse function of \(\text {Re}\). Interestingly, both turbulent and laminar inflow cases lie on the same trend-line, suggesting that the nature of the boundary layer upstream of the shock has no influence on the SBLI severity and on the subsequent recovery of the boundary layer. In conclusion, a normal shock impinging on a laminar boundary layer above a curved surface, and in the presence of adverse pressure gradients, does not appear to result in more pronounced detrimental effects compared to its fully turbulent counterpart. However, as inertial forces become progressively more dominant the boundary layer recovery downstream of the normal shock wave-boundary layer interaction is noticeably thinner and recovers a fuller velocity profile.