Accuracy and error analysis of optical liquid film thickness measurement with total internal reflection method (TIRM)

Abstract

The characterization of thin liquid films is relevant to many engineering applications, ranging from oil and chemical industry to refrigeration systems, to cooling of light water nuclear reactors. The total internal reflection method (TIRM) is an optical method known for decades for being able to non-intrusively measure film thickness of a wide range of fluids flowing over a transparent wall, but systematic studies on the accuracy of the method are still missing. In this work, TIRM is presented and all the main potential error sources related to the application of such measurement are thoroughly characterized. The analysis includes the potential impact of variation of the refractive index on the measured thickness, the extension of the experimental calibration range to a broader set of measurable thicknesses and the effect of the inhomogeneity of the film free surface on the measured thickness. This latter aspect was never investigated in detail before because of the inherent complexity of the involved physical phenomena, but an in-house developed ray-tracing simulation allows new insights into the problem. Overall, the present paper redefines the utilization limitations and the accuracy of TIRM.

1 Introduction

1.1 Complexity of thin films

The characterization of thin liquid films over a wall is central in many applications, ranging from oil and chemical industry to refrigeration systems and cooling of light water nuclear reactors. Thin water films are often created in so-called annular flow regime (Cuadros et al. 2019) which is a two-phase flow in which a gaseous phase occupies the center of a pipe while a liquid phase flows along the walls in a thin annular film. In this flow regime, a strong shear force typically characterizes the phases interface, so that the film is always turbulent. Such films, as well as others, such as free-falling films, exhibit a wavy interface (Belt et al. 2010), which leads to the need of accurate local measurements to be able to resolve the liquid film thickness. Some of the most common methods for film thickness measurement include: conductance-based methods in which single probes or arrays of multiple electrodes are used to measure conductivity of the liquid film (Rivera et al. 2022; Ju et al. 2018; Damsohn and Prasser 2009); brightness-based methods that measure fluorescence intensity of liquid films in which a dye is dissolved (Cherdantsev et al. 2023; Fan et al. 2020); interferometry-based methods that take advantage of the optical phase variation of light when reflected from surfaces at a different distance (Conroy and Armstrong 2005) with both highly coherent monochromatic light sources (Nozhat 1997) or with broad spectrum ‘white’ sources (Ferraro et al. 2021; Berto et al. 2022; Sullivan 1972); high speed photography with strong contrast back illumination (Pan et al. 2015); radiological methods to detect the film interface with X-rays (Robers et al. 2021) or gamma-rays (Berto et al. 2019). All these techniques are non-intrusive, which is necessary in the case of thin films. However, another less common non-intrusive technique presents the additional advantage of being fast and relatively easy to implement, namely the method based on total internal reflection originally described by Hurlburt and Newell (1996) and Shedd and Newell (1998) and recently employed again by Pautsch and Shedd (2006), Rodríguez and Shedd (2004) and Baptistella et al. (2023). In this paper, we will refer to this method as TIRM (total internal reflection method). Previous works have treated the uncertainty of TIRM referring to specific experimental conditions or considering simplifying assumptions which mostly work for averaged quantities (Moreira et al. 2020; Yu, et al. 1996). On the contrary, the aim of this research is to better define the boundaries of this technique in real conditions and regardless of the experimental apparatus.

1.2 Description of the TIRM for liquid film thickness measurement

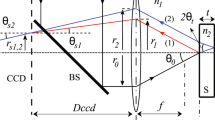
As a reference, the TIRM for liquid film thickness measurement is thoroughly explained in Moreira et al. (2023) and Shedd and Newell (1998). The TIRM is an optical method based on Snell’s Law of optics and total internal reflection. In TIRM, a laser beam is sent through a transparent wall on which a liquid film is present. The liquid film will also have an interface with a gas phase. Looking at Fig. 1, the lower surface of the transparent wall is covered with a light diffuser; consequently, light beams will hit the wall–liquid interface and then the liquid–gas interface at all possible angles. All the beams hitting one of these interfaces at the corresponding critical angle or bigger angles will be reflected back onto the diffuser layer. The most important rays for TIRM are the former ones which intersect the film free surface precisely at the liquid–gas critical angle. These beams will create a circular pattern on the diffusive surface of the transparent wall from which information on the film thickness can be extracted by taking images of the circles. In particular, referring to Fig. 1, the radius r of the circular pattern when there is a water film is always given by the sum of the ‘dry radius’ when there is no liquid ${r}_{dry}$ and an additional contribution from the ‘liquid radius’ ${r}_{l}$ which is due to the presence of the liquid film. One can easily derive all the necessary mathematical relations for measuring the liquid film thickness LFT as in Eq. (1) where $\theta_{{{\text{lg}}}} ,\theta_{{{\text{gw}}}}$ and $\theta_{{{\text{lw}}}}$, respectively, are the critical angles at the liquid–gas, gas–wall and liquid–wall interfaces. Overall, the liquid film thickness is then measured as a spatial average over a ring with diameter r. It must be noted that $r_{{{\text{dry}}}}$ can be computed analytically knowing the wall thickness t, using Eq. (2), but it is recommended to directly measure it, since manufacturing inaccuracies could otherwise affect the results. In this work, it is always going to be measured, not computed.

Fig. 1

Scheme of light rays trajectories when using TIRM (transmitted rays are dotted, reflected rays are dashed/solid lines depending on the interface and angle of the reflection)

A total internal reflection will also occur at the transparent wall–liquid interface. In this case, the reflected circular pattern will always be present with the same size ${r}_{2}$ regardless of the thickness of the liquid film because it only depends on the thickness of the wall and on the refractive indexes of the liquid and the wall, as in Eq. (3). Once again, in practical applications, it is recommended to measure this radius rather than compute it.

$${\text{LFT}} = 0.5\left( {r - r_{{{\text{dry}}}} } \right)/\tan \theta_{{{\text{lg}}}}$$

(1)

$$r_{{{\text{dry}}}} = 2\tan \left( {\theta_{{{\text{gw}}}} } \right)t$$

(2)

$$r_{2} = 2\tan (\theta_{{{\text{lw}}}} )t$$

(3)

This second circle can disturb the measurements, as pointed out in Moreira et al. (2023), because it may overlap with the circular pattern that we want to measure thus becoming hard to distinguish. However, this ‘double circle issue’ may be avoided either by selecting a wall such that the second circle size is always going to be very different than the diameter of the expected circular pattern of interest (which can be derived from the expected liquid film thickness) or by applying some additional post-processing to the images of interest, as explained in Sect. 2.2.

1.3 Previous attempts of uncertainty quantification of the TIRM

As highlighted in Shedd and Newell (1998), in the presence of tilted free surfaces the reflections from the film might happen in unexpected directions, thus affecting the accuracy of TIRM. The same is true in the case of other interfacial disturbances such as waves. This also applies to very thin films, since old and recent studies (Hewitt et al. 1990; Xue et al. 2022) have shown that thin films below 1 mm can also be strongly disturbed under certain conditions. In Alekseenko et al. (2009), it has been shown that applying laser-induced fluorescence to an annular flow it is possible to visualize detailed wave structures along a plane, and that even with films in the range of 0.1 mm thickness it is possible to obtain waves which have a slope of several degrees with a width of a few millimeters. This means that the uncertainty in applying TIRM might arise from both the slope of the film surface and the presence of small interfacial disturbances. In line with the latest considerations, in Moreira et al. (2020) and Moreira et al. (2023), the authors acknowledge potential uncertainties deriving from the not flat interface of the film, and they account for these uncertainties by estimating the slope of the film as if it was flat or with two-dimensional schemes, which always results in a negligible uncertainty with respect to experimental accuracy. A first attempt to estimate the accuracy of the measuring principle of TIRM fully taking the irregular shape of the film into account was performed by Yu et al. (1996) and later by de Oliveira et al. (2006). However, in both the works, the investigated film surfaces are either flat or characterized by one-dimensional disturbances. Overall, these studies show the awareness of the need to assess the accuracy of the method with wavy and irregular film surfaces, but they also show the difficulty of performing such assessment for films that are strongly irregular and three dimensional by nature. Ideally, fewer approximations on the shape of the irregularity of the film surface should be employed when assessing the limits of the technique for film thickness measurement.

2 Methods—Analysis of error sources in TIRM

In this section, it is explained how a more consistent and systematic characterization of the uncertainties of TIRM can be performed. In particular, this is done by detailing the different error sources that can be encountered and how they can be quantified. The error sources that will be discussed in the upcoming subsections are: refractive index, circle detection, camera resolution and inhomogeneity of the film interface.

2.1 Refractive index

The refractive index is needed for the computation of the critical angle, which appears in Eq. (1) for the determination of the LFT. Since the refractive index comes into play through a tangent operator, the effect of an error on the refractive index on the LFT is nonlinear. The error in the measured film thickness ${err}_{thick}$ due to an error in the refractive index ${err}_{n}$ on the liquid phase can be easily derived from Eq. (1) as follows

$$err_{{{\text{thick}}}} = \tan \left( {\arcsin \left( {\frac{{n_{{{\text{gas}}}} }}{{n_{{{\text{liquid}}}} }}} \right)} \right)/\tan \left( {\arcsin \left( {\frac{{n_{{{\text{gas}}}} }}{{err_{n} \cdot n_{{{\text{liquid}}}} }}} \right)} \right)$$

(4)

Based on Eq. (4), it is clear that the smaller the refractive index ${n}_{liquid}$, the larger the impact of an error in the refractive index on the measured film thickness. Moreover, an error of a few percent decimal points in the refractive index of the medium of interest can cause a much greater percent error in the computed thickness. It is important to point out that in the case of non-adiabatic experiments, changes in the refractive index might occur due to temperature changes (Kasarova et al. 2010). In Bashkatov and Genina (2003), the refractive index of water is measured at different temperatures and they show that, for a fixed light wavelength, the refractive index can change more than 1% between 0 °C and 100 °C, which could cause an $err_{{{\text{thick}}}}$ of 2.4% if not accounted for in TIRM experiments with air as a gas.

Inaccuracy can also concern the refractive index of the gaseous phase (which can be both a gas and a vapor). With the same reasoning followed for the refractive index in the liquid phase, one can derive that the larger the refractive index of the gas/vapor, the larger an error on its estimation will impact the measured film thickness. However, in the case of diluted gas and vapors, the refractive index is often very close to unity and exhibits small variations with temperature, so that its influence on TIRM is limited. As an example, using the data provided by Schiebener et al. (1990) for saturated steam, it can be seen that for a temperature range between 0 and 100 °C, the change in the refractive index of steam would be less than 0.02%, thus implying an $err_{{{\text{thick}}}}$ of less than 0.05%. Similar results can be obtained for the case of air, taking as a reference the data provided by Shaheen et al. (2023). Nonetheless, depending on the specific conditions, desired accuracy and type of the gaseous phase, one might have to be careful also with the gas-phase refractive index, as from Eq. (4).

2.2 Circle detection

TIRM requires some initial calibration, failing to perform this step might affect the precision of all the subsequent measurements by adding a bias. The current section describes the steps that need to be undertaken to limit this bias and therefore improve the TIRM accuracy. TIRM should always be calibrated versus a known film thickness. This is first because the total reflection does not take place sharply at the critical angle but within a range of ± 1° around it Hurlburt and Newell (1996). Moreover, the characteristics of the laser beam could also affect the sharpness of the circular pattern edges. This means that failing to calibrate the image detection algorithm might affect the accuracy of the estimation of the pattern radius. In the next two subsections, the calibration and the circle detection procedure are described.

2.2.1 Calibration

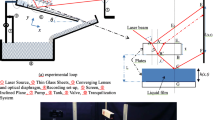
Calibration of the technique is performed on stagnant water films against a conductance probe realized with a metallic needle. The probe is mounted on a TOSAG micrometer screw with 0.01 mm precision, which is fixed at the bottom of a 5-mm-thick glass tank where the water film is placed. The needle can be moved up and down with the screw; when the needle touches the film, the current position is recorded. Below the tank, aligned with the conductance probe, a TIRM setup is installed, to measure the film thickness at the same time and in the same location as the conductance probe. The TIRM setup consists of a CNI MGL-FN-532-1W green laser module with a 0.1 mm diameter at 100 mm focal distance and a Nikon D80 camera with an optical setup consisting of a SIGMA teleconverter TC-2001 and a SIGMA DC 18–125 objective allowing 0.02 mm/pixel resolution. It should be noted that the laser was always operated at minimum power by supplying a current of 1.2 mA. A schematic of the calibration setup is illustrated in Fig. 2.

Fig. 2

Scheme of the calibration setup

The camera is activated with an infrared remote control and about 35 images are captured for each tested film thickness. The bottom of the tank is sprayed with a thin layer of paint to make the circular pattern visible. Prior to that, camera calibration is performed by fixing an optical target to the bottom of the tank. It should be noted that the presence of the conductance probe above the laser spot in the tank caused some unavoidable reflections, which are registered by the camera and have to be systematically cropped out from the images before the image processing. The calibration is performed using water in solution with soap to reduce the surface tension and help obtain flatter films, limiting the effects of the meniscus. The addition of soap is also affecting the refractive index of water, which is then measured as 1.3329 using a SPER SCIENTIFIC Digital Refractometer model 300036 with an accuracy up to the fourth decimal point. For air, a refractive index of 1 is assumed. In Fig. 3a-b, the results of the calibration are presented for films ranging between 0.1 and 8 mm, which includes data points where the ‘double circle issue’ appears. This area is highlighted with a red band in Fig. 3a. More details on the aspect of the double circle are provided in Sect. 2.2.2. The error bar on the probe measurements is taken as the maximum offset between several measurements of the same film, while the error bar on the camera measurements is given by the standard deviation of the thickness measured from each individual image.

Fig. 3

a Calibration results with conductance probe thickness versus thickness measured with TIRM for water films thicker than 1.2 mm; b calibration results with conductance probe thickness versus thickness measured with TIRM for water films thinner than 1.2 mm

Referring to Fig. 3a, the agreement of the two film thickness measuring methods is pretty good, with all the data points falling within a 2% uncertainty band within the measurement uncertainty. As expected, uncertainty does not depend on the film thickness. Notably, although the algorithm for extracting the radii is described in the following subparagraph, it is clear already that also in the double circle cases, which are more challenging, the deviation never goes beyond 2%. A similar outcome is found for the calibration with thinner films up to 1.2 mm, as shown in Fig. 3b. It is noticeable that, within the measurement uncertainty, the mismatch is slightly larger for the thinner films, up to 4%. For thinner films, there might be an inherent inaccuracy in the experimental setting due to the fact that for thin films the deforming effect of surface tension cannot be fully eliminated. In any case, the uncertainty is found to be fully acceptable and the calibration can be considered successful.

2.2.2 Circle detection algorithm

The proposed steps for the circles detection are illustrated in Fig.4. At first the regions in the image that are outside of the area of interest have to be masked out. Then, images are normalized and binarized according to prescribed brightness thresholds and a median filtering is applied to reduce noise. Eventually, edges of the circular pattern are detected from the changes in the derivative of the brightness along straight lines in each image. Once the edges of the circular patterns have all been detected, a circle is fit through the points identified as belonging to the circle, as shown in Fig. 5c, similarly to Pautsch and Shedd (2006). This procedure is effective when double circle patterns do not appear, as pointed out in Moreira et al. (2023). In the case of double circle patterns a different post-processing is necessary. An image with the double circle should be saved in advance, and the radius of the double circle should be measured and saved. This is going to be a reference image. Then, whenever the detected radius in the analyzed images is close in size to the known radius of the second circle, the value of each pixel of the reference double circle image needs to be subtracted from the image of interest.

Fig. 4

Algorithm for circle detection

Fig. 5

Image with double circle issue (a); image with double circle being smaller than the circular pattern of interest (very thick film) (b); image with double circle issue after elimination of the double circle (c); blurred circular pattern from irregular film (visible laser spot) (d)

After subtraction of the reference image, resulting pixels with negative values can be offset to 0 to prevent potential algorithm errors, but overall the second circle can be easily distinguished from the first and eliminated from the images, leaving a clear image containing only the circular pattern of interest. In Fig. 5a-c (in this case the laser spot at the center of the image is hidden by the laser pointer which, as from Fig. 2, is on top of the camera), the result of the three post-processing steps is shown: a) an image with the double circle issue; b) an image that can be subtracted from the first one to eliminate the double circle; and c) the final subtracted image, in which the double circle has been removed and the circle of interest is detected. In the case in which long measurements are performed, it is possible to eliminate the double circle by subtracting from each image the mean of all the images. This is because all images will contain the same double circle, while the circle of interest will be subject to change according to changes in the film thickness. This second approach was tested and delivered comparable results (within 1% resulting thickness) to the first approach described earlier. However, this second approach is harder to generalize because the results will depend on the amount of images with double circle patterns compared to the total number of available images. The aforementioned result in which no difference larger than 1% was found refers to a dataset in which 25% of the images presented the double circle, which proves that at least in principle the method can work. In general, since the size of the double circle depends on the thickness of the used transparent wall, one could always tune the thickness of the wall to the intended application (to the thickness of the expected film) so that the double circle is not an issue. Moreover, there can be many applications in which the double circle simply never appears, whenever the measured film is much thinner than the used wall.

2.3 Resolution of the camera

The resolution of the camera is an important factor in determining the accuracy of the TIRM since the variations in the size of the circular pattern to be detected can be very small, depending on the film thickness and material properties. Using Eq. (1), the ratio between the measured film thickness and the corresponding circle radius provides an indication of the sensitivity required in the detection of radii variations in order to capture a corresponding film thickness variation. Results obtained using Eq. (1) for different liquid refractive indexes are reported in Table 1, where air is assumed as the gas. The larger the refractive index, the more a small variation in the circle radius will affect the magnitude of the corresponding film thickness. The table can help determine the required camera resolution in terms of pixel/mm depending on the medium of interest and on the film thickness variations of interest.

Table 1 Ratios of film thickness over corresponding circle size for several liquid refractive indexes and air as gas

2.4 Non-homogeneity of the liquid film interface

The least studied source of uncertainty in TIRM is given by the topology of the film interface, mostly because it is the one uncertainty which is harder to control. In the case of the still water basin used for the calibration, the boundaries of the circle were perfectly aligned in a circular shape. However, this is not necessarily always the case: in Fig. 5d, an example of circle from a film with disturbed (wavy) surface from an air–water annular flow is shown. (In this case, the laser spot is visible at the center of the image.) In these situations distorted circular patterns are going to be recorded by the camera.

In the case of distorted circular patterns, looking for the best approximation of a circle will still deliver a reasonable estimate of the mean film thickness along the measured circumference, as pointed out in Moreira et al. (2020). However, it can be hard to precisely define how far from the true mean thickness the approximation is, since the real topology of the surface is not known. In this paper, we propose to estimate the uncertainty of the surface topology using a ray-tracing algorithm that can replicate the physical phenomena of the total internal reflection and refraction for the thickness measurements of thin films. The algorithm is discussed in detail in the next section.

3 Description of ray-tracing algorithm for TIRM simulation

Ray-tracing is a technique aiming at creating realistic images by calculating the path of light rays through regions characterized by varying geometrical and optical properties. It is based on the assumption that light rays are transmitted along a straight line in a homogeneous medium and can be transmitted, reflected or refracted at every interface between different media. Ray-tracing of light has many applications ranging from biomedicine (Wei et al. 2014) to material surface characterization (Bergström et al. 2007), but most relevant for the present study, it has recently been proposed in fluid measurements. As an example, ray-tracing has been used for correcting (Mushin Can et al. 2020), calibrating (Mitzushima 2021) or post-processing fluid measurements (Luthman et al. 2019).

For the interested reader, a full overview of the technique and how to implement it in coding is provided in Glassner (1989), in which chapters 3 and 4 are especially relevant to what implemented in this article. The flowchart of the ray-tracing algorithm developed for the assessment of TIRM accuracy is presented in Fig. 6. First of all, the geometrical boundaries of the problem are defined with three interfaces: two parallel planes, bottom of the wall and wall–film interface, respectively, and the three-dimensional film–gas interface. The computational domain is shown in Fig. 7, where a laser beam is also exemplary plotted. The film–gas interface can be obtained from a user-defined mathematical function or it can be extracted from available measurements, if any. The three-dimensional surface of the liquid film is fit by scaling it on an x–y mesh grid with the desired spatial resolution. (Cubic interpolation is employed.) From the center of the coordinate system, several light beams are emitted and tracked in all directions. Iterations are performed over several equally spaced polar and azimuthal angles (α and i, respectively) ranging from 0° to 90° because of symmetry (occasionally the polar angle α is spanned from 0° to 180° in those cases when symmetry is not ensured with a span up to 90°. When this occurs, it will be specified). Each beam is analytically intersected with the wall–film interface plane where it is refracted according to Snell’s law. As also highlighted by Luthman et al. (2019), Snell’s law is a reasonable approximation in the case of distinct media with different refraction index, as in this case. Each of these refracted beams is then intersected with the initially fitted surface representing the film–gas interface. This intersection is found numerically with a tolerance in the order of ${10}^{-3}$ mm. At the intersection point, the normal vector to the fitted surface is computed using MATLAB surfnorm function. This normal vector is used to compute the angle with the incoming beam. The computed angle is compared to the critical angle $\theta_{{{\text{lg}}}}$ to assess if it is reflected or not. Reflected beams keep being tracked according to a new direction given by a rotation matrix, otherwise they are discarded, since physically they would be transmitted through the film and therefore would not be useful for TIRM. The tracked beams are then refracted again at the wall–film interface until they intersect the bottom of the wall plane. Eventually, full reconstructed trajectories of the tracked beams are obtained and the final pattern that they generate on the bottom of the wall-base plane surface is visualized. The radius of such pattern is then correlated with the film thickness. The algorithm validation and convergence analysis are discussed in the following subsections.

Fig. 6

Computational flowchart of the ray-tracing algorithm

Fig. 7

Computational domain of the ray-tracing simulation in the case of a water film on a glass wall with the film surface boundary in blue, the wall–film interface in green and the bottom of the wall in black. A laser beam is also plotted as an example with the corresponding polar and azimuthal angles α and i

3.1 Validation of the TIRM ray-tracing algorithm

The ray-tracing algorithm has been successfully validated on flat horizontal films (0° inclination at the interface), by comparing its results to the reference analytical solution given by Eq. (1). In the case of flat films, no random reflections of rays can occur which might result in blurring of the circular pattern edges. Therefore, the ray-tracing algorithm will produce circular patterns with very sharp edges, making the radius determination straightforward. For the validation, a glass wall is considered with a water film and air as a gas, with corresponding refractive indexes of 1.49, 1.3329 and 1, respectively. A total number of 213′500 rays is tracked with an angular resolution of 0.25 mrad. In the case of flat films the grid resolution is not particularly relevant since all the boundaries are planes and interpolation over a coarse or fine grid does not play a big role when dealing with linear functions. Several cases are used for the validation, with wall thicknesses ranging between 1 and 5 mm and film thicknesses ranging between 0.25 and 2 mm. Overall, it is found that the radius computed with the in-house ray-tracing code matches the analytical solution with a maximum error well below 1%. For illustration purposes, in Fig. 8, the circular pattern obtained with the ray-tracing algorithm is compared with the analytical solution for a case characterized by a 5-mm-thick glass wall and 1-mm-thick water film, showing a perfect match.

Fig. 8

Comparison of tracked rays from the ray-tracing code to the analytical circle for a 5-mm glass wall with a 1-mm water film in contact with air

4 Use of ray-tracing algorithm to assess TIRM uncertainty

Once validated, the ray-tracing algorithm has then been applied also in case of not flat horizontal surfaces of known thickness in order to assess the uncertainty of TIRM under different conditions. In particular, in the next subsections, two cases are investigated: the case of flat but not horizontal films and the case of not flat wavy films. The two cases are separated since different difficulties characterize the two situations. The same media (glass, water and air) introduced for the validation are also going to be used in the analysis of this section.

4.1 Flat tilted films

With the presence of flat tilted surfaces, the circular patterns are going to be distorted. However, as for the case of flat horizontal films, the absence of curvature on the film interface will produce circular patterns with very sharp edges, making the radius determination straightforward and not requiring a convergence study. For the same reason, only the rays that are reflected first need to be tracked, which helps save computational time.

4.1.1 Tested dataset

This set of simulations is performed on a domain with 0 < α < 180° in order to capture the full asymmetry of the reflected pattern. The radius which is used for the thickness measurement is computed as the average of all the local radii, just as would be done with standard TIRM. The reference thickness used for comparison is instead given by the average film thickness, corresponding to the thickness at the very center of the domain, on the same vertical where the light beams are emitted. The following conditions are tested:

• Wall thickness: 1,3 and 5 mm

• Film thickness: 0.25, 0.5, 0.75, 1 and 2 mm

• Inclination of the film surface: 1°, 3°, 5°, 7° and 10°

The same number of rays and angular resolution of the validation on flat horizontal films are used.

4.1.2 Results

The deviation between the mean film thickness obtained with the ray-tracing algorithm and the reference solution is plotted in Fig. 9 as a function of the film inclination angle, for several different film thicknesses, with a 5-mm-thick wall (Fig. 9a) and a 1-mm-thick wall (Fig. 9b). For thicker walls fewer film inclination angles can be tested because of the geometrical characteristics of the problem.

Fig. 9

Percent deviation in measured from mean thickness from the distorted circular pattern deriving from a tilted water film in air versus the tilting angle of the film for several film thicknesses and a wall thickness of 5 mm (a) and 1 mm (b)

It is found that the accuracy of the film thickness estimated based on the detection of distorted circles is higher when the wall is thinner. This result is to be expected considering that the distorted reflected beams can travel longer if the wall is thicker, thus increasing the effect of the distortion on the final circular pattern. So, for example, in the case of air and water, for a 1-mm film using a 5-mm-thick wall, the deviation of measured from mean thickness can increase up to 5.7% if the slope of the film is 9°, while this would be less than 4% for a 1 mm wall. However, as previously mentioned for the case of air–water annular flows, even if steep slopes of several degrees are not impossible in thin film flows, in most cases no slopes higher than 5° will be encountered (Paras and Karabelas 1991). Under these more frequent conditions with slopes below 5°, the deviation from true mean thickness would never exceed 3%.

In addition, as shown in Fig. 10, the error associated with the measurement of the film thickness increases much faster for thin films than it does for thicker films. For example, the error on a 2-mm-thick film (Fig. 10b) barely doubles when the wall thickness is varied from 1 to 5 mm, even with a 10° tilted film. For a 0.5-mm-thick film instead (Fig. 10a), already with a tilting angle of 5°, changing the wall thickness from 1 to 5 mm will result in an error almost three times larger. Overall, with increasing wall thickness, thinner films are going to be proportionally more impacted by systematic distortion of the film interface.

Fig. 10

Percent deviation in measured from mean thickness from the distorted circular pattern deriving from a tilted water film in air versus the tilting angle of the film for several wall thicknesses and a film thickness of 0.5 mm (a) and 2 mm (b)

Based on the obtained results, it can be concluded that when applying TIRM, the transparent wall of the test section should be as thin as possible in order to limit the errors deriving from distortions of the circular pattern of interest, especially if very thin films are to be measured. However, it has to be taken into account that thinner walls can potentially make the double circle issue more pronounced.

4.2 Wavy films

With wavy film interfaces the circular shape of interest is blurred and/or distorted. Specifically, since the edges of the circle are not going to be sharp anymore and since the film interface is not going to be a linear function anymore, a circle detection approach similar to the one introduced in Sect. 2.2 is needed in addition to a convergence analysis in terms of number of rays and grid resolution. In the next subsections, these latter aspects are discussed before presenting the tested datasets and the resulting analysis. Following the conclusions from Sect. 4.1.2, in all the next subsections, we will refer to a wall of 5 mm (the thicker tested and also a quite thick wall for any not pressurized application). In this way, all the next results can be interpreted as a conservative worst-case scenario.

4.2.1 Circle detection from ray-tracing with sensitivity analysis

In order to apply to the simulations the previously described circle detection procedure, some modifications to the algorithm are necessary. This is because the type of images obtained from simulations is strongly discretized (i.e., they are clouds of discrete points), so the brightness method based on spatial derivative used previously cannot be applied here. Instead, the PDF of the radii corresponding to every tracked beam is used as an equivalent for brightness. By detecting at which distance from the light source (i.e., at which radius) the majority of the beams land, thus causing a steep rise in the PDF, the true edge of the blurred circular pattern of interest can be identified. To identify the exact point at which the PDF rises significantly, the PDF is first smoothed with a mild Savitzky–Golay filter in order to eliminate high frequency variations. Then, the maximum peak of the distribution is located, as well as the base noise level corresponding to the mean value of the distribution for the smallest radii before the steep increase. Finally, the selection of the bin of interest in the PDF is done by picking the first radius to exceed a given percent value p of the prominence of the filtered distribution peak. An example of such PDF distribution next to the corresponding cloud of tracked points is shown in Fig. 11a-b.

Fig. 11

Example of probability density function of the radii distribution with identified radius of the circular pattern (a) and corresponding pattern with identified circle (b) for a film generating many random reflections leading to blurring of the final image

An empirically determined percentage of p = 12% is selected for the detection of the radius from the PDF for the measurement of film thickness. The identification of the correct bin of the PDF is of course very important, and the overall result is therefore depending on the p threshold. Nonetheless, the previously described procedure is found to be very robust, as confirmed by a sensitivity analysis performed on the choice of the parameter p. This sensitivity is tested for different number of rays and changing grid size for two different film topological configurations. Both correspond to artificially generated films obtained from a combination of sinusoidal functions given by the general Eq. (5). The parameters used for Eq. (5) are summarized in Table 2 and based on worst-case scenarios wave characteristics of real films from Grasso et al. (2023). The corresponding functions are plotted in Fig. 12, where it is visually clear how challenging these films can be for TIRM in terms of complexity of the interface.

$$z = b + A\cos \left( {k_{1} x} \right)\left[ {\cos \left( {k_{2} y} \right) + a\cos \left( {k_{3} y} \right)} \right]$$

(5)

Table 2 Parameters defining tested geometries of films for sensitivity analysis of ray-tracing simulations

Fig. 12

Top view plots of the functions of geometry #1 (a) and #2 (b) used for the sensitivity analysis

The advantage of using a combination of sinusoidal functions with relatively high frequency is in their short wavelength periodicity, which makes the results less dependent on the specific point where the rays intersect the film. This will contribute to the generality of the results. Moreover, in both these geometries, there is no flat horizontal surface, which is a more challenging condition for TIRM than what typically encountered in real cases, as it is known that real waves are normally separated by flatter flow regions (Kokomoor and Schubring 2014; Han et al. 2006). This implies that such artificial films generate many distortions as well as significant blur in the final circular pattern, providing more challenges to the ray-tracing algorithm than many real cases would. The idea here is to provide worst-case scenarios and, in this way, determine a upper boundary for the error in film thickness that is to be expected in real cases, for which less distortions and blur will exist.

Not surprisingly, given the steep slope of the PDF distribution, it is found that the estimated film thickness is quite insensitive to the threshold p for both tested geometries. In particular, a change in the value of p does not affect the resulting thickness for more than 2%, as far as the error in the estimation of the parameter is within ± 15% with respect to the chosen value of 12%, as shown in Fig. 13 for two exemplary cases. To note that an error of 2% is within the same range of uncertainty associated with the calibration method applied to real experiments.

Fig. 13

Effect of change of measured thickness with respect to change of p in the case of geometry #1 and #2, respectively, for the cases of 8000 and 8334 rays with 0.015 mm grid

4.2.2 Grid size and number of rays—convergence analysis

The convergence of the ray-tracing algorithm results with grid size and number of rays has been investigated. At this aim, the same geometries described in the previous section are used. The results of the convergence study are reported in Fig. 14 as a function of the grid size (a) for geometry #2 and as function of the number of rays (b) for both geometries. 120 cores are used to track the individual rays. It is found that convergence is obtained for grid sizes below 0.015 mm. Therefore, a grid size of 0.015 mm is adopted as a good compromise between computational cost and accuracy. With regard to the number of tracked rays (Fig. 14b), good convergence is found as long as the number of tracked rays is not below 1000 per core. 3500 rays per core is therefore selected adopting a substantial safety margin.

Fig. 14

a Measured film thickness versus grid size with 700 tracked rays per core using geometry #2; b measured film thickness versus number of tracked rays for both the tested geometries with a grid size of 0.015 mm

4.2.3 Tested dataset

The validated ray-tracing algorithm has been used to assess the accuracy of TIRM under both the cases of real and artificially generated films. Over 50 simulations are performed to explore the limits of the TIRM technique. Each test case required almost 20 h of computation on 120 parallel cores AMD EPYC 7742 (2.25 GHz), therefore, for the sake of time, not too many frames could be analyzed. Nonetheless, the authors acknowledge that the ray-tracing algorithm could probably be further optimized in terms of efficiency of the computation. Roughly half of the simulations are performed on artificial films generated from a combination of sinusoidal functions, as from Eq. (5), while the other half of the simulations are performed on real wavy film surfaces measured using a high-resolution conductivity film sensor applied to the investigation of falling water films (Grasso et al. 2023). The conductivity film sensor presented a spatial resolution of 2 mm, so the measured data are interpolated on a finer grid before applying the ray-tracing TIRM algorithm. Artificial sinusoidal waves are defined keeping in mind realistic values of wave parameters published in the literature for annular flows, such as wave steepness (Paras and Karabelas 1991), wave to base ratio (Kokomoor and Schubring 2014), roughness height and ratio of wave volume over total volume (Han et al. 2006). The wave volume is relevant because it correlates with the roughness of the film. Since the sinusoidal films obtained with Eq. (5) lack a proper wave spacing, an important parameter for assessment of film roughness needs to be adapted, namely the previously mentioned ratio of wave volume to total volume. The wave volume would normally be considered as the total volume of liquid below the wave, but without wave spacing this would imply that the ratio with the total volume is always going to be unitary. So the definition here is changed and the wave volume is only considered as the volume between the wave crest and the base film thickness. In Table 3, the ranges used for the parameters characterizing the tested films are listed. The overall tested dataset presents a wide range of film's characteristics.

Table 3 The minimum and maximum values of each of the parameters characterizing thin films in the tested dataset

In Fig. 15, the normalized covariance obtained using the reciprocal products of standard deviations of each film parameter is presented. This shows that although the tested dataset cannot be considered fully exhaustive and representative of any possible film, it has a broad variability and can be used as a reference benchmark for assessing the general limitations and accuracy of TIRM.

Fig. 15

Normalized covariance of all the parameters characterizing the tested films

4.2.4 Results

As could be expected, it is found that with TIRM one should always pay attention to sudden distortion of the light from the passing of local disturbances whose shape deeply affects the reflected rays. As an example, a sinusoidal film is designed on purpose to show a potential worst case scenario. Equation (5) with parameters: b = 0.5, A = 0.25, $k_{1}$ = 0.7, $k_{2}$ = 0.7, $k_{3}$= 0, a = 0 is used to generate the film. In this case, as it is clear from Fig. 16, the point of contact of the light rays with the film is happening along the tilted side of a sinusoidal surface (Fig. 16b), so that the reflected rays distort the reflected pattern (Fig. 16a) in this particular frame. In a normal data analysis, since the resulting pattern is completely off with respect to a circle (in this case it is closer to a square), this would require some additional processing to extract information on film thickness; otherwise, the result should be discarded.

Fig. 16

Pattern (a) and trajectory (b) of tracked rays in a TIRM simulation in the specific case of a strong distorted resulting pattern

Within the available dataset, among the artificially generated films, some films are designed with comparable characteristics. (Some films are kept the same, but the base thickness is varied, and in some other cases, wave spacing is kept the same while changing the other waves characteristics.) Some general trends could be observed, even if they are based on a small number of observations and should therefore be considered carefully. In particular that thinner films are more prone to deviations in measured from mean thickness deriving from distortions of circular patterns than thicker films with the same characteristics, which is shown in Fig. 17a. Moreover, while it is to be expected that films with bigger wave spacing will be measured more precisely, since they will be overall flatter, it was observed that steeper waves cause the deviations in measured from mean thickness to generally increase, probably because random scattered reflections will be more likely to happen, as shown in Fig. 17b for two sinusoidal films with similar characteristics. The deviation of measured from mean thickness for the whole simulated dataset is plotted versus mean thickness in Fig. 18, where a distinction is made between sinusoidal (red) and measured (blue) films. It is possible to see that while the mean film thickness is pretty homogeneously distributed for the measured films, there is a concentration of the sinusoidal films around 0.6 mm. This is the case because the author tried to artificially generate as many films as possible with similar characteristics in order to compare them and possibly infer some trends. However, given the limited number of simulations which was possible to perform, as mentioned, no strong trends could be found.

Fig. 17

Comparison of deviation of measured from mean thickness for some films with comparable characteristics. In (a) films with the same sinusoidal function but varying mean thickness, in (b) films with the same sinusoidal function but varying amplitude which implies different wave slope

Fig. 18

Deviation of measured from mean thickness for all the simulated films versus their mean thickness. In red are the artificial sinusoidal films and in blue are the measured ones

On the whole, the main conclusion from the several simulations is the assessment of the average effect of circle distortion on the measurement of mean film thickness of films exhibiting very different characteristics. In the case of the artificial sinusoidal films the resulting mean deviation in measured from mean thickness inside the circular pattern was found to be 1.22 ± 4.28% with a 95% confidence interval from t-score distribution using standard error, while in the case of real films it was found to be 8.92 ± 4.02%. Overall, a mean deviation in measured from mean thickness of 5.71 ± 3.08% was determined over a dataset of more than 50 ray-tracing simulations. When considering the thickness of the considered films, always below 1 mm, a 5.7% mean error seems a satisfying result, especially considering that it is in the same order of magnitude as the calibration uncertainty.

The most relevant conclusion is that at least within the variance expressed by the considered dataset, the main source of uncertainty for TIRM is not necessarily to be searched in the calibration or in the presence of an inclination in the film but also the presence of the interfacial disturbances cannot be neglected, which were rarely accounted for in previous studies. Before using TIRM, one should make sure what the conditions of the dataset are likely to be and assess the main source of uncertainty, for which this work could be a useful first reference.

5 Conclusions

In this study, TIRM has been investigated as an effective and practical method for experimental measurement of liquid film thickness, and its accuracy and limitations have been systematically characterized. All the main sources of error which might affect TIRM measurements are investigated in detail, namely inaccuracy in refractive index of the flowing medium, accuracy of circle pattern detection, camera resolution and inhomogeneity of the film free surface. Errors related to the assessment of the refractive index of the medium and to the resolution of the camera are determined analytically, and tools to assess the error on measured film thicknesses based on the specific test conditions are provided.

A circle detection algorithm has been developed and validated against film thickness measurements performed with a conductance probe. The algorithm proves to be rather effective in circle detection with all the data points for films thinner than 1.2 mm falling within a 4% uncertainty band and all the data points for thicker films falling within a 2% uncertainty band with respect to the conductance probe measurements. Moreover, the algorithm proves to also effectively work in the case in which ‘double circle issue’ occurs, thus extending the usability range of TIRM.

For the assessment of inaccuracies arising from the disturbed free surface of the measured films, for the first time, a ray-tracing algorithm is developed and validated to simulate TIRM in the cases of: flat tilted films, artificial films obtained from the combination of sinusoidal functions and real films extracted from a high-resolution conductivity film thickness sensor. The analysis shows that the effect of tilted water–air film surfaces on the measured thickness with TIRM results in mean film thickness errors of no more than 6% in the case of walls up to 5 mm thick and liquid films up to 2 mm thickness for the worst-case scenario of a film inclination of 10°. Overall, it is proven that deviations from the true mean caused by tilted films increase with thicker transparent walls and thinner films. Noteworthy, it can be highlighted that thicker walls will most likely eliminate the ‘double circle issue’ in an experiment but they will lead to an increase of the overall measurement uncertainty. Moreover, testing the effect of inhomogeneous film free surfaces on the measured thickness with TIRM on a diversified dataset of more than 50 films thinner than 1 mm, the mean deviation in measured from mean thickness was found to have a value of 5.71% with a 95% confidence interval of ± 3.08%. These findings imply that the main source of uncertainty of TIRM is not necessarily to be searched in the calibration procedure but potentially also in the inhomogeneity of the film free surface.

In future, the proposed ray-tracing simulations could be accelerated by running on GPUs rather than CPUs, thus enabling to run more test cases and develop better confidence intervals for the mean uncertainty of TIRM. Predictive error algorithms based on measured film characteristics could be deployed as well. Finally, since cylindrical pipes are common in the investigation of thin flowing films, ray-tracing simulations could be adapted to also run on cylindrical geometries. This would allow to assess the effect of image distortion from curved surfaces in case TIRM is applied to pipes.