Abstract
Studying turbulent heat transfer over rough surfaces is vital for enhancing heat transfer efficiency in various practical applications. This research presents an in-depth examination of the commissioning of a heated floor boundary layer wind tunnel facility, specifically focussing on addressing the uncertainties in measuring heat transfer over rough walls. Our findings show that minor variations in the slope of the inner-scaled mean temperature profile (\(\kappa _h\)) on a heated smooth wall have a marginal effect on the estimates of friction temperature and heat transfer coefficients across a range of friction Reynolds numbers (\({900 \lesssim \textrm{Re}_\tau \lesssim 3700}\)) when using the Clauser fit method. Direct heat transfer measurements using power metres validate this conclusion. Temperature measurements over a three-dimensional sinusoidal roughness indicate constant \(\kappa _h\) within uncertainty limits across the examined range \({2300 \lesssim \textrm{Re}_\tau \lesssim 10{,}400}\), contingent on prior knowledge of the roughness’s virtual origin. Nevertheless, measuring heat transfer coefficients and roughness functions entails large uncertainty due to challenges in estimating heat losses and applying the modified Clauser method. Recommendations for enhancing accuracy in heated rough wall measurements include direct measurement of wall shear stress and heat flux, selecting low emissivity heated plates and ensuring precise control of heated wall conditions. This work also emphasises the significance of conducting a comprehensive uncertainty analysis as a valuable tool for identifying and addressing any shortcomings in the measurement facility and equipment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Forced convective turbulent heat transfer over rough walls has been a topic of intense research interest for some time now, primarily due to its pertinence to practical applications such as gas turbines and heat exchangers (Kays et al. 2005; Chung et al. 2021). Roughness augments the heat transfer, but often at the expense of even greater increases in drag or pressure drop, and hence can negatively affect heat transfer efficiency. Currently these effects are poorly quantified. To address this issue, it is essential to develop appropriate facilities, measurement techniques and methodology to accurately predict turbulent heat transfer over rough walls.
The intricacy of heat transfer experiments is notably higher than that of momentum transfer experiments. This can be attributed to the inclusion of heated components and temperature controllers, as well as the difficulties associated with minimising and accurately measuring heat losses. As such, measurements of heat transfer are typically associated with a high level of uncertainty. The origins of this uncertainty may include but are not limited to, the difficulties in precisely setting the temperature differential between the wall and flow, accurately measuring the local surface temperature, quantifying and limiting (non-convective) heat loss through conduction and radiation and determining the wall heat flux.
In a majority of prior experiments, rough walls were heated through the utilisation of a boiling water chamber (e.g. Perry and Hoffmann 1976; Moretti and Kays 1965) or an electrical heater (e.g. Dipprey and Sabersky 1963; Jayatilleke 1966). The electrical heater could take the form of a resistance wire or coil that is embedded in a high thermal conductivity material or situated between silicone sheets or thermofoil layers (Lau et al. 1991b; Scibilia 2000; Chakroun and Quadri 2002). To avoid non-uniformity in the temperature distribution of the test surface, a layer of high thermal conductivity material, such as aluminium or copper, or thermal epoxy is often employed as a thermal buffer (Choi and Hamid 1991; Chakroun and Quadri 2002; Léon et al. 2020). The multi-layer construction between the heater and the test surface causes significant temperature variation and thermal lag. To mitigate this issue, direct temperature measurement of the test surface is essential. As flow disruptive measurement techniques, such as the direct placement of a temperature sensor on the surface, might not be desirable for some cases, passive temperature measurement techniques, such as thermal imaging or thermochromic liquid crystal paint, are often utilised (Hippensteele and Russell 1988; Tanda 2004; Adhikari et al. 2020). While feasible, employing methods such as thermal cameras for real-time monitoring of wall temperature in a wind tunnel can pose setup challenges, including the requirement for multiple high-speed thermal cameras, which are costly and complex to install while mitigating reflections. An alternative, simpler, and cost-effective approach involves installing a thermocouple between the heater and the surface, as demonstrated in studies such as Léon et al. (2020).
The quantification of non-convective heat loss from the heaters via conduction through the walls of the facility or via radiation from the surface has been a persistent source of uncertainty in heated floor experiments. The heat loss from a heated surface can be a substantial proportion of the measured signal, particularly at lower Reynolds numbers where the convective heat flux contributes a relatively minor portion. In most cases, conductive heat loss, computed using Fourier’s law, is mitigated by thermally insulating the sides and bottom of the heaters (Lau et al. 1991a). As a result, conductive heat loss is typically associated with less than 10% of the total power consumption (Lau et al. 1991a; Choi 1993). It should be noted that the accurate estimation of the proportion of the total power consumption due to conductive heat loss will depend on surface temperature and the freestream velocity. Given its minimal percentage, its contribution to the overall loss is commonly neglected (Blair and Werle 1980; Blair 1983; Hippensteele et al. 1987; Hippensteele and Russell 1988; Choi and Hamid 1991). Various methods have been utilised in the literature to predict radiative heat loss. For example, the radiative heat loss of heated rough walls is typically estimated using the Stefan–Boltzmann equation (Choi and Hamid 1991). Despite the widespread use of the Stefan–Boltzmann equation (e.g. Choi and Hamid 1991; Chakroun and Taylor 1993), its applicability is uncertain due to the geometry and orientation of the rough surfaces involved (Siegel 2001). Hippensteele et al. (1987) also estimated radiative heat loss by extrapolating the curve of heat transfer against flow speed to the zero flow condition. Alternatively, radiative heat transfer can be predicted experimentally by computing the difference in total heat transfer at a specific flow speed with and without heating the tunnel side and top walls to a temperature similar to the surface temperature, as discussed in Choi and Hamid (1991); Choi and Orchard (1997). This study will comprehensively examine and test methods for predicting convective heat transfer and heat losses (i.e. conductive and radiative) from a heated surface.
The convective heat flux is commonly assessed through three main methods in the literature. The direct method for measuring convective heat flux involves determining the electrical power input to the heating elements and subtracting the conductive and radiative heat loss (Hosni et al. 1991; Brójo et al. 1997). This approach is straightforward, yet its accuracy is contingent upon the estimation of heat loss, as previously discussed and also the accurate determination of power input. It is also contingent on an ability to accurately control heat flux or surface temperature to constant conditions. Convective heat flux can also be predicted through the streamwise gradient of the enthalpy thickness, as detailed by White and Majdalani (2006). This method necessitates measurements of the momentum and thermal boundary layer at various streamwise positions, making it inaccessible in certain flow facilities. This methodology involves not only the accurate determination of mean velocity and temperature but also requires the inclusion of streamwise gradients. These gradients require a sufficient resolution in the direction of flow. Additionally, this approach assumes a two-dimensional flow; and thus, the presence of any three-dimensional effects in the experimental setup could adversely affect the accuracy of measurements. The third method for measuring convective heat flux is through the friction velocity (\(U_\tau \)) and friction temperature (\(\Theta _\tau \)) obtained by fitting the velocity and temperature profiles with the logarithmic law of the wall (Hoffmann and Perry 1979). However, as recently highlighted by Alcántara-Ávila et al. (2021) and Pirozzoli et al. (2022), this method may not be a suitable approximation due to the variation of the logarithmic temperature law slope \(\kappa _h\) with Reynolds number. This study will measure and compare the convective heat flux using the three methods mentioned above.
Schematic showing the tunnel multi-layer floor construction, including the test plates, insulation and wooden frame. The location of the embedded thermocouples is shown with green marks. To provide visual access to the configuration of the test surfaces, a portion of the tunnel walls has been removed (indicated by the red dotted line). The insets show schematic samples of the smooth and rough tiles, and a zoomed view of the rough tile illustrating the fading of the roughness near the spanwise edges
The current paper provides a comprehensive overview of the commissioning of a heated floor tunnel facility, particularly addressing the sources of uncertainty discussed above. Section 2 introduces the heated floor facility and its temperature control system. Following this, Sect. 3 focuses on the measurement techniques and methodologies employed to ascertain heat losses, skin friction and heat transfer coefficients. The validation of the experiment is undertaken on a smooth heated wall in Sect. 4; while, Sect. 5 extends this validation to a three-dimensional sinusoidal roughness, which has previously been investigated through direct numerical simulations (DNS) by MacDonald et al. (2019).
2 Heated floor wind tunnel
The wind tunnel and heated wall are discussed in Sect. 2.1. The wall temperature control equipment and software are discussed in Sect. 2.2. Supplementary material is also included to discuss: Sect. S1 testing the temperature influence on the velocity field with dual-wire sensor, Sect. S2 manufacturing steps of three-dimensional sinusoidal roughness and Sect. S3 temperature control procedure and developed code.
2.1 Heated floor tunnel facility
The experimental apparatus employed in this study is an open-return boundary layer wind tunnel facility located in the Walter Basset Aerodynamics Laboratory at the University of Melbourne. The wind tunnel comprises of a settling chamber consisting of a honeycomb and five screens, followed by a three-dimensional contraction with an area ratio of 8.9:1. The working cross section dimensions are \({0.94\times 0.38}\) m2 in the spanwise (y-) and wall-normal (z-) directions, and the total working section length is 6.7 m in the streamwise (x-) direction, see Fig. 1. A strip of P40 grit sandpaper is installed on the bottom wall at the inlet of the working section to trip the boundary layers to the turbulent state. The upper wall of the working section has spanwise slots every \({x = 0.5}\) m, which allow measurement access for a spanwise/wall-normal traverse at different streamwise locations. Additionally, the upper wall is adjustable and has 12 static pressure taps to permit adjustment of the pressure gradient. For all experiments detailed here the condition is set to zero pressure gradient with \(C_p(x)\) within \(\pm 0.01\). The freestream velocity is obtained using a national physical laboratory (NPL) Pitot-static tube mounted to the tunnel’s sidewall. The tunnel is capable of operating at a maximum freestream velocity of \(U_\infty = 30.0\) m s\(^{-1}\) (Kevin 2018).
The floor of the working section allows for floor temperature adjustment and easy reconfiguration of the surface topography. As illustrated in Fig. 1, the test surface consists of eleven aluminium \(500\times 720\) mm2 (\(x\times y\)) main plates with a thickness of 6.35 mm, spanning a total streamwise fetch of 5.5 m of the test section from \(0 \lesssim x \lesssim 5.5\) m, where \(x=0\) is located at the downstream edge of the P40 trip. This investigation employs two primary sets of main plates, consisting of a smooth set and a rough set (with three-dimensional sinusoidal roughness), as shown in the insets of Fig. 1. The specifications and fabrication methodology for the sinusoidal roughness tiles are detailed in S2 of the supplementary documentation. The amplitude of the roughness on the spanwise edges of the plates is linearly blended to zero over a distance of \({\approx 20}\) mm (depicted in the inset of Fig. 1) to prevent abrupt variations in surface roughness that could potentially trigger the development of secondary flows. There are also eight aluminium side rails arranged symmetrically on either side of the tunnel. Underneath every aluminium main plate and side rail, there is a custom-made electrical pad heater matched in size to the aluminium (Holroyd Components Ltd with a maximum heat flux of 3.4 kW m\(^{-2}\)). The side rails are designed to be heated to the same temperature as the main plates to mitigate conductive heat loss from the main plates to the tunnel side walls. The conductive heat loss through the bottom of the tunnel is also minimised through the use of a 3 mm thick calcium–magnesium silicate thermal insulation sheet with thermal conductivity of \({K_{\textrm{in1}} = 0.23}\) W (mK)\(^{-1}\), and a 50 mm layer of polyisocyanurate foam thermal insulation (Bondor Insulated Panel) with \({K_{\textrm{in2}} = 0.20}\) W (mK)\(^{-1}\) between the pad heaters and the wooden frame of the tunnel. This multi-layer floor construction is depicted in Fig. 1. The conductive and radiative heat loss estimation is discussed in Sect. 4.2.
2.2 Temperature control system
Studies on heated walls are frequently conducted under conditions of either uniform heat flux at the wall (Antonia and Danh 1977; Taylor et al. 1989; Virgilio et al. 2020) or a constant wall temperature difference with the freestream (Hoffmann and Perry 1979; Subramanian and Antonia 1981; Taylor et al. 1989; Mayo et al. 2018). Our current experimental facility is designed to accommodate both conditions; however, we have chosen to conduct the measurements at a constant wall temperature difference with the freestream. This decision was guided by the desire to directly estimate the enhanced heat transfer associated with a rough wall in comparison with a smooth wall, both operating under identical flow conditions. Additionally, this approach eliminates the need for control of the freestream temperature, or laboratory temperature in our case which we lack accurate control of and which is crucial in the uniform heat flux method.
To operate at a constant wall temperature difference with the freestream, the temperature of the tunnel floor is continuously monitored through thermocouples embedded 2.5 mm beneath the aluminium surface. There are thirty type-E thermocouples (Omega 5TC-TT-36), two in each main plate and one in each side rail, as indicated by the green circle symbols in Fig. 1. All thermocouples are calibrated using an in-house water bath against a Traceable Scientific Thermistor (FSH15-077-7) with an accuracy of less than \(\pm 0.05\,^{\circ }\)C. Using Fourier’s law to estimate heat conduction, it is found that impact on temperature measurements (the maximum computed difference in temperature between the top surface and the embedded thermocouple location) is \( < 0.005^\circ \)C, which is below the accuracy threshold of the thermocouples. This prediction is confirmed for the metallic smooth wall with high thermal conductivity by comparison with thermocouples placed directly on the aerodynamic surface. Additional details regarding the uniformity of the temperature across the roughened surface are discussed in Sect. 5.
Example of \(\Theta _{\textrm{w}} - \Theta _\infty \) in time of a heated smooth main plate located at \(x=3.5 - 4.0\) m when the wall temperature is controlled by the PID controller at \({U_\infty = 20\,\mathrm {m~s^{-1}}}\). The insets show a zoomed view of \(\Theta _{\textrm{w}} - \Theta _\infty \) for the smooth (black line) and rough (blue line) walls. The red dashed lines show the temperature variation \(\pm 0.3 ^\circ \)C and \(\pm 0.4 ^\circ \)C around the set temperature \({20 ^\circ }\)C over the smooth and rough walls, respectively
In order to regulate the temperature of the individual heaters, a control box is constructed, which contains fifteen zero-cross solid-state relays (SSRs) (Celduc-SUL842070) and two microcontrollers (Arduino Mega 2560). Eleven of the SSRs are dedicated to controlling the main heaters individually, while the remaining four SSRs are employed to control the side rails. A proportional-integral-derivative (PID) controller developed in-house using Mathworks MATLAB is utilised in conjunction with the control box to achieve temperature regulation. For each heater, the temperature controller modulates the duty cycle of the power supplied to the pad heater to maintain a constant temperature difference (\({\Theta _{\textrm{w}} - \Theta _\infty }\)), where \(\Theta _{\textrm{w}}\) is the average wall temperature measured by the two embedded thermocouples associated with that particular plate and pad heater, and \(\Theta _\infty \) is the freestream temperature obtained from a thermocouple placed at the freestream (at \({z = 100\,\textrm{mm}}\) or \({\approx 2\delta }\) from the wall, at \(x = 3.8\) m). Here, \(\delta \) is the thickness of the boundary layer. The step-by-step procedure of the controller for adjusting the floor temperature is further explained in the supplementary material (S3). The developed temperature control codes for MATLAB and the microcontrollers are available on GitHub (Abu Rowin and Xia 2022). As can be seen from Fig. 2, the PID controller can, for example, maintain a constant set temperature for a smooth and rough walls at \({U_\infty = 20}\) m s\(^{-1}\) with variations of approximately less than \(\pm 0.4\,^{\circ }\)C. For all the heated wall measurements presented in this work, the temperature difference is maintained at \({\Theta _{\textrm{w}} - \Theta _\infty = 20\,^\circ }\)C. This value is chosen to maximise the measurable temperatures while ensuring a neutrally stable thermal boundary layer (i.e. negligible buoyancy effects and purely shear-driven flow). The Monin–Obukhov stability parameter for all cases discussed in this work is \(\delta _\Theta /L_o \lesssim 0.003\), where \(\delta _\Theta \) is the thermal boundary layer thickness and \(L_o = -U_\tau ^3 \Theta _{\textrm{w}}/ (\kappa g q_{\textrm{conv}}^{''})\) is the Obukhov length. Here g is gravitational acceleration, \(\kappa \) is the Von Kármán constant and \(q_{\textrm{conv}}^{''}\) is the convective heat flux. The low value of the Monin–Obukhov stability parameter indicates that all tested conditions are in the near-neutral regime; and hence, buoyancy effects can be assumed negligible. Validation of the near-neutral regime assumption is further discussed in Sect. 4.3 and in the supplementary material (S1).
3 Measurement techniques and methodology
The measurement of the heat transfer coefficient is facilitated through the recording of the power consumption for each heater, as outlined in Sect. 3.1. The temperature and velocity measurements are made using cold-wire (constant current mode) and hot-wire anemometry (constant temperature mode), respectively, which are detailed in Sects. 3.2 and 3.3.
3.1 Electrical power measurement
To determine the electrical power consumption of each heater, nineteen power metres (Peacefair PZEM-004T-10A) with \(\pm 1\) W accuracy are utilised (11 for the main plates, and 8 for the side rails). These power metres have been factory calibrated and subsequently verified with an oscilloscope (Silgent SHS806) and an ammeter (FLUKE i200s) to measure the instantaneous voltage and current. The power data from the nineteen metres is recorded at a rate of 5 Hz through the two microcontrollers included in the control box (the highest sample rate allowable by the metres). The estimation of the conductive heat transfer from the electrical power consumption is discussed in Sect. 4.2.
3.2 Cold-wire measurements
Cold-wires are used to measure temperature fluctuations across a thermal boundary layer, using an anemometer circuit (AA-lab AN-1003) operating with the constant current at 0.15 mA. The wire diameter is 5.0 µm, and the length-to-diameter ratio l/d is approximately \(\approx 250\). In situ calibration of the cold-wire probe is performed using a jet facility, with procedures provided in the work of Xia et al. (2022). As a result, a linear relationship between cold-wire output voltage (\(E_{\textrm{cw}}\)) and temperature can be established and used for the subsequent temperature measurements in the wind tunnel.
Though for most measurements, we observe a negligible drift of the cold-wire calibration over the duration of the profile measurements, we nonetheless also employed an intermediate calibration method [introduced by Talluru et al. (2014) for hot-wire calibration] to overcome any cold-wire calibration drift that might occur. For this method, the probe is traversed at every seventh data point during the measurement of the temperature profile in the thermal boundary layer to the location adjacent to the freestream thermocouple. We apply linear interpolation between the intermediate calibration points to obtain the corresponding calibration curve fit constants for each measurement station during the profile measurement.
The viscous-scaled length of the cold-wire sensor, \(l U_\tau /\nu _{\textrm{w}}\) varied from 26.8 to 67.9 for the tested range of Reynolds numbers. It is noted that the cold wires are only used here to measure the mean temperature profiles. Although \(l U_\tau /\nu _{\textrm{w}}\) is relatively large and \({l/d \approx 250}\) is smaller than required to resolve the highest frequency temperature fluctuations, it has been demonstrated by Xia et al. (2022) that the mean temperature measured by cold wires is not subject to spatial or temporal attenuation.
3.3 Hot-wire anemometry
Velocity measurements are conducted using a single-normal sensor hot-wire probe with a diameter of 5.0 µm and a length-to-diameter ratio of \({l/d \geqslant 200}\). The probe is operated in constant temperature mode using an in-house designed Melbourne University constant temperature anemometer (MUCTA), with an overheat ratio of 1.8. The hot-wire probe is calibrated in the freestream of the wind tunnel before and after each velocity measurement. The hot-wire probe is calibrated at a range of freestream velocities (fifteen data points) from zero to 1.2 times the freestream velocity of the measurement. A third-order polynomial curve fit is applied to the obtained curves of the hot-wire voltage. For each boundary layer measurement, the wire traverses at least 40 locations spaced logarithmically in the z-direction from \(z \approx 0.7 {-} 110\) mm. The signal is sampled at 40 kHz for a duration of 120 s at every z location. The non-dimensional sample interval is \(\Delta t U_\tau ^2/\nu _{\textrm{w}} \approx 0.09 {-} 1.57\) and sample duration in boundary layer turnover times is \({TU_\infty /\delta \gtrsim 40{,}000}\), where \(\nu _{\textrm{w}}\) is the kinematic viscosity of the fluid considered at the wall temperature (\(\Theta _{\textrm{w}}\)) and \(\delta \) is the momentum boundary layer thickness. Since the hot-wire length (\(l \approx 1\) mm) and diameter (\(d \approx 5\) µm) are kept constant for different Reynolds number cases, the viscous-scaled wire length varies from \({21.4 \lesssim l U_\tau /\nu _{\textrm{w}} \lesssim 54.4}\) for the smooth wall case. For the mean velocity profiles, the spatial resolution effects due to the variations of \(l^+\) are expected to be negligible (Örlü and Alfredsson 2010).
The measurements of velocity obtained from a hot-wire probe are commonly subject to contamination by non-isothermal flow fields due to the hot-wire’s sensitivity to variations in ambient fluid temperature. All subsequent measurements presented in this report were conducted with the heaters switched off to mitigate the impact of temperature variations on velocity measurements. In this case, the approach is valid due to the near-neutral thermal boundary layer, which suggests that the temperature field will act as a passive scalar (see discussion of the Monin–Obukhov stability parameter in Sect. 2.2). Consequently, the heated wall will not be anticipated to impact the velocity field. This assumption has been tested using a custom sensor capable of simultaneously measuring velocity and temperature (with the heated wall active). Full details of the custom sensor and the validation are available in the supplementary material (S1). The results reveal that no noticeable differences (within the measurement uncertainty) are observed between the velocity profiles recorded when the heaters are switched on or off. Nevertheless, when measurements are performed with the heaters switched on in Sects. 4.4 and 5, we will attempt to account for the expected modified wall shear stress (e.g. \(U_\tau \)) due to the small change in fluid properties.
Given the significant impact of accurate estimation of wall location on the prediction of inner-scaled parameters and roughness functions over rough walls, we employed a high-resolution imaging system to perform online estimation of the wall and wire wall-normal positions during measurement. This system is also accurate enough to account for wall displacement resulting from floor expansion during the operation of the heaters. The digital resolution of the imaging system is \(\approx 12\) µm pixel\(^{-1}\). A Mathworks MATLAB code was developed and made available on our GitHub repository (Abu Rowin and Xia 2022) to facilitate wire and wall detection, as well as to monitor any changes in the wall and wire positions across the series of images collected during the measurements. The overall positional uncertainty is a combination of the encoder system precision (5 µm pixel\(^{-1}\)), the wall-normal traversing microscope system depth of field (30 µm), which was initially used to find the wire wall-normal distance with respect to the wall, and the high-resolution imaging system (12 µm pix\(^{-1}\)) used to monitor changes in the wall and wire positions during the course of measurements. The overall wall-normal positional error for the current study is estimated as \(\pm 35\) µm. The uncertainty associated with this technique is considered in the full uncertainty analysis as discussed in Appendix 1
4 Measurement validation over the base smooth wall
4.1 Velocity measurements
To serve as a benchmark for rough wall results and validate the facility, velocity and temperature measurements have first been conducted over a heated smooth surface. The smooth wall is constructed from eleven aluminium cast plates, each measuring \(500 \times 720\) mm\(^{ 2}\) in \(x \times y\) and with a thickness of 6.35 mm. Ten of these plates are black anodised to eliminate reflections in thermal imaging, which is used to evaluate uniformity of the surface temperature; while, the remaining un-anodised plate is used to validate the radiation heat loss estimation of the anodised plates, as will be discussed in Sect. 4.2. These measurements are conducted at a streamwise location of \({x = 3.8}\) m (see Fig. 1) and a range of freestream velocities of \({U_\infty = 8-30}\) m s\(^{-1}\) for validation purposes.
Non-dimensionalised mean streamwise velocity \(U/U_\tau \) over smooth wall versus \(zU_\tau /\nu _{\textrm{w}}\) at \(x = 3.8\) m and range of \({U_\infty = 8-30}\) m s\(^{-1}\). For this measurement the heaters are not activated, thus \(\nu _{\textrm{w}} = \nu _\infty \). The simulated smooth wall data by Schlatter and Örlü (2010) ( ) at \(\textrm{Re}_{\tau } = 1271\), the law-of-the-wall (
) at \(\textrm{Re}_{\tau } = 1271\), the law-of-the-wall ( ) and the log-law (
) and the log-law ( ) are also plotted for comparison. Higher freestream velocities correspond to darker grey colours as shown in Table 1. The inset displays \(C_f\) versus \(\textrm{Re}_{\delta _2}\). The dashed black line (
) are also plotted for comparison. Higher freestream velocities correspond to darker grey colours as shown in Table 1. The inset displays \(C_f\) versus \(\textrm{Re}_{\delta _2}\). The dashed black line ( ) in the inset represents the Coles–Fernholz relation \({C_f = 2[\kappa ^{-1} \ln {\textrm{Re}_{\delta _2}}+C]}\) with \({C = 4.127}\). The grey and magenta symbols in the inset indicate \(C_f\) of smooth walls with and without heating, respectively
) in the inset represents the Coles–Fernholz relation \({C_f = 2[\kappa ^{-1} \ln {\textrm{Re}_{\delta _2}}+C]}\) with \({C = 4.127}\). The grey and magenta symbols in the inset indicate \(C_f\) of smooth walls with and without heating, respectively
The inner-scaled streamwise velocity, \(U/U_\tau \), versus the wall-normal distance, \(zU_\tau /\nu _{\textrm{w}}\) at \({U_\infty = 8-30~\textrm{m}~\textrm{s}^{-1}}\) is shown in Fig. 3. The friction velocity, \(U_\tau \), is estimated from the Clauser fit with the logarithmic profile of \({U/U_\tau = \kappa ^{-1} \ln (zU_\tau /\nu _{\textrm{w}}) + A}\). The logarithmic profile constants are \({\kappa = 0.384}\) and \({A = 4.17}\) (Nagib and Chauhan 2008). Here, the assumed extent of the logarithmic region is \(80 \lesssim zU_\tau /\nu _{\textrm{w}} \lesssim 0.15Re_\tau \) for the smooth wall. Uncertainty of the Clauser fit is discussed in detail in Appendix 1. A summary of the parameters for the smooth wall measurements from \({U_\infty = 8-30~\textrm{m}~\textrm{s}^{-1}}\) is included in Table 1. For validation, the velocity profile at friction Reynolds number \({\textrm{Re}_{\tau } = \delta U_\tau /\nu _{\textrm{w}} = 1271}\) from the smooth wall DNS by Schlatter and Örlü (2010) is included in Fig. 3. The logarithmic profile and viscous sublayer (\({U/U_\tau = zU_\tau /\nu _{\textrm{w}}}\)) are also included in Fig. 3. As expected, the mean velocity profiles of the smooth wall overlap with the numerical profile in the buffer and log-law regions regardless of the freestream velocity, demonstrating the Reynolds number invariance of the inner-scaled velocity profiles in the inner and log regions. In the inset of Fig. 3, \(C_f\), is plotted against the momentum-thickness Reynolds number, \({\textrm{Re}_{\delta _2} = \rho _\infty U_\infty \delta _2 /\mu _\infty }\), where \(C_f\) is evaluated from
Here the subscripts \(\infty \) and \(\textrm{w}\) denote air properties evaluated at \(\Theta _\infty \) and \(\Theta _{\textrm{w}}\). The momentum boundary layer thickness \(\delta _2\) is computed from
where \(\rho \) and U are the density and the mean streamwise velocity at each wall-normal location. Since all the velocity measurements here are performed; while, the heaters are switched off, the density did not vary across the boundary layer (i.e. \(\rho _{\textrm{w}} = \rho = \rho _\infty \)) and \(C_f\) is computed as \({C_f = 2{U_\tau ^2}/ U_\infty ^2}\). Later, when the heaters are switched on for the temperature measurements, the density variations are considered. The inset of Fig. 3 also includes the Coles–Fernholz relation of \({C_f = 2[\kappa ^{-1} \ln {\textrm{Re}_{\delta _2}}+C]}\) shown by the black dashed line. The constant \({C = 4.127}\) obtained from Nagib et al. (2007) results in good agreement with the current data. The error bars are the measurement and processing uncertainties discussed in Appendix 1.
4.2 Power consumption
Before presenting the mean temperature profiles and heat transfer coefficient results, we present here the power consumption of the heaters and discuss the prediction of heat loss. The average electrical power consumed by each heater is measured by the power metres as discussed in Sect. 3.1. The metres employed in the PID controller average the power signal internally at 5 Hz and thus are not suitable for estimating power supplied to the rapidly switched heater pads when the temperature controller is active. Instead, the electrical power consumption is estimated as average power \(\overline{P}_{100}\) when a heater is operating at 100% duty cycle multiplied by the time-averaged duty cycle (DC) at which the SSR is operating to maintain a constant floor temperature (\(\overline{P}_{DC} = \overline{P}_{100}\times DC\)). Since the SSRs used here are zero-crossing type relays (i.e. they switch on/off only when the mains AC voltage supply crosses zero), the pulse-width-modulated (PWM) signal sent by the micro-controller to the SSR might differ from the actual attained duty cycle supplied to the heaters. To validate the power consumption by the method mentioned above, we used the oscilloscope and ammeter (mentioned in Sect. 3.1) to acquire the instantaneous voltage and current consumed by each heater at a sampling rate of 10 kHz. The instantaneous voltage v(t) (dashed black line) and current i(t) (red dash-dotted line) fed to the heater and PWM output of micro-controller at 20% duty cycle (solid magenta line) are shown in Fig. 4. As expected, the zero-crossing SSR switches on the power only when the mains voltage crosses zero. However, the SSR switches the power off at a non-zero mains voltage, presumably due to some inductive loads, as indicated by the SSR manufacturer. To avoid any future mismatch between the PWM and the power switching, it is recommended to use an immediate switching (or random switching) SSR. Nonetheless, the uncertainty between the assumed duty cycle due to the zero-crossing SSR is small. It can also be seen that the phase shift (i.e. desynchronisation) between v(t) and i(t) is small enough (\(\lesssim 10\) ms) to yield only positive instantaneous power \({p(t) = v(t) \times i(t)}\), as shown by the blue solid line in Fig. 4.
In order to verify the assumption that the average electrical power consumed by a heater is given by \({\overline{P}_{DC} = \overline{P}_{100} \times DC}\), we evaluate the expression \({\overline{P}_{\textrm{osc}} = \frac{1}{T}\int _{0}^{T} p(t)\textrm{d}t}\), where \({p(t) = v(t) \times i(t)}\). A comparison of the computed value of \(\overline{P}\) obtained by both methods reveals a discrepancy of only \(2\%\), thus indicating that the former approach is a viable means of determining \(\overline{P}\). This discrepancy is considered as the uncertainty of the power metre results, as discussed in Appendix 1.1.
The mean electrical power consumption, represented as \(\overline{P}\), is perceived as the sum of the convective heat transfer to the thermal boundary layer and other heat loss components (\({\overline{P} = q_{\textrm{conv}} + q_{\textrm{loss}}}\)). The heat loss term, \(q_{\textrm{loss}}\), is inclusive of conductive and radiative heat transfer (\(q_{\textrm{loss}} = q_{\textrm{cond}}+q_{\textrm{rad}}\)). The conductive heat loss is deemed to occur in a one-dimensional manner towards the floor of the tunnel only, as a result of the implemented side rails heated to the same temperature as the main plates—minimising lateral conductive heat losses. It is important to clarify that the one-dimensional assumption regarding conductive heat transfer specifically addresses the heat loss from the bottom of the main plate the tunnel floor. This assumption does not extend to the consideration of local conductive heat transfer that may occur due to variations in temperature on the flow side topography of the roughness. However, as stated in Sect. 5, we expect such variations on the rough wall to be minimal (due to the use of aluminium which has a high thermal conductivity relative to air). The estimation of the conductive heat loss is derived from Fourier’s law as
where \(\Theta _{b}\) is the temperature of the tunnel floor from the laboratory side, c is the thickness and K is the thermal conductivity of the insulation layers (calcium–magnesium silicate and polyisocyanurate foam) or wood frame. The double quotation marks denote the heat flux (i.e. parameter normalised by the plane area). The radiative heat loss is calculated from the Stefan–Boltzmann law as \(q_{\textrm{rad}}^{\prime \prime } = \sigma \varepsilon (\Theta _{\textrm{w}}^4-\Theta _{\mathrm {s-wall}}^4)\), where \(\sigma = 5.67 \times 10^{-8}\) W m\(^{-2}\) K\(^{-4}\) is the Stefan–Boltzmann constant, \(\varepsilon \) is the emissivity and \(\Theta _{\mathrm {s-wall}}\) is the tunnel side and top walls temperature assumed here to be equivalent to \(\Theta _\infty \). The emissivity of the anodised smooth wall is estimated by covering a portion of the anodised aluminium test surface with a black tape of known emissivity. The temperature of the test surface is raised to a minimum of \(20~^\circ \)C above the ambient temperature, and thermal images of both the anodised aluminium surface and the black tape are captured using a thermal camera (FLIR T1040). This camera operates within a spectral range of \(7.5 {-}14\) µm and can measure object temperatures ranging from \(-40\) to \(2000~^\circ \)C. The environment surrounding the thermal camera operation field is regulated to prevent any direct reflections from biasing the recorded signal. Additionally, the camera settings are fine-tuned to account for the ambient temperature and any energy radiated by the surroundings. The surface temperature over the known emissivity black tape is estimated and compared with the temperature readings from the embedded thermocouples, and then the emissivity is adjusted until the anodised aluminium surface appears to have the same temperature as the black tape. This methodology resulted in a determination of \(\varepsilon = 0.77\) for the black anodised aluminium surface. The validity of this method for estimating the emissivity was confirmed by comparing it to the prediction of emissivity based on the power difference when a plate was replaced with an un-anodised aluminium plate with \(\varepsilon \approx 0.09\). The emissivity of the un-anodised plate is obtained from Incropera et al. (1996) for polished aluminium at \({\approx 47 ^\circ }\)C. This comparison assumes that the convective and conductive heat transfer are equivalent for the anodised and un-anodised plate under the same \(U_\infty \) conditions and that any increase in the power consumption of the anodised plate is due to radiation alone. The discrepancy between the two methods for estimating the emissivity, \(\Delta \varepsilon = \pm 0.03\), is considered a source of uncertainty in predicting radiative heat loss. For the current smooth wall experiments, the conductive heat loss to the tunnel floor is \(\approx 7.4\) W m\(^{-2}\) and the radiative heat loss \(q_{\textrm{rad}}^{\prime \prime }\) for the anodised plates is 99.2 W m\(^{-2}\). It is important to note that the application of the Stefan–Boltzmann equation does not account for any transmittance or reflectance of heat between the bottom wall and other tunnel walls. Instead, it assumes that all heat radiated by the bottom wall is absorbed by the surrounding. Consequently, the radiative heat loss estimated by the Stefan–Boltzmann equation may be overestimated. In the current study, considering the absorption of heat by the bottom wall through the assumption of radiation within the cavity, we found that the radiative heat loss is approximately 4% lower than when calculated solely using the Stefan–Boltzmann equation. The total heat loss \(q_{\textrm{loss}}\) for the heated smooth wall ranges from \(\sim 30 - 10\%\) of the convective heat for \({U_\infty = 8 - 30}\) m s\(^{-1}\), respectively. Note that had we used un-anodised aluminium plates for the smooth surface, these heat losses would be reduced to 5–2% for \(U_\infty \) = 8 to 30 m s\(^{-1}\), respectively, based on the reduced emissivity of the un-anodised plates.
Relationship between freestream velocity \(U_\infty \) and the total power consumption normalised by the surface area (\(750 \times 500\) mm2) (i.e. heat flux) of a heater located at \({x = 3.5 - 4.0}\) m, for smooth ( ) and rough (
) and rough ( ) walls. The black and blue dashed lines depict the linear fits of the smooth and rough walls data, respectively
) walls. The black and blue dashed lines depict the linear fits of the smooth and rough walls data, respectively
The total heat loss can also be estimated using the approach proposed by Hippensteele et al. (1987), Choi and Hamid (1991), where the average electrical power consumption of a heater as a function of \(U_\infty \) is extrapolated to \(U_\infty = 0\) m s\(^{-1}\). In this method, Choi and Hamid (1991) assumes that at zero tunnel speed, the electrical power consumption is solely due to radiative heat transfer, neglecting any conductive or free convective heat transfer. The extrapolation method applied for the current study is shown in Fig. 5 and yields a total flowoff heat flux loss of \(q_{\textrm{0}}^{\prime \prime } = 209.9\) W m\(^{-2}\), which is significantly higher than the \(q_{\textrm{loss}}^{\prime \prime } \approx 106.6 \) W m\(^{-2}\) calculated by summing the conductive and radiative heat loss. The discrepancy between the two methods is likely due to the unrealistic assumption that the total power consumption at \(U_\infty = 0\) m s\(^{-1}\) is exclusively composed of conductive and radiative heat loss. In reality, as proposed by Hippensteele and Russell (1988) and Jayamaha et al. (1996), at \(U_\infty = 0\) m s\(^{-1}\), the total heat flux (i.e. total power consumption per unit area) is equal to the sum of the heat flux loss and the free convection heat flux, \(q_{\textrm{fconv}}^{''} = h_{0}(\Theta _{\textrm{w}} - \Theta _\infty )\), where \(h_0\) is the natural convection heat transfer coefficient. Here, we estimated \(h_0\) using correlations from literature that relate \(h_0\) to the Rayleigh number, Ra, and the thermal conductivity of air, \(K_\textrm{a}\), expressed as \({h_0 = f(\textrm{Ra}, K_\textrm{a})}\). Since various expressions can be found in literature, as summarised by Kitamura and Kimura (1995), we report a range of \(h_0\) estimated from these expressions to be within \(4.3 \lesssim h_0 \lesssim 5.5\) W m\(^{-2}\) K\(^{-1}\). In this measurement scenario, when the wall temperature difference equals \(20~^\circ \)C, the free convection heat flux (\(q_{\textrm{fconv}}^{''}\)) ranges from approximately 86–110 W m\(^{-2}\), which closely matches the discrepancy between the estimated heat loss obtained from extrapolation and that derived from direct measurement. Therefore, extrapolating total power consumption to zero tunnel velocity can effectively determine heat loss, incorporating free convective heat transfer.
Viscous-scaled mean temperature profiles, \({(\Theta _{\textrm{w}} - \Theta )/\Theta _\tau }\), of the smooth wall against \(zU_\tau /\nu _{\textrm{w}}\). Darker grey refers to increasing freestream velocity as indicated in Table 1. The DNS of Xia et al. (2022) ( ) at \(\textrm{Re}_{\tau } = 395\), the linear thermal sublayer law (
) at \(\textrm{Re}_{\tau } = 395\), the linear thermal sublayer law ( ) and the temperature log-law are shown. The left inset (
) and the temperature log-law are shown. The left inset ( ) shows the inverse of the logarithmic law slope \(\kappa _h\) with increasing \(\textrm{Re}_\tau \). In the left inset (
) shows the inverse of the logarithmic law slope \(\kappa _h\) with increasing \(\textrm{Re}_\tau \). In the left inset ( ) is \(\kappa _h = \kappa /Pr_t = 0.47\). The right inset shows the temperature diagnostic function \(\beta _\Theta \) versus \(zU_\tau /\nu _{\textrm{w}}\)
) is \(\kappa _h = \kappa /Pr_t = 0.47\). The right inset shows the temperature diagnostic function \(\beta _\Theta \) versus \(zU_\tau /\nu _{\textrm{w}}\)
4.3 Temperature measurements
The inner-scaled mean temperature profile \({(\Theta _{\textrm{w}}-\Theta )/\Theta _{\tau }}\) for the heated smooth wall is shown in Fig. 6 for a range of freestream velocities at \(U_\infty = 8-30\) m s\(^{-1}\). Here \(\Theta \) is the mean temperature and \(\Theta _{\tau }\) is the wall friction temperature estimated as \({\Theta _\tau = q_{\textrm{conv}}^{\prime \prime }/(\rho _{\textrm{w}} c_{p} U_\tau )}\) (Patel et al. 2017), where \(c_{p}\) is the air specific heat and \(q_{\textrm{conv}}^{\prime \prime }\) is obtained from the power measurements as detailed above in Sect. 4.2. The estimated \(\Theta _\tau \) for smooth cases at different \(U_\infty \) is included in Table 1. Given that the heaters are activated during these measurements, air properties are computed at \(\Theta _{\textrm{w}}\), and this necessitates a corresponding adjustment to the normalisation, such that the viscous-scaled wall-normal distance is given by \(z U_\tau /\nu _{\textrm{w}}\), where \(\nu _{\textrm{w}} = \mu _{\textrm{w}}/\rho _{\textrm{w}}\) represents the air kinematic viscosity at \(\Theta _{\textrm{w}}\), with \(\mu _{\textrm{w}}\) the dynamic viscosity determined by Sutherland’s formula and \(\rho _{\textrm{w}}\) the air density from the ideal gas law both at \(\Theta _{\textrm{w}}\). In order to ascertain the significance of temperature variations across the boundary layer on the momentum boundary layer, the velocity was obtained through the use of the dual probe (hot- and cold-wire), as discussed in the supplementary material (S1), at two freestream velocities of \(U_\infty = 12\) and 20 m s\(^{-1}\). Analysis of the mean temperature profile, when the heaters were activated, revealed a slight alteration of the slope of the logarithmic regions, resulting in a \(\sim 2\%\) variation of \(U_\tau \) obtained via the Clauser method as compared with the \(U_\tau \) of the unheated case. The skin-friction coefficient \({C_f = 2\rho _{\textrm{w}}/\rho _\infty (U_\infty /U_\tau )^2}\) was also observed to vary by \(\sim 3\%\) between these cases, as demonstrated by magenta symbols in the inset of Fig. 3. It is noteworthy that \(\delta _2\) for the heated smooth wall was computed using Equation (2), with the density \(\rho \) varying across the boundary layer in correspondence with the measured temperature at each z location measured by the cold wire. Since the measured differences in \(U_\tau \) and \(C_f\) between the heated and unheated cases fall within the limits of current measurement uncertainties, we have made the assumption that the Coles–Fernholz relation holds true for all subsequent analyses of the heated wall. In order to estimate \(\textrm{Re}_{\delta _2}\), we utilised Equation (2) while taking into account the variations in density across the boundary layer, and obtained \(C_f\) values directly from the Coles–Fernholz relation. Nonetheless, we emphasise the need for caution in conducting heated wall measurements, as variations in flow properties may significantly influence wall shear stress. This would particularly be the case where there were larger temperature differences between the wall and freestream. Direct measurements of wall shear stress on the heated wall, could yield a more precise evaluation of the impact of temperature on the momentum boundary layer.
As noted by Abe et al. (2004), Pirozzoli et al. (2016), Alcántara-Ávila et al. (2021), and Pirozzoli et al. (2022), there is a possibility of a marginal change in the slope of \((\Theta _{\textrm{w}} - \Theta )/\Theta _\tau \) in the logarithmic region, represented by \(\kappa _h\), with an increase in \(\textrm{Re}_\tau \). This suggests that the commonly employed thermal version of the Clauser method, which utilises a logarithmic temperature law to fit temperature profiles, may produce erroneous estimates of \(\Theta _\tau \) since it assumes constant \(\kappa _h\). To assess this, in Fig. 6 we plot the temperature profiles of the heated smooth wall, alongside the thermal sublayer \({(\Theta _{\textrm{w}} - \Theta )/\Theta _\tau = Pr (zU_\tau /\nu _{\textrm{w}})}\) and the logarithmic thermal log-law \({(\Theta _{\textrm{w}} - \Theta _{\textrm{log}})/\Theta _\tau = \kappa _h^{-1}\textrm{log}(zU_\tau /\nu _{\textrm{w}}) + A_r(Pr)}\). Here, \(\kappa _h = \kappa / Pr_t = 0.47\), where \(Pr_t = 0.82\) represents the turbulent Prandtl number and the intercept is given by \({A_r = (3.85Pr^{1/3}-1.3)^2 + (Pr_t/\kappa ) \textrm{log}(Pr) \approx 3.8}\) (Kader 1981), where Pr is the molecular Prandtl number. Although \(\Theta _\tau \) is computed from \({\Theta _\tau = q_{\textrm{conv}}^{\prime \prime }/(\rho _{\textrm{w}} c_{p} U_\tau )}\), where \(q_{\textrm{conv}}^{\prime \prime }\) is measured by the power metres, the temperature profiles exhibit satisfactory agreement with the linear relationship in the thermal sublayer. The slope of \((\Theta _{\textrm{w}} - \Theta )/\Theta _\tau \) within the logarithmic region (i.e. \(\kappa _h\)) appears to vary with \(\textrm{Re}_\tau \), as shown in the inset of Fig. 6. Alcántara-Ávila et al. (2021) suggested that this variation could be attributed to the lack of a fully developed logarithmic region. To confirm the development of the temperature logarithmic region of the current results, we use a temperature diagnostic function denoted as \(\beta _\Theta = z/\Theta _\tau (\textrm{d}\Theta /\textrm{d}z)\), which is analogous to the velocity diagnostic function \(\beta _U = z/U_\tau (\textrm{d}U/\textrm{d}z)\), as proposed by Alcántara-Ávila et al. (2021). We observe that no clear plateau of \(\beta _\Theta \) is present at \(\kappa _h^{-1}\) for \(\textrm{Re}_\tau \approx 900\), indicating an underdeveloped thermal boundary layer. However, for \(\textrm{Re}_\tau \gtrsim 1600\) (i.e. \(U_\infty = 12\) m s\(^{-1}\)), a distinct plateau of \(\beta _\Theta \) at \(\kappa _h^{-1}\) is evident, indicating a fully developed logarithmic region. Even beyond this limit, the data in Fig. 6 continue to exhibit a valid trend of increasing \(\kappa _h\) with \(\textrm{Re}_\tau \). The observed variation of \(\kappa _h\) with \(\textrm{Re}_\tau \), raises questions over the reliability of the Clauser method for estimating \(\Theta _\tau \) under the conditions of a heated smooth wall. Additionally, errors may arise when attempting to estimate \(\Theta _\tau \) using freestream flow properties for \(\rho \) and \(c_p\) within the expression \({\Theta _\tau = q_{\textrm{conv}}^{\prime \prime }/(\rho _{\textrm{w}} c_{p} U_\tau )}\). However, it is important to note that the current results do not conclusively settle this matter. Despite the \(\kappa _h\) variation, when we apply the Clauser method, the results of the heat transfer coefficient from the power method and Clauser method (as will be discussed in the following section) still overlap within the measurement uncertainty.
4.4 Estimates of heat transfer coefficient
As previously stated in the introduction, the wall heat flux can be measured either directly, as explained in Sect. 4.2 by evaluating power consumption, or indirectly, either by analysing the streamwise gradient of the enthalpy thickness or through the logarithmic temperature law to the measured temperature profiles (a Clauser type fit). This section aims to verify the reliability of indirect methods by comparing them with the direct power consumption method, utilising the Stanton number St as the metric for heat transfer coefficient. The calculation of St for the directly measured wall heat flux through power consumption is as follows (Ligrani and Moffat 1985):
The measured St from Eq. (4) is shown by the red shaded symbols in Fig. 7 versus \(\textrm{Re}_{\delta _2}\). The empirical relationship for St by Mukerji et al. (2004) is also included in Fig. 7, as
where
This expression includes the virtual streamwise origin for the momentum boundary layer \(\zeta \). For the current smooth wall case, \({\zeta \approx - 0.49}\) m is estimated from extrapolation of the measured \(\delta _2\) against streamwise location x to the location where \(\delta _2 = 0\). It is clear from Fig. 7, that the measured St given by the power consumption agrees well with the relationship suggested by Mukerji et al. (2004) within the measurement uncertainty.
The Stanton number can also be determined by examining the evolution of the boundary layer’s enthalpy thickness (\(\delta _h\)) along the streamwise axis (x) through the calculation of \(St = \textrm{d}\delta _h/\textrm{d}x\). The enthalpy thickness can be obtained from the expression presented in Crawford et al. (1980).
where the thermal boundary thickness \(\delta _\Theta \) is defined as the point where the mean temperature \(\Theta \) recovers to 99% of (\(\Theta _{\textrm{w}} - \Theta _\infty \)). For the present analysis, the momentum and thermal boundary layers were evaluated at four distinct streamwise locations: \(x = 1.88\), 2.3, 3.1 and 3.8 m. During the measurement of the thermal boundary layer in the region near the tunnel entrance (\(x \lesssim 1.8\) m), we observed discrepancies between the thickness of the thermal boundary layer and the energy consumption of the heater pads in this area. Specifically, we found that the thermal boundary layer was more inconsistent at lower flow velocities, with variations extending up to \(x \approx 3.0\) m at \(U_\infty = 8.0\) m s\(^{-1}\). These variations may be attributed to the entrance conditions of the tunnel, as previously suggested based on the surface temperature coefficient (analogous to the pressure coefficient) as documented by Perry and Hoffmann (1976).
The St values computed from the enthalpy thickness are shown with the green symbols in Fig. 7 for flow velocities of \({U_\infty = 12}\) (round filled green symbols) and 20 m s\(^{-1}\) (square green filled symbols). The individual points are from the gradient \(\textrm{d}\delta _h/\textrm{d}x\) computed at \(x = 1.88, 2.3, 3.1\) and 3.8 m. The St values obtained at \(U_\infty = 20\) m s\(^{-1}\) using the enthalpy thickness method exhibit good agreement with the St values determined from energy consumption measurements. Conversely, significant disparity (of up to \(12 \%\)) is noticeable in St values computed using the gradient of enthalpy thickness and the energy consumption technique at a flow velocity of \({U_\infty = 12}\) m s\(^{-1}\). The observed discrepancy may plausibly be ascribed to a range of contributing factors, including inadequate tripping at low tunnel velocities, which results in a delay in the development of the turbulent state. The lack of thermal insulation between the initial tile and the upstream tunnel wall may introduce additional conductive heat loss at \(x = 0\), a factor not considered in the power measurements. Moreover, the individual control of heat flux to each of the eleven plates means that the surface temperature of the first streamwise plate (spanning from \(0< x < 0.5\) m) will not remain constant in the streamwise direction, arising from the rapid initial reduction in St as the newly formed thermal boundary layer thickens along x (refer to Fig. 7 for an example). It is also important to acknowledge the presence of weak secondary flows in wind tunnels, often referred to as Klebanoff modes (Watmuff 1998). These modes can cause velocity fluctuations (and presumably temperature variations as well) across the span. Their slight variations under different tunnel operating conditions can impact the effectiveness of using the momentum integral approach to measure \(C_f\) (Walsh 1990; Anders 1990), thus potentially influencing the enthalpy thickness approach for determining St. In view of these outcomes, estimating St using the enthalpy thickness method appears unreliable. Hence, for these reasons, this method will not be employed to determine St for the rough wall in Sect. 5. To understand the effect of any spanwise uniformities due to Klebanoff modes or secondary flows on this method would be quite complicated (requiring a three-dimensional control volume analysis for the energy balance, as opposed to the two-dimensional balance used here). However, a useful first step would be to document any spanwise variations in forced convective heat flux or temperature. This can be achieved through various methods, including the utilisation of a, temperature-sensitive paint such as liquid crystal (e.g. Fisher and Eibeck 1990), thermal cameras and heated thin-foil (e.g. Gurka et al. 2004; Nakamura and Yamada 2013).
Stanton number, St, of heated smooth surface obtained by ( ) power consumption, (
) power consumption, ( ) enthalpy thickness at \({U_\infty = 12}\) m s\(^{-1}\), (
) enthalpy thickness at \({U_\infty = 12}\) m s\(^{-1}\), ( ) enthalpy thickness at \({U_\infty = 20}\) m s\(^{-1}\) and (
) enthalpy thickness at \({U_\infty = 20}\) m s\(^{-1}\) and ( ) Clauser fit. The St model (
) Clauser fit. The St model ( ) of Mukerji et al. (2004) is presented here
) of Mukerji et al. (2004) is presented here
The third approach for calculating St involves fitting the temperature profile to the thermal log law. It is important to emphasise that this method does not take into account the variations of \(\kappa _h\) with the Reynolds number (as previously discussed in Sect. 4.3). Instead, a constant value of \(\kappa _h = 0.47\) is utilised. The expression for this method combines Equation (4) with the definition of \(\Theta _\tau \),
where \(\Theta _\tau \) and \(U_\tau \) are both obtained from Clauser fits to the mean temperature and velocity profiles, respectively. The St values derived from this methodology are presented in Fig. 7 using grey shaded symbols. The error bars in the figure represent both measurement and processing uncertainties, as detailed in Appendix 1 and 2. Notably, the calculated St values obtained from this technique exhibit similar values with those derived through the power consumption approach (utilising Eq. 4). It is pertinent to underline that the observed variation of \(\kappa _h\) concerning \(\textrm{Re}_\tau \), as expounded earlier, does not seem to hold critical significance in the results of St obtained from the smooth wall. The marginal differences between the St from the power metre and those from the Clauser fit, as depicted in Fig. 7, are presumably attributable solely to the misapplication of an inaccurate \(\kappa _h\) value and measurement and processing uncertainties.
5 Velocity and temperature measurement over roughness
In this section, we present and compare the results of momentum and thermal boundary layer measurements for a three-dimensional (3D) sinusoidal rough surface. Details about the manufactured roughness are included in the supplementary material (S2). Figure 8 shows the non-dimensionalised streamwise velocity, \(U/U_\tau \), plotted against \({(z-d)U_\tau /\nu _{\textrm{w}}}\) in the freestream velocity range of 8–30 m s\(^{-1}\). The virtual origin, d, is derived from the direct numerical simulation of Abu Rowin et al. (2022) for a roughness geometry that is matched to that of the current study. Abu Rowin et al. (2022) estimated d as the value that yields a close approximation of \(\kappa \) in the logarithmic region of the mean velocity profiles to that of the smooth wall. They found that d/k increases with \(kU_\tau /\nu _{\textrm{w}}\) before approaching a constant \(d/k \approx 0.42\) at \(kU_\tau /\nu _{\textrm{w}} \gtrsim 40\). Based on this, d/k is assumed constant \(d/k = 0.42\) for all the cases presented in the current work since \(kU_\tau /\nu _{\textrm{w}} > 40\). The Clauser method is also used for the rough wall to estimate the friction velocity, \(U_\tau \) within the logarithmic limits of \(0.5\lambda U_\tau /\nu _{\textrm{w}}\lesssim zU_\tau /\nu _{\textrm{w}}\lesssim 0.15Re_\tau \), where \(0.5\lambda _y\) represents the assumed limit of the roughness sublayer (Chan et al. 2015) and \(\lambda _y\) is the roughness spanwise wavelength. If the estimated roughness sublayer limit is below \(zU_\tau /\nu _{\textrm{w}} < 80\), the logarithmic region range is adjusted as \(80 \lesssim zU_\tau /\nu _{\textrm{w}}\lesssim 0.15Re_\tau \). In this case, the gradient of the measurement is fitted with the modified logarithmic profile \({U_{\textrm{log}}/U_\tau = \kappa ^{-1}\textrm{log}(zU_\tau /\nu _{\textrm{w}})+A-(\Delta U/U_\tau )}\), where \(\Delta U/U_\tau \) represents the velocity roughness function (Clauser 1954; Hama 1954).
It is worth noting that the velocity profile of the rough wall, when using this method, is assumed to maintain the same slope (\(\kappa \)) in the log region as its smooth wall counterpart. However, certain roughness geometries might not align with this assumption (e.g. the riblet surface in Endrikat et al. 2022). Moreover, when using the modified Clauser method over rough surfaces, the derived value of \(U_\tau \) is noticeably influenced by d. In future improved studies, where possible, it is recommended to measure the wall shear stress directly on the test surface to estimate \(U_\tau \). A summary of the bulk parameters for the 3D sinusoidal roughness measurements is provided in Table 2.
As shown in Fig. 8, the rough wall displays a downward shift in \(U/U_\tau \) compared to the smooth wall, with the magnitude of this shift, represented by \(\Delta U/U_\tau \), increasing as \(kU_\tau /\nu _{\textrm{w}}\) increases. The figure also shows \(U_\infty /U_\tau \) appears to approach a constant value for \({U_\infty \gtrsim 12.0}\) m s\(^{-1}\), suggesting constant value of \(C_f\) as shown in the inset of Fig. 8. The inset also includes the Coles–Fernholz relation of the smooth wall. The magnitude of \(C_f\) increases in the transitionally rough regime, ranging from approximately \(5.6 \times 10^{-3}\) to \(6.2 \times 10^{-3}\) for \(kU_\tau /\nu _{\textrm{w}} \approx 40\) to 62 (i.e. \(U_\infty = 8\) to 12 m s\(^{-1}\)). At higher \({U_\infty > 12.0}\) m s\(^{-1}\), \(C_f\) over the 3D sinusoidal roughness attains a plateau, indicating the onset of the fully rough regime.
Viscous-scaled mean streamwise velocity, \(U/U_\tau \), profiles of the rough wall against \({(z-d)U_\tau /\nu _{\textrm{w}}}\). The darker blue indicates higher freestream velocity as listed in Table 2. The law-of-the-wall ( ) and the log-law for the smooth wall (
) and the log-law for the smooth wall ( ) are also shown. The inset shows \(C_f\) as a function of \(\textrm{Re}_x\). Coles–Fernholz relation for the smooth wall is included (
) are also shown. The inset shows \(C_f\) as a function of \(\textrm{Re}_x\). Coles–Fernholz relation for the smooth wall is included ( ). In the inset (
). In the inset ( ) is at the \({C_f \approx 6.1 \times 10^{-3}}\)
) is at the \({C_f \approx 6.1 \times 10^{-3}}\)
Viscous-scaled mean temperature, \((\Theta _{\textrm{w}} - \Theta )/\Theta _\tau \), profiles of the heated 3D sinusoidal roughness against \({(z-d)U_\tau /\nu _{\textrm{w}}}\). The darker blue refers to higher \(U_\infty \) as listed in Table 2. The linear thermal sublayer law ( ) and the temperature log-law (
) and the temperature log-law ( ) are included. The left inset shows \(\kappa _h\) as a function of \(\textrm{Re}_\tau \). In the left inset (
) are included. The left inset shows \(\kappa _h\) as a function of \(\textrm{Re}_\tau \). In the left inset ( ) is \(\kappa _h \approx \kappa /Pr_t = 0.47\) and (
) is \(\kappa _h \approx \kappa /Pr_t = 0.47\) and ( ) is at \(\kappa _h = 0.38\) when the origin is assumed at the mid-plane k/2. The right inset shows the temperature profile difference between the logarithmic profile \(\Theta _{\textrm{log}}/\Theta _\tau \) and rough wall mean temperature \(\Theta /\Theta _\tau \) up to the upper limits of the logarithmic region
) is at \(\kappa _h = 0.38\) when the origin is assumed at the mid-plane k/2. The right inset shows the temperature profile difference between the logarithmic profile \(\Theta _{\textrm{log}}/\Theta _\tau \) and rough wall mean temperature \(\Theta /\Theta _\tau \) up to the upper limits of the logarithmic region
Figure 9 displays the inner-scaled mean temperature profiles, \((\Theta _{\textrm{w}} - \Theta )/\Theta _\tau \), for the 3D sinusoidal roughness. We use the power consumption method to obtain the friction temperature \(\Theta _\tau \). Since we heat the wall in this measurement, we consider air properties at \(\Theta _{\textrm{w}}\) for normalisation. It is important to acknowledge that we make the assumption of uniform temperature across the roughened surface, with temperatures equivalent to those measured by the embedded thermocouples. However, it is essential to note that this assumption has not been experimentally validated due to challenges in measuring surface temperature at various locations of the roughness topography, such as crest and trough, primarily because of potential flow blockage with thermocouples placed on the aerodynamic surface or issues with surface reflections in thermal imaging. Despite this limitation, our choice of using a material with high thermal conductivity, specifically aluminium in this case, supports our heat transfer analysis, which suggests minimal temperature variation between the peaks and troughs of the rough surface. Additionally, findings from the DNS study on conjugate heat transfer with rough surfaces by Orlandi et al. (2016) also lend support to our assumption by indicating that temperatures across rough surfaces with high thermal conductivity materials tend to be uniform. The conductive and radiative heat loss of the rough wall is estimated from Fourier’s law and the Stefan–Boltzmann equation, similar to that of the smooth wall. However, estimating the emissivity of rough walls is challenging due to the high reflection from the roughness features, resulting in greater uncertainty in the emissivity of rough walls compared to smooth walls, as discussed in Appendix 1. Alternatively, the total heat loss of the heated rough surfaces could also be estimated by extrapolating the total power consumption to \(U_\infty = 0\) (as shown in Fig. 5) and subtracting the natural convection heat transfer. The total heat loss using this technique is calculated to be \(\approx 145\) W/m2, comparable with the 132 W/m2 obtained through direct estimation method. While we assumed that the natural heat transfer coefficient in the current roughness case approximates that of a smooth surface, it is crucial to acknowledge that the presence of roughness may influence natural heat transfer, as e.g. demonstrated by Wagner and Shishkina (2015). Consequently, uncertainty persists regarding the validity of this assumption.
In contrast to the observed change in \(\kappa _h\) over a smooth wall, shown in Fig. 6, \(\kappa _h\) for the rough wall appears to remain constant with increasing Reynolds number, within the bounds of measurement uncertainty, as illustrated in the inset of Fig. 9. To further illustrate that \(\kappa _h\) for the rough wall shares the same value as the assumed \(\kappa _h\) for the smooth wall (\(\kappa _h \approx \kappa /Pr_t = 0.47\)), the difference between logarithmic temperature profile \(\Theta _{\textrm{log}}\) (shown by the green line in Fig. 9) and the rough wall temperature profile results in an approximate plateau within the assumed logarithmic region range \(0.5\lambda U_\tau /\nu _{\textrm{w}}\lesssim zU_\tau /\nu _{\textrm{w}}\lesssim 0.15 \textrm{Re}_\tau \) as shown in the lower inset of Fig. 9.
Notably, \(\kappa _h\) for the rough wall varies significantly with the virtual origin. For instance, when the virtual origin is assumed to be at the mid-plane (\(d=k/2\)), as previously assumed by MacDonald et al. (2019), \(\kappa _h\) is reduced to 0.38 (indicated by the dashed red line in the inset of Fig. 9). This indicates that if the Clauser method is applied to estimate \(\Theta _\tau \) for a rough wall measurement without prior knowledge of the correct \(\kappa _h\) and d values for the corresponding rough wall, a significant degree of uncertainty is expected in the reported results.
Figure 10 compiles St obtained from the power and Clauser methods for the 3D sinusoidal roughness along with the smooth wall St model of Mukerji et al. (2004). (The estimation of St through the enthalpy thickness is omitted in this section due to the unsuitability of this approximation for the current facility, as demonstrated in Sect. 4.4). The computed St decreasing from both methods follow the same overall trend of decreasing St with \({kU_\tau /\nu _{\textrm{w}} > 65}\). This trend of St with increasing Reynolds number for transitionally and fully rough regimes walls is previously reported in the simulations of 3D sinusoidal roughness of MacDonald et al. (2019). The difference between the results of the two techniques lie within the error margins of these two techniques. The computed error bars from an evaluation of different sources of uncertainty (see Appendix 1 and 2) are shown in Fig. 10.
Stanton number, St, of heated 3D sinusoidal roughness obtained from ( ) power consumption and (
) power consumption and ( ) Clauser fit. For comparison, the St model (
) Clauser fit. For comparison, the St model ( ) by Mukerji et al. (2004) for the smooth surface is also presented
) by Mukerji et al. (2004) for the smooth surface is also presented
To further illustrate the effect of the roughness at different flow regimes and validate the rough wall results against the simulation of MacDonald et al. (2019), the inner-scaled velocity roughness function, \({\Delta U/U_\tau = (U_{\textrm{log}} - U)/U_\tau }\) (diamond symbols) and temperature roughness function, \(\Delta \Theta /\Theta _\tau = (\Theta _{\textrm{log}} - \Theta )/\Theta _\tau \) (square symbols) are plotted as a function of the normalised roughness height, \(k U_\tau /\nu _{\textrm{w}}\), in Fig. 11. Due to the lack of smooth wall cases at equivalent large \(\textrm{Re}_\tau \) for the rough wall, we use the logarithmic laws (\(U_\textrm{log}\) and \(\Theta _\textrm{log}\)) as reference smooth profiles while neglecting any variations of the logarithmic region slope. In order to ensure a justifiable comparison between the current research findings and those of MacDonald et al. (2019), we have re-evaluated the values of \(\Delta U/U_\tau \) and \(\Delta \Theta /\Theta _\tau \) reported by MacDonald et al. (2019), taking into account the virtual origin as described in Zhong et al. (2023). Furthermore, we have computed \(\Delta U/U_\tau \) and \(\Delta \Theta /\Theta _\tau \) at a single wall-normal location within the logarithmic region, which is equivalent to that used by MacDonald et al. (2019) (at the critical height of the minimal channel technique), in order to facilitate a valid comparison between our results and those of MacDonald et al. (2019).
Velocity roughness function ( ) \(\Delta U/U_\tau \) and temperature roughness function (
) \(\Delta U/U_\tau \) and temperature roughness function ( ) \(\Delta \Theta /\Theta _\tau \) versus \({k U_\tau /\nu _{\textrm{w}}}\). The darker blue shading refers to higher \(U_\infty \), as indicated in Table 2. Other symbols are (
) \(\Delta \Theta /\Theta _\tau \) versus \({k U_\tau /\nu _{\textrm{w}}}\). The darker blue shading refers to higher \(U_\infty \), as indicated in Table 2. Other symbols are ( ) \(\Delta U/U_\tau \) and (
) \(\Delta U/U_\tau \) and ( ) \(\Delta \Theta /\Theta _\tau \) for the 3D sinusoidal roughness data of MacDonald et al. (2019). A log liner dash-dotted and dashed fitted lines of \({\Delta U^+ = \kappa ^{-1} \textrm{log}(k U_\tau /\nu _{\textrm{w}}) + A - C_k}\) are fitted to the data of MacDonald et al. (2019) and current results, respectively, with \(C_k = 4.9\) and 5.8. The horizontal solid line is at a constant value of \(\Delta \Theta ^+ = 4.3\). The inset shows \(\Delta U/U_\tau \) and \(\Delta \Theta /\Theta _\tau \) as a function of the normalised equivalent sand-grain roughness height, \({k_s U_\tau /\nu _{\textrm{w}}}\). The solid line in the inset illustrates the fully rough asymptote \({\Delta U^+ = \kappa ^{-1} \textrm{log}(k_s U_\tau /\nu _{\textrm{w}}) + A - C_N}\), where \(C_N = 8.5\) is Nikuradse’s fully rough constant (Nikuradse 1933). For the current data \(k_s/k = 2.8\)
) \(\Delta \Theta /\Theta _\tau \) for the 3D sinusoidal roughness data of MacDonald et al. (2019). A log liner dash-dotted and dashed fitted lines of \({\Delta U^+ = \kappa ^{-1} \textrm{log}(k U_\tau /\nu _{\textrm{w}}) + A - C_k}\) are fitted to the data of MacDonald et al. (2019) and current results, respectively, with \(C_k = 4.9\) and 5.8. The horizontal solid line is at a constant value of \(\Delta \Theta ^+ = 4.3\). The inset shows \(\Delta U/U_\tau \) and \(\Delta \Theta /\Theta _\tau \) as a function of the normalised equivalent sand-grain roughness height, \({k_s U_\tau /\nu _{\textrm{w}}}\). The solid line in the inset illustrates the fully rough asymptote \({\Delta U^+ = \kappa ^{-1} \textrm{log}(k_s U_\tau /\nu _{\textrm{w}}) + A - C_N}\), where \(C_N = 8.5\) is Nikuradse’s fully rough constant (Nikuradse 1933). For the current data \(k_s/k = 2.8\)
The current behaviour of \(\Delta U/U_\tau \) exhibits a logarithmic-linear trend, closely following the asymptotic equation \({\Delta U^+ = \kappa ^{-1} \textrm{log}(k U_\tau /\nu _{\textrm{w}}) + A - C_k}\) for \(kU_\tau /\nu _{\textrm{w}} \gtrsim 67\), as illustrated in Fig. 11. In this context, the constant \({C_k = 5.8}\) has been utilised to fit the logarithmic-linear asymptote to the current dataset. This logarithmic behaviour suggests that the roughness approaches the fully rough regime, a concept originally introduced by Nikuradse (1933). The simulation results of \(\Delta U/U_\tau \) by MacDonald et al. (2019) also exhibit a tendency towards the logarithmic-linear asymptote, albeit with a different constant value of \({C_k = 4.8}\), but at a somewhat lower value of \(kU_\tau /\nu _{\textrm{w}} \gtrsim 40\). This discrepancy in the onset of the fully rough regime between our present study and the work of MacDonald et al. (2019) can perhaps be attributed to the differences between channel and boundary layers, and perhaps also due to the uncertainty in determining \({\Delta U^+}\) in experiments. For completeness, the inset of Fig. 11 plots the roughness functions from the current dataset and MacDonald et al. (2019) as functions of the equivalent sand-grain roughness height, denoted as \({k_s U_\tau /\nu _{\textrm{w}}}\). The ratio of \(k_s/k\) for our current results is \(k_s/k = 2.8\), while for MacDonald et al. (2019), it is \(k_s/k = 4.1\). These values are derived by aligning \(\Delta U/U_\tau \) with the fully rough asymptote \({\Delta U^+ = \kappa ^{-1} \textrm{log}(k_s U_\tau /\nu _{\textrm{w}}) + A - C_N}\), where \(C_N = 8.5\) represents Nikuradse’s fully rough constant (Nikuradse 1933).
The temperature roughness function, \(\Delta \Theta /\Theta _\tau \), derived from the current experiments, remains approximately constant (\({\Delta \Theta /\Theta _\tau \approx 4.3}\)) across the entire tested range of \({41 \lesssim kU_\tau /\nu _{\textrm{w}} \lesssim 158}\). This trend aligns well with the findings reported by MacDonald et al. (2019). The inset of Fig. 11. In both studies, it is observed that \({k_s U_\tau /\nu _{\textrm{w}}}\) reaches a plateau when \({k_s U_\tau /\nu _{\textrm{w}}\gtrsim 160}\).
The distinct different trends observed between \({\Delta U/U_\tau = f(k U_\tau /\nu _{\textrm{w}})}\) and \({\Delta \Theta /\Theta _\tau \ne f(k U_\tau /\nu _{\textrm{w}})}\) are indicative of the breakdown of the Reynolds analogy between momentum and heat transfer (MacDonald et al. 2019). This observation aligns with the recent findings of Abu Rowin et al. (2024), which suggest that the onset of this breakdown occurs when the roughness approaches a fully rough condition. The study by Abu Rowin et al. (2024) indicates that the changes in heat transfer with varying \(k^+\) may be linked to localised heat transfer over the roughness. Specifically, it suggests that lower heat transfer rates are anticipated at the reversed-flow regions of the roughness compared to the exposed regions experiencing high shear rates.
In summary, Fig. 11 illustrates that the experimental results for the velocity and temperature roughness functions of the 3D sinusoidal surface closely match the minimal channel DNS results for the same surface within the specified uncertainty limits of the experiments. Future efforts aimed at refining these types of measurements could focus on minimising errors through direct wall shear stress measurements and improved strategies for assessing conductive and radiative heat losses.
6 Conclusion
This manuscript provides complete details on commissioning a heated wind tunnel facility designed to accurately measure heat transfer over smooth and rough surfaces. A comprehensive review and comparison of various measurement techniques and methods are also presented to highlight the main sources of uncertainty involved in heated wall measurements.
The present findings demonstrate that variations in the slope of the inner-scaled mean temperature profile in the log region, denoted as \(\kappa _h\), measured over a heated smooth wall within the range of \({900 \lesssim \textrm{Re}_\tau \lesssim 3700}\) have only a marginal influence on the estimation of friction temperature and heat transfer coefficient when employing the Clauser fit approach. A comparative analysis between results derived from the Clauser fit method and those obtained from direct heat transfer techniques using power metres confirms this observation. The results also show that the enthalpy thickness method of measuring the heat transfer coefficient is not recommended due to several factors including, insufficient tripping at low tunnel velocities, lack of thermal insulation between the initial tile and the upstream tunnel wall, and the presence of weak secondary flows.
The temperature measurements over a rough wall (3D sinusoidal roughness) indicate that \(\kappa _h\) remains independent of \(\textrm{Re}_\tau \) within the tested range of \({2300 \lesssim \textrm{Re}_\tau \lesssim 10{,}400}\). Notably, the experimental results over the rough wall exhibit good agreement with the data obtained from the 3D sinusoidal surface studied by MacDonald et al. (2019), within the specified uncertainty limits of the experiments. It is worth noting here that rough wall measurements, such as heat transfer coefficient and roughness functions, exhibit a large level of uncertainty. Heat losses can account for a substantial portion of the measured power consumption (up to 5% for un-anodised aluminium plates and up to 30% for anodised plates). Uncertainty in estimating these losses can be a substantial source of error, as can uncertainty associated with the application of the modified Clauser method for measurement of \(U_\tau \) (specifically when the logarithmic intercept is assumed to be unknown).
Drawing from the uncertainty analysis conducted in this study, influenced by both measurement and processing techniques, we propose several recommendations to mitigate sources of uncertainty in heated rough wall measurements. These recommendations include the necessity for direct measurement of wall shear stress, which can aid in estimating the virtual origin and skin friction (i.e. friction velocity), as well as the direct measurement of heat flux, effectively addressing uncertainties related to variations in \(\kappa _h\) with \(\textrm{Re}_\tau \). If direct measurement of wall shear stress using for example a floating element, can be conducted while the heaters are active, it would be possible to account for any changes in the momentum boundary layer arising from gradients in fluid properties near the heated wall. We also stress the importance of accurate assessment and mitigation of heat losses in heated wall measurements, while cautioning against the anodisation of heated test plates. Our study also underscores the critical need for careful control of the heated wall to maintain a constant \(\Theta _{\textrm{w}} - \Theta _\infty \). Finally, the incorporation of a rigorous uncertainty analysis, as outlined in the Appendix of this manuscript, serves as a tool for identifying and addressing any shortcomings in the measurement facility and equipment.
Availability of data and raw materials
Not applicable.
References
Abe H, Kawamura H, Matsuo Y (2004) Surface heat-flux fluctuations in a turbulent channel flow up to \({\rm Re}_\tau \)= 1020 with \({P}r\)= 0.025 and 0.71. Int J Heat Fluid Flow 25(3):404–419
Abu Rowin W, Xia Y (2022) Heated floor tunnel codes. https://github.com/Aburowin/Heated_tunnel
Abu Rowin W, Saurav T, Jelly T, Hutchins N, Chung D (2022) Turbulent forced convection over roughness with different heights and densities. In: Australasian heat and mass transfer conference, number 12-AHMTC
Abu Rowin W, Zhong K, Saurav T, Jelly T, Hutchins N, Chung D (2024) Modelling the effect of roughness density on turbulent forced convection. J Fluid Mech 979:A22
Adhikari R, Wood D, Pahlevani M (2020) An experimental and numerical study of forced convection heat transfer from rectangular fins at low Reynolds numbers. Int J Heat Mass Transf 163:120418
Alcántara-Ávila F, Hoyas S, Pérez-Quiles MJ (2021) Direct numerical simulation of thermal channel flow for. J Fluid Mech 916:A29
Anders J (1990) Outer-layer manipulators for turbulent drag reduction. Viscous Drag Reduct Bound Layers 123:263–284
Antonia RA, Danh HQ (1977) Structure of temperature fluctuations in a turbulent boundary layer. Phys Fluids 20:1050–1057
Blair M (1983) Influence of free-stream turbulence on turbulent boundary layer heat transfer and mean profile development, Part I—experimental data. J Heat Transf 105:33–40
Blair M, Werle M (1980) The influence of free-stream turbulence on the zero pressure gradient fully turbulent boundary layer. Technical report, UTRC
Brójo FP, Gonçalves LC, Silva PD (1997) Determination of heat transfer coefficients over ribbed surfaces with infrared thermography. In: Turbo expo: power for land, sea, and air, vol 78675, p V001T07A002. ASME
Chakroun W, Quadri MMA (2002) Heat transfer measurements for smooth and rough tilted semi-cylindrical cavities. Int J Therm Sci 41(2):163–172
Chakroun W, Taylor RP (1993) Heat transfer and fluid dynamics measurements in accelerated rough-wall boundary layer. In: Turbo expo: power for land, sea, and air. ASME
Chan L, MacDonald M, Chung D, Hutchins N, Ooi A (2015) A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J Fluid Mech 771:743–777
Choi KS (1993) Breakdown of the Reynolds analogy over drag-reducing riblets surface. In: Nieuwstadt FTM (ed) Advances in turbulence IV. Springer, Berlin, pp 149–154
Choi KS, Hamid S (1991) Heat transfer study of riblets. In: Choi KS (ed) Recent developments in turbulence management. Springer, Berlin, pp 25–41
Choi K-S, Orchard D (1997) Turbulence management using riblets for heat and momentum transfer. Exp Therm Fluid Sci 15(2):109–124
Chung D, Hutchins N, Schultz M, Flack K (2021) Predicting the drag of rough surfaces. Annu Rev Fluid Mech 53:439–471
Clauser F (1954) Turbulent boundary layers in adverse pressure gradients. J Aeronaut Sci 21(2):91–108
Crawford M, Kays W, Moffat R (1980) Full-coverage film cooling—part I: comparison of heat transfer data for three injection angles. J Eng Power 102:1000–1005
Dipprey D, Sabersky R (1963) Heat and momentum transfer in smooth and rough tubes at various Prandtl numbers. Int J Heat Fluid Flow 6(5):329–353
Endrikat S, Newton R, Modesti D, García-Mayoral R, Hutchins N, Chung D (2022) Reorganisation of turbulence by large and spanwise-varying riblets. J Fluid Mech 952:A27
Fisher EM, Eibeck PA (1990) The Influence of a horseshoe vortex on local convective heat transfer. J Heat Transf 112(2):329–335
Gurka R, Liberzon A, Hetsroni G (2004) Detecting coherent patterns in a flume by using PIV and IR imaging techniques. Exp Fluids 37:230–236
Hama F (1954) Boundary-layer characteristics for smooth and rough surfaces. Trans Soc Nav Archit Mar Eng 62:333–358
Hippensteele SA, Russell LM (1988) High-resolution liquid-crystal heat-transfer measurements on the end wall of a turbine passage with variations in Reynolds number. In: NHTC, number NASA-TM-100827
Hippensteele SA, Russell LM, Torres FJ (1987) Use of a liquid-crystal, heater-element composite for quantitative, high-resolution heat transfer coefficients on a turbine airfoil, including turbulence and surface roughness effects. Technical report
Hoffmann P, Perry A (1979) The development of turbulent thermal layers on flat plates. Int J Heat Mass Transf 22(1):39–46
Hosni M, Coleman HW, Taylor RP (1991) Measurements and calculations of rough-wall heat transfer in the turbulent boundary layer. Int J Heat Mass Transf 34(4–5):1067–1082
Incropera FP, DeWitt DP, Bergman TL, Lavine AS et al (1996) Fundamentals of heat and mass transfer, vol 6. Wiley, New York
Jayamaha S, Wijeysundera N, Chou S (1996) Measurement of the heat transfer coefficient for walls. Build Environ 31(5):399–407
Jayatilleke CLV (1966) The influence of prandtl number and surface roughness on the resistance of the laminar sub-layer to momentum and heat transfer
Kader B (1981) Temperature and concentration profiles in fully turbulent boundary layers. Int J Heat Mass Transf 24(9):1541–1544
Kays WM, Crawford ME, Weigand B (2005) Convective heat and mass transfer. McGraw-Hill, New York
Kevin K (2018) Reorganising wall turbulence using directional surface roughness. PhD thesis, University of Melbourne
Kitamura K, Kimura F (1995) Heat transfer and fluid flow of natural convection adjacent to upward-facing horizontal plates. Int J Heat Mass Transf 38(17):3149–3159
Lau S, Kukreja R, McMillin R (1991a) Effects of v-shaped rib arrays on turbulent heat transfer and friction of fully developed flow in a square channel. Int J Heat Mass Transf 34(7):1605–1616
Lau S, McMillin R, Han J (1991b) Turbulent heat transfer and friction in a square channel with discrete rib turbulators. J Turbomach 113:360–366
Léon O, Reulet P, Chedevergne F (2020) Aerodynamic and heat transfer effects of distributed hemispherical roughness elements inducing step changes in a turbulent boundary layer. Int J Heat Fluid Flow 85:108672
Ligrani PM, Moffat RJ (1985) Thermal boundary layers on a rough surface downstream of steps in wall temperature. Bound-Layer Meteorol 31(2):127–147
MacDonald M, Hutchins N, Chung D (2019) Roughness effects in turbulent forced convection. J Fluid Mech 861:138–162
Marusic I, Monty JP, Hultmark M, Smits AJ (2013) On the logarithmic region in wall turbulence. J Fluid Mech 716:R3
Mayo I, Virgilio M, Cernat BC, Arts T (2018) Measurement uncertainty in liquid crystal thermography applied to internal cooling research: two practical examples. In: Vol. 5B heat transfer, p V05BT13A011, Oslo, Norway, June 2018. American Society of Mechanical Engineers. ISBN 978-0-7918-5109-8
Moffat R (1988) Describing the uncertainties in experimental results. Exp Therm Fluids Sci 1(1):3–17
Moretti P, Kays W (1965) Heat transfer to a turbulent boundary layer with varying free-stream velocity and varying surface temperature-an experimental study. Int J Heat Mass Transf 8(9):1187–1202
Mukerji D, Eaton JK, Moffat RJ (2004) Convective heat transfer near one-dimensional and two-dimensional wall temperature steps. J Heat Transf 126(2):202–210
Nagib HM, Chauhan KA (2008) Variations of von Kármán coefficient in canonical flows. Phys Fluids 20(10):101518
Nagib HM, Chauhan KA, Monkewitz PA (2007) Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Philos Trans R Soc 365(1852):755–770
Nakamura H, Yamada S (2013) Quantitative evaluation of spatio-temporal heat transfer to a turbulent air flow using a heated thin-foil. Int J Heat Mass Transf 64:892–902
Nikuradse J (1933) Laws of flow in rough pipes. In: VDI Forschungsheft
Orlandi P, Sassun D, Leonardi S (2016) DNS of conjugate heat transfer in presence of rough surfaces. Int J Heat Mass Transf 100:250–266
Örlü R, Alfredsson PH (2010) On spatial resolution issues related to time-averaged quantities using hot-wire anemometry. Exp Fluids 49:101–110
Patel A, Boersma BJ, Pecnik R (2017) Scalar statistics in variable property turbulent channel flows. Phys Rev Fluids 2(8):084604
Perry A, Hoffmann P (1976) An experimental study of turbulent convective heat transfer from a flat plate. J Fluid Mech 77(2):355–368
Pirozzoli S, Bernardini M, Orlandi P (2016) Passive scalars in turbulent channel flow at high Reynolds number. J Fluid Mech 788:614–639
Pirozzoli S, Romero J, Fatica M, Verzicco R, Orlandi P (2022) DNS of passive scalars in turbulent pipe flow. J Fluid Mech 940:A45
Schlatter P, Örlü R (2010) Assessment of direct numerical simulation data of turbulent boundary layers. J Fluid Mech 659:116
Scibilia M-F (2000) Heat transfer in a forced wall jet on a heated rough surface. J Therm Sci 9(1):85–92
Siegel R (2001) Thermal radiation heat transfer. CRC Press, Boca Raton
Squire DT, Morrill-Winter C, Hutchins N, Schultz MP, Klewicki JC, Marusic I (2016) Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J Fluid Mech 795:210–240
Subramanian C, Antonia R (1981) Effect of Reynolds number on a slightly heated turbulent boundary layer. Int J Heat Mass Transf 24:1833–1846
Talluru K, Kulandaivelu V, Hutchins N, Marusic I (2014) A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas Sci Technol 25(10):105304
Tanda G (2004) Heat transfer in rectangular channels with transverse and v-shaped broken ribs. Int J Heat Mass Transf 47(2):229–243
Taylor RP, Coleman HW, Hosni M, Love PH (1989) Thermal boundary condition effects on heat transfer in the turbulent incompressible flat plate boundary layer. Int J Heat Mass Transf 32:1165–1174
Virgilio M, Dedeyne JN, Van Geem KM, Marin GB, Arts T (2020) Dimples in turbulent pipe flows: experimental aero-thermal investigation. Int J Heat Mass Transf 157:119925
Wagner S, Shishkina O (2015) Heat flux enhancement by regular surface roughness in turbulent thermal convection. J Fluid Mech 763:109–135
Walsh M (1990) Riblets. Viscous drag reduction in boundary layers: progress in astronautics and aeronautics
Watmuff JH (1998) Detrimental effects of almost immeasurably small freestream nonuniformities generated by wind-tunnel screens. AIAA J 36(3):379–386
White FM, Majdalani J (2006) Viscous fluid flow, vol 3. McGraw-Hill, New York
Xia Y, Abu Rowin W, Jelly T, Marusic I, Hutchins N (2022) Investigation of cold-wire spatial and temporal resolution issues in thermal turbulent boundary layers. Int J Heat Fluid Flow 94:108926
Zhong K, Hutchins N, Chung D (2023) Heat-transfer scaling at moderate Prandtl numbers in the fully rough regime. J Fluid Mech 959:A8
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. The authors gratefully acknowledge the support of the Australian Research Council (ARC) and Mitsubishi Heavy Industries (MHI), via the ARC Linkage program (LP180100712).
Author information
Authors and Affiliations
Contributions
W.A., Y.X. and S.W. conducted the experiments, analysed the data and prepared the figures. W.A. and Y.X. wrote the manuscript. N.H. conceptualised the research, provided supervision and developed the key ideas. All the authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors report no Conflict of interest.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendices
Appendices
1.1 Appendix 1: Uncertainty analysis
Various sources of uncertainty contribute to the observed differences in the experimental results. In this section, we categorise these sources of uncertainty into two distinct classes: measurement uncertainty, which encompasses variables like equipment precision (as shown in Appendix 1), and processing or data analysis uncertainty, which can arise from the manipulation of data, such as determining the inner scale parameters through the application of the Clauser fit (as discussed in Appendix 2). It is crucial to emphasise that all uncertainties discussed here are expanded uncertainties. The figures presented in the main body of this work feature error bars of combined uncertainty stemming from these two primary sources. It is important to note that estimates of uncertainty are also expected to vary depending on the test surface (i.e. smooth or rough). Notably, the presence of roughness elements introduces distinct sources of uncertainty, such as radiative heat loss and wall-normal virtual origin. Consequently, the following sections are structured to expound upon uncertainty analysis in the contexts of both smooth and rough surfaces.
1.1.1 Appendix 1.1: Smooth wall measurement uncertainty
Quantifying the measurement uncertainty is typically not straightforward due to the coupled effect when different equipment/devices are used for measurements. One of the ways to estimate the percentage of measurement uncertainty is the propagation of error method. The error for a quantity with this method is estimated as,
where \(\epsilon \) is the error of a parameter, X is the parameter that we wish to obtain the error for, \({\frac{\partial X}{\partial A_i}}\) is the partial derivative of X with respect to \(A_i\) where \(A_i\) is a variable that X depends on (i.e. \({X = f(A_i)}\)) and N is the number of variables. It worth noting that based on the expression in (9), if the uncertainty of each parameter \(\epsilon (A_i)\) is expanded, the resulting uncertainty \(\epsilon (X)\) will also be expanded.
An example of using the propagation of error (9) to get the error of Stanton number as computed from the power consumption (4), where the subscript ‘P’ indicates a parameter obtained from the power consumption measured by the power metre, yields
The uncertainty of \(\Theta _{\textrm{w}}\) and \(\Theta _\infty \) are obtained from the thermocouple calibration. We also apply propagation of error for \(\epsilon (\rho _\infty ), \epsilon (c_{p})\) and \(\epsilon (U_\infty )\), where \({\rho _\infty = f(p,\Theta _\infty )}\), \({C_{p} = f(\Theta _\infty )}\) and \(U_\infty = f(p, \Theta )\), where p is the pressure measured by the Pitot-static tube. While the uncertainties provided by manufacturers, such as those for the differential pressure sensor or thermistor, may not explicitly state whether they are expanded uncertainties, we have treated them as such due to their inclusion of biased errors. Additionally, uncertainties reported with notations such as the expression ‘±’ are assumed to be expanded uncertainties in our analysis.
The uncertainty of \(q_{\textrm{conv}}''\) is obtained from the difference between \(\overline{P_{\textrm{DC}}}\) and \(\overline{P_{\textrm{osc}}}\). As described in Sect. 4.2, the main source of uncertainty here arises from the emissivity term to account for the radiative heat losses. To predict the emissivity, we followed a specific procedure involving thermal imaging with a FLIR T1040 thermal camera. We covered a portion of the heated rough plate with electrical tape, which has an approximate emissivity of \(\varepsilon \approx 0.95\). The measurement setup ensured controlled conditions with no direct radiative interference apart from the camera user. We recorded the actual surface temperature as captured by the thermal camera on the electrical tape; while, the temperature on an area without the tape remained considerably lower. The apparent surrounding temperature is included in the camera setting to account for energy radiated by the surroundings on the test surface. We then adjusted the emissivity on the camera’s settings until the surface temperature matched that of the tape. As previously discussed in Sect. 4.2, an alternative method to determine the true surface temperature is to employ an embedded thermocouple for direct temperature measurement instead of reading the signal on the electrical tape. While we observed minimal temperature differences between the thermocouple and the thermal camera reading on the electrical tape in our current measurements, we recommend using the tape approach. This approach accounts for potential temperature changes caused by the reflection of nearby sources, ensuring greater accuracy. The total uncertainty associated with estimating \(q_{\textrm{loss}}\) for a smooth wall is determined to be \(\epsilon (q_{\textrm{loss}}) = 3\) W.
Accounting for all these errors in Eq. (10), \(\epsilon (St_P)\) is estimated to be ±\(0.14\times 10^{-3}\) to ±\({0.10\times 10^{-3}}\) for freestream velocities ranging from \({U_\infty = 8}\) to 30 m s\(^{-1}\), respectively. The lower uncertainty at higher freestream velocities is due to the fact that the heat loss compared to the total power usage becomes relatively smaller. We apply the same methodology to assess the uncertainty of \({\Theta _\tau = q_{\textrm{conv}}^{\prime \prime }/(\rho _{\textrm{w}} c_{p} U_\tau )}\), and for a smooth wall, we determine it to be \({\epsilon (\Theta _{\tau ,P}) = }\)±\({0.13-0.05~^\circ }\)C for \({U_\infty = 8}\) to 30 m s\(^{-1}\). All the smooth wall measurement uncertainties are included in Table 3.
1.1.2 Appendix 1.2: Rough wall measurement uncertainty
Estimating the emissivity of a rough surface presents a greater challenge compared to smooth surfaces, primarily due to the surface reflections caused by the roughness elements. We did not make the assumption that the emissivity of the rough wall is similar to that of the un-anodized aluminium smooth wall (\(\varepsilon \approx 0.09\)). This decision was based on the fact that the current rough wall is machined in-house, and the effect of surface texture and finish on emissivity is unknown. This inherent complexity leads to increased uncertainty in the determination of radiative heat loss, as discussed in Appendix 1.1. Consequently, \(\epsilon (q_\textrm{loss})\) for the rough wall is estimated to be 10 W. This larger uncertainty translates into corresponding uncertainties for \({\epsilon (St_P)}\) of approximately \({0.21\times 10^{-3}}\) to \({0.09\times 10^{-3}}\), over the freestream velocity range of \({U_\infty = 8}\) to 30 m s\(^{-1}\), respectively. Detailed information regarding the measurement uncertainties for rough wall experiments is included in Table 3.
1.2 Appendix 2: Processing uncertainty
1.2.1 Appendix 2.1: Smooth wall processing uncertainty
In the previous section, we were able to employ propagation of error Eq. (9), since most of the parameters involved had explicit expressions and straightforward partial derivatives. However, parameters such as \(U_\tau \), \(\Delta U/U_\tau \) and \(\Delta \Theta /\Theta _\tau \) are obtained through a sequence of calculations. For such quantities, a more generalised technique of error estimation, as proposed by Moffat (1988), is deployed. This method suggests that the error in a quantity X can be estimated from,
where \(A_i\) is a variable on which X depends, and \(\epsilon (A_i)\) is the uncertainty in that variable. A significant processing step that introduces notable variations in the results is the utilisation of the Clauser method to derive \(U_\tau \) and \(\Theta _\tau \) from the mean streamwise velocity and temperature profiles, respectively. In the case of a mean streamwise velocity profile for a smooth wall, the gradient \(\kappa ^{-1}\) and the intercept A within the logarithmic region are typically constant and reasonably well-established. Here, we assume that \(\kappa \) and A are constants for the smooth wall. Another processing step that can significantly impact the results is the choice of limits for the logarithmic region. In the literature for the smooth wall, the limits for the logarithmic region are not well-defined and vary from \(zU_\tau /\nu _{\textrm{w}} = 30\) to 200 for the lower limit and from \(zU_\tau /\nu _{\textrm{w}} = 0.1 \textrm{Re}_\tau \) to \(0.15 \textrm{Re}_\tau \) for the upper limit (Squire et al. 2016; Marusic et al. 2013). Upon a close check of the velocity and temperature diagnostic functions (\(\beta _U\) and \(\beta _\Theta \), see Sect. 4.3), we determine that the reliable velocity and temperature logarithmic region limits for the smooth wall is \(80 \lesssim zU_\tau /\nu _{\textrm{w}} \lesssim 0.15 \textrm{Re}_\tau \). Thus, here we do not consider uncertainty due to the variations of the logarithmic region limits. From this analysis, we find that the uncertainty associated with using the Clauser method to estimate \(U_\tau \) for a smooth wall is \(\epsilon (U_{\tau ,C}) = 0.038 - 0.051\) m s\(^{-1}\) for \({U_\infty = 8 - 30}\) m s\(^{-1}\), where the subscript ‘C’ indicates parameters obtained from the Clauser method. It is essential to note that this \(\epsilon (U_{\tau ,C})\) encompasses all the uncertainties linked to wall location detection issues due to the use of imaging system and manufacturer (see \(\epsilon (z)\) in Table 3), and all other equipment and device uncertainties, such as \(\epsilon (\rho _\infty )\), \(\epsilon (c_{p})\), and \(\epsilon (U_\infty )\), which can influence the value of \(U_\tau \). From this uncertainty analysis of \(U_\tau \), we now use the propagation of error (9) for \(C_f\) and St for Eqs. (1) and (8), respectively. We find \(\epsilon (C_{f,C}) \approx 0.76\times 10^{-3} - 0.35\times 10^{-3}\) and \(\epsilon (St_C) \approx 0.32\times 10^{-3} - 0.12\times 10^{-3}\) for the smooth wall.
1.2.2 Appendix 2.2: Rough wall processing uncertainty
In the current rough wall investigation, to shed light on the expected uncertainty in the modified Clauser fit, we only allow the intercept to be an unknown variable while maintaining a fixed gradient of \(\kappa ^{-1}\) for the mean viscous-scaled velocity profile within the logarithmic region. This approach diverges from the classical Clauser technique for smooth walls, where both A and \(\kappa \) are assumed to be known, and \(U_\tau \) is extracted to minimise the regression error between the log-law and the viscous-scaled measured mean profile. The reason for not allowing \(\kappa \) also to vary here is that as shown from previous DNS studies over 3D sinusoidal surface (e.g. MacDonald et al. 2019; Zhong et al. 2023; Abu Rowin et al. 2024), this roughness geometry does not alter \(\kappa \) or \(\kappa _h\).
Like for the smooth wall, the logarithmic region limits are not well-defined for rough walls. For the 3D sinusoidal roughness in our study, we selected fixed logarithmic limits ranging from the roughness sublayer \((0.5\lambda ) U_\tau /\nu _{\textrm{w}}\) to \(0.15 \textrm{Re}_\tau \) for velocity and temperature profiles. As a result, we do not introduce additional uncertainty for \(\epsilon (U_{\tau ,C})\), \(\epsilon (C_{f,C})\), and \(\epsilon (St_C)\) due to varying the logarithmic limits. The uncertainties associated with employing the modified Clauser fit for the rough wall is then, \({\epsilon (U_{\tau ,C}) = 0.044 - 0.076}\) m s\(^{-1}\), \({\epsilon (C_{f,C}) \approx 1.09\times 10^{-3}} - {0.70\times 10^{-3}}\), and \({\epsilon (St_C) \approx 0.58\times 10^{-3}} - {0.22\times 10^{-3}}\) for \({U_\infty = 8 - 30}\) m s\(^{-1}\), respectively.
The above uncertainty estimates exclude the effect of the virtual origin, which can lead to significantly higher uncertainty when applying the modified Clauser method. To assess the effect of the virtual origin (d), we shifted the origin to both the mid-plane and the crest of the roughness. These changes resulted in variations of approximately 16.0% and 14.0% for \(U_\tau \) and \(\Theta _\tau \), respectively. It is important to note that the uncertainty resulting from varying the virtual origin to these extreme limits likely represents an overestimate of the error associated with d, representing a worst-case scenario. In our current study, the virtual origin was directly obtained from the DNS data of Abu Rowin et al. (2022) for a surface comparable to the one used in our research. Therefore, its effect was not considered as a source of error. Detailed information regarding processing uncertainties for the rough wall case is also provided in Table 3.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abu Rowin, W., Xia, Y., Wang, S. et al. Accurately predicting turbulent heat transfer over rough walls: a review of measurement equipment and methods. Exp Fluids 65, 86 (2024). https://doi.org/10.1007/s00348-024-03812-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-024-03812-1


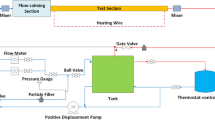






 ) left axis, current i(t) (
) left axis, current i(t) ( ) red right axis and power
) red right axis and power  ) blue right axis obtained by the oscilloscope for a PWM input single to a SSR, varying from 0 to 5 volts shown with (
) blue right axis obtained by the oscilloscope for a PWM input single to a SSR, varying from 0 to 5 volts shown with ( ), at
), at 





