The effect of high values of relative surface roughness on heat transfer and pressure drop characteristics in the laminar, transitional, quasi-turbulent and turbulent flow regimes

Abstract

This study investigated the effect of large values of relative surface roughness on the heat transfer and pressure drop characteristics using simultaneously measured heat transfer and pressure drop data. Experiments were conducted using a horizontal circular tube with a base inner diameter of 5 mm and length of 4 m. One smooth and two rough tubes, with relative roughnesses of 0.04 and 0.11, were tested at different constant heat fluxes between Reynolds numbers of 100 and 8 500. Water was used as the test fluid and the Prandtl number varied between 3 and 7. Contrary to the trend in the Moody Chart, a significant increase in laminar friction factors with increasing surface roughness was observed. Both the friction factors and Nusselt numbers as functions of Reynolds number showed a clear upward and leftward shift with increasing surface roughness across the different flow regimes. Furthermore, the boundaries between the flow regimes were the same for the pressure drop and heat transfer results. The width of the transitional flow regime was narrower for rough tubes and had a differing trend. The quasi-turbulent and turbulent flow regimes occurred at lower Reynolds numbers for increasing roughness. When investigating the relationship between heat transfer and pressure drop, it was found that an increase in surface roughness favoured heat transfer in the quasi-turbulent flow regime. This is useful for rough tubes as the quasi-turbulent flow regime onsets early with regards to the Reynolds number in tubes with large roughnesses.

1 Introduction

Heat exchangers play vital roles in numerous industries and aid cycles by rejecting or consuming heat, thereby maintaining the heat transfer between fluids in a process. Improving the efficiency of industrial processes directly depends on improving the effectiveness of heat transfer equipment, for example, heat exchangers. On improving the effectiveness of heat exchangers, less energy is consumed in an application for the same heat transfer performance, which decreases operational costs.

Single-phase flow through tubes can be classified into four flow regimes [1]: laminar, transitional, quasi-turbulent, and turbulent. In practice, engineers are advised to design heat exchangers to operate within the laminar and turbulent flow regimes due to limited design information outside of these two flow regimes. Engineers design for high heat transfer rates and low pressure drops, as optimized heat transfer is excellent for improved efficiency, while the required pumping power (and thus operational running costs) can be minimized by reducing the pressure drops. The laminar flow regime has low pressure drops and low heat transfer rates compared to the turbulent flow regime, which has high heat transfer rates and high pressure drops. For some cases, the optimum operating range would be in or close to the transitional flow regime, because the heat transfer rate is better than in the laminar flow regime, while the pressure drop is smaller compared to that in the turbulent flow regime. Furthermore, heat exchangers that were not designed to operate in the transitional flow regime might later on operate in this regime due to scaling and corrosion that changes the flow characteristics, or due to additional equipment and possible changes concerning the operating conditions [2].

Due to their importance in our everyday lives, fluid flow characteristics were investigated from as early as 1883 [3]. The initial research was primarily focused on the laminar and turbulent flow regimes, while studies on transitional flow began in the 1990s. The initial research on transitional flow focussed on the effect of inlet geometries on the isothermal and diabatic friction factors, as well as the heat transfer coefficients using a constant heat flux boundary condition and ethylene glycol–water mixtures with Prandtl numbers between 40 and 160 [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Studies that considered a constant surface temperature boundary condition used water, with Prandtl numbers of approximately 7, as the test fluid [2, 18,19,20,21]. Overall, it was concluded that the onset of the transitional flow regime was delayed for smoother inlet geometries, as well as increasing heat fluxes. An increase in heat flux also increased the friction factors and heat transfer coefficients in the laminar and transitional flow regimes, but had a negligible effect in the turbulent flow regime. Thereafter, a series of studies were conducted investigating the effect of enhanced tubes [20, 21], mixed convection [1, 22], developing flow [23,24,25,26], flow regime boundaries [27], nanofluids [28,29,30], multiple tubes [31], twisted tape inserts [32], annuli [33, 34], inclination angles [22, 35] and forced convection [36] on transitional flow. These studies, however, were all limited to transitional flow through smooth tubes, except for the studies conducted using enhanced tubes [20, 21] and a recent study that investigated tubes with low values of relative surface roughness [37].

Enhanced tubes have been proven effective to enhance heat transfer and thus increase the efficiency by creating turbulence and flow rotation along the axial direction of the tube [15, 20, 21]. Older literature termed some of these studies on enhanced tubes as artificial roughness. However, enhanced tubes differ from ‘natural roughness’ [38], for example - gluing sand grains, electroplating, corrosion, and scaling, because of its differing shape, size, randomness, asymmetry, and nonuniformity. Fluid flow properties are highly dependent on the surface roughness type. According to Webb et al. [39], flow lines would follow the shape of the element and only reattach a distance six to eight times the height of the element, therefore fluid flow characteristics of rough and enhanced tubes may differ and should be studied separately [37, 39, 40].

The relative surface roughness is the ratio of the mean height of the surface roughness inside the tube to the inner tube diameter [41] and has been studied extensively. Unfortunately, theoretical analysis cannot produce a functional form showing the dependence of pressure drop on fluid flow in rough tubes as there are many unknown variables in the analysis. The dependence was rather shown through an experimental analysis where artificially rough surfaces were produced and then tested. As early as 1858, Darcy concluded from experimental pressure drop results that flow through tubes depended on the surface roughness, slope, and tube diameter [42]. This was followed by pioneering work conducted by Nikuradse [41], who conducted rough tube experiments by gluing sand grains of different sizes to the inside surface of tubes, and Colebrook and White [43], who developed an implicit relation to quantify the effect of relative roughness on the friction factors. The widely used Moody chart [42] is essentially the Colebrook equation plotted over a range of Reynolds numbers and relative surface roughnesses.

Many studies focussed on the effects of surface roughness on pressure drop, however, less studies investigated the effects of surface roughness on heat transfer and are mostly limited to micro- and mini-tubes [15, 44,45,46,47,48,49,50,51,52,53,54,55]. This is mainly due to challenges associated in roughening the inner surfaces of tubes without adding a thermal resistance layer to the inside of the tube or changing the physical properties of the tube [37, 38, 56]. It is also generally easier to obtain significant relative roughnesses in micro- and mini-tubes than in macro-tubes, due to the smaller diameters of the tubes. Meaningful relative surface roughness can be obtained in mini- and micro-tubes using acid etching methods [55, 57,58,59], sanding [60], or by considering the surface finish of the tube itself when the diameters are minimal [8]. Smooth micro-tubes and rough macro-tubes may have the same relative surface roughness value.

Numerous studies concerning the effect of relative surface roughness on the friction factors in the transitional flow regime using micro- and mini-channels as well as micro- and mini-tubes, have been conducted. A commonality across the studies suggests that the critical Reynolds number of the transitional flow regime occurs at lower Reynolds numbers when the surface roughness increases [8, 55, 57,58,59, 61]. Tam et al. [55] and Ghajar et al. [8] found that in larger tubes (> 0.84 mm), the transitional flow regime was not influenced by surface roughness, whereas in smaller tubes (≤ 0.84 mm), the onset of transitional flow regime was advanced for increasing relative surface roughness. Ghajar et al. [8] noted a considerably higher effective surface roughness (ε_eff) than the measured mean roughness (Ra); this was due to tolerances and non-uniformities caused by the tube's smaller diameter (micro-channels). A smaller diameter partially explains the differences observed between the behaviour of mini- and micro-channels of the same relative surface roughness, determined by Ra. When investigating both the isothermal and the diabatic friction factors, Tam et al. [55] discovered that heating resulted in a delayed onset of the transitional flow regime, but had a negligible effect on the end of the transitional flow regime. Everts and Meyer [23] found similar results when investigating smooth tubes. Tam et al. [55] concluded that the effect of surface roughness on transitional flow was greater at the onset than at the end. Therefore, it also impacted the prominence and width of the transitional flow regime, representing the Reynolds number range in which transition occurs [55].

Limited studies investigated the effect of relative surface roughness on the friction factors on the transitional flow regime using macro-tubes. Nikuradse [41] and Huang et al. [40, 62] roughened their tubes by gluing sand grains of different sizes to the inside. The results of these studies, focusing solely on isothermal friction factors, concluded an inverse relationship between surface roughness and the critical Reynolds number and found that as surface roughness increased, the critical Reynolds number decreased. Additionally, the width of the transitional flow regime decreased.

Kandlikar et al. [58] and Everts et al. [37, 56, 63] conducted studies that considered the influence of surface roughness on heat transfer in the transitional flow regime. Kandlikar et al. [58] considered the effects of heat transfer in stainless-steel mini-tubes with diameters of 1 067 μm and 620 μm. The internal surfaces of these tubes were acid etched, which resulted in average surface roughnesses measuring between 0.001 and 0.003. In the 1 067 μm tube, it was found that the surface roughness had no effect. In the smaller 620 μm tube, with the same relative surface roughness as the larger tube, it was found that there was an increase in Nusselt numbers in the laminar flow regime and the transitional flow regime started earlier. Everts et al. [56, 63] focused explicitly on the transitional flow regime in rough tubes by gluing uniformly sized sand grains to the inside of copper tubes using cyanoacrylate. It was found that the surface roughness resulted in increased heat transfer coefficients and advanced the onset of transitional flow regime. Due to difficulty characterizing the thermal resistance that the cyanoacrylate adhesive and sand grains imparted on the tube, this study was limited to qualitative heat transfer results.

While most studies either focussed on friction factors or heat transfer coefficients, Everts et al. [37] studied the effects of surface roughness on simultaneous heat transfer and pressure drop measurements of fully developed laminar and transitional flow using macro-tubes. Contrary to previous studies, it was found that an increase in surface roughness delayed the onset of the transitional flow regime and decreased the width of the transitional flow regime. Furthermore, to quantify the effect of surface roughness on the onset of the transitional flow regime, three distinct regions were identified and defined. The regions defined were the dampening region (low relative surface roughnesses, typically less than 0.001), enhancing region and saturating region (high relative surface roughnesses, typically larger tan 0.1). Their focus was specifically on the dampening region where the relative surface roughness was less than 0.001. The low surface roughness dampened the effect of the inlet disturbance and caused a delay on the onset of the transitional flow regime. An increase in heat flux caused a further delay in the onset of the transitional flow regime.

Everts et al. [37] also noted that most of the previous studies that investigated the influence of surface roughness in the transitional flow regime can be grouped in the enhancing region and more studies are required to further our understanding of the influence of surface roughness in the saturating region. Only the study of Wu and Little [45] that investigated gas flow through fine channels in the laminar and turbulent flow regimes, considered large relative roughnesses which can typically be expected to fall in the saturating region. These test sections had unique features such as large asymmetric and random relative roughnesses, which made it challenging to quantify the relative roughness of the tube. Due to the unique roughness features, it was found that the Reynolds analogy no longer applied and that the experimental data did not correlate with the general rough tube correlations, which were developed for artificial rough tubes and rough tubes of close-packed sand grains.

The challenge in obtaining large relative roughnesses in macro-tubes, without creating a significant thermal resistance layer, is probably one of the main reasons why limited studies investigated the effects of large relative roughness on the heat transfer characteristics of single-phase flow through tubes. The purpose of this study was therefore to experimentally investigate the effect of large relative surface roughnesses on the simultaneous heat transfer and pressure drop characteristics of transitional and quasi-turbulent flow through horizontal tubes.

2 Experimental set-up and test section

The experimental set-up in Fig. 1 was a closed-loop system in which water was pumped from a thermostat-controlled bath and tank through a filter, flow meter, mixers, flow-calming section, test section, and back to the storage tank. A secondary closed-loop system was connected to the tank to maintain a constant temperature by use of a thermostat-controlled bath with a heating power input of 3.5 kW and cooling power input of 0.9 kW.

Fig. 1

Schematic of the experimental set-up that was used to conduct the simultaneous heat transfer and pressure drop experiments. The test section shown in orange was changed for each relative roughness test

A 420 ℓ/hr magnetic gear pump was used to circulate the water through the system. The speed of the pump was controlled through the Labview program by changing the voltage signal to it. The pump was connected to the flow loop using a rubber hose to dampen vibrations to the test section. A pressure gauge was attached before the flow meters to monitor the pressure of the system. If the pressure went too high, a pressure relief valve allowed the water return to the tank, thus depressurizing the system. To prevent solid particles from being circulated through the system, a 120-micron filter was included. After the filter, a bypass valve was incorporated to increase the backpressure and minimize flow pulsations in the test section in order to improve the accuracy of the results [64]. The mass flow rate was measured by one of two Coriolis flow meters, CMF010 or CMF015, depending on the Reynolds number that was being tested. The two flow meters had a full-scale of 330 ℓ/hr and 108 ℓ/hr, respectively, and accuracies of ±0.05% of the full-scale value, thus 0.165 ℓ/hr and 0.054 ℓ/hr.

The same flow-calming section that was used by Bashir et al. [36] was used in this study to ensure a uniform velocity distribution before the flow entered the test section. The flow-calming section was manufactured from a clear acrylic tube with an outer diameter of 180 mm, length of 616 mm and contraction ratio of 33. Mixers were placed before the flow-calming section and after the test section to mix the fluid before measuring uniform inlet and outlet temperatures. The mixer consisted of alternating left and right-hand helical plates [65] that repeatedly sliced the thermal boundary layers to produce a uniform cross-sectional temperature. The inlet and outlet fluid temperatures were measured using Pt100 probes, which were calibrated to an accuracy of 0.06 °C using a digital thermometer (accuracy of 0.03 °C) and the thermostat-controlled bath.

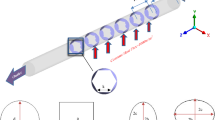
Figure 2 contains a schematic of the test section, indicating the axial positions of the thermocouple stations (A-U) and the pressure taps (P1 and P2). The inlet of the test section was connected flush to the flow-calming section to obtain a square-edged inlet, while the outlet of the test section was connected to the mixing section. To prevent axial heat conduction from the test section to the flow-calming and mixing sections, the flow-calming section flange and mixing section were manufactured from acetal (which has a low thermal conductivity of 0.31 W/m.K).

Fig. 2

Schematic of the test section indicating the axial positions of the thermocouple stations (A-U) and pressure taps (P1 and P2), as well as a cross-sectional view to indicate the alternating thermocouple stations on the left and right side of the test section. The placement of the flow-calming section and the mixing section with respect to the test section is also shown

The test section was manufactured from a hard-drawn copper tube with inner and outer diameters of 5 mm and 6.1 mm, respectively, and a total length of 4 m. The maximum length to diameter ratio, x/D, was 589. A total of 21 thermocouple stations were spaced along the tube length to measure the surface temperatures. As indicated by the cross-sectional view in Fig. 2, each thermocouple station contained three thermocouples to investigate the circumferential temperature distributions caused by free convection effects. Each thermocouple station contained a thermocouple at the top (T1) and bottom (T3) of the test section, while the third thermocouple, T2, alternated between the left and right of the test section along the tube length. The thermocouples were spaced close to each other near the inlet of the test section to accurately capture the developing temperature profile. Furthermore, a length of 400 mm was left between the last thermocouple station, U, and the mixer to prevent upstream effects from influencing the temperature measurements at the last measuring station. Araldite 2014-2 adhesive with a thermal conductivity of 0.34 W/m.K was used to glue the thermocouples into indentations of approximately 50% of the tube’s wall thickness. The thermocouples were calibrated in-situ to an accuracy of 0.1 °C using the thermostat-controlled bath and the calibrated Pt100 probes as the reference temperature.

Pressure taps P1 and P2 in Fig. 2 were made from a 30 mm long capillary tube, which was silver soldered to the test tube. A 0.4 mm diameter hole was drilled through the capillary and test tubes. This hole was less than 10% of the inner diameter of the test section which prevented the pressure taps from affecting the flow through the tube [66]. All burrs were carefully removed from the inside of the tube. A bush tap with a quick-release coupling was installed onto the pressure tap and nylon tubing was used to connect the pressure taps to the pressure transducer which contained interchangeable diaphragms. Three different diaphragms with full-scale values of 2.2 kPa, 14 kPa and 55 kPa were used. The accuracy of each diaphragm was 0.25% of the full-scale value. The pressure transducers were calibrated using Beta T-140 manometers and a water column to accuracies of 5.5 Pa, 35 Pa and 137.5 Pa, respectively.

The pressure taps were placed at the latter part of the test section, 0.97 m apart, where fully developed flow was expected depending on the Reynolds number, heat flux and surface roughness. At a Reynolds number of 1 200, the laminar forced convective [1] and mixed convective [25] thermal entrance lengths were calculated to be 3.8 m and 0.64 m, respectively. The entrance lengths would decrease as the Reynolds number decreases. The average Nusselt numbers and friction factors were calculated in the last 1 m of the test section between the pressure taps (stations O to U in Fig. 2). Therefore, the average Nusselt numbers and friction factors contained fully developed flow for mixed convection conditions but contained some developing flow (depending on the Reynolds number) for forced convection conditions.

Different methods were investigated to obtain a uniform surface roughness on the inside of the tube. Ultimately, a unique roughening method was used to achieve a uniform surface roughness over a tube length of 4 m, while minimizing the additional thermal resistance. Because of their high thermal conductivity, copper particles were glued to the inside of the test section. The copper particles were sifted and sorted according to different sizes (75–150 μm and 150–300 μm) to achieve the different surface roughnesses in the tubes. Soudal Cyanofix 84A was used to glue the copper particles to the inside of the tube, because its low viscosity made it possible to cover the tube with a uniform thin glue layer. To ensure a uniform thin glue layer, the glue was first blown through the tube using pressurized air and thereafter, copper particles were blown through the tube from a pressurized container. The particles and glue formed a ripple texture on the tube surface and the heights depended on the size of the particles used. This ripple texture was the primary degree of roughness that disturbed the flow.

The roughness of the smooth tube was measured using a portable roughness tester, Mitutoyo Surftest SJ-210, with a range of -200 μm to 160 μm and a resolution of 0.02 μm. As the surface roughness of the rough tubes exceeded the ranges of the available instrumentation, the surface roughness was obtained using a milling machine and a dial indicator, which had an accuracy of 12 μm. The tube was cut into 12 sample lengths and three readings were taken at different locations on each sample. The readings were then averaged to get a good representation of the average surface roughness along the tube length and the results are summarised in Table 1. For rough 1, 67% of the measured data fell within one standard deviation, 93% of the data fell within two standard deviations, and all the data fell within three standard deviations. The uniformity of rough 2 was better as 84% of the measured data fell within one standard deviation and 95% within two standard deviations.

Table 1 Summary of the roughness (mm) and relative roughness values for the test sections tested

To obtain a constant heat flux boundary condition, two 0.38 mm diameter constantan heating wires were tightly wound around the test section and connected to a direct current (DC) power supply. The power supply had a range of 0-1.5 kW and accuracy of 3 W. The heating wires were connected in parallel with opposing currents to dampen the electromagnetic interference [67]. Care was taken not to coil the heating wire over the thermocouple junction (where the thermocouple was glued onto the tube) to prevent the surface temperature measurements from being affected. A gap of 1 mm, which was found to be sufficient [67], and was left on either side between the thermocouple junction and the coiled heating wire.

To prevent heat losses from the flow-calming section, test section, and mixers to the surroundings, these components were well-insulated using Armaflex Class O insulation with a thermal conductivity of 0.035 W/m.K. Using one-dimensional heat transfer calculations, an insulation thickness of 80 mm was found to be sufficient to limit the maximum heat losses from the test section to 2%.

A data acquisition system was used to capture the experimental data. This data was then recorded with a National Instruments Labview program. The data acquisition system comprised an SCXI (Signal Conditioning eXtensions for instrumentation), a computer, and National Instruments Labview Software which was used to log the data. Mass flow rates, temperatures, and pressure drops were recorded through the Labview program. The data reduction and plots were completed using Matlab software.

3 Data reduction

The data reduction method used the measured temperature, pressure, mass flow rate, and tube dimensions collectively. By replacing D, the measured inner diameter of the smooth tube, with D_r, the measured inner diameter of the rough tube (or the constricted flow diameter), the same methodology can be applied for rough tubes.

The mean fluid temperature, T_m, was calculated using a linear temperature distribution over the heated tube length, L_h, where x is the distance on the tube to a specific axial position. T_o is the outlet temperature measured by the Pt100 probe in the mixing section, and T_i is the inlet temperature measured by the Pt100 probe in the flow-calming section.

$${T}_{m}=\left(\frac{{T}_{o}-{T}_{i}}{{L}_{h}}\right)x+{T}_{i}$$

(1)

The bulk fully developed fluid temperature, T_b,FD, was calculated midway between the two pressure taps (at x = 2.7 m) in Fig. 2.

$${T}_{b,FD } =\left(\frac{{T}_{o}-{T}_{i}}{{L}_{h}}\right)2.7 +{T}_{i}$$

(2)

The thermophysical correlations of water [68] were used to calculate the specific heat capacity, C_p, thermal conductivity, k, Prandtl number, Pr, dynamic viscosity, μ, density, ρ, and the thermal expansion coefficient, $\beta$. The fully developed bulk fluid temperature was used to calculate the bulk fluid properties, while the mean fluid temperatures were used to calculate the local fluid properties.

The Reynolds number, Re, is a function of the mass flow rate, $\dot{m}$, dynamic viscosity, μ, and inner diameter, D:

$$Re=\frac{4\dot{m}}{\mu D\pi }$$

(3)

The electrical power input from the power supply was calculated as the product of the voltage and current (Q_e = VI). The heat transfer rate to the water (Q_w = ṁC_p(T_o- T_i)) should be close to the electrical power input in a well-insulated system, and the energy balance error, EB, quantifies the heat losses:

$$EB= \left|\frac{VI-\dot{m}{C}_{p}({T}_{o}-{T}_{i}) }{VI}\right|\times 100$$

(4)

To account for minor heat losses to the ambient surroundings, the heat transfer rate to the water was used to calculate the heat flux:

$$\stackrel{.}{q}\:=\frac{\stackrel{.}{Q}}{\pi D{L}_{h}}=\frac{\dot{m}{C}_{p}\left({T}_{o}-{T}_{i}\right)}{\pi D{L}_{h}}$$

(5)

The total thermal resistance across the tube wall, R_total, due to the different thermal resistances caused by the glue layers and copper particles, are summarised in Fig. 3, and was calculated as:

Fig. 3

Schematic of the axial cross-section of a rough tube indicating the different thermal resistances presented in the heat transfer analysis

$${R}_{total}= \frac{{\text{ln}}\left(\frac{{D}_{o,g}}{{D}_{o}}\right)}{2\pi {L}_{h}{k}_{o,g}} + \frac{{\text{ln}}\left(\frac{{D}_{o}}{D}\right)}{2\pi {L}_{h}{k}_{cu}}+ \frac{{\text{ln}}\left(\frac{D}{{D}_{i,g} }\right)}{2\pi {L}_{h}{k}_{i,g}}+\frac{{\text{ln}}\left(\frac{{D}_{i,g}}{{D}_{r} }\right)}{2\pi {L}_{h}{k}_{cu}}$$

(6)

D_o,g accounts for the thin glue layer between the thermocouple and the surface of the tube, D_o and D are the outer and inner diameters of the tube, D_i,g is the inner diameter of the tube with an inner glue layer that fixes the copper particles to the inner tube surface and D_r is the constricted inner diameter of the rough tube. The thermal conductivities of materials with a significant thermal resistance are the thermocouple glue, k_o,g, and the cyanoacrylate, k_i,g, that fixed the copper particles to the inner surface of the tube, which had thermal conductivities of 0.34 W/m.K and 0.1 W/m.K, respectively. In Eq. 6, the diameters remain the same in this instance when analysing rough tubes. The second and last terms of Eq. 6, which represented the thermal resistance across the copper tube wall and copper particles, were negligible due to the high thermal conductivity of copper, k_cu, being 401 W/m.K.

The temperature difference between the inner surface (in contact with the fluid) and the temperature measured by the thermocouple on the outer surface of the test section was thus calculated as the product of the heat input and the total thermal resistance:

$$\Delta T=\: \stackrel{.}{Q}\,{R}_{total}$$

(7)

The average outer surface temperature at a thermocouple station, T_s,o, was taken as the sum of T₁, T₃ and two times T₂ (Fig. 2), thus the thermocouple temperature measurements at the thermocouple station divided by four. This accounted for any circumferential temperature differences from free convection effects. The average inner surface temperature at a thermocouple station was then obtained by subtracting the temperature drop due to the thermal resistance of the glue layers:

$${T}_{s}= {T}_{s,o}- \Delta T$$

(8)

The average surface temperature along the tube length was calculated as follows:

$${\overline{T}}_{s}=\frac{1}{L}\underset{0}{\overset{L}{\int }}{T}_{s}(x){\text{d}}x$$

(9)

The average surface temperature in the fully developed section, was obtained by applying Eq. 9 between thermocouple stations O and U in Fig. 2. The average heat transfer coefficient, h, was calculated from the heat flux, average surface temperature and bulk fluid temperature:

$$h=\frac{\stackrel{.}{q}}{({\overline{T}}_{s}-{T}_{b})}$$

(10)

The average Nusselt numbers, Nu, were calculated from the average heat transfer coefficient as follows:

$$Nu=\frac{hD}{k}$$

(11)

The local heat transfer coefficient, h, was calculated from the heat flux, local surface temperature (Eq. 8) and mean fluid temperature (Eq. 1), and the local Nusselt numbers, Nu, were calculated from the local heat transfer coefficients.

The friction factors, f, were calculated using the mass flow rate and pressure drop measurements taken between the two pressure taps, a distance 0.97 m apart:

$$f=\frac{\Delta P\rho {D}^{5}{\pi }^{2}}{(0.97)8\dot{m}}$$

(12)

To determine the Grashof numbers, Gr, the gravitational acceleration constant, g, was taken as 9.81 m/s² and the kinematic viscosities, υ, were determined from the viscosities and densities, by $\nu =\mu /\rho$.

$$Gr=\frac{g\beta \left({T}_{s}-{T}_{m}\right){D}^{3}}{{v}^{2}}$$

(13)

The Graetz numbers, Gz, were determined as follows:

$$Gz=RePr\frac{D}{L}$$

(14)

Finally, the Colburn j-factors were calculated as:

$$j=\frac{Nu}{ReP{r}^{1/3}}$$

(15)

For validation purposes, the percentage error for a value (M) was calculated as follows:

$$\%error=\frac{|{M}_{exp}-{M}_{cor}|}{{M}_{cor}}$$

(16)

The uncertainties were calculated within a 95% confidence interval using the method of Dunn and Davis [69] and examples of the calculations can be found in the work of Everts [67] as well as Everts and Meyer [70]. The bias error was obtained from the accuracies of the instrumentation, as summarised in Table 2, and the precision error was obtained from the standard deviation of 200 data points.   

Table 2 Summary of the ranges and accuracies of the instrumentation used

Due to the high accuracy of the Coriolis flow meters, the Reynolds number uncertainties remained less than 1.2% and 2% and the smooth and rough tubes, respectively, irrespective of the Reynolds number and heat flux. For the smooth tube, the average Nusselt number and Colburn j-factor uncertainties at a heat flux of 3 kW/m² varied between 3.5–15% and 3.9–15% for Reynolds numbers between 1 100 and 5 000, respectively. There Nusselt number and Colburn j-factor uncertainties increased with increasing Reynolds number and decreasing heat flux due to the decreasing surface-fluid temperature differences. The friction factor uncertainties at a heat flux of 3 kW/m² varied between 2 and 3% and was not significantly affected by heat flux. When the surface roughness was increased to rough 2, the average Nusselt number and Colburn j-factor uncertainties varied between 3.9–11% and 4.4–11%, respectively, for Reynolds numbers between 1 100 and 3 000 at a heat flux of 3 kW/m². The corresponding friction factor uncertainties were ranged between 2 and 4%. The slight increase in the Nusselt number uncertainties with increasing surface roughness was again due to the smaller surface-fluid temperature differences. It should be noted that when increasing the surface roughness, the flow regimes occurred at lower Reynolds numbers. Therefore, although the uncertainties were expected to increase with increasing surface roughness (due to the decreased surface-fluid temperature differences), the uncertainties remained relatively similar in comparison to the smooth tube.

4 Experimental procedure and test matrix

Before any readings were taken, steady-state conditions were sought after. Approximately two to three hours were required to reach steady-state conditions after the daily start-up. Steady state was assumed once there was no significant change in temperature, pressure drop, mass flow rates, and energy balance readings for approximately five minutes. Thereafter, 200 data points were taken at a frequency of 20 Hz, which were then averaged to obtain a single value. Experiments were done by setting the mass flow rate to the maximum Reynolds number and thereafter, reducing the mass flow rate by reducing the pump speed. The bypass and inlet valves were used to further adjust the mass flow rate and minimise pulsations created by the magnetic drive gear pump.

The focus of this study was on transitional and quasi-turbulent flow. Therefore, most of the experiments involved testing ranges around these flow regimes, while sufficient portions of the laminar and turbulent flow regimes were also covered for the smooth tube. The significant surface roughnesses of the rough tubes caused the flow regimes to occur at significantly lower Reynolds numbers than for a smooth tube. Limiting factors of the experimental set-up determined the tested Reynolds number range which is shown in Table 3. The minimum and maximum Reynolds numbers were chosen such that the outlet water temperature was kept below 60 °C and the system pressure below 2.5 bar. As summarised in Table 3, a total of 557 mass flow rate measurements, 25 560 temperature measurements and 557 pressure drop measurements were taken.

Table 3 The experimental test matrix summarising the number of mass flow rate measurements, pressure drop measurements, temperature measurements for the different heat fluxes and Reynolds number ranges tested

5 Validation

To verify the accuracy and reliability of the experimental data, an extensive validation was conducted using the results of the smooth tube. The validation consisted of isothermal friction factors, average Nusselt numbers, as well as local laminar Nusselt numbers for both forced and mixed convective flow.

5.1 Fully developed isothermal friction factor

A total of 38 data points was taken to validate the fully developed isothermal friction factors between Reynolds numbers 500 and 8 300 in Fig. 4. Comparing the laminar friction factors to the Poiseuille [71] friction factor in Eq. 17 between Reynolds numbers of 500 and 1 900, the friction factors had an average deviation of 2.2%. The deviation increased from 1% at a Reynolds number of 500 to 7.9% at a Reynolds number of 1 900, which was within the uncertainty of the experimental data for Reynolds numbers less than 1 200. For laminar Reynolds numbers between 1 200 and 1 900, the deviation was greater than the experimental uncertainties. This was due to the thermal entrance length which increased with increasing Reynolds number and started to extend into the tube portion across which the pressure drops were measured.

Fig. 4

Validation of the fully developed isothermal friction factors as a function of Reynolds number with the correlations of Poiseuille [71] and Blasius [72] in the laminar and turbulent flow regimes, respectively

The transitional flow regime started at a Reynolds number of 2 850 and had a deviation of 18.1% from the Poiseuille equation.

$$f=\frac{64}{Re}$$

(17)

In the turbulent flow regime, the friction factors were compared to the Blasius [72] correlation in Eq. 18 between Reynolds numbers of 3 470 and 8 300. The average deviation was 0.9% with the maximum deviation of 1.8% occurring at a Reynolds number of 3 470. The deviation was well within the uncertainties of the experimental data.

$$f=0.316R{e}^{-0.25}$$

(18)

5.2 Average nusselt numbers

To calculate the average fully developed Nusselt numbers, only the thermocouple stations between the pressure taps (stations O to U in Fig. 2) were used. A heat flux of 7 kW/m² was applied to the test section and measurements were taken between Reynolds numbers of 1 200 to 3 100 in the laminar flow regime and 3 600 to 8 100 in the turbulent flow regime to validate the average Nusselt numbers in Fig. 5.

Fig. 5

Validation of the average Nusselt numbers as a function of Reynolds number at a heat flux of 7 kW/m² with the correlation of Meyer and Everts [1] in the laminar flow regime and the correlations of Meyer et al. [73] and Gnielinski [74] in the turbulent flow regime

The laminar Nusselt numbers were validated using the correlation of Meyer and Everts [1] in Eq. 19, which is valid for both developing and fully developed mixed convective laminar flow. The average laminar Nusselt numbers were significantly greater than the theoretical fully developed forced convective Nusselt number of 4.36 for a constant heat flux boundary condition, as free convection effects increased the Nusselt numbers. The average deviation was 1.2% between Reynolds numbers of 1 200 and 2 000 when compared with the correlation of Meyer and Everts [1], which were well within the uncertainties of the experimental data. There was an increase in Nusselt numbers between Reynolds numbers of 2 000 to 3 050 because of developing flow and the average deviation was 12.9%. The mixed convection thermal entrance lengths were 2.5 m and 5 m, respectively, for Reynolds numbers of 2 000 and 3 050. Therefore, at a Reynolds number of 2 000 the fully developed section between the pressure taps contained 0% developing flow, however, at a Reynolds number of 3 050 it contained 100% developing flow. As the local heat transfer coefficients are higher for developing flow than fully developed flow, the average Nusselt numbers increased.

$$\begin{array}{c}\overline{Nu}=4.36+\overline{Nu_1}+\overline{Nu_2}\\\overline{Nu_1}=\frac1L\int_0^{Lt_{MCD}}Nu_1dL=\frac1L\left(-0.84Pr_b^{-0.2}Lt_{MCD}+0.72\left(Re_bD\right)^{0.54}Pr_b^{0.34}Lt_{MCD}^{0.46}\right)\\\overline{Nu_2}=\frac1L\int_{Lt_{MCD}}^LNu_2dL=\frac1L\left(0.207Gr_b^{0.305}-1.19\right)Pr_b^{0.42}\left(Re_bD\right)^{-0.08}\left(L-Lt_{MCD}\right)\\Lt_{MCD}=\frac{2.4Re_bPr_b^{0.6}D}{Gr_b^{0.57}}\,\text{f}\text{o}\text{r}\,L>Lt_{MCD}\\Lt_{MCD}=L\,\text{f}\text{o}\text{r}\,L<Lt_{MCD}\\\text{.}\end{array}$$

(19)

For turbulent flow, the experimental data compared well with the correlation of Meyer et al. [73] in Eq. 20 with an average deviation of 1% between Reynolds number 3 600 to 8 400. The maximum deviation of 6.9% was found at a Reynolds number of 8 400. When comparing the experimental data with the correlation of Gnielinski [74] in Eq. 21, an average deviation of 2% was obtained between Reynolds numbers of 3 600 and 8 400. The minimum deviation was found to be 0.3% at a Reynolds number 4 100, while the maximum deviation was 5.3% at a Reynolds number of 7 000. The increased deviation at higher Reynolds numbers was due to the increased uncertainties caused by the decreased surface-fluid temperature differences, however, the deviations from both correlations over the entire turbulent Reynolds number range were well within the uncertainties of the experimental data.

$$Nu=0.018R{e}^{-0.25}{\left(Re-500\right)}^{1.07}{Pr}^{0.42}{\left(\frac{Pr}{{Pr}_{w}}\right)}^{0.11}$$

(20)

$$\begin{array}{c}Nu=\frac{(\xi /8)(Re\mathop{-}1000)Pr}{1\mathop{+}12.7\sqrt{(\xi /8)}\left({Pr}^{2/3}\mathop{-}1\right)}\left[1+{\left(\frac{D}{L}\right)}^{2/3}\right]{\left(\frac{Pr}{{Pr}_{S}}\right)}^{0.11}\\ \xi ={\left(1.8{\:{\text{log}}}_{10}\,Re-1.5\right)}^{-2}\end{array}$$

(21)

5.3 Local laminar nusselt numbers: forced convection

It is very challenging to experimentally obtain fully developed forced convection conditions in macro-tubes [25]. To achieve this, a small heat flux must be applied such that free convection effects caused by heating are negligible. To validate the local forced convective Nusselt numbers in Fig. 6, a heat flux of only 0.3 kW/m² was applied at a bulk Reynolds number of 700. The experimental data was compared to the correlation of Shah and London [75] in Eq. 22, which is valid for simultaneously hydrodynamically and thermally developing flow. The horizontal black dotted line represents the theoretical Nusselt number of 4.36 for fully developed forced convective flow through tubes heated at a constant heat flux [42]. The data was checked against the flow regime map of Everts and Meyer [27] which is valid for developing flow and confirmed that forced convection conditions were to be expected.

Fig. 6

Comparison of the local Nusselt numbers as a function of axial position for forced convective laminar flow at Reynolds number of 700 and heat flux of 1 kW/m² with the correlation of Shah and London [75] and the theoretical Nusselt number of 4.36 [42]

$$\begin{array}{c}Nu=N{u}_{1}\times N{u}_{2}-1\\ N{u}_{1}={\left[1+{\left(\frac{\pi /\left(115.2{z}^{*}\right)}{{\left\{1\mathop{+}\,(Pr/0.0207{)}^{2/3}\right\}}^{1/2}{\left\{1\mathop{+}{\left(220{z}^{*}/\pi \right)}^{-10/9}\right\}}^{3/5}}\right)}^{5/3}\right]}^{3/10}\\ \begin{array}{c}N{u}_{2}=5.364{\left[1+{\left(220{z}^{*}/\pi \right)}^{-10/9}\right]}^{3/10}\\ {z}^{*}=\frac{\pi }{4Gz}\end{array}\end{array}$$

(22)

The local Nusselt numbers compared very well with the correlation of Shah and London [75], with an average deviation of 4.4%. The fully developed Nusselt numbers between x/D = 135 and x/D = 590 had an average deviation of 15.2% from 4.36, which was within the uncertainties of the experimental data. The maximum local Nusselt number uncertainty of 31.4% was found at the inlet, due to the very small surface-fluid temperature difference of only 0.33 °C at the first thermocouple station. The surface-fluid temperature difference increased along the tube length to 0.46 °C and the average uncertainty was 22.9%. The high uncertainties were due to the very small surface-fluid temperature differences and the difference between the inlet and outlet temperatures was only 1.60 °C.

5.4 Local laminar nusselt numbers: mixed convection

The local mixed convective laminar Nusselt numbers were obtained at a heat flux of 7 kW/m² and a bulk Reynolds number of 1 200. The flow regime map of Everts and Meyer [27] for developing flow was used to verify that mixed convection conditions were to be expected. Fig. 7 indicates that the Nusselt numbers were on average 77% greater than the theoretical forced convection Nusselt number of 4.36 due to the heat transfer enhancement caused by free convection effects. The Nusselt numbers compared very well with the correlation of Meyer and Everts [1] in Eq. 23, with an average deviation of 1.5% and the deviation was comparable to the uncertainties of the experimental data.

Fig. 7

Comparison of the local Nusselt numbers as a function of axial position for mixed convection laminar flow at Reynolds number of 1 200 and heat flux of 7 kW/m² with the correlation of Meyer and Everts [1]. The dotted line shows a Nusselt number of 4.36

$$\begin{array}{c}Nu=4.36+{\left({Nu}_{1}^{6}+{Nu}_{2}^{6}\right)}^{1/6}\\ {Nu}_{1}=\left(0.33{Gz}^{0.54}-0.84\right){Pr}^{-0.2}\\ {Nu}_{2}=\left(0.207{Gr}^{0.305}-1.19\right){Pr}^{0.5}{Gz}^{-0.08}\end{array}$$

(23)

6 Pressure drop results

6.1 Effect of surface roughness

The isothermal (heat flux of 0 kW/m² and represented using the black markers) and diabatic (heat flux of 3 kW/m² and represented using the red markers) friction factors as a function of Reynolds number are compared in Fig. 8 for the smooth, rough 1, and rough 2 test sections to investigate the effect of surface roughness on the friction factors in the different flow regimes. In general, there is a clear upward and leftward shift in the friction factors with increasing surface roughness across the different flow regimes. From laminar flow theory, the friction factors for a smooth tube can be given as f = 64/Re [71] and indicated by the dashed green line. For the smooth tube, the isothermal laminar friction factors correlated very well with the Poiseuille equation [71] with an average deviation on 2.2%. As the Reynolds number was increased, the deviation increased slightly. Although there was a negligible difference between the isothermal and diabatic laminar friction factors, the Reynolds number at which the deviation started was lower for the isothermal (Re ≈ 1 150) than the diabatic (Re ≈ 1 730) friction factors due to the lower viscosity of the heated fluid.

Fig. 8

Comparison of the isothermal (heat flux of 0 kW/m²) and diabatic (heat flux of 3 kW/m²) friction factors for smooth, rough 1, and rough 2 as a function of Reynolds number, using black and red markers, respectively. Also included are the flow regime boundaries and the Poiseuille equation [71]

Contrary to the Moody Chart, which indicates that surface roughness has a negligible effect on the laminar friction factors, a significant increase in friction factors with increasing surface roughness was observed in the laminar flow regime was observed in Fig. 8. At a Reynolds number of 190, the friction factors for rough 1 and rough 2 were 126% and 158% higher than those predicted using the Poiseuille equation. The surface roughness breaks up the boundary layers and increases the flow resistance and friction factors, especially in mini- and microtubes [76]. For large values of relative roughness, the flow lines near the roughness elements at the surface would follow the shape of the roughness elements becoming curved lines instead of parallel lines [40]. It was observed by Webb et al. [39] that these flow curves separated from the wall surface and then only reattached a distance six to eight times the height of the roughness elements. This results in a decreased effective flow diameter and thus increased pressure drop and friction factor.

Similar to the findings of previous studies on rough tubes [8, 40, 55, 57, 58, 60,61,62], an increase in relative surface roughness significantly advanced the onset of the transitional flow regime of both the isothermal and diabatic friction factors due to the increased flow disturbances caused by the roughness elements. However, it follows from Fig. 8 that the transitional flow regime became less pronounced for rough 1 and even more challenging to identify for rough 2. The roughness elements disturbed the boundary layer and increased the flow swirls to such an extent that the transitional flow behaviour was significantly different from smooth tubes or tubes with lower values of relative surface roughness. The friction factors no longer increased with Reynolds number in the transitional flow regime, but continued to decrease, although the gradient was less than in the laminar flow regime. Therefore, for the two rough tubes, the critical Reynolds number was considered to be the Reynolds number at which the friction factors began to deviate from the Poiseuille trend (the linear behaviour when plotted on a log-log graph). For isothermal flow, the critical Reynolds numbers corresponded to 350 and 300 for rough 1 and rough 2, respectively, which is significantly earlier than a critical Reynolds number of 2 810 for the smooth tube.

When comparing the isothermal and diabatic friction factors in rough 1 and rough 2, there were minor differences in the boundaries of the transitional flow regime at a fixed surface roughness. This implies that the disturbances caused by the roughness elements dominated the heat transfer characteristics and dampened free convection effects inside these rough tubes. Similar to the trends observed by Everts et al. [37], the critical Reynolds number of the smooth tube was delayed from 2 810 to 2 970 when comparing the isothermal (0 kW/m²) and diabatic (3 kW/m²) friction factors. Furthermore, the transition gradients increased, which implies that the flow transitioned faster from the laminar to the quasi-turbulent flow regimes. A similar trend was observed in the diabatic friction factors of rough 1. Unfortunately, it was not possible to conduct experiments at Reynolds numbers below 390 at a heat flux of 3 kW/m², because the outlet bulk fluid temperatures became too high. Therefore, the critical Reynolds number could not be identified for rough 2 as sufficient portion of the laminar flow regime could not be covered.

In the quasi-turbulent flow regime, the friction factors continued to decrease with increasing Reynolds number in both the smooth and rough tubes. However, the gradient of the friction factors was less than in the laminar flow regime, but more than in the turbulent flow regime. As indicated by the arrows in Fig. 8, an increase in surface roughness also advanced the onset of the turbulent flow regime. In the turbulent flow regime, the gradient of the friction factors became approximately zero which indicates that the frictions factors were independent of Reynolds number, but increased significantly with increasing surface roughness. These trends are in good agreement with the findings of Nikuradse [41] as well as the well-known Moody chart [42]. The negligible difference between the isothermal and diabatic friction factors in the quasi-turbulent and turbulent flow regimes, as well as the boundaries between these flow regimes, were as expected, as any free convection effects were suppressed by the velocity of the fluid.

6.2 Effect of heat flux

The friction factors as a function of Reynolds number for heat fluxes of 1 kW/m², 2 kW/m², 3 kW/m², and 5 kW/m² are compared in Fig. 9 for rough 1 to investigate the effect of heat flux on the friction factors in rough tubes. At low Reynolds numbers in the laminar flow regime, typically below 500, an increase in heat flux increased the friction factors. This was due to the thermal gradient between the bulk fluid and surface temperature caused by mixed convection, which affected the velocity profile. Increasing the heat flux increased the shear stresses due to changes in the velocity profile, while the fluid density slightly decreased, causing the friction factors to increase [9].

Fig. 9

Friction factors as a function of Reynolds number for rough 1 at 1 kW/m² (blue), 2 kW/m² (green), 3 kW/m² (red) and 5 kW/m² (purple) between pressure taps 1 and 2. The flow regime boundaries for all the heat fluxes are labeled with arrows

An increase in the heat flux caused a delay in the onset of the transitional flow regime, which agreed well with the findings of Everts et al. [37]. This was due to the decreased viscosity of the heated fluid. It was concluded from Fig. 8 that the flow disturbances caused by the roughness elements resulted in the transitional flow regime being less pronounced than in smooth tubes. However, it follows from Fig. 9 that as the heat flux was increased, the transition gradient increased which also made the transitional flow regime more pronounced. An increase in heat flux resulted in increased free convection effects and temperature fluctuations, which assisted the flow in transitioning from laminar to quasi-turbulent flow. This also decreased the width of the transitional flow regime from a Reynolds number range of approximately 300 at a heat flux of 1 kW/m² to 200 at a heat flux of 3 kW/m².

Despite the increasing heat flux that caused a slight delay in the onset of the transitional flow regime, the roughness inside the tube significantly advanced the onset of all the flow regimes, compared to the smooth tube trends in Fig. 8. Therefore, the majority of the experimental data fell in the quasi-turbulent and turbulent flow regimes. In these flow regimes, free convection effects were suppressed by the velocity of the fluid, which explains why increasing the heat flux had a negligible influence on the magnitude and trend of the friction factors. The Reynolds number ranges of these flow regimes were therefore independent of heat flux and dependent on surface roughness (Fig. 8) only.

7 Relationship between pressure drop and heat transfer

Although the boundaries between different flow regimes are often obtained from visual inspection, it followed from Fig. 8 that it became increasingly difficult when tubes with large values of relative roughness, such as in this study, were used. This became even more challenging when the heat transfer results were investigated in terms of the Nusselt numbers, as will be shown in Fig. 11. Everts and Meyer [26] found that a direct relationship between pressure drop and heat transfer is valid for all flow regimes in a smooth tube, while Everts et al. [37] confirmed that the boundaries between the different flow regimes are also similar for the pressure drop and heat transfer results when using rough tubes. Therefore, the friction factors could be used as a guideline to identify the different flow regimes in the heat transfer results. Fig. 10(a), (c), (e) compares the pressure drop results in terms of the friction factors, and the heat transfer results in terms of the Colburn j-factors for smooth, rough 1, and rough 2, respectively. Only heat fluxes of 3 kW/m² and 5 kW/m² were considered in this analysis due to the high uncertainties in the heat transfer results at the lower heat fluxes (caused by the small surface-fluid temperature differences).

Fig. 10

Comparison of friction factors and Colburn j-factors between x/D = 431 and x/D = 621 (a, c and e), and f/j-factors as a function of Reynolds number (b, d and f), for smooth (a, b), rough 1 (c, d), and rough 2 (e, f), respectively

Similar to the findings of Everts et al. [37], the trends of the friction factors and Colburn j-factors were similar in all flow regimes for the smooth and rough tubes. Furthermore, as indicated by the red lines, the boundaries between the flow regimes were the same for both the pressure drop and heat transfer results. To investigate the relationship between pressure drop and heat transfer in rough tubes and determine the influence of surface roughness on the heat transfer and pressure drop characteristics, the friction factors were divided by the Colburn j-factors and compared in Fig. 10(b), (d), (f), for smooth, rough 1 and rough 2, respectively. This ratio is valuable to identify operating conditions of heat exchangers in which an increase in surface roughness would favour an increase in heat transfer rather than an increase in pressure drop. Therefore, lower values indicate favourable conditions for heat exchanger operation.

Although the friction factor and Colburn j-factor trends seemed similar in Fig. 10(a), it follows from Fig. 10(b) that for a smooth tube, the f/j-factors decreased significantly in the transitional flow regime, remained approximately constant in the quasi-turbulent flow regime and then decreased further with increasing Reynolds number in the turbulent flow regime. This indicates that the turbulent flow regime is a favourable flow regime for heat exchangers to operate in and explains why many heat exchangers in practice are designed to operate in this flow regime. For rough 1, Fig. 10(d) indicates that when the surface roughness is increased, the f/j-factors decreased with increasing Reynolds number in the laminar and transitional flow regimes, reached a minimum and remained approximately constant in the quasi-turbulent flow regime, before increasing with Reynolds number in the turbulent flow regime. Furthermore, there was a negligible difference between the f/j-factors of the two heat fluxes, which indicated that the free convection effects were suppressed by the additional fluid motion caused by the roughness elements. When the surface roughness was increased further to rough 2, Fig. 10(f) indicates that the f/j-factors again decreased with increasing Reynolds number in the transitional flow regime, reached a minimum in the quasi-turbulent flow regime, however, increased significantly in the turbulent flow regime as the Reynolds number was increased further.

It can therefore be concluded that although the turbulent flow regime is a favourable flow regime for heat exchangers containing smooth tubes to operate in, this is no longer the case for rough tubes. For rough tubes, the quasi-turbulent flow regime was found to be a promising flow regime for heat exchanger operation due to the lower f/j-factors. As the onset of the different flow regimes occurred earlier with increasing surface roughness, the heat exchangers can also operate at lower mass flow rates which decreases the pressure drop, pumping power and thus operational running costs. When comparing the magnitude of the f/j-factors in the smooth and rough 1 test sections, it follows that increasing the surface roughness increased the quasi-turbulent f/j-factors by a factor of approximately 2.5. However, when increasing the surface roughness further to rough 2, the magnitude of the average f/j-factors were not significantly affected (although a slight decrease can be observed). This indicates that smooth tubes remain preferable for heat exchangers, however, in situations were surface roughness is unavoidable, the efficiency of heat exchangers can be improved by changing the operating flow regime from turbulent to quasi-turbulent flow.

Everts and Meyer [23] found although the heat transfer coefficients in the quasi-turbulent flow regime are slightly less than for turbulent flow, the heat transfer characteristics are very similar to turbulent flow. Furthermore, as the temperature and pressure drop fluctuations for quasi-turbulent flow are significantly less than for transitional flow, it can be considered a more stable. The transitional flow regime was previously identified as a flow regime that gives an excellent compromise between the low pressure drops associated with laminar flow and the high heat transfer coefficients of turbulent flow [2]. However, the benefits quasi-turbulent flow regime should not be overlooked, especially when using rough tubes in heat exchangers.

8 Heat transfer results

8.1 Effect of surface roughness

To investigate the effect of surface roughness on the heat transfer characteristics in the different flow regimes, the average fully developed Nusselt numbers (431 < x/D < 621) at a heat flux of 3 kW/m² for smooth, rough 1, and rough 2 are compared in Fig. 11. Similar to the friction factor results, a general trend in this figure is that the Nusselt numbers shifted to the left with increasing surface roughness, implying that the onset of the different flow regimes occurred at lower Reynolds numbers. For the smooth tube, the average fully developed Nusselt number was 6.6 at a Reynolds number of 1 100 in the laminar flow regime. This was higher than the theoretical Nusselt number of 4.36, and the increase in Nusselt number can primarily be attributed to the enhanced heat transfer caused by free convection effects. Using the flow regime map of Everts and Meyer [27], it was confirmed that mixed convection conditions existed. The Nusselt numbers increased further as the Reynolds number increased from 2 000 to 3 000, however, this was due to developing flow rather than mixed convection. As the thermal entrance length extended into the fully developed region, the average heat transfer coefficients increased, because the heat transfer coefficients of developing flow are higher than for fully developed flow.

Fig. 11

Average fully developed Nusselt numbers for smooth, rough 1 and rough 2 tubes at a heat flux of 3 kW/m² as a function of Reynolds number. The flow regime boundaries are labeled and indicated using red arrows

For rough 1, the Nusselt numbers increased significantly with increasing Reynolds number throughout the laminar flow regime and the gradient was steeper than for the smooth tube. This suggests that an increase in surface roughness increased the thermal entrance length to such an extent that the region 431 < x/D < 621 contained developing flow even at Reynolds numbers as low as 500. As it was not possible to decrease the Reynolds number further, due to the limitations of the experimental setup, it was not possible to obtain fully developed laminar flow in rough 1 or any laminar flow in rough 2. Furthermore, due to the significant shift in the flow regime boundaries between smooth and rough 1, it was not possible to have comparable results to quantify the influence of surface roughness at a fixed Reynolds number in the laminar flow regime. Therefore, to gain a better understanding of the effect of surface roughness on thermal entrance length in the laminar flow regime and to develop appropriate heat transfer correlations, it is suggested to conduct additional experiments using tubes with lower values of relative surface roughness and longer tube lengths.

Another interesting observation from Fig. 11 was that for rough 1 and rough 2, the Nusselt numbers in the laminar flow regime decreased significantly with decreasing Reynolds number and when extending this trend to lower Reynolds it does not seem to approach the theoretical fully developed laminar Nusselt number of 4.36 for flow through a tube heated at a constant heat flux. Instead, it can be postulated from this graph that the Nusselt numbers would approach unity when the Reynolds number tends to zero. This was similar to results obtained by Everts et al. [35] who investigated opposing and assisting flow in vertical tubes. At a Reynolds number of zero, the heat transfer is by conduction only and therefore the Nusselt number is expected to be unity. As the Reynolds number is increased, convection effects become significant, which increases the Nusselt numbers. Due to the very low flow rates that were associated with the laminar flow regime in these rough tubes, the convection heat transfer component was very low and therefore led to decreased Nusselt numbers compared to smooth tubes.

Other authors such as Li et al. [52] and Liu et al. [51] found similar trends when using rough microtubes. At low Reynolds numbers, the Nusselt numbers did not correlate with classical laminar theory and were lower than expected. Li et al. [52] concluded that this was due to the variation in the thermophysical properties which caused the Nusselt number to be less than that of Shah and London [75]. Liu et al. [51] found that their experimental data deviated from conventional theory when the relative roughness was greater than 1.5% and the discrepancies seemed to increase at low Reynolds numbers and larger relative tube wall thickness. They concluded that such discrepancies were because of the tube wall axial heat conduction occurring at low Reynolds numbers. Maranzana et al. [50], Gamrat et al. [53], Herwig and Hausner [77], and Li et al. [78] also indicated that at low Reynolds numbers, conduction along tube walls becomes significant and competes with internal forced convection heat transfer. The relative roughness in this study was 4% and 11%, respectively, and the copper particles used to roughen the tube contributed to an increased the wall thickness of the copper tube. Therefore, the heat conduction along the tube walls of the rough tubes competed with the internal convection heat transfer and affected the heat transfer coefficients.

It follows from Fig. 11 that the transitional flow regime began at a Reynolds number of 3 050 in the smooth tube and ended at a Reynolds number of 3 180. For rough 1, the transitional flow regime occurred between Reynolds number of 560 and 760. An interesting finding is that although an increase in surface roughness advanced the onset of the transitional flow regime, it did not decrease the width of the transitional flow regime. Instead, the width of the transitional flow regime increased slightly from a Reynolds number range of 130 in the smooth tube to 200 in rough 1. However, the transition gradient decreased with increasing surface roughness and the transitional flow regime became less pronounced because roughness elements were sufficient to cause fluctuations in the flow, breaking up the laminar sublayers and disturbed the general fluctuating transitional flow behaviour that is typically found in smooth tubes [56, 63]. When using rough tubes, the heat transfer characteristics throughout the different flow regimes therefore had some elements of turbulent flow behaviour, which also explains the trend of increasing Nusselt numbers with increasing Reynolds number.

The onset of the quasi-turbulent and turbulent flow regimes for the smooth tube occurred at Reynolds numbers of 3 180 and 6 000, respectively. As the surface roughness was increased, the onset of the quasi-turbulent and turbulent flow regimes for rough 1 occurred at Reynolds numbers of 760 and 1 200, respectively, while it advanced to Reynolds numbers of 490 and 930, respectively, in rough 2. Therefore, the Reynolds number range of the quasi-turbulent flow regime was approximately 2 820 in the smooth tube and decreased significantly to 440 for both rough 1 and rough 2. In both the quasi-turbulent and turbulent flow regimes, an increase in surface roughness increased the Nusselt numbers due to the enhanced mixing caused by the roughness elements.

8.2 Effect of heat flux

To investigate the effects of heat flux on the heat transfer characteristics in rough tubes, Fig. 12 compares the average Nusselt numbers obtained in smooth and rough 1 at different heat fluxes. The Reynolds numbers at which laminar flow existed where significantly lower for rough 1 than for the smooth tube. Therefore, the surface-fluid temperature differences were generally higher which led to decreased Nusselt number uncertainties. Furthermore, for rough 1, the velocity of the fluid was not sufficient to suppress free convection effects in the laminar flow regime. It is interesting to note that the laminar Nusselt numbers decreased with increasing heat flux, which is contrary to the usual trend of laminar flow through horizontal tubes. However, the laminar trends in Fig. 12 is in good agreement with the trends for opposing flow observed by Everts et al. [35] which confirms that the roughness elements inside the tube obstruct the free convection effects inside the tube.

Fig. 12

Average Nusselt number as a function of Reynolds number for smooth (circles) and rough 1 (triangles) at 1 kW/m² (blue), 2 kW/m² (green) – rough 1 only, 3 kW/m² (red) and 5 kW/m² (purple) between x/D = 431 and x/D = 621. The flow regime boundaries for all the heat fluxes are labeled with arrows

For the smooth tube, the critical Reynolds numbers were 2 920, 3 050 and 3 072 for the 1 kW/m², 3 kW/m² and 5 kW/m², respectively. Similar to previous studies [9, 32, 64], an increase in heat flux delayed the onset of transitional flow due to the lower viscosity of the heated fluid, which led to increased Reynolds numbers. However, these changes were very small. The relative surface roughness of rough 1 is expected to fall into the saturating region, as defined by Everts et al. [37]. In this region the influence of heat flux and thus the Grashof number is expected to have negligible effects on the critical Reynolds number, as flow fluctuations inside the rough tube suppress free convection effects. Despite the tubes being rough, it follows from Fig. 12 that an increase in heat flux increased the transition gradient and therefore the increased free convection effects still assisted the flow in transitioning from laminar to quasi-turbulent flow.

The effect of heat flux on the onset of transitional and the quasi-turbulent flow regimes was slight and negligible, respectively. As the Reynolds number was increased, free convection effects decreased, and heat flux was expected to have a negligible influence on the turbulent flow regime. This explains why the differences between the Nusselt numbers at heat fluxes of 3 kW/m² and 5 kW/m² were negligible. However, at heat fluxes of 1 kW/m² (smooth and rough 1) and 2 kW/m² (rough 1), the turbulent Nusselt numbers diverged from the higher heat fluxes. This was not due to enhanced heat transfer, but rather due to the increased uncertainties caused by the small surface-fluid temperature differences at these lower heat fluxes.

9 Conclusions

This study experimentally investigated the effect of large relative surface roughnesses on the simultaneous heat transfer and pressure drop characteristics of transitional and quasi-turbulent flow. In general, it was found that the onset of the transitional, quasi-turbulent and turbulent flow regimes occurred at lower Reynolds numbers for an increase in relative roughness, while the magnitude of the friction factors and heat transfer coefficients increased.

For rough tubes at a constant heat flux of 3 kW/m², the onset of the transitional flow regime for the tube with a relative roughness of 0.04 (rough 1) occurred at a Reynolds number of 560 while for the tube with larger roughness of 0.11 (rough 2), the critical Reynolds number was below 390. Furthermore, the quasi-turbulent flow regime occurred at a Reynolds number of 760 and 490, respectively.

Tubes with large relative roughnesses showed a non-linear behaviour for the friction factors and did not correlate with classical laminar theory even at low Reynolds numbers. This was mainly attributed to the constricted flow diameter and flow obstructions by the roughness elements. The boundaries between the flow regimes, as well as the friction factors and Colburn j-factors trends were similar for both the pressure drop and heat transfer results in all the flow regimes for the smooth and rough tubes. For rough tubes, there negligible difference between heat fluxes further indicated that the free convection effects were suppressed by the additional fluid motion caused by the roughness elements.

The turbulent flow regime is generally considered as the favourable flow regime for heat exchangers containing smooth tubes to operate in, however, this is no longer the case for rough tubes. In tubes with significant surface roughness, the quasi-turbulent flow regime was found to be the most appealing flow regime for heat exchangers, as the f/j-factors were the lowest. Additionally, the flow regimes occurred earlier with increasing surface roughness, therefore, heat exchangers can operate at lower mass flow rates which decreases the pressure drop, pumping power and thus operational running costs. The quasi-turbulent flow regime is also less unpredictable and chaotic than the transitional flow regime. Engineers can optimize their design by working within the quasi-turbulent flow regime for significantly rough tubes to minimize pressure drop with the best heat transfer results.