1 Introduction

In many cases, flows are associated with the transport of scalar quantities, e.g., concentration or temperature. One prominent example is thermal convection that drives many astrophysical and geophysical flows (Schumacher and Sreenivasan 2020; Guervilly et al. 2019; Marshall and Schott 1999; Mapes and Houze 1993). Beyond that, thermal convection plays an important role in various fields of engineering, e.g., the cooling of electronic components (Bessaih and Kadja 2000) or inherent temperature-driven flows in large-scale thermal energy storages (Otto et al. 2023). While measuring the flow itself can oftentimes be challenging (Cierpka et al. 2019), the complexity increases further when the scalar is also measured, e.g., due to deterioration of the fluorescent dye (Sakakibara and Adrian 1999) and increased hardware requirements (Moller et al. 2021). Meanwhile, optical velocity measurements techniques like particle image velocimetry (PIV) are well-established and sophisticated tools in experimental fluid mechanics (Kähler et al. 2016). Hence, novel methods that would assist with the scalar measurement are highly desirable.

Recently, machine learning and deep learning-based methods have emerged as well-suited tools in fluid mechanics (Ling et al. 2016; Mendez et al. 2023; Brunton et al. 2020; Brunton and Kutz 2022; Raissi et al. 2019; Liu et al. 2020; Yu et al. 2023) with and increasing number of applications in flow measurement techniques (Rabault et al. 2017; König et al. 2020; Moller et al. 2020; Sachs et al. 2023), data reduction (Mendez 2022), forecast (Ghazijahani et al. 2022; Heyder and Schumacher 2021; Pandey et al. 2022) and super-resolution (Fukami et al. 2021; Gao et al. 2021). Deep neural networks turned out to be a powerful tool, and effort is spent to make their predictions consistent with physical laws by incorporating the governing equations, making them “physics-informed” (Raissi et al. 2020; Cai et al. 2021a, b). In many cases, solving the governing equations requires knowledge of all gradients, hence demanding fully volumetric measurements and knowledge of the thermal boundary conditions, which still remain the exception (Schiepel et al. 2021; Kashanj and Nobes 2023). Therefore, a purely data-driven model that processes far more common planar data as input would be of great use. In this manuscript, we present a u-net-based model (cp. Figure 2) which is well-suited to process multidimensional data in different fields (Jansson et al. 2017; Zhang et al. 2018; Fonda et al. 2019; Schonfeld et al. 2020) and thus provides a profound studied and versatile basis. The objective of the u-net is to predict the temperature field \(\tilde{T}\) for the given velocity fields \(u_x\), \(u_y\) and \(u_z\), as conceptualized in Fig. 1. The u-net is trained and tested with experimental temperature and velocity data obtained from joined stereoscopic particle image velocimetry and particle image velocimetry measurements (PIT) in the horizontal mid-plane of a large aspect ratio Rayleigh–Bénard convection (RBC) experiment. The Rayleigh–Bénard setup is a well-studied, simplified model experiment for natural convection and hence ideal to evaluate the u-net performance (Ahlers et al. 2009; Chillà and Schumacher 2012). RBC usually consists of fluid confined by adiabatic side walls, which is heated from below and cooled from above. The resulting dynamical system is governed by the Rayleigh number \(\textrm{Ra} = g\alpha \Delta T H^3/(\nu \kappa )\) and the Prandtl number \(\textrm{Pr} =\nu /\kappa\) which are defined by acceleration due to gravity g, the thermal expansion coefficient \(\alpha\), the temperature difference between heating and cooling plate \(\Delta T\), the domain height H, the kinematic viscosity \(\nu\) and the thermal diffusivity \(\kappa\) of the fluid. Additionally, the aspect ratio \(\Gamma =W/H\) as the ratio of domain width W and height H and the container’s shape affects the flow (Shishkina 2021; Ahlers et al. 2022). In the present large aspect ratio experiment, so-called turbulent superstructures emerge (Pandey et al. 2018; Stevens Richard et al. 2018; Moller et al. 2022; Käufer et al. 2023).

Fig. 1
figure 1

Conceptual sketch of our goal to predict the temperature by using three velocity components in the horizontal mid-plane of a large aspect ratio RBC experiment

Full size image

The remainder of the paper is structured as follows. Section 2 describes the architecture of the u-net together with applied modifications. In Sect. 3, we introduce the data sets as well as the experiment and methods used for their generation. Thereupon, in Sect. 4, we discuss the results of the hyper-parameter study and define two real-world application scenarios in Sect. 5. We subsequently analyze and interpret the prediction of both scenarios in Sect. 6 and conclude with a summary and future research perspectives in Sect. 7.

2 Deep learning model architecture

The u-net proposed by Ronneberger et al. (2015) is an autoencoder-like architecture that consists of two parts, the encoder and the decoder. Depending on the task, the encoder consists of one or multiple fully connected or convolutional layers (LeCun et al. 1989) where each layer provides fewer output values (neurons) than the previous. The decoder is typically constructed as an inverted version of the encoder; thus, the layers inflate their input instead of reducing it. Ronneberger et al. originally proposed u-net for biomedical image segmentation. Its architecture is enriched with additional residual connections that give the decoder additional vision on the different encoder layer outputs. In contrast to conventional residuals, here, the parallel branches are not added together but are appended along the channel dimension. The residuals clearly nullify the original autoencoder idea since the decoder is not able to expand the data solely from its reduced representation. However, this does not affect its applicability for non-reconstruction tasks. This can be tasks where the model performs a local feature extraction instead.

There are already several studies based on u-net, some of which propose improved and more complex u-net architectures (Çiçek et al. 2016; Zhou et al. 2019; Oktay et al. 2018; Wang et al. 2019; Alom et al. 2019; Zhang et al. 2020; Huang et al. 2020). A detailed overview of u-net and its variants is given by Siddique et al. (2021). Most applications here are still related to medical image segmentation/processing. Apart from that, the u-net was successfully utilized in other scientific fields like the analysis of turbulent Rayleigh–Bénard convection (Fonda et al. 2019; Wang et al. 2020; Esmaeilzadeh et al. 2020; Pandey et al. 2020). With each encoder layer, the model captures more abstract visual features of the input snapshot and passes them directly to the decoder using residual connections. This way, the decoder has access to features of different level of detail when step-wise constructing the output scalar. Therefore, we choose to use u-net as the basis for our deep learning experiments.

Fig. 2
figure 2

Basic u-net architecture (based on Ronneberger et al. (2015))

Full size image

Figure 2 shows the basic u-net architecture (Ronneberger et al. 2015). It consist of three different types of building blocks convolutional, max-pooling and up-convolution layers. An encoder layer is a sequence of 3 convolutional layers with an increasing number of \(3\times 3\) filters with a rectified linear unit (ReLU) activation. Here, the path splits, and one branch forms a skip connection to the decoder and the other goes through a max-pooling layer following the U-shape. A corresponding decoder block concatenates data directly from the encoder via the skip connection with data from the previous layer that is passed through an up-convolution which is composed of an up-sampling layer and a convolutional layer with \(2\times 2\) filters. The concatenated data goes through a sequence of three convolutional layers with a decreasing number of \(3\times 3\) filters and ReLU activation. The final output is passed through an additional \(1\times 1\) convolutional layer. Further details regarding the architecture can be found in the original publication by Ronneberger et al. (2015).

For our study, we utilize the u-net architecture as model backbone but altered and added concepts that we deemed more appropriate for the problem of temperature field prediction. These concepts are batch normalization, sub-pixel convolutions instead of up-sampling layers and several alternative ReLU-like activations. We discuss each concept in more detail below.

2.1 Activation function

The original u-net architecture uses ReLU activation after its convolutional layers (except the output layer). Although the ReLU (Eq. 10) activation function, which was first proposed by Nair and Hinton (2010), is still widely and successfully applied, more sophisticated successors were proposed in recent years. A well-known downside of the original ReLU is the “dying ReLU” problem. This problem appears when the model enters a state (weight configuration) where all inputs of the ReLU are non-positive and thus produce zero gradients. Leaky ReLU is a variant that ensures nonzero gradients in the whole domain, which often makes it the superior choice (Xu et al. 2020). Clevert et al. (2015) proposed the exponential linear unit (ELU). ELU allows negative activations and moves their mean toward zero, which alleviates the bias shift effect and speeds up training. A similar improvement inspired by the ideas of ReLU, dropout (Hinton et al. 2012) and Krueger et al. (2016) is the Gaussian error linear unit (GELU) activation. It uses the cumulative normal distribution function to imitate the stochastic effect of dropout and zoneout depending on the input o by applying the Gaussian cumulative distribution function \(\Phi\) and have shown to improve classification results for MNIST and CIFAR-10/100 by the inventors (Hendrycks and Gimpel 2016). Along with the introduction of self-normalizing neural networks (SNNs) came another ReLU-like activation function scaled exponential linear unit (SELU) (Klambauer et al. 2017). The authors proved the self-normalizing properties of SELU for \({\lambda _{01} \approx 1.0507}\) and \({\alpha _{01} \approx 1.6733}\), which stabilize training of deeper neural networks. They show that SELU preserves approximately zero mean and unit variance through multiple layers.

All these variants were proposed to improve training behavior and their utilization can have regularizing and stabilizing effects or improve training speed and the overall prediction performance of the model. However, their actual usefulness cannot be taken for granted for any case. Hence, we test different activation functions for our setup to elaborate which one is most suitable for our needs.

In the supplementary material, Fig. 18 displays the above activation functions.

2.2 Batch normalization

Batch normalization layers (Ioffe and Szegedy 2015) are typically added before the layer activation (e.g., ReLU) to process each batch of inputs o as follows:

$$\begin{aligned} {\hat{o}} = \gamma \frac{o - \mu _o}{\sqrt{\sigma _o^2 + \epsilon }} + \beta , \end{aligned}$$
(1)

where \(\mu _o\) and \(\sigma _o\) are the mean and standard deviation of the moving average batch, respectively. \(\epsilon\) is added for numerical stability and \(\gamma\) and \(\beta\) are trainable shift and scale parameters. Batch normalization ensures that the input o is scaled and shifted to have \(\beta\) mean and \(\gamma\) variance, thereby helping the model to reduce the internal covariate shift of layer inputs, increasing training speed and preventing exploding gradients for deeper networks and larger learning rates, resulting in overall better model performance (Santurkar et al. 2018; Bjorck et al. 2018).

2.3 Sub-pixel convolution

Shi et al. (2016) proposed sub-pixel convolutions instead of conventional bi-linear or bi-cubic up-sampling to improve the reconstruction and super-resolution (SR) quality of deep neural networks. They were frequently used for state-of-the-art deep learning approaches to perform image super-resolution tasks (Wang et al. 2020). The sub-pixel layer consists of two operations. To scale two-dimensional input feature maps \(c_{{\rm in}}\) by a factor r a sub-pixel layer first applies a convolution operation with \(c_{{\rm out}}=r^2c_{{\rm in}}\) filters. After that, a pixel-shuffle operation is applied. It re-arranges the output feature maps of the convolution in a deterministic way, as shown in Fig. 3. The number of feature maps can also be referred to as the number of channels, e.g., an RGB image as input means three input channels, where each channel provides the information for either red, green or blue. The figure displays an exemplary application of a sup-pixel convolution. On the left side, the low-resolution (LR) layer input is shown with only a single channel. Four convolutional filters are applied, and their outputs are shown in the middle of the figure. Finally, in the outer right area, the re-arranged convolution outputs that form the super-resolution (SR) version of the layer input can be seen. Here, the small squares stand for pixels and their colors indicate the corresponding convolutional filter. During the re-arrangement, the most upper-left pixel of each filter’s output are combined to form the four most upper-left pixels of the SR output. The same pattern applies to all other pixel positions. This behavior persists during inference as well as during training, such that the convolutional filters are trained best to predict their specific sub-pixel value. Instead of RGB pixels, our data consists of the different velocity components and temperature, which are also spatially dependent. This makes our data likewise suitable to be processed by super-resolution layers.

Fig. 3
figure 3

Operation of a sub-pixel layer that takes a single low-resolution (LR) input feature map (just \(c_{{\rm in}}=1\) channel), with width w and height h, and creates a corresponding (super-resolution) SR output feature map with scaling factor r

Full size image

3 Experiment

The training, testing, and validation data used in this paper were obtained from experiments in a cuboid aspect ratio \(\Gamma =25\) RBC cell with a lateral size W = 700 mm and a height H = 28 mm. A schematic view of the experiment is shown in Fig. 4.

Fig. 4
figure 4

Sketch of the experiment and the measurement arrangement

Full size image

The working fluid inside the cell is water at a mean temperature \(T_{{{\text{ref}}}} \approx 19.5\,^{^\circ } {\text{C}}\), which has a Prandtl number Pr=7.1 The fluid is confined by glass sidewalls, an aluminum heating plate at the bottom and a cooling plate assembly made from glass at the top. The cooling plate assembly consists of two horizontally oriented, slightly separated glass sheets. This arrangement allows the adjustment of the cooling plate’s temperature by cooling water while maintaining optical transparency. The temperature of both plates can be precisely and independently controlled by adjusting the temperature of the through-flowing water. The transparent cooling plate enables the application of optical measurement techniques for spatially and temporally resolved velocity and temperature measurements of a large part of the flow domain, which otherwise would not be possible due to the small height of the experiment. To visualize the flow, polymer-encapsulated thermochromic liquid crystals (TLCs) are added to the fluid. When illuminated by a continuous wavelength spectrum, the color of light reflected by the particles is temperature-dependent, which is leveraged to estimate the temperature of the fluid by particle image thermometry (PIT) (Dabiri 2009). Beyond the temperature, the color is also influenced by other factors, most importantly the observation angle \(\phi\), which is the angle between illumination and observation, and the illumination spectrum (Moller et al. 2019). During the experiments, a slice of approximately 3 mm thickness around the horizontal mid-plane was illuminated by a custom white light LED array with integrated light sheet optics. The flow in the measurement plane was then observed by two monochrome cameras under an oblique viewing angle of \(\approx 55^\circ\), which recorded the data used for the stereoscopic PIV processing (Prasad 2000; Raffel et al. 2018). An additional color camera was positioned with an observation angle \(\phi\) \(\approx\) 65\(^\circ\), which was used to capture the particle color for the subsequent PIT analysis. The observation angle of \(\phi\) \(\approx\) 65\(^\circ\) was chosen as a trade-off to achieve a large field of view with high sensitivity in the desired temperature range. For this study, a processing scheme based on the local calibration curves of the hue was used. Therefore, the color images were sliced into interrogation windows, and the color values were averaged within the windows and then transformed into the hue, saturation, and value (HSV) color space. Since the hue is sufficient to describe the color change, saturation and value are neglected. During the calibration, a known temperature was adjusted in the domain, and color images were recorded for several temperature steps across the temperature range of the experiment. Thereby the relation between the temperature and the hue was obtained for each interrogation window individually. This local calibration effectively eliminates the influence of the observation angle on the reflected color. During the processing of the convection data, the hue calibration curves were then used to derive the temperatures from the measured hue values. Further details on the technique can be found in Moller et al. (2019, 2020).

Utilizing the aforementioned experiment and methods, three data sets at different \(\textrm{Ra} \in \{2\times 10^5, 4\times 10^5, 7\times 10^5\}\) of spatially and temporally resolved, simultaneously measured planar temperature and velocity data were obtained. The data sets consist of long-time data of all three velocity components \({{\textbf {u}}} = (u_x, u_y, u_z)\) and the temperature T to catch the reorganization of the superstructures (Moller et al. 2022). Since the focus of the experimental setup is set on the investigation of the large-scale structures, neither the Batchelor scale nor the Kolmogorov scale are resolved. For the highest Rayleigh number, the Kolmogorov scale and the Batchelor scale are estimated to be 1.8 and 0.7 mm, which is smaller than the interrogation window size of 3.2 mm. Due to the otherwise enormous amount of data, a special recording scheme, visualized in Fig. 5, was applied.

Fig. 5
figure 5

Structure of the data sets and bursts

Full size image

Instead of continuously recording, the data were recorded in bursts of 200 corresponding to at least 44 free-fall times \(t_\textrm{f}\) (Eq. 2) seconds with gaps of approximately 1000 s or at least 221 \(t_\textrm{f}\) in between. Hence, the data provide sufficient variety within the burst and between the bursts to be used as training data. From each burst, 200 snapshots were obtained. For each data set, a total of 19 bursts were recorded and processed, totaling a number of 5700 snapshots. The initial processing of the data were performed on different grids, which were slightly coarser for \(\textrm{Ra} \in \{2\times 10^5, 4\times 10^5\}\). To train the u-net, the data were interpolated on a common grid, resulting in a slight up-sampling for the lower two \(\textrm{Ra}\) . For the analysis, the data were transferred into their non-dimensional representation denoted by \(\sim\) according to

$$\begin{aligned}&{\tilde{t}}=t/t_{\textrm{f}}=\frac{t}{\sqrt{H/\alpha g (T{_\textrm{h}}-T_{\textrm{c}})}} \end{aligned},$$
(2)
$$\begin{aligned}&{\tilde{T}}=\frac{T-T_{\textrm{c}}}{T_{\textrm{h}}-T_{\textrm{c}}}, \end{aligned}$$
(3)
$$\begin{aligned}&\tilde{\textbf{u}}=({\tilde{u}}_{x}, {\tilde{u}}_{y}, {\tilde{u}}_{z})=\frac{\textbf{u}}{\sqrt{H \alpha g (T_{\textrm{h}}-T_{\textrm{c}})}}, \end{aligned}$$
(4)
$$\begin{aligned}&\tilde{\textbf{x}}=({\tilde{x}}, {\tilde{y}}, {\tilde{z}})=\frac{\textbf{x}}{H}. \end{aligned}$$
(5)

The most important parameters of the experimental run are shown in Table 1; further details can be found in Moller (2022) and Käufer et al. (2023).

Table 1 Overview of the data sets at different Rayleigh numbers Ra and the most important parameters. Data adapted from Moller (2022)
Full size table

4 Model training and optimization

For our network training procedure, we split the data into a training, a validation and a test subset. We split the dataset between the bursts to avoid highly similar snapshots in different subsets. Thus, the snapshots of any burst are all within the same subset. Similar to the representation of a color image, we consider each snapshot as a two-dimensional tensor of size \(295 \times 287\) and four channels that contain the velocity and temperature. We consider the velocity fields \({\tilde{u}}\) as input and the temperature field \({\tilde{T}}\) in the remaining channel as the target or ground truth for our model. We want to point out that ground truth refers to the measured temperature, which itself differs from the exact fluid temperature due to measurement uncertainties. The training was structured into epochs, and each epoch into steps. Within each epoch, the model sees each training snapshot exactly once. The number of epochs is determined by early stopping (Prechelt 2012). Thus, we watch the validation loss and stop the training when it did not improve for 10 patience epochs. This is a best practice value high enough to ensure the convergence of the model while keeping the training duration reasonable. If the number of patience epochs is chosen too small, it may result in an under-fitting of the model. The processing of one batch within an epoch is followed by a stochastic gradient descent back-propagation step to adjust the model weights. Other hyper-parameters are the learning rate \(\eta\) and the channel factor \(\rho\). The latter is bound to the model architecture and determines the number of channels used in each layer. Therefore, the l-th encoder layer has \(c_e^{(l)}=\rho 2^{l - 1}\) channels. Due to u-net’s symmetric architecture, the l-th decoder layer has \(c_d^{(l)}=\rho 2^{L - l}\) channels, where L is the number of encoder respectively decoder layers. During the hyper-parameter tuning of \(\eta\) and \(\rho\), we use a fixed batch size of 64 snapshots to ensure a stable and efficient training behavior. A too small batch size leads to increased training duration and less general validity of each gradient descent step. A too large batch size may exceed the memory limits. It is important to note that the hyper-parameter tuning in Sect. 4.1 is only valid for this batch size.

For transparency and reproducibility, we provide configurations for \(\eta\) and \(\rho\) for all tests. Since we train our model to solve a regression task, we use the mean squared error (MSE) (6) as loss function for all trained models. The MSE of a single dimensionless temperature snapshot \({\tilde{T}}_\textrm{GT}\) and its prediction \({\tilde{T}}_\textrm{P}\) with \(d = \Vert {\tilde{T}}_\textrm{GT}\Vert = \Vert {\hat{T}}_\textrm{P}\Vert\) values each is formalized as:

$$\begin{aligned} \textrm{MSE}({\tilde{T}}_{\textrm{GT}}, {\tilde{T}}_{\textrm{P}}) = \frac{1}{d} \sum _{i=1}^{d}({\tilde{T}}_{\textrm{GT}, i} - {\tilde{T}}_{\textrm{P},i})^2.\ \end{aligned}$$
(6)

In the consideration of validation losses as in Fig. 7, we report the average MSE across all validation snapshots. We performed all experiments on an NVIDIA A40 GPU with 40GB VRAM.

Fig. 6
figure 6

Data bursts split into subsets for the P0 scenario

Full size image

4.1 Hyper-parameter optimization

Before we begin to train our model, we structure the data as sketched in Fig. 6. We shuffle the whole dataset B on burst level. Then, we divide it into a training set \(B_{\textrm{train}}\), a validation set \(B_{\textrm{valid}}\) and a testing set \(B_{\textrm{test}}\). These subsets hold \({b_{\textrm{train}}:=\Vert B_{\textrm{train}}\Vert =15}\) bursts for training and \({b_{\textrm{valid}}:=\Vert B_{\textrm{valid}}\Vert =b_{\textrm{test}}:=\Vert B_{\textrm{test}}\Vert =2}\) bursts for validation and test phase respectively, which leaves us with an approximate 80 : 10 : 10 split. We refer to this training scenario as P0.

Before moving on to more complex scenarios, we determine appropriate values for \(\eta\) and \(\rho\). Therefore, we perform a full grid search for these hyper-parameters with a basic u-net model and P0 conditions (see Fig. 6) with \(\text {Ra}=2\times 10^5\). We test all combinations of \({\eta \in \{0.01, 0.005, 0.001, 0.0005, 0.00001\}}\) and \({\rho \in \{8, 12, 16, 24, 32, 48, 64\}}\). Each combination is replicated 5 times with a different random seed \({s \in \{0, 1, 2, 3, 4\}}\). Figure 7 provides the MSE averaged over all replications of each tested hyper-parameter combination. It indicates that the predictions tend to worsen for increasing \(\eta\) and \(\rho\). It also appears that smaller \(\rho \le 8\) are more robust against larger \(\eta\). It also seems that for learning rates \(\eta \le 0.0001\) , it is beneficial to increase the channel factor. Though, the performance gain is rather small, given the memory effort. Therefore, we set our limit to the capacity of a single GPU. For our setup, this is the case for a \(\rho = 64\). Here, we receive the most promising validation MSE for \(\rho = 48\) and a learning rate of \(\eta = 0.0005\).

Fig. 7
figure 7

Mean of the validation MSEs for all tested \(\eta\)-\(\rho\)-combinations as heat map

Full size image

For the ablation study, we want to add the different architectural variations described in Sect. 2 separately to the model architecture and observe the effect on performance. Table 2 shows the different architecture configurations and the resulting mean absolute error (MAE) (7) that is calculated as follows:

$$\begin{aligned} \textrm{MAE}({\tilde{T}}_\textrm{GT}, {\tilde{T}}_\textrm{P}) = \frac{1}{d} \sum _{i=1}^{d}\Vert {\tilde{T}}_{\textrm{GT},i} - {\tilde{T}}_{\textrm{P},i}\Vert .\ \end{aligned}$$
(7)

The smallest and therefore best MAE result is printed in bold. As mentioned above, we run each experiment with five different initializations. Therefore, the reported MAE is actually the average of these runs together with the standard deviation. Due to the preprocessing of our data, the target temperature values lie within 0 and 1. We ensure the same limits for the predicted temperature with a sigmoid activation at the last decoder layer. This is due to the fact that the sigmoid activation also projects to the interval [0, 1]. A ReLU-like activation, as used for the other layers, would allow unbounded positive output values, which is not desirable for our task. It also implies that the MAE is within the same limits and is given in arbitrary units (AU). The ablation study shows that only the batch normalization improves the performance of the base model. Hence, we add batch normalization layers to all our subsequent models. These also increase the resilience of our model against larger learning rates and thus allow for faster training convergence. In addition, the dependence on the random seed is less prominent (as indicated by the low standard deviation) which is important if the model will be applied for other tasks in the future.

Table 2 Results of the ablation study
Full size table

5 Application scenarios

So far, we shuffled our data before splitting. This, however, does not resample many possible applications. Since the u-net is trained on the measurement data, these must be either generated during the experimental run in temporal succession, e.g., at the beginning or taken from a different run. Hence, we consider two different scenarios. First, we investigate the neural network’s performance when trained on the data of the same experimental run, one model for each Ra. We call this scenario P1. This scenario could help to further expand the accessible measurement time when the measurement of the scalar quantity is not possible anymore. For example, due to the degeneration of the tracer or dye to visualize the scalar quantity due to photobleaching for LIF (Sakakibara and Adrian 1999) or luminescent two-color tracer particle measurements (Massing et al. 2016) limits the time in which scalar measurements can be performed while velocity measurements are still viable. Another reason could be the increased computer memory requirements for the scalar measurement, e.g., the combination of two-color LIF and planar time-series PIV increases the amount of data by 200 \(\%\) compared to simple PIV setup (Sakakibara and Adrian 1999).

For this scenario, it is essential to know how much training data are needed for reliable results, or in other words, for how long simultaneous scalar and velocity measurements are required until the u-net can replace the scalar measurements. Therefore, we systematically investigated the influence of \(B_{\text {train}}\) on the loss, as conceptualized in Fig. 8. It shows out of which bursts the training \(B_{\text {train}}\) (pink), validation \(B_{\text {valid}}\) (purple) and test subset \(B_{\text {train}}\) (blue) are composed for different amounts of training data \(b_{\text {train}}\) in scenario P1. Here, \(B_{\text {valid}}\) and \(B_{\text {test}}\) are fixed and consist of burst 1 and 2 respectively burst 18 and 19 in all P1 experiments.

Fig. 8
figure 8

Data bursts split into subsets to produce results for different \(b_{\text {train}}\) in the P1 scenario

Full size image
Fig. 9
figure 9

MAE for different \(b_{\text {train}}\) in the P1 scenario

Full size image

The first P1 results are presented in Fig. 9, which shows the MAE on the test subset for different \(b_{\text {train}}\). We observe that the MAE decreases for increased \(b_{\text {train}}\). However, considering the value of the MAE, the improvement of additional training data is limited, especially when three or more bursts are used for training. Hence, we considered \(b_{\text {train}} = 3\), which corresponds to a measurement time of approximately an hour, as an appropriate trade-off between the u-net performance and effort on generating the training data for further experiments. At first glance, it seems surprising that MAE for a fixed \(B_{\text {train}}\) decreases with increasing Ra considering that the flow becomes increasingly turbulent but likewise the free-fall time \(t_\textrm{f}\) as the characteristic time scale of the flow decreases. Hence, a burst at higher Ra contains more temporal information. Furthermore, the turbulent superstructures that are characteristic of the flow are more distinct for lower Ra (Käufer et al. 2023).

Considering these results is insufficient to ensure that the u-net generalizes well. It additionally requires testing whether the neural network learns the characteristics of the flow and does not rely upon temporal information. Therefore, we systematically investigate the effect of temporal distance, measured in the number of bursts \(\Delta b\) between the last training burst and the first testing burst. We refer to these bursts as \(\Delta B\) as shown in Fig. 10.

Fig. 10
figure 10

Data bursts split into subsets to produce results for different \(\Delta b = \Vert \Delta B\Vert\) in the P1 scenario

Full size image

To analyze the effect, we plotted the MAE in dependence of \(\Delta b\) in Fig. 11.

Fig. 11
figure 11

MAE for different \(\Delta b\) and fix \(b_{\text {train}} = 3\)

Full size image

The plot shows some fluctuations, but overall, no systematic dependence of the MAE on \(\Delta B\) for any Ra, which indicates that our deep learning model does not rely on temporal similarities between testing and training data which decreases with increasing \(\Delta B\).

In a nutshell, our systematic investigation showed that the u-net requires relatively little training data and produces time-independent predictions.

The second scenario we consider is training the u-net on data from a different experimental run with a slightly different Ra, which we call scenario \({\textbf {P2}}\). When previously obtained data from similar experimental conditions are available, new measurements of the scalar quantity are not feasible anymore. For this scenario, we train the u-net on data of two Rayleigh numbers and apply the model on data of the remaining Ra experiment as sketched in Fig. 12, which means for one case interpolation and extrapolation for the others.

Fig. 12
figure 12

Data bursts split into subsets for the P2 scenario

Full size image

In total, 30 bursts of two different Ra are used for training. Since the training and prediction are performed on different experimental runs, the data are time-independent by default.

6 Results

In Sects. 4 and 5, we showed that the u-net can predict temperature from velocity data after an initial training phase and identified a channel factor \(\rho =48\) and a learning rate \(\eta =0.0005\) as optimal hyper-parameter. We defined two different scenarios P1 and P2 as potential use cases and determined three bursts of training data as optimum between model performance and data generation effort. To fully evaluate the u-net’s performance on the given task, a rigorous physical interpretation and comparison of the results is required. The subsequent analysis is performed only on the test data, which the u-net has never seen during training.

6.1 Temperature prediction

We start by comparing the MAEs (reported in Kelvin and arbitrary unit) of the final trained model u-net for scenario P1 (Table 3) and P2 (Table 4) and of a respective naive approach that simply shifts and scales the vertical velocity field to approximate temperature. This way, the predicted temperature field is composed as \({\tilde{T}}_{\textrm{naive}}=\sigma _T\frac{\tilde{{{\textbf {u}}}}_z - \mu _z}{\sigma _{z}} + {\tilde{T}}_{\textrm{mean}}\). Here, \(\mu _z\) and \(\sigma _{z}\) are the average vertical velocity and its standard deviation, while \(\sigma _T\) corresponds to the standard deviation of the temperature. \({\tilde{T}}_{\textrm{mean}}=0.5\) denotes the mean temperature in the horizontal mid-plane which would emerge under the idealized Boussinesq assumption.

While a fluid mechanical interpretation of the MAE is not straightforward, it nevertheless is a clear indicator of the model’s performance. In Tables 3 and 4, the MAE is reported for the dimensionless temperature fields and lies within 0 to 1, just as in Table 2.

Table 3 Test results of the P1 models (same Ra)
Full size table
Table 4 Test results of the P2 models (varying Ra)
Full size table

When comparing the different MAE values, we clearly see that the u-net in any scenario outperforms the naive approach by an order of magnitude in MAE, demonstrating the usefulness of the u-net. Furthermore, the u-net trained in the P1 scenario achieves better prediction results compared to the u-net trained in the P2 scenario. This is expected since the training data in the P1 scenario is generated from the same experimental run at the same Ra and thermal boundary conditions and, therefore, inheres a better representation of distinct flow compared to the u-net trained in the P2 scenario. With the single exception of the \(\textrm{Ra} =4\times 10^5\) case in the P2 scenario, the MAE of the u-net predictions decreases with Ra. While this, at first glance, seems to be counter-intuitive since flows get more complex with increasing Ra, it is a consequence of the measurement technique and turbulent superstructures. On the one hand, the experiment and the measurements were designed and performed to investigate the development of large-scale turbulent superstructures, and due to the inherent trade-off between the field of view and spatial resolution, the measurements do neither resolve the smallest temperature nor velocity structures, and these are averaged out. On the other hand, the turbulent superstructures are more distinct and pronounced at lower Ra, and the temperature fields appear smoother at higher Ra (Moller et al. 2022), which tends to be beneficial for the u-net. The lower MAE for the P2 u-net predictions at \(\textrm{Ra} =4\times 10^5\) is a consequence of the training data, which only for this Ra incorporates a lower and higher Ra. Hence, the u-net performs an “interpolation” compared to the “extrapolation” of the other P2 cases.

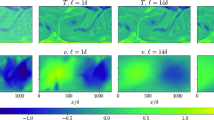
To gain more physical insights, we continue with comparing exemplary instantaneous snapshots of the temperature fields for \(\textrm{Ra} =4\times 10^5\) shown in Fig. 13.

Fig. 13
figure 13

Comparison of exemplary measured and predicted temperature fields \({\tilde{T}}_{\textrm{GT}}\) (a), \({\tilde{T}}_{\textrm{P1}}\) (b), \({\tilde{T}}_{\textrm{P2}}\) (c) and the difference fields \(\tilde{T}_{GT}-\tilde{T}_{naive,P1}\) (d), \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P1}}\) (e) and \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P2}}\) (f) at \(\textrm{Ra} =4\times 10^5\)

Full size image

Here, we contrast the ground truth temperature \({\tilde{T}}_{\textrm{GT}}\) with the temperature predicted by the u-net trained with scenario P1 \({\tilde{T}}_{\textrm{P1}}\) and scenario P2 \({\tilde{T}}_{\textrm{P2}}\). We observe that the dominant structures in the temperature field, the so-called turbulent superstructures, are clearly distinguishable in both predicted temperature fields. However, small-scale features appear to be smoothed out in the predictions. This observation also persists in the fields of the temperature differences \({\tilde{T}}_\textrm{GT} - {\tilde{T}}_\textrm{naive,P1}\), which resembles the difference of the naive approach, \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P1}}\) and \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P2}}\). Looking at the \({\tilde{T}}_\textrm{GT} - {\tilde{T}}_\textrm{naive,P1}\) field, we observe differences significantly larger than those of any u-net prediction. Hence, the naive approach is not suitable at all. For the difference \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P1}}\), we note that for large parts of the field, the absolute value of the deviation is below 0.1. However, there are localized spots, especially for \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P1}}>0\), where the deviations are slightly larger. Nevertheless, the absolute value for 90\(\%\) of the differences is below 0.15, and larger outliers are unlikely since the temperature measurement is itself associated with measurement uncertainty. Likewise, we observe localized spots of higher deviations in the difference field \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P2}}\), but additionally, it seems to be somewhat biased toward \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P2}}<0\) which indicates a slight overestimation of the temperature predicted by the u-net trained in scenario P2. Still, the absolute value for 90\(\%\) of the differences is below 0.15. To further quantify how well ground truth and prediction align, we computed the Pearson correlation coefficient \(C({\tilde{T}}_\textrm{GT}, {\tilde{T}}_\textrm{P})\) (8) for each \({\tilde{T}}_\textrm{GT}\) the corresponding \({\tilde{T}}_\textrm{P}\) as:

$$\begin{aligned} C({\tilde{T}}_\textrm{GT}, {\tilde{T}}_\textrm{P}) = \frac{\textrm{cov}({\tilde{T}}_\textrm{GT},{\tilde{T}}_\textrm{P})}{\sigma _{{\tilde{T}}_\textrm{GT}}\sigma _{{\tilde{T}}_\textrm{P}}}, \ \end{aligned}$$
(8)

where \(\textrm{cov}({\tilde{T}}_\textrm{GT},{\tilde{T}}_\textrm{P})\) is the covariance between ground truth and prediction and \(\sigma _{{\tilde{T}}_\textrm{GT}}\) and \(\sigma _{{\tilde{T}}_\textrm{P}}\) are their standard deviations. The resulting mean correlation coefficient C for all Ra and scenarios is shown in Table 5.

Table 5 Overview average Pearson correlation coefficient C for various Ra and scenarios
Full size table

Looking at the table, we observe a high degree of correlation for the u-net predictions for all cases with a correlation coefficient C of 0.7 or higher. The naive approach for both scenarios results in the same correlation coefficient, which is at least 0.2 lower compared to the u-net prediction and decreases with Ra. This shows that temperature \({\tilde{T}}\) and vertical velocity \({\tilde{u}}_{z}\) are not highly correlated, especially at high Ra and, hence, the simple re-scaling approach of the vertical velocity field is unsuitable. Similar to the MAE, we see that for the P2 scenario, the u-net performs best for \(\textrm{Ra} =4\times 10^5\). In the next step, we computed the probability density functions (PDFs) of the temperatures \({\tilde{T}}\) from all snapshots in the test data set to understand further the deviation between measured and predicted temperature. Contrasting the PDFs shown in Fig. 14, we observe a good agreement for the lowest Rayleigh number \(\textrm{Ra} =2\times 10^5\) especially for the P1 case, albeit the PDFs of the predicted temperature show a lower probability of extreme temperature events and specifically high temperatures, which is in line with the smooth appearance of the predicted temperature fields.

Fig. 14
figure 14

PDFs of the temperature \({\tilde{T}}\) for various Ra

Full size image

This trend continues and increases with the Rayleigh number. For \(\textrm{Ra} =4\times 10^5\), we furthermore observe that the PDFs of the predictions for \({\tilde{T}}<0.5\) no longer collapse on each other. While the PDF of the P1 u-net predictions agrees rather well with the PDF of the measurement data, the P2 u-net underestimates the probability of \({\tilde{T}}<0.4\) events and overestimates the probability of \({\tilde{T}}\approx 0.6\) events. This coincides with the bias we observed in the temperature difference field \({\tilde{T}}_{\textrm{GT}}-{\tilde{T}}_{\textrm{P2}}\). For the highest \(\textrm{Ra}\) most dominantly but also for the lower \(\textrm{Ra}\), we observe that the statistics of the temperature PDFs are not symmetric. This is mostly an effect of the asymmetric boundary conditions of the experiment, which resembles almost perfect isothermal boundary conditions at the bottom plate in contrast to the cooling plate made from glass where the conductive heat transfer within the plates is comparable to the convective heat transfer at the surface of the plate. This results in an increased probability of inverted heat transfer and limits the global heat transfer of the system. Further details can be found in Käufer et al. (2023). Nevertheless, we see a PDF of the P1 predictions and the measured temperature in the range \(0.2<{\tilde{T}}<0.65\) almost match. Unlike the P1 predictions, the PDF of the P2 predictions shows a significant overestimation of cold temperatures. This is expected since the probability density function of the test and training cases differs significantly.

As the final step of our analysis of the predicted temperature data, we compare the azimuthally averaged power spectra of the temperature. These spectra indicate how the temperature is distributed over the different spatial scales or wavelengths. They are also commonly used to determine the size of the turbulent superstructures (Pandey et al. 2018; Moller et al. 2022). To determine the azimuthally averaged spectra, we compute the temperature field’s two-dimensional discrete Fourier transform (DFT). We then compute the power spectrum and average the data azimuthally. We apply a spectral filter where we discard wavelengths that are larger than the field of view and therefore have no physical meaning. Additionally, we zero-pad the temperature fields to increase the number of spectral bins. Further details on the procedure can be found elsewhere (Moller 2022). The computed dimensionless wavelength \({\tilde{\lambda }}\) is normalized by H.

Fig. 15
figure 15

Power spectra of instantaneous temperature (black, red, and blue) and vertical velocity fields (green) for various Ra

Full size image

Figure 15 shows the power spectra calculated from a single exemplary instantaneous temperature snapshot (black, red, and blue) and the corresponding vertical velocity snapshot (green). Looking at the spectra, we observe excellent agreement between the spectra of the measured temperature data and their respective predicted counterparts in all cases, especially for wavelength \({\tilde{\lambda }}>0.5\). For smaller scales, we see an increased power spectral density \(E({\tilde{\lambda }})\) for the measurement data as a consequence of the smoother appearance of the predictions. Of high interest in large aspect ratio, RBC are the turbulent superstructures whose size is commonly determined by the maximum of the power spectrum. Thus, a magnification of the peak region is shown in the bottom right of each plot. The dashed, gray line indicates the wavelength \({\tilde{\lambda }}\) corresponding to the peak in the power spectrum, which is additionally written in the inset. For \(\textrm{Ra} =4\times 10^5\) and \(\textrm{Ra} =7\times 10^5\) , we observe a good agreement between the measured and predicted temperatures, especially for \(\textrm{Ra} =7\times 10^5\) where all peaks virtually collapse. In contrast, for \(\textrm{Ra} =2\times 10^5\), the peak of the P2 prediction shows a reduced power spectral density compared to the peak obtained from the measurement data. Nevertheless, the shapes of the peaks still agree well.

Beyond that and even most importantly, the plots show that for all cases, the wavelength \({\tilde{\lambda }}\) belonging to the peak is the same for the predictions and the measurements, which underlines that the u-net in both scenarios is a suitable tool capable of correctly predicting the size of the temperature superstructures.

Comparing the temperature spectra with the vertical velocity spectra, we can see a similar trend; however, the vertical velocity spectra are offset from the temperature and have a less pronounced peak at a large wavelength, which indicates the superstructure size. Especially for \(\textrm{Ra} =7\times 10^5\), we see a significant difference between the temperature and vertical velocity spectra since the spectral peak of the vertical velocity is shifted toward a smaller wavelength. This indicates that the u-net learns to transfer spatial scales rather than just augmenting the vertical velocity field.

So far, we have investigated the performance of the u-net models of both scenarios P1 and P2 by means of fields, probability density functions and power spectra of the temperature. We saw that for both scenarios P1 and P2, the u-net is able to accurately predict the temperature and, specifically, the large-scale structures in the temperature field. Overall the predicted temperature data are smoother, containing fewer extreme temperature events. This aligns with our expectations since the smallest-scale structures are lost in the convolutional layer of the contraction branch of the u-net despite the skip connections. On the one hand, this means the u-net does not reproduce the smallest-scale features. On the other hand, it makes it robust against measurement noise and acts like a filter. In fact, both autoencoders and u-nets were also successfully used for denoising tasks in the past (Vincent et al. 2010; Bao et al. 2020).

6.2 Heat transfer prediction

An important quantity of any RBC setup is the system’s heat transfer, which is described by the Nusselt number Nu. Since we obtain temperature and vertical velocity data at the same point in space and time, we are able to determine the local Nusselt number

$$\begin{aligned} \textrm{Nu}_{\text {loc}} = {\sqrt{\text {RaPr}}} \, {\tilde{u}}_z\left( \tilde{{{\textbf {x}}}}, {\tilde{t}} \right) {\tilde{\Theta }}\left( \tilde{{{\textbf {x}}}}, {\tilde{t}} \right) . \end{aligned}$$
(9)

Here, \({\tilde{\Theta }}\) denotes the temperature fluctuation, which we obtain by decomposing \({\tilde{T}}\) into the linear conduction profile \({\tilde{T}}_{\text {lin}}\) and the fluctuations \({\tilde{\Theta }}\) according to \({\tilde{T}} \left( \tilde{{{\textbf {x}}}}, {\tilde{t}} \right) = {\tilde{T}}_{\text {lin}} \left( {\tilde{z}} \right) + {\tilde{\Theta }} \left( \tilde{{{\textbf {x}}}}, {\tilde{t}} \right)\) with \({\tilde{T}}_{\text {lin}} = 1 - {\tilde{z}}\). Thus \({\tilde{T}}_{\text {lin}} = 0.5\) at the horizontal mid-plane where the data were measured. Further details on the derivation of the \(\textrm{Nu}_{\text {loc}}\) can be found in Käufer et al. (2023).

Figure 16 shows exemplary snapshots of the \(\textrm{Nu}_{\text {loc}}\) field computed from \({\tilde{u}}_z\) and \({\tilde{T}}_{\textrm{GT}}\) (a), \({\tilde{u}}_z\) and \({\tilde{T}}_{\textrm{P1}}\) (b), and \({\tilde{u}}_z\) and \({\tilde{T}}_{\textrm{P2}}\) (c), respectively.

Fig. 16
figure 16

Comparison of exemplary local Nusselt number fields at \(\textrm{Ra} =4\times 10^5\) calculated from purely measurement data (a) and from measured velocity and predicted temperature (b, c)

Full size image

Comparing all three fields, we can easily detect the same patterns, albeit the fields of the ground truth \(\textrm{Nu}_{\text {loc}}\) number and \(\textrm{Nu}_{\text {loc}}\) calculated from the P1 predictions are substantially more similar. Yet, most strikingly, is the fact that we observe negative \(\textrm{Nu}_{\text {loc}}\) events in the u-net predictions independent of the training scenario. In general, high temperature and upward velocity, as well as low temperature and downward velocity, are strongly correlated since temperature-induced local changes in density drive the flow. Hence, the neural network could achieve low MAE values by predicting high temperatures where upward velocities occur and vice versa. In practice, we also observe events \(\textrm{Nu}_{\text {loc}} <0\) where heat is transferred from top to bottom, even though with a much lower probability. The occurrence of negative \(\textrm{Nu}_{\text {loc}}\) events in the \(\textrm{Nu}_{\text {loc}}\) field obtained from both predictions, furthermore, at the same locations as in the ground truth fields, proves that the u-net learns a representation of the flow that goes far beyond the simple correlation of velocity and temperature. To further investigate this intriguing insight, we turn our attention to the PDFs of \(\textrm{Nu}_{\text {loc}}\) in Fig. 17.

Fig. 17
figure 17

PDFs of the local Nusselt number \(\textrm{Nu}_{\text {loc}}\) for various Ra

Full size image

We note that PDFs agree well, especially in the range \(0<\textrm{Nu}_{\text {loc}} <50\) for all Ra. With the exception of the P2 case for \(\textrm{Ra} =7\times 10^5\), \(\textrm{Nu}_{\text {loc}} >50\) events seem to be slightly underrepresented in the \(\textrm{Nu}_{\text {loc}}\) calculated from predicted temperature data. Again this can be linked to the smoother temperature field obtained from the predictions. Furthermore, the absolute probability of these events is low.

Looking at the probability for \(\textrm{Nu}_{\text {loc}} <0\) , we see that the data obtained from the u-net predictions correctly represents the probability of low-intensity reversed heat transfer events, but the negative far-tail events are underrepresented. As mentioned above, those events are the toughest to predict due to the preferential correlation between temperature and velocity. Considering the low value of the absolute probability of these events, those might be altered by the measurement uncertainty. An exception is the PDFs obtained from the P2 data at \(\textrm{Ra} =2\times 10^5\). Solely based on the PDFs, for this Ra, the P2 model seems to outperform the P1 model since it better matches the PDF of the measured ground truth data, even for extreme \(\textrm{Nu}_{\text {loc}} <0\) events. At first glance, this seems surprising, but recalling that the P2 model for this Ra was trained only with data of higher Ra, which have a broader distribution of \(\textrm{Nu}_{\text {loc}} <0\) events, it is unsurprising that these are embedded into the trained model.

Lastly, we want to quantify and compare the global heat transfer characterized by the global Nusselt number \(\textrm{Nu}=\langle \textrm{Nu}_{\text {loc}} \rangle _{{\tilde{A}},{\tilde{t}}}\) which we obtain by averaging \(\textrm{Nu}_{\text {loc}}\) over the field of view \({\tilde{A}}\) and time \({\tilde{t}}\).

Table 6 Overview of the global Nusselt Nu for all combinations of Ra and temperature determination methods
Full size table

Looking at the resulting values in Table 6, we observe that the ground truth Nu and the Nu calculated from the P1 agree well with relative differences, which are defined as the absolute value of the difference between reconstructed and measured global Nusselt number divided by the measured global Nusselt number, between 14.1\(\%\) and 0.3\(\%\). As a rule of thumb, Nu obtained from the P1 predictions is slightly higher. In contrast, the deviations for Nusselt numbers obtained from the P2 predictions—which undoubtedly are the more difficult predictions—are significantly larger with relative values between 47.6\(\%\) and 13.5\(\%\). Contributing to this large deviation is that in the experimental setup, a change in Ra also affects the thermal boundary conditions, additionally influencing the flow physics. Nevertheless, we see qualitative agreement. In both cases, the relative deviation is the lowest for \(\textrm{Ra} =4\times 10^5\) which is reasonable in the P2 case but unexpected for the P1 case where the MAE of the temperature prediction is lowest for \(\textrm{Ra} =7\times 10^5\).

To summarize, we have shown that the u-net predictions allow us to compute physically plausible \(\textrm{Nu}_{\text {loc}}\) fields, albeit underestimating the probability of extreme \(\textrm{Nu}_{\text {loc}} <0\) events. Comparing the global values of Nu, we observed good quantitative agreement between ground truth and the P1 case but only qualitative agreement for the P2 case.

7 Conclusion and perspectives

In this paper, we proposed a purely data-driven, supervised, deep learning-based method to derive the distribution of a scalar quantity from experimental velocity data. We demonstrate it for the example of large aspect ratio RBC and extract temperature data from stereoscopic PIV velocity data. We used data from experiments at \(\textrm{Ra} =2\times 10^5, 4\times 10^5, 7\times 10^5\) and chose the u-net architecture as a baseline. Starting from this point, we investigated the influence of several modifications, namely the choice of the activation function, the up-sampling and the batch normalization. We observed that only batch normalization had a positive effect on our task. Thereupon, we identified the optimal values for the channel factor \(\rho =48\) and the learning rate \(\eta =0.0005\) in an extensive grid search. We observed that u-net exhibits stable training behavior, yielding only minor deviation in performance when trained with different random initial weights. The chosen parameter combination shows a low standard deviation of the validation MSE and the grid search heat map a clear convergence, indicating the robustness of the parameter selection. Subsequently, we defined two real-world application scenarios, P1 and P2. In scenario P1, we trained the u-net on data of the same experimental run. We studied the influence of the amount of training data on the MAE and selected the number of three training bursts as the best compromise between model performance and training data generation effort. Furthermore, we proved that the predictions are independent of the temporal distance between training and prediction. The MAE, which is like the MSE a common loss metric in the field of machine learning, for all models in scenario P1 is below 0.065. For scenario P2, we trained the u-net on the data of two \(\textrm{Ra}\) and predicted the temperature for the remaining third Ra. In this scenario, all models achieve MAE values below 0.085. We demonstrated that the u-net prediction in any scenario significantly outperforms the naive assumption of \({\tilde{T}}_{\textrm{naive}}\).

We rigorously analyzed the performance of the models in both scenarios by comparing the temperature fields, PDFs, and power spectra with the ground truth data. We observed that the characteristic superstructures are clearly recognizable in the predictions of both scenarios, albeit smoothed. The signs of smoother predictions are also remnant in the PDFs and the power spectra, which show a lower probability for extreme temperature events and lower power spectral density on smaller scales, respectively. Even though the P2 predictions tend to be biased, the size of the temperature superstructure can be correctly determined from the spectra in all cases. Our comparison of the heat transfer associated with the temperature predictions unveiled similarities in the field of ground truth \(\textrm{Nu}_{\text {loc}}\) field and the \(\textrm{Nu}_{\text {loc}}\) fields obtained from the predicted temperature. Remarkably, the \(\textrm{Nu}_{\text {loc}}\) fields obtained from the u-net predictions feature the occurrence and location of \(\textrm{Nu}_{\text {loc}} <0\) correctly, especially for the P1 scenario. The PDFs of \(\textrm{Nu}_{\text {loc}}\) show a good agreement with ground truth data for \(\textrm{Nu}_{\text {loc}} >0\). However, extreme \(\textrm{Nu}_{\text {loc}} <0\) events are underrepresented. The comparison of the global Nu displayed quantitative agreement between measurement and P1 scenario data but only qualitative agreement for the P2 scenario.

Our study showed that the u-net has proven to be a suitable and robust tool. When trained on data of the same experimental run, it is capable of physically consistent predictions from noisy measurement data. In the future, we want to incorporate information about the heat transfer into the training of the u-net. Therefore, we want to add an additional loss term determined from the difference between the PDF of \(\textrm{Nu}_{\text {loc}}\) obtained from measured temperature and vertical velocity and the PDF of \(\textrm{Nu}_{\text {loc}}\) obtained from predicted temperature and measured vertical velocity. Thereby, we expect the model to better estimate the negative tails of the \(\textrm{Nu}_{\text {loc}}\) PDFs.