Measurement of high-Re turbulent pipe flow using single-pixel PIV

Abstract

In this paper are presented PIV measurements of turbulent pipe flow at bulk Reynolds numbers Re$_D$ between 3.4$\times$10$^5$ and 6.9$\times$10$^5$. So-called single-pixel correlation is applied that yields a superior spatial resolution that is slightly larger than the equivalent size of a pixel in the flow. The location and shape of the averaged correlation peak give the mean velocity and normal and Reynolds stresses. A novel aspect of the single-pixel correlation approach is the extension to determine the 2-point spatial correlation of the velocity fluctuations and the spectrum of the longitudinal velocity fluctuations. Detailed results are presented for Re$_D$ = 4.98$\times$10$^5$, corresponding to a shear Reynolds number Re$_\tau$ = 10.3$\times$10$^3$, with a spatial resolution in wall units of $\varDelta y^+$ = 19.

1 Introduction

One of the main limitations in obtaining experimental data of wall turbulence at very high Reynolds number is the limited spatial resolution, especially in the near-wall region. Intrusive measurement methods, such as Pitot tube and hot-wire anemometry, are limited by the dimensions of the probe. Therefore, there has been a drive to design smaller measurement probes (Vallikivi et al. 2011). An alternative is to change the scale of the facility relative to the typical dimensions of the probe (Vinuesa et al. 2016). Particle image velocimetry (PIV) is a non-intrusive measurement method where commonly the instantaneous flow velocity field is estimated in small interrogation regions (Adrian and Westerweel 2011). The finite dimensions of the interrogation windows, here 32$\times$32 pixels, limit also the spatial resolution in the near-wall region. Using an optical system with a high magnification and elongated interrogation windows of 6$\times$64 pixels to accommodate strong velocity gradients in the wall-normal direction, Willert et al. (2017) obtained detailed measurements in the near-wall region of the CICLoPE facility, although a mirror needed to be introduced into the facility to accommodate the measurements.

Another approach is to extend the spatial resolution of the PIV measurement to a single pixel. This approach was first described for microfluidic applications (Westerweel et al. 2004), and that was later also applied to measure the mean velocity profile in the near-wall region of a turbulent boundary layer (Kähler et al. 2006). The shape of the displacement correlation peak represents the local probability-density function for the displacement that is convoluted with the particle image self-correlation (Westerweel 2008). This makes it possible to not only estimate the mean velocity from the location of the averaged displacement correlation peak, but also the turbulent normal stresses and Reynolds stress from the measured shape of the correlation peak (Scharnowski et al. 2012). However, to fully describe the turbulent flow statistics, it is necessary to also measure the local length scales. In this paper, we present a further extension to estimate the local spatial correlation of the velocity fluctuations that is based on the single-pixel algorithm.

Fig. 1

Setup of the PIV system used to measure the flow in the Alpha Loop. From: Sridharan (2018)

Fig. 2

Friction factor as measured and simulated in different pipe flow facilities as a function of the Reynolds number Re$_D$. The lines represent: (1) the friction factor for laminar Poiseuille flow ($c_f$= $64/\textrm{Re}_D$); (2) the friction law for a smooth wall, (Zagarola and Smits 1998); (3) the Blasius friction law ($c_f$ = 0.316/Re$_{D}^{1/4}$). Experimental and numerical data from: Eggels et al. (1994), den Toonder and Nieuwstadt (1997), McKeon et al. (2004), Wu and Moin (2008), Ahn et al. (2015), and present data. The inset shows the present data along with lines for different values of the relative roughness $k_s/D$ according to Colebrook (1939). The present data agrees with $k_s/D$ = 0.00003, leading to $k_s$ = 6.2 $\mu$m

2 Experimental set-up

The ability to improve the spatial resolution by means of the single-pixel PIV approach is demonstrated by measuring the turbulent flow in the ‘Alpha Loop’¹ at Deltares (Delft, The Netherlands); see Fig. 1. This facility is a closed-loop water-filled pipe with a length of 320 m and an inner diameter D of 206 mm. The flow loop is intended for industrial-scale testing of multiphase flows and is made of a nearly smooth steel pipe. In Fig. 2, we show the friction coefficients based on the measured pressure gradient and measured bulk flow rate. The inset of Fig. 2 shows that the pipe has a low roughness of $k_s/D = 3\times 10^{-5},$ corresponding to $k_s = 6.2~\mu$m. Separate roughness measurements on 20$\times$20 mm$^2$ samples of pipe material using a confocal microscope yield similar values; see “Appendix A”.

For the PIV measurements, the pipe is fitted with a transparent test section (made of PMMA) enclosed in a rectangular transparent water-filled box that can withstand the operating pressure (3 bar) and avoids serious light refraction from the curved pipe wall; the placement of external slits reduces internal reflections of the light sheet from the recorded images (Sridharan 2018); see “Appendix B”. The PIV test section is located approximately 530D downstream of the pumps. The flow is seeded with 10 $\mu$m diameter tracer particles (Sphericel 110P8, Potters Industries Inc.). A planar cross section of the flow is illuminated with a 0.8 mm thick light sheet generated from the beam of a frequency-doubled dual Nd:YAG laser (Spectra-Physics PIV 400) using light sheet forming optics. Images are recorded using a CCD camera (SensiCam QE) with a 1376$\times$1040-pixel image format and 6.45 $\upmu$m pixel pitch, equipped with a 50 mm focal length lens (Micro Nikkor) using a f/4 aperture stop. Image pairs are recorded using frame straddling with a framing rate of 5 Hz. The image magnification is $M_0$=0.035, ensuring ample focal depth and diffraction-limited particle images. The theoretical value for the diffraction-limited particle image diameter would be 5.4 $\upmu$m diameter, but in practice the diffraction-limited spot diameter is generally 2–4 times larger than the theoretical value for low aperture numbers (e.g. Adrian and Westerweel 2011, Fig. 10.6). The actual particle image diameter for the recorded images is determined from the particle image self-correlation, giving an $e^{-2}$ value of 10.9 $\upmu$m (1.7 px).

The recorded images are pre-processed using the proper² min-max filter (Adrian and Westerweel 2011) with a 5$\times$5-px filter size to enhance the image contrast and to reduce the number of spurious vectors (see below) by a factor of 4–6. Remnants of the internal reflections, which occur as thin horizontal lines near the pipe walls, are removed using a Fourier filter, similar to the method for removing striations in laser induced fluorescence (LIF) images (Westerweel et al. 2011). Using the method described by Adrian and Westerweel (2011, pp. 505–8), the image density $N_I$ in the pre-filtered images is 19–20 for 32$\times$32-px interrogation windows. The properties of the experimental set-up are summarized in Table 1.

Calibration of the measurement is performed by inserting a calibration grid with ‘+’ marks into the liquid-filled pipe and performing a linear scaling from pixel coordinates to physical coordinates. In order to obtain a high resolution calibration, a ray-tracing model of the transparent test section is used, which yields a correction to the calibration of up to 4.74 px in the near-wall area; see "Appendix C".

To carefully determine single-pixel PIV results, it is required to identify the location of the pipe wall. An intense reflection in the shape of a thin line in the lower half of the image identifies the pipe wall (pixel row 1234 from the top of the image); see Fig. 3. The reflection is directed away from the pipe axis at the far upstream side of the image and towards the pipe axis at the far downstream side of the image. Hence, there is a small misalignment and imaging error of the image rows with respect to the pipe axis of not more than ±1 px. Given that it is less than a pixel over the measurement range, no corrections are considered to be necessary. When approaching the pipe wall (e.g., the lower pipe wall at image row 1234), the single-pixel correlation displays a distinct peak, which vanishes when the wall is passed (i.e., image row 1235). After comparing the results for the mean streamwise velocity profiles with the familiar log law expression, it was concluded that the lower pipe wall is actually located at pixel 1235. It should be noted that here an integer-pixel wall location is used, but possibly fractional pixel wall locations can be considered due to the large influence on the near-wall part of the logarithmic velocity profile.

The flow rate is measured using an electromagnetic flow meter (ABB, type MAG-SM DS41F) located approximately 40D downstream of the pumps. The flow meter is calibrated to a full range of 300 l/s. The accuracy for the current discharge is 1% according to the product sheet. The pressure drop across one pipe section of length 6.125 m is measured using a differential pressure sensor (Rosemount 3051) calibrated to a full scale differential pressure of 62 mbar and corrected for the static pressure difference. The up- and downstream tube connections to the sensor are located at the side of the pipe sections (oriented horizontally), and there is one pair of flanges located between the up- and downstream tubes. The upstream connection of the differential pressure sensor is located at approximately 390D downstream of the pumps and 210D upstream of the PIV measurement section. During the measurements the water temperature increases due to frictional heating. The water temperature is measured using a Pt-100 temperature sensor mounted at the bottom of the pipe section downstream of the PIV section at approximately 500D upstream of the pumps. The temperature rise is measured for all cases; for Re$_D$ = 6.93$\times 10^5$ the temperature rise is not more than 0.4° C over the full duration of the measurement.

All signals are acquired by measuring the potential difference (in volts) over appropriate resistors using a data acquisition board (National Instruments 6210) at a rate of 1 Hz using custom software (LabView). The measured values are averaged over the full measurement period of approximately 4000 s for each case.

Fig. 3

Image processing steps: a recorded image; b after contrast normalization by means of a 5$\times$5-pixel min-max filter (Adrian and Westerweel 2011); c detail near the lower pipe wall in image b with reflections (the wall reflection occurs at image row 1234), and: d removal of remaining reflections in (c) by means of a Fourier filter (Westerweel et al. 2011). Image gray values are inverted in all images

Table 1 Experimental properties

3 Methodology

3.1 Mean velocity and velocity fluctuations

The conventional PIV method determines the local instantaneous particle image displacement by computing the spatial correlation in typically 32$\times$32-pixel interrogation windows and identifying the location of the displacement correlation peak; the velocity is obtained by dividing the particle image displacement by the exposure time-delay between the two laser light pulses that illuminate the flow (Adrian and Westerweel 2011).

Fig. 4

Principle of single-pixel PIV. For a set of image pairs the intensity at a given pixel location in the first exposure is correlated over a small region in the second exposure. The velocity is determined from the location of the displacement correlation peak. The shape and orientation of the correlation peak yield $\overline{{u'}^2}$, $\overline{{v'}^2}$, and $\overline{{u'v'}}$. After: Westerweel et al. (2004) and Kähler et al. (2006)

Alternatively, the particle image displacement can be found by correlating a single pixel in the first image frame with pixels in a small domain in the second frame, and summing the correlations over many frame pairs; see Fig. 4. When one uses 1024 frames, in principle the same amount of information is processed as for a single 32$\times$32-pixel (=1024 pixels) interrogation window. The gain is that the spatial resolution is now determined by the dimension of a single pixel, at the cost of losing the ability of recording time-resolved flows. This is attractive for stationary laminar and turbulent flows where a high spatial resolution is required.

In the present work, we make use of the fact that a fully developed turbulent pipe flow is homogeneous in the axial direction, and the single pixel approach is implemented by calculating the cross-correlation between a single image row of 922 pixels length in the first frame of a frame pair and a domain of a specified width and also a length of 922 pixels in the second frame. To accommodate the variations in particles-image displacement a domain width of 4 pixels is used for the mean flow quantities and a width of 8 pixels for the fluctuating quantities and spatial correlations. The computation of the correlation by means of Fourier transforms is implemented with zero padding (Adrian and Westerweel 2011). The particle image self-correlation is computed in a similar fashion, by means of auto-correlation of the second frame only. Both the cross-correlation and auto-correlation are summed over 20,000 recorded frame pairs for all cases. It is noted that in the vicinity of the reflections in the images (see Fig. 3), the resulting correlations appear to include a self-correlation peak at zero displacement that originates from the reflections. We therefore excluded in these cases a 3$\times$3-pixel domain centered around the zero displacement location in the spatial correlation to ignore the self-correlation peak.

Fig. 5

Examples of a fitted Gaussian two-dimensional peaks in a 5$\times$5 domain for single-pixel correlation averaging, taken at a pipe radius of approximately r = 85.2 mm and Re$_\tau =$ 10.3$\times$10$^3$. The numbers below the graphs show the preset values (‘Set’) and fitted values (‘Fit’) for the peak amplitude, sub-pixel location, widths ($\sigma _X$,$\sigma _Y$) along the principal axes (red and green lines), and angle $\alpha$ of orientation for the main principal axis. Subplots above and to the right show the fits along the principle axes. (top) Cross-correlation peak with widths ($\sigma _X$,$\sigma _Y$) = (1.04,0.76) [px] and angle $\alpha$ = 0.27 rad (15°). (bottom) The corresponding (nearly) circular self-correlation peak with $\sigma$ = 0.6 [px], which corresponds to a particle image diameter of $d_\tau$ = $2\sqrt{2}\sigma$ = 1.7 [px]. (Graphs and fitting by MATLAB macro D2GaussFit by Gero Nootz.$^{3}$)

Figure 5 shows a measured displacement correlation peak in a 5$\times$5 domain for Re$_\tau$ = 10,254 at a radial distance of r = 85.2 mm from the pipe centerline, i.e. r/D = 0.414. A two-dimensional elliptical Gaussian is fitted to the correlation data, using the MATLAB routine lsqcurvefit and based on the routine D2GaussFit³ by Gero Nootz. The result shows that the correlation peak is elliptical, oriented with its long axis (red) over an angle of 0.269 rad (15.4°) with a half-width of 1.037 px and a short-axis (green) half-width of 0.763 px. The profiles to the right and on top compare the fitted curves to the measured correlation data along the two principal axes. The fit requires a priori estimates for the location, widths, and orientation of the Gaussian peak, for which we use the results of the 3-point Gaussian fits (Adrian and Westerweel 2011) and zero-angle for the orientation. In the remainder of this paper, we use 3$\times$3-data fits for estimating the mean displacement, and 5$\times$5-data fits for the normal and Reynolds stresses.

Fig. 6

The deconvolution of the single-pixel correlation average $\langle R_D({\textbf{s}})\rangle$ with the particle image self-correlation $F_\tau ({\textbf{s}})$ to obtain the local velocity joint probability density function (PDF) $F_\varDelta ({\textbf{s}})$; see text. After: Strobl (2017)

To correct for the effect of the finite particle image diameter on the measured probability density function, the measured displacement correlation peak needs to be deconvoluted with the (measured) particle image self-correlation peak. Given a large enough ensemble of image pairs, the displacement correlation peak can be expressed as the convolution of the particle image self-correlation $F_\tau ({\textbf{s}})$ and the (in-plane) displacement distribution $F_\varDelta ({\textbf{s}})$ (Westerweel 2008; Adrian and Westerweel 2011):

$$\begin{aligned} \langle R_D({\textbf{s}})\rangle \sim F_\tau *F_\varDelta = \int F_\tau ({\textbf{s}}-{\textbf{s}}')F_\varDelta ({\textbf{s}}') d{\textbf{s}}', \end{aligned}$$

(1)

where ${\textbf{s}}$ is a vector in the correlation plane. The exact derivation of this expression and a convenient generalized approximation are given by Westerweel (2008). To extract the displacement distribution, it is assumed that both $F_\tau$ and $F_\varDelta$ are two-dimensional Gaussian functions (Scharnowski et al. 2012); in the case of diffraction-limited imaging, the particle image self-correlation $F_\tau ({\textbf{s}})$ is approximately a two-dimensional circular Gaussian function with a width $d_\tau \sqrt{2}$, where $d_\tau$ is the particle image diameter (Adrian and Westerweel 2011), while the displacement distribution $F_\varDelta ({\textbf{s}})$ is approximately a two-dimensional elliptical Gaussian function where the widths in axial and radial directions are directly proportional to the local normal stresses and the orientation of the ellipse depends on the Reynolds stress.

For the deconvolution of the displacement correlation peak we follow the method proposed by Strobl (2017): (i) first a two-dimensional elliptical Gaussian is fitted to the displacement correlation peak, which gives the orientation angle $\alpha$ of the long axis of the ellipse; (ii) the elliptical Gaussian peak is rotated over $-\alpha$, so that the main axes of the ellipse align with the horizontal (X) and vertical (Y) axes, and the widths of the Gaussian are given by $d_{\textrm{X}}$ and $d_\textrm{Y}$ respectively; (iii) given that $F_\tau$ is well approximated by a two-dimensional circular Gaussian function with an $e^{-2}$ width $d_\tau \sqrt{2}$ (Adrian and Westerweel 2011), the widths after deconvolution are given by:

$$\begin{aligned} d^*_{\textrm{X}}= \sqrt{d_{\textrm{X}}^{\ 2}-2d_\tau ^2} \quad \text {and:}\quad d^*_{\textrm{Y}}= \sqrt{d_{\textrm{Y}}^{\ 2}-2d_\tau ^2}, \end{aligned}$$

(2)

respectively; (iv) the new two-dimensional ellipse is rotated back over an angle $\alpha$ to its original orientation; see Fig. 6.

After deconvolution, the resulting two-dimensional Gaussian is normalized, so that it represents the local two-dimensional probability density function $f(u^*,v^*)$, with: $\iint f(u^*,v^*)du^* dv^* \equiv 1$, where $f(u^*,v^*)du^* dv^*$ represents the probability that $u^*< u < u^*+du^*$ and $v^*< v < v^*+dv^*$ (Nieuwstadt et al. 2016). To obtain the mean velocities, i.e. first-order moments, and normal and Reynolds stresses, i.e. second-order moments, at each location the integration is carried out numerically as:

$$\begin{aligned} {\overline{u}}= & {} \iint u^* \cdot f(u^*,v^*)\ du^* dv^*, \end{aligned}$$

(3)

$$\begin{aligned} {\overline{v}}= & {} \iint v^* \cdot f(u^*,v^*)\ du^* dv^*, \end{aligned}$$

(4)

$$\begin{aligned} \overline{u'^2}= & {} \iint (u^*-{\overline{u}})^2 \cdot f(u^*,v^*)\ du^* dv^*, \end{aligned}$$

(5)

$$\begin{aligned} \overline{v'^2}= & {} \iint (v^*-{\overline{v}})^2 \cdot f(u^*,v^*)\ du^* dv^*,\quad \text {and:} \end{aligned}$$

(6)

$$\begin{aligned} \overline{u'v'}= & {} \iint (u^*-{\overline{u}})(v^*-{\overline{v}})\cdot f(u^*,v^*)\ du^* dv^*. \end{aligned}$$

(7)

In Fig. 7, the measured correlation function and the corresponding two-dimensional Gaussian representations, before and after deconvolution, are shown for case Re$_D$ = 4.98$\times$10$^5$ at a radial distance of r = 85.2 mm from the centerline. This approach appears to work well for the axial normal stress and the Reynolds stress, but appears to yield elevated values for the radial normal stress. It is conjectured that the variation in axial displacement is comparable to or larger than the particle image diameter, but this is not the case for the variation in the radial displacement, which appears to be smaller than the particle image diameter. As a result, the deconvolution procedure as described above may not yield accurate results for the radial normal turbulent stress. Instead, we use an effective particle image diameter ${\hat{d}}_\tau$ for the deconvolution in (2) that is found by matching the single-pixel result for the radial normal stress to the data that was obtained by the conventional PIV in the overlap region where both methods were applied.

In the work of Scharnowski et al. (2012), it is mentioned that bias effects may occur in estimates of the normal and Reynolds stresses due to large gradients in the particle image displacement in combination with a large particle image diameter. In the present measurements, the largest variation in displacements due to velocity gradients occurs near the pipe wall, where it is estimated to be at most 0.25 [px/px] (see Figs. 9 and 10 below), and the particle image diameter is measured at 1.7 px (see Fig. 5); hence, given these values, no significant bias is expected for the present measurement data.

Fig. 7

(left) Measured displacement correlation $\langle R_D({\textbf{s}})\rangle$ for Re$_D =$ 4.98$\times$10$^5$ at a radial distance of $r = 85.2$ mm from the pipe centerline; (center) two-dimensional Gaussian representation of $\langle R_D({\textbf{s}})\rangle$; (right) correlation peak after deconvolution with the particle image self-correlation

Fig. 8

Principle of measuring spatial correlation of the axial velocity fluctuations using single-pixel PIV. The joint probability density function is constructed via diadic multiplication and summation of the correlation data in two points separated over a distance $\varDelta x = x_2-x_1$; see text for further explanation. The inset shows the convergence of the estimated relative error for the spatial correlation as a function of the number of processed frames. Data taken from the spatial correlation for $\varDelta x$ = 3.68 mm at the pipe centerline. On the right is reproduced the corresponding joint pdf, with an enlargement of the 5$\times$5 domain that contains the main peak that is used to determine the spatial correlation. An animated version of the central cartoon and the summation of the correlation are available as supplementary material

3.2 Spatial correlation of velocity fluctuations

In this paper, we introduce an extension to the single-pixel approach, and that is the evaluation of spatial correlations of the velocity fluctuations, defined as (Hinze 1975; Adrian and Westerweel 2011):

$$\begin{aligned} Q_{uu}(\varDelta x) = \overline{u'(x)u'(x+\varDelta x)} = \overline{{u'}^2}\rho _{uu}(\varDelta x), \end{aligned}$$

(8)

where $\rho _{uu}(\varDelta x)$ is the correlation coefficient for velocity data separated by a distance $\varDelta x$ = $x_2-x_1$ along a homogeneous direction in the flow (here the axial velocity fluctuations $u'$ along the axial direction x of the pipe flow). Conventionally, $Q_{uu}(\varDelta x)$ is estimated from PIV data by multiplying the velocity fluctuations at locations separated by a distance $\varDelta x$, and then averaging over data along the homogeneous direction (if any) and over all recorded frames. This yields a biased estimate of $Q_{uu}$ with an expectation value:

$$\begin{aligned} E\{{\hat{Q}}_{uu}(\varDelta x)\} \cong Q_{uu}(\varDelta x)\left( 1-|\varDelta x| / L\right) \end{aligned}$$

(9)

(Adrian and Westerweel 2011), with $|\varDelta x|<L$ where L is the length along the homogeneous direction of the region where PIV data is taken. The second factor on the righthand side is known as a Bartlett window.

An alternative approach is to estimate $Q_{uu}(\varDelta x)$ from the joint probability density function of the velocity fluctuations $(u'_1,u'_2)$ at two distinct points $(x_1,x_2)$ in the flow:

$$\begin{aligned} Q_{uu}(\varDelta x) = \iint (u_1^*-{\overline{u}})(u_2^*-{\overline{u}}) f(u_1^*,u_2^*|x_1,x_2) du_1^* du_2^*, \end{aligned}$$

(10)

The two-point joint pdf $f(u_1^*,u_2^*|x_1,x_2)$ is constructed as illustrated in Fig. 8: We multiply the instantaneous intensity in a single pixel at $x_1$ in frame A with the intensities in a given number of pixels in frame B. When a particle image is present at $x_1$ in frame A and also in the range of pixels in frame B, then this gives a peak at an offset of $u_1$ equal to the instantaneous particle image displacement; see the red pixels and signal peak in Fig. 8. At the same time, we multiply the instantaneous intensity of a single pixel at $x_2$ in frame A with the intensities of a given number of pixels in frame B. If there happens to be a particle image present at $x_2$, this gives a signal peak at an offset $u_2$ equal to the instantaneous particle image displacement; see the blue pixels and correlation peak in Fig. 8. We subsequently perform a dyadic multiplication of the two signals, i.e. $f_1(u_1|x_1) \otimes f_1(u_2|x_2)$ (where each signal is represented as a vector), to construct a matrix containing a peak in the $(u_1,u_2)$ plane; green dot in Fig. 8. This is then repeated for all pixels along a row in frames A and B, which is the homogeneous direction for the current flow, and over all frame pairs (A,B). This then builds up an estimate for the joint probability density function $f(u_1^*,u_2^*|x_1,x_2)$:

$$\begin{aligned} f(u_1^*,u_2^*|x_1,x_2) \doteq \sum \limits _{\langle i \rangle } f_1^{(i)}(u_1|x_1) \otimes f_1^{(i)}(u_2|x_2), \end{aligned}$$

(11)

where the sum over i means averaging data in the homogeneous direction and over all frame pairs. Note that only when there is a particle image present at $x_1$ and at the same moment another particle image at $x_2$ that there is a contribution to the estimation of the joint pdf; without a particle image present in either $x_1$ or $x_2$ the net contribution to the estimate is effectively nihil. Hence, a large volume of data is required to obtain a reliable unbiased estimate $Q^*_{uu}(\varDelta x)$. Given that the image density for a 32$\times$32-pixel area is 10, the probability to find a particle image in a single pixel is 0.010; to find two particle images simultaneously in two pixels is then only 10$^{-4}$. In the present data we have around 900 pixels per line, and 20,000 frame pairs, yielding a total of 18$\times$10$^6$ sample pairs, so that one can expect 1800 simultaneously matching particle image pairs (or more when the image density is above 10). This is why a large number of image frame pairs is required for the estimation of the spatial correlation. Furthermore, there is a finite probability that erroneous matches occur, but these are expected to be randomly distributed over the $(u_1,u_2)$ domain and do not seriously affect the estimation of spatial correlation. The inset in Fig. 8 shows the convergence of the relative statistical error for the two-point spatial correlation as a function of the number of frames (each containing 900 pixels per row) that was processed. The data in this graph were determined via so-called bootstrapping. The results indicate that the error converges proportional to $1/\sqrt{N}$, where N is the number of pixels; this is indicative of a linear process for correlation averaging (Meinhart et al. 2000; Westerweel et al. 2004; Scharnowski et al. 2012).

A typical result for the joint PDF is shown in the right inset in Fig. 8. The joint PDF appears as an elongated 2D Gaussian distribution that is always oriented along the diagonal. The correlation estimate $Q^*_{uu}$ follows from the mixed moment, defined in (10).

As for the point-wise PDF’s, the joint PDF’s are convoluted by the particle image self-correlation. To correct for this, we normalize the measured correlations $Q^*_{uu}$ with those of the conventional PIV analysis, similar to the normalization of the wall-normal stresses. However, the conventional PIV data yields a biased estimate ${\hat{Q}}_{uu}$ of the spatial correlation (Priestley 1992; Adrian and Westerweel 2011), so in order to compare the two results, the estimate $Q^*_{uu}$ is multiplied with a Bartlett window to match the biased estimate ${\hat{Q}}_{uu}$.

In the current work, the spatial correlation is determined for an axial spatial range of 800 pixels. To properly estimate the integral scale from the spatial correlation, its tail is extended by fitting of an exponential tail from the data between offsets of 400 to 800 pixels. In a region of approximately 7 pixels near $\varDelta x = 0,$ the spatial correlation shows erratic results; see “Appendix D”. Hence, the data for the spatial correlation over a separation of less than 7 pixels is ignored and replaced by the results of a parabolic fit over the remaining data. Finally, the Fourier transform is taken of the single-pixel spatial correlation data to yield the power spectrum of axial velocity fluctuations. To attenuate the noise in the tails of the spatial correlation, a moving mean filter with a variable filter size ranging from 4 to 132 pixels is applied. Furthermore, the spectral data is averaged in equally spaced spectral windows in logarithmic wavenumber-space (Priestley 1992, p. 580).

4 Results

4.1 Acquired data

Measurements are performed at bulk Reynolds numbers Re$_D$ ($= 2U_bR/\nu$) between 3.4$\times$10$^5$ and 6.9$\times$10$^5$ (where $U_b$ is the bulk velocity, $R = \frac{1}{2}D$ is the pipe radius, and $\nu$ the kinematic viscosity of the fluid). The main flow conditions are shown in Table 2. The wall shear stress is calculated from the measured pressure drop and used to obtain the friction velocity as $u_\tau =\sqrt{\tau _w/\rho }$. The friction factor is determined via $c_f = 8 (u_\tau / U_b)^2$. The water density and kinematic viscosity are taken at the measured mean temperature.

Table 2 The flow conditions and exposure time delay for the measurements

For each Reynolds number a total of 20,000 double-frame images are recorded. We mainly present results obtained at Re$_D$ = 4.98$\times$10$^5$, with a corresponding shear Reynolds number Re$_\tau$ ($\equiv u_\tau R/\nu$) = 10.3$\times$10$^3$.

4.2 Conventional PIV method

For the conventional PIV processing, the images are pre-processed using a 5$\times$5-px min-max filter (Adrian and Westerweel 2011). A multi-grid approach is used with initially 64$\times$64-px interrogation areas and 50% overlap. After determining the median vectors in a 5$\times$5 neighborhood, the result is interpolated to a 32$\times$32-px grid with 50% overlap for the second interrogation pass. After the second pass, any outliers are detected using universal outlier detection (Westerweel and Scarano 2005) and replaced by means of linear interpolation. The 32$\times$32-pixel interrogation result for the case Re$_D$ = 4.98$\times$10$^5$ contains 1.8% spurious vectors (67 outliers per image pair yielding 3763 vectors each, with 45 and 96 as the 5- and 95-percentiles, respectively); this indicates that there is sufficient seeding and negligible loss-of-correlation due to out-of-plane motion. These numbers are also representative for the measurements taken at the other Reynolds numbers presented in Table 2, with the exception of the image pairs for the highest flow rate (i.e., 97 lps), where the working fluid became slightly polluted.

The final grid consists of 71$\times$53 interrogation areas leading to a vector spacing of 2.94 mm. Profiles of the mean velocity, normal stresses and Reynolds stress are determined by pointwise averaging of the interrogation results over all image pairs followed by averaging the data along rows (in the homogeneous direction of the turbulent pipe flow). For the conventional PIV results only the first 5000 images are used for all cases. All PIV processing is performed using in-house MATLAB software based on the methods documented by Adrian and Westerweel (2011).

4.3 Single-pixel PIV results

The spatial resolution of the conventional PIV is given by the dimensions of the 32$\times$32-pixel interrogation window. For the measurement presented here this corresponds to a resolution of $\varDelta y^+ \cong$ 600. Evidently, this is too crude to make measurements in the near-wall region. The single-pixel approach gives a measurement at each (radial) pixel location, and thus gives a spatial resolution of $\varDelta y^+$ = 19. This would in principle be sufficient to determine the flow profiles in the entire log-region.

Fig. 9

(top) Measured mean axial velocity profile from the wall to the axis of the pipe. Black markers represent the conventional PIV with 32$\times$32-pixel interrogation windows; colored markers are the single-pixel correlation results. (bottom) Detail for the 10 mm region near the wall. Open markers indicate reflection locations except for the data points directly adjacent to the wall, where the result is possibly influenced by optical effects due to the presence off the wall

Figure 9 shows the measured velocity profiles with both the conventional and the single-pixel PIV approaches. The results cover a displacement range between 4 and 11 pixels and appear to be free from pixel locking errors. The conventional PIV was performed over the entire flow, while the single-pixel results were only done for the near-wall flow region, with a sufficient overlap with the conventional PIV data.

Fig. 10

The mean axial velocity profile in wall units for all values of Re$_\tau$ in Table 2. The black symbols represent the conventional PIV results using 32$\times$32-pixel interrogation regions; the colored symbols represent the single-pixel PIV result. Open symbols indicate locations with interference from reflections or locations where the result is possibly influenced by the presence of the wall. The horizontal error bars indicate the influence of a variation in wall location of 0.5 px further towards lower $y^+$ values (error bar on right side of symbol) and 0.25 px towards higher $y^+$ values (error bar on left side of symbol). The dashed lines indicate $(\ln {y^+}+ \Pi )/k$ where $\Pi = 1.8$ and $k = 0.405$. Lines for increasing values of $Re_\tau$ are shifted by 5 plus units. The solid red line indicates the data of McKeon et al. (2004)

Figure 10 shows the velocity profiles for all Reynolds numbers, but now in a semi-log plot, which illustrates the high level of accuracy of the single-pixel PIV results and the extension of the range in the log-region by a decade in wall units. Note that the results are converged up to the size of the symbols and also note that the data point nearest to the wall for case $Re_\tau$ = 7162 is the only near-wall data point that is increasing in value during the convergence process. To assess the quality of the mean flow, the data of McKeon et al. (2004) for $Re_{\tau } = 10,914$ is compared with the present case $Re_{\tau } = 10,254$. The agreement up to symbol size indicates that the quality of the mean flow is comparable. The profiles coincide with the log profile with a von-Kármán constant of k = 0.405. This value for k is in agreement with the value found by Nagib and Chauhan (2008) for pipe flow.

Fig. 11

The normal and Reynolds stresses in wall units for Re$_\tau$ = 10.3$\times 10^3$ Top: Reynolds stress $\overline{u'v'}^+$. Bottom: normal stresses represented by $\overline{u'}^+$ $\equiv$ ($\overline{{u'}^2}/u_\tau ^2)^{1/2}$ and $\overline{v'}^+$ $\equiv$ $(\overline{{v'}^2}/u_\tau ^2)^{1/2}$. Black dots represent the 32$\times 32$-pixel PIV data and light red dots represent the single-pixel PIV results. The red line is the three-point moving average excluding data at the reflections in Fig. 3; see also text

Figure 11 shows the results for the normal stresses and the Reynolds stress, as determined by the procedure explained in Sect. 3. The conventional PIV method using 32$\times$32-pixel interrogation windows shows erroneous results for the radial normal stress and the Reynolds stress close to the pipe wall (for $|r|/D > 0.43$), which corresponds to a distance $y^+ < 10^3$ from the wall. The single-pixel PIV results appear to give reliable results when approaching the wall. As explained in Sect. 3, the results for the radial normal stress $\overline{{v'}^2}$ are deconvoluted by matching the deconvoluted single-pixel correlation results with the conventional 32$\times$32-pixel results for $\overline{{v'}^2}$. The single-pixel PIV results for the Reynolds stress appear to deviate occasionally from the surrounding data, which can be attributed to interference of the remaining reflections with the single-pixel estimate of the displacement correlation peak.

One of the features observed in high-Re turbulent pipe flow is the emergence of a so-called outer peak in the streamwise normal stress $\overline{{u'}^2}$ (Hultmark et al. 2013; Willert et al. 2017). The outer peak begins to emerge at a Reynolds number Re$_\tau$ larger than 2$\times$10$^4$, which is just outside the range of our measurements. However, at a Reynolds number Re$_\tau \sim 10^4$ a clear ‘plateau’ is visible in the profile for $\overline{{u'}^2}$, which is evident when comparing with results for much lower Reynolds numbers (e.g., den Toonder and Nieuwstadt 1997).

Fig. 12

The streamwise normal stress $\overline{{u'}^2}^+$ as a function of the distance from the wall for Re$_\tau$=10, 254 (Re$_D$ = 4.98$\times$10$^3$). The light red circles represent the 32$\times$32-px PIV data (for $y^+ > 665)$, the light red dots the single-pixel PIV data. The red line is a tenth-order fitted polynomial that excludes the data at the reflections in Fig. 3, indicated by the arrows at the top. The dash-dotted green curve represents the data of Willert et al. (2017) at Re$_\tau$= 11.7$\times$10$^3$; the dashed blue curve represents the data of Hultmark et al. (2013) at Re$_\tau$= 10.5$\times$10$^3$. The continuous maroon line and the continuous purple line indicate the data of den Toonder and Nieuwstadt (1997) at Re$_\tau$ = 338 and 1382, respectively

In Fig. 12, the normalized normal stress $\overline{{u'}^2}^+$ is plotted as a function of the distance from the wall $y^+$. The data is compared with data obtained by Hultmark et al. (2013) at Re$_\tau$ = 10.5$\times$10$^3$ in the Princeton Superpipe and by Willert et al. (2017) at Re$_\tau$ = 11.7$\times$10$^3$ in the CICLoPE facility. The single- pixel results match the conventional 32$\times$32-px PIV data that is available for $y^+>$ 665 only. The original single-pixel PIV data show occasional fluctuations in the range $250< y^+ < 10^3$. This can be attributed to the reflections that occur close to the pipe wall; see Fig. 3. By expanding the number of modes in the Fourier filter to six in the images prior to the single-pixel correlation in the affected area, the effect of these reflections could be substantially suppressed only at the locations in between the reflections. A tenth order polynomial is fitted to the PIV and single-pixel data. The results show an acceptable agreement with the Superpipe and CICLoPE data to within an error margin that corresponds to variations in the particle displacement of 0.11 px. Note that the so-called inner peak, located at $y^+ \approx$ 10–20 could not be resolved. The plateau in $\overline{u'^2}^+$ that occurs at these high Reynolds numbers can be resolved down to $y^+ \cong 150$ from the pipe wall. This is approximately 500 wall units closer to the wall than for conventional PIV.

In Fig. 13, we present the results for the spatial correlation coefficient $\rho _{uu}(\varDelta x)$ of the axial velocity fluctuations at five wall distances, ranging from the pipe centerline to $y^+ = 172$. Upon integrating the area below the spatial correlation we obtain the longitudinal integral turbulence length scale L/D. The inset in Fig. 13 shows the integral length scale as a function of the distance from the wall. The length scale decreases in size upon approaching the wall, as is expected. Towards the pipe centerline the length scale again decreases.

Fig. 13

The full longitudinal spatial correlation coefficient $\rho _{uu} (\varDelta x)$ for the axial velocity fluctuations at locations: $y^+ = 172$, 423, 791, 1580, and 10,254 (pipe centerline). Successive data are shifted vertically by 0.3 for clarity. Light-blue dots: single-pixel correlation results; blue lines: same data after applying moving average filter with increasing filter length (indicated at the lower axis); red line: fitted exponential tail; green dots: fitted central peak. The inset shows the integral length scale L, obtained by L = $\int \rho _{uu}(s) ds$, relative to the pipe diameter D. Dashed line in inset is the integral length scale estimated from the 32$\times$32-px PIV data

By taking the Fourier transform of $\rho _{uu}(\varDelta x)$ we find the longitudinal spectrum $F_{uu}(\kappa )$. In Fig. 14, the spectrum as derived from the single pixel data is shown, along with the binned results and an indication of a $-5/3$ slope. The single-pixel PIV result extends the range in wavenumber by more than a decade (owing to the 16–32 times higher resolution compared to the conventional 32$\times$32-px PIV data), but also becomes noisy at the higher wave numbers. By using binning over equal sections along the logarithmic axis (red dots in Fig. 14), a consistent result is obtained for $\kappa D < 10^3$, whereas the conventional PIV data appears to give consistent results for $\kappa D < 100$. This demonstrates the potential of single-pixel PIV to provide information of the spatial structure of the turbulence. The results of Laufer (1954) for the measured turbulence spectrum at the centerline ($y/R=1.0$) and $y/R=0.074$ at Re$_D$ = 500$\times$10$^3$ are included in Fig. 14.

Fig. 14

The one-dimensional turbulent power spectra $F_{uu}(\kappa )$ as a function of the wavenumber $\kappa$, normalized by the pipe diameter D, corresponding to the data in Fig. 13. Graphs are shifted vertically by two decades for visibility. The light blue lines correspond to the spatially filtered data in Fig. 13, where the open red dots represent data for $\kappa D < 20$; the solid red dots represent binned data over equal intervals $\log (\varDelta \kappa /\kappa )$ (see text). The cross symbols represent the data from the 32$\times$32-px PIV data. The dashed blue lines indicate a $-5/3$ slope. The open circles and triangles are (normalized) data from Laufer (1954) at y/R = 1.0 and 0.074, respectively

5 Conclusions

We present high-resolution PIV results (ultimately limited by the pixel size) of turbulent pipe flow, using a single-pixel PIV approach. This improves the spatial resolution by more than an order of magnitude over conventional PIV methods, while still recording the data over the full pipe diameter. This is applied to an industrial-style pipe flow facility, at shear Reynolds numbers between Re$_\tau$ = 7.2$\times$10$^3$ and 13.9$\times$10$^3$. Detailed results are presented for the measurement at a shear Reynolds number of Re$_\tau$ = 10.3$\times$10$^3$. Conventional PIV using 32$\times$32-pixel interrogation windows only covers the wake region of the turbulent pipe flow, with the interrogation region closest and non-overlapping to the wall residing at the outer edge of the log-layer. The single-pixel PIV result is obtained by processing 20$\times$10$^3$ image pairs. Making use of the homogeneous axial direction in turbulent pipe flow, 18$\times$10$^6$ pixel pairs are processed and resulting in a 3$\times$3-pixel correlation peak for each radial position. Sub-pixel interpolation yields the mean velocity profile and makes it possible to resolve the full log layer down to the buffer layer.

For single-pixel PIV, the data spacing is equal to the equivalent size of a pixel in the object domain. In the original design of the experiment, the theoretical value for the diffraction-limited particle image diameter is computed as 4.0 $\upmu$m (Adrian and Westerweel 2011, Fig. 3.19), which is less than the size of a pixel (see Table 1). However, from the particle image self-correlation peak an effective particle image diameter of 10.9 $\mu$m is determined ($e^{-2}$-value), so that the actual spatial resolution in the object domain is somewhat larger than the equivalent size of a pixel.

From the shape of the 5$\times$5-pixel correlation peak also the axial and radial normal stresses and the Reynolds stress can be extracted. The accuracy of the single-pixel PIV result is demonstrated by resolving the plateau in the axial normal stress that forms into an outer peak at higher Reynolds numbers down to $y^+ \cong 150$ from the pipe wall. This is approximately 500 wall units closer to the wall than for conventional PIV. However, it appears that the result is sensitive to the presence of reflections in the image. These reflections arise from the laser light sheet that enters the optical box and inner and outer transparent pipe walls within the optical box. In the present application, conventional non-fluorescent tracer particles were used; the interference of these reflections could be avoided by the use of fluorescent tracer particles in combination with an appropriate optical filter. A novel aspect of the work is the extension of single-pixel PIV from single-point to two-point flow statistics, demonstrated by a high-resolution result for the spatial correlation of the axial velocity fluctuations. This makes it possible to obtain a reliable estimate of the turbulent spectral density for the axial velocity fluctuations. These results were obtained with a standard PIV system with a modest resolution of 1376$\times$1040 pixels. This demonstrates the capabilities of single-pixel PIV for turbulence measurements of high-Re wall turbulence, without recourse to specialized equipment or dedicated flow facilities. Using cameras with a larger format would make it possible to resolve the turbulence statistics even closer to the wall.

Appendices

Appendix A: Wall roughness

At very high Reynolds numbers, the roughness of the pipe wall can become an issue (Shockling et al. 2006; Langelandsvik et al. 2008). In the present measurements, the wall roughness is determined from the Colebrook correlation in Fig. 2. In order to obtain a separate quantification of the surface roughness of the pipe, a measurement was performed by a commercial enterprise using a confocal microscope (type Sensofar S Neox 090) with a Nikon EPI 10$\times$ objective. Scans are made of an area of 6.24$\times$5.23 mm$^2$ located centrally on the sample with a spatial resolution of 1.38 $\mu$m/px. Four samples (1–4) of 20$\times$20 mm$^2$ each from a visibly smooth section of pipe and three (5–7) similarly sized samples from a visibly corroded section of pipe were removed and measured using a combination of depth-from-defocus and confocal microscopy. The result for Sample 4 is shown in Fig. 15.

Fig. 15

Image of Sample 4 of a visually smooth section of the pipe wall. The size of the sample is 20$\times$20 mm$^2$

Resulting images of the surface of Sample 4 are shown in Fig. 16. The root mean square roughness height for the depicted sample is 4.0 $\mu$m. The results for all samples are tabulated in Table 3.

Fig. 16

Surface roughness quantification result for sample number 4. The data shown has been corrected for the curvature of the pipe wall

Table 3 Surface roughness quantification results. $S_q$ is the root mean square roughness height from confocal microscopy; see text

Appendix B: Effect of external slits

In the PIV measurement section use was made of two externally mounted slits with an approximate width of 2 mm to eliminate some of the occurring reflections. The slits were mounted on the laser side and opposite side of the test section. An indication of the reflections that were removed is shown in Fig. 17.

Fig. 17

Effect of external slits. Top: ray tracing diagram (not to scale) representing the bright lines appearing in the raw PIV images. Bottom left: raw PIV image without external slits. Bottom right: raw PIV image after using external slits. After: Sridharan (2018)

Appendix C: Near-wall correction to calibration

In the current work, the transformation from pixel units to physical units is performed using a linear scaling. The scaling factor is derived from the distance between the + marks on the calibration plate. This leads to a scaling factor of 0.1839 mm/px. Upon modelling the propagation of light rays in the PIV test section using a ray tracing approach, it was found that in a near-wall area of approximately 100 pixels the magnification varies significantly and the internal cylinder acts somewhat as a convex cylindrical lens, i.e. the imaged radial distance from the wall is compressed with respect to the physical distance. The ray tracing model result of the light ray intersecting the inner pipe wall of the measurement section is shown in Fig. 18.

Fig. 18

Ray tracing model of the PIV test section, consisting of a rectangular glass box that enclosed a PMMA pipe, both filled with water. The refractive indices of the glass, PMMA, and water, are 1.51, 1.49, and 1.33, respectively. The camera is positioned left of the measurement section at 1626 mm from the light sheet plane represented by the green vertical line) coming in from the bottom. The solid blue ray intersects with the inner wall of the test section; the blue and dotted lines represent the (continued) refracted and reflected rays, respectively. The dashed blue line represents the imaginary unrefracted ray. Black lines represent primary and secondary reflected and refracted rays (for the lower half of the images in Fig. 3) from where the light sheet intersects optical interfaces. Solid lines represent reflections (partly) visible in the images; dashed lines are reflection that are not visible. The numbers on the left represent the image row numbers, relative to the image location of the wall (‘0’); Reflections 1, 2, and 3 in Fig. 3 occur at lines 15, 31, and 50, respectively. All dimensions are in mm

Using the ray-tracing model, a correction to the scaling as obtained from the calibration markers is computed. This correction is shown in Fig. 19 along with the interpolation to absolute pixel values. The final radial locations are determined by adding the correction to the distance from the wall in pixels and then applying the previously mentioned scaling factor. The values of the refractive indices used in the ray tracing computation are given in the caption of Fig. 18.

The correction is validated by extrapolating the physical distance between the calibration markers to the wall location (column 1235 in the raw image). Upon performing the linear extrapolation the location where the wall ($r = 103$ mm) is expected to be without correction is 1238, whereas in the images the wall is at pixel 1235; see Fig. 20. This agrees with the model results up to approximately 2 pixels; see Fig. 19.

Fig. 19

Correction to the linear calibration scaling as computed by ray-tracing. Left: correction over the full pipe radius. Right: correction and for the first hundred pixels from the wall (covering the inner layer up to the edge of the log-layer)

Fig. 20

Ray-tracing validation: pixel locations of the calibration markers versus calibration marker inter mark distance, including linear extrapolation towards the image row for the anticipated wall location (1238); the actual wall location is found at image row 1235

The same ray tracing can be applied to reconstruct the locations of the reflections observed in Fig. 3; see Fig. 18.

Fig. 21

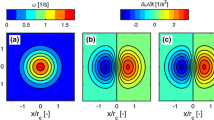
The estimate of the joint probability function (pdf) $f(u_1^*,u_2^*|x_1,x_2)$ with $\varDelta x = x_2-x_1$ determined with the method described in Fig. 8 for offsets between $\varDelta x$ = 0 and 7 [px]. The appearance of the auto-correlation band (offset by a distance $\varDelta x$) and a mirror image of the joint pdf is explained in the diagram on the right

Appendix D: Single-pixel spatial correlation for small separations

The estimation of the joint PDF $f(u_1^*,u_2^*|x_1,x_2)$, as explained in Fig. 8, gives erratic results for an offset $\varDelta x$ = $x_2-x_1$ less than 5–7 pixels. Examples of the computed joint PDF for $\varDelta x$ between 0 and 7 [px] are shown in Fig. 21. A self-correlation band may overlap with the joint PDF. This band is due to the self-correlation of particle images that appear both in $f_1(u_1^*|x_1)$ and $f_1(u_2^*|x_2)$; see the diagram in Fig. 21. It is conjectured that incomplete transfer of charge between pixels on the CCD sensor during image readout may also contribute to the appearance of this band. Also, a mirror image of the joint PDF appears on the opposite side of the self-correlation band, which is also explained in the diagram in Fig. 21.