1 Introduction

The schlieren method is a technique used to visualize light refraction caused by density gradients. It enables to observe the instantaneous flow geometry of a wide area without disturbing the flow and is an essential tool for studying compressible flows, such as jets, wakes, mixing layers, and shock waves (Van Dyke 1982; Settles 2001). A variant of the schlieren method, background-oriented schlieren (BOS) (Raffel 2015), has also been widely used. The patterns on the background behind the flows appeared to shift because of light refraction caused by density gradients. The magnitude of refraction can be obtained quantitatively by measuring the displacement of the patterns in an image captured with a camera. Although BOS has some disadvantages, such as blurred images of the flow owing to out-of-focus and inferior spatial resolution compared with the schlieren method, it has gained interest because of its simple apparatus.

A problem with these visualization methods is that three-dimensional (3D) flows are difficult to capture because all refractions along the light path are integrated into visualized data. This can be solved by reconstructing the 3D density distribution using computed tomography (referred to as 3D-BOS in this paper). Numerous studies have explored applications from relatively simple flows, including (i) axisymmetric or (ii) steady/periodic flows measured using a single camera, to (iii) more complicated, non-axisymmetric, and unsteady flows measured using multiple cameras. Group (i) includes jets (Venkatakrishnan et al. 2011; van Hinsberg and Rösgen 2014; Tan et al. 2015), flows around wind tunnel models (Venkatakrishnan and Meier 2004; Venkatakrishnan and Suriyanarayanan 2009; Sourgen et al. 2012; Leopold et al. 2013), shock waves (Hayasaka et al. 2016), candle plumes (Guo and Liu 2017), and combustion flows (Wahls and Ekkad 2022a, b). Group (ii) includes non-axisymmetric jets (Venkatakrishnan 2005; Goldhahn and Seume 2007; Tipnis et al. 2013; Lang et al. 2017; Kirby 2018; Lee et al. 2021) and flows around non-axisymmetric wind tunnel model (Ota et al. 2011). Group (iii) includes natural convection (Zeb et al. 2011), flow around projectiles (Yamagishi et al. 2021), wing tip vortices (Klinge et al. 2004), cascade wake (Hartmann et al. 2015), jets (Adamczuk et al. 2013; Nicolas et al. 2016, 2017a, b; Hartmann and Seume 2016; Lanzillotta et al. 2019), candle plumes (Nicolas et al. 2016), flames (Atcheson et al. 2008; Grauer et al. 2018; Liu et al. 2021), and fuel sprays (Lee et al. 2012). In recent years, further studies have been conducted on the implementation in wind tunnels (Bathel et al. 2019, 2022; Weisberger et al. 2020), improvement of analysis methods (Unterberger et al. 2019; Grauer and Steinberg 2020; Unterberger and Mohri 2022; Cai et al. 2022), uncertainty analysis (Rajendran et al. 2020), velocity field estimation using physics-informed neural networks (Cai et al. 2021; Molnar et al. 2023a, b), high-speed measurements using various devices such as optical fibers (Liu et al. 2020; Ukai 2021; Gomez et al. 2022), and the use of speckle BOS (Amjad et al. 2023) and plenoptic BOS (Davis et al. 2021).

Despite the progress of these studies, the application of the 3D-BOS method for measuring the density distributions near a wall is still challenging. This is because the wall blocks most of the light paths, resulting in a lack of light from multiple directions for obtaining the refraction data for reconstructing the density distributions. This problem may arise for near-wall flows, such as transonic buffets (Kouchi et al. 2016), shock wave–boundary layer interactions (Bolton et al. 2017), and supersonic impinging jets (Akamine et al. 2021). In the third case, a supersonic jet impinges on an inclined flat plate, forming a 3D shock structure on the wall, that interacts with a turbulent jet shear layer to produce intense acoustic waves. To further understand the noise source mechanism, it is necessary to measure the unsteady behavior of 3D shock structures and the large-scale turbulent fluctuations of shear layers. Such measurements have been difficult because, for example, all fluctuations on the wall are integrated into schlieren images and the shear layers slightly distant from the wall cannot be captured by measuring the wall pressures. These difficulties can be overcome if the 3D-BOS can measure near-wall density distributions.

For near-wall density measurements based on the 3D-BOS method, modifications are required to provide sufficient light paths near the wall. One possible approach is the use of transparent walls; however, the light direction is still restricted because of the total internal reflection (the critical angle is approximately 42° for glass with a typical refractive index of 1.5). To the best of the authors’ knowledge, two extensions have been proposed (Hashimoto et al. 2017; Bühlmann 2020), although each has its limitations. The method of Hashimoto et al. is an application of near-field BOS (van Hinsberg and Rösgen 2014), in which a wall surface is used as a background of the BOS optical system. This has the advantage of enabling density measurements with only minor modifications from the conventional 3D-BOS. However, for example, Fig. 3 of van Hinsberg and Rösgen (2014) shows that the smallest detectable refraction angle of the near-field BOS rapidly deteriorates when the distance between the wall and density distribution approaches about 40 mm or less. The other method by Bühlmann uses the speckle BOS instead of conventional BOS. It uses a speckle pattern created by the reflection of the laser on the rough surface of the wall instead of the usual background pattern, enabling measurements up to the vicinity of the wall. However, Bühlmann also noted that a phenomenon called speckle decorrelation occurs, in which the speckle pattern not only shifts but also deforms when the refraction angle is large. A method for designing optical systems to avoid speckle decorrelation has not yet been established. A method that is more similar to the conventional BOS with higher sensitivity in the vicinity of the wall would be useful.

This paper proposes a new extension, 3D-BOS using Mirror, to measure the density field near the wall surface to overcome the limitations. The proposed method uses the wall as a mirror to provide sufficient light paths for the reconstruction. Unlike the method of Hashimoto et al., the sensitivity in the near-wall region can be maintained by using the mirror image of the background away from the density distribution. Additionally, unlike Bühlmann’s method, most of the optical settings are the same as in the conventional 3D-BOS (Nicolas et al. 2017a). A major difference from the conventional method is that the light paths are reflected by the mirror. The refraction data for the reconstruction becomes complicated because both the direct and mirror-reflected images are superposed. This paper first proposes a formulation for such complicated data. Next, the proposed method is validated using artificially generated model data of an ideal axisymmetric density distribution. The differences between the true and reconstructed distributions are compared with those of the conventional method. Finally, the proposed method was experimentally demonstrated by measuring density distributions of a candle plume.

2 Methods

The proposed method, 3D-BOS using Mirror, shares most of the concepts of the measurement and analysis with the conventional 3D-BOS (Nicolas et al. 2016, 2017a). In this section, the methods are described in four parts to illustrate the similarities and differences between the conventional and proposed methods: (i) measurement setup (Sect. 2.1), (ii) measured data (Sect. 2.2), (iii) reconstruction analysis from the measured data (Sect.  2.3), and (iv) camera calibration in experiments (Sect. 2.4).

2.1 Measurement setup

Figure 1a shows a typical measurement setup for a conventional 3D-BOS. Around the target density distribution, multiple cameras are placed within 180° on one side, and background boards with patterns are placed on the other side. In contrast, the proposed method considers a case in which a flat wall is located adjacent to the density distribution, as shown in Fig. 1b. Unlike conventional methods, the cameras cannot be placed behind walls. Thus, the cameras are placed within 90° on one side and the background boards on the other side. Using the wall as a mirror to reflect light, the proposed method provides light paths from directions blocked by the wall (Cam 1 to Cam 11 in Fig. 1b). It may be desirable to provide light paths that are almost parallel to the mirror to accurately measure the density gradient normal to the mirror plane. However, depending on location of the background boards and the sizes of the density distribution and mirror, there is a minimum camera direction relative to the mirror plane at which the reflected images of the background boards can be captured. In the experiment described in Sect. 3.2, an additional camera was placed almost parallel to the mirror (Cam 12 in Fig. 1b).

Fig. 1
figure 1

Examples of the setup for the conventional 3D-BOS and proposed 3D-BOS using Mirror (not to scale)

Full size image

2.2 Measured data

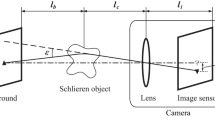
The data measured in the setups described in Sect. 2.1 is explained using the schematic of the light paths shown in Fig. 2. Despite differences owing to the mirror reflection, both the conventional and proposed methods capture images with cameras and calculate the light direction vectors before and after passing through the reconstructed region including the target density distribution. The directional changes of those vectors are used to reconstruct the density distribution in Sect. 2.3. Specifically, the light direction vectors are calculated based on the following concepts.

Fig. 2
figure 2

Schematic views of the light paths for disturbed (orange) and quiescent (blue) cases (not to scale)

Full size image

Figure 2a shows the light paths in the conventional method. Images are captured by cameras when the density distribution is present (disturbed case) and removed (quiescent case). The shifts of the background pattern between the two images due to light refraction are measured using methods such as optical flow. Figure 2a shows the case when the pattern appearing at D1 in the disturbed case is shifted to Q1 in the quiescent case. Under the camera model assuming that all the projecting light paths are through a pinhole O, the straight light paths Q1–O and D1–O are calculated from the pixel coordinates of Q1 and D1, respectively. In the quiescent case, by extending Q1–O, the location of point Q2 is obtained as the intersection with the background board. In the disturbed case, the unit light direction vectors changes from the vector \({{\varvec{e}}}_{\mathrm{in}}\) at point D2, where the light enters the reconstructed region, to the vector \({{\varvec{e}}}_{\mathrm{out}}\) at point D3, where the light exits the reconstructed region, owing to the refraction caused by the density distribution between D2 and D3. Though the light path D2–D3 is actually a curved line, the displacement from a straight line is small because the refraction angle is small (Nicolas et al. 2016). Thus, approximating the light path D2–D3 with a straight line extended the line D1–O, the locations of points D2 and D3 are calculated as the intersections with the surfaces of the reconstructed region. From the directions of the straight lines D1–D2 and D3–Q2, the unit light direction vectors \({{\varvec{e}}}_{\mathrm{in}}\) and \({{\varvec{e}}}_{\mathrm{out}}\) are obtained, respectively.

Figure 2b shows the light paths in the proposed method. The light paths are reflected at the mirror located at a surface of the reconstructed region. As in the conventional method, the lines D1–O and Q1–O are first extended to calculate points D2 and D3 in the disturbed case and Q2 in the quiescent case. By reflecting and extending the line Q1–Q2, the location of point Q3 is obtained as the intersection with the background board. The intersection point D4 with the surface of the reconstructed region can also be determined by reflecting and extending the line D1–D3 based on the approximation of the conventional method that the light paths in the reconstructed region can be considered straight lines. From the directions of the straight lines D1–D2 and D4–Q3, the unit light direction vectors \({{\varvec{e}}}_{\mathrm{in}}\) and \({{\varvec{e}}}_{\mathrm{out}}\) are obtained, respectively. These vectors represent the light directions at points D2 and D4 where the light path enters and exits the reconstructed region, respectively.

2.3 Reconstruction of density distribution

2.3.1 Fundamentals

This section describes the method of reconstructing the density distribution using the changes between the light direction vectors \({{\varvec{e}}}_{\mathrm{in}}\) and \({{\varvec{e}}}_{\mathrm{out}}\) obtained in Sect. 2.2. In this study, the proposed method was formulated based on a direct approach (Nicolas et al. 2016; Grauer et al. 2018) among the various conventional 3D-BOS methods. In both the conventional and proposed methods, a measurement vector \({\varvec{b}}\) defined in Sects. 2.3.2 and 2.3.3 is first calculated from the light direction vectors \({{\varvec{e}}}_{\mathrm{in}}\) and \({{\varvec{e}}}_{\mathrm{out}}\) corresponding to each pixel on the image plane of each camera. Next, a reconstructed region is defined that includes the target density distribution. A vector \({\varvec{\rho}}\) denotes the density vector, which is reshaped from the density values on a grid discretizing the reconstructed region, and a matrix \(A\) represents the transformation from \({\varvec{\rho}}\) to \({\varvec{b}}\). The vector \({\varvec{\rho}}\) is calculated such that the norm of the difference between \({\varvec{b}}\) and \(A{\varvec{\rho}}\), \({\Vert {\varvec{b}}-A{\varvec{\rho}}\Vert }_{2}^{2}\), is minimized:

$$\begin{array}{*{20}c} {\mathop {{\text{argmin}}}\limits_{{\varvec{\rho}}} \left\{ \left\Vert \varvec{b} - A \varvec{\rho} \right\Vert_2^2 + \lambda \left\Vert \nabla \varvec{\rho} \right\Vert_2^2 \right\}. } \\ \end{array}$$
(1)

The second term is a regularization term to keep the solution smooth. The regularization parameter \(\lambda\) is determined using the L-curve method for every data point (Nicolas et al. 2016), which was \(\lambda ={10}^{-4}\) in Sect. 3.1 and \(\lambda ={10}^{-5}\) in Sect. 3.2. This paper uses an iterative method called LSQR (Paige and Saunders 1982) to solve the minimization problem in Eq. (1). The obtained density distribution has an arbitrary constant corresponding to the constant of integration. The constants are determined to minimize the difference from the true distribution in Sect. 3.1, and to make the densities at the outer surfaces of the reconstructed region become the atmospheric density in Sect. 3.2.

The matrix \(A\) and vector \({\varvec{b}}\) in Eq. (1) were derived from the following two basic equations. One is the ray equation in geometric optics (Eq. 2.27 in (Träger 2012)):

$$\begin{array}{*{20}c} {\frac{{\text{d}}}{{{\text{d}}s}}\left( {n{\varvec{e}}} \right) = \varvec{\nabla} n,} \\ \end{array}$$
(2)

where \(s\) is the distance along the light path, \({\varvec{e}}\) is the unit light direction vector, and \(n\) is the refractive index. The other equation is the Gladstone–Dale law (Merzkirch 1987):

$$\begin{array}{*{20}c} {n = G\rho + 1,} \\ \end{array}$$
(3)

where \(G=2.26\times {10}^{-4}\) m3/kg is the Gladstone–Dale constant for dry air. In the succeeding subsections, the formulations of the conventional and proposed methods are explained based on these equations. For simplicity, the light beams were treated as the principal rays in this study.

2.3.2 Conventional 3D-BOS

Although the conventional and proposed methods share the basic Eqs. (2) and (3), they differ in the definition of the measurement vector \({\varvec{b}}\) and transformation matrix \(A\) in Eq. (1) owing to the mirror reflection of the light paths. This subsection summarizes the derivation of the measurement vector \({\varvec{b}}\) and transformation matrix \(A\) for the conventional method. Substituting Eq. (3) into Eq. (2) and integrating over the interval D2–D3 in Fig. 2a,

$${\frac{{n_{0} }}{G}\left( {{\varvec{e}}_{{{\text{out}}}} - {\varvec{e}}_{{{\text{in}}}} } \right) = \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s,}$$
(4)

where \({n}_{0}\) is the refractive index of the surrounding atmosphere, and \({s}_{D2}\) and \({s}_{D3}\) are the distances measured along the light path from D1 to D2 and D3, respectively. By selecting two vectors \({{\varvec{e}}}_{\xi }\) and \({{\varvec{e}}}_{\eta }\) such that \(\left\{{{\varvec{e}}}_{\xi }, {{\varvec{e}}}_{\eta }, {{\varvec{e}}}_{\mathrm{in}}\right\}\) is an orthonormal basis, and transforming the coordinates of Eq. (4) to this basis by determining the inner product,

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {b_{\xi } \equiv \frac{{n_{0} }}{G}{\varvec{e}}_{\xi } \cdot {\varvec{e}}_{{{\text{out}}}} = {\varvec{e}}_{\xi } \cdot \mathop \int \nolimits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s} \\ {b_{\eta } \equiv \frac{{n_{0} }}{G}{\varvec{e}}_{\eta } \cdot {\varvec{e}}_{{{\text{out}}}} = {\varvec{e}}_{\eta } \cdot \mathop \int \nolimits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s} \\ {\frac{{n_{0} }}{G}\left( {{\varvec{e}}_{{{\text{in}}}} \cdot {\varvec{e}}_{{{\text{out}}}} - 1} \right) = {\varvec{e}}_{{{\text{in}}}} \cdot \mathop \int \nolimits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s} \\ \end{array} } \right..} \\ \end{array}$$
(5)

Only two of three equations in Eq. (5) are independent because \({{\varvec{e}}}_{\mathrm{out}}\) is the unit vector, i.e., \({\left({{\varvec{e}}}_{\xi }\cdot {{\varvec{e}}}_{\mathrm{out}}\right)}^{2}+{\left({{\varvec{e}}}_{\eta }\cdot {{\varvec{e}}}_{\mathrm{out}}\right)}^{2}+{\left({{\varvec{e}}}_{\mathrm{in}}\cdot {{\varvec{e}}}_{\mathrm{out}}\right)}^{2}=1\). We select the first and second equations in Eq. (5).

By using the scalars \({b}_{\xi }\) and \({b}_{\eta }\) on the left-hand side of the first and second equations in Eq. (5), the measurement vector \({\varvec{b}}\) in Eq. (1) can be constituted as follows. By writing \({{\varvec{e}}}_{\xi }={\left(\begin{array}{ccc}{e}_{\xi x}& {e}_{\xi y}& {e}_{\xi z}\end{array}\right)}^{T}\), the right-hand side of the first equation in Eq. (5) becomes

$${b_{\xi } =\, e_{\xi x} \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \frac{\partial \rho }{{\partial x}} {\text{d}}s + e_{\xi y} \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \frac{\partial \rho }{{\partial y}} {\text{d}}s + e_{\xi z} \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \frac{\partial \rho }{{\partial z}} {\text{d}}s,}$$
(6)

where the \(x, y,\) and \(z\) axes are those of the grid of the reconstructed region. By discretizing Eq. (6) and summarizing those for all the pixels of all the cameras,

$$\begin{array}{*{20}c} {{\varvec{b}}_{\xi } \approx E_{\xi x} PD_{x} \varvec{\rho} + E_{\xi y} PD_{y} \varvec{\rho} + E_{\xi z} PD_{z} \varvec{\rho} .} \\ \end{array}$$
(7)

The vector \({{\varvec{b}}}_{\xi }\) consists of the scalars \({b}_{\xi }\) of all the pixels of all the cameras. The vector \({\varvec{\rho}}\) is the density vector as in Eq. (1), which consists of the density values on the grid points. The numbers of elements of the vectors \({{\varvec{b}}}_{\xi }\) and \({\varvec{\rho}}\) are denoted by \({N}_{i}\) and \({N}_{j}\), respectively. The \({N}_{j}\times {N}_{j}\) matrices \({D}_{x}, {D}_{y},\) and \({D}_{z}\) are the operators that transform the density vector \({\varvec{\rho}}\) into vectors consisting of the density gradients \(\frac{\partial \rho }{\partial x},\frac{\partial \rho }{\partial y},\) and \(\frac{\partial \rho }{\partial z}\) on the grid points. In this paper, these are defined as the coefficient matrices for the second-order central difference or, at the end points, second order one-sided differences. The \({N}_{i}\times {N}_{j}\) matrix \(P\) is the operator that transforms the values on the grid points to the integral between D2 and D3. In this paper, this is defined as the coefficient matrix for the trapezoidal integration of the values on the light path linearly interpolated from the grid points. The \({N}_{i}\times {N}_{i}\) matrices \({E}_{\xi x}, {E}_{\xi y},\) and \({E}_{\xi z}\) are the diagonal matrices consisting of the scalars \({e}_{\xi x}, {e}_{\xi y},\) and \({e}_{\xi z}\) for all the pixels of all the cameras, respectively. For the scalar \({b}_{\eta }\) in Eq. (5), we can express the same form as in Eq. (7); thus,

$$\begin{array}{*{20}c} {\mathop {\mathop {\underbrace{ \left( {\begin{array}{*{20}c} {{\varvec{b}}_{\xi } } \\ {{\varvec{b}}_{\eta } } \\ \end{array} } \right)}_{\varvec{b}} } } \approx \mathop {\mathop { \underbrace{ \left( {\begin{array}{*{20}c} {E_{\xi x} } & {E_{\xi y} } & {E_{\xi z} } \\ {E_{\eta x} } & {E_{\eta y} } & {E_{\eta z} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} P & O & O \\ O & P & O \\ O & O & P \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right) }_{A}} } \varvec{\rho} ,} \\ \end{array}$$
(8)

where \(O\) is the \({N}_{i}\times {N}_{j}\) zero matrix, and the \({N}_{i}\times {N}_{i}\) matrices \({E}_{\eta x}, {E}_{\eta y},\) and \({E}_{\eta z}\) are the diagonal matrices consisting of the scalars \({e}_{\eta x}, {e}_{\eta y},\) and \({e}_{\eta z}\) for all the pixels of all the cameras, respectively, where \({{\varvec{e}}}_{\eta }={\left(\begin{array}{ccc}{e}_{\eta x}& {e}_{\eta y}& {e}_{\eta z}\end{array}\right)}^{T}\). The \(2{N}_{i}\)-vector on the left-hand side and \(2{N}_{i}\times {N}_{j}\) matrix on the right-hand side in Eq. (8) are the vector \({\varvec{b}}\) and matrix \(A\) in Eq. (1), respectively, for the conventional method.

2.3.3 Proposed 3D-BOS using mirror

This subsection summarizes the derivation of the measurement vector \({\varvec{b}}\) and transformation matrix \(A\) for the proposed method. The major difference from the conventional method is an additional refraction in the light path after the mirror reflection, D3–D4, as shown in Fig. 2b. Substituting Eq. (3) into Eq. (2) and integrating between D2–D3 and D3–D4, respectively,

$${\frac{{n_{0} }}{G}\left( {{\varvec{e}}_{D3} - {\varvec{e}}_{{{\text{in}}}} } \right) = \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s,}$$
(9a)
$${\frac{{n_{0} }}{G}\left( {{\varvec{e}}_{{{\text{out}}}} - {\varvec{e}}_{D3}^{\prime} } \right) = \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \varvec{\nabla} \rho {\text{d}}s,}$$
(9b)

where \({s}_{D2},{s}_{D3},\) and \({s}_{D4}\) are the distances measured along the light path from D1 to D2, D3, and D4, respectively. The unit vectors \({{\varvec{e}}}_{D3}\) and \({{\varvec{e}}}_{D3}^{\prime}\) represent the light directions before and after the mirror reflection, and they have the following relationship (Householder transform):

$$\begin{array}{*{20}c} {{\varvec{e}}_{D3}^{ {\prime }} = {\varvec{e}}_{D3} - 2\left( {{\varvec{e}}_{D3} \cdot {\varvec{e}}_{n} } \right){\varvec{e}}_{n} ,} \\ \end{array}$$
(9c)

where \({{\varvec{e}}}_{n}\) is the unit normal vector of the mirror plane. Using \({{\varvec{e}}}_{\xi }\) and \({{\varvec{e}}}_{\eta }\) defined as in the conventional methods, Eqs. (9a)–(9c) can be summarized into two equations as follows. By determining the inner product of Eq. (9a) and \({{\varvec{e}}}_{\xi }\),

$${\frac{{n_{0} }}{G}{\varvec{e}}_{\xi } \cdot {\varvec{e}}_{D3} = {\varvec{e}}_{\xi } \cdot \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s.}$$
(10a)

By determining the inner product of Eq. (9b) and the vector \({{\varvec{e}}}_{\xi }^{\prime}={{\varvec{e}}}_{\xi }-2\left({{\varvec{e}}}_{\xi }\cdot {{\varvec{e}}}_{n}\right){{\varvec{e}}}_{n}\), which is the mirror reflection of \({{\varvec{e}}}_{\xi }\),

$${\frac{{n_{0} }}{G}\left( {{\varvec{e}}_{\xi }^{ {\prime }} \cdot {\varvec{e}}_{{{\text{out}}}} - {\varvec{e}}_{\xi }^{ {\prime }} \cdot {\varvec{e}}_{D3}^{ {\prime }} } \right) = {\varvec{e}}_{\xi }^{ {\prime }} \cdot \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \varvec{\nabla} \rho {\text{d}}s.}$$
(10b)

By determining the inner product of Eq. (9c) and \({{\varvec{e}}}_{\xi }^{\prime}\), and using that \({{\varvec{e}}}_{n}\) is a unit vector, i.e., \({\Vert {{\varvec{e}}}_{n}\Vert }_{2}^{2}={{\varvec{e}}}_{n}\cdot {{\varvec{e}}}_{n}=1\),

$$\begin{aligned} {\varvec{e}}_{\xi }^{ {\prime }} \cdot {\varvec{e}}_{D3}^{ {\prime }} = & \left\{ {{\varvec{e}}_{\xi } - 2\left( {{\varvec{e}}_{\xi } \cdot {\varvec{e}}_{n} } \right){\varvec{e}}_{n} } \right\} \cdot \left\{ {{\varvec{e}}_{D3} - 2\left( {{\varvec{e}}_{D3} \cdot {\varvec{e}}_{n} } \right){\varvec{e}}_{n} } \right\} \\ = & {\varvec{e}}_{\xi } \cdot {\varvec{e}}_{D3} - 2\left( {{\varvec{e}}_{D3} \cdot {\varvec{e}}_{n} } \right)\left( {{\varvec{e}}_{\xi } \cdot {\varvec{e}}_{n} } \right) - 2\left( {{\varvec{e}}_{\xi } \cdot {\varvec{e}}_{n} } \right)\left( {{\varvec{e}}_{D3} \cdot {\varvec{e}}_{n} } \right) + 4\left( {{\varvec{e}}_{\xi } \cdot {\varvec{e}}_{n} } \right)\left( {{\varvec{e}}_{D3} \cdot {\varvec{e}}_{n} } \right) = {\varvec{e}}_{\xi } \cdot {\varvec{e}}_{D3} . \\ \end{aligned}$$
(10c)

Substituting Eqs. (10c) and (10a) into Eq. (10b),

$${\frac{{n_{0} }}{G}\left( {{\varvec{e}}_{\xi }^{ {\prime }} \cdot {\varvec{e}}_{{{\text{out}}}} - {\varvec{e}}_{\xi } \cdot {\varvec{e}}_{D3} } \right) = \frac{{n_{0} }}{G}{\varvec{e}}_{\xi }^{ {\prime }} \cdot {\varvec{e}}_{{{\text{out}}}} - {\varvec{e}}_{\xi } \cdot \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s = {\varvec{e}}_{\xi }^{ {\prime }} \cdot \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \varvec{\nabla} \rho {\text{d}}s. }$$
(10d)

After performing Eq. (10d), and similarly for \({{\varvec{e}}}_{\eta }\) and its mirror reflection \({{\varvec{e}}}_{\eta }^{\prime}\), we obtain the following equations:

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {b_{\xi } \equiv \frac{{n_{0} }}{G}{\varvec{e}}_{\xi }^{ {\prime }} \cdot {\varvec{e}}_{{{\text{out}}}} = {\varvec{e}}_{\xi } \cdot \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s + {\varvec{e}}_{\xi }^{ {\prime }} \cdot \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \varvec{\nabla} \rho {\text{d}}s} \\ {b_{\eta } \equiv \frac{{n_{0} }}{G}{\varvec{e}}_{\eta }^{ {\prime }} \cdot {\varvec{e}}_{{{\text{out}}}} = {\varvec{e}}_{\eta } \cdot \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \varvec{\nabla} \rho {\text{d}}s + {\varvec{e}}_{\eta }^{ {\prime }} \cdot \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \varvec{\nabla} \rho {\text{d}}s} \\ \end{array} } \right..} \\ \end{array}$$
(11)

This is the equation for the proposed method corresponding to Eq. (5) in the conventional method.

The right-hand side of the first equation in Eq. (11) can be expressed as follows, similar to Eq. (6) in the conventional method:

$$b_{\xi } = e_{\xi x} \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \frac{\partial \rho }{{\partial x}} {\text{d}}s + e_{\xi y} \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \frac{\partial \rho }{{\partial y}} {\text{d}}s + e_{\xi z} \mathop \int \limits_{{s_{D2} }}^{{s_{D3} }} \frac{\partial \rho }{{\partial z}} {\text{d}}s + e_{\xi x}^{ {\prime }} \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \frac{\partial \rho }{{\partial x}} {\text{d}}s + e_{\xi y}^{ {\prime }} \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \frac{\partial \rho }{{\partial y}} {\text{d}}s + e_{\xi z}^{ {\prime }} \mathop \int \limits_{{s_{D3} }}^{{s_{D4} }} \frac{\partial \rho }{{\partial z}} {\text{d}}s,$$
(12)

where \({{\varvec{e}}}_{\xi }^{\prime}={\left(\begin{array}{ccc}{e}_{\xi x}^{\prime}& {e}_{\xi y}^{\prime}& {e}_{\xi z}^{\prime}\end{array}\right)}^{T}\), and the \(x, y,\) and \(z\) axes are those of the grid of the reconstructed region. By discretizing Eq. (12) and summarizing those for all the pixels of all the cameras,

$$\begin{array}{*{20}c} {{\varvec{b}}_{\xi } \approx E_{\xi x} PD_{x} \varvec{\rho} + E_{\xi y} PD_{y} \varvec{\rho} + E_{\xi z} PD_{z} \varvec{\rho} + E_{\xi x}^{ {\prime }} P^{ {\prime }} D_{x} \varvec{\rho} + E_{\xi y}^{ {\prime }} P^{ {\prime }} D_{y} \varvec{\rho} + E_{\xi z}^{ {\prime }} P^{ {\prime }} D_{z} \varvec{\rho} .} \\ \end{array}$$
(13)

The matrices \({D}_{x}, {D}_{y}, {D}_{z}, P, {E}_{\xi x}, {E}_{\xi y}\), and \({E}_{\xi z}\) are the same as in Eq. (7). The \({N}_{i}\times {N}_{j}\) matrix \({P}^{\prime}\) is the operator that transforms the values on the grid points to the integral between D3 and D4. The \({N}_{i}\times {N}_{i}\) matrices \({E}_{\xi x}^{\prime}, {E}_{\xi y}^{\prime},\) and \({E}_{\xi z}^{\prime}\) are the diagonal matrices consisting of the scalars \({e}_{\xi x}^{\prime}, {e}_{\xi y}^{\prime},\) and \({e}_{\xi z}^{\prime}\) for all the pixels of all the cameras, respectively. For the scalar \({b}_{\eta }\) in Eq. (11), we can express this in the same form as in Eq. (13); thus,

$$\begin{array}{*{20}c} {\mathop {\mathop { \underbrace{ \left( {\begin{array}{*{20}c} {{\varvec{b}}_{\xi } } \\ {{\varvec{b}}_{\eta } } \\ \end{array} } \right)}_{\varvec{b}} } } \approx \mathop {\mathop { \underbrace{ \left( {\begin{array}{*{20}c} {E_{\xi 1} } & {E_{\xi 2} } & {E_{\xi 3} } & {E_{\xi 1}^{ {\prime }} } & {E_{\xi 2}^{ {\prime }} } & {E_{\xi 3}^{ {\prime }} } \\ {E_{\eta 1} } & {E_{\eta 2} } & {E_{\eta 3} } & {E_{\eta 1}^{ {\prime }} } & {E_{\eta 2}^{ {\prime }} } & {E_{\eta 3}^{ {\prime }} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} P & O & O \\ O & P & O \\ O & O & P \\ {P^{\prime}} & O & O \\ O & {P^{\prime}} & O \\ O & O & {P^{\prime}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right)}_{A} } } \varvec{\rho} ,} \\ \end{array}$$
(14)

where the \({N}_{i}\times {N}_{i}\) matrices \({E}_{\eta x}^{\prime}, {E}_{\eta y}^{\prime},\) and \({E}_{\eta z}^{\prime}\) are the diagonal matrices consisting of the scalars \({e}_{\eta x}^{\prime}, {e}_{\eta y}^{\prime},\) and \({e}_{\eta z}^{\prime}\) for all the pixels of all the cameras, respectively, where \({{\varvec{e}}}_{\eta }^{\prime}={\left(\begin{array}{ccc}{e}_{\eta x}^{\prime}& {e}_{\eta y}^{\prime}& {e}_{\eta z}^{\prime}\end{array}\right)}^{T}\). The \(2{N}_{i}\)-vector on the left-hand side and \(2{N}_{i}\times {N}_{j}\) matrix on the right-hand side in Eq. (14) are the vector \({\varvec{b}}\) and matrix \(A\) in Eq. (1), respectively, for the proposed method.

2.4 Camera calibration

Before the analysis described in Sects. 2.2 and 2.3, camera calibration was performed to obtain the locations and attitudes of the cameras, background boards, and mirror. Similar to the camera calibration for the conventional method (Le Sant et al. 2014), a marker board of known size was placed near the target density distribution and several images were captured with the cameras while changing the attitude of the marker board, as shown in Case A of Fig. 3a. The pixel coordinates of the markers were detected from the images, providing the intrinsic parameters, locations, and attitudes of the cameras relative to the marker boards (Zhang 2000), and thus the relative locations and attitudes between the cameras. Furthermore, as shown in Case B in Fig. 3b, the locations and attitudes of the background board were obtained by attaching the markers to the background board and applying the same analysis.

Fig. 3
figure 3

Data for the camera calibration in 3D-BOS using Mirror (top, configurations; bottom, examples of data (detected markers are shown as orange marks))

Full size image

The proposed method additionally requires the location and attitude of the mirror. In this study, the location and attitude of the mirror were obtained by fixing the marker board and capturing several images while changing the mirror attitudes (Takahashi et al. 2012, 2016), as shown in Case C in Fig. 3c.

To further reduce the error in the location and attitude of the mirror, we captured the mirror-reflected images while changing the attitude of the marker board placed near the density distribution, as shown in Case D in Fig. 3d, to obtain information about the locations of the light paths reflected by the mirror. A parameter optimization called the bundle adjustment (Hartley and Zisserman 2004) was then performed to minimize the difference between the pixel coordinates of the measured markers and those calculated with the obtained parameters for all the data in Cases A–D.

In Cases A and D, a circle grid (3 rows × 7 columns asymmetric grid with 2 mm dot diameter and 5 mm column spacing) was used because the markers were not in focus, and in Cases B and C, ChArUco markers (Garrido-Jurado et al. 2014) with a chessboard square length of 10 mm and marker square size of 5 mm were used for robust detection. Both the markers were detected using the OpenCV library implementation. In Zhang’s method, an ideal simple camera was assumed to stabilize the estimation of the intrinsic parameters: the scale factors of the pixel coordinate in the horizontal and vertical directions were \(\alpha =\beta\), the skew factor between the two axes on the image plane was \(\gamma =0\), the pixel coordinates of the pinhole \(\left({u}_{0}, {v}_{0}\right)\) was fixed to the image center, and the lens distortion was ignored.

3 Results and discussion

3.1 Model data tests

The proposed method, 3D-BOS using Mirror, was validated by examining whether the reconstructed distribution agrees with the true distribution for an artificially generated model data. First, a model data of an ideal axisymmetric distribution was generated. By setting cameras virtually, the values \({b}_{\xi }\) and \({b}_{\eta }\) were calculated for the model data using the right-hand sides of the first and second equations of Eq. (5) for the conventional method and Eq. (11) for the proposed method. With the calculated \({b}_{\xi }\) and \({b}_{\eta }\), we reconstructed the distribution using the conventional and proposed methods, respectively. The differences between the reconstructed and true distributions were compared for the conventional and proposed methods to examine whether the differences between these two methods affected the reconstructed results. Because the number of cameras was known to affect the reconstruction error (Nicolas et al. 2016), we varied the number of cameras in the range \({N}_{\mathrm{cam}}=3-24\).

The model data were defined as an axisymmetric distribution around \(y\)-axis in the region \(\left[-0.5, 0.5\right]\times \left[-0.5, 0.5\right]\times \left[-0.5, 0.5\right]\) with a radial profile:

$$\begin{array}{*{20}c} {\rho \left( r \right) = \frac{1}{2}\left( {1 - \tanh \frac{{r - r_{e} }}{{\delta_{e} }}} \right),} \\ \end{array}$$
(15)

where \(r= \sqrt{{x}^{2}+{z}^{2}}\), and the radius and boundary thickness of the cylinder were set at \({r}_{e}=0.25\) and \({\delta }_{e}=0.08\), respectively. The grid resolution was heuristically determined to be 31 × 31 × 31. The isosurfaces in Fig. 4a show the 3D distribution of the model data, and the gray surface (\(z=0.5\)) indicates the mirror plane when the proposed method was examined. Figure 4b shows the distribution on the plane perpendicular to the \(y\)-axis in Fig. 4a. The distributions on the horizontal and vertical dashed lines are plotted on the upper and right sides, respectively.

Fig. 4
figure 4

Model data for the validation

Full size image

Figure 5a and b show examples of virtual camera configurations for the conventional and proposed methods, respectively. The red and blue lines indicate the image plane and its normal vector, and the thin gray lines are the light paths indicating the angle of view for each camera. The orange lines show the reconstructed region, and the thick gray line in Fig. 5b indicates the mirror plane. In the conventional method, \({N}_{\mathrm{cam}}\) cameras were equally spaced on a semicircle of a radius of 10 centered at the origin. In the proposed method, \({N}_{\mathrm{cam}}\) cameras were equally spaced within the range of 10 to 75 degrees to the \(z\)-axis, on a circle of a radius of 10 centered at the point \(\left(x, y, z\right)=(0, 0, 0.5)\) located on the mirror plane. The resolution of each camera was \(51\times 29\) pixels, and the scale factor to the pixel coordinates (Sect. 2.4) was set at \(\alpha =300\).

Fig. 5
figure 5

Configurations and distributions of \({b}_{\xi }\)

Full size image

Using these configurations, the values \({b}_{\xi }\) and \({b}_{\eta }\) were computed with the right-hand side of the first and second equations in Eq. (5) for the conventional method and Eq. (11) for the proposed method. It should be noted that the principal rays (i.e., infinite depth of focus) were assumed for simplicity. The Gauss–Kronrod quadrature was used to calculate each integral, and the density gradient was obtained analytically from Eq. (15) as

$$\begin{array}{*{20}c} {\varvec{\nabla} \rho = \frac{{{\text{d}}\rho }}{{{\text{d}}r}}\frac{1}{r}\left( {\begin{array}{*{20}c} x \\ 0 \\ z \\ \end{array} } \right), \frac{{{\text{d}}\rho }}{{{\text{d}}r}} = - \frac{1}{{2\delta_{e} \cosh^{2} \frac{{r - r_{e} }}{{\delta_{e} }}}}.} \\ \end{array}$$
(16)

Figure 5c and d show the horizontal components, \({b}_{\xi }\), of each camera in the conventional and proposed methods, respectively, when the number of cameras was \({N}_{\mathrm{cam}}=8\); the vertical components, \({b}_{\eta }\), whose values were approximately zero, are not shown. For the conventional method, Fig. 5c shows red and blue vertical lines, which were caused by refraction at the edge of the cylindrical distribution shown in Fig. 4a. Because of the axial symmetry, the same distributions were obtained for all the cameras. In contrast, for the proposed method, Fig. 5d shows a more complicated distribution, where the direct and mirror-reflected images overlapped depending on the camera directions.

Figure 6 shows the distribution reconstructed by solving Eq. (1) with the proposed method with \({N}_{\mathrm{cam}}=8\) cameras. The 3D isosurfaces in Fig. 6a show an axisymmetric distribution as in Fig. 4a. Figure 6b shows the slice view as in Fig. 4b. In the upper and right plots, the orange lines coincide with the black lines, indicating that the reconstructed distribution agreed with the true distribution. The near-wall cylindrical distribution could be accurately reconstructed from the complicated data in Fig. 5d using the proposed method.

Fig. 6
figure 6

Reconstructed distribution of model data for proposed 3D-BOS using Mirror for \({N}_{\mathrm{cam}}=8\)

Full size image

Figure 7 shows that the proposed method can accurately reconstruct the distribution with a different number of cameras. Figure 7a shows the relative error \({\Vert {\varvec{\rho}}-{{\varvec{\rho}}}_{\mathrm{true}}\Vert }_{2}/{\Vert {{\varvec{\rho}}}_{\mathrm{true}}\Vert }_{2}\) between the true distribution \({{\varvec{\rho}}}_{\mathrm{true}}\) and reconstructed distribution \({\varvec{\rho}}\). The horizontal axis is the number of cameras. For both the conventional and proposed methods, the error decreased to approximately 2%–3% as the number of cameras increased. These two plots almost agreed, indicating that there is no significant error inherent to the proposed method.

Fig. 7
figure 7

Effects of the number of cameras, \({N}_{\mathrm{cam}}\), on the reconstructed distributions with the conventional and proposed methods

Full size image

Figure 7b shows the reconstructed distributions for \({N}_{\mathrm{cam}}=3, 4, 6, 8,\) and \(24\) cameras. The left two columns show the reconstructed distributions of the conventional method, and the right two columns show those of the proposed method. The profiles on the vertical dashed lines in the first and third columns are plotted on the second and fourth columns, where the orange and black lines represent the reconstructed and true distributions, respectively. For \({N}_{\mathrm{cam}}=8\) and \({N}_{\mathrm{cam}}=24\), the reconstructed distributions agreed well with the true distributions for both the conventional and proposed methods, indicating that the distributions were accurately reconstructed. Additionally, for \({N}_{\mathrm{cam}}=3, 4,\) or \(6\), the reconstructed distributions of the proposed method did not exhibit significant errors compared with the conventional method. The proposed method could reconstruct the distribution as accurately as the conventional method for all the number of cameras examined. The remaining errors may be attributed to the discretization and approximation common to both the conventional and proposed methods.

In addition to the basic validation of the concept of simple cylindrical distribution described above, we investigated whether the proposed 3D-BOS using a mirror could reconstruct more complicated model data. Future applications of the proposed method, such as supersonic jets impinging on an inclined flat plate, should include wall-attached asymmetric density distributions. Additional model data were reconstructed to investigate the applicability of measuring these distributions. The model data were defined using the following profile:

$$\begin{array}{*{20}c} {\rho \left( {r, \theta ,\zeta } \right) = \frac{1}{4}\left( {1 - \tanh \frac{{r - \left( {r_{0} + {\Delta }r\sin n\theta } \right)}}{{\delta_{e} }}} \right)\left( {1 - \tanh \frac{{\left( {\zeta - \zeta_{0} } \right)}}{{\delta_{\zeta } }}} \right),} \\ \end{array}$$
(17)

where \(\zeta\) is the distance on a line inclined at 30° relative to the mirror plane (the origin is the center of the mirror plane), and \(r\) and \(\theta\) are the radial distance and azimuthal angle around the \(\zeta\)-axis, respectively. The mean radius of the cylinder was \({r}_{0}=10\) mm, the thickness was \({\delta }_{e}=3\) mm, the azimuthal wavenumber was \(n=8\), the amplitude was \(\Delta r=1\) mm, the length of the cylinder was \({\zeta }_{0}=20\) mm, and the boundary thickness in \(\zeta\)-direction was \({\delta }_{\zeta }=3\) mm. As a realistic setting, the grid and camera resolutions were the same as those employed in the experiments in Sect. 3.2. The grid discretized the 60 mm × 60 mm × 30 mm region into \(81\times 81\times 41\) voxels (0.75 mm-side). \({N}_{\mathrm{cam}}=12\) cameras were equally spaced within the range of 10–75° of the \(z\)-axis on a circle with a radius of 500 mm from the mirror center. The resolution of each camera was \(180\times 135\) pixels, and the scale factor of the pixel coordinates (Sect. 2.4) was set at \(\alpha =925\).

Figure 8a shows the 3D isosurface of the true distribution. The slice view of the center plane is shown on the left side of Fig. 8b, and the profile of the dashed line is shown on the right side. Figure 8c shows the distributions of \({b}_{\xi }\) and \({b}_{\eta }\) (horizontal and vertical components, respectively) obtained through numerical integration as in the case of the simple model data described above. Using these data, the distributions shown in Fig. 8e and f were reconstructed using the proposed method. Features such as overall shape and azimuthal wavenumber were qualitatively captured. Although optimization of factors such as the camera layout is required, this result indicates the applicability of the proposed method to a wall-attached asymmetric density distribution.

Fig. 8
figure 8

Additional model data test for the proposed 3D-BOS using a mirror

Full size image

3.2 Experimental demonstration for a candle plume

As an experimental demonstration of the proposed method, 3D-BOS using Mirror, the density distributions of a candle plume was measured. The candle plume was used for demonstration in a previous study of the conventional 3D-BOS (Nicolas et al. 2016), because the density gradient is large, making it easy to measure, and the density distribution is simple and almost cylindrical immediately above the flame.

The experimental setup is shown in Fig. 9a. A 200 mm × 200 mm, 2 mm-thick first-surface mirror was used as the wall, and a candle was placed at a distance of approximately 20 mm from the wall. Twelve cameras (The Imaging Source, DMK33GX273) and background boards were placed around the candle. The parameters of the BOS optical systems were determined by considering the sensitivity and diameter of the circle of confusion, as in the conventional method (Nicolas et al. 2017a), because mirror reflection does not affect these factors. The distance from the camera to the candle was \(m\approx 500\) mm and the distance from the candle to the background was \(l\approx 300\) mm. A focal length was \(f=25\) mm and the f-value was \({f}_{\#}\approx 8\). The diameter of the circle of confusion at the density distribution (Nicolas et al. 2017a) was \(\frac{fl}{\left(f+l\right) {f}_{\#}}\approx 1.2\) mm. Although the camera had a resolution of 1440 × 1080 pixels, the resolution was reduced to 1/8 (i.e., 180 × 135 pixels at maximum) after the optical flow analysis described below was conducted, resulting in a scale factor of the pixel coordinates (Sect. 2.4) of \(\alpha \approx 925\). The exposure time was 2 ms and the frame rate was 1 Hz. A total of 231 images were captured by synchronizing all the cameras with a pulsed signal. For the background, semi-randomly distributed dots proposed by Nicolas et al. (2017a) were used (dot diameter = 0.4 mm, average dot spacing = 0.6 mm, and standard deviation of dot displacement = 0.1 mm). A K-type thermocouple was placed approximately 80 mm above the candle to measure temperature.

Fig. 9
figure 9

Experimental data of candle plume

Full size image

Before the measurement, the camera calibration described in Sect. 2.4 was performed by capturing a total of 1754 images, as shown in the bottom row of Fig. 3. Figure 9b shows the obtained locations and attitudes of the cameras, background boards, and mirror: the thick gray lines are the mirror and background boards, the thin gray lines indicate the angle of view of the cameras, and the red and blue lines represent the image plane and its normal vector of each camera. The 60 mm × 45 mm × 45 mm region immediately above the candle, indicated by the orange lines, was set as the reconstructed region. The grid resolution was heuristically determined to be 81 × 61 × 61 (0.75 mm-side voxels).

Figure 9c shows an example image captured with Cam 6 in the disturbed case. The direct and mirror-reflected images of the thermocouple and flame appear on the right and left sides, respectively. Behind them, the dots drawn on the background board appeared as shown in the enlarged part (100 × 100 pixels). The shifts in these dots were measured using the Farnebäck method, a type of optical flow implemented in the OpenCV library, with an averaging window size of 15 × 15 pixels. To reduce the extra resolution, the images were resampled by averaging each 8 × 8 pixel window. The displacement due to thermal deformation of the mirror was subtracted, resulting in the distribution as shown in Fig. 9d. Only the distributions of the horizontal displacements are shown; the vertical components, which were approximately zero, are not shown. Similar to Fig. 5d of the model data, the direct and mirror-reflected images were superposed, producing a complicated distribution that differed for each camera. Excluding the shaded areas in which the flame or thermocouple prevent the dot-shift measurements, we calculated the values \({b}_{\xi }\) and \({b}_{\eta }\) using the left-hand side of Eq. (11).

Figure 10 shows examples of the instantaneous density distributions reconstructed from \({b}_{\xi }\) and \({b}_{\eta }\) by solving Eq. (1) using the proposed method. Figure 11 shows the time-averaged density distribution. Both show the value \(\rho -{\rho }_{0}\), where \({\rho }_{0}\) is the atmospheric density. In the instantaneous distributions, the high-temperature, low-density region owing to the candle plume appeared to be circular (Fig. 10a and b) or deformed (Fig. 10c and d). The time-averaged distribution in Fig. 11 captures a nearly cylindrical distribution of the candle plume. These results showed that the proposed method can experimentally reconstruct the almost cylindrical density distribution near the wall.

Fig. 10
figure 10

Examples of the reconstructed relative density distribution in the candle plume experiment

Full size image
Fig. 11
figure 11

Time-averaged relative density distribution reconstructed in the candle plume experiment

Full size image

The white circles in Figs. 10a, c, and 11a show the location of the thermocouple determined from the images. The temperature history measured using this thermocouple is shown in the upper part of Fig. 12, and density history converted by the equation of state for the ideal gas is shown in the lower part of Fig. 12 as a blue line. The orange line in Fig. 12 shows the density history immediately below the thermocouple reconstructed with the proposed method. Both plots show a fluctuating but almost steady densities. The time-averaged density was approximately \(-0.81\) kg/m3 for the thermocouple and \(-0.88\) kg/m3 for the proposed method, with a difference of approximately 9%. This may be attributed to the composition of the candle plume. These plots were obtained using the gas constant of air, \(R\approx 287.1\) J/kg-K, to convert the thermocouple temperature to density, and the Gladstone–Dale constant of air, \(G=2.26\times {10}^{-4}\) m3/kg, to calculate Eq. (11), although the candle plume contained the combustion gas. If all the oxygen in the air were used to combustion of the paraffin wax of the candle, the gas constant would be \(R\approx 288.4\) J/kg-K, a change of approximately 0.5%, and the Gladstone–Dale constant would be \(G\approx 2.41\times {10}^{-4}\) m3/kg, a change of approximately 7%, which was roughly estimated based on the studies of Merzkirch (1987) and Qin et al. (2002). Considering these uncertainties, the densities obtained from the thermocouple and reconstructed with the proposed method were consistent.

Fig. 12
figure 12

Time histories of the temperature (top) and relative density (bottom)

Full size image

4 Conclusions

This paper proposes a new extension, 3D-BOS using Mirror, of the conventional 3D-BOS to measure three-dimensional near-wall density distribution by using the wall as a mirror to reflect light. The modifications to the formulation of the conventional method to incorporate the mirror-reflected light paths were presented. A validation using the artificially generated model data of the ideal axisymmetric distribution showed that the proposed method could reconstruct the density distribution as accurately as the conventional 3D-BOS for all the number of cameras examined. In an experimental demonstration using a candle plume, the proposed method reconstructed the almost cylindrical density distribution near the wall.

Future work will include improving the results using newer optical flow algorithms, a more realistic treatment of light rays as conical beams, and more parametric studies on grid resolutions and camera configurations. It is also expected that the proposed method can be applied to unknown density distributions such as supersonic jets impinging on an inclined flat plate.