1 Introduction

Shock-wave/boundary-layer interactions (SWBLI) are a common phenomenon in compressible viscous flows and are encountered in many air and space transportation systems (Dolling 2001). Strong interactions, caused for instance by large discontinuities on the surface or steep impinging shocks, impose large adverse pressure gradients that can compel the boundary layer to separate. SWBLIs and the associated flow separation are highly unsteady. A wide range of characteristic frequencies are relevant, most notably, the low-frequency unsteadiness of the shock-wave/separation-bubble system (Clemens and Narayanaswamy 2014). Unsteady separation events are strongly unfavourable and can induce fluctuating pressure and thermal loads on the surface, resonant structural vibrations, et cetera. To eliminate or curb these adverse phenomena, the development of flow-control strategies is necessary (Delery 2000).

An established control technique uses mechanical vortex generators, such as vanes or ramps, to manipulate the incoming boundary layer by inducing streamwise vortices downstream of their installation (Taylor 1947). These vortices increase the near-wall momentum by transporting high-momentum fluid towards the wall, thereby enhancing the boundary layer’s ability to resist separation. Mechanical vortex generators, both with heights above the boundary-layer thickness and of sub-boundary layer type, have been widely studied and proven to be very effective (Pearcey 1961; Lin 2002; Babinsky et al. 2009; Blinde et al. 2009; Giepman et al. 2014; Titchener and Babinsky 2015; Schreyer et al. 2021). However, they induce parasitic drag due to their permanent presence on the surface and thus decrease the efficiency and performance of a vehicle during phases when they are not needed. An effective alternative are air-jet vortex generators (AJVGs) (Wallis 1952), which generate streamwise vortices by injecting steady jets of air (Szwaba 2005; Souverein and Debiève 2010; Sebastian et al. 2020) into the incoming cross-flow, thereby achieving a similar separation-control effectiveness as mechanical vortex generators (Wallis and Stuart 1958; Pearcey 1961; Pearcey et al. 1993).

Effective AJVG control entails low jet penetration (to minimize parasitic drag) and, subsequently, delayed lift-off of the jet-induced vortices, which leads to improved mixing downstream of jet injection.

Progress has been made in describing and understanding the effects of various parameters influencing AJVG control. Szwaba (2013) showed that AJVG arrays with jet-orifice diameters (\(hd_{jet}\)) below \(25\%\) of the boundary-layer thickness (\(\delta\)) improve effectiveness, as the jet-induced vortices stay within the boundary layer. Furthermore, to avoid lift-off of the induced vortices and to reduce the penetration depth of the jets into the boundary layer, spanwise-inclined jet injection was proposed (Wallis and Stuart 1958; Johnston and Nishi 1990) and has been adopted in later investigations (Szwaba 2005, 2011; Souverein and Debiève 2010; Verma et al. 2014; Ramaswamy et al. 2020; Ramaswamy and Schreyer 2021, 2022). Spanwise-inclined injection of jets into supersonic crossflow was studied in detail using LES by Sebastian et al. (2020), who reported the formation of asymmetric counter-rotating vortex pairs, with a stronger clockwise-rotating vortex, that sustain for a longer downstream distance.

The separation control effectiveness is also affected by the jet/jet spacing (D) (Verma and Manisankar 2019; Ramaswamy et al. 2020): the degree of interaction between adjacent jet-induced vortices directly influences the strengthening or dissipation of their vorticity (Ramaswamy and Schreyer 2022; Sebastian and Schreyer 2022b). Moderate jet spacings of \(D \approx 7-13hd_{jet}\) result in favourable control effectiveness, and both very small (\(D \sim O(4 hd_{jet})\)) and very large spacings (\(D \sim O(25 hd_{jet})\)) are ineffective (Ramaswamy and Schreyer 2022). Furthermore, for these favourable jet spacings, good control effectiveness can be achieved with a jet-stagnation pressure equal to or slightly higher than the wind-tunnel stagnation pressure (Wallis and Stuart 1958; Szwaba 2005; Souverein and Debiève 2010; Verma and Manisankar 2012; Verma et al. 2014; Ramaswamy et al. 2020; Ramaswamy and Schreyer 2021, 2022), which eliminates the need for complex and energy-intensive AJVG installations.

Almost all investigations and optimisation studies on separation control using AJVGs focus exclusively on jet injection via circular orifices, presumably due to their ease of manufacturing. However, vortical structures and mixing characteristics that appear favourable for control purposes have been revealed by several studies of jet-in-supersonic-crossflow (JICF) configurations with jet-injection via non-circular orifices in other contexts (see, e.g. Gruber et al. (1995, 2000); Barber et al. (1997); Foster and Engblom (2004); Tomioka et al. (2003); Wang et al. (2013); Rizzetta (1992) and Mahesh (2013) for a review). Specifically, JICF studies aiming at improved mixing for fuel-injection applications have inspected non-circular jet-orifice shapes like rectangles (Rizzetta 1992), diamonds (Tomioka et al. 2003), and most notably, ellipses (Gruber et al. 1995, 1996, 1997, 2000; Zhang et al. 2009; Wang et al. 2013).

Due to the observed enhanced spreading rate and better mixing performance of an elliptical supersonic free-jet (Gutmark et al. 1989), Gruber et al. (1995, 1996, 1997, 2000) studied a low-aspect-ratio elliptical jet (with the major-axis aligned along the streamwise direction) in supersonic crossflow extensively. Low aspect-ratio elliptical jets possess a smaller separation zone along the streamwise direction due to their slender geometry (Gruber et al. 1996), and vice versa for high-aspect ratio elliptical jets (Zhang et al. 2009).

Furthermore, the non-axisymmetric configuration of elliptical jets tends to exhibit an axis-switching phenomenon when transversely injected: the major and minor axes of the jet-induced structures switch periodically, which results in an enhanced lateral spreading rate along the jet-minor axis (Gruber et al. 1995, 2000) and a \(20\%\) reduction in transverse penetration in comparison to a corresponding circular jet.

Elliptical JICF thus offer promising prospects for AJVG control. However, almost all cases mentioned above employ wall-normal jets with jet diameters in the order of the boundary-layer thickness, i.e. \(hd_{jet} \sim O(\delta )\). Such jets disturb the external flow, thereby increasing parasitic drag. To identify flow features that improve the flow-control prospects, Sebastian and Schreyer (2022a) studied single spanwise-inclined elliptical jets in a supersonic crossflow with \(hd_{jet} \le 0.25\delta\) (as identified as favourable by Szwaba (2013)). The jet-induced vortices of these jets are larger and stronger than for spanwise-inclined circular jets. They improve the streamwise vorticity with minimal disturbance to the external flow and are therefore promising candidates for separation control (Sebastian and Schreyer 2022a).

However, to conclusively recognize the potential of elliptical jets for control purposes, their direct application on a shock-induced flow separation needs to be studied. To the authors’ knowledge, such a study has not yet been reported. The only application of non-circular AJVGs for such purposes by Rao (1988) reports enhanced control performance for spanwise-inclined rectangular AJVGs in comparison to circular AJVGs of similar cross-sectional area.

In the present study, we methodically assess the potential of elliptical jets for separation control by investigating the influence of rows of elliptical AJVGs of two different aspect ratios on a \(24^o\) compression-ramp interaction in comparison to equivalent circular orifices.

2 Experimental set-up

2.1 Experimental facility and wind-tunnel model

Table 1 Experimental conditions
Full size table

Experiments were carried out in the in-draft trisonic wind tunnel, equipped with the supersonic test section, at the Institute of Aerodynamics, RWTH Aachen University. At the investigated Mach number of \(M=2.52\), the stable run time is about 3 s. The ambient conditions in the laboratory determine the wind-tunnel stagnation conditions, and for \(M=2.52\), the freestream unit Reynolds number is \(9.6 \times {10^6}\,\text {m}^{-1}\). To avoid condensation effects, the air is dried with a silica-gel-based drier, achieving a relative humidity below \(5\%\). The \(0.4\,\text {m} \times 0.4\,\text {m}\) test section is equipped with two side windows and a top-wall window for optical access. The experimental conditions are summarised in Table 1.

Fig. 1
figure 1

Schematic of the wind-tunnel model and PIV setup. The subfigure in b shows the main AJVG parameters. All dimensions are in mm

Full size image

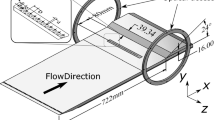
A fully separated shock-wave/boundary-layer interaction was generated with a \(24^o\) compression ramp installed on a flat plate (see Fig. 1a). The model has an overall length of \(902\,\text {mm}\) and spans the entire width of the test section. A zigzag trip \(\sim 1\delta\) downstream of the flat-plate leading edge ensured a uniform turbulent boundary layer around the interaction region. Particle-image-velocimetry measurements indicated a boundary-layer thickness \(\delta = 10.4\) mm at \(4.5\delta\) upstream of the ramp corner (Ramaswamy and Schreyer 2021).

A modular control insert with an array of 23 AJVG orifices was placed \(7.69\delta\) upstream of the ramp corner. A schematic of the AJVG module, depicting various design parameters, is included in Fig. 1b (zoomed detail). The jets are pitched within the spanwise/wall-normal plane at an angle of \(\phi = 45^o\) and skewed at an angle of \(\theta = -90^o\), resulting in a pure spanwise injection. Jets with similar orientation were investigated extensively in literature (Wallis 1952; Szwaba 2005, 2011, 2013; Souverein and Debiève 2010; Ramaswamy and Schreyer 2021). A pressure plenum located underneath the AJVG module ensures uniform injection of air with a total pressure equal to the wind-tunnel stagnation pressure. The total pressure and total temperature in the plenum were monitored using a WIKA S-20 pressure transducer and a J-type thermocouple. Earlier parametric studies (Ramaswamy et al. 2020; Ramaswamy and Schreyer 2022) at similar flow conditions revealed a most effective jet spacing of \(D = 0.76\delta\) (D = \(8hd_{jet}\)). All tested geometries in the current study use this spacing. The AJVG parameters are summarized in Table 2.

Table 2 AJVG parameters
Full size table

Three AJVG arrays with single rows of jet orifices are studied: elliptical orifices with cross sections of aspect ratios AR = 0.5 and 2, as well as a circular array (AR = 1). The aspect ratio was defined as the ratio of the spanwise (S) to the streamwise lengths (L), hence AR = S/L. The dimensions of the elliptical orifices were chosen to maintain a constant hydraulic diameter (\(hd_{jet} = 1\) mm) to allow for comparisons with the corresponding circular orifice. The hydraulic diameter is defined as the ratio of four times the cross-sectional area of the orifice to its wetted perimeter. With \(hd_{jet} = 1\) mm, the dimension of the ellipses are calculated using their corresponding area, perimeter, and desired aspect ratio. LESs of a jet flow in a spanwise-inclined plenum-pipe configuration (Sebastian and Schreyer 2022a) confirmed that the hydraulic diameter is an appropriate way to characterise and compare non-circular jet-orifices, with \(\le 8\%\) difference in the momentum-flux ratios between the different cases, as calculated based on jet exit conditions.

A conventional drilling process was used to manufacture the circular AJVGs. The non-circular orifices were drilled using a laser fine-cutting process at the Fraunhofer Institute for Laser Technology in Aachen. An IPG Photonics YLS-2000/20,000-QCW laser with a peak pulse power of 8kW, equipped with a Precitec YK52 cutting head, was used for this purpose. The laser focal diameter was \(100\,\mu\)m. Table 3 provides a summary of the geometric parameters of all orifice shapes. Assuming inviscid flow under sonic exit conditions, an estimate for the array mass-flow-rate (\(\dot{m}\)) is also included in the table. Note that the orifice shapes depicted in the table correspond to the cross-sectional dimensions.

Table 3 Geometric and flow parameters of the orifices. The black down-arrow represents the crossflow direction
Full size table

2.2 Flow diagnostics and data analysis

The general flow topology was assessed using an in-house built focusing-schlieren setup (Schauerte and Schreyer 2018) with the focus plane along the model centreline. While a conventional schlieren is based on a single-point light source, a focusing-schlieren system consists of a 2D array of slit light sources (source grid), that is mapped on to a plane coinciding with a cut-off grid. The individual pairs of source slit/cut-off slit behave as independent schlieren systems, each at a different inclination with respect to the optical axis. The focusing ability arises from the superposition of images from the individual schlieren system. Given their advantages in characterising strongly 3D interactions, as in the present study, a focusing-schlieren setup was preferred over conventional schlieren. Further details on the setup can be found in Schauerte and Schreyer (2018). The focusing-schlieren images were acquired at 20 kHz using a Photron SA.5 high-speed camera with an image resolution of \(704\text {px} \times 520\text {px}\). The camera was exposed for a duration of \(2\mu \text {s}\). Additionally, surface-flow features were studied with an oil-flow visualisation technique, using a mixture of Shell Tellus type 22 oil, \(\text {TiO}_2\) particles, and a trace amount of oleic acid. We recorded the oil-flow patterns at a digital resolution of 0.20 px/mm using a PCO Pixelfly camera placed above the optical access in the upper wind-tunnel wall. The transient oil-flow images were taken during the stable phase of the wind tunnel runs.

We characterised the velocity field at selected planes along the streamwise/wall-normal (WN) and streamwise/spanwise (WP) directions in two independent particle image velocimetry (PIV) campaigns.

To seed the flow, Di-Ethyl-Hexyl-Sebacate (DEHS) was atomised using an in-house particle generator and filtered with a cyclone separator. The air reservoir was globally seeded prior to each wind tunnel run. The filtered particles have a mean diameter of \(0.7\mu \text {m}\) and a response time of \(2.6\mu \text {s}\) (Marquardt et al. 2019). The corresponding Stokes number (\(\tau _p U_\infty / \delta\)) was 0.14.

For the WN-PIV campaign, the PIV setup consisted of a Litron NANO-L pulsed double-cavity Nd:YAG laser and four Dantec FlowSense EO 11 M cameras, which were synchronised using two BNC 575-8 pulse/delay generators. Dantec DynamicStudio was used to control the system. The laser has a wavelength of 532nm and a pulse width of \(\sim 6\) ns. The beam was shaped into a light sheet of \(\sim 1\) mm thickness and was introduced into the test section via the optical access on the upper test-section wall. Laser reflections on the model surface were minimised by a coating of matte-black paint on the flat-plate and ramp surfaces.

The camera arrangement is shown in Fig. 1b. Two beam splitter cubes split the light emanating from the illuminated particles and direct it to two cameras each. Cameras C1 and C2 realise a field of view (FoV1) of \(9\delta \times 6 \delta\) at a resolution of 43.5 px/mm, cameras C3 and C4 realise a marginally larger field of view (FoV2) of \(10.5\delta \times 7 \delta\) at a slightly lower resolution of 36.5 px/mm. However, the maximum streamwise extent of usable data upstream of the ramp corner was limited by the laser light-sheet length and the optical access to the test section. Hence, the data presented in this study covers a total effective range of \(12\delta \times 6\delta\).

Each camera was equipped with a Tamron SP AF 180 m f/3.5 objective. Cameras C1 and C3 received a larger proportion of the light and were set at \(f\# = 5.6\), while the apertures of cameras C2 and C4 were set at \(f\# = 3.5\). These settings ensured uniform particle-image intensity for all cameras. Each camera acquires double-exposure images at a frame rate of 3Hz. To improve the acquisition rate, one cameras pair (C1 and C3) was triggered alternately with respect to the other pair (C2 and C4), with the laser firing dual-pulses during every camera pair’s acquisition window. This doubled the effective acquisition rate of the system to 6 Hz. The low acquisition rates of the individual cameras prevent any visible overlap of particle exposures.

Measurements were taken in two WN-Planes, at \(z = 0\)D and \(z = 1.5\)D, which correspond to locations at the jet-centreline and in-between two orifices, respectively.

To characterise the jet-induced vortices, a second PIV campaign was carried out in the streamwise/spanwise plane (WP-PIV) at \(y = 0.24\delta\), for which a Quantronix Darwin-Duo 100 Nd:YLF laser was used to create a \(\sim 1.5\) mm thick laser light sheet to illuminate the DEHS particles. The laser was operated at 1000 Hz, with a pulse energy of 30mJ per oscillator. An ILA high-speed synchronizer was used to synchronise the laser pulses to the exposures of a Photron SA.5 high-speed camera (C5), placed above the top-wall optical access. A FoV of \(8.6\delta \times 8.6\delta\) was captured by the camera’s full-frame CMOS sensor (1024px \(\times\) 1024px), at a resolution of \(\sim 11.1\)px/mm. Note that the ‘high-speed’ acquisition of 1000Hz is orders of magnitude smaller than the characteristic timescales of this flow, and is hence not viewed as a 'time-resolved' acquisition.

All acquired images were pre-processed to account for model vibrations, camera noise, and reflections (see Ramaswamy and Schreyer (2021) for more details). PIV images were processed with DynamicStudio 6.4, using an adaptive PIV algorithm. We used final interrogation-window sizes of 32px \(\times\) 32px at \(75\%\) overlap for the WN-PIV images and of 16px \(\times\) 16px at \(50\%\) overlap for the WP-PIV images. For further details on the PIV setup, equipment, and post-processing routines of both campaigns, see Ramaswamy and Schreyer (2022). Mean and turbulent quantities were calculated from normalised instantaneous velocity vectors to account for freestream-velocity variations between measurements from multiple days (Ramaswamy and Schreyer 2021).

2.3 Measurement uncertainty

The measurement conditions are susceptible to variations due to wind-tunnel runs distributed over multiple days. Hence, an estimation of uncertainties is crucial to correctly interpret the data. All reported uncertainties are based on a \(95\%\) confidence interval.

The Mach number, defined by the area-ratio of the facility, varied by less than \(0.6\%\). The total pressure and temperature fluctuated by \(1.5\%\) and \(1.3\%\) during the course of the measurement campaign. This resulted in a \(1.5\%\) uncertainty in free-stream unit Reynolds number. Variations in the air supply affect the AJVG injection pressure, which has an uncertainty of \(2.9\%\).

Assuming particles that accurately follow the flow, we calculated statistical uncertainties of the mean and turbulent quantities with the approach of Benedict and Gould (1996). For WN-PIV, the error in the root-mean-square (rms) of streamwise and wall-normal velocity fluctuations at \(50\%\) of the boundary-layer thickness is below \(5.1\%\) and \(9.8\%\), respectively, and below \(17\%\) for the Reynolds-shear stress. The corresponding uncertainties for WP-PIV are \(3.66\%\) and \(3.74\%\) for the streamwise and spanwise components, respectively. Uncertainties due to PIV cross-correlation and laser-pulse jitter (\(\sim 0.5ns\)) are estimated to \(\sim 1\%\). Assuming statistical independence, the uncertainties in boundary layer integral parameters due to the wall-position and the minor changes in wind tunnel total conditions are less than \(1.5\%\), \(2.4\%\) and \(1\%\) for the momentum-thickness (\(\theta _c\)), the displacement-thickness (\({\delta ^*}_c\)) and the boundary-layer thickness (\(\delta\)), respectively, based on the compressible turbulent-boundary-layer calculations of Stratford and Beaver (1959).

The long-pulse width (\(\sim 200ns\)) of the WP-PIV system coupled with temporal non-uniformities in laser intensity cause a disparity between the pulse-separation time set by the high-speed synchroniser and the effective pulse-separation time; this results in a systematic error of \(\sim 3\%\) of the mean velocities. We applied the correction suggested by Marquardt et al. (2019) to account for the \(\sim 40\) ns shift in pulse separation time, thereby reducing this error to \(\sim 1\%\).

Near the AJVG inlet, close to the surface, unphysical flow interpretations may be caused by laser reflections and since the jets themselves were not seeded. We therefore masked the affected regions and did not include the corresponding data points in the presented mean and turbulent profiles.

Finally, the separation-length estimates from oil-flow visualisations are accurate by \(\pm 2\)px. With the magnification used during image acquisition, the resulting uncertainty in baseline total separation length is \(1.4\%\).

3 Results and discussion

3.1 Incoming boundary-layer characterisation

The mean and turbulent velocity statistics of the incoming boundary layer are assessed on the basis of PIV data at \(4.5\delta\) upstream of the ramp corner (see Fig. 2). The mean velocity profile outside of the viscous sub-layer is scaled using the logarithmic law of the wall

Fig. 2
figure 2

Boundary-layer profiles: a mean, b turbulent

Full size image
$$\begin{aligned} {u^+}_{vd} = \frac{1}{\kappa } \ln y^+ + C \quad \textrm{and}\quad {y^+} = \frac{y\cdot u_{\tau }}{\nu _w} \end{aligned}$$
(1)

where, \({u^+}_{vd}\) is the van Driest effective velocity (Van Driest 1951) in inner scaling, \(u_{\tau }\) is the friction velocity, and \(\nu _w\) is the kinematic viscosity at the wall. The log-law shows good agreement with the measured mean velocity with the constants \(\kappa = 0.4\) and \(C = 5\) between \(65 \le y^+ \le 250\). The friction velocity (\(u_{\tau }\)) and hence the skin-friction coefficient were determined using the Clauser chart method (Clauser 1956) and are \(u_\tau = 25\,\text {m/s}\) and \(C_f = 0.0017\), respectively. The boundary-layer density profile was calculated using the ideal-gas law and the Crocco-Busemann relation (see White (2006)), following the assumption of an adiabatic, fully developed, zero-pressure-gradient boundary layer with a recovery factor of \(r = 0.89\). Subsequently, the compressible boundary-layer displacement and momentum thicknesses were estimated as \({\delta ^*}_c = 2.66\,\text {mm}\) and \({\theta }_c = 0.85\,\text {mm}\), respectively. The results from a large-eddy simulation (Sebastian et al. 2020) of a compressible turbulent boundary layer under similar conditions (\(M = 2.5\) and \(Re_{\theta _c}\) = 7000) are also included in Fig. 2a and show good agreement with the present dataset.

The streamwise (\(\sqrt{\overline{u^\prime }}\)) and wall-normal (\(\sqrt{\overline{v^\prime }}\)) rms velocity fluctuations from WN-PIV are shown in Morkovin scaling (Morkovin 1962) in Fig. 2b. Recent PIV data from the same facility by Marquardt et al. (2019) (\(M_e = 2.45\), \(Re_{\theta _c}= 7011\)) and the LES of a supersonic turbulent boundary layer under similar conditions by Sebastian et al. (2020) are also shown, along with the turbulent-boundary-layer measurements of Klebanoff (1955) (\(Re_{\theta _{in}} = 7447\)) and Elena and Lacharme (1988) (\(M_e = 2.32\), \(Re_{\theta _c} = 4700\)). The streamwise velocity component is marginally over-predicted, which appears to be an artefact of the facility. The wall-normal component on the other hand is under-predicted: a typical oblique shock-wave test overestimates the particle frequency response to weak disturbances such as wall-normal fluctuations in the undisturbed boundary layer (Williams et al. 2015). However, under-prediction due to this issue decreases once the flow undergoes compression due to the separation shock, resulting in higher fluid viscosity and density and hence a better particle response (Schreyer et al. 2018).

The streamwise and spanwise (\(\sqrt{\overline{w^\prime }}\)) rms velocity fluctuations from WP-PIV, measured at \(y = 0.24\delta\), are also included in Fig. 2b. The applied high-speed PIV system features long temporal laser profiles (\(\sim 200\) ns) and large camera pixels (\(\sim 20\mu\)m). These features complicate accurate turbulence measurements, in supersonic flows in particular, due to challenges with non-uniform seeding (Scarano 2008). Consequently, the streamwise velocity fluctuations are weakly under-predicted. We use the WP-PIV data solely to study topological modifications; the weak under-prediction will thus not deter any interpretations. The spanwise velocity fluctuations from WP-PIV are of much lower magnitude and follow the trends of the wall-normal component, as expected for 2D canonical turbulent boundary layers (Guarini et al. 2000).

3.2 Baseline shock-wave/boundary-layer interaction

Fig. 3
figure 3

a Normalised mean streamwise velocity and b rms of streamwise velocity fluctuations of the baseline interaction

Full size image

We first present a brief assessment of the fully separated \(24^o\) compression-ramp interaction for later comparisons. Contours of the normalised mean streamwise velocity and normalised streamwise velocity fluctuations are shown in Fig. 3. The undisturbed boundary-layer far upstream of the ramp corner is clearly visible. At \(x = -3.9\delta\), the adverse pressure gradient induces separation; consequently, a separation shock and a detached shear layer downstream form. The separation shock oscillates at low frequency (Clemens and Narayanaswamy 2014), as visible in a broad region of increased turbulence intensity tracing the entire length of the separation shock. The flow separates from the surface at \(x = - 2.5\delta\) and reattaches on the ramp surface at \(x = 1.1\delta\); a large recirculation region forms. The zero-velocity streamline, which outlines the extent of the recirculation zone, is marked with red dash lines in Fig. 3. For the present study, the scale of separation is in the order of the ramp length; the proximity of separation to the expansion corner has been shown to influence the mean development of SWBLIs (Larcheveque et al. 2022a). Nevertheless, the separation-bubble is closed at all times for the present case, and the breathing motion of the shock-bubble system was verified to stay within the ramp length. The flow compression amplifies the turbulent stresses (see, e.g. Andreopoulos et al. (2000)), which leads to large regions of high fluctuation intensity above the recirculation region and downstream of reattachment.

Fig. 4
figure 4

rms of streamwise velocity fluctuations of the baseline case at \(y = 0.24\delta\)

Full size image

Figure 4 shows the normalised streamwise velocity-fluctuation contour along the streamwise/spanwise plane at \(y = 0.24\delta\). A mean surrogate separation line was identified, following the definition of Ganapathisubramani et al. (2009), as the streamwise location where the local velocity is less than \(\overline{u} - 4\sigma _u\) (\(\overline{u}\) and \(\sigma _u\) are the line-averaged mean and standard deviation of the streamwise velocity in the upstream boundary layer) and is shown as black dashed lines in Fig. 4. The uncontrolled interaction is nearly 2-dimensional along the entire width of the measurement domain, and no corner-effects due to the wind-tunnel side walls are visible.

For additional information on the uncontrolled interaction, see Ramaswamy and Schreyer (2021).

3.3 Effect of flow control

Fig. 5
figure 5

Instantaneous focusing-schlieren visualisation of the baseline and elliptical cases

Full size image

The global modification of the shock structures in the SWBLI due to the injection of the AJVGs is assessed using the instantaneous focusing-schlieren images in Fig. 5, which includes the baseline SWBLI and the two elliptical AJVG cases. The flow features for AR1 are similar to the elliptical cases and hence not shown here.

The typical features of a ramp-induced SWBLI (incoming boundary layer, ramp-induced separation shock, separated shear layer, etc.; see Sec. 3.2) are nicely visualised for the baseline case (see Fig. 5a).

The injection of the jets (see Figs. 5b,5c) imposes an obstruction to the incoming supersonic flow, which induces a shock wave upstream of the jet. This jet-induced shock, however, is relatively weak and does not noticeably modify the external freestream flow properties (Ramaswamy and Schreyer 2022).

Apart from the jet-induced shock, the overall arrangement of the SWBLI is not fundamentally changed by the control. The boundary layer separates from the flat-plate surface, and a ramp-induced separation shock forms. The separated shear layer reattaches on the ramp surface and generates weak compression waves that coalesce into the reattachment shock. Note that in the absence of spanwise integration in the focusing-schlieren method, the images do not capture a well-defined reattachment shock for all cases.

Fig. 6
figure 6

Oil-flow visualisation of all cases. S - separation line; C - ramp corner; R - reattachment line

Full size image

What does change, however, is the spanwise behaviour of the interaction: the extent of the ramp-induced separation varies periodically. The global flow topology is visible in the oil-flow visualisations shown in Fig. 6, representing the top view of the interactions with the crossflow direction from top to bottom. For all cases, the central \(\sim 30\%\) span of the AJVG array are shown to allow for comparisons unhindered by edge effects that may locally alter the control behaviour. The thin-film of oil under wind-on conditions responds to surface pressure and shear forces (Squire 1961), and the images therefore visualise typical surface features.

A region of accumulated oil just upstream of the air-jet orifices indicates the jet-induced separation. The jets interact with the crossflow and form uneven pairs of counter-rotating vortices, where one vortex is stronger and sustains longer in the streamwise direction (Sebastian et al. 2020). The vortices generate spanwise periodic up- and downwash, causing the streamwise oil streaks visible in Fig. 6. Consequently, the originally 2D separation line (S) upstream of the ramp corner for the baseline case is now corrugated. The reattaching shear layer forms a clear interface on the ramp surface, from which the surface streaklines diverge in the up- and downstream directions. This helps identify the flow reattachment line (R). For all control cases, the flow separation line moves downstream, and the flow reattachment line moves upstream, in comparison with the baseline case.

Fig. 7
figure 7

a Mean streamwise velocity and b rms of streamwise velocity fluctuations of ellipse AR2 at \(y = 0.24\delta\)

Full size image

To quantitatively characterise the jet-induced modifications, we performed 2C-PIV in a wall-parallel plane at \(y = 0.24\delta\); the normalised streamwise mean-velocity and the rms of streamwise-velocity-fluctuation for case AR2 are shown in Figs. 7a and 7b, respectively. The jet-induced vortices are seen to induce a spanwise-periodic modulation of mean streamwise velocity. Furthermore, they also exhibit longitudinal streaks of increased turbulent intensity. Both WP-PIV and the oil-flow visualisations (Fig. 6) show a slight spanwise skew of these structures as they convect downstream. This skew is a consequence of the spanwise-inclined nature of jet injection, and its strength directly depends on the spanwise jet/jet spacing (Ramaswamy and Schreyer 2022; Sebastian and Schreyer 2022b). For the present configuration, the skew angle is \(\sim 3^o\) along the direction of jet-injection and is mostly invariant to the jet-orifice geometry.

The red dashed lines in Fig. 7 indicate the identified surrogate separation line, and the black dashed line shows the corresponding line for the uncontrolled baseline case from Fig. 4. For case AR2, the surrogate separation line is displaced downstream along the entire spanwise extent of the measurement domain. It is shifted farthest downstream at the approximate spanwise locations of increased turbulent intensity.

Fig. 8
figure 8

Separation length reduction of the control cases

Full size image

We compare the separation-control behaviour of the three control cases on the basis of the spanwise-averaged separation lengths. The results were normalised with the corresponding length from the baseline case and are shown in Fig. 8. The respective mean values (blue circular markers) and the standard deviation (blue error-bars) measured from WP-PIV are presented, and the latter represent the degree of separation-line corrugation. For both elliptical orifices, the reduction in separation length is greater than for the more commonly used circular orifice.

To corroborate this trend, we also show the separation lengths from surface oil-flow visualisations (black markers in Fig. 8). For these, we extracted the most upstream and downstream points of the corrugated separation line along one jet pitch (\(-0.5hd_{jet} \le z = 0 \le -0.5hd_{jet}\)) from multiple frames of the stable oil-flow video and averaged. The results from both methods are in good agreement; in the AR1 case, the separation length is reduced by \(\sim 17\%\), while both elliptical cases achieve a nearly \(25\%\) reduction in separation length as measured from the oil-flow visualisations. The corresponding separation lengths are listed in Table 4.

Table 4 Total separation lengths from oil-flow visualisations
Full size table

3.4 Jet-induced coherent structures

To better understand the observed trend in separation-control effectiveness, it is essential to analyse the jet-induced structures and their relationship to the orifice geometry. In this section, we examine the PIV results in detail to assess the jet-in-crossflow characteristics.

Upon jet-injection, the streamwise velocity fluctuations induced by the jet vary in the spanwise direction and perturb the otherwise spanwise-homogeneous boundary layer. An amplitude of this modulation can be estimated at every location and is defined as follows:

$$\begin{aligned} A(x,z) = \frac{{\sqrt{{u^\prime }^2}}_{control}(x,z) - {\sqrt{{u^\prime }^2}}_{baseline}(x,z)}{{\sqrt{{u^\prime }^2}}_{baseline}(x,z)} \end{aligned}$$
(2)
Fig. 9
figure 9

Jet-wake amplitude at \(x = -5\delta\). The solid lines are the corresponding first order Fourier model

Full size image

The resulting modulation amplitude A(z) at \(x = -5\delta\) is presented in Fig 9 for the three control cases. While all cases exhibit a periodic fluctuation-intensity oscillation in the spanwise direction, the intensity is much lower (by approx. \(35\%\)) for the circular AR1 case than for the two elliptical cases.

The control effect of AJVGs relies on the transport of high-momentum fluid to the near-wall region. To asses the relevant jet mixing characteristics, jet-in-crossflow studies commonly study the downstream evolution of the width of the jet wake (see Mahesh (2013)). The procedure is fairly straightforward for single jets. In the present case of a jet array, however, neighbouring jets interact. We therefore adopted a Fourier-model-based technique, which has been shown to be robust in extracting major length/time scales from spatially/temporally periodic signals (Fujita and Chen 2008; Gehrmann and Harding 2018).

As the jet-wake amplitude is nearly sinusoidal in nature, we used a first-order approximation:

$$\begin{aligned} F(z) = a_0 + a_1 cos(\omega z) + b_1 sin(\omega z) \end{aligned}$$
(3)
$$\begin{aligned} \lambda = \frac{2\pi }{\omega } \end{aligned}$$
(4)

where \(\lambda\) indicates the period of the sinusoidal signal computed from the first-order best-fit Fourier model. \(\lambda\) is equivalent to the width of a single sinusoidal wave, i.e. a single jet-induced wake in the array. The streamwise evolution of \(\lambda\), normalised with the orifice hydraulic diameter is shown in Fig. 10. For comparison, we also estimated the wake width for a single spanwise-inclined circular jet with the same geometrical and flow properties as the current case via this technique (represented by case D25 from Ramaswamy and Schreyer (2022)).

Fig. 10
figure 10

Streamwise evolution of jet wake-width

Full size image

The AR1 single jet interacts with a ramp-induced shock beyond \(x = -4.5\delta\), and thus the first-order Fourier model cannot capture the wake amplitude anymore. For the jet-array cases, the control effectiveness is larger, and therefore the separation line and the separation shock shift downstream. The jets thus do not experience effects of the shock – and hence endure spanwise-periodic flow modulations—until approximately \(x = -3.5\delta\).

The AR1 single-jet shows the expected rise in wake-width with streamwise distance. For all jet-array cases, the wake widths saturate at \(\lambda = 8hd_{jet}\), which is equal to the jet/jet spacing within the arrays. These observations clearly show that, while a single jet-in-crossflow can spread without impedance, the jets in an array configuration are confined, and their lateral spreading is limited to the spacing between the jets.

Since the wake width is already equal to the jet spacing at the most upstream available location in Fig. 10, we expect that flow-field modulations brought about by the strong influence of the jet/jet interactions will dominate any modulations due to jet-orifice shape.

Fig. 11
figure 11

TKE of Ellipse AR2 at \(z = 1.5D\). The corresponding profiles are superimposed at three exemplary locations

Full size image

Regarding the induced parasitic drag of AJVGs, a second quantity of interest in these jet-in-crossflow configurations is the penetration of the jets into the crossflow. Earlier jet-in-crossflow studies have detected the jet trajectory on the basis of the jet-centreline streamline (Muppidi and Mahesh 2005) or the local scalar concentration (Smith and Mungal 1998), or by tracking the local velocity maxima (Kamotani and Greber 1972) or turbulent kinetic energy (TKE) (Gutmark et al. 2010). The latter technique was most suitable for our study, since the jet-momentum-flux ratio (J) and \(d/\delta\) are low for the cases studied here, and tracking the jet streamlines in experimental studies is challenging. Gutmark et al. (2010) has shown that this detection method can trace the streamwise evolution of jet penetration as effectively as tracking the local velocity maxima.

To illustrate the ability to trace the peak of TKE profiles, in order to track the penetration depth of jet-induced structures, we show an exemplary TKE contour from WN-PIV at \(z = 1.5D\) in Fig. 11. TKE profiles at three locations are superimposed. The extracted jet-penetration trajectories for our three cases are plotted in Fig. 12 as a function of the streamwise distance.

Fig. 12
figure 12

Jet-penetration based on peak TKE intensity at \(z = 1.5D\)

Full size image

On average, the elliptical cases penetrate approx. \(25\%\) deeper into the boundary layer than the circular jet at similar conditions. This stronger effect on the boundary layer is also indicated by stronger jet-induced separation upstream of the air-jet orifices (see Fig. 6): for case AR1, the jet-induced separation length is \(\sim 4.8 hd_{jet}\), while it is approx. \(30\%\) higher (\(\sim 6.2 hd_{jet}\)) for the two elliptical cases.

Nevertheless, the penetration stays below \(y = 0.6\delta\), so that the jet-induced parasitic drag is still small. The relatively deeper penetration, combined with the larger vortex footprints observed by Sebastian and Schreyer (2022a), could mean that jets from elliptical orifices can access the high-momentum fluid at the upper part of the boundary layer more effectively than their circular counterparts.

3.5 Mean-flow modification of the SWBLI

Fig. 13
figure 13

Normalised streamwise mean velocity for the baseline and control cases. The top row (a–f) corresponds to WN1 location and the bottom row (g–l) corresponds to WN2 location at every presented streamwise position

Full size image

To assess the influence of jet injection on the evolution of the mean and turbulent velocities in the boundary layer, we discuss boundary-layer profiles at various streamwise locations across the interaction region, both for the circular and elliptical air-jet vortex generators. At all locations, the streamwise and wall-normal velocity components along the respective local wall-parallel and wall-normal directions are given. Furthermore, it has to be noted that, while the flow downstream of jet-injection is skewed along the jet-injection direction, the reported boundary-layer profiles are aligned along the global streamwise/wall-normal directions.

The normalised streamwise mean velocity profiles from WN-PIV are presented in Fig. 13. Six selected locations provide insight into the boundary-layer evolution: around the location of jet injection (\(x = -6\delta\); \(x = -4\delta\)), throughout the compression-ramp interaction along the flat plate (\(x = -3\delta\); \(x = 0\delta\)), and around reattachment on the ramp surface (\(x = 1\delta\); \(x = 3\delta\)). The uncontrolled case is shown for comparison.

We present profiles at two spanwise locations to get insight into the three-dimensional nature of the interaction. Location WN1 (at \(z = 0D\)) corresponds to the plane aligned along the centreline of a jet orifice, and WN2 (at \(z = 1.5D\)) is located mid-plane in between two jet orifices. The corresponding PIV measurement planes are marked with green dash lines in Fig. 7.

The impact of the jets on the boundary layer upstream of the ramp-induced shock wave is visible on the profiles at \(x = -6\delta\) and at \(x = -4\delta\). At \(x = -6\delta\), in the jet near field (jets are injected at \(x = -7.69\delta\)), the boundary layer is heavily perturbed, especially at WN2 (see Fig. 13g). At WN2, the flow deceleration is larger for the two elliptical cases than for the circular case. This effect is due to the larger jet-induced separation and a slightly stronger jet-induced shock wave (see Sec. 3.3). At WN1, the flow deceleration is marginal, which may be related to the alleviating effect of added jet-momentum downstream of each orifice.

Shortly downstream, the momentum redistribution effected by the jet-induced vortices is visible: at \(x = -4\delta\), the profiles at WN2 are distinctly S-shaped (see Fig. 13h). The jet-induced longitudinal vortices transfer momentum from the outer boundary layer towards the wall, which makes the mean boundary-layer profiles fuller for the control cases (see Figs. 13b).

In Sec. 3.4, we saw that interactions between adjacent jets in AJVG arrays are evident as far upstream as \(x = -6.4\delta\). These favourable interactions amplify the streamwise vorticity (Sebastian and Schreyer 2022b). Moreover, Sebastian and Schreyer (2022a) found that (single) elliptical jets in crossflow induce larger and stronger counter-rotating vortex pairs than circular jets. Therefore, arrays of elliptical jets should further improve favourable jet/jet interactions and increase the vorticity. These effects are indeed visible in the mean velocity profiles at \(x = -4\delta\), and the jet/jet interactions are strongest at location WN2 (Figs. 13h). Here, the degree of entrainment, as indicated by the S-shaped profiles, is much stronger for the two elliptical cases than for the circular case. The stronger entrainment thus directly coincides with the downstream movement of the ramp-induced separation line (as observed in Fig. 8).

Farther downstream, at \(x = -3\delta\), the baseline boundary layer is on the verge of separation, as visible in strong boundary-layer decelerations (see Figs. 13c, i). The control cases, however, still sustain a high-momentum region close to the wall due to the downstream shift of the separation shock. The velocity profile close to the wall is fullest for the high-aspect ratio elliptical AR2 case (at \(x = -4\delta\) and \(x = -3\delta\)). This effect is most probably responsible for the slightly higher performance of the AR2 ellipse AJVGs in controlling the \(24^o\) shock-induced flow separation (see Sec. 3.3).

Moreover, at \(x = -3\delta\), all three control cases feature spanwise undulations between WN1 and WN2. This behaviour indicates that the jet-induced vortices also corrugate the separated shear layer, not only the separation line. The structure of the entire SWBLI region thus becomes inherently 2.5D–3D (spanwise periodic) when subjected to separation control with AJVGs.

Within the separation bubble, at \(x = 0\delta\), reverse flow occurs in all cases (see Figs. 13d, j). The large recirculation bubble in the baseline case has a maximum height of \(y = 0.3\delta\). The injected air jets achieve large reductions in mean separation area; for the control cases it reduces to a maximum height of \(y < 0.2\delta\).

As the flow reattaches and develops over the ramp surface (\(x = 1\delta\) & \(x = 3\delta\); see Figs. 13e, k f, l, respectively), the influence of the jet-induced vortices on the velocity profiles decreases, and their shapes are very similar to the corresponding baseline boundary-layer profiles. The reattachment line at around \(x=0.8\delta\) is thus not corrugated (as the separation line was; see Fig. 6), which is consistent with previous AJVG-control studies (Szwaba 2005; Souverein and Debiève 2010; Verma and Manisankar 2012). Also at \(x = 3\delta\), no major spanwise variations occur anymore, and the boundary layer begins its recovery to an equilibrium state.

The observed differences in separation and reattachment may be explained with the behaviour of the jet-induced structures. Spanwise-inclined jets sustain low penetration depths (see the LESs of Sebastian et al. (2020) & Sebastian and Schreyer (2022a) and Fig. 12 in the current study). Furthermore, the streamwise vortices lift off of the surface with the separated shear layer in the SWBLI (see Ramaswamy and Schreyer (2022)), so that they only minimally interfere with the boundary layer in the reattachment region. Therefore, the separation line and the separated shear layer upstream of the ramp corner are spanwise corrugated, and the reattachment lines maintain nearly constant positions.

3.6 Turbulence behaviour

AJVGs also modify the turbulence behaviour. The boundary-layer turbulence is amplified both due to the injection of the jets (Santiago and Dutton 1997) and due to the shock-wave/boundary-layer interaction downstream (see, e.g. Andreopoulos et al. (2000)). In the following section, we will quantify and compare the changes brought about by elliptical and circular AJVGs on the boundary-layer turbulence.

Fig. 14
figure 14

Normalised streamwise velocity fluctuations for the baseline and control cases

Full size image

Figure 14 shows the evolution of the rms of the streamwise velocity fluctuations at several streamwise locations for the baseline and control cases, at spanwise locations WN1 (top row) and WN2 (bottom row). Also here, the velocities and coordinate system are aligned along the respective local surface coordinates.

Directly downstream of jet injection (\(x = -6\delta\)), the expected turbulence amplification due to the induced vortical structures is observed for all cases (see intensity peaks at \(y/\delta \sim 0.30\) at WN1 and \(y/\delta \sim 0.40\) at WN2). The intensity maxima are larger for the elliptical than the circular jets in between two jet orifices (WN2), but slightly smaller at WN1. This behaviour is due to the jets’ spanwise inclination, as well as the increased strength of the introduced vortices and their subsequent jet/jet interactions. The overall maximum of \(0.11 U_\infty\) occurs for the elliptical cases at WN2.

The disparity in wall-normal peak intensity location at \(x = -4\delta\) (Fig. 14f) shows that the penetration depths of the jet-induced structures vary with orifice aspect ratio in their downstream evolution.

Downstream of the ramp-induced shock, at \(x = -1\delta\), the turbulence intensity is amplified and the peak shifts away from the wall, along with the separated shear layer. For the control cases, the intensity peak is much closer to the wall (\(y \sim 0.3\delta - 0.4\delta\)) than for the baseline case (\(y \sim 0.6\delta\)) due to the delayed separation.

The separated shear layer reattaches on the ramp-surface and the boundary layer begins its recovery back towards an equilibrium state. For circular jets, the turbulence intensity decreases to a level slightly below the uncontrolled conditions after the SWBLI-induced amplification (see Ramaswamy and Schreyer (2021)). This behaviour is also observed for the elliptical cases studied here at locations downstream of reattachment (see \(x = 3\delta\)). Beyond that, no major effects of the jets are visible at \(x=3\delta\) any more, and the profiles do not vary greatly in the spanwise direction.

Fig. 15
figure 15

Normalised wall-normal velocity fluctuations for the baseline and control cases

Full size image

The behaviour of the wall-normal turbulence intensities is qualitatively similar as the streamwise component (see Fig. 15). However, at WN2, the degree of amplification upon injection varies much more between the elliptical and circular AJVGs (see Fig. 15(e), \(x=-6\delta\)). The two elliptical cases show the strongest amplification (by a factor of 3.5 compared with the uncontrolled case), followed by the circular case (factor 2). At WN1, the amplification is nearly equal for all control cases.

Farther downstream (\(x = -4\delta\)), both elliptical cases maintain high-intensity turbulent structures, while the wall-normal turbulent-intensity magnitudes are lower for the circular orifices at both WN1 and WN2.

Downstream of the separation shock (\(x = -1\delta\)), the previously uneven amplification for the different cases has subsided, and all cases show maximum intensities of approx. \(0.07U_{\infty }\). At subsequent streamwise locations throughout flow reattachment and the expansion at the end of the ramp surface, the wall-normal velocity fluctuations behave similarly as the streamwise component in that the profiles closely follow the trends of the uncontrolled case. The continuous turbulence amplification due to, inter alia, the streamline curvature, however, is slightly stronger for the uncontrolled case.

Fig. 16
figure 16

Normalised Reynolds shear stress for the baseline and control cases

Full size image

We discuss the mixing characteristics in the boundary layer downstream of the AJVG array on the basis of the Reynolds shear stresses. As the jet-induced vortices convect downstream, they interact with spanwise-adjacent vortices and thereby increase the turbulent mixing within the boundary layer. The shear stress amplifies for all AJVG geometries, particularly in the WN2 plane, where the jet/jet interactions are strongest.

To highlight differences related to AJVG-orifice shape, selected Reynolds-stress profiles at streamwise locations across the interaction region are shown in Fig. 16. Note that Figs. 16a - c correspond to spanwise location WN1 and Figs. 16d - f correspond to WN2.

In the near wake of the AJVGs (\(x = -6\delta\)), high Reynolds shear stresses and hence strong turbulent mixing occur predominantly at WN2, where jet/jet interactions are strongest (see Fig. 16d).

For the elliptical orifices, the jet-induced structures and hence jet/jet interactions are stronger, and the shear-stress magnitude is approximately five times the value of the baseline case at WN2. For the circular orifices, it is only double the baseline level. This stronger turbulent mixing for the elliptical cases most likely contributes to their better flow-control effectiveness. Disparities in shear-stress magnitude between the different control cases disappear upon flow separation (see Fig. 16b and e, at \(x = -1\delta\)).

Across the SWBLI, the turbulent shear stresses are substantially amplified for all cases. However, the intensity is, on average, \(28\%\) lower for the controlled cases than for the uncontrolled SWBLI on the ramp surface (\(x = 3\delta\); see Figs. 16c and f). This result confirms the relieving effect of AJVG control on the turbulent stresses observed in Ramaswamy and Schreyer (2021).

Overall, any boundary-layer modifications brought about by the jet-induced vortices are limited to the region upstream of the shock-induced separation, and variations at locations farther downstream are minor.

4 Conclusion

We studied the effect of orifice shape on the separation-control effectiveness of elliptical air-jet vortex generators (AJVGs). The AJVGs were used to control the separation at a \(24^o\) compression-ramp interaction at Mach 2.52 and \(Re_{\theta _c} = 8225\). We investigated single-row arrays of spanwise-oriented steady air jets from three orifice shapes with the same hydraulic diameter: two ellipses of aspect ratios (AR) 0.5 and 2 and a circular orifice (AR 1). The mean-flow organisation and turbulence behaviour were assessed using oil-flow and focusing-schlieren visualisations, as well as PIV in streamwise/spanwise and streamwise/wall-normal planes.

Under the influence of control, the previously nearly 2D separation line becomes corrugated. All tested AJVG configurations achieve a reduction in separation length along the entire span of the air-jet array: the corrugated separation line is shifted downstream, and the nearly 2D reattachment line is shifted upstream. Both elliptical AJVGs achieve better control effectiveness than the circular case, with a \(25\%\) reduction in spanwise-averaged separation length compared with only \(17\%\), respectively.

Upon injection, the jets induce streamwise vortices. The jet-to-jet spacing was selected in such a manner that these vortices interact favourably with the adjacent jet-induced structures. Jet/jet interactions between adjacent jets begin as early as \(1.2\delta\) downstream of jet injection, as concluded from the restricted wake width downstream of the individual jets.

On average, the elliptical cases penetrate \(25\%\) deeper into the boundary layer than the corresponding circular case, which provides access to higher momentum fluid in the outer parts of the boundary layer. Furthermore, elliptical AJVGs generate larger streamwise vortices, which strengthens the jet/jet interactions and increases turbulent mixing. Both effects combine and result in the observed better control effectiveness.

Influences of both above-described effects are visible in the mean and turbulent velocity profiles. For the elliptical AJVGs, the velocity profiles downstream of jet injection are fuller due to the stronger streamwise vortices and the associated increase in entrainment. Also the streamwise and wall-normal turbulent intensities are larger for the elliptical than for the circular AJVGs.

AJVGs have a relieving effect on the turbulence amplification across the SWBLI: for all control cases, the turbulent intensities along the ramp surface are lower than in the uncontrolled SWBLI.

While elliptical AJVGs clearly improve the separation-control effectiveness, the differences between the AR0.5 and 1.5 cases are minor. Any effects of the orientation of the elliptical AJVGs (AR0.5 vs AR1.5) appear to be masked by the stronger jet/jet interactions.