On the feasibility of selective spatial correlation to accelerate convergence of PIV image analysis based on confidence statistics

Abstract

This paper presents a method which allows for a reduced portion of a particle image velocimetry (PIV) image to be analysed, without introducing numerical artefacts near the edges of the reduced region. Based on confidence intervals of statistics of interest, such a region can be determined automatically depending on user-imposed confidence requirements, allowing for already satisfactorily converged regions of the field of view to be neglected in further analysis, offering significant computational benefits. Temporal fluctuations of the flow are unavoidable even for very steady flows, and the magnitude of such fluctuations will naturally vary over the domain. Moreover, the non-linear modulation effects of the cross-correlation operator exacerbate the perceived temporal fluctuations in regions of strong spatial displacement gradients. It follows, therefore, that steady, uniform, flow regions will require fewer contributing images than their less steady, spatially fluctuating, counterparts within the same field of view, and hence the further analysis of image pairs may be solely driven by small, isolated, non-converged regions. In this paper, a methodology is presented which allows these non-converged regions to be identified and subsequently analysed in isolation from the rest of the image, while ensuring that such localised analysis is not adversely affected by the reduced analysis region, i.e. does not introduce boundary effects, thus accelerating the analysis procedure considerably. Via experimental analysis, it is shown that under typical conditions a 44% reduction in the required number of correlations for an ensemble solution is achieved, compared to conventional image processing routines while maintaining a specified level of confidence over the domain.

Graphic abstract

1 Introduction

Particle image velocimetry (PIV) is used extensively to experimentally investigate the characteristics of fluid dynamics. By analysing a pair of images of tracer particles separated by a small time delay, $\delta t$, an instantaneous displacement field may be obtained. While such instantaneous displacement measurements may be of interest by themselves, PIV is also extensively used to acquire time-averaged solutions of a wide variety of flows around objects such as rotorcraft (Jenkins et al. 2009), formula 1 cars (Michaux et al. 2018), or cyclists (Jux et al. 2018). Typically, time-averaging is applied to many instantaneous displacement fields, providing the mean solution as well as other statistics about the flow, for example, the standard deviation or kurtosis. Alternatively, ensemble cross-correlation can be utilised, wherein the cross-correlation operator is applied to all N pairs of images in the ensemble, resulting in N correlation maps for each sample location within the image. At each location, all N correlation maps are averaged and a single displacement vector, equivalent to the time-averaged solution, is retrieved (Meinhart et al. 2002). This approach is frequently used in micro-PIV or when experimental conditions, such as seeding, are poor and would result in instantaneous cross-correlation failing (Wereley et al. 2002). The limitation of this approach, however, is that it can only produce the mean displacement field. While both approaches have their advantages and disadvantages, the primary benefit to the former is the ability to easily obtain statistical quantities about the flow.

Such statistics may be of interest to the experimentalist but must be reliable, i.e. converged to the user’s requirements. Satisfactory convergence of the mean displacement field may be obtained using relatively few, $N<100$, image pairs for reasonably steady or straightforward flows, although the number of images may be several times larger for more unsteady flows. Conversely, (Ullum et al. 1998) note that reliable convergence of higher order statistics may require a dramatic increase in the required number of image pairs towards $N=20,000$, posing significant demands on computational resources. While the computational cost to obtain a single mean displacement field may not be significant in and of itself, it is often desirable to test many parameter configurations, which can rapidly increase the number of mean displacements to be analysed. Meanwhile, access to wind tunnels (WT) is often restricted due to their running costs, availability, or regulatory bodies, as is the case in Formula 1¹ FIA (2019). As such, the experimentalist must often decide which parameter configurations are likely to be the most informative in advance, to maximise WT utilisation. Reductions in computational requirements to obtain the desired results may, conversely, enable the user to adjust model-parameter configurations on the fly, based upon results obtained concurrently with WT run-time, thus offering a considerable benefit towards maximising the efficiency of WT usage.

Fig. 1

Evolution of the confidence interval (95% confidence level) of the mean displacement for an axisymmetric turbulent jet, provided for the second PIV challenge (Stanislas et al. 2005), using a 20 image pairs, b 50 image pairs, c 100 image pairs. The confidence interval lower limit is capped at 0.1 for the purpose of illustration. Units in pixel

When calculating ensemble-averaged solutions, the underlying displacement field (i.e. flow) is required to be quasi-stationary, although some temporal fluctuations are unavoidable and the magnitude of such will naturally vary over the domain due to the underlying flow behaviour. Furthermore, flow features captured within the field of view typically vary spatially, presenting a range of displacement gradients, which have been previously shown to be detrimental to the accuracy of the correlation outcome (Westerweel 2008), adding increased uncertainty in the form of artificial displacement fluctuations. In addition, it has been previously demonstrated that cross-correlation response is non-linear and is biased towards regions of curvature (Theunissen and Edwards 2018). While this produces a constant bias to the mean, it also influences the measured temporal variance; the amount of bias per-image basis will vary depending upon the realisation of particle images within the correlation window. Due to these factors, the number of image pairs required for local statistical convergence will vary over the field of view (FOV). To exemplify, the captured FOV may contain regions of little temporal variance (e.g. laminar flow), requiring only few velocity samples to reach statistical convergence in the temporal average, whereas more turbulent regions will demand a large number of realisations, implying that in some image regions statistical convergence might have been reached while additional data analyses are driven by isolated, non-converged, image portions.

Spatially adaptive sampling strategies may ameliorate the situation by reducing locally the number of correlation windows (Theunissen et al. 2007; Edwards and Theunissen 2019), although such approaches do not consider the local convergence and will continue to place correlation windows, albeit fewer of them, in regions which may already be satisfactorily converged. Confidence intervals provide an insight into the convergence of a statistic, by indicating the bounds within which there is a certain confidence that the true statistic value lies. If the width of the interval is smaller than some user-defined threshold value, then the solution at that location can be considered sufficiently accurate for the user’s needs. Figure 1 shows the magnitude of the 95% confidence interval (CI) for a turbulent jet flow, as provided with the Second International PIV Challenge (Stanislas et al. 2005), as the number of images contributing to the ensemble increases. Regions in which confidence in the solution is sufficient, i.e. regions in Fig. 1 where the CI ≤ 0.1, can be considered to have reached statistical convergence. Since confidence intervals can be easily computed per pixel, it is possible to determine only those pixels which require further sampling to reach the target threshold, herein referred to as the region of interest (ROI).

In theory, the image outside of the ROI need not be sampled any further, which could be achieved by imposing a sampling mask in a similar methodology as image masks are applied. Referring again to Fig. 1, the regions in dark green represent the regions which do not need further analysis, whereas the central turbulent jet region represents the ROI. Applying a mask immediately surrounding the ROI, however, would artificially truncate information along the flow-mask boundary, something which has repeatedly been found to influence correlation (Masullo and Theunissen 2017; Gui et al. 2003; Ronneberger et al. 1998). Provided a global interpolant is not used to interpolate displacement vectors, then beyond some distance, which shall be referred to as the analysis support radius (ASR), changes to the solution will no longer influence the point in question. Therefore, a sampling mask could be imposed around the ASR, in turn reducing computation, without adversely affecting the solution within the ROI in any way.

In the following section, this paper explains how confidence intervals can be calculated efficiently, and subsequently how they allow automatic detection of the ROI within the image. Following this, a novel methodology is introduced which allows calculation of the sampling support radius for arbitrary analysis configurations, and details on how to implement this within a typical image analysis routine are given. The methodology is then proven on a set of experimental images of the flow over a blunt trailing edge, showing the potential computational savings which can be achieved by the proposed method.

2 Background theory

The level of convergence in a particular statistic can be inferred by considering its confidence interval (CI). Broadly speaking, the CI represents the range around the observed statistic mean within which there is a certain probability, $\alpha$, typically 0.95 in engineering applications, of the true statistic mean occurring. More accurately, the confidence level indicates the proportion of calculated confidence intervals which would contain the true value, if infinitely many intervals were calculated from the same underlying distribution (Neyman 1937). Increasing the required confidence level for a given distribution will increase the width of the interval—thus giving more chance of the true value being within the calculated bands; a 100% confidence level, $\alpha = 1$, although not realistic, would result in an infinitely large interval to be certain of containing the true value. The CI is proportional to a scaling term which varies depending on the underlying distribution of the data; if the underlying data are normally distributed, and the true standard deviation of the population, i.e. $\sigma _{u}$, is known, then the critical value, denoted by $z^*$ in this case, is obtained from the standard normal distribution. However, if the sample size is very small, or the standard deviation must be estimated from the observed data, then the Student’s t distribution should be used to obtain the critical value, denoted by t. The equation to calculate the confidence interval of the mean of the horizontal displacement is shown in Eqs. (1a) and (1b), where N is the number of samples, $\sigma _{u}$ is the true population standard deviation, and $S_{u}$ is the observed sample standard deviation. The critical values $z^* = f(\alpha )$ and $t = f(\alpha , N)$ will be covered in more detail in the remainder of this section. To clarify, the calculated interval would be $\overline{u} \pm \mathrm{CI}_{\overline{u}}$ where $\overline{u}$ is the observed mean of the data. A similar equation is obtained for the vertical displacement.

Fig. 2

Comparison of the normal- and Student’s t distributions, and the effect of the number of degrees of freedom, $\nu$, on calculating the confidence interval

Attention now turns to the critical values, $z^*$ and t. These values represent the width, in terms of the number of standard deviations either side of the mean such that the contained cumulative probability is equal to the imposed confidence level, $\alpha$. In other words, the area under the PDF curve (see Fig. 2a) between $\sigma = \pm \ z^*$, or $\sigma = \pm \ t$, equals $\alpha$. For the standard normal distribution, with $\mu =0$ and $\sigma = 1$, depicted in Fig. 2a by the solid line, this critical value is purely a function of $\alpha$. Common values of $\alpha$ are 0.68, 0.95, and 0.997 which correspond to $z^*$ values of 1, 1.96, and 3, respectively. The solid vertical lines in Fig. 2a represent $z^*\pm 1.96$, i.e. $\alpha =0.95$, and, therefore, contain 95% of the distribution within these bounds. Alternative values can be found in lookup tables, or by numerically solving the cumulative density function (CDF) of the standard normal distribution for some target $\alpha$, for which functions are readily available in most public statistics libraries.

The Student’s t distribution, on the other hand, depends on the number of degrees of freedom, $\nu = N - 1$. When there are few degrees of freedom, there is more uncertainty in the estimate of the standard deviation; the t distribution accounts for this uncertainty by having larger tails, allowing for more samples further from the mean. This can be seen in Fig. 2a by the increased probability for large $\sigma$, and decreased probability for low $\sigma$. Consequently, the critical value t, which is to contain some proportion $\alpha$ of the distribution, must be larger, and this can also be seen in Fig. 2a. Similar to the above, values of t for various degrees of freedom can be found in lookup tables or calculated with functions from readily available libraries. It should be noted that as the degrees of freedom, $\nu$, increases, the Student’s t distribution tends towards the normal distribution, and in turn $t\rightarrow z^*$, as shown in Fig. 2b, allowing t to be approximated with $z^*$ when $\nu$ is sufficiently large.

Calculation of the confidence interval requires the standard deviation of the displacement to be estimated. A simple implementation to estimate the standard deviation is to store all the displacement fields, $u_{i}(x, y), v_{i}(x, y)$, for $i=1, 2, ... N$ where x and y are the coordinate locations in the image. As a new image is analysed, the standard deviation may be updated using Eq. (2), where $S_{u,N}$ is the sample standard deviation for the horizontal displacement, calculated from of N displacement fields. The notation (x, y) has been dropped for clarity.

$$\begin{aligned} S_{u,N} = \sqrt{\frac{1}{N-1} \sum _{i=1}^N (u_i - \overline{u})^2}. \end{aligned}$$

(2)

This implementation, however, requires re-calculating for every additional displacement field and, furthermore, requires all previous displacement fields to be stored in memory. Efficient and stable updating algorithms exist for both the mean and variance, which can calculate these values without the need to store all contributing data (Chan et al. 2017). In Eq. (3), $u_N$ signifies a component of the Nth displacement field, $\overline{u}_N$ is the mean of all N samples ($u_i$ with $i=1\ldots N$) and ${S^*}^2_{u,N}$ is the sum of squared differences to the mean, which estimates the variance, $S^2_{u,N}$, via the relationship $S^2_{u,N} = {S^*}^2_{u,N}/(N-1)$.

$$\begin{aligned} \overline{u}_N= & {} \overline{u}_{N-1} + (u_N - \overline{u}_{N-1})/N, \end{aligned}$$

(3a)

$$\begin{aligned} {S^*}^2_{u,N}= & {} {S^*}^2_{u,N-1} +(u_N - \overline{u}_{N-1})\cdot (u_N - \overline{u}_N). \end{aligned}$$

(3b)

Fig. 3

Depiction of the analysis support radius for an arbitrary region of interest (yellow) showing the interpolation kernel A, the vector validation kernel B, image deformation kernel C, and finally the region with no influence over the ROI, D, for both bi-linear, (b), and bi-cubic, (c), interpolation kernels. Red dots represent sample locations for a 50% overlap ratio, while the red square depicts an individual correlation window

Having estimated the sample standard deviation, $S_u$, the confidence interval can then be calculated for each vector location using (1b), as in Fig. 1. Comparison of this confidence interval to some threshold value is then used to indicate convergence. For PIV applications, a suitable threshold value for the confidence interval of the mean could be 0.1px, in line with the commonly assumed uncertainty of PIV (Westerweel and Scarano 2005). Although this uncertainty level depends on many parameters, both experimentally and in regard to the analysis procedure, it serves as a reasonable threshold to demonstrate the presented methodology and is generally appropriate for uncertainty in the mean displacement. It should be emphasised, however, that this parameter should be selected by the user depending on the particular conditions of the experiment, analysis procedure, and on the statistic of interest. While this paper focuses on confidence intervals of the mean, it is worth noting that the aforementioned methodology can be extended to essentially arbitrary statistic properties. Doing so requires calculating the standard deviation of the statistic in question, which can be obtained formally, using standard expressions of variance (Benedict and Gould 1996), or may be approximated using techniques such as bootstrapping (Efron and Tibshirani 1986; Theunissen et al. 2008). However, further discussion of such is beyond the intended scope of this paper.

In the extensive paper by Sciacchitano and Wieneke (2016), the authors discuss how instantaneous uncertainty propagates to ensemble statistical uncertainty. In their paper, the uncertainty of the mean is shown to decrease with increasing effective number of independent samples, $N_{\mathrm{eff}}$, and increase as the local, spatial, standard deviation² relative to the displacement magnitude increases, i.e. as the instantaneous uncertainty increases. In this context, $N_{\mathrm{eff}} \le N$ and accounts for any time-dependency between successive snapshots, such as in time-resolved data sets. Understanding the increase in temporal uncertainty of the mean due to instantaneous uncertainty can, and should, be used to aid selection of the user-imposed threshold in the currently proposed methodology. Since the proposed methodology considers only the measured temporal fluctuations, which contains both the actual flow fluctuations and measurement error, the imposed threshold should be appropriately reduced if a certain confidence in just the underlying flow fluctuations is desired. The amount to reduce the threshold can be approximated by the uncertainty mean square, which can be found using accurate uncertainty quantification methods such as those in Sciacchitano et al. (2015).

3 Methodology

Fig. 4

Flowchart showing masking process. Note that k corresponds to the iteration number in the WIDIM analysis, and that masks are created working backwards from the final WIDIM iteration, due to the forward dependency of iterations. Letters in parentheses reflect the regions depicted in Fig. 3

Using the theory introduced previously, the ROI can be determined by comparing the CI, for each vector location, to the user-defined threshold. The subsequent goal is to minimise the computation required to resolve the displacement at these locations, without artificially introducing numerical artefacts associated with image masks. Each sample, i.e. correlation window, will have a support radius, termed the analysis support radius, within which changes to the sampled value will influence the final solution in some way, yet beyond such distance, there will be no effect on the solution. A typical analysis algorithm, e.g. WIDIMScarano and Riethmuller (2000), can be roughly divided into four steps: (1) interrogating the image at pre-defined locations, (2) validating the results of such interrogation by comparing each vector to its neighbours, (3) interpolating the validated vectors onto a pixelwise grid, called the dense predictor, (4) deforming the raw images according to the dense predictor. Steps 1–4 are then repeated several times to improve the spatial resolution, by reducing the interrogation window sizes, and/or inter-sample spacing, i.e. vector-pitch. The methodology presented herein aims to minimise the number of correlation locations in step 1, while ensuring that the solution at step 3, within some arbitrary region, is unaffected. Note that although the initial ‘region’ of interest is defined only at vector locations, intermediate steps in the algorithm must be able to handle a pixel-wise defined ROI, as will be explained in the remainder of this section. Accordingly, an overview of the methodology, for an arbitrary circular ROI, is depicted in Fig. 3, with each component being further broken down and discussed in isolation. Due to the forward dependency of PIV analysis algorithms, i.e. that later iterations in the analysis rely on the output of previous iterations, the proposed method obtains sampling masks in reverse order. In other words, the minimum region that must be sampled in the first analysis iteration cannot be determined until it is known which regions are required in the second iteration, which in turn relies on the third iteration, and so on. To avoid confusion, that the first sampling mask obtained is to be used in the last analysis iteration, any references to a particular ‘iteration’ refer exclusively to the analysis iteration in which the mask is applied.

3.1 Interpolation

The methodology proceeds by working backwards, step-by-step, from the desired final solution to the very first correlation. Referring to the previously described steps 1–4, it is noted that in the final iteration of a typical PIV algorithm steps 3 and 4 may often be neglected, provided the interpolated displacement field is not required, e.g. for post-processing, nor the final deformed image required, e.g. for particular uncertainty quantification (Sciacchitano et al. 2013). While dilation of the sampling mask to account for interpolation may be omitted if the displacements are only required at vector locations, in the case that the ROI is defined per pixel, as it is for intermediate iterations (see Sect. 3.3), the sampling mask must be dilated to consider the spatial requirements of interpolation. Typically, bi-cubic interpolation is used to obtain the dense predictor from vector information, balancing speed and accuracy (Astarita 2008), as well as being simple to implement. More accurate schemes, such as cardinal sin or FFT interpolation, can be used at the expense of computation, whereas bi-linear interpolation may be used to accelerate analysis at the expense of accuracy. While the choice of scheme is ultimately left to the user, the principles described herein can be applied to any scheme, provided that the interpolation kernel can be determined a-priori, i.e. is not data dependent, and is finite in nature. Due to their popularity, this paper shall focus on bi-linear and bi-cubic interpolants.

The first step in finding the ASR is, therefore, to find the vectors whose interpolation kernel overlaps with the ROI. For bi-linear interpolation, each pixel is only influenced by the four immediate neighbouring vectors, which form a 2 × 2 stencil. Dilating the ROI by the inter-sample distance, $h_k$, where k is the iteration number, in both x and y, therefore, ensures that all vectors which would influence the interpolation within the ROI are contained within the dilated region. This region is depicted by region A in Fig. 3b. In contrast, bi-cubic interpolation requires a 4 × 4 stencil and hence the ROI must be dilated by $2h_k$ to ensure all influencing vectors are contained within the new region. This is depicted by region A in Fig. 3c. These regions indicate all the samples which are needed to obtain the correct interpolation within the ROI.

3.2 Vector validation

Prior to interpolation, vectors are typically subject to validation, using schemes such as the normalised median threshold test (NMT) (Westerweel and Scarano 2005) to detect outliers. Since validation may influence the values of samples within the region A, all of the information required for this step must be collected. Vector validation can be broken down into two steps; invalid vector detection, and vector replacement. The NMT compares each vector to its eight surrounding neighbours from a 3 × 3 grid, if the vector disagrees with its neighbours beyond some pre-defined threshold, then it is replaced by the analysis routine. The replacement vector is typically calculated as the mean of the valid eight neighbours, or zero if all are invalid. Therefore, to correctly detect outliers within region A, the sampling mask must be extended to include the immediately neighbouring vectors, i.e. dilate region A by a further $h_k$. This intermediate region shall be denoted as region B’. However, if a vector at the edge of region A is determined to be an outlier, it must be replaced by the average of its neighbours, excluding any outliers. This, of course, is logical; values that have been identified as being erroneous should not be considered. Yet this requires validation of vectors at the limit of region B’, which itself requires the neighbouring eight vectors to be present. As such, for uninhibited validation, region A must, in fact, be dilated by $2h_k$. The resulting region, region B, can be seen in Fig. 3b and c³.

While dilation by $2h_k$, to obtain region B, is required to guarantee numerical equivalence to an equivalent conventional solution, dilating by $h_k$ is generally sufficient for approximate results. This is for two reasons: first, the final solution for instantaneous image analysis is only affected if a vector at the perimeter of region A is identified as an outlier, which represents only a small proportion of the samples. Samples not on the edge of region A would have access to vectors $2h_k$ away and would be unaffected. Second, vectors along the perimeter of region B are still guaranteed to have at least three immediate neighbours, and typically at least five, which can be used for an approximate vector validation attempt. Furthermore, the influence of outliers on the solution is likely to be corrected, at least partially, by subsequent iterations, and therefore, only outliers on the perimeter of region A in the final iteration are likely to cause any significant disturbance to the ensemble solution. Herein, dilation by $2h_k$ for vector validation, ensuring numerical equivalence, will be referred to using NMT, whereas dilation by $h_k$, accepting some numerical differences, will be referred to as NMT*. Differences of the ensemble mean values using NMT compared to NMT* are typically $<1\%$, i.e. at least two orders of magnitude smaller than the imposed ‘acceptable’ threshold, yet, require fewer correlations to obtain.

3.3 Image deformation

Considering that many PIV analyses make use of iterative routines to obtain improved spatial resolution (Scarano 2002), the implications of image deformation must also be considered. For each of the locations which must be correlated in iteration k, i.e. region B, the correlation response must be identical to an equivalent complete analysis routine. Accordingly, each pixel within each correlation window in region B, iteration k, must be appropriately deformed. This region can be found by convoluting each sample location in region B with the current window size (WS), as indicated by region ‘C’ in Fig. 3b and c. Since image deformation, following the methodology of Unser et al. (1993), requires the predictor for iteration $k-1$ at each of these pixels to be correct, region C effectively serves as the ROI for iteration $k-1$. The process is repeated until the first iteration is reached and a sample mask is obtained for each iteration. The described approach is presented as a flowchart in Fig. 4, and with each specific sampling region graphically highlighted in Fig. 3 for clarity. A standard image analysis routine can then be modified to correlate only sample locations which lie within this region and ignore everything else, i.e. region ‘D’, with no negative effects on the solution in the ROI.

3.4 Implementation

In its simplest form, the proposed sampling masks may be imposed in the same way that a conventional image mask is applied, i.e. skipping correlations where the window is in the inactive region, requiring minimal code modifications. Yet, further modifications to various components of the analysis process, e.g. interpolation and image deformation, which continue to operate on the entire image, can yield further optimisations. It is relatively straightforward to modify vector validation and structured interpolation codes to consider only the ‘active’ region. In doing so, the computational cost for these processes is proportional to the number of vector locations, i.e. the number of cross-correlation operations. Image deformation requires interpolating the image based on the predictor values over the image. This image interpolation operates pixel-wise and hence the code can be easily modified to exclude pixels outside of the sampling mask from the deformation process, resulting in a computational cost scaling with the number of pixels in the ROI. When using B-Spline image interpolation, as recommended by Astarita for the best accuracy (Astarita and Cardone 2005), efficient implementation relies on a finite-impulse response (FIR) filter, which is applied to the entire raw image concurrently (Unser et al. 1993). Such filtering is not easily reduced to arbitrary sub-regions; however, this step is only required once per image and yields a marginal computational overhead. Finally, calculation of the sampling mask can be obtained through a series of binary image dilations, wherein the ROI or sampling region is denoted by True (1) and False (0) elsewhere, which can be optimised using bitwise logical operators and are computationally cheap (van den Boomgaard and van Balen 1992). Hence, the method computational savings scale roughly linearly with decreasing ROI extent.

Since the calculation of the standard deviation requires at least two data points, this methodology can, in theory, be implemented from the third image pair onwards. In practice, however, confidence intervals calculated with such few samples are likely to be large, and would accordingly necessitate ubiquitous sampling. To mitigate unnecessary computation, the first $N_t\approx 10$ timesteps are, therefore, obtained using a conventional structured approach, without computing confidence intervals. This number effectively represents the lowest number of images which are expected to be required for convergence of any pixel. Values of $N_t = 10-30$ are reasonable if mean displacements of reasonably steady flows are sought. When the flow is more turbulent $N_t$ may be closer to 100, further still, if higher order statistics are to be obtained, $N_t$ may be in the thousands. Furthermore, it is generally not worth proceeding with the adaptive approach if the size of the ROI is $>\approx 95\%$ of the entire image. In part, the overhead to calculate the sampling masks must be considered, although this is small. Though more importantly, the ASR is typically larger than the ROI, particularly in the intermediate iterations of the analysis, implying that the vast majority of the domain is likely to be sampled anyway and, therefore, computational savings are likely to be small.

4 Results

4.1 Numerical investigation

According to this methodology, the ASR is influenced by the following parameters: correlation window size (WS), window overlap ratio (WOR), number of iterations wherein the WS and vector spacing is refined ($N_k$), number of iterations wherein the WS and spacing are kept constant, ($N_{\mathrm{kr}}$), interpolation methodology (linear or cubic), vector validation methodology and parameters (for example, NMT or NMT*) Changing such PIV interrogation parameters will naturally affect the extent of the resulting sampling masks. For example, cubic interpolation requires dilation by 2h, instead of h for linear interpolation, therefore demanding more correlations to be performed for a given region of interest (ROI) (Fig. 3). In addition to the parameter configuration, the constitution, i.e. the size and shape, of the ROI will also influence the total number of correlations. Figure 5 demonstrates this by comparing the number of samples required for a single block of pixels acting as the ROI, to the number of samples that would be required if the same number of pixels were to represent a more distributed ROI. Due to the practically infinite number of ways to compose the ROI, quantifying this behaviour is difficult, yet a generally valid tendency is that fewer, larger, contiguous ROIs (which are typically encountered in practical situations) will be more effective at reducing the required number of correlations than many scattered regions.

Fig. 5

Influence of the composition of the ROI on the number of samples required for a a single contiguous ROI, requiring 56 samples (red dots) using the proposed method, and b several distributed ROIs, requiring 150 samples, for an equivalent cumulative extent of ROI. Note that colours are the same as in Fig. 3. To simplify the illustration, a linear interpolation is imposed, which results in the interpolation kernel (which would be orange) being identical to the ROI in this case, since the linear kernel does not extend beyond sample locations

To better understand the extent to which each parameter affects the total number of correlations required for a given ROI size, a parameter study was conducted, within which the shape of the ROI was kept as a single central square. This parametric study intends to identify which analysis parameters have the most impact on the size of the sampling mask. To investigate, a default parameter configuration was constructed, as shown in Table 1. For each parameter, a range of typical values were then applied while keeping the other parameters fixed, over a range of ROI sizes. The resulting number of correlations were then recorded and compared to the total number of correlations required for full analysis with the same settings.

To simplify the discussion, the dilation of the ROI per iteration can be approximated as some scalar multiple of the sample spacing, i.e $\eta \cdot h$. For example, a single iteration with linear interpolation (dilation by h) and NMT validation (dilation by 2h) would result in $\eta = 3$. When varying the interpolation kernel or vector validation method, $\eta$ is modified, whereas h remains constant. Accordingly, there is an approximately constant increase in the fractional number of correlations, i.e. the number of correlations performed as a fraction of the total possible for that particular parameter configuration, shown in Fig. 6c and f. Similarly, the more iterations there are, the more times that the ROI is dilated by $\approx \eta \cdot h$, thus we see again a steady increase in the fractional number of samples as the number of iterations increases.⁴ Conversely, parameters such as the WS and overlap ratio alter the spacing, h, instead of $\eta$, and can have a much more significant impact on the fraction of correlations which need to be performed for a given ROI, as shown by Fig. 6a and b. The spatial dependency of the analysis is reduced, and hence the computational cost more closely correlates with the amount of domain to be analysed. Put differently, the smaller spacing increases the total number of sample locations in the entire domain, yet the absolute number of samples required for a particular ROI remains approximately the same⁵, increasing the number of samples which are now not needed to be correlated, significantly improving its efficiency. The key corollary from this study is that more computationally intensive interrogation parameters, with fewer analysis iterations, will benefit the most from the presented methodology.

Table 1 Values used for each setting as part of the parameter sweep

Fig. 6

Comparison of the speedup effect of a locally selective WIDIM approach for changing a final WS. b WOR. c Vector validation approach. d Number of iterations. e Number of refinement iterations. f Interpolation method

4.2 Experimental analysis

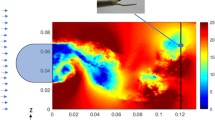
To verify the methodology in a real application, it was applied to the flow behind a blunt trailing edge, investigated by Elsahhar et al. (2018) for its aeroacoustic properties. In this study, the effect of trailing edge bluntness on the generation of wake-vortex noise was investigated using particle image velocimetry. The case treated in the following is that of a bluff body with a bluntness thickness, $h_b$, of 46 mm and freestream velocity of approximately 11.6 m/s, equivalent to a chord-length (350 mm)-based Reynolds number of 2.75 × $10^5$. Shown in Fig. 7 is the reference flow field for this particular case. Experiments were performed by means of Dantec Dynamics planar PIV system in the low-turbulence wind tunnel of the University of Bristol, which produces background RMS turbulence levels below 0.03%. It is worth noting that the exemplary PIV recording shown in Fig. 8 combines image recordings of two, simultaneously triggered, FlowSense EO cameras, each with a sensor of 2072 × 2072 px. The time delay between snapshots was chosen to achieve a freestream displacement of approximately 4 px. The first field of view (FOV) observed the boundary layer near the trailing edge while the second covered the near-wake region. Each FOV corresponded to an observed field of view of 161 mm × 161 mm, equivalent to approximately 3.5$h_b$ × 3.5$h_b$. The reader is referred to Elsahhar et al. (2018) for further details regarding the PIV setup and experimental parameters.

Fig. 7

Ensemble averaged, reference flow field obtained by averaging all 115 measured displacement fields in their entirety. The contour represents the vertical displacement component. Units in pixel

Since the FOV contains both uniform flow and regions of more turbulence, these images serve as ideal candidates to test the proposed method. Figure 8 shows one of the (in total) 115 raw images and highlights the strong reflection present in nearly all of the images. While the presence of such reflections would not adversely affect the methodology presented within, reflections may still influence the solution accuracy. Since the reflection varies slightly in time, correlations in this region will be influenced to a varying degree per snapshot—leading to increased RMS, or temporal standard deviation. Furthermore, it is expected that some correlations in this vicinity would fail, producing outliers. While the majority of these outliers should be captured by the outlier detection algorithm, some will persist—further increasing the RMS at these locations. Referring back to (1b), this would increase the number of samples required for a given CI; therefore, if the reflections can be mitigated with simple pre-processing, then both the solution and computational performance improve. An ensemble-minimum background subtraction (Wereley et al. 2002) was, therefore, applied to all images, which removed the majority of the reflections (Fig. 8b). Nevertheless, remnants remain in the images due to the temporally fluctuating nature of the reflection. While more advanced pre-processing techniques could certainly have been employed to further improve image quality, however, since it does not adversely affect the demonstration of the proposed methodology’s efficacy, these techniques were not investigated any further. It can be seen in Fig. 9 that more samples are required to contribute to the solution where these artefacts remain, corroborating the expected influence of reflections on the methodology described above.

The ensemble of images was analysed according to three different schemes. First, a reference conventional solution was established using conventional WIDIM (Scarano 2002) adopting the default parameters as in Table 1.

Fig. 8

Exemplary PIV image from Elsahhar et al. (2018). a Raw image with zoom inset showing reflection, b pre-processed image with inset showing diminished reflection. Contrast enhanced for clarity

However, the discrete displacement data (following the cross-correlation of interrogation windows) were interpolated pixel-wise using bi-cubic kernels rather than the bi-linear scheme listed in Table 2. Subsequently, the presented methodology was used to obtain the ensemble mean at a 95% confidence, of being within 0.1 px and 0.05 px, using the same parameter configuration as the reference solution. Due to the relatively small number of samples (115) and the unknown standard deviation, (1b) was used to obtain the pixel-wise confidence interval after each time step, using the Student’s t distribution to calculate t. Regions where the adaptive method uses all 115 images, e.g. regions where the CI exceeds the threshold, such as in the wake region of Fig. 7, the solution is numerically equivalent to the reference solution. Outside of these regions, where less than the full 115 images have been considered, the solution is expected to differ from the reference to some degree, depending on the threshold level. Figure 10 shows how much the adaptive solutions differ from the reference WIDIM solution. Plotting the histogram of the magnitude of such differences, i.e. $|U_l - U_w|$, where $U_l$ is the solution from the proposed methodology, and $U_w$ is the reference WIDIM solution, over the domain, Fig. 11 shows how these follow roughly a normal distribution. In the limit as the number of images increases, this distribution will tend towards a normal distribution with properties equivalent to the imposed conditions, e.g. for 95% confidence of 0.1 px, the distribution will have zero mean and a standard deviation of $\approx 0.05$, such that $2\sigma$ corresponds to 0.1 px. The distribution presented within is expected to have a bias towards zero since the solution in the proposed methodology’s solution represents a considerable proportion of the reference solution. Consider a region wherein 100/115 images contribute to the reduced solution. For quasi-steady flow, variations in the final 15 images are unlikely to have a significant impact on the reference solution, yet it is expected that if the reference solution contained many more snapshots, for example in the order of thousands, from the same underlying statistical distribution, then the histogram of differences would tend to the normal distribution as described previously.

The number of samples contributing to the ensemble mean, over the entire domain, for each threshold setting is shown in Fig. 9. In both cases, the freestream requires relatively few samples to reach convergence compared to the wake. This is in line with the expressions for the confidence levels in (1b). As the local standard deviation increases, the number of independent samples required to reach a pre-defined confidence level increases quadratically. It can also be seen that the stricter tolerance requires more samples in the fringes of the wake, relative to the more relaxed threshold. Although the majority of the image reflection was removed, its influence can still be observed by the increase in the number of contributing samples in Fig. 9. Comparing the total number of correlations for the entire ensemble, Table 2, the strength of the proposed method is made apparent. A reduction of 44% and 28% in the number of correlations is achieved for the 0.1 px and 0.05 px thresholds, respectively. While overheads exist beyond the correlations, such as interpolation and image deformation, these typically represent a small proportion of the overall computational cost. The number of total correlations is further reduced using the NMT* approach as described previously, reducing the number of correlations by $\approx$5% in both cases.

Fig. 9

Number of contributing samples for a threshold of a 0.1 px, and b 0.05 px

Table 2 Comparison of the number of correlations performed for each of the approaches

Fig. 10

Effect of changing confidence interval threshold on the magnitude difference to a reference full solution, for a 0.1 px threshold and b 0.05 px threshold. Units in pixel

Fig. 11

Histogram of the delta to the reference WIDIM solution from all pixels where the number of contributing samples is less than that of the reference

5 Conclusions

A method has been proposed which automatically reduces the interrogation domain subject to satisfactory convergence of the flow field statistics. The method has been demonstrated based on the mean flow field, and the concept may be easily extended to arbitrary flow statistics. Convergence is determined by calculating the confidence interval and comparing to a user-defined threshold value, for example, a 95% confidence of 0.1 px difference to the expected mean. A region of interest (ROI) is obtained automatically and efficiently based on the flow statistics and used to develop a sampling mask for each iteration. Generation of the sampling masks considers the imposed interrogation parameters, e.g. WS and overlap ratio, and determines the minimum region of the image which must be analysed to avoid introducing artificial numerical artefacts, known to be associated with image or mask boundaries.

This approach significantly reduces the computational cost required to obtain domain-wide ensemble statistics converged to a pre-defined level by reducing the total number of correlations required. The method was applied to the flow behind a blunt trailing edge, being investigated for its aero-acoustic properties. A numerical assessment revealed that for typical PIV settings, the number of correlations to obtain the ensemble mean was reduced by 44%. The method is expected to be particularly of use when rapid mean solutions are required, i.e. analysing images concurrently with wind tunnel utilisation, or when processing higher order statistics. Notably, computational savings are made by a reduction in the number of correlations performed, which represents the most time-consuming process in a typical PIV analysis algorithm. Therefore, regardless of the particular hardware configuration, e.g. the use of graphical processing units (GPUs) to accelerate the computation of each individual FFT, or the use of large clusters to distribute computations, the proposed methodology still offers potential computational savings as fewer correlations must be computed.