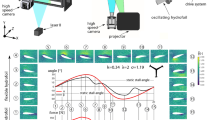
Abstract
The characteristics of the fluid–structure interaction on the flexible blades of a horizontal-axis water turbine are studied; this bioinspired technology features mechanical simplicity, performance and lifetime improvement, and low fish impact risk, all characteristics of a truly sustainable renewable energy exploitation. A surface-tracking method synchronized with force measurements was applied on a surrogate model of single-bladed, vertical-axis water turbine in a water channel. This allows for the characterization of the structural deformations and their link to the hydrodynamic forces, over a large range of turbine designs and operating points. It is shown that the phase angles of the maxima in blade deformation coincide with those of the load maxima on a rigid blade in identical flow conditions. The influence of the turbine’s tip/speed ratio on the blade deformation and blade load is investigated. With the chosen blade design, hydrofoil deformation is found to be maximum in the operating points where the performance improvement is maximized (\(k_o=0.3\)). With lower values of reduced frequency (corresponding to lower rotation speed), fluid-induced forces dominate the fluid–structure interaction. Conversely, at higher frequencies, structural inertia dominates the interaction, and blade deformation is again reduced. Results suggest that the optimal blade rigidity may depend on the operating point; nevertheless the potential of the flexible-blade design is demonstrated through clear linking of fluid-induced forces and blade deformation in the complex flow conditions of the Darrieus water turbine.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The exploitation of marine energy resources, like tidal or marine currents, would provide a vast, currently almost unused source of renewable energy. It represents one of the most promising and challenging tasks in renewable energy engineering: the technology must cope with the rough conditions of a marine environment, including saltwater, but also meet demands for sustainable technologies with low ecological impact. This, in combination with the need for high efficiency, translates into contradicting requirements for turbine design.
A rigid and a flexible NACA0018 hydrofoil. The large deformations change the rotor flow characteristics significantly. Left: rigid hydrofoil without deformation with speed triangles as a result of the inclination angle \(\alpha\). Right: flexible foil for the same \(\alpha\) (cross section retrieved from the experiment, as explained later in the text)
Vertical-axis hydrokinetic water turbines (VAWT) could provide a simple and robust technology to meet this challenge. They operate independently from the flow direction and do not require any housing or guiding apparatus. They also have low ecological impact: no fish injury was reported in turbine assessments for marine current turbines operating with low rotational speed (Amaral et al. 2011; Zhang et al. 2017). Hydrokinetic water turbines mostly operate under low tip/speed ratio (\(\lambda\), see Eq. 2) conditions compared to wind turbines. This is due to their high solidity (\(\sigma\), see Eq. 4), which is required by the higher density of water. Fish impact probability models take into account the rotational speed of the rotor (Turnpenny et al. 2000; Deng et al. 2007 or Müller et al. 2018); a common finding is that the impact risk rises along with the rotor frequency. The pressure drop, which is the other main cause of fish injury during turbine passage (Stephenson et al. 2010), is negligible in hydrokinetic turbines.
Nevertheless, the most important particularity of VAWT may be their high area-based energy density for installations in turbine arrays, as reported by Whittlesey et al. (2010), Dabiri (2011) and Brownstein et al. (2016). This is an obvious advantage compared to horizontal-axis water turbines (HAWT) in farm installations, even if VAWT cannot yet compete with them in terms of single-turbine efficiency. Theoretical, momentum-based methods based on two-actuator disk models of the cross-flow turbine predict that the Betz-Joukowski limit should be slightly overcome (Loth and McCoy 1983; Newman 1986). Common magnitudes for maximum power coefficients measured in literature are about \(c_{\mathrm{p}_{\mathrm{max}}}=0.35\) (Maître et al. 2013).
For low-\(\lambda\) operating points (\(\lambda <3\)), the flow in the rotor region is dominated by highly unsteady hydrodynamics such as dynamic stall, as reported by Laneville and Vittecoq (1986) and later observed with particle image velocimetry measurements by Fujisawa and Shibuya (2001), Ferreira et al. (2009), Gorle et al. (2014) and Buchner et al. (2018). These conditions generate cyclic structural loads and can lead to material failure from fatigue, which is an important point in the design of a VAWT (Buchner et al. 2018). Additionally, the efficiency in low-\(\lambda\) operating points is low for conventional VAWT designs (Shiono et al. 2000). For high-\(\lambda\) operation points, strut and tip losses become dominant (Daróczy et al. 2015). Those forces are affected by the square of the angular velocity \(\omega\). Blade–blade interaction also rises along with \(\lambda\). At high tip/speed ratios, the successor blade enters the wake of its predecessor because wake downstream convection becomes small compared to the blade speed.
The flow regime in the rotor is complex. The phenomenon of dynamic stall shows nonlinear, chaotic characteristics with high instability: small initial differences in the flow conditions can translate into massive changes in the resulting flow. The numerical modeling of these flow conditions and its impacts on applications like turbomachinery is challenging. Even when simplified geometries such as pitching plates are used, obtaining accurate results requires costly three-dimensional simulations with high spatial and temporal resolution (Zanotti et al. 2014). The loads on a VAWT can successfully be reproduced with numerical methods like large- or detached-eddy simulations, but underlying flow dynamics such as the onset of leading-edge vortices or the occurrence of the vortex shedding are not always reproducible with satisfying accuracy (Ferreira et al. 2007). In parallel, experimental research is carried out on dynamic stall and its influence on VAWT, such as in Buchner et al. (2017) or Miller et al. (2018), or with a focus on simplified models like pitching plates or profiles (Benton and Visbal 2019) in order to provide deeper insights in the underlying mechanism and to develop control strategies for technical applications.
Beside more fundamental research on the flow characteristics themselves, numerous strategies have been pursued to overcome the negative effects of dynamic stall in these turbines, such as adaptive blowing (Müller-Vahl et al. 2014) or plasma actuators (Greenblatt et al. 2014). A common approach is to balance the rotor blades during the rotation with active or passive pitch motion of the blades in order to avoid deep dynamic stall, as shown by Pawsey et al. (2002), Lazauskas and Kirke (2012), Mauri et al. (2014), Liang et al. (2016), Chatellier et al. (2018) or Abbaszadeh et al. (2019).
Strom et al. (2016) introduced a control of the angular velocity based on the azimuth angle that can significantly improve the performance of a two-blade VAWT.
A bioinspired approach to control and improve the stall characteristics of a hydrofoil is the use of an optimized morphology, e.g., protuberances or tubercles on the leading edge (Hansen et al. 2016 or Pérez-Torró and Kim 2017). The study at hand makes use of a bioinspired, adaptive structural design of the blade itself. This approach is inspired by observations of the fins of sea mammals, whose flexibility improves their propulsion efficiency significantly (Fish 1993). Such a flexible blade adapts itself to the flow by deformation, which affects the hydrodynamic forces (see Fig. 1). In particular, the drag of such flexible structures is decreased. A transfer of this passive flow control mechanism to VAWT is presented in this study. The deformations result in a morphing of the foil toward a cambered profile operating at a lower angle of incidence. The aim of the approach is to inhibit or lower the deep dynamic stall phase and to reduce phases of significant loss of lift with high drag. These states occur at low-\(\lambda\) operating points for a significant fraction of each period. Figure 2 demonstrates this shape morphing effect for an angle of incidence of 30\(^\circ\). The rigid hydrofoil (left) shows no deformation, while the flexible profile (right) morphs to a shape comparable to a highly cambered NACA15518. The geometry of the cambered foil (gray) is overlaid on a profile outline (black line) derived from a high-speed video recording of the cross section.
Zeiner-Gundersen (2015) successfully unified a blade pitch method with adaptive blades for a VAWT operating in very low-\(\lambda\) conditions. MacPhee and Beyene (2016) found corresponding results for a flexible blade without additional pitch function from numerical investigations. The influence of flexibility on performance and lifetime was investigated for multiple operating points and turbine designs without hardware variations by Hoerner et al. (2019). An experimental surrogate model for a single-blade VAWT was used. It could be shown that significant improvements can be achieved for \(\lambda =2\) and for multiple turbine designs. This was the case in particular for \(\sigma =1\) on a three-bladed rotor, such as investigated by Maître et al. (2013).
In the present study, a structured-light-based profilometry method, introduced by Takeda et al. (1982) and adapted to a high-speed surface tracking (SFT) method for FSI by Hoerner and Bonamy (2019), is combined with a synchronous measurement of the hydrodynamic forces (Hoerner et al. 2019). The surface deformations and force characteristics of a flexible blade are compared to a rigid structure for reference.
The following section will give an overview of the experimental concepts and methodology used. Then, the results for two operation points (\(\lambda =2\) and \(\lambda =3\)) and several design points (\(\sigma\)) will be shown and subsequently discussed.
2 Experimental model and setup
2.1 Modeling
In order to simplify the complex flow characteristics in a VAWT rotor and to focus on the dynamics at the blade level, a surrogate model for a single-blade VAWT was used. This well-known simplification, already introduced in former studies such as Ly and Chasteau (1981), substitutes the static reference frame of the observer with the rotating reference frame of the turbine rotor. The result is an oscillating hydrofoil, performing a nonsinusoidal pitch motion, with a pitch angle \(\alpha\), that is equal to the angle of incidence for the rotor blade. Its trajectory is defined by Eq. 1 and shown in Fig. 2 (Laneville and Vittecoq 1986).
with the rotor’s azimuth angle \(\theta\) and tip/speed ratio \(\lambda\) given from Eq. 2:
The tangential velocity \(\omega R\) of the rotor, which is the product of the angular velocity and the radius, is expressed as a function of the far-field flow velocity \(v_{\infty}\). The relative flow velocity at blade level w varies as a function of the azimuth angle \(\theta\), expressed by Eq. 3:
This model reduction allows for a clear observation of the flow characteristics at the blade level. However, it neglects some effects applying to the real turbine, such as a reduced angle of attack in the downstream region of the rotor reported by Delafin (2014) or Bianchini et al. (2018). During the experimental investigations, w is set constant, since the flow speed \(v_{\mathrm{ch}}\) in a water channel cannot be varied in the required timescales. The solidity \(\sigma\) of a VAWT is defined as a function of the chord length C, the number of blades n and the radius R as Eq. 4:
The simplified physical model allows to vary the solidity of the investigated turbine by varying the oscillation frequency \(f_{\mathrm{o}}\) in the experiment. This allows for the investigation of the influence of flexible blades for multiple turbine designs without hardware changes in the experiment. This relation of \(f_{\mathrm{o}}\) to \(\sigma\) can be found by the definition of reduced frequency k (Eq. 5) and its adaptation to the oscillating profile case (Eq. 6), which characterizes the flow dynamics at blade level. It was first introduced by McCroskey et al. (1976) and later adapted to VAWT by Laneville and Vittecoq (1986) for a vertical axis turbine:
As an example, for \(\lambda =2\), a reduced frequency of \(k=0.16\) would result in a very fragile design of \(\sigma =0.5\) and lead to a radius \(R=0.4\) m in the given experimental setup. For \(k=0.56\), a very solid machine of \(\sigma =1.75\) would result in a radius of \(R=0.113\) m. A scaled version of the LEGI turbine model (Maître et al. 2013), with \(\sigma \approx 1\), operates at \(k=0.32\) with a radius of \(R=0.2\) for a chord length \(C=0.066\) m. The reduced frequency \(k_o\) (Eq. 6), derived for the current setup, was introduced in Hoerner et al. (2019). It is derived from Eq. 5 by replacing the radius with an expression that involves the tip/speed ratio and the oscillation frequency of the pitching hydrofoil:
A qualitative transfer of the results from the reduced model to a VAWT is made possible by the definition of a normal \(c_{\text{N}}\) and thrust coefficient \(c_{\text{T}}\). They are based on the nondimensionalized lift \(c_{\text{L}}\) and drag coefficients \(c_{\text{D}}\).
Within this model, \(c_{\text{T}}\) is the share of the hydrodynamic loads that provides propulsion and should become maximal. \(c_{\text{N}}\) generates structural loads without benefit and should be minimized. Since the angles of incidence remain below \(30^\circ\), the drag plays a crucial role, due to its relative amplification through the trigonometric functions involved.
A more detailed description of the experimental model and extended force measurements is presented in Hoerner et al. (2019).
Setup of the experiment at the water tunnel including force measurement and surface tracking. Both the projector and the high-speed camera (which together measure the deformation) are positioned underneath the water tunnel. The six-axis load cell is positioned fully submerged in the water between the drive system and the hydrofoil
2.2 Setup and force measurements
The experiment was conducted in the hydrodynamic tunnel at the LEGI labs Grenoble. The channel test section is of dimensions (\(X\times Y\times Z){:} 1000\times 280\times 175\) [mm]. Two NACA0018 hydrofoils were investigated in the present study: a rigid hydrofoil made from solid aluminum and a flexible composite hydrofoil. The deformations of the rigid foil remain below the measurement accuracy. The flexible hydrofoil mounted in the test section is shown in Fig. 3. The leading edge up to the first-quarter chord is made out of milled aluminum, while the rest of the foil is flexible, with a skeleton consisting of a thin (0.3 mm thick) carbon-fiber composite blade surrounded by a hyper-flexible silicone body. The main advantages of such a design are an almost uniform stiffness in the axis of the rotation and a high camber-wise flexibility, which amount to a nearly two-dimensional characteristic of the structural deformation. Furthermore, this design allows for a simple change of the foil stiffness, by variation of the thickness of the carbon skeleton. The design allows for a simplified mechanical modeling of the structural deformation characteristics with use of a clamped beam and the Euler–Bernoulli beam theory. A preliminary estimation of an expected deformation magnitude of 15\(^\circ\) for a maximum angle of incidence of \(\alpha =30^\circ\) (with forces achieved from numerical simulations) leads to a skeleton thickness of 0.5 mm. The deformation magnitude was chosen with respect to the static stall angle of roughly \(\alpha _{\mathrm{stall}}=16^\circ\) for the Reynolds number envisaged for a NACA0018. Three different stiffness of 0.3, 0.5 and 0.7 mm thickness was investigated in a preliminary study (Hoerner et al. 2019). The most flexible structure showed the highest flow adaptation and thrust improvement. It was chosen for further investigations in consequence. The structured light projection on the hydrofoil surface, which is used for the deformation measurements, is visible in Fig. 3.
The general experimental setup is shown in Fig. 4. A six-axis load cell was positioned behind the mounting plate of the hydrofoil, which allowed to capture the hydrodynamic forces and torques in three dimensions with 1 kHz sample rate. A drive system governed by a highly accurate position control system follows the trajectory of the pitch motion. This trajectory is given in Eq. 1 and provides, for each reduced frequency \(k_o\), conditions corresponding to an operating point \(\lambda\) for a specific solidity \(\sigma\). The load cell follows the forced rotational pitch motion from the drive system. The lift and drag forces are obtained by transformation of the forces measured in the static reference frame, with help of the drive’s position feedback.
Lift and drag forces acquired from the six-axis load cell were nondimensionalized with the corresponding instantaneous value of \(v_{\text{ch}}\):
Values for \(c_{\mathrm{D}}\), \(c_{\mathrm{L}}\) and \(\alpha\) at any time point within a period were averaged across periods. For example, in a representative period constructed with n periods for each sample j of the position feedback \(\alpha\), the period-averaged lift coefficient \(\overline{c_{\mathrm{L}}}(\alpha _j)\) is obtained as:
The constant channel flow velocity was set to \(v_{\mathrm{ch}}=3\) m/s which results in a blade-based Reynolds number Re = 200,000 for a hydrofoil of \(C=66\) mm chord length. The general sensor accuracy of the six-axis load cell is of \(<2\%\) reading from the manufacturer. However, channel cross-talk was in particular for high lift with low-drag scenarios that were found for nonstalled profiles. The hydrofoil inertia is considered to be not significant. The load difference in between the flexible and the rigid hydrofoil, a result of the different mass, was found to be close to the sensor uncertainty (1 N in drag and 0.5 N in lift) at the maximum acceleration point in the fastest motion investigated. The details of the experimental setup including extensive considerations regarding measurement uncertainty are given in Hoerner et al. (2019).
2.3 Surface tracking
In FSI with large deformations, the structure gives feedback to the flow field, which, in consequence, back-couples both flow and structure in a strong manner. In order to get insight in these fluid–structure interaction mechanisms, the deformations of the structure are captured synchronized with the hydrodynamic forces.
For the deformation measurements, a structured-light-based profilometry method introduced by Takeda et al. (1982) was adapted to the requirements of the present study, as described by Hoerner and Bonamy (2019). The source code of the analysis software is published and freely available (Augier and Bonamy 2019).
The core of the method is the projection of a fringe pattern of a sinusoidal grayscale distribution on a surface (see Fig. 3). Any change in the surface height will defocus the pattern, and the phase angle \(\phi\) of the sinusoidal pattern will be shifted. A high-speed recording of the projection allows to retrieve the structural deformations \(\Delta h\) compared to a reference surface. The knowledge of the geometrical setup, such as the distance of the projector to the camera \(D_{\mathrm{PC}}\) and to the surface baseline D, as well as the wave length of the projection \(l_{\lambda}\), allows to calculate the height \(\Delta h\) of the surface for each pixel of the recording at the position i, j for a given sample s.
In consequence, the method allows to retrieve a three-dimensional surface with high temporal and spatial resolution, from a two-dimensional recording. In the present setup, the patterns were recorded with 4 kHz temporal (frame rate) and 0.25 mm spatial (retrieved from the camera) resolution. Details of the method and of the two-dimensional spectral analysis of the deformations, including uncertainty considerations, are given in Hoerner and Bonamy (2019). In the present setup, the method showed an averaged measurement uncertainty of 0.66 mm, which is about 1.06 % of the pitch amplitudes observed at \(\lambda =2\).
Surface tracking measurements (SFT) are taken for the rigid and for the flexible hydrofoil in identical conditions. The subtraction of one from the other provides the instantaneous deformation field of the flexible hydrofoil. In the subsequent section, this comparison for two operating points (\(\lambda =2\) and \(\lambda =3\)) is shown along with the corresponding forces.
Calculation of the hydrofoil (deformation) angle \(\beta\) shown in subsequent Figs. 6, 7, 8, 9, 10, 11, 12, 13 and 14 for the flexible (\(\beta _1\)) and the rigid hydrofoil (\(\beta _2\)) for the same inclination angle (\(\alpha =\beta _2\)). The surface height h is projected on a fixed-size pixel lattice. This leads to a constant projected foil length (see Hoerner and Bonamy 2019 for details)
Deformation (top) and hydrodynamic forces (bottom) for \(\lambda =2\) and \(k_o=0.06\) (transition between quasi-static (\(k_o<0.05\)) and dynamic state). The stall point is shifted to higher angles of incidence. The force peaks on the rigid hydrofoil (bottom: gray dashed line) occur at the same pitch angle as the deformation peaks on the flexible structure (top: solid black line). One oscillation period is shown
In the subsequent paragraphs, the results of the surface tracking are shown along with those of the force measurements, for both the rigid and flexible hydrofoil. This allows to compare the characteristics of the deformation and their influence on the hydrodynamic forces as the reduced frequency is varied. In upcoming Figs. 6, 7, 8, 9, 10, 11, 12, 13 and 14, the upper graph shows the position feedback of the drive system (dashed black for the flexible and dashed gray for the rigid foil) in order to show the repeatability of the motion through the drive system. The deformation of the foil is characterized with a single parameter, the angle \(\beta\), which can be seen as an equivalent angle to alpha for the deformed structure. As shown in Fig. 5, it represents the angle of a triangle in between the measured trailing edge height h, the pivot point at quarter chord and the height at zero angle \(h_0\) at trailing edge and the pivot point, using Eq. 15:
The projected chord length C remains constant during the oscillations, as the height matrix from the measurement is projected to a fixed-size lattice (see Hoerner and Bonamy 2019 for details).
In a previous publication, the highest potential for turbine improvement through flexible blades was found to occur at \(\lambda =2\) (Hoerner et al. 2019). In this case, the maximum inclination angles \(\alpha\) are approximately 50% higher compared to the \(\lambda =3\) case. This is also true for the lift force in the experiment, which peaks at up to 150 N (cases with \(k_o> 0.16\)) for \(\lambda =2\).
Adapting the flexible blades to the lower lift forces observed at higher tip/speed ratios may require lower foil stiffness. However, centrifugal loads on the blades increase together with the tip/speed ratio. The approach presented may fail if centrifugal forces on the structure start to dominate fluid forces. This is likely to occur for wind turbines, whose rotational speed is typically higher.
The data presented are filtered after the SFT processing and force measurement using a zero-phase, low-pass, second-order 35-Hz Butterworth filter, in order to fully eliminate the effects of a 60-Hz flicker from the projector and vibrations from load-cell measurements (unfiltered raw data were presented in Hoerner et al. 2019; Hoerner and Bonamy 2019).
3 Results and discussion
The measurement results are presented in Figs. 6, 7, 8, 9, 10 and 11 for \(\lambda =2\), and selected further results are presented for \(\lambda =3\) in Figs. 12, 13 and 14. This extensive description is presented to provide a complete description of the foil deformation as one transits from quasi-static state to the high-frequency state. In the following paragraphs, a systematic description is provided; the diagrams are also annotated to point out notable visible features. Nevertheless, it is important to highlight the main trends that stem as \(k_o\) is increased:
At low \(k_o\), the flexible blade adapts accurately to the flow. Fast changes in the hydrodynamic loads get balanced by structural deformation, which becomes visible by the repeatedly coincidence of deformation peaks for the flexible structure to the loads on the rigid structure, which results in a smoother trajectory of the load over a period. In this case, the fluid–structure interaction is dominated by the fluid flow with a low impact of the profile motion to the dynamics.
As \(k_o\) is progressively increased, the flexible blade deforms with increasing amplitude and increasing structural delay, until both reach a maximum. The inertial effects in the flow lead to delayed flow separation with increasing effects along with \(k_o\) and an increasing speed in the blade motion.
At high \(k_o\), the flexible blade features dynamics largely similar to the rigid blade, with smooth, low-amplitude deformations. Here, the profile motion governs the dynamics of the fluid–structure interaction.
Finally the connection between relative deformation, which expresses the degree of adaptation of the structure, and hydrodynamic loads as a function of the reduced frequency is provided in Fig. 15).
3.1 The \(\lambda =2\) case
The experimental setup includes six variations of the reduced frequency \(k_o\) realized with the oscillation frequency \(f_{\mathrm{o}}\):
\(k_o\) = [0.06, 0.16, 0.28, 0.33, 0.46, 0.71]
\(f_{\mathrm{o}}\) = [0.45, 1.30, 2.25, 2.63, 3.64, 5.68] Hz
Deformation (top) and hydrodynamic forces (bottom) for \(\lambda =2\) and \(k_o=0.16\) (dynamic state is reached). The stall point is further shifted. The force peaks on the rigid hydrofoil (bottom: gray dashed line) occur earlier than the deformation peaks on the flexible structure (top: solid black line). Lift loss and drag peak occur at the same moment
Deformation (top) and hydrodynamic forces (bottom) for \(\lambda =2\) and \(k_o=0.28\). The trend of Fig. 7 continues. Lift loss and drag peak do not occur at the same moment anymore. Force and deformation peaks are gained
Deformation (top) and hydrodynamic forces (bottom) for \(\lambda =2\) and \(k_o=0.45\). The force and deformation peaks diminish after a maximum at \(k_o=0.33\) in Fig. 9. The highest peak is shifted to the descending branch of the trajectory of \(\alpha\) for the flexible hydrofoil
3.1.1 Transitional state (\(k_o=0.06\), \(f_{\mathrm{o}}=0.45\) Hz)
The campaign starts with a transitional case (Fig. 6). The flow dynamics for a reduced frequency \(k<0.05\) can be considered to be quasi-static (McCroskey et al. 1981): here, flow convection dominates over the pitch motion. The rigid profile static stall angle was found experimentally to be at 16\(^\circ\). The pitch motion shifts the stall point of the rigid foil to 22\(^\circ\). The lift force peak is about 120 N on the rigid hydrofoil. The deformation peaks of the flexible hydrofoil and the lift peaks of the rigid foil coincide. The lift curves for the flexible hydrofoil show none of the “classical” characteristics of static foil stall (abrupt drop in lift with increase in drag). Local maxima in rigid lift force and flexible deformation coincide repeatedly, e.g., at 1800, 2000, 5400, 5600 samples. The lift force drops occur simultaneously with the drag peaks.
3.1.2 Dynamic stall (\(k_o=0.016- 0.33\), \(f_{\mathrm{o}}=1.30- 2.63\) Hz)
At \(k_o=0.016\), a fully dynamic state is reached (see Fig. 7). The pitch motion leads to a further phase shift of the stall point toward higher angles of incidence and increased lift force peaks (\(F_{\mathrm{L}}>150\) N for \(k_o=0.33\)). However, these peaks are smoothed out compared to the previous case, which is also caused by the shorter period length. The structure deflects more than before, due to the increased lift forces.
The rigid force peaks still coincide with the flexible deformation peaks. However a short delay time becomes visible. This trend continues with rising \(k_o\). At \(k_o=0.28\) and \(k_o=0.33\) (see Figs. 8 and 9), the deflections increase and further shift to later occurrences in the phase angle, while the lift and drag peaks further increase. The deflection of the flexible structure and the lift peaks still coincide, but the coincidence is less evident than for the transitional state, since the delay time becomes more important relative to shorter oscillation periods.
The lift and drag peaks do not coincide anymore, with the drag peaks occurring later than the drops in the lift forces. For the case of \(k_o=0.33\) (\(\sigma \approx 1\) with \(n=3\)), the deformation peaks of the flexible structure remain for a quarter of the period.
Analysis of the results from the force measurements showed an improvement of 20% on the blade thrust coefficient compared to the rigid hydrofoil. This improvement is explained by the significant reduction observed in the drag (of around 50%) along with relatively smaller reductions in the lift forces (30%).
3.1.3 Fully dynamic state (\(k_o=0.45- 0.71\), \(f_{\mathrm{o}}=3.64-5.68\) Hz)
In the fully dynamic state, the pitch motion dominates over the flow convection. For \(k_o=0.45\) (see Fig. 10), the stall point of the flow is phase-shifted from the ascending branch at 16\(^\circ\) to the descending branch at 5\(^\circ\). The peaks in the lift and drag usually associated with stall become invisible. The deflection peaks of the flexible structure remain only for a shorter (about 15%) share of the period. However, the drag remains at a high level of up to 60 N for the rigid hydrofoil.
For the highest reduced frequency investigated, \(k_o=0.71\) (see Fig. 11), the dynamics were characterized by strong vibrations in the forces (even after low-pass filtering), but without any visible impact on the structure. The trend from the previous case continued. The deformation leads to a delay in the height trajectory compared to the inclination angle. The zero crossing of the flexible hydrofoil occurs later in the period than for the rigid structure (zero crossing of \(\beta\) at a pitch angle \(\alpha =-12^\circ\)). This is not the case for lower reduced frequencies.
3.2 The \(\lambda =3\) case
The surface tracking measurements were taken once again for seven oscillation frequencies, corresponding to seven reduced frequencies:
\(k_o\) = [0.07, 0.13, 0.24, 0.34, 0.49, 0.62, 0.65]
\(f_{\mathrm{o}}\) = [0.70, 1.33, 2.46, 3.42, 4.84, 6.20, 6.45] Hz
The results are displayed in Figs. 12, 13 and 14. Generally the results show comparable characteristics to the \(\lambda =2\) case and will not be described in a systematic manner. However, the main difference is the decreased maximum pitch angle \(\alpha _{\text{max}}=20^\circ\). The curve shape of the pitch trajectory is smoother than the sawtooth-like shape of the \(\lambda =2\) case. In consequence, the maximum deformation of the hydrofoils is smaller as well. This is due to the smaller lift forces of \(F_{\mathrm{L}}=100\) N, which is, compared to the \(\lambda =2\) case, a reduction of 33% and comes along with the reduction of the angle of incidence of 33%.
The characteristics reported in the previous operating point occur already for lower \(k_o\) in the \(\lambda =3\) case. The rigid hydrofoil stalls only in the quasi-static/transitional cases at \(k_o<0.24\). The shape characteristics of \(k_o=0.07\) are comparable to those from \(k_o=0.16\) at \(\lambda =2\). Even there, the drag peaks remain very moderate compared to the previous case. For higher \(k_o\) values, no drag peak can be observed at all. The characteristics of deformations at \(k_o=0.71\) for \(\lambda =2\), are already found at \(k_o=0.24\) for \(\lambda =3\): this is especially true for the phase shift of the deformation. The curve shape is once more reminiscent of a sine function, and the structural relaxation from the deformation is delayed compared to the hydrodynamic forces. For \(\lambda =3\), a typical VAWT (with \(\sigma \approx 1\)) operates at \(k_o\approx 0.26\). This operation point is shown in Fig. 13 with \(k_o=0.24\). In general no significant influence of \(k_o\) on the deformation is observed. This is maybe due to the low angles of incidence and to an excessive hydrofoil stiffness for this condition.
3.3 The influence of \(k_o\) and \(\lambda\)
The results from all experiments are summed up in Fig. 15, which displays the influence of the reduced frequency on the deformation characteristics and the hydrodynamic loads for two different operation points.
In that figure, three parameters are plotted. The first is the deformation d, calculated as the maximum height difference between the rigid and the flexible surface at the trailing edge over a period. It is expressed as a percentage of the chord length:
The last 10 pixels (2.4 mm) on the borders were removed in the calculation because of the inaccuracy of the measurement method in these regions. The uncertainty bandwidth for d is based on the accumulated measurement error of \(\delta =0.66\) mm for all hydrofoils.
The two other parameters are the hydrodynamic loads (lift and drag) acting on the flexible foil. The absolute maximum of the forces averaged over the periods is shown. The generally higher peak loads on the rigid hydrofoil are not shown. The uncertainty on the hydrodynamic loads has a sensor uncertainty of \(\approx 2\%\), mainly originating from channel cross-talk, which is due to the sensor design (Hoerner et al. 2019).
A regression based on radial-basis functions has been applied to display trend curves on the data. The areas where the highest blade thrust improvements were observed, identified in previous work (Hoerner et al. 2019), are also highlighted in Fig. 15.
For \(\lambda =2\) (Fig. 15left), the deformation is strongly influenced by \(k_o\) and has a maximum at about \(k_o=0.3\). This coincides with the best-efficiency point of common VAWT. Lower values of \(k_o\) result in smaller lift force peaks and smaller deformations. For \(k_o>0.2\) the flow dynamics lead to increased lift force peaks of about 40% compared to the static cases. The lift forces remain constant beyond \(k_o>0.2\). The drag forces first increase along with the lift, but decrease again once the deformation peak at \(k_o=0.3\) has been reached. This reduction in the drag is small compared to the overall hydrodynamic loads, and its impact on the structural deformation can be considered to be small.
The deformation peaks decrease strongly beyond \(k_o>0.3\). In this case, the structural inertia damps the deformations—as the period length decreases, a delay time in the structural response becomes more important. This results in decreased deformation amplitudes.
Above \(k_o>0.4\), changes in measurement values are small (\(<2.5\%\)).
For \(\lambda =3\) (Fig. 15right), the deformation is not significantly influenced by the reduced frequency. The range of the measured values (2.5% deformation) is within the range of the accumulated uncertainty in the SFT measurement itself. It is probable that this independence is a consequence of the lower hydrodynamic loads: the profile is then too stiff to adapt to the flow under such conditions. Additionally, outside of the quasi-static flow state (\(k_o>0.05\)), the lower maximum angle of incidence does not lead to profile stall, since the (dynamic) stall angle is not reached anymore.
4 Conclusions
The structured-light-based SFT method developed by Takeda et al. (1982) was successfully adapted to the FSI case and implemented in the Python framework Fluidimage (Hoerner and Bonamy 2019). The surface height is acquired instantaneously with high temporal (4 kHz) and spatial (\(\sim 0.25\) mm) resolution. The average uncertainty within the method is 0.66 mm. The method requires only equipment commonly found in a fluid mechanics laboratory and provides a credible and affordable alternative to commonly used laser interferometer or stereoscopic digital image correlation techniques.
In the present setup, the hydrodynamic forces were captured together with the synchronized SFT measurements. This allows to link hydrodynamic forces with structural deformations. The investigations led to the following conclusions:
- 1.
The structural deformation of the flexible profile coincides with the hydrodynamic forces acting on the rigid hydrofoil. This effect is particularly clear at \(\lambda =2\) and low \(k_o\). The coupling becomes less significant with rising \(k_o\) and \(\lambda\).
- 2.
The maximum deformation of the flexible hydrofoils depends on the character of the forces acting on the surface, which is dominated by the reduced frequency \(k_o\) and tip/speed ratio \(\lambda\):
for low \(k_o\) and low \(\lambda\), the magnitude of the lift and drag forces governs the behavior; the magnitude of the deformation is proportional to those forces;
the magnitude of the deformation decreases with increasing \(k_o\) once the peak deformation has been reached. There, the inertial forces become dominant over the hydrodynamic forces;
- 3.
The temporal occurrence of the deformation peak within an oscillation period depends on the reduced frequency \(k_o\) as well:
when \(k_o\) is increased, the deformation peak occurrence is phase-shifted to a later point in the period;
inertial effects in both structure and flow lead to delay in the relaxation of the structure. They keep the structure bent for a significant part of the period after the zero crossing of the profile inclination. This happens for high \(k_o\) values for \(\lambda =2\) (Fig. 11) and also for fully dynamic cases at \(\lambda =3\) (Figs. 13 and 14).
- 4.
Regarding the blade thrust, the highest improvements had been found to occur in a range of \(k_o=0.28\)–0.35 (Hoerner et al. 2019). It is shown here that those reduced frequencies feature the highest deformation peaks. In a three-bladed turbine design, this range corresponds to a solidity of about \(\sigma =1\) (retrieved from Eq. 6). Such a turbine’s best efficiency point is found at \(\lambda =2\), as shown by Shiono et al. (2000). It is a common design point for three-bladed H-rotors studied in the literature: for example, the VAWT investigated by Maître et al. (2013) performs best at \(\lambda =2\) with \(k_o=0.35\). This turbine was chosen as a reference design for the experimental setup, and key features as Reynolds number were kept similar. The turbine blades are shaped as a NACA0018 hydrofoil, with a slightly cambered shape to take into account the flow curvature from the cycloidal motion.
The results suggest that the stiffness of the present flexible hydrofoil is too high for the smaller pitch angles occurring in the \(\lambda =3\) case, and that the blade design should be adapted to the operating point.
A design dependence on the operating point would be a drawback of the method, and further investigations with different blade flexibilities should investigate this aspect. However, the proposed method already provides interesting benefits: it is mechanically simple compared to fully controlled active blade pitch mechanisms and is less prone to failure. Most importantly, it is suitable for performance and lifetime improvements on low-\(\lambda\) turbines, which are of high interest from an ecological point of view.
Abbreviations
- w :
-
Relative velocity (\(\text{ms}^{-1}\))
- s :
-
Surface (\(\text{m}^2\))
- \(v_{\mathrm{ch}}\) :
-
Channel inlet velocity (m/s)
- \(v_{\infty}\) :
-
Flow velocity (m/s)
- \(l_{\lambda}\) :
-
Wave length (m)
- k :
-
Reduced frequency (–)
- h :
-
Height (m)
- n :
-
Number (–)
- l :
-
Length (m)
- f :
-
Frequency (Hz)
- \(c_{\mathrm{L}}\) :
-
Lift force coefficient (–)
- \(c_{\mathrm{D}}\) :
-
Drag force coefficient (–)
- \(c_{\mathrm{P}}\) :
-
Power coefficient (–)
- R :
-
Radius (m)
- C :
-
Profile chord length (m)
- T:
-
Oscillation period (–)
- D :
-
Distance between projector and zero plane (m)
- \(D_{\mathrm{PC}}\) :
-
Distance between projector and camera (m)
- F :
-
Force (N)
- \(F_{\mathrm{D}}\) :
-
Drag force (N)
- \(F_{\mathrm{L}}\) :
-
Lift force (N)
- \(\sigma\) :
-
Solidity (–)
- \(\omega\) :
-
Angular velocity (\(\text{s}^{-1}\))
- \(\rho\) :
-
Density (kg/\(\text{m}^3\))
- \(\lambda\) :
-
Tip/speed ratio (–)
- \(\alpha\) :
-
Angle of incidence (rad)
- \(\beta\) :
-
Deformation angle of incidence (\(^\circ\))
- \(\phi\) :
-
Phase angle (rad)
- \(\theta\) :
-
Azimuth angle (rad)
- FSI:
-
Fluid–structure interaction
- Re:
-
Reynolds number
- VAWT:
-
Vertical-axis water turbine
- HAWT:
-
Horizontal-axis water turbine
References
Abbaszadeh S, Hoerner S, Maître T, Leidhold R (2019) Experimental investigation of an optimised pitch control for a vertical-axis turbine. IET Renew Power Gener 13(6):3106–3112. https://doi.org/10.1049/iet-rpg.2019.0309
Amaral S, Perkins N, Giza D, McMahon B (2011) Evaluation of fish injury and mortality associated with hydrokinetic turbines (1024569). Technical report, Electrical Power Research Institute Palo Alto
Augier P, Bonamy C (2019) Fluidimage. https://foss.heptapod.net/fluiddyn/fluidimage. Accessed 29 May 2020
Benton S, Visbal M (2019) The onset of dynamic stall at a high, transitional Reynolds number. J Fluid Mech 861:860–885. https://doi.org/10.1017/jfm.2018.939
Bianchini A, Balduzzi F, Ferrara G, Persico G, Dossena V, Ferrari L (2018) A critical analysis on low-order simulation models for Darrieus VAWTs: how much do they pertain to the real flow? J Eng Gas Turbines Power. https://doi.org/10.1115/1.4040851
Brownstein I, Kinzel M, Dabiri J (2016) Performance enhancement of downstream vertical-axis wind turbines. J Renew Sustain Energy 8:053306. https://doi.org/10.1063/1.4964311
Buchner AJ, Honnery D, Soria J (2017) Stability and three-dimensional evolution of a transitional dynamic stall vortex. J Fluid Mech 823:166–197. https://doi.org/10.1017/jfm.2017.305
Buchner AJ, Soria J, Honnery D, Smits A (2018) Dynamic stall in vertical axis wind turbines: scaling and topological considerations. J Fluid Mech 841:746–766. https://doi.org/10.1017/jfm.2018.112
Chatellier L, Gorle J, Pons F, Malick B (2018) Towing tank testing of a controlled-circulation Darrieus turbine. In: Advances in renewable energies offshore, pp 195–201, ISBN 9781138585355. https://doi.org/10.1201/9780429505324
Dabiri J (2011) Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J Renew Sustain Energy doi. https://doi.org/10.1063/1.3608170
Daróczy L, Janiga G, Petrasch K, Webner M, Thévenin D (2015) Comparative analysis of turbulence models for the aerodynamic simulation of H-Darrieus rotors. Energy 90:680–690. https://doi.org/10.1016/j.energy.2015.07.102
Delafin PL (2014) Analyse de l’écoulement transitionnel sur un hydrofoil: application aux hydroliennes à axe transverse avec contrôle actif de l’angle de calage (French). Université de Bretagne occidentale - Brest, Thesis https://tel.archives-ouvertes.fr/tel-01147402
Deng Z, Carlson T, Ploskey G, Richmond M, Dauble D (2007) Evaluation of blade-strike models for estimating the biological performance of Kaplan turbines. Ecol Model 208(2):165–176. https://doi.org/10.1016/j.ecolmodel.2007.05.019
Ferreira CS, Bijl H, van Bussel G, van Kuik G (2007) Simulating dynamic stall in a 2D VAWT: modeling strategy, verification and validation with particle image velocimetry data. J Phys Conf Ser 75(1):012023. https://doi.org/10.1088/1742-6596/75/1/012023
Ferreira CS, van Kuik G, van Bussel G, Scarano F (2009) Visualization by PIV of dynamic stall on a vertical axis wind turbine. Exp Fluids 46(1):97–108. https://doi.org/10.1007/s00348-008-0543-z
Fish F (1993) Power output and propulsive efficiency of swimming bottlenose dolphins (Tursiops truncatus). J Exp Biol 183:179–193
Fujisawa N, Shibuya S (2001) Observations of dynamic stall on Darrieus wind turbine blades. J Wind Eng Ind Aerodyn 89:201–214. https://doi.org/10.1016/s0167-6105(00)00062-3
Gorle J, Bardwell S, Chatellier L, Pons F, Ba M, Pineau G (2014) PIV investigation of the flow across a Darrieus water turbine. In: 17th international symposium on applications of laser techniques to fluid mechanics—Lisbon
Greenblatt D, Ben-Harav A, Müller-Vahl H (2014) Dynamic stall control on a vertical-axis wind turbine using plasma actuators. AIAA J 52:456–462. https://doi.org/10.2514/1.J052776
Hansen K, Rostamzadeh N, Kelso R, Dally B (2016) Evolution of the streamwise vortices generated between leading edge tubercles. J Fluid Mech 788:730–766. https://doi.org/10.1017/jfm.2015.611
Hoerner S, Bonamy C (2019) Structured-light-based surface measuring for application in fluid–structure interaction. Exp Fluids 60(11):168. https://doi.org/10.1007/s00348-019-2821-3
Hoerner S, Abbaszadeh S, Maître T, Cleynen O, Thévenin D (2019) Characteristics of the fluid–structure interaction within Darrieus water turbines with highly flexible blades. J Fluids Struct 88C:13–30. https://doi.org/10.1016/j.jfluidstructs.2019.04.011
Laneville A, Vittecoq P (1986) Dynamic stall: the case of the vertical axis wind turbine. J Sol Energy Eng Trans ASME 108:140–145. https://doi.org/10.1115/1.3268081
Lazauskas L, Kirke B (2012) Modelling passive variable pitch cross flow hydrokinetic turbines to maximize performance and smooth operation. Renew Energy 45:41–50. https://doi.org/10.1016/j.renene.2012.02.005
Liang Y, Zhang L, Li E, Zhang F (2016) Blade pitch control of straight-bladed vertical axis wind turbine. J Cent South Univ 23(5):1106–1114. https://doi.org/10.1007/s11771-016-0360-0
Loth J, McCoy H (1983) Optimization of Darrieus turbines with an upwind and downwind momentum model. J Energy 7(4):313–318. https://doi.org/10.2514/3.62659
Ly K, Chasteau V (1981) Experiments on an oscillating aerofoil and applications to wind-energy converters. J Energy 5(2):116–121. https://doi.org/10.2514/3.62511
MacPhee D, Beyene A (2016) Fluid–structure interaction analysis of a morphing vertical axis wind turbine. J Fluids Struct 60:143–159. https://doi.org/10.1016/j.jfluidstructs.2015.10.010
Mauri M, Bayati I, Belloli M (2014) Design and realisation of a high-performance active pitch-controlled H-Darrieus VAWT for urban installations. In: 3rd renewable power generation conference. https://doi.org/10.1049/cp.2014.0930
Maître T, Amet E, Pellone C (2013) Modelling of the flow in a Darrieus water turbine: wall grid refinement analysis and comparison with experiments. Renew Energy 51:497–512. https://doi.org/10.1016/j.renene.2012.09.030
McCroskey W (1981) The phenomenon of dynamic stall. Technical report, NASA TM-81264
McCroskey W, Carr L, McAlister K (1976) Dynamic stall experiments on oscillating airfoils. AIAA J 14(1):57–63. https://doi.org/10.2514/3.61332
Miller M, Duvvuri S, Brownstein I, Lee M, Dabiri J, Hultmark M (2018) Vertical-axis wind turbine experiments at full dynamic similarity. J Fluid Mech 844:707–720. https://doi.org/10.1017/jfm.2018.197
Müller-Vahl H, Strangfeld C, Nayeri C, Paschereit C, Greenblatt D (2014) Control of thick airfoil, deep dynamic stall using steady blowing. AIAA J 53(2):277–295
Müller S, Cleynen O, Hoerner S, Lichtenberg N, Thévenin D (2018) Numerical analysis of the compromise between power output and fish-friendliness in a vortex power plant. J Ecohydraul 3(2):86–98. https://doi.org/10.1080/24705357.2018.1521709
Newman B (1986) Multiple actuator-disc theory for wind turbines. J Wind Eng Ind Aerodyn 24(3):215–225. https://doi.org/10.1016/0167-6105(86)90023-1
Pawsey N (2002) Development and evaluation of passive variable-pitch vertical axis wind turbines. Ph.D. thesis, School of Mechanical and Manufacturing Engineering, The University of New South Wales
Pérez-Torró R, Kim J (2017) A large-eddy simulation on a deep-stalled aerofoil with a wavy leading edge. J Fluid Mech 813:23–52. https://doi.org/10.1017/jfm.2016.841
Shiono M, Suzuki K, Kiho S (2000) An experimental study of the characteristics of a Darrieus turbine for tidal power generation. Electr Eng Jpn 132(3):38–47. https://doi.org/10.1002/1520-6416(200008)132:3<38::AID-EEJ6>3.0.CO;2-E
Stephenson J, Gingerich A, Brown R, Pflugrath B, Deng Z, Carlson T, Langeslay M, Ahmann M, Johnson R, Seaburg A (2010) Assessing barotrauma in neutrally and negatively buoyant juvenile salmonids exposed to simulated hydro-turbine passage using a mobile aquatic barotrauma laboratory. Fish Res 106(3):271–278. https://doi.org/10.1016/j.fishres.2010.08.006
Strom B, Brunton S, Polagye B (2016) Intracycle angular velocity control of cross-flow turbines. Nat Energy. https://doi.org/10.1038/nenergy.2017.103
Takeda M, Ina H, Kobayashi S (1982) Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J Opt Soc Am 72(1):156–160. https://doi.org/10.1364/JOSA.72.000156
Turnpenny A, Clough S, Hanson K, Ramsay R, McEwan D (2000) Risk assessment for fish passage through small, low-head turbines. Technical report, Atomic Energy Research Establishment, Energy Technology Support Unit, New and Renewable Energy Programme
Whittlesey R, Liska S, Dabiri J (2010) Fish schooling as a basis for vertical axis wind turbine farm design. Bioinspir Biomim. https://doi.org/10.1088/1748-3182/5/3/035005
Zanotti A, Nilifard R, Gibertini G, Guardone A, Quaranta G (2014) Assessment of 2D/3D numerical modeling for deep dynamic stall experiments. J Fluids Struct 51:97–115. https://doi.org/10.1016/j.jfluidstructs.2014.08.004
Zeiner-Gundersen D (2015) A novel flexible foil vertical axis turbine for river, ocean and tidal applications. Appl Energy 151:60–66. https://doi.org/10.1016/j.apenergy.2015.04.005
Zhang J, Kitazawa D, Taya S, Mizukami Y (2017) Impact assessment of marine current turbines on fish behavior using an experimental approach based on the similarity law. J Mar Sci Technol 22(2):219–230. https://doi.org/10.1007/s00773-016-0405-y
Acknowledgements
Open Access funding provided by Projekt DEAL. The corresponding author is grateful for the funding of his thesis by the Rosa-Luxemburg-Stiftung Berlin, the Wachstumskern Flussstrom Plus Project (03WKC02B), financed by the German Federal Ministry of Education and Research and the funding of German-French-University Saarbrücken. The authors thank Roumaissa Hassaini (LEGI) for her support during the method development. The support of Shokoofeh Abbasazdeh, Roberto Leidhold (OvGU), Michael Haarman (CATLAB, Berlin), Michel Riondet and Jean-Marc Barnoud (LEGI) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hoerner, S., Bonamy, C., Cleynen, O. et al. Darrieus vertical-axis water turbines: deformation and force measurements on bioinspired highly flexible blade profiles. Exp Fluids 61, 141 (2020). https://doi.org/10.1007/s00348-020-02970-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-020-02970-2