Abstract
This study presents an approach for obtaining full-field dynamic surface-pressure reconstructions with low differential amplitudes. The method is demonstrated in a setup where an air jet is impinging on a flat plate. Deformations of the flat plate under dynamic loading of the impinging jet were obtained using a deflectometry setup that allows measurement of surface slopes with high accuracy and sensitivity. The measured slope information was then used as input for the virtual fields method to reconstruct pressure. Pressure fluctuations with amplitudes of down to \({\mathcal {O}}(1)~\text {Pa}\) were extracted from time-resolved deflectometry data using temporal band-pass filters. Pressure transducer measurements allowed comparisons of the results with an established measurement technique. Even though the identified uncertainties in fluctuations were found to be as large as 50%, the spatial distributions of dynamic pressure events were captured well. Dynamic mode decomposition was used to identify relevant spatial information that correspond to specific frequencies. These dynamically important spatio-temporal events could be observed despite their low differential amplitudes. Finally, the limitations of the proposed pressure determination method and strategies for future improvements are discussed.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The measurement of dynamic surface pressure distributions is crucial for a range of applications in fluid dynamics, material design and testing, as well as for the investigation of impinging jets for heat and mass transfer. Time-resolved measurements that provide a large number of data points for low-range differential pressures are challenging for current techniques, which are discussed in the following. Microphones have high sensitivities for differential pressure amplitudes of \((1)~\text {Pa}\) and well below, depending on the type of microphone and experimental noise sources, but they allow only point-wise measurements. However, fitting these microphones requires drill-holes in the investigated specimen, which change the material response. Further, the achievable spatial resolution is generally limited by the size of the sensors, see, e.g., Corcos (1963, 1964). Small-amplitude vortices may thus still be detected, but with low spatial accuracy. The spatial resolution may be increased using pinhole-mounting, e.g., (Robin et al. 2012; Van Blitterswyk and Rocha 2017). This requires a large amount of sensors when measuring pressure over even a moderately large area. Larger differential pressure amplitudes of \({\mathcal {O}}(100)~\text {Pa}\) and above can be measured optically in full-field using pressure-sensitive paints (PSP), e.g., in transonic and supersonic scenarios (Engler et al. 2000; Liu et al. 2008). As PSP is a technique for the measurement of absolute pressure, it is generally difficult to resolve small differential amplitudes (Beverley and McKeon 2007, chapter 4.4). Using phase averaging to address the restricting factor of camera noise, as well as a porous paint formulation, acoustic pressure amplitudes of down to \(500~\text {Pa}\) were measured in Gregory et al. (2006). Using phase averaging in combination with proper orthogonal decomposition to measure the interaction between a rotor wake and a cylinder, PSP measurements of fluctuations within 100 Pa were achieved with good agreement to microphone measurements in Jiao et al. (2019). Particle image velocimetry (PIV) and particle tracking velocimetry (PTV) are well-established techniques that allow full-field pressure reconstructions from flow field measurements. These methods generally perform best when dense Lagrangian velocity and acceleration information can be achieved close to the investigated surface. In Jeon et al. (2016), tomographic time-resolved PIV was used to measure the pressure field around an inclined airfoil. 2D and 3D reconstructions for 2 and 3 components were conducted and found to yield similar results. The reconstructed differential pressures of \({\mathcal {O}}(100)~\text {Pa}\) agreed reasonably well with pressure tap measurements and further allowed identifying vortex shedding frequencies. Time-resolved measurements with high speed cameras are typically restricted by the limited amount of pixels on the imaging device. Since a certain number of pixels is required for each interrogation window, this limits the achievable accuracy in pressure and the size of the field of view. In Schneiders et al. (2016a) helium-filled soap bubbles were tested as tracer particles for tomo-PIV to increase the size of the field of view for practical engineering applications. The authors reconstruct the pressure field with differential amplitudes of \({\mathcal {O}}(1)~\text {Pa}\) around a cylinder and find good agreement with transducer measurements on the cylinder surface. They achieved a measurement volume of \(20 \times 17 \times 18 ~\text {cm}^3\). In Gesemann et al. (2016) B-Spline based methods are used to improve the accuracy and resolution of velocity, acceleration and pressure fields in the presence of noise. Synthetic data are used to quantify the achieved improvements in reconstruction performance for each method. Tomographic PTV was used in Schneiders et al. (2016b) for pressure volume reconstructions with four high-speed cameras for a wind tunnel flow around a cylinder. The accuracy was estimated by comparing the reconstructed pressure values along the surface of the cylinder to microphone measurements. Discrepancies between microphone and tomo-PTV results of only 0.5 Pa were found. In Huhn et al. (2018) 3D pressure fields were reconstructed within the flow field of an impinging jet using dense Lagrangian particle tracking (LPT) by Shake-The-Box (STB) processing with six high-speed cameras. Pressure reconstructions obtained along the impingement wall were compared with microphone measurements and yielded an uncertainty of \(0.3~\text {Pa}\). Tomo-PIV and LPT with STB processing were compared on simulated measurements of a flow around a step change in a wind tunnel in van Gent et al. (2017). The authors also investigate different available pressure reconstruction techniques. Accuracies of \({\mathcal {O}}(1)~\text {Pa}\) were achieved for all of the investigated methods. Using time-resolved Lagrangian particle tracking with the Vortex-in-Cell+ technique, an accuracy of approximately \(0.5~\text {Pa}\) was achieved. Generally, PIV and PTV approaches require optical access to the flow field, as well as suitable seeding particles and a sufficiently transparent fluid. Near the surface, the techniques are often restricted by shadowing effects, reflections and the finite size of the reconstruction window. The computational effort for processing the acquired images is relatively high due to the large amount of data points from potentially multiple cameras. If only the surface pressure distribution is of interest, this leads to a significant overhead and to a large amount of potentially unnecessary flow field data.
Alternatively, surface deformation measurements can be used to calculate the pressure acting on a specimen by solving the mechanical equilibrium equations. For thin plates in pure bending, which will be discussed in the following, the local equilibrium equation can be obtained using the Love–Kirchhoff theory, which involves fourth-order derivatives of the surface deflections, (Timoshenko and Woinowsky-Krieger 1959). Such high-order derivatives lead to significant noise amplification and therefore require regularization. In Pezerat and Guyader (2000) numerical simulations were used to obtain local deflections of a thin-plate specimen under a given load. Noise was added numerically. Wave number filters were then applied prior to solving the equilibrium equation locally, which allowed an identification of the external vibration sources. In the same study, the technique is also applied to an experiment where an aluminium plate of \(0.5~\text {mm}\) thickness is excited with a shaker with pseudo-random noise. The reconstructed force amplitude of \(0.15~\text {N}\) was reasonably close to the directly measured force of \(0.17~\text {N}\). The acoustic component of a turbulent boundary layer flow at an air flow speed of \(25~\text {ms}^{-1}\) with a parallelepiped as turbulence source was identified on an aluminium plate with \(0.6~\text {mm}\) thickness with a similar approach in Lecoq et al. (2014). The amplitudes identified using the equilibrium equation were, however, found to underestimate the pressure levels when compared to microphone measurements.
The virtual fields method (VFM) is an alternative identification method. It is based on the principle of virtual work. For the purpose of pressure identification, the VFM requires full-field kinematic data, the mechanical constitutive material parameters of the specimen, and suitable virtual fields. The latter need to be selected with respect to the theoretical and practical requirements of the investigated problem, such as boundary conditions and continuity. The virtual fields can also be selected to provide different levels of regularization adapted to a given signal-to-noise ratio. In the case of thin plates in pure bending, the principle of virtual work yields an equation that only involves second-order deflection derivatives. The VFM is described in detail with a range of applications in Pierron and Grédiac (2012). It was used in combination with scanning Laser Doppler Vibrometer (LDV) measurements for investigating acoustic loads on thin plates. This allowed reconstructing spatially averaged sound pressure levels in Robin and Berry (2018) and transverse loads and vibrations in Berry et al. (2014), as well as random external wall pressure excitations in Berry and Robin (2016). In an investigation of the sound transmission of thin plates, comparisons of spatially averaged pressure auto-spectra with microphone array measurements showed good agreement except at structural resonance frequencies in Robin and Berry (2018). A limitation of these studies was that full-field data could not be obtained simultaneously with LDV measurements. This can be addressed using alternative measurement techniques. Deflectometry is an optical full-field technique for the measurement of surface slopes, (Surrel et al. 1999), which can be combined with high-speed cameras to investigate dynamic events. It can achieve very high slope sensitivities, in the present study \({\mathcal {O}}(1)~\text {mm km}^{-1}\). In Devivier et al. (2016), deflections of ultrasonic Lamb waves were imaged using deflectometry on thin vibrating mirror glass and carbon/epoxy plates. Since deflectometry measurements yield surface slopes, the required order of derivatives of experimental data in the VFM is reduced to one. In Giraudeau et al. (2010) this was used to identify the Young’s modulus, Poisson’s ratio and the associated damping parameter on vibrating, thin, polycarbonate plates. A combination of deflectometry and the VFM was also employed in O’Donoughue et al. (2017) to reconstruct dynamics of mechanical point loads of several \({\mathcal {O}}(1)~\text {N}\) on an aluminium plate with \(3~\text {mm}\) thickness. Spatially averaged random excitations were identified with this method in O’Donoughue et al. (2019). In Kaufmann et al. (2019) it was used to measure mean pressure distributions of an impinging air jet with differential pressure amplitudes of several \({\mathcal {O}}(100)~\text {Pa}\) on thin glass plates of \(1~\text {mm}\) thickness. The study also proposes a methodology to assess the accuracy of pressure reconstructions and to select optimal reconstruction parameters. However, in several aerodynamic and hydrodynamic applications, it is important to obtain surface-pressure fluctuations (both broadband as well as at certain frequencies). In the present study, the work of Kaufmann et al. (2019) is extended to measure the spatio-temporal evolution of low differential pressure events which are generated by the flow on a surface. The method is demonstrated in a canonical flow problem: a jet impinging on a flat surface. This work is specifically concerned with reconstructing and extracting the pressure footprint of large-scale vortices impinging on the plate. These pressure fluctuations will have very low differential pressure compared to the mean flow, typically of \({\mathcal {O}}(10)~\text {Pa}\) for broad band events and well below for single-frequency events. This specific flow problem is chosen to highlight the pros and cons of the proposed surface pressure determination technique.
2 Theory
2.1 Deflectometry
Deflectometry is an optical technique that allows full-field slope measurements on specular reflective surfaces using a periodic spatial signal (Surrel et al. 1999). A schematic of the setup is shown in Fig. 1. \(p_{\text {G}}\) is the pitch of the spatial signal, here a cross-hatched grid, and \(h_{\text {G}}\) the distance between grid and specimen surface. The camera is placed next to the grid, such that a pixel directed at point M on the specimen surface records the reflected grid at point P. Applying a load deforms the surface locally, resulting in a change in surface slope, d\(\alpha\), such that the same pixel will now record the reflected point \(P^{\prime }\). Rigid body movements and out-of-plane deflections are neglected here, as the specimen bending stiffness is sufficiently large and the investigated loads small.
Phase maps are extracted from grid images using a spatial phase-stepping algorithm featuring a windowed discrete Fourier transform algorithm with triangular weighting and using a detection kernel size of two periods (Surrel 2000; Badulescu et al. 2009). This algorithm suppresses some harmonics resulting from the use of a non-sinusoidal signal and mitigates the effects of miscalibration. The displacement, u, between P and \(P^{\prime }\) is calculated iteratively from the obtained phase maps, \(\phi\), (Grédiac et al. 2016, section 4.2):
where the subscripts def and ref refer to a deformed and a reference configuration, respectively, as the phase difference between a loaded and unloaded configuration is of interest.
For sufficiently small d\(\alpha\), \(h_{\text {G}} \gg {u}\), small angle \(\theta\) and assuming that the camera records images in normal incidence, geometric considerations yield a simplified, linear relationship between the change in surface slope d\(\alpha\) and u (e.g., Ritter 1982):
where \(u_{x}\) and \(u_{y}\) are the components of u in x- and y-direction, respectively. If this hypothesis is not valid, then full calibration needs to be performed, which is more complex, see Balzer and Werling (2010) and Surrel and Pierron (2019). The printed grid pitch \(p_{\text {G}}\) drives the spatial resolution. The slope resolution depends on measurement noise as well as \(p_{\text {G}}\) and \(h_{\text {G}}\).

[redrawn from (Kaufmann et al. 2019)]
Top view of deflectometry setup and working principle
2.2 Pressure reconstruction
Assuming that the plate material is linear elastic, isotropic and homogeneous, the principle of virtual work is expressed by (e.g., Pierron and Grédiac 2012, chapter 3):
where S denotes the surface area, p the investigated pressure, \(D_{xx}\) and \(D_{xy}\) the plate bending stiffness matrix components, \(\kappa\) the curvatures, \(\rho\) the plate material density, \(t_S\) the plate thickness, a the acceleration, \(w^{*}\) the virtual deflections and \(\kappa ^{*}\) the virtual curvatures. In the present study \(D_{xx}\), \(D_{xy}\), \(\rho\) and \(t_S\) were known from the plate manufacturer. \(\kappa\) and a were obtained from deflectometry measurements. The virtual fields \(w^{*}\) and \(\kappa ^{*}\) have to be chosen with respect to theoretical as well as practical restrictions of the problem such as continuity and boundary conditions. They can further be optimized to minimize the effects of noise (Pierron and Grédiac 2012, chapter 3.7). Assuming constant pressure within a piecewise virtual field and approximating the integrals in Eq. (3) with discrete sums, one obtains a simplified expression for the pressure:
where N is the total number of discrete surface elements.
2.3 Virtual fields
In this study, 4-node Hermite 16 element shape functions were used to define virtual fields over subdomains of the plate surface S. The formulation of these fields can be found in Pierron and Grédiac (2012, chapter 14). They provide \(\hbox {C}^{1}\) continuous virtual deflections, which yield the required continuous virtual slopes. They also allow defining virtual displacements and slopes that are zero over the edges of each element, which eliminates the unknown contributions of virtual work along the plate boundaries. The definition of virtual fields over subdomains, also called piecewise virtual fields, provides more flexibility than globally defined virtual fields, in particular when unknown and complex load distributions are investigated. In the following, the subdomain over which a virtual field was defined is referred to as pressure reconstruction window (PRW). Nine nodes were defined for one PRW. All degrees of freedom were set to zero except for the virtual deflection of the center node, which was set to 1. One pressure value was calculated for each window. Example fields are shown in Fig. 2. The size of the PRW has to be chosen according to the signal-to-noise ratio as well as the spatial distribution of the signal. Larger windows filter noise more efficiently as they effectively average over a larger area, but they can lead to a loss of signal amplitude and limit the spatial resolution.
Example Hermite 16 virtual fields with superimposed virtual elements and nodes (black). \(\xi _1\), \(\xi _2\) are parametric coordinates. The example window size is 24 points in each direction. Full equations can be found in Pierron and Grédiac (2012, chapter 14)
3 Experimental methods
3.1 Setup
The experiment consisted of a deflectometry setup with a reflective specimen and an impinging air jet (see Fig. 3). The cross-hatched grid used for deflectometry was printed on transparency with \(600~\text {dpi}\) using a Konica Minolta bizhub C652 printer. A custom made panel with \(9\times 100~\text {W}\) LEDs was used as white light source. The camera was placed at an angle beside the printed grid to record the reflected grid in normal incidence. Table 1 lists the relevant experimental parameters. 5400 images were recorded per deflectometry measurement series due to limited camera storage, which corresponds to \(1.35~\text {s}\). A \(1~\text {mm}\) thick first-surface glass mirror served as specimen. Since the camera is not focused on the plate surface, but on the reflected grid, small deformations and imperfections quickly lead to a lack of depth of field. This was addressed by closing the aperture. The achieved slope resolution, which is defined as the standard deviation of a slope map calculated with two grid images in an unloaded configuration here, was approximately \(3~\text {mm km}^{-1}\).
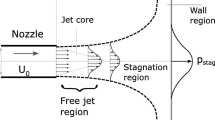
A fan-driven, round air was used to generate the investigated flow impinging on the flate plate specimen. This flow was chosen as a canonical flow problem to demonstrate the measurement technique and highlight its pros and cons. Figure 4 shows a schematic of such an impinging jet, which can be divided into a free jet, stagnation and wall region, see, e.g., Kalifa et al. (2016) and Zuckerman and Lior (2006). Its properties are governed by the ratio between downstream distance and nozzle diameter, \(h_{\text {N}}\)/D, nozzle geometry and Reynolds number, Re. The free jet develops if \(h_{\text {N}}\)/D \(~\gtrsim ~ \,\)2 (Zuckerman and Lior 2006). Downstream from the nozzle exit, a shear layer forms around the jet core, leading to entrainment and causing the mean velocity profile to spread. So-called primary vortices form in the shear layer around the jet core, propagate downstream, impinge on the specimen and are then deflected to propagate radially outward along the wall (Zuckerman and Lior 2006). Their strength scales with the Reynolds number. A stagnation region forms as the jet approaches the impingement plate. Here, the static pressure rises up to the stagnation point and the resulting pressure gradients divert the flow radially away from the jet center line. This laterally diverted flow forms the wall region. In this region, merging of primary vortices occurs (Pieris et al. 2019). Further, counter-rotating secondary vortices form along the impingement surface as a result of impinging primary vortices (Walker et al. 1987). These can deflect the primary vortices away from the wall. Tertiary structures resulting from interactions between primary and secondary ones are also sometimes observed. The shedding frequencies of the secondary vortices have a higher variability than those of primary vortices (Pieris et al. 2019). The mean pressure distribution on the impingement surface is approximately Gaussian (Beltaos 1976). The spectrum of frequencies at which primary vortices are shed typically has a maximum that depends on the nozzle exit velocity and the nozzle diameter, characterized by the Strouhal number (Becker and Massaro 1968):
For the given setup parameters, it follows that the shedding frequency spectrum has an expected maximum at about \(f_{{\text {shed}}} = 800~\text {Hz}\). Thus, the 5400 images captured for one measurement series at 4000 frames per second correspond to \(1080~f^{-1}_{{\text {shed}}}\). The jet parameters, also given in Table 1, were chosen to generate dynamic events, particularly primary vortices, that could likely be resolved with the available deflectometry grid pitch and camera frame rate at full spatial resolution.

[redrawn from (Kaufmann et al. 2019)]
Experimental setup

[redrawn from (Kaufmann et al. 2019)]
Impinging jet setup and flow features
3.2 Validation
Reference pressure measurements were conducted using Endevco 8507C-2 type pressure microphones with piezoresistive transducer elements. These microphones have a diameter of \(2.5~\text {mm}\). According to the manufacturer, they have an amplitude linearity of \(\pm 1~\text {dB}\) in a range between 100 and 173 dB and a frequency response of \(\pm 5~\text {dB}\) to more than \(20~\text {kHz}\). Here, the experimentally observed noise level had a standard deviation of up to \(1.5~\text {Pa}\). The microphones were placed along a line beginning from the stagnation point radially outwards with a spacing of \(5~\text {mm}\). An NI PXIe-4330 module was used for data acquisition. Data were acquired over \(20~\text {s}\) at \(20~\text {kHz}\). The microphones were placed along an aluminium plate of \(1~\text {cm}\) thickness at the same distance from the jet as the glass specimen used in deflectometry measurements. The setup of the jet relative to the plate was the main error source in microphone measurements, since no high precision equipment like e.g., micro stages were available. Eight separate measurements were conducted to account for this repeatability error.
Accelerations were measured using a Polytec PDV 100 Laser Doppler Vibrometer (LDV). The acquisition frequency was \(4~\text {kHz}\) and the acquisition time \(20~\text {s}\).
3.3 Data processing
One phase map was calculated from each grid image. A windowed discrete Fourier transform phase detection algorithm using a rectangular window of two grid pitches length was employed for phase detection (Surrel 2000). One data point per full grid pitch was calculated in x- and y-direction, respectively. Curvatures were calculated from slope maps with three-point centered finite differences. Deflections were obtained from the slope maps using an inverse (integrated) gradient based on a sparse approximation (D’Errico 2009). The second time derivative of these deflections yields accelerations. Central differences were used here. However, this requires knowledge of the integration constant, i.e., of the deflection at one reference point at each time step. These were not measured in the present setup. Instead, plate deformations were assumed to be quasi-static, which allows neglecting the acceleration term in Eq. (3). While this assumption is unlikely to be entirely accurate, it is reasonable to assume that for thin plates in bending sufficient relevant information about the spatial shape of the pressure distribution is contained in the curvature information. Separate LDV acceleration measurements were used to obtain an estimate for the resulting error. VFM pressure reconstructions were conducted as described in Sect. 2.2. The pressure reconstructions were oversampled in space by shifting the PRW by one data point in either direction until the entire surface was covered. Figure 5 shows a flow chart of the main processing steps. For the calculation of standard deviations, data from 20 runs were used to improve convergence.
The mean pressure distributions obtained from time-resolved measurements in the present study are compared to the mean distributions obtained from uncorrelated snapshots in Kaufmann et al. (2019). Figure 6 shows the azimuthally averaged mean pressure distribution for both methods and pressure transducer data for comparison. Even though the presented time-resolved measurements suffer from a lower signal-to-noise ratio due to the much higher shutter speed employed here, the results agree well. The mean surface pressure distributions was captured well using the VFM in both the snapshot data and the time-resolved data, but the amplitude is underestimated by approximately 30%. It was shown that this discrepancy between VFM and transducer data is largely due to the systematic processing error of the VFM. Further, it could be reduced to approximately 10% using a finite element correction procedure in Kaufmann et al. (2019). For amplitudes of this magnitude, this is comparable to other optical based pressure determination techniques like PSP, see, e.g., Beverley and McKeon (2007) and Jiao et al. (2019). Further details of the mean surface pressure comparison can be found in Kaufmann et al. (2019), where the influence of the processing parameters as well as of noise is investigated in experimental and numerical data. The study also investigates the systematic error using finite element simulations and artificial grid deformation. Given the agreement in the mean distributions, the time-resolved data can now be further examined to obtain surface-pressure fluctuations. These dynamic events were investigated here with two different filtering approaches.
First, a temporal bandpass filter was implemented by calculating the Fourier transform of the slope maps and setting the amplitudes of filtered frequencies to zero. This filter has a poor impulse response, i.e., a poor response to finite length input signals, but yields the best achievable frequency resolution, which allows an application down to very narrow frequency bands. Second, dynamic mode decomposition (DMD) (Schmidt 2010) was applied to instantaneous pressure reconstructions. The technique dedicated to using DMD on large and streaming data sets introduced in Hemati et al. (2014) was employed here.
Comparison between transducer measurements and VFM pressure reconstructions for different processing parameters. r denotes the radial distance from the stagnation point. Snapshot and transducer data from Kaufmann et al. (2019)
3.4 Processing parameters
A methodology for selecting optimal processing parameters based on simulated experiments and artificial grid deformation was proposed in Kaufmann et al. (2019, section 5). It requires an estimate of the expected load distribution to obtain model slope maps. These allow calculating the deformations of a corresponding, artificial reflected grid image, which is used as input to the processing algorithm. By systematically varying the PRW size, its influence on pressure reconstruction can be evaluated to identify its optimal value.
This simulation also allows an estimation of the systematic processing error for the chosen reconstruction parameters by comparing the input and reconstructed pressure distributions. Since this study aims at identifying dynamic events which are governed by the primary vortices impinging on the specimen, a circular load distribution with a peak amplitude of \(10~\text {Pa}\) was chosen as model input, see Fig. 7a. Here, \(\hbox {r}_x\) and \(\hbox {r}_y\) denote the radial distance from the stagnation point in x- and y-direction, respectively. D is the nozzle diameter. The results of this analysis are shown in Fig. 7b. The error estimate, \(\epsilon\), is defined as the difference between reconstructed and input pressure amplitude, \(p_{{\text {rec}}, i}\) and \(p_{{\text {in}}, i}\), divided by the local amplitude of the input pressure distribution at each point i:
where N is the number of points. With an estimated average error of ca. 20%, \(\text {PRW} = 24\) was identified as optimal size and will therefore be employed in the following. Note that a PRW side length of 24 data points corresponds to a physical distance of 0.6 D, or \(12~\text {mm}\). Despite the PRW size of 0.6 D, it will be shown later that the smaller spatial structures of the impinging vortices are well captured. The outcomes can be further improved by optimizing the setup.
4 Experimental results
4.1 Fluctuations
Instantaneous pressure maps were reconstructed from each measured slope map. The corresponding standard deviations, \(s_p\), obtained from these maps allowed a first evaluation of the captured pressure fluctuations. Figure 8a shows that the spatial distribution obtained for \(s_p\) appears to resemble noise patterns. These data were compared to microphone measurements. VFM standard deviation results were averaged over all data points with the same radial distance from the stagnation point at \(rD^{-1} = 0\). Figure 8b shows that the VFM results significantly overestimate the standard deviations when compared to microphone data.
To investigate the reason for the poor agreement of these results, the power spectral densities (PSDs) of slope maps obtained from deflectometry measurements were compared with those of pressure amplitudes from microphone measurements. The amplitude spectrum obtained from microphone data are shown in Fig. 9a. Slope data (Fig. 9b) was averaged over 21 data points which corresponds to an area of \(5.3~\text {mm}^2\), approximately matching the \(4.9~\text {mm}^2\) surface area of the microphone. The comparison shows that the slope measurements capture relevant information on the dynamics of the impinging jet in the observed slope amplitude spectrum between ca. \(0.25~f_{{\text {shed}}} - 1.88~f_{{\text {shed}}}\). Both figures show a maximum of the respective amplitude spectra close to the expected frequency \(f_{{\text {shed}}}\). However, the pressure amplitude spectrum obtained from VFM pressure reconstructions (Fig. 9c) shows mostly random noise for all frequencies above ca. \(0.6~f_{{\text {shed}}}\) (\(50~\text {Hz}\)). This suggests that low frequencies contain sufficient noise sources to overwhelm the signal when the slopes are converted to pressure using the VFM. This is likely because the VFM requires processing the slopes to accelerations (obtained from slopes by spatial integration and subsequent double temporal differentiation) and curvatures (computed from slopes by spatial differentiation). Obtaining these quantities appears to amplify noise to the extent that the low differential pressures are masked. However, the VFM is a linear method and therefore the methodology can be applied either to the entire range of frequencies or to specific frequency bands. If the method were applied to specific bands, then it might be possible to obtain the sought low differential pressure events since the lower frequency noise sources could be effectively filtered out. It is therefore necessary to employ further processing steps to extract dynamic pressure information from the slope measurements.
4.2 Temporal filter
A temporal band-pass filter was applied to the slope maps (see Sect. 3.3) to extract information on dynamic flow events in the identified relevant frequency range between \(0.25~f_{{\text {shed}}} - 1.88~f_{{\text {shed}}}\) (200–1500 Hz). Figure 10 shows instantaneous VFM pressure reconstructions from the band pass filtered slope map at two different points in time. The observed pressure distributions agree qualitatively with the expected distributions from primary vortices impinging on the flat surface, as they form around the upstream jet, i.e., with a radius of approximately 0.5 D and spread radially outward along the impingement plate. Figure 11 shows the corresponding PSD. The PSD of pressure reconstructions from a series of noise images which were processed in the exact same way is shown in the same figure for comparison. While the signal-to-noise ratio is relatively low, the signal is still clearly above noise level. The PSD further shows low amplitude noise in the band widths that were previously set to zero in the slope spectra, which is a result of the VFM processing steps.
The standard deviations of the VFM pressure reconstructions from the broad band pass filter (see Fig. 12a) are compared with microphone data, which are filtered within the same frequency band as the slope maps (see Fig. 12b). The VFM reconstructions still overestimate the standard deviations when compared to the microphone measurements by up to 50%. The shape of the distribution seems to be captured however. The distribution found in Fig. 12a agrees reasonably well with the expectations, as the fluctuations increase for radii above 0.5 D around the stagnation point. This is where primary vortices are expected to impinge on the plate to propagate radially outwards, with secondary vortices forming in the wall flow.
The results show that information on surface-pressure fluctuations was captured by the deflectometry measurements and that it is possible to reconstruct the corresponding pressure distributions qualitatively. The corresponding amplitudes of the standard deviations are however overestimated, likely due to the assumption of quasi static bending and systematic processing error and low signal-to-noise ratio. To further investigate the pressure fluctuations, methods to address the low signal-to-noise ratio and to extract additional dynamic information from the data are employed in the following section.
4.3 Dynamic mode decomposition
Dynamic mode decomposition (DMD) is a suitable tool for extracting relevant dynamic information from a data sequence. It allows identifying spatially coherent features and their temporal behaviour within the entire observed frequency spectrum. The main challenge in applying this technique to the present case is that the computational cost and required resources increase with the amount of data points in space as well as with the number of snapshots. The approach introduced in Hemati et al. (2014) allows processing all instantaneous pressure maps by incrementally updating the calculated POD basis as well as the DMD modes and coefficients. It is therefore employed here.
DMD was applied to VFM pressure reconstructions from slopes which were filtered within a band pass range from \(0.25~f_{{\text {shed}}} - 1.88~f_{{\text {shed}}}\) (200–1500 Hz). This eliminated modes stemming from the mean surface pressure and from low frequency experimental noise sources. The calculated POD basis was truncated at 200 modes, since higher modes primarily stem from random noise. Figure 13a, b show the amplitude and damping coefficients. The modes identified for frequencies below \(0.25~f_{{\text {shed}}}\) (200 Hz) stem from noise introduced by data processing, since this frequency range was filtered out from the slope information. These modes resemble noise patterns, have low amplitude and high damping coefficients. The most relevant modes corresponding to the impinging primary vortices were identified to be around \(0.97~f_{{\text {shed}}}\), which is reasonably close to the maximum that was expected from theoretical considerations in the frequency spectrum (see Sect. 3.1). They have the highest amplitude and the lowest damping coefficients of all identified modes. Examples of pressure reconstructions from two modes are shown in Fig. 13c, d. The modal shapes are coherent with only small amounts of noise and resemble the expected spatial distributions. A video of the \(0.97~f_{{\text {shed}}}\) (776 Hz) mode with damping coefficient set to zero can be found in the supplementary material of this paper.
This clearly shows that the low differential pressure events generated by impinging vortices were captured by the new surface pressure determination method. It should be noted that the differential pressure amplitudes extracted here are below \({\mathcal {O}}(1)~\text {Pa}\). Despite the uncertainty in amplitude identified above, it would be impossible to capture these events in full-field with any extant measurement technique. More importantly, the method allows to identify the spatio-temporal evolution of the pressure footprint of flow structures on a surface, which is otherwise currently only possible with Tomographic PIV or PTV, which would require optical access to the flow side of the experiment and the entire area over the impingement surface for several cameras. It should however be noted that these results could only be extracted using the filter techniques detailed above, which require time redundancy and are only applicable to flows with events occurring at discrete frequencies. Combining deflectometry and VFM with flow measurements will allow investigations of the flow-structure interactions in more detail in the future. To improve this methodology for further applications requires considerations of the error sources and future ways in which these can be minimized. This is discussed in the next section.
5 Error sources
This section discusses the systematic error sources encountered in the experimental setup as well as in the processing technique. In terms of experimental error sources, several elements of the deflectometry setup should be considered. Irregularities in the recorded grid as well as miscalibration, i.e., non-integer numbers of pixels per grid pitch, can lead to errors in the detected phases. The main factors causing these irregularities are damages on the specimen surface and defects of the printed grid. Miscalibration can be caused by misalignments between camera sensor and printed grid, as well as by irregularities and harmonics in the printed grid. Misalignment can also result in fringes. These error sources and their effect are highly dependent on the precise alignment between grid, specimen surface and camera. They can further be time dependent, because the specimen deforms under the dynamic load. Using the LDV to measure vibrations of the camera, it was also found that the camera cooling fans caused vibrations at several frequencies below 100 Hz, which were also identified in the measured slope spectrum. Based on comparisons with numerical data presented in Kaufmann et al. (2019), the effect of these experimental errors could amount to up to 10% of the peak pressure value for the mean surface pressure.
An additional issue concerning experimental bias is that the mechanical constitutive material parameters provided by the plate manufacturer, in particular the Young’s modulus, may not be accurate. In Kaufmann et al. (2019) it was estimated that the resulting error on pressure amplitudes was up to 10%.
The systematic error resulting from the processing approach employed in this study was investigated in Kaufmann et al. (2019). VFM pressure reconstructions were found to underestimate the local amplitudes because the virtual fields act as a low pass spatial filter over the area of a reconstruction window. The exact error value depends on the chosen reconstruction parameters as well as the investigated load distribution and signal-to-noise-ratio. In the present study, the error associated with data processing can be estimated using the analysis presented in Sect. 3.4. It is approximately 20% for instantaneous pressure maps when using a PRW size of 24 data points side length. Note that this estimate does not take into account the influence of random noise or the filtering techniques.
The error resulting from assuming quasi-static behaviour was assessed using LDV measurements to obtain accelerations at discrete points along the specimen surface. Values of up to \(1.4~\text {ms}^{-2}\) were found for the standard deviation of the accelerations. A worst case estimate for the resulting error in pressure was obtained by assuming an acceleration value of \(a=1.4~\text {ms}^{-2}\) over the entire specimen. The resulting dynamic pressure value was calculated using the acceleration term in Eq. (4). For pressure reconstructions from unfiltered slopes, it yields a value of \(p_{{\text {dyn}}} = 84~\text {Pa}\), which corresponds to approximately 13% of the estimated peak pressure amplitude of 630 Pa. For reconstructions from bandpass filtered slopes, significantly lower error values were identified. Using a bandpass filter range of \(0.25~f_{{\text {shed}}} - 1.88~f_{{\text {shed}}}\) (200–1500 Hz) for slope maps, worst case estimates of \(a=0.1~\text {ms}^{-2}\) and \(p_{{\text {dyn}}}=6~\text {Pa}\) were obtained.
Based on the low amplitude of noise patterns in the extracted dynamic pressure distributions, it appears that experimental errors from the deflectometry setup were filtered efficiently. The systematic processing errors as well as the assumption of quasi-static behaviour are likely to result in an underestimation of instantaneous pressure reconstructions, which can be estimated to up to 30%. The latter is also the most likely reason for the increasing discrepancy between pressure fluctuations identified from transducer data and from VFM reconstructions when moving into the region in which vortices first impinge on the plate.
6 Limitations and future work
Low-amplitude differential pressure fluctuations were extracted from VFM pressure reconstructions using two techniques. To address the large discrepancy between microphone data and VFM reconstructions, the present setup could be improved to obtain accurate acceleration information. This could potentially be achieved by simultaneously measuring deflections at a known point in the field of view using an LDV. Further, to achieve convergence and due to the low signal-to-noise ratio, a large number of snapshots was required. This is a challenge for available high-speed cameras due to limited storage and data transfer rates. Experiments based on phase-locked measurements can address this issue. This also allows using cameras with higher resolutions, which can be combined with smaller grid pitches to increase slope resolution. Slope resolution can also be improved by increasing the distance between grid and sample, though the quality and availability of suitable camera lenses is an issue. Another limitation of the approach presented here is that the specimen is required to be of optical mirror quality. Non-mirror-like, but reasonably smooth surfaces were successfully used for deflectometry measurement using an infrared camera and heated grids (Toniuc and Pierron 2019). Due to the relatively long wavelength of infrared light, sufficiently specular reflection for slope measurements was achieved using unpolished metal plates as well as perspex with approximately 1.5\(~\upmu \text {m}\) surface RMS roughness. An approach for applications of deflectometry measurements to curved surfaces is proposed in Surrel and Pierron (2019). Though the results were promising, a sophisticated calibration was required and time-resolved measurements are currently not possible. Finally, improved virtual fields and higher order pressure reconstruction approaches could reduce the systematic processing error of the VFM.
7 Conclusion
This study presents an approach for obtaining full-field dynamic pressure information from surface slope measurements. Surface slopes were measured using a highly sensitive deflectometry setup. Pressure reconstructions were obtained using the VFM. The extracted differential pressure amplitudes range down to few \({\mathcal {O}}(1)~\)Pa. \(85 \times 85\) data points were obtained, corresponding to a field of view of \(4.25~\text {cm}\times 4.25~\text {cm}\). For band pass filtered data VFM results were found to capture the expected pressure distribution well, but to overestimate the standard deviations of the pressure amplitudes by up to 50% when compared to microphone data. DMD was used to extract relevant dynamic information. Error sources associated with experimental limitations and the processing technique were identified and discussed. Despite the low accuracy in amplitude, the achieved high data point density and the low magnitude of the extracted pressure amplitudes make the presented technique highly relevant for a large range of applications in engineering and science.
8 Data provision
All relevant data produced in this study is available under the DOI https://doi.org/10.5258/SOTON/D1165.
References
Badulescu C, Grédiac M, Mathias JD (2009) Investigation of the grid method for accurate in-plane strain measurement. Measur Sci Technol 20(9):95–102
Balzer J, Werling S (2010) Principles of shape from specular reflection. Measurement 43(10):1305–1317
Becker HA, Massaro TA (1968) Vortex evolution in a round jet. J Fluid Mech 31(3):435–448
Beltaos S (1976) Oblique impingement of circular turbulent jets. J Hydraul Res 14(1):17–36
Berry A, Robin O (2016) Identification of spatially correlated excitations on a bending plate using the virtual fields method. J Sound Vib 375:76–91
Berry A, Robin O, Pierron F (2014) Identification of dynamic loading on a bending plate using the virtual fields method. J Sound Vib 333(26):7151–7164
Beverley J, McKeon RHE (2007) Springer handbook of experimental fluid mechanics, chapter 4, vol 4. Springer, Berlin, pp 188–208
Corcos GM (1963) Resolution of pressure in turbulence. J Acoust Soc Am 35(2):192–199
Corcos GM (1964) The structure of the turbulent pressure field in boundary-layer flows. J Fluid Mech 18(3):353–378
D’Errico J (2009) Inverse (integrated) gradient.https://de.mathworks.com/matlabcentral/fileexchange/9734-inverse-integrated-gradient. Accessed on 12 June 2019
Devivier C, Pierron F, Glynne-Jones P, Hill M (2016) Time-resolved full-field imaging of ultrasonic Lamb waves using deflectometry. Exp Mech 56:345–357
Engler RH, Klein C, Trinks O (2000) Pressure sensitive paint systems for pressure distribution measurements in wind tunnels and turbomachines. Meas Sci Technol 11(7):1077–1085
Gesemann S, Huhn F, Schanz D, Schroeder A (2016) From noisy particle tracks to velocity, acceleration and pressure fields using b-splines and penalties. In: Proceedings of the 18th international symposium on applications of laser techniques to fluid mechanics, July 4–7, Lisbon, Portugal, pp 2684–2694
Giraudeau A, Pierron F, Guo B (2010) An alternative to modal analysis for material stiffness and damping identification from vibrating plates. J Sound Vib 329(10):1653–1672
Grédiac M, Sur F, Blaysat B (2016) The grid method for in-plane displacement and strain measurement: a review and analysis. Strain 52(3):205–243
Gregory JW, Sullivan JP, Wanis SS, Komerath NM (2006) Pressure-sensitive paint as a distributed optical microphone array. J Acoust Soc Am 119(1):251–261
Hemati M, Williams M, Rowley C (2014) Dynamic mode decomposition for large and streaming datasets. Phys Fluids 26(11):111–701
Huhn F, Schanz D, Manovski P, Gesemann S, Schröder A (2018) Time-resolved large-scale volumetric pressure fields of an impinging jet from dense lagrangian particle tracking. Exp Fluids 59(5):81
Jeon Y, Earl T, Braud P, Chatellier L, David L (2016) 3D pressure field around an inclined airfoil by tomographic TR-PIV and its comparison with direct pressure measurements. In: Proceedings of the 18th international symposium on the application of laser and imaging techniques to fluid mechanics. In: Proceedings of the 18th international symposium on the application of laser and imaging techniques to fluid mechanics, July 4–7, Lisbon, Portugal, pp 1060–1069
Jiao L, Chen Y, Wen X, Peng D, Liu Y, Gregory JW (2019) Resolving vortex-induced pressure fluctuations on a cylinder in rotor wake using fast-responding pressure-sensitive paint. Phys Fluids 31(5):55–106
Kalifa RB, Habli S, Saïd NM, Bournot H, Palec GL (2016) The effect of coflows on a turbulent jet impacting on a plate. Appl Math Model 40(11):5942–5963
Kaufmann R, Pierron F, Ganapathisubramani B (2019) Full-field surface pressure reconstruction using the Virtual Fields Method. Exp Mech 59(8):1203–1221
Lecoq D, Pézerat C, Thomas JH, Bi W (2014) Extraction of the acoustic component of a turbulent flow exciting a plate by inverting the vibration problem. J Sound Vib 333(12):2505–2519
Liu Q, Sleiti A, Kapat J (2008) Application of pressure and temperature sensitive paints for study of heat transfer to a circular impinging air jet. Int J Therm Sci 47(6):749–757
O’Donoughue P, Robin O, Berry A (2017) Time-resolved identification of mechanical loadings on plates using the virtual fields method and deflectometry measurements. Strain 54(3):e12–e258
O’Donoughue P, Robin O, Berry A (2019) Inference of random excitations from contactless vibration measurements on a panel or membrane using the virtual fields method. In: Ciappi E, De Rosa S, Franco F, Guyader JL, Hambric SA, Leung RCK, Hanford AD (eds) Flinovia-flow induced noise and vibration issues and aspects-II. Springer International Publishing, Cham, pp 357–372
Pezerat C, Guyader JL (2000) Force analysis technique: reconstruction of force distribution on plates. Acta Acust United Acust 86(2):322–332
Pieris S, Zhang X, Yarusevych S, Peterson SD (2019) Vortex dynamics in a normally impinging planar jet. Exp Fluids 60(5):84
Pierron F, Grédiac M (2012) The virtual fields method. Extracting constitutive mechanical parameters from full-field deformation measurements. Springer, New York
Ritter R (1982) Reflection moire methods for plate bending studies. Opt Eng 21:21–9
Robin O, Berry A (2018) Estimating the sound transmission loss of a single partition using vibration measurements. Appl Acoust 141:301–306
Robin O, Moreau S, Padois T, Berry A (2012) Measurement of the wavenumber-frequency spectrum of wall pressure fluctuations: spiral-shaped rotative arrays with pinhole-mounted quarter inch microphones. In: 19th AIAA/CEAS Aeroacoustics Conference, May 27–29, Berlin, Germany, pp 881–898
Schmidt PJ (2010) Dynamic mode decomposition of numerical and experimental data. J Fluid Mech 656:5–28
Schneiders JFG, Caridi GCA, Sciacchitano A, Scarano F (2016a) Large-scale volumetric pressure from tomographic PTV with HFSB tracers. Exp Fluids 57:1–8
Schneiders JFG, Caridi GCA, Sciacchitano A, Scarano F (2016b) Large-scale volumetric pressure from tomographic PTV with HFSB tracers. Exp Fluids 57(11):164
Surrel Y (2000) Photomechanics, chap fringe analysis. Springer, Berlin, pp 55–102
Surrel Y, Pierron F (2019) Deflectometry on curved surfaces. In: Lamberti L, Lin MT, Furlong C, Sciammarella C, Reu PL, Sutton MA (eds) Advancement of optical methods and digital image correlation in experimental mechanics, vol 3. Springer International Publishing, Cham, pp 217–221
Surrel Y, Fournier N, Grédiac M, Paris PA (1999) Phase-stepped deflectometry applied to shape measurement of bent plates. Exp Mech 39(1):66–70
Timoshenko S, Woinowsky-Krieger S (1959) Theory of plates and shells. Engineering societies monographs. McGraw-Hill, New York
Toniuc H, Pierron F (2019) Infrared deflectometry for slope deformation measurements. Exp Mech 59(8):1187–1202
Van Blitterswyk J, Rocha J (2017) An experimental study of the wall-pressure fluctuations beneath low reynolds number turbulent boundary layers. J Acoust Soc Am 141(2):1257–1268
van Gent PL, Michaelis D, van Oudheusden BW, Weiss PÉ, de Kat R, Laskari A, Jeon YJ, David L, Schanz D, Huhn F, Gesemann S, Novara M, McPhaden C, Neeteson NJ, Rival DE, Schneiders JFG, Schrijer FFJ (2017) Comparative assessment of pressure field reconstructions from particle image velocimetry measurements and lagrangian particle tracking. Exp Fluids 58(4):33
Walker JDA, Smith CR, Cerra AW, Doligalski TL (1987) The impact of a vortex ring on a wall. J Fluid Mech 181:99–140
Zuckerman N, Lior N (2006) Jet impingement heat transfer: physics, correlations, and numerical modeling. Adv Heat Transf 39(C):565–631
Acknowledgements
This work was funded by the Engineering and Physical Sciences Research Council (EPSRC). F. Pierron acknowledges support from the Wolfson Foundation through a Royal Society Wolfson Research Merit Award (2012–2017).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
348_2019_2850_MOESM1_ESM.mp4
A video of a DMD reconstruction showing the well-defined spatial structure of an impinging vortex can be found in the supplementary material of this publication. It shows a reconstruction of the \(0.97~\text {f}_{shed}\) (\(776~\text {Hz}\)) DMD mode identified in section 4.3. This mode corresponds to the highest identified amplitude coefficient, which is reasonably close to the theoretically expected maximum at \(\hbox {f}_{{shed}}\) (\(800~\text {Hz}\)) in the amplitude spectrum. The video shows 100 frames at a rate of 33 fps. The acquisition frequency was \(4~\text {kHz}\). Damping was set to zero for this video. (mp4 1359 KB)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kaufmann, R., Ganapathisubramani, B. & Pierron, F. Reconstruction of surface-pressure fluctuations using deflectometry and the virtual fields method. Exp Fluids 61, 35 (2020). https://doi.org/10.1007/s00348-019-2850-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-019-2850-y