Characterization of spray-induced turbulence using fluorescence PIV

Abstract

The strong shear induced by the injection of liquid sprays at high velocities induces turbulence in the surrounding medium. This, in turn, influences the motion of droplets as well as the mixing of air and vapor. Using fluorescence-based tracer particle image velocimetry, the velocity field surrounding 125–135 m/s sprays exiting a 200-$\upmu$m nozzle is analyzed. For the first time, the small- and large-scale turbulence characteristics of the gas phase surrounding a spray has been measured simultaneously, using a large eddy model to determine the sub-grid scales. This further allows the calculation of the Stokes numbers of droplets, which indicates the influence of turbulence on their motion. The measurements lead to an estimate of the dissipation rate $\epsilon \approx 35$ m$^{2}$ s$^{-3}$, a microscale Reynolds number Re$_{\lambda } \approx$ 170, and a Kolmogorov length scale of $\eta \approx 10^{-4}$ m. Using these dissipation rates to convert a droplet size distribution to a distribution of Stokes numbers, we show that only the large scale motion of turbulence disperses the droplet in the current case, but the small scales will grow in importance with increasing levels of atomization and ambient pressures.

1 Introduction

When a high-speed liquid jet breaks up into a spray, it drags along the air surrounding it, generating strong shear forces in the ambient gas. This shear can be the driving force for generating turbulence. This turbulence, in turn, can influence the mixing and dispersion of the droplets in the spray itself (Bharadwaj et al. 2009; Bocanegra Evans et al. 2016). Little information exists on spray-induced turbulence, due to the challenge of measuring the velocity field in such a complex environment, as well as obtaining the number of measurements required to obtain statistical information. The small-scale turbulence characteristics, such as the dissipation rate, determine the influence of the gas-phase turbulence on the motion and mixing of droplets in turbulence (Shaw et al. 1998; Reveillon and Demoulin 2007). A dimensionless quantity called the Stokes number quantifies the response of droplets to velocity fluctuations of the surrounding gas. It is the ratio of two time scales: the viscous response time over the Kolmogorov time scale $\tau _{\eta }$. A measurement of $\tau _{\eta }$ requires a measurement of the turbulent energy dissipation rate $\epsilon$. This is an experimental challenge, as this requires measurements at the resolution of the smallest length scales. In this paper a large-scale eddy approach is used in which properties of small-scale motion are inferred from a measurement of large-scale velocity statistics (Pope 2000).

One of the challenging aspects of obtaining gas-phase velocities close to a spray is the inherent multi-phase environment. Hot-wire anemometers, often used for 1D measurements of turbulence (Laufer 1954; Wyngaard 1968; Ligrani and Bradshaw 1987), are influenced by impacting droplets (Siebert et al. 2007) in both the processing and longevity of the (fragile) probe. Direct-scattering techniques that determine the displacement of small particles/droplets that follow the flow (tracers) using pulsed lasers, such as Particle Image Velocimetry (PIV), are affected by the large range of scales, and are visualizing foremost the liquid phase of the spray (Paulsen Husted et al. 2009; Cao et al. 2000).

In the past, fluorescent tracers have been used to circumvent this problem (Lee et al. 2002; Zhu et al. 2012; Rottenkolber et al. 2002; Kosiwczuk et al. 2005; Driscoll et al. 2003; Zhang et al. 2014; Boëdec and Simoëns 2001). By adding a fluorescent molecule to tracers in the ambient gas ($\upmu$m-sized droplets), the laser light scattered by the liquid phase can be filtered from the images, and only the luminescent gas phase is then recorded. In this way, the velocity field of the gas-phase can be determined independently, and the applied method is commonly referred to as Laser-Induced Fluorescence PIV (LIF-PIV). These investigations often focus on visualizing large-scale flow structures (Rottenkolber et al. 2002; Kosiwczuk et al. 2005; Lee et al. 2002) or measuring the mean velocity induced by sprays (Zhu et al. 2012; Zhang et al. 2014).

A measurement of the statistical properties of the turbulent flow induced by the breaking jet aims to measure its small- and large-scale properties. The first is characterized by the dissipation rate $\epsilon$, which sets the length $\eta$ and the timescale $\tau _{\eta }$ of the smallest vortices, $\eta = (\nu ^{3} / \epsilon )^{1/4}$ and $\tau _{\eta }=(\nu /\epsilon )^{1/2}$, respectively, where $\nu$ is the kinematic viscosity of the surrounding gas. A value of the droplet Stokes number $St\ll$1 signifies that droplets can follow the turbulent velocity fluctuations at the smallest scale (and thus also at all larger scales). The turbulent velocity $u_\mathrm{rms}(\mathbf {x})=\langle (u(\mathbf {x},t) - \overline{u}(\mathbf {x}))^{2} \rangle ^{1/2}$, with $\mathbf {x}$ the position in space and $\overline{u}$ the mean velocity $\overline{u}(\mathbf {x})=\langle u(\mathbf {x},t) \rangle$, where $\langle \rangle$ indicates an average over time, determines the dispersion of droplets that follow the flow exactly ($St\le$ 1). As the droplets predominantly behave like passive tracers down to the Kolmogorov scale their dispersion should behave like those of fluid elements. At times much shorter than the large eddy turnover time T, droplets disperse in a ballistic manner, with the mean separation between droplets $\sigma$ increasing as $\langle \sigma ^{2}(t) \rangle = u_\mathrm{rms}^{2} t^{2}$. However, at times much larger than T, the droplets disperse diffusively, as $\langle \sigma ^{2}(t) \rangle = T u_\mathrm{rms}^{2} t$. Therefore, to obtain an accurate picture of the mixing and dispersion of droplets, the correlation properties of the velocity field have to be measured in addition to the turbulent velocity.

2 Experimental setup

The fluorescent tracer agent used in this work is Fluorescein sodium salt (Sigma-Aldrich), an organic compound with a broadband absorption in the ultraviolet and a peak luminescence at 521 nm. The compound is dissolved in water in near-saturated concentrations to ensure high luminescence yield. To follow the motion of the air precisely, the fluorescent dye is atomized to droplets with a mean diameter of 0.3 $\upmu$m with a geometric standard deviation of less than 2.0, using a six-jet atomizer (Model 9306, TSI). The atomized tracers are injected 1000 nozzle diameters downstream of a continuous water or heptane spray, generated by a pressurized straight single-hole nozzle capillary (see Figs. 1 and 2), with a diameter of 200 $\upmu$m and a length of 2 mm. The nozzle is surrounded by a container ($400\times 400\times 800$ mm) to obtain a uniform dense seeding of the atomized tracers, with optical access for the camera and laser sheet. The gas phase is set in motion through the heptane and water spray, which mixes the fluorescein-doped micro-droplets into the spray surroundings. A double-pulsed Nd:YAG laser (PIV-300, Spectra Physics) is custom-fitted to generate third harmonic (355 nm) pulses at a repetition rate of 10 Hz and a time delay between the pulses of 60 $\upmu$s. These pulses are formed into a sheet with a thickness of approximately 100 $\upmu$m and a fluence of 300 mJ/cm$^{2}$. Following a laser pulse, the luminescent micro-droplets are recorded through a high-pass 420 nm filter (Schott, GG420) using a PIV camera (Redlake) with a resolution of 1600 $\times$ 1200 pixels and at a magnification of 10.4 $\upmu$m per pixel. The sprays are continuously generated by pressurizing the liquid reservoir connected to the nozzle with a pressure of 10 MPa (surrounded by air at atmospheric pressures). This is done for approximately 1–2 min, leading to approximately 200–300 image pairs. This measurement is repeated up to three times, resulting in 700–900 image pairs for both the water and heptane sprays.

The continuous nature of the spray may introduce recirculated droplets in addition to the large (outlier) droplets from the aerosol generator. The jet velocity was measured using laser-induced phosphorescence (Voort et al. 2016a, b), with $v_{\text {jet}}$ = 135 m/s for the heptane jet and $v_{\text {jet}}$ = 125 m/s for the water jet. This leads to Reynolds Re $= v_{\text {jet}}d_{\text {nozzle}}/\nu$ and Weber We $= \rho _{g}v_{\text {jet}}^{2}d/\gamma$ numbers of Re $\simeq 4.5\times 10^{4}$, We $\simeq 220$ and $Re\simeq 2.5\times 10^{4}$, We $\simeq 125$ for the heptane and water jet, respectively, with $\nu$ the kinematic viscosity, $d_{\text {nozzle}}$ the nozzle diameter, and $\gamma$ the surface tension of the liquid.

Fig. 1

Schematic of the experimental spray setup. Micro-droplets containing fluorescent tracers are added to a chamber containing a spray mount. A double-pulsed ultraviolet laser sheet is used to excite the micro-droplets surrounding the spray. The spray surroundings are visualized with a PIV camera

Fig. 2

Diffuse background (DBI) image of the heptane spray at an injection pressure of $P_{\text {inj}}=10$ MPa.

Figure 3a shows a single fluorescence image. Both the fluorescent tracers and the direct scattering of the UV light off the liquid phase (jet, drops) can be seen. Although the observation of direct scattering is strongly suppressed by the UV filter, additional image processing is necessary to reduce the contribution of liquid drops to the PIV calculation. First, the images are filtered using a 5 $\times$ 5 pixel binomial filter, after which an 8 $\times$ 8 sliding minimum was subtracted. Next, all drops with a diameter $d_{\text {thr}}$ larger than 2 pixels ($\approx 20 \upmu$m) and intensity larger than an intensity threshold $I_{\text {thr}}=100$ counts (see Fig. 3d) are located in the image. At a turbulent dissipation rate of $\epsilon = 50$ m$^{2}$s$^{-3}$, these drops have a Stokes number of St $\approx 2$. Smaller drops are considered as tracers, while the contribution of larger drops on the PIV correlation is minimized by setting their intensity equal to the background intensity sampled on a radius of $d_\mathrm{thr}$ around them. The result is shown in Fig. 3c. This elimination of droplets is based on their size, not directly on their intensity. The PIV correlations are done using DaVis PIV software (LaVision GmbH, Germany), with 48 $\times$ 48 pixel interrogation windows that started at 128 $\times$ 128 pixels. The planar velocity gradients, needed for the measurement of the dissipation rate, were computed using central differences. As the PIV interrogation window size $\simeq$ 5$\eta$, large eddy PIV implies a correction factor of $\simeq$ 3.4, which multiplies with the standard value of the Smagorinsky constant $C_{\epsilon }=0.17$ (Bertens et al. 2015). Statistics over 700–900 vector fields are computed over displacement vectors corresponding to correlation peak ratios larger than 1.15. Furthermore, the nozzle exit and jet were obscured by a mask. Performing PIV in this multiphase environment is a challenge. However, we believe that we have obtained a good estimate of the mean and turbulent flow magnitudes, and an order of magnitude estimate of the small-scale turbulence properties.

Fig. 3

Overview of the LIF fluorescein image a surrounding a $\approx$135 m/s heptane spray. b Enlargement (width 3 mm) of the image in (a) showing both fluorescent tracers and direct UV scattering of the liquid. After image processing c droplets larger than $~20 \upmu$m are identified and replaced by the background intensity. The arrows in (b) and (c) point to the spot of a large liquid drop. The intensity pdf (d) of the images before (b) and after (c) image processing show a clear segmentation threshold for drops larger than $d_{\rm thr}$

3 Results

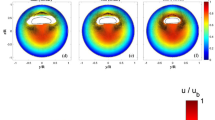
Figure 4 shows the mean velocity field of the gas phase. There appears to be a net influx of mass into the measurement volume. This must be offset by a large downstream (upward) flow induced by the strong shear at the liquid–gas interface. This flow could not be visualized, as the current setup and imaging method cannot image close enough to the spray edge. Additionally, a small crossflow is anticipated by the observed asymmetry of the pattern of radially inward flowing gas (compare left and right part of Fig. 4). This crossflow is orders of magnitude lower than the spray velocity ($\mathcal {O}(10^{-1})$ vs $\mathcal {O}(10^2)$ m/s), too weak to influence the breakup of the spray itself.

Fig. 4

The velocity magnitude of the gas-phase mean velocity field surrounding a 135 m/s heptane spray. The lines indicate the direction and magnitude of the velocity vector. A mask was placed over the image to obscure the liquid jet

While the mean velocity gives information on spray-induced entrainment, the velocity fluctuations are a measure of the turbulence. The induced turbulence is strongest near the liquid–gas boundary, and is stronger for the heptane jet than for the water jet, see Fig. 5. A possible explanation is the different morphology of the jets: The heptane jet breaks up more atomized (more droplets, smaller core) than the water jet, and the liquid–gas interface will contain a larger number of droplets. The different structure of the root mean square (RMS) velocity for the left ($x<0$) side of the heptane spray can be explained by an increased scattering of the laser sheet, reducing the signal-to-noise ratio (SNR).

Fig. 5

The turbulent velocity in the near-nozzle region of the spray, defined as $u' = (\langle (u-\bar{u})^{2}\rangle + \langle (v-\bar{v})^{2}\rangle )^{1/2}$. The lower graph shows the measured turbulent velocity $u'(x)$ at $y=5$ mm. Few valid PIV vectors were obtained on the left side of the heptane jet, likely due to scattering of the laser sheet on the spray, leading to a large variation of $u'$

The size of the large-scale turbulent vortices is set by the integral scale, which quantifies the decay length of the two-point correlation function. The longitudinal correlation function can be used to estimate the length scales in the spray-induced turbulence. The longitudinal correlation function (Pope 2000), averaged over all measurements and positions in the unmasked region of the flow, is

$$\begin{aligned} C(r)= \langle (v(\mathbf {x}+\mathbf {e}_{y}r),t) v(\mathbf {x},t) \rangle / \langle v^{2} \rangle , \end{aligned}$$

where $\mathbf {e_{y}}$ is the unity vector in the y-direction, and the average $\langle \rangle$ is done over time and locations $\mathbf {x}$ in the unmasked region of the flow. For the computation of C(r), we correct for the inhomogeneity of the velocity field u(x, t) by subtracting the mean and dividing by the fluctuation velocity. The correlation in the radial (x) direction is omitted due to the inhomogeneity of the turbulent flow, but should be equal to C(r) in isotropic turbulence. The function C(r) is shown in Fig. 6 for both the water and heptane jets. The exponential decay of the $C_{yy}(r)$ correlation function, $C_{yy}(r) \sim e^{-r/L_{y}}$, gives $L_{y, \text {water}}\approx 6$ mm and $L_{y,\text {heptane}} \approx 8$ mm. The magnitude of $L_{y}$ demonstrates that the largest eddies are much smaller than the circulatory flow in this experiment, and are therefore generated by the shear at the liquid–gas interface.

Fig. 6

The black and gray are C(r) for the heptane and water spray, respectively. The dashed lines are a fit of $C(r)\sim exp(-r/L_{y})$, with $L_{y,\text {heptane}}\approx$ 8 mm and $L_{y,\text {water}}\approx$ 6 mm.

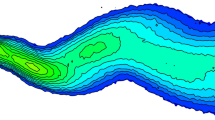
The smallest scales of the induced turbulence are determined by the turbulent dissipation rate $\epsilon$. It is a challenge to measure the dissipation rate because the velocity field is averaged over the PIV interrogation windows and the turbulence is inhomogeneous. In isotropic and homogeneous turbulence, the true dissipation rate can be obtained using a large eddy correction of the measured velocity gradients (Bertens et al. 2015). In our case, while using the measured planar gradients, this would result in $\epsilon = 2^{3/2} (C_{\epsilon } \Delta )^{2} \langle S_{2}\rangle ^{3/2}$, with $C_{\epsilon }$ the Smagorinsky correction factor, $\Delta$ the PIV window size, and the strain rate $S=\frac{3}{2}\langle (\partial _y u)^2 + (\partial _x v)^2\rangle ^2 + \frac{3}{4}\langle (\partial _x u)^2 + (\partial _y v)^2\rangle ^2$, with $\partial _y u=\partial u/\partial y$, etc. Using this, we define a local $\epsilon (\mathbf {x})$, with the understanding that the dissipation rate is the spatial average of $\epsilon (\mathbf {x})$. In Bertens et al. (2015), we argue that the value of the constant $C_{\epsilon }$ should depend on the ratio of $\Delta$ over the Kolmogorov length scale $\eta$, the window overlap in the PIV calculations, and the discrete approximation of the derivatives. Figure 7 shows the local dissipation rate for the water and heptane case. Clearly, this local dissipation rate is very inhomogeneous, with a poorly defined average. The resulting averaged dissipation rates are $\epsilon _{\text {hep}}=50$ $\text {m}^{2} \text {s}^{-3}$ and $\epsilon _{\text {wat}}=35$ $\text {m}^{2} \text {s}^{-3}$ for the heptane and water jets, respectively. For the Kolmogorov length and time scales, this corresponds to $\eta \approx 9 \times 10^{-5}$ m, $\tau _{\eta } \approx 6 \times 10^{-4}$ s and $\eta \approx 10^{-4}$ m, $\tau _{\eta } \approx 7 \times 10^{-4}$ s for the heptane and water sprays, respectively, with a lambda Reynolds number of 170 and 140.

Fig. 7

Local dissipation field of the heptane (a) and water (b) case, computed from the velocity gradients, $\epsilon = 2^{3/2} (C_{\epsilon } \Delta )^{2} \langle S_{2}\rangle ^{3/2}$, with $S=\frac{3}{2}\langle (\partial _y u)^2 + (\partial _x v)^2\rangle ^2 + \frac{3}{4}\langle (\partial _x u)^2 + (\partial _y v)^2\rangle ^2$, with $\partial _y u=\partial u/\partial y$, etc., and $\Delta$ the interrogation window size, and the Smagorinsky constant $C_{\epsilon }$ = 0.58 (in accordance with the large eddy correction)

Whether the droplet dispersion is affected by the small-scale turbulence induced by the jet depends on two properties: The droplet Stokes number and the size of the turbulent velocity fluctuations as compared to the axial and radial release velocities at breakup. If the Stokes number is small ($St\ll$ 1), the droplets will disperse with the turbulent air surrounding the spray. If the Stokes number is large ($St\gg$1), they will mostly travel ballistically away from the spray with the radial velocity induced by the breakup of the ligament at the liquid–gas interface (which can be approximated from measurements of liquid dispersion van der Voort et al. 2016a). Using the measured $\epsilon$ and $\tau _{\eta }$, and the individual fluid properties to determine the droplet response time $\tau _{d}=\rho _{d} d^{2} / 18 \mu _{g}$, with $\mu _{g}$ the viscosity of air, the droplet Stokes number can now be determined. Taking the droplet size d from the size distribution of the droplets from the investigated sprays (measured with interferometric particle imaging), the size distribution can be translated to a distribution of Stokes numbers (see Fig. 8). The range of Stokes numbers indicates that these droplets will follow the turbulent eddies.

Fig. 8

The PDF of the droplet size distribution (a) and Stokes distribution (b) for the heptane (red) and water (blue) sprays. The gray area indicates the cut-off, determined by the lower limit of the IPI droplet sizing measurement range (van der Voort et al. 2016b)

4 Conclusions

The Stokes number quantifies the response of the droplets in the spray environment to the smallest timescale (eddy turnover time) of the spray-induced turbulence, estimated from the measured dissipation rate to be $\tau _{\eta } \approx 6 \times 10^{-4}$ s. On the other hand, the estimate of the integral length scale leads to a large eddy turnover time $\tau _{L} = L / u' \approx 10^{-2}$ s, one order of magnitude larger than $\tau _{\eta }$, corresponding to a turbulent diffusion rate $D_{turb} \approx \tau _{L} u'^{2} \approx 10^{-2}$m$^{2}/$s. From the measured size distribution, we conclude that most droplets will be dispersed by turbulence. This includes the formation of large-scale clusters and voids (of recirculated droplets), as is illustrated in Fig. 9. However, the initial velocity of the droplets will determine if the dispersion will occur in the near-nozzle regime investigated in this work.

A separation has to be made between the recirculated droplets already present in the spray environment (such as would occur in sprays in a confined environment, as piston engines), and the droplets newly generated by the jet itself.

Fig. 9

Complementary image of the post-processed PIV images, showing the locations of droplets with diameters $\ge$ 20 $\upmu {\rm m}$ surrounding the spray at a single instance of time. The variation in droplet density indicates turbulent clustering in the regions of strain between the turbulent eddies

The average radial and longitudinal velocity of the liquid part of the spray was measured using laser-induced phosphorescence, which tracks the displacement of a small luminescent volume of liquid using molecular tracers and intensified high-speed cameras (Voort et al. 2016b). The distance each droplet travels before it is adapted to the turbulent flow (droplet response length) is given by $\tau _{d} v_{jet}$, which is in the order of 30 mm for 10 $\upmu$m droplets ($St\approx$ 1). This distance is much larger than our interrogation area, and only reaches the investigated area for droplets < 5 $\upmu$m ($St<$0.1), which is outside of our droplet sizing measurement range. Under the present conditions, the influence of turbulence on the dispersion of spray droplets is small. However, if the atomization level is increased, by increasing ambient pressure, or changing the liquid properties, the mean jet velocity will decrease while the turbulent fluctuations will grow stronger. This will shift the droplet distribution towards smaller Stokes numbers and shorter droplet response lengths. As the ratio of $u'$ to the radial release velocity becomes larger, and the distribution shifts towards smaller Stokes numbers, the spray-induced turbulence becomes increasingly important in determining the droplet dispersion, and thus the mixing of spray and air.