On dealing with multiple correlation peaks in PIV

Abstract

A novel algorithm to analyse PIV images in the presence of strong in-plane displacement gradients and reduce sub-grid filtering is proposed in this paper. Interrogation windows subjected to strong in-plane displacement gradients often produce correlation maps presenting multiple peaks. Standard multi-grid procedures discard such ambiguous correlation windows using a signal to noise (SNR) filter. The proposed algorithm improves the standard multi-grid algorithm allowing the detection of splintered peaks in a correlation map through an automatic threshold, producing multiple displacement vectors for each correlation area. Vector locations are chosen by translating images according to the peak displacements and by selecting the areas with the strongest match. The method is assessed on synthetic images of a boundary layer of varying intensity and a sinusoidal displacement field of changing wavelength. An experimental case of a flow exhibiting strong velocity gradients is also provided to show the improvements brought by this technique.

Introduction

Standard analysis of PIV images generally involves the division of sequential recordings into smaller interrogation areas and estimating the displacement of recorded particle images captured within those areas by means of cross-correlation. Particle images moving together in the same direction will produce a single strong peak in the cross-correlation map, allowing the retrieval of a representative displacement vector. For this analysis to be conducive, local in-plane displacement gradients must be negligible and an upper limit of 0.05 pixels/pixel is often suggested in literature (Keane and Adrian 1992). When strong in-plane displacement gradients are present, interrogation areas are populated by particle clusters moving in different directions. As a consequence, the correlation peak will broaden and deform as the gradients increase, until the peak splinters into multiple peaks (Fig. 1) (Scarano 2002). The unique displacement vector obtained from the correlation map is then no longer representative of the underlying flow field. Non-uniform displacement fields and deformations in the particle image pattern therefore constitute a strong source of error for PIV (Huang et al. 1993) and must be treated carefully. While smaller interrogation window sizes are preferential to reduce the effect of local velocity gradients, such reduced windows contain fewer particle images thereby increasing the measurement uncertainty and limiting the maximum displacement measurable (Adrian 1991). Both contradicting requirement on the sizing of the correlation windows contribute to a limitation in the achievable dynamic velocity range of PIV (Adrian 1999).

One of the prevailing solutions adopted to increase attainable spatial resolution and dynamic velocity range is the iterative multi-grid approach proposed by Scarano and Riethmuller (2000). The technique suggested involves the analysis of images with wide interrogation areas first, used as “predictor” of the displacement field. Velocity predictors are adopted to deform consecutive image snapshots with the aim of reducing the relative particle images displacement. This step is typically combined with a reduction of the window size and a displacement correction using the velocity predictors. The initial window size should be large enough to capture the largest displacement in the flow field while the final size should be appropriately sized to achieve the desired spatial resolution, ensuring a sufficient amount of particle images are captured. The benefit of the multi-grid algorithm is an increase in spatial resolution and an improved velocity dynamic range, which is the reason of its widespread use and success. However, in the presence of splintered peaks in the first iteration of the analysis, a reliable estimation of the flow field is impossible. This gives rise to an unrepresentative displacement predictor, which influences the remainder of the iterative process.

Beside the use of advanced image processing algorithms, a straightforward lowering of the time-separation between sequential images can be applied to reduce the displacement peak discrepancy. This yields however a reduction in dynamic velocity range while augmenting the relative error (Boillot and Prasad 1996). In case of time-resolved PIV datasets, Hain and Kähler presented a strategy to selectively interrogate image snapshots temporally separated by locally optimised values to increase accuracy and dynamic range (Hain and Kähler 2007). Persoons et al. on the other hand devised an intricate multi-pulse separation technique, where pulse separations across several exposures are adjusted to increase dynamic range (Persoons and ODonovan 2010). The majority of PIV applications continue to rely on standard double-pulsed systems however, imposing a unique separation time between recordings. As such, a solution to the problematic of multiple correlation peaks appearing must be sought from an algorithmic perspective.

Fig. 1

Effect of displacement gradients on the correlation map. The figure illustrates the correlation map between interrogation windows subjected to a shear flow of varying intensity. In-plane gradients are respectively: a 0.01, b 0.05, c 0.1 and d 0.5 pixels/pixel. As the gradient increases, the correlation map contains multiple detectable peaks, marked with red dots

The standard approach adopted in many PIV algorithms to circumvent the problem of numerous peaks in the correlation map is to simply discard peaks below a certain Signal-to-Noise (SNR) threshold (typically 1.2–1.5) (Keane and Adrian 1990). SNR is defined as the ratio between the highest and the second highest peak and can be indicative of measurement quality (Xue et al. 2014), However, a SNR below the threshold does not necessarily imply unreliable peaks. Multiple correlation peaks can be of equal height and well above the noise level. This SNR-based solution thus helps to increase the robustness of the measurement by dealing with the ambiguity of multiple peaks, but does not offer a solution to the problem of displacement vector representativeness. It will be shown in this paper that complex displacement fields with high amplitude oscillations indeed remain impossible to be measured even with the adoption of a SNR threshold. A particular solution utilising correlation peak amplitudes was proposed in Roth and Katz (2001); peak-height weighted averaging of the displacements related to all the peaks in the correlation map. While this suggestion mitigates the problem when multiple peaks relate to similar displacements, it remains insufficient in case of very dissimilar displacements. When dealing with high intensity opposite velocities such as in case of shear layers, shock waves, vortices, etc., the average of the peaks will produce a nearly zero displacement, augmenting the possibility of iterative multi-grid schemes to fail. To deal with velocity gradients in a recursive local-correlation algorithm, (Hart 2000) proposed to start with a large initial window and use the identified peak in the correlation map as an estimate to limit the range of possible particle displacements in sub-regions. Although this process can, in theory, be carried out down to correlation windows containing a single particle image, the dependency on the initial displacement estimate remains. Exactly this value can be compromised by the appearance of multiple peaks in case of strong displacement gradients. A “Reverse Hierarchical process” was proposed in Rohály et al. (2002). Rather than initiating the analysis from the largest scale, the solution proposed was to build a correlation map by starting from the smallest scale and adding interrogation areas based on inter-level correlation correction and validation. Also in this case, dynamic range and spatial resolution are shown to be improved, although no mention is made in case of splintered peaks. Corresponding correlation windows can also be sized differently (Liang et al. 2002). Such an approach could potentially help mitigate the problem of multiple peaks by taking the advantages of using small and large correlation window together. However, correlation maps produced were shown to be noisier and less reliable due to the smaller regions correlated. More importantly, improvements in accuracy and measurement range were shown to rely on displacement vectors obtained in the previous iteration. Alternatively, the interrogation process follows the standard implementation and image intensities captured within correlation windows are altered. Spatial resolution in case of non-uniform velocity fields was shown to be drastically improved in Nogueira et al. (2001) by multiplying interrogation windows with a weighting function prior to correlation, thereby increasing the importance of central pixels within a correlation window compared to those on the periphery. Several shapes and sizes of weighting functions were tested in Astarita (2007), proving that the adoption of weighting functions can improve the spatial results more than simply reducing the interrogation window size. Notwithstanding the great improvements shown, the use of weighting functions was demonstrated with velocity fields of small-scale amplitudes. Weighting functions reduce the luminosity of particles on the edges of the interrogation area, thus inherently discarding the information pertaining the displacement of those particle images. Weighting functions therefore lower the probability of multiple correlation peaks appearing, but simultaneously produce velocity vectors which are not necessarily representative of the underlying displacement field captured within the interrogation areas. Irrespective of the correlation response, also the vector location must be appropriate. In Young et al. (2004), the problem of velocity gradients has also been tackled in terms of vector location. Displacement vectors are usually anchored in the geometric centre of the interrogation area. This is not necessarily representative of the fluid motion in case of non-uniform velocity fields. The solution proposed by Young et al., was to anchor the vectors to a location more representative of the underlying flow motion. This involved shifting the particle image intensities according to the identified displacement, multiplying the shifted intensity fields and anchoring the vector to the location of the maximum element in their multiplication plane. In spite of the improvements produced by this method, a single vector per correlation window was produced, limiting its application in case of multiple peaks.

The algorithms mentioned afore all highlight the problematic surrounding the appearance of multiple peaks in a correlation map when high velocity gradients are present, yet, none offer a satisfactory solution. In this paper a novel Multiple Peak PIV algorithm (MP-PIV) is proposed, capable of dealing with splintered peaks in the correlation-map. Details of the methodology are provided in Sect. 2. In short, every prominent peak is considered to be a potential displacement. The suggested methodology enables the measurement of these displacements by detecting and analysing all the peaks of the correlation map, producing multiple vectors per correlation window. This approach thus improves the measurement of displacements in case of strong in-plane gradients. The procedure is articulated in two sub-processes. First, strong significant peaks are selected and discerned from random noise. This process is carried out through an automatic thresholding method exploiting the correlation map histogram. Each selected peak then produces one or more vectors anchored to a sub-correlation grid. Vector locations are chosen by shifting the images according to each displacement and by checking the quality of the overlapping images through cross-correlation. Not only is all the valid information contained in the correlation map used to the fullest, also vector locations become more accurate allowing a better estimation of the velocity predictor. Numerical analyses through Monte-Carlo simulations are presented for a boundary layer of varying amplitude and a sinusoidal velocity field of variable frequency in Sect. 3. Together with an experimental test case (Sect. 4) all assessments indicate the proposed solution to yield a drastic improvement in PIV measurements’ accuracy and attainable resolution.

Methodology

The Multiple Peak PIV (MP-PIV) methodology proposed in this work utilises aspects of the iterative predictor-corrector algorithm presented in Scarano and Riethmuller (2000) and is outlined in Fig. 2. Interrogation areas are still distributed on a Cartesian grid and cross-correlated. Contrary to the standard approaches however, vectors are not located in the geometrical centres of these areas. Instead, once each pair of correlation windows is evaluated, multiple peaks are detected and discerned from the correlation noise as described in Sect. 2.1. A second layer of sub-correlation windows (or sub-interrogation areas) is then used to select the displacement vectors and anchor them to the sub-windows’ geometrical centres (Sect. 2.2). As per common multi-grid approaches where interrogation windows are iteratively halved, sub-correlation window sizes are half the size of the parent window with a minimum of 17 pixels. In order to find the most adequate sub-interrogation area for each vector, the initial interrogation areas are shifted (not deformed) according to each of the peaks’ displacement. A secondary cross-correlation between the shifted images is performed once more in the sub-interrogation areas and high signal-to-noise ratios indicate the sub-window’s centre to be appropriate to allocate the vector. Otherwise the node is left available for the analysis of a different peak. Peaks for which no good match was found are automatically discarded.

Fig. 2

Flow chart of the MP-PIV algorithm. Notice the collocation of two different sets of correlation points: correlation windows to detect displacements and sub-correlation windows to anchor vectors

Once correlation windows have been analysed, the displacement field is validated using a normalised median threshold (Westerweel and Scarano 2005) and corrupted vectors are replaced using the median of their neighbours. The final displacement field is then interpolated to produce a displacement predictor for the successive iterations.

Multiple peak detection

Several situations can cause multiple peaks. If particle images move uniformly, and sufficient particle images are in the interrogation region, a single peak will appear in the correlation map. If clusters of particles move in different directions within the same interrogation area, the correlation map will show distinct peaks for each cluster. Also when individual particle images move in random directions, particles disappear from the first to the second image or images are poorly seeded and contaminated with noise, cross-correlation will equally produce a map presenting multiple peaks. These peaks are not necessarily related to actual displacements though (Fig. 3a). It is therefore essential to discern proper peaks associated to displacements from random noisy peaks (see Fig. 3b). In MP-PIV, this task is automatically carried out in three successive steps. Peaks are first detected as local extrema in the correlation map through a simple local maxima detection in an 8-by-8 neighbourhood. These local correlation maxima include both displacement peaks and correlation noise and require further filtering. In the second step candidate displacement peaks are selected using the automatic triangle threshold method (Zack et al. 1977). Details about the method are provided in the next paragraph. Finally, valid peaks are retained through a user-defined SNR.

Fig. 3

Examples of correlation maps with multiple peaks due to a bad correlation and b multiple displacements

Triangle thresholding

The automatic thresholding method adopted in this work to distinguish displacement peaks from correlation noise was proposed for the first time in Zack et al. (1977) to discern bright objects from a dark background. The method is used here to exploit the histogram of the correlation map and, in particular, its peculiar shape in case of PIV images. Since correlation peaks only constitute a small portion of the histogram, they can be easily distinguished from background noise with a geometrical process of maximization. Given the histogram of the correlation map, as depicted in Fig. 4, the line between the maximum number of elements (Max pdf) and the maximum correlation peak amplitude (Max corr) is considered. When dealing with most commonly correlation coefficients, Max corr will equal one. For each bin of the histogram, the distance between its value and the max-max line is evaluated. This distance is plotted in red in Fig. 4 above the triangle. The bin location corresponding to the maximum distance, incremented by a normalized offset (typically 0.1), is considered as a threshold to discern good peaks from correlation noise, i.e. the first peak-selection is done on the basis of correlation peak amplitude.

Fig. 4

The principle of triangle thresholding as an automated method to discern strong peaks from correlation noise. The blue plots represents the histogram (PDF) of the correlation map, with the black line connecting the maximum of the correlation (on the x axis) with the maximum value of the PDF (on the y axis). The red plots represents the distance between the max-max line and the values of the histogram. The maximum value of this distance, shifted by an offset of typically 0.1, yields the automatic threshold

Peak refinement by Signal-to-Noise ratio

An accustomed measure of the correlation peak’s reliability and validation heuristic of the obtained particle image displacement estimate is the common ratio between the highest and second highest peak amplitude. In MP-PIV the authors revisit this definition since a SNR close to one actually implies both correlation peaks to be of equal magnitude and to potentially contain particle image displacement information provided they are both above the correlation noise. The afore triangle threshold presents an automatic means of discerning strong peaks from the correlation noise based on the peak heights. However, in case of noisy correlation maps (Fig. 3a), displacement peaks might be hard to detect or not even exist, potentially compromising the triangle threshold. For this reason, a secondary peak refinement is implemented.

Given N candidate peaks selected by the triangle threshold (e.g. the five highest peaks in Fig. 5), and denoting the set of sorted correlation peak values in descending order as $P=\{P_1,P_2,\ldots ,P_N\}$, the SNR of the $i\mathrm{th}$ peak is defined as

$$\begin{aligned} \mathrm{SNR}_i = \frac{P_{i}}{P_{i + 1}}. \end{aligned}$$

(1)

The subset of peaks considered for further investigation are then all peaks preceding the first peak within the set P (hence of higher amplitude) for which the $\mathrm{SNR}_i$ is higher than a user-defined threshold $\sigma _{{\mathrm{thr}}}$. Figure 5 shows an example of this filter for 50 peaks. The first five peaks are considered on the basis of the triangle threshold. With a typical SNR threshold of 1.3, the third peak is the first for which the $\mathrm{SNR}_i$ is above the threshold. Accordingly, only the first three peaks are retained for further consideration as these peaks are supposed to be sufficiently distinguishable from correlation noise. Once the selection of correlation peaks is refined, displacement vectors are collocated on a sub-correlation grid, as described in the next section.

Fig. 5

Illustration of the correlation peak refining process using Signal-to-Noise ratio (SNR). The example shows an application containing 50 randomly generated peaks, extracted from a normal distribution, sorted from the highest to the smallest. The first peak selection is based on peak amplitude through the triangle-threshold method. The secondary selection is based on the consecutive SNR with a user-defined lower limit

Vector allocation

The detection of multiple peaks in the correlation map provides the necessary information regarding the captured particle image displacements. The missing information is still the spatial distribution of these displacements i.e. where displacement vectors should be positioned in the interrogation area. The solution proposed in this work is to anchor the displacement vectors to a grid of sub-correlation windows, as shown in Fig. 6, thus retaining a structured vector distribution. Peaks selected from the previous step are processed from the highest to the lowest. For each peak, interrogation areas are simply shifted using the sub-pixel peak displacement. The grid of sub-interrogation areas (shown in red in Fig. 6) is subsequently cross-correlated to measure the quality of mutual particle image overlap. Sub-correlation maps presenting one single peak (high SNR) indicate good locations to anchor the considered displacement vector in its centre. If multiple peaks appear (low SNR), the grid node will be left for the analysis of the next peak. In order to increase the displacement accuracy and speed up the predictor-corrector convergence, sub-correlation maps are also used to provide an additional sub-pixel correction to the displacement corresponding to the scrutinized correlation peak (Willert and Gharib 1991).

Fig. 6

Layout of correlation and sub-correlation windows adopted in the MP-PIV algorithm. Correlation windows (green) are used to detect multiple displacements peaks. No vector is allocated in these areas. Instead, sub-correlation windows (red) are used to assess each of the selected potential particle displacements. Displacements yielding the highest correlation peak within a sub-window are anchored to the geometrical centre of the sub-correlation window

This vector positioning procedure ensures that higher peaks will always have a priority on smaller peaks, increasing the robustness of the algorithm. Moreover, velocity vectors will only be generated if good particle image matching locations are available. A detailed description of the algorithm can be found in Algorithm 1. The method is implemented in a predictor-corrector fashion, as already shown in Fig. 2. Once all the correlation windows are processed, displacement vectors are validated using the normalized median threshold (Westerweel and Scarano 2005) and interpolated on a pixel-grid using quintic spline (Astarita and Cardone 2005).

¹

Numerical assessment

Improvements achieved with MP-PIV by resolving splintered peaks have been quantified through Monte-Carlo analyses. Assessments have been performed on synthetic images involving two different velocity fields: a boundary layer of increasing free-stream velocity, tested for different seeding densities, and a sinusoidal field of varying frequency, tested for different amplitudes. Synthetic images were generated following the approach described in Lecordier and Westerweel (2004) using Gaussian shaped tracer images, with diameters drawn from a normal probability $\mathcal {N}(\mu ,\sigma ^2)=\mathcal {N}(3{\mathrm{\ pixel}},1{\mathrm{\ pixel}}^2)$. The mean intensity of particles was 50% of the maximum gray scale and the standard deviation was 18%. Intensity profiles were integrated over pixel elements adopting a pixel fill-ratio of unity and discretised in 16 bits. The synthetic images were not altered with artificial noise , such that observed differences in performance could be ascribed solely to algorithmic variations..

MP-PIV was tested and compared to four different PIV techniques. The first technique, referenced hereafter as MGRID, is similar to the multi-grid algorithm of Scarano and Riethmuller (2000) but without any vector validation. In a slightly modified version of MGRID, MGRIDF, a SNR filter is introduced to automatically exclude vectors with a SNR below 1.3. MGRIDF is thus identical to standard multi-grid methods. In order to investigate the improvements in terms of spatial resolution, intensity weighting as suggested by Nogueira et al. (2001) has been included and is referred to as LFC (local field correction). Finally, a PIV algorithm adopting cross-correlation between windows of different sizes (DSIW, different sized interrogation windows) was also considered as described by Liang et al. (2002). An overview of the considered algorithms in terms of their difference in settings is given in Table 1.

Table 1 Summary of the algorithms used in the numerical assessment

Boundary layer

The displacement field (u, v) related to a laminar boundary layer on flat plate was simulated by resolving Prandtl’s equations (Prandtl 1938) in the vicinity of a wall, i.e. Blasius’ solution;

$$\begin{aligned}&2\frac{\mathrm{d}^{3}f}{\mathrm{d} \eta ^3}+f\frac{\mathrm{d}^2 f}{\mathrm{d} \eta ^2}=0 \quad \text{ with } \quad f(0)=\frac{\mathrm{d}f}{\mathrm{d} \eta }(0)=0 \quad \text{ and } \quad \underset{\eta \rightarrow \infty }{lim}\frac{\mathrm{d}f}{\mathrm{d} \eta }(\eta )=\infty \nonumber \\&\quad u=U_{\infty }\frac{\mathrm{d}f}{\mathrm{d} \eta }, \quad v=\frac{1}{2}\root \of {\frac{\nu U_{\infty }}{x}}\left\{ \eta \frac{\mathrm{d}f}{\mathrm{d} \eta }-f\right\} , \quad \eta =y\root \of {\frac{U_\infty }{\nu x}} \quad \text{ and } \quad \delta =\frac{5.0}{\root \of {U_{\infty }/\nu x}}. \end{aligned}$$

(2)

The free-stream displacement $U_\infty$ was adjusted from 0.5 to 33 pixels with increments of 0.5 pixels. A total of 5000 independent simulations were performed for each displacement field. The simulations were repeated for three seeding densities: 0.03, 0.1 and 0.3 particles per pixel (ppp). The boundary layer thickness $\delta$ was set to a constant 64 pixels and the error analysis was focused on an image portion of 65-by-65 $\mathrm{pixels}^2$ in size adjacent to the wall. Window sizes WS were reduced from 65 to 17 pixels in three refinement steps. Imposing a 75% window overlap, a final displacement field with a constant vector spacing of 4 pixels was obtained giving a total of 225 vectors. A plot of the velocity profiles is presented in Fig. 7.

Fig. 7

Boundary layer profiles across the initial interrogation window ($WS_{init}=65$ pixels), for different free-stream pixel displacements ($U_\infty$), imposed in the numerical assessments

Due to the potential appearance of multiple valid correlation peaks, the single resulting velocity vector is highly dependent on the underlying flow and instantaneous seeding distribution. To quantify the correspondence between the imposed ideal $(u_{{\mathrm{id}}},v_{{\mathrm{id}}})$ and measured $(\hat{u},\hat{v})$ displacements, results are shown in terms of normalised root of the averaged mean square error in the velocity components ($\epsilon$, hereafter referred to as error) (Schluchter 2005). This heuristic does not distinguish between bias and random error but is indicative of how representative the measurement is of the underlying flow, and was evaluated as ($N=1000\times 225$):

$$\begin{aligned} \varepsilon = \frac{1}{U_{{\mathrm{ref}}}}\sqrt{\frac{1}{N}\sum _{i=1}^{N}\left[ \frac{\left( u_{{\mathrm{id}}}-\hat{u_i}\right) ^2+\left( v_{{\mathrm{id}}}-\hat{v_i}\right) ^2}{2}\right] }, \end{aligned}$$

(3)

where $U_{{\mathrm{ref}}}$ is the spatially averaged velocity $U_{{\mathrm{ref}}}=\frac{1}{N}\sqrt{\sum _i \left( u_{{\mathrm{id}}}^2+v_{{\mathrm{id}}}^2\right) /2}$. Plots of the measurement error are presented against the free-stream velocity $U_\infty$ and the maximum rate of strain S;

$$\begin{aligned} S_{\max }\equiv \frac{\partial u}{\partial y}\Bigr |_{y=0}=\frac{5.0 U_\infty }{\delta }\frac{\mathrm{d}^2 f}{\mathrm{d} \eta ^2}\Bigr |_{\eta =0}\equiv \frac{1.6605 U_\infty }{\delta}. \end{aligned}$$

(4)

Equation 4 expresses the velocity gradient in terms of pixels/pixel, which, given the imposed values, ranged from 0.013 pixels/pixel ($U_{\infty }=0.5\, \mathrm{pixels}$) to 0.85 pixels/pixel ($U_{\infty }=33\, \mathrm{pixels}$).

Figure 8a presents the results of the error analysis for a seeding density of 0.03 ppp. For such a small seeding density, DSIW is unable to produce a reliable correlation map and produces noisy results even for the smallest gradients tested. By increasing the free-stream velocity, $\epsilon$ for DSIW appears to initially decrease. However, the reader should note that the absolute error ($\epsilon U_\mathrm{ref}$) is actually increasing. The observable tendency is only due to the adopted normalization in Eq. 3. The other image processing approaches present a constant normalised error $\epsilon$ of approximately 0.03 up to a gradient of 0.2 pixels/pixel. After this point, MGRID, MGRIDF and LFC present a sharp increase in error while MP-PIV remains constant. When gradients are increased up to 0.5 pixels/pixel, the normalised error for MP-PIV increases to 0.10 compared to 0.20 (MGRIDF), 0.25 (LFC), 0.32 (MGRID) and 0.36 (DSIW). Increasing the velocity gradients even further from 0.5 to 0.6 pixels/pixel, standard PIV algorithms produce error levels which are more than 20% the $U_{{\mathrm{ref}}}$ whereas the error with MP-PIV remains below 20% up to a gradient of 0.7 pixels/pixel.

Fig. 8

Results for the boundary layer simulation. Normalised error plots are presented for three different levels of seeding density: a 0.03, b 0.1 and c 0.3 ppp. MGRID multi-grid, MGRIDF multi-grid with SNR filter, LFC local field correction, DSIW different sized interrogation windows, MP-PIV multiple peak PIV. See Table 1 for details

In Fig. 8b, the curves for a seeding density of 0.1 ppp show a similar behaviour to the case of lower seeding density (Fig. 8a), with the biggest difference being the change in error with DSIW. For this seeding density, the reliability of DSIW has improved, yielding error levels on par with the other methodologies tested. It is worth noting the difference between MGRID and MGRIDF. The mere implementation of a SNR threshold in MGRIDF allows a reduction of the error when dealing with less severe gradients, confirming the detrimental effect of multiple correlation peaks if left untreated. However, at higher gradients imposing a SNR threshold inhibits the detection of a valid correlation peak among multiple peaks of (near-)equal magnitude, increasing the overall error. Best results are obtained by MP-PIV with lowest error levels throughout the entire range of gradients tested. LFC, which aims to enhance spatial resolution, produces error levels which are slightly lower than the other techniques tested, but only in the lower range of gradients (between 0 and 0.25 pixels/pixel). The adoption of a weighting window is well-documented to increase the spatial resolution of the measurement (Astarita 2007; Nogueira et al. 1999). Current results show though that weighting can be harmful if the linear size of the window is not increased accordingly. Particles belonging to the periphery of the window will contribute less to the correlation peak, producing worse results in case of high amplitude displacements. This observation is confirmed by the error levels produced by LFC in case of high gradients. Figure 8a–c show that the error generated by LFC for gradients higher than 0.5 pixels/pixel can be more than twice the error produced by the other techniques.

With increasing seeding density error levels generally reduce. At a seeding density of 0.3 ppp (Fig. 8c) DSIW produces results which are slightly better than MGRID, MGRIDF and LFC, especially in case gradients are higher than 0.5 pixels/pixel. However, also in this case, MP-PIV obtains the lowest error levels across almost the entire range of gradients tested, confirming it being the most suitable methodology for complex velocity fields.

Sinusoid test

To characterise the behaviour and improvements of MP-PIV even further, the algorithms’ response to a one-dimensional sinusoidal displacement field was considered:

$$\begin{aligned} u_{{\mathrm{id}}}(x,y) = A\sin \left( y \frac{2\pi }{\lambda } + \phi \right) . \end{aligned}$$

(5)

Sinusoidal displacements were imposed by adjusting the normalised wavelength from 0.25 to 1.5 and randomly selecting the phase $\phi$ in a Monte-Carlo fashion. The normalised wavelength was defined as the ratio between the smallest correlation window size ${\rm WS_{\min }=17 pixels}$ and imposed sinusoidal wavelength $\lambda$; $\lambda ^* ={\mathrm{WS}}_{\min }/\lambda$. Amplitudes A of 3, 5 and 7 pixels were imposed. Measured displacement fields were fitted with a sinusoid and the reconstructed amplitude $\hat{A}$ was normalised with the imposed A producing an evolution in normalised amplitude $\hat{A}/A$ with normalised wavelength $\lambda ^*$. For all sinusoids tested, the seeding density was kept at a constant value of 0.1 ppp. Images were analysed once again with initial window sizes of 65 pixels and iteratively halved to 17 pixels. A mutual window overlap of 75% was set to obtain a final vector spacing of 4 pixels.

Fig. 9

Plots of the normalised amplitude $\hat{A}/A$ for the numerical assessment involving a sinusoidal displacement field considering three different amplitudes: a A=3, b A= 5 and c A=7 pixels. MGRID multi-grid, MGRIDF multi-grid with SNR filter, LFC local field correction, DSIW different sized Interrogation Windows), MP-PIV multiple peak PIV. See Table 1 for details

For a sinusoid of 3 pixels of amplitude, results are presented in Fig. 9a. The plots show that only for small amplitudes the frequency response of cross-correlation resembles the expected behaviour of a moving average (Scarano 2003; Theunissen 2012). MP-PIV performs slightly better compared to the other approaches, except for LFC. For this specific velocity field, the spatial resolution obtained using LFC is superior to the other techniques tested, with values of normalized amplitude higher than 0.5 up to $\lambda ^*\approx 1.1$. This increased spatial resolution is to be expected as the advantages of using a weighting functions have already been shown in the literature (Astarita 2007). From a practical perspective however, smaller amplitudes demand reduced temporal separation between snapshots, which as advocated is not always optimal. When the sinusoid amplitude is increased from 3 to 5 pixels (Fig. 9b), LFC begins to show the same deficiencies as presented in Sect. 3.1 with an increased amplitude modulation for $\lambda ^*<0.6$ compared to the other analysis approaches. At $A=5 \mathrm{pixels}$, MP-PIV behaves slightly better than the other methods tested, offering a marginally higher spatial resolution in the range $\lambda ^*=0.3$–0.7. Increasing the sinusoid amplitude even further (Fig. 9c) to $A=7 \mathrm{pixels}$, the frequency response of all the algorithms becomes completely different from the standard moving average assumption, confirming the strong non-linearity of the PIV algorithm (Theunissen 2012). When a sinusoid of 7 pixels amplitude is analysed, MP-PIV presents the best spatial resolution among all the algorithms tested, with LFC showing the worst spatial resolution for the same reason as described in Sect. 3.1.

Computational effort

An absolute measurement of the computational effort for MP-PIV is impossible to provide since it is entirely dependent on the complexity of the flow. In case of simple velocity fields (i.e. flow gradients are such that correlation maps contain a single peak), the computational overload is only constituted by the vector positioning process. All the parameters being equal to a standard PIV algorithm (i.e. correlation window size, vector spacing, number of iterations, interpolation technique, etc.), the additional overload for MP-PIV slows down the analysis by a factor of 1.5. However, such a comparison is unfair. In fact, MP-PIV produces a denser displacement field from the first iteration and could potentially reduce the number of iterations required for the predictor-corrector to converge, saving computational time compared to a standard PIV algorithm.

When multiple peaks are present, the computational overload depends on several factors, including but not limited to: the quality of the images, the seeding density, the complexity of the flow, the sensitivity ($\sigma _\mathrm{thr}$) chosen by the user, etc. For very complex interrogation windows (more than five peaks detected), a computational time up to six times higher was experienced. However, the reader should note that the additional computational time for a single correlation window does not necessarily imply a slower analysis for the entire image, since a slower but more accurate displacement field in the first iteration allows a potential reduction in the required number of successive iterations.

Fig. 10

Computational time for different techniques analysed in Table 1. The computational time for MP-PIV is strongly dependent on the complexity of the flow field. MGRID multi-grid, MGRIDF multi-grid with SNR filter, LFC local field correction, DSIW different sized interrogation windows, MP-PIV multiple peak PIV. See Table 1 for details

Figure 10 presents the computational time for MP-PIV and other techniques described in Table 1 for a pair of synthetic images of a boundary layer as described in Sect. 3.1. As the amplitude of the boundary layer increases, the flow becomes more complex and the computational time of MP-PIV rises as advocated. MP-PIV has been tested for three different seeding densities, 0.03, 0.1 and 0.3 ppp (particles per pixel) to show the dependency of the computational time on the amount of particle images. As the seeding becomes denser, the underlying flow is better sampled and correlation maps will contain more information, enabling an increased number of correlation windows to be elaborated by MP-PIV and rendering a more accurate flow field (cf. Fig. 8).

Experimental application

To assess the proposed MP-PIV algorithm in more realistic conditions, an application to experimental PIV images of the wake flow behind a porous disc is proposed. Measurements were conducted behind a circular disc placed in the low turbulence wind tunnel of the University of Bristol. This tunnel attains turbulence levels below 0.05% and has an octagonal test section of 0.8 m$\times$0.6 m. Four 3 mm diameter piano-wires held the disc in place, which was subjected to a freestream velocity of 30 m/s impinging perpendicular to the frontal surface. The disc had a thickness of 6 mm and a diameter $D_{{\mathrm{disc}}}$ of 6 cm resulting in a negligible blockage of 0.16% at a diameter-based Reynolds number $Re_D$ of $11.6\times 10^4$. Six perforations, each with a radius $r_{\rm p}$ of 3.87 mm ($r_p\approx 0.065 \times D_{{\mathrm{disc}}}$), were located at a radius $r_{\rm a}$ of 1.08 cm to establish a porosity $\beta$ (open/closed area) of 0.10 (Fig. 11a).

Fig. 11

a Sketch of the porous disc tested. The green line indicates the location of the PIV measurement plane. b Exemplary PIV image recording illustrating the reflections off the disc surface (left) and mirror images/reflections (middle). Flow is from left to right

Seeding was generated by atomizing a mixture of PEG-80 and water producing $1\,\upmu \text{m}$ tracer particles. Illumination was provided by a Litron 200 mJ laser with a repetition rate of 15 Hz. An optical arrangement of cylindrical and spherical lenses transformed the laser beam into a 1 mm thick laser sheet positioned along the centre of two pores. Images were recorded with a Speedsense M340 camera. A 75 mm focal length lens with f-stop set at 16 was utilized, producing particle image diameters of approximately 2–3 pixels. The CMOS sensor consisted of $10\,\upmu \text{m}$ pixels arranged in a $2560 \times 1600$ array. With a calibration factor of 15.5 pixels/mm the corresponding field of view covered approximately 2.75 disc diameters downstream and $1.72\times D_{{\mathrm{disc}}}$ in vertical direction. The separation between laser pulses was set at $40\,\upmu \text{s}$, producing a maximum particle image displacement of approximately 25 pixels at the pores. An exemplary image snapshot is depicted in Fig. 11b.

Fig. 12

Average displacement field (sub-sampled for displaying purpose) and average velocity magnitude for the disc images. Red dashed lines are the locations where profiles are extracted (Figs. 13, 14)

Images were analysed using the same algorithms adopted in the previous section. The window size was reduced from 256 to 16 pixels in five predictor-corrector iterations and a mutual overlap of 75% between correlation windows was imposed. Images were interpolated using quintic spline (Astarita and Cardone 2005) and velocity fields were validated using the normalized median threshold (Westerweel and Scarano 2005). A mask was automatically generated to ignore pixels belonging to the disk².

The average velocity field is shown, together with the displacement magnitude, in Fig. 12. With a jet-like flow issuing from the pores, velocity gradients in the order of $\frac{\partial u}{\partial y}\equiv 0.6\,\, \mathrm{pixels/pixel}$ are encountered near the geometrical pore boundaries. Horizontal gradients $\frac{\partial u}{\partial x}$ can be as high as 1.1 pixels/pixel. Velocity profiles for the horizontal displacement are extracted along the red dashed lines and are presented in Figs. 13 and 14. The first remarkable result is the behaviour observed with DSIW. Due to the low seeding density of the images, estimated to be approximately 0.05 ppp, DSIW produces correlation maps which are far too noisy to produce a reliable displacement field. As a result, velocity profiles for DSIW, presented in Figs. 13 and 14 differ completely from the other techniques tested. This behaviour was already shown in the numerical assessment (Fig. 8a) and is confirmed by this experiment. The use of DSIW is therefore strongly discouraged in case of images presenting low seeding density.

Results of Figs. 13 and 14 are in agreement with the observation of the numerical assessment in that LFC is unable to measure gradients in case of high intensity displacements. This is the case near the pores of the disc. From the horizontal profile, the maximum displacements measured on the jet centerlines with LFC are 22.1 (upper jet) and 23.0 pixels (lower jet), whereas MP-PIV is able to measure displacements, in identical locations, of 23.6 and 24.0 pixels. Measured displacements with MGRID and MGRIDF are between those obtained with LFC and MP-PIV, in accordance with the synthetic results for the boundary layer (Fig. 8).

Fig. 13

Profiles of mean horizontal velocity component extracted along respectively $y/D_{disc}\approx \pm \frac{1}{6}$ in Fig. 12. See Table 1 for a description of the considered methods. MGRID multi-grid), MGRIDF multi-grid with SNR filter, LFC local field correction, DSIW different sized interrogation windows), MP-PIV multiple peak PIV. See Table 1 for details

The discrepancies in vertical velocity profiles depicted in Fig. 14 are consistent with the previous observations. The velocity profiles in Fig. 14a, taken in vicinity of the jets show strong modulations in peak jet velocity depending on the image processing methodology; LFC attains a maximum displacement of 17.0, MGRID and MGRIDF of 23.2 and MP-PIV of 24.0 pixels. DSIW returns entirely erroneous results. For the velocity profiles in Fig. 14b, extracted further downstream, gradients are less intense and the velocity profiles agree more closely, which supports the results of the numerical assessments.

Fig. 14

Vertical profiles of the u component of the mean velocity extracted along the vertical red dashed lines of Fig. 12 at respectively $x/D_\mathrm{disc}=\,\approx 0.1$ and $x/D_\mathrm{disc}=\,\approx 0.45$. MGRID multi-grid, MGRIDF multi-grid with SNR filter, LFC local field correction, DSIW different sized interrogation windows, MP-PIV multiple peak PIV. See Table 1 for details

Residual displacements

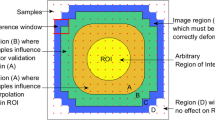
The higher displacements measured by MP-PIV are not necessarily an indication of better measurements. In order to investigate the quality in case of experimental images, a post-processing analysis which the authors refer to as residual displacements is proposed. For each pair of analysed snapshots the final displacement field is used to deform the initial images, as per standard predictor-corrector iterations. Deformed images are then re-analysed, independently, with three different window sizes: 17, 33 and 65 pixels. The vector spacing is kept constant to 33 pixels and the norm of the displacement, for each window size, is stored. The maximum displacement among the three windows tested is then selected and referred to as the residual displacement (RD). This analysis of RD provides a robust indicator of quality of the measurement for experimental images; a displacement vector is correct when the PIV images, deformed with that vector, are perfectly overlapping in the vector’s neighbourhood, in which case RD = 0. The detrimental effect of erroneous and unrepresentative displacement estimates will echo throughout the iterative process and may appear as large displacement inaccuracies in the final result. These are detectable (large RD) with only the larger window sizes.

The authors would like to highlight the existence of uncertainty quantification methodologies such as particle disparity (Andrea et al. 2013) and correlation statistics (Bernhard 2015). These methods work on the presumptions that the scrutinised displacement is within only a few pixels of the true value and only one dominant vector is encountered in the correlation map. Neither of the assumptions necessarily hold in the cases considered in the present work, necessitating the new heuristic RD. The reader should also note that RD cannot be used as a correction for local vectors (as per standard multi-grid algorithms) since vectors from the RD result from a process involving multi-sized interrogation areas and do not follow from an iterative window size halving.

Fig. 15

Average residual displacements for a MP-PIV, b LFC, c MGRID, d MGRIDF, e DSIW. Values of the residual for e DSIW were cut because the same scale as other methods was used for consistency. MP-PIV attains the lowest levels of residual near the jets area, where gradients are the strongest

A comparison for all the methodologies tested in terms of ensemble averaged RD is presented in Fig. 15. In the vicinity of the jets high particle displacement approximating 25 pixels can be encountered as the pores act as vena contracta, accelerating the flow. The velocity gradients in this area are too high for a standard PIV algorithm as corroborated by the RD-values shown in Fig. 15b–e. The residual displacement for DSIW is extremely high and not even comparable with the other techniques tested. This behaviour is in agreement with the velocity profiles shown in the previous section and provides another confirmation of the unsuitability of DSIW for lower seeding densities. Figure 15a–d show very similar RD fields with the main difference being near the pore exits and disc rim ($y/D_{\rm disc}\approx \pm 0.5$) whereas the bulk of the flow presents resolvable velocity gradient magnitudes. Here, the residual displacements for MP-PIV are shown to be the lowest among all the techniques tested, with LFC being the highest and MGRID/MGRIDF being in between.

Fig. 16

Horizontal profiles of the residual displacement extracted along the red dashed lines ($y/D_\mathrm{disc}\approx \pm \frac{1}{6}$ respectively) of Fig. 12. MGRID multi-grid, MGRIDF multi-grid with SNR filter, LFC local field correction, DSIW different sized interrogation windows, MP-PIV multiple peak PIV. See Table 1 for details

Horizontal profiles for the average RD are presented in Fig. 16 for the red dashed lines of Fig. 12. The profiles show MP-PIV attaining RD levels below 3 pixels, confirming its better suitability to describe the flow displacement in case of strong gradients and high intensity displacements. Values of RD near the jets for MGRID/MGRIDF are around 4–5 pixels, and 8–9 pixels for LFC, with more than 18 pixels for DSIW. Far away from the jets, similar values of RD are experienced for all the methodologies tested, with DSIW still producing the highest RD.

Fig. 17

Vertical profiles of the residual extracted at respectively $x/D_\mathrm{disc}\approx 0.1$ and $x/D_\mathrm{disc}\approx 0.45$ (red dashed lines of Fig. 12)

The vertical profiles for RD are finally shown in Fig. 17. The plots present once again a generally higher value of RD in the vicinity of the jets ($x/D_{{\mathrm{disc}}}\approx 0.05$) where gradients are the highest and standard PIV algorithms fail to measure the displacements. MGRID and MGRIDF produce a RD of about 4 pixels, LFC values are around 8 pixels and DSIW is completely out of line with RD in excess of 18 pixels. Results are the best for MP-PIV, with levels of RD below 2 pixels across the entire profile.

Conclusions

Correlation maps in PIV image analyses can present multiple peaks when strong gradients in particle image displacement are encountered within interrogation windows. A method to detect relevant correlation peaks and generate multiple vectors per interrogation region was proposed. Strong peaks are automatically discerned from the correlation noise using a threshold based on the histogram of the correlation map. Selected peaks are analysed in sequence to understand which areas of the interrogation window contribute to which identified correlation peak. This task is fulfilled through a secondary grid of sub-interrogation areas, each half the size of the parent correlation window. The geometrical centres of these sub-windows serve as anchor locations for subsequent displacement vectors. For each identified correlation peak, sub-interrogation windows are translated according to the corresponding displacement. The most suitable displacement for each sub window is then found through a secondary cross-correlation based on, among all the tried displacements pertaining the identified peaks, the strongest SNR.

The algorithm has been assessed with Monte-Carlo simulations performed with two synthetic flow fields: a boundary layer of varying intensity and a one dimensional sinusoidal field of varying frequency and amplitude. Results indicated the proposed algorithm, MP-PIV, was able to outperform existing PIV methodologies by allowing a lower measurement error in the presence of strong velocity gradients, attaining errors which are as low as half the alternatives tested. Moreover, results for the sinusoid test showed an improved spatial resolution in case of high amplitudes.

Finally, an experimental test case offered a further opportunity to explore the advantages of MP-PIV in case of real images. Images for a porous disc were analysed with different image processing methodologies and residual displacements were presented and compared. Velocity profiles and residual displacements confirmed the results obtained for the synthetic test cases with MP-PIV allowing a better measurement of image displacements in the flow area most affected by velocity gradients.