Temperature decline thermography for laminar–turbulent transition detection in aerodynamics

Abstract

Detailed knowledge about laminar–turbulent transition and heat transfer distribution of flows around complex aerodynamic components are crucial to achieve highest efficiencies in modern aerodynamical systems. Several measurement techniques have been developed to determine those parameters either quantitatively or qualitatively. Most of them require extensive instrumentation or give unreliable results as the boundary conditions are often not known with the required precision. This work introduces the simple and robust temperature decline method to qualitatively detect the laminar–turbulent transition and the respective heat transfer coefficients on a surface exposed to an air flow, according to patent application Stadlbauer et al. (Patentnr. WO2014198251 A1, 2014). This method provides results which are less sensitive to control parameters such as the heat conduction into the blade material and temperature inhomogeneities in the flow or blade. This method was applied to measurements with NACA0018 airfoils exposed to the flow of a calibration-free jet at various Reynolds numbers and angles of attack. For data analysis, a post-processing method was developed and qualified to determine a quantity proportional to the heat transfer coefficient into the flow. By plotting this quantity for each pixel of the surface, a qualitative, two-dimensional heat transfer map was obtained. The results clearly depicted the areas of onset and end of transition over the full span of the model and agreed with the expected behavior based on the respective flow condition. To validate the approach, surface hotfilm measurements were conducted simultaneously on the same NACA profile. Both techniques showed excellent agreement. The temperature decline method allows to visualize laminar–turbulent transitions on static or moving parts and can be applied on a very broad range of scales—from tiny airfoils up to large airplane wings.

Introduction

For the design of modern aircraft engines with highest possible efficiencies, it is of great interest to optimize airfoils regarding their losses and performance at design conditions. To design the layout of such airfoils, a detailed knowledge of the boundary layer state for all points on the blade surface and for all operating conditions is crucial. This is hard to access for most measurement techniques on fast rotating parts. Due to increasing drag and efficiency losses, the presence of laminar–turbulent transition on laminar airfoils is not desirable and needs to be fully accessed in measurements to prove the performance of the blade design and to validate CFD calculations.

During the last five decades, many measurement techniques have been developed with the purpose of detecting transitional behavior of boundary layers. A distinction can be drawn between mechanical, electrical, and optical methods accessing boundary layer information in one or two spatial dimensions. A still used mechanical approach for flow visualization is, for example, the oil flow technique (Maltby 1962; Schülein 2004; Radespiel et al. 2013). Oil flows deposit colored pigments on the wall and provide two-dimensional information of boundary layer phenomena such as flow separation in complex geometries. This relatively simple technique is, however, limited by a low repeatability and centrifugal forces on the pigments in rotating applications.

Another extensively used electrical, but one-dimensional technique is based on surface hot films. These films consist of an insulating and isolating material which has very thin electrically conducting traces on its surface. By keeping the temperature of these traces constant, by regulating the electrical current that flows through them, the heat transfer from the blade/film surface into the flow can be determined either qualitatively or even quantitatively after a respective calibration (van Heiningen et al. 1976; Haselbach and Nitsche 1996). A major advantage of these sensors is their high data acquisition frequency and thus the possibility to detect transient behavior in fluid flows. However, the instrumentation is laborious and for measurements on rotating parts, a telemetry system including anemometer electronics would increase the complexity of the setup even more, which is often not tolerable.

To reduce instrumentation and to minimize distortion of the fluid flows, several optical methods have been developed to contactless access the boundary layer with high spatial resolution. Here, particle image velocimetry was used by Ol et al. (2005) to detect laminar–turbulent transition after laminar separation bubbles. Another common optical approach is the utilization of infrared thermography. For example, Bouchardy and Durand (1983) measured the adiabatic temperature distribution on the surface of a blade in a wind tunnel with an infrared camera to detect the transition region. Quast (1987) and more recently Crawford et al. (2013) and Richter and Schülein (2014) applied this technique also in free flight experiments and moving rotor blades. Major drawbacks are, however, the always present reflections of surrounding surfaces on the investigated blade, the varying emissivity of the surface and the dependency on the viewing angle. These effects can easily interact and thus hide the effect of the changing surface temperature caused by transition.

To bypass these effects, a novel approach for measuring the laminar–turbulent boundary layer transition by means of active thermography was filed as an application for a patent by Stadlbauer et al. (2014). Since heat transfer coefficients differ strongly between laminar and turbulent flow state, the transitional behavior of the flow can be accessed by measuring the heat transfer between surface and flow. Therefore, the use of a high-speed infrared camera was proposed for analyzing the temporal temperature decline on a surface after a short heat pulse. Due to higher heat transfer coefficients in turbulent regions, the calculated decline rate is higher than in laminar flow and transition can thus be detected.

Conceptionally, similar approaches were developed by Raffel et al. (2015), where subsequent thermograms of a high-speed infrared camera were evaluated. They proved the application of this technique on freestanding moving rotor blades and demonstrated that the movement of an unsteady transition could be detected. Grawunder et al. (2016) preheated a helicopter model in a wind tunnel to measure the onset and end of transition by analyzing the difference between two normalized thermograms. This analysis approach was proposed by Gartenberg and Wright (1994). In contrast to Raffel et al. (2015) and Grawunder et al. (2016), which use a constant heat source, a pulsed light source was used in this work to make this technique usable for the analysis of fast rotating devices. Furthermore, the present paper refines the idea of the patent document by proposing a beneficial combination of measurement method and physically based post-processing to detect laminar–turbulent transition. It strongly reduces interfering influences due to reflections or irregular surfaces and can, therefore, be used for transition detection even in hard-to-access areas, e.g., on rotating blades in turbo machinery where preheating is not possible. Based on an underlying physical model, the resulting temperature decline rate can be related to the heat transfer coefficient which can be accessed along the analyzed profile.

In the literature, quantitative infrared thermography (QIRT) is used to calculate heat transfer properties from transient temperature data. Therefore, an analytical model by Cook and Felderman (1966) is applied to determine the heat flux based on infrared wall temperature measurements (Schrijer 2012; Astarita and Carlomagno 2012). Especially for fast transient conditions such as in short duration facilities, it is advantageous to use a numerical approach by applying a non-linear least-square fit to the measured data (Schultz and Jones 1973; Schülein 2006). The present study uses a 1D heat transfer simulation for a multi-layer system to access heat transfer coefficients from data measured by the proposed method.

In the following, the measurement principle will be explained. Then, the physical model is described to motivate the proposed post-processing. A possibility to quantitatively measure heat transfer coefficients with this approach is indicated by fitting a numerical model to the measured data. Finally, the performance of this method is examined using a symmetric NACA0018 profile in a free jet facility under different angles of attack and Reynolds numbers. For comparison, surface hot film measurements were performed under equal conditions which are eventually compared to the results of the presented method.

Measurement principle

General setup

Like all IR-based techniques, the approach described here requires a coating of the surface with low thermal conductivity and high emissivity. By heating the respective surface with a short light pulse (generated, e.g., by a flash lamp or a laser), the topmost layer of the coating is heated up a few degrees. Two-dimensional areas can be illuminated at once so that no scanning of the surface is necessary. After the light source has been switched off, a high-speed infrared camera is used to detect the temperature decline for every pixel. This temperature decline is evaluated in a post-processing algorithm resulting in a quantity proportional to the heat transfer coefficient and the wall shear stress. Figure 1 schematically explains the measurement setup.

Fig. 1

Measurement setup

In IR-based measurements, different parameters can interfere with the measured signal and lead to inaccurate results. These include irregular thermal coatings due to varying thicknesses, heat loss into the blade due to non-ideal insulation, inhomogeneous heating of the used light source and interfering reflections due to surrounding components. For the proposed measurement technique, these effects can be distinctively reduced by a novel post-processing method and a reference measurement which is performed without any airflow and subtracted from the measurement with flow. Both measures significantly improve data quality and will be theoretically motivated in the following.

Theory and measurement data analysis

To analyze the data and to determine a quantity proportional to the heat transfer coefficient and the wall shear stress, the simplified model of an ideal thermal insulator is used. The temperature rise ($T^{\prime} = T - T_{\infty }$) directly after the heating pulse is given as

$$T^{\prime}_{0} = \frac{{q_{\text{pulse}} }}{{c_{\text{e}} \rho_{\text{e}} h}},$$

(1)

where $q_{\text{pulse}}$, $c_{\text{e}}$ and $\rho_{\text{e}}$ are the energy density of the heating pulse, the specific heat and the density of the coating, while $h$ denotes the penetration depth of the light pulse. Due to Newton’s law of cooling, the heat flux from the heated surface to the air flow is given by

$$\dot{q}_{\text{w}} = - \alpha T^{\prime},$$

(2)

and therefore, the differential equation for the simplified model of an ideal insulator can be written as

$$\dot{T}^{\prime} = - \frac{\alpha }{{c_{\text{e}} \rho_{\text{e}} h}}T^{\prime},$$

(3)

with the solution

$$T^{\prime}(t) = T^{\prime}_{0} \exp \left( { - \frac{\alpha }{{c_{\text{e}} \rho_{\text{e}} h}}t} \right),$$

(4)

where $\alpha$ represents the heat transfer coefficient.

In the case of an ideal insulator, the heat transfer into the flow can be expressed as

$$\alpha = - c_{e} \rho_{e} h\varLambda$$

(5)

with $\varLambda$ as the temperature decline rate. After thermal excitation, $\varLambda$ is constant and can be determined by the following expression

$$\varLambda = \frac{1}{\Delta t}\ln \left( {\frac{{T^{\prime}_{m + 1} }}{{T^{\prime}_{m} }}} \right) \approx \frac{{2\left( {T^{\prime}_{m + 1} - T^{\prime}_{m} } \right)}}{{\Delta t\left( {T^{\prime}_{m + 1} + T^{\prime}_{m} } \right)}},$$

(6)

where $\frac{1}{\Delta t}$ is the frame rate of the camera and $m$ is the picture index, while the logarithm was approximated by its series expansion. For subsonic air flows with Prandtl number $Pr \approx 1$, the Reynolds analogy factor

$$s = \frac{{c_{\text{f}} }}{2St}$$

(7)

is approximately equal to unity and constant (Incropera and De Witt 1985; Luca et al. 1990). $c_{f}$ denotes the coefficient of friction while $St$ is the Stanton number. The coefficient of friction in the flow is given as

$$c_{\text{f}} = \frac{{\tau_{\text{w}} }}{{\frac{\rho }{2}U_{\infty }^{2} }},$$

(8)

with $\tau_{\text{w}}$ as wall shear stress, $\rho$ as the density of the fluid, and $U_{\infty }$ as the unperturbed velocity of the fluid (Schlichting and Gersten 2006). The heat transfer $\alpha$ and the Stanton number are related by

$$St = \frac{\alpha }{{\rho c_{\text{p}} U_{\infty } }},$$

(9)

with $c_{\text{p}}$ as the isobar heat capacity of the fluid. Equations (5), (7), (8) and (9) can be combined to the following expression

$$\tau_{\text{w}} = \frac{\alpha }{{c_{\text{p}} }}sU_{\infty } = \varLambda \frac{{c_{\text{e}} \rho_{\text{e}} h}}{{c_{\text{p}} }}sU_{\infty } ,$$

(10)

which shows that the wall shear stress, the heat transfer coefficient and the temperature decline rate are proportional if the coating resembles an ideal insulator. For data analysis, Eq. (6) is used to calculate $\varLambda$ for every pixel of subsequent thermograms and directly relate it to $\alpha$ and $\tau_{\text{w}}$. By definition, $\varLambda$ is independent from the absolute temperature level. Consequently, inhomogeneities of the initial heat pulse are of minor importance and reflections of surrounding components can be strongly reduced by the usage of the proposed analysis method.

Numerical simulations

With thermal conductivities of about 0.1 W/(m K), the condition of an ideal insulator is not achievable even with modern coatings. Especially on complex shapes which often lead to a varying thickness of the coating, the heat loss into the blade cannot be neglected. To analyze the sensitivity of the present approach to this effect, a simplified 1D numerical simulation was used, which calculates the heat transport processes for given heat transfer coefficients and heat conduction rates. Furthermore, thermal coatings consisting of more than one layer (e.g., high emissivity coating and an additional insulating layer) with differing material parameters and thicknesses can be simulated to determine the temperature decline on the surface.

An implicit simulation based on Bender–Schmidt’s method is used which approximates the heat conduction equation at every grid point (Golub and Ortega 1995; Jaluria and Torrance 2003). Only the heat transport perpendicular to the surface is taken into consideration. This approximation is justifiable under several circumstances, namely an approximately constant temperature distribution on the surface, very small thicknesses of the thermal coating layers or if the spatial resolution of the measured image (defined by the optics of the infrared camera and the detector) is by far coarser than the distance given by the propagation velocity of the heat waves through the thermal coating within the observed time frame.

This numerical method was used to calculate the temperature decline rate versus time for a three-layer thermal insulation system (Fig. 2, left). At 0.07 s, where $\varLambda$ is approximately constant, several $\varLambda$ values were evaluated for different heat transfer coefficients between 0 and 2800 W/(m² K). By plotting the respective $\varLambda$ values versus heat transfer (Fig. 2, right), it can be shown that the relation between heat transfer and $\varLambda$ is approximately linear for small variations in $\varLambda$ and $\alpha$, which corresponds to the described theory of the ideal insulator [see Eq. (5)]. The major deviation to this theory lies in the offset of the linear relation since in reality heat loss due to conduction into the material also occurs at $\alpha = 0$. To take this into account, a measurement in a reference situation without flow ($\alpha = 0$) must be subtracted from a measurement with flow: $\varLambda - \varLambda_{\text{ref}}$. This reduces interfering effects such as variation in thickness of thermal coatings and inhomogeneous illumination while preserving the linear relation between $\varLambda$ and $\alpha$.

Fig. 2

Left $\varLambda$ values for different heat transfer values $\alpha$ versus time calculated with the described numerical 1D-tool. Right if the $\varLambda$ values from the quasi-constant time region between 0.06 and 0.08 s are plotted versus heat transfer, the relation between reference ($\alpha = 0$) and measurement ($\alpha \ne 0$) can be deduced

Experiments and results

Measurements of laminar–turbulent transitions

The proposed technique was demonstrated on a standard NACA-0018 profile with a cord length of 51 mm, which was manufactured from aluminum and coated with a dual-layer film consisting of a thermally insulating layer (material I) with a thickness of 70 µm and a high emissivity paint of 100 µm thickness (material II). Both thicknesses were mainly defined by the deposition processes. To minimize the heat loss into the blade, an insulating layer with a very low thermal conductivity of 0.08 W/(m K) was used.

This profile was mounted in a free jet facility with 100 mm exit nozzle diameter (see Fig. 3). To generate the heat pulse, a commercial flash lamp (Broncolor, Pulso G) with 3200 J pulse energy and a pulse duration of 7 ms was used. Depending on the distance between lamp and sample, a temperature rise of about 40 K was achieved. An infrared camera (Thermosensorik, CMT 640 M HS) with a CMT detector was used to detect the temperature decline after the heat pulse. It was operated in a subframe mode with 256 × 256 pixels to achieve a sampling rate of 500 fps. The camera recorded 200 frames beginning immediately after the heat pulse generated by the flash lamp.

Fig. 3

Schematic view of the NACA airfoil in the free jet facility. $\beta$ Denotes the angle of attack

Several different flow conditions were investigated with this setup by varying the Reynolds number and the angle of attack. For each combination of Reynolds number and angle of attack, 20 sequences of 200 images were generated and averaged so that one mean sequence could be used for further processing. Furthermore, for each angle of attack, reference sequences with 200 images were recorded with exactly the same setup and geometry.

For each pixel in these image sequences, the temporal behavior of the temperature decline rate $\varLambda (t)$ as described in Eq. (6) was calculated for both the measurement with flow ($\varLambda$) and the reference situation ($\varLambda_{\text{ref}}$). After that, a time span was identified in which $\varLambda$ and $\varLambda_{\text{ref}}$ are nearly constant. Within this time interval, a 2D-image was calculated by plotting the difference between the mean value of $\varLambda$ and $\varLambda_{\text{ref}}$, leading to a representation where high readings represent large heat transfers. It should be noted, that for this analysis no temperature calibration of the infrared camera is needed if raw intensities correlate linearly with temperature values within the relevant temperature region. In this case, Eq. (6) can likewise be used with raw intensities rather than calibrated temperature values which, however, constituted no significant difference for the present measurements.

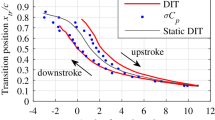
The left-hand side of Fig. 4 shows the resulting 2D-plots of $\varLambda - \varLambda_{\text{ref}}$ for all Reynolds numbers and angles of attack. The leading and trailing edges are marked with LE and TE. Large values (=bright color) represent regions with large heat transfers (large wall shear stress), whereas low values (=dark color) are those with low heat transfer (i.e., low wall shear stress). For all angles at Re = 230,000, the values of $\varLambda - \varLambda_{\text{ref}}$ were extracted along the central cross section and plotted versus axial chord length on the right-hand side of Fig. 4.

Fig. 4

Left 2D-plots of $\varLambda - \varLambda_{\text{ref}}$ for different Reynolds numbers and angles of attack. The leading and trailing edges of the airfoil are denoted with LE and TE. In the used greyscale colormap, white represents regions with high heat transfer. Right extracted $\varLambda - \varLambda_{\text{ref}}$ curves at Re = 230,000 for all angles of attack along the central chord line of the 2D-plots (indicated by white-dashed lines on the left-hand images). The transition region from onset to end of transition is clearly detectable. With increasing $\beta$ the position of the transition region is shifted towards the leading edge

To compare measurement and simulation, the $\varLambda$ and $\varLambda_{\text{ref}}$ curves of the mean value from a 10 × 10 pixel area within the transition region for the measurement at Re = 190,000 and $\beta = 15^\circ$ were plotted versus time in Fig. 5. The circles and crosses show the measured temperature decline rates in comparison with the simulations for the known material parameters and thicknesses of materials I and II. The region of constant $\varLambda$ and $\varLambda_{\text{ref}}$ values is detectable within 0.05 and 0.17 s after the heating pulse. To achieve good agreement between the $\varLambda$ curve of the simulation and the measurement (each with flow), the heat transfer into the fluid was adjusted such that the deviation between the measured and the simulated curve is minimized, leading to a heat transfer of about $\alpha = 300$ W/(m² K).

Fig. 5

$\varLambda$ (heat transfer $\alpha \ne 0$) and $\varLambda_{\text{ref}}$ curve (heat transfer $\alpha = 0$) versus time for an area directly inside the transition region on the blade in measurement (circles and crosses with four times-reduced frame rate for visualization purposes) and simulation (lines) for comparison. Within the time region between 0.05 and 0.17 s, the agreement between measurement and experiment is sufficiently good if $\alpha$ is set to 300 W/(m² K)

Comparison of transition measurement techniques

To compare the proposed method to other techniques, another NACA-0018 profile with equal dimensions was equipped with surface hot films as well as the previously used high emissivity paint. Surface hot films come with their own insulating layer, thus no additional thermal barrier was added underneath the paint. The configuration is shown in Fig. 6 where 43 hot films are mounted in 1.25 mm intervals along the suction side of the profile.

Fig. 6

NACA-0018 profile equipped with surface hot films. The electric connections are coated with high emissivity paint for temperature decline measurements. Leading and trailing edge are marked by LE and TE

As described in Sect. 3.1, the profile was positioned in the free jet facility and measurements for different Reynolds numbers (150,000, 230,000) and angles of attack (0°, 8°, 15°) were performed. Here, hot film and temperature decline measurements were executed successively to prevent mutual interference. Additionally, the hot films were measured one by one to exclude disturbances of downstream sensors. For surface hot film measurements, an anemometer circuit keeps the temperature of a sensor constant, while recording the required voltage V. In the literature, different methods exist to calculate a quantity proportional to wall shear stress from the voltage signal. For this case, the semi-quantitative evaluation after Hodson et al. (1993) was used

$$\tau_{\text{w}} \propto \left( {\frac{{V^{2} - V_{0}^{2} }}{{V_{0}^{2} }}} \right)^{3} ,$$

(11)

where V ₀ is the voltage of the reference measurement without flow.

The data analysis of the temperature decline measurements was performed as in the previous experiment via Eq. (6) and by subtracting a reference measurement $\varLambda - \varLambda_{\text{ref}}$. Figure 7 shows a comparison of both measurement techniques at two different angles of attack. Additionally, to surface hot film measurements, the proposed data analysis approach was compared to a second post-processing method. As mentioned in the introduction, Gartenberg and Wright (1994) and later Grawunder et al. (2016) developed a method based on differential infrared thermography. To detect boundary layer transition, they subtracted the raw sensor intensities of two thermograms $\Delta I = I_{1} - I_{2}$ of subsequent infrared measurements with changing temperature. This method was applied to the present dataset using the raw intensity signal of the infrared camera. For $I_{1}$ a steady-state thermogram before the heating pulse was used, whereas $I_{2}$ represents a transient thermogram that captured the maximum temperature difference between the turbulent and laminar areas (Gartenberg and Wright 1994). The results are shown as dashed lines in Fig. 7. The two-dimensional spatial information for both analysis methods are depicted in Fig. 8. For better visualization, image contrasts are optimized within the measurement area.

Fig. 7

Comparison of surface hot film signal and temperature decline signal at Re = 230,000 for different angles of attack (8° and 15°) along the chord line. All data were normalized and offset corrected to simplify comparison. The dashed lines show the results of the thermogram subtraction method developed by Gartenberg and Wright (1994) and others

Fig. 8

Post-processed images of a NACA0018 profile after the proposed temperature decline method (left) and after Gartenberg and Wright’s method (right). Exemplarily, the data of the measurement with a Reynolds number of 230,000 and an angle of attack of 15° were chosen

Discussion

The proposed temperature decline method for transition detection uses a beneficial combination of illumination and measurement setup and a post-processing method based on the model of an ideal insulator. This model sets the measured temperature decline rate $\varLambda$ in a proportional relation to heat transfer coefficient $\alpha$ and within the Reynolds analogy to wall shear stress $\tau_{\text{w}}$. By means of a numerical simulation, it could be shown that this model can be used even for non-ideal insulators for small variations in $\varLambda$ and $\alpha$. Additionally, a reference measurement $\varLambda_{\text{ref}}$ can be subtracted to reduce interfering effects without influencing the proportional behavior.

By evaluating the quantity $\varLambda - \varLambda_{\text{ref}}$ for every pixel, 2D images can be calculated which qualitatively show shear stress behaviors and present boundary layer transitions. On the left-hand side of Fig. 4, as expected, the images are in general brighter for larger Reynolds numbers which is due to higher fluid velocities. For the negative angle of attack, no transition occurs. For angles greater than zero, a clearly visible transition region is detected, which shifts towards the leading edge of the blade with increasing angles of attack. All images show a slight bending of the transition line near the image borders. This comes from the limited core region of the free stream. The data from these regions were not used for analysis. The left-hand side of Fig. 4 shows the typical wall shear stress curves with onset and end of transition. Again, the shift of the transition region towards the leading edge with increasing angles of attack is clearly detectable, which results from the increasing pressure gradient along the suction side of the profile. For these measurements, the heating pulse caused a temperature rise of about $\Delta T = 40\,{\text{K}}$. Keeping $\Delta T$ as low as possible is desirable to not alter the boundary layer too much. However, there is a trade-off between temperature rise and thermal resolution of the used camera. An optimal range for $\Delta T$ was found between 20 and 50 K where camera noise is still acceptable and effects on transitional behavior are negligible.

A possibility of accessing quantitative data with this method was indicated in Fig. 5. Here, the numerical simulation was used to calculate the heat transfer coefficient within the transition region by fitting the model to regions of nearly constant $\varLambda$ and $\varLambda_{\text{ref}}$ values. This, in principle leads to quantitative heat transfer coefficients and could be evaluated for every pixel in the generated images. However, determining heat transfer coefficients in this way should be validated in detail. This requires additional measurement techniques and will be the subject of future experiments.

To validate the qualitative shear stress behaviors and transition detection, the temperature decline method was compared to surface hot-film measurements in Fig. 7. Here, both measurement techniques coincide very well. In both plots, the temperature decline data is less noisy than the surface hot-film results. This may come from electrical interferences in the test facility environment disturbing the surface hot-film measurement. Good agreement was achieved also for angles of attack and Reynolds numbers are not shown in Fig. 7.

Additionally to surface hot films, a comparison to another post-processing method by Gartenberg and Wright (1994) is given. Grawunder et al. (2016) used this method to automatically detect transition on a preheated model in a wind tunnel. In complex geometries such as turbine rigs, preheating the object of interest is not feasible and might lead to unwanted changes in aerodynamic behavior. Therefore, heating only the surface with a short heating pulse is considered. Gartenberg and Wright’s thermogram subtraction method was applied to this measurement approach and compared to the proposed temperature decline method in Figs. 7 and 8. Here, both methods render the transition onto the same area. Since the high emissivity paint was applied on the metallic contacts of the hot films, the heat is partially dissipated by those rather than emitted into the flow. Consequently, different heat transfer conditions appear on the metallic contacts leading to a striped pattern perpendicular to flow direction (Fig. 8, right). This bias effect is strongly reduced if the temperature decline method is used which takes advantage of the described post-processing and a reference measurement without flow (Fig. 8, left). In Fig. 7 a deviation of Gartenberg and Wright’s method to surface hot-film- and temperature decline measurement can be identified for downstream chord positions. This deviation results from an inhomogeneous heating of the coated surface. The anisotropic illumination of the used flash lamp and the curved surface of the NACA-0018 profile lead to varying energy densities along the model surface. In this experiment, trailing and leading edge were thus less heated than the central part of the profile causing higher $\Delta I$. In the case of the temperature decline method, this effect is considerably reduced by subtracting a reference measurement and applying the proposed analysis method.

Conclusion and outlook

With the presented method, the temperature decline rate and the heat transfer between flow and surface can be qualitatively determined and transition regions can be reliably detected and visualized. A novel post-processing method and the subtraction of a reference situation allow to correct for several interfering effects such as inhomogeneous thermal coating and surface heating or reflections from surrounding components. Based on the post-processing method, it is furthermore in principle possible to quantitatively measure the heat transfer coefficient for every pixel of the image by fitting a numerical model to the obtained data. In comparison with surface hot films, the temperature decline method vastly reduces the amount of instrumentation since no wiring is necessary. Compared to other post-processing techniques for IR-based approaches, it combines short heating and measuring times with strongly reduced interfering effects making it suitable for measurements in complex and fast rotating systems.

In future experiments, the temperature decline method will be applied on rotating blades of a gas turbine. Modern high-speed infrared cameras have shutter times down to 1 µs, which allow to measure the temperature decline rate on rotating blades with velocities up to 1000 m/s if spatial resolutions of ±1 mm are acceptable. In this case, the surface temperature for every pixel must be determined for many subsequent rotations. Since the involved heat transport mechanisms are relatively slow, unsteady phenomena cannot be resolved. Nevertheless, the result in a rotating rig experiment will be a mean distribution of the heat transfer on the investigated surfaces which is very helpful to prove the performance of blades and to validate numerical flow simulations.