1 Introduction

Thermographic particle image velocimetry (thermographic PIV) is a recently introduced technique for simultaneous 2D temperature and velocity measurements in gaseous flows. In essence, it is a combination of laser-induced phosphorescence (LIP) and particle image velocimetry (PIV). The temperature field is detected from the ratio of the phosphorescent emitted at two spectral lines from phosphor particles excited by a UV light source, while the velocity field is calculated from the cross-correlation of two consecutive images that record the Mie scattering from the same particles illuminated by a double-pulsed laser. This technique is of interest primarily due to the capability of revealing the correlation between the structures of temperature and velocity field in turbulent flows or flames.

Thermographic phosphors were previously investigated for surface thermometry on engines and gas turbines, and a comprehensive review of such studies has been produced (Allison and Gillies 1997; Brübach et al. 2013; Aldén et al. 2011). There are numerous types of phosphor, and their detectable temperature range varies, according to the dependence of their life time, spectral characteristics and fluorescence yield on temperature. In general, both fluorescence yield and lifetime decrease with temperature, often limiting the range of application. The theory of phosphorescence is a continuing topic in material science due to its wide application to devices such as LEDs and solid-state lasers. Most thermographic phosphor tracers consist of a ceramic lattice doped with one or more types of rare-earth ions (Khalid and Kontis 2008), which can sustain temperatures up to 2000 K (Fond et al. 2012). Following photo-excitation, typically by UV light, ions in the host lattice in a phosphor particle are raised to higher energy states, and their relaxation to the ground state is accompanied by both radiative emission and non-radiative quenching. The possibility of the latter increases with stronger thermal vibrations of the host and becomes predominant at high temperatures, which leads to temperature sensitivity of both emission spectrum and decay time (Feist et al. 1999). For most types of phosphor, the emission shows both a spectral shift and a faster decay time at higher temperature. These two temperature dependent characteristics have been used for surface thermography and developed as two different approaches: an intensity ratio method and a decay time method. Fuhrmann et al. (2013) compared these two approaches for surface thermography and reported that the lifetime method was superior over the ratio-based method because of its high accuracy and precision especially at high temperatures. However, this time-resolved method may not be suitable for fast moving objects, because the lifetime of the chosen phosphor (\(\text {Mg}_{4}\text {FGeO}_{6}\):Mn) (hence the measurement time) is too long to properly resolve the temperature field. The ratio method has more recently been used in a number of studies for 2D gas-phase temperature measurements based on the intensity ratio of the phosphorescent emission of particles at different wavelengths (Brübach et al. 2006; Hasegawa et al. 2007; Rothamer and Jordan 2011; Lipzig et al. 2013; Lawrence et al. 2013; Jovicic et al. 2015).

The emission characteristics of different phosphors have been investigated for decades, but most of these studies were based on phosphor particles in bulk or bonded to a surface. Recently, the photo-luminescent behavior of phosphor particles dispersed in flows was shown to be quite different from that observed in the bulk material (Fond et al. 2012; Jovicic et al. 2015), suggesting that the calibration of the relationship between temperature to intensity ratio must be conducted in flowing systems. A particle counting system was developed to investigate the emission characteristics based on individual BAM:Eu\(^{2+}\) particles in dispersed form (Fond et al. 2015a, b), while considering different laser fluences, seeding densities and their effects on the accuracy of the temperature measurement. The result showed that the intensity ratio is dependent on the local laser fluence, and a normalization by the mean intensity-ratio field obtained at room temperature was proposed to eliminate the effects of spatial variation.

The LIP technique also shows potential for achieving multi-physics measurements in turbulent flows (Yi and Kim 2014). Omrane et al. (2008) demonstrated simultaneous 2D measurements of gas-phase temperature and velocity for the first time, where two systems were used: an Nd:YAG laser operating at 355 nm to form a UV laser sheet and an ICCD camera with a stereoscope for two-color imaging, and a double-pulsed PIV laser providing a laser sheet at 532 nm in the same plane, collected by a non-intensified PIV double-frame imaging camera. This two-system setup was followed by Jovicic et al. (2012) and Neal et al. (2013): the former demonstrated simultaneous 2D temperature and velocity measurements on a heated jet with Dy:YAG and Dy:Er:YAG tracers, while the latter achieved such measurements in a diesel engine with Pr:YAG tracers. Fond et al. (2012) demonstrated simultaneous 2D measurements of temperature, velocity and mixture fraction on a heated jet, where the ICCD cameras were replaced by two non-intensified cameras. The result shows that non-intensified CCD cameras performed well in capturing the phosphorescence emission from BAM:Eu\(^{2+}\) at a temperature below 800 K. The same technique was repeated with two high-speed laser systems with additional three non-intensified CMOS cameras (Abram et al. 2013). Recently, point-based simultaneous temperature and velocity measurements with phosphor particles were also achieved by combining LDA and LIP (Ojo et al. 2015).

The ratio-based thermographic PIV demonstrated by all aforementioned studies was realized using two systems, consisting of 2 lasers and at least 3 cameras [or 2 with a stereoscope (Omrane et al. 2008)] running simultaneously, making it a resource-intensive technique. The exact overlap of two laser sheets requires additional dichroic optics, and proper alignment. Using lifetime-based thermographic PIV, Someya et al. (2012) seeded MFG particles, a phosphor with a lifetime much longer than BAM:Eu\(^{2+}\), into an optical engine and excited by a single-pulsed UV laser sheet. A high-speed camera running at 40,000 fps recorded the signal decay of the MFG tracers. The phosphor lifetime (hence the temperature) was estimated from the first four consecutive images after each pulse, and the velocity was also calculated based on the same images (single-pulse multi-frame PIV). According to the reported result, the lifetime thermographic PIV suffers from weaknesses such as long measurement time (hence not suitable for turbulent flows), narrow applicable temperature range (decay time drops drastically as temperature rises), and small field of view/poor resolution (the camera is running at high recording rate). However, this novel lifetime-based technique sheds light on an interesting idea regarding to thermographic PIV: apart from Mie scattering, the phosphorescence can also be used to perform PIV. Although there have been some previous studies on micro-PIV with luminescent tracer particles (Pouya et al. 2005; Guasto et al. 2006; Guasto and Breuer 2008), most such studies were conducted in liquids with quantum dots. The study by Someya et al. (2012) demonstrated the feasibility of combining the PIV system and two-color system into one, which can greatly simplify the experimental setup.

In the present study, the possibility of using a double-pulsed UV light source (UV-PIV system) and two non-intensified CCD cameras to implement thermographic PIV is demonstrated. Although in general it should be possible to capture the Mie scatter at 355 nm instead of the the fluorescence signal, the quantum efficiency of most (inexpensive) PIV cameras such as those used in the present experiment is nearly zero at 355 nm. Alternatively, it may also be possible to use the residual 532 nm if the laser has sufficient energy. The present approach focuses on using the phosphorescent signal for both PIV and LIP.

For purposes of demonstration, easily obtainable ZnO particles were selected as tracer particles for both thermography and velocimetry, as it displays high temperature sensitivity (Abram et al. 2015) and short decay time (\(<1\;\upmu\)s) (Rodnyi and Khodyuk 2011) within 300–500 K. According to Abram et al. (2015), most commercial ZnO contains some level of impurities that can serve as an activator for phosphorescent emission, and its photo-luminescent behavior is similar to commercial phosphor ZnO:Zn in which Zn is deliberately added as a dopant. The use of ZnO is limited to temperatures lower than about 500 K, as the fluorescence signal becomes too weak to be captured by a non-intensified CCD camera. However, the same principles used in the present technique are transferrable to fast-decay phosphors such as BAM:Eu, which yield suitable signal at higher temperatures, at sufficiently short decay times.

In this paper, the experimental setup is described in Sect. 2, followed by the in-flow calibration of the signal in Sect. 3, including a method for correcting for effects of laser fluence non-uniformity on the intensity ratio. Instead of the normalization method proposed in Abram et al. (2015), the calibration was conducted at different pulse energies and the corresponding laser profiles were measured, hence the local laser fluence was introduced into the calibration function. Sections 4, 5 and 6 show a demonstration of simultaneous temperature and velocity measurements based on the obtained calibration function.

2 Experimental setup

2.1 Flow system

For both calibration of ZnO and thermographic PIV demonstration, an air jet of 7.2 mm diameter was used. The flow rate was 40 slpm at room temperature, controlled by a mass flow controller (Alicat MCR-250SLPM) for an bulk jet velocity of 17 m/s at standard conditions, and jet Reynolds number of Re = 8000. A co-flow of 0.4 m/s over a surrounding diameter 80 mm shielded the jet from ambient air. The jet was heated by rope heaters (Omega FGR-100) wrapped around the tube, providing a maximum outlet temperature of about 450 K for this flow rate. In-line heaters could not be used in this experiment, as aggregates of ZnO particles were found to stick between the coils and block the flow.

The ZnO particles (Sigma-Aldrich 96479) were heated to 120 \(^{\circ }\)C and dried for 8 hours in an oven before the experiment. Unlike several commercial phosphor particles used in previous literature, ZnO particles ordered from Sigma-Aldrich were not coated with anti-agglomeration agents. Although the primary particle size of this product was reported to be about 200 nm and most aggregates measured approximately 1–2 \(\,\upmu\)m (Abram et al. 2015), a few aggregates of much larger size (>20  \(\upmu\)m) could still be observed even after a long drying time, probably due to inter-particle forces. These large aggregates can result in error for both temperature and velocity measurements due to its long temperature response time (Fond et al. 2012) and non-negligible particle slip. Hence, they were removed from the images during the preliminary processing stage.

ZnO particles were dispersed into the jet by a seeder (Texas Airsonics AJ-1), in which particles are fluidized by a vibrator. For this seeder, the minimum flow-rate that could efficiently seed particles into the jet was about 30 slpm, below which the particle seeding density was too low to produce a detectable signal. The co-flow was not seeded with particles due to the limited flow rate of the available seeders. This of course biases the velocity and temperature measurements in favour of the seeded flow, and prevents measurements further away from the mixing layer of the jet.

2.2 Optical system

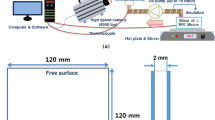
The optical system is illustrated in Fig. 1. Typical dual-cavity lasers for PIV irradiate at 532 nm wavelength, while Nd:YAG lasers or pumped lasers that can produce UV light generally deliver a single-pulse per flashlamp pulse. This is one of the reasons why all previous studies have used two separate laser systems for LIP and PIV, respectively. The laser used in the present study is an Nd:YAG laser (Continuum, Surelite III) operating with a third harmonic generator which produces pulsed illumination at 355 nm. Although the laser only has one cavity, it can produce two laser pulses each time by enabling the laser Q-switch to be opened twice during one flashlamp discharge, and the total energy is evenly distributed to each pulse by adjusting the Q-switch delay time (Continuum 1995). However, this double pulse mode is optimized for pulse separation \(\Delta\) t = 60  \(\upmu\)s. The total energy of two pulses decreases drastically as \(\Delta\) t deviates from this optimized value. In the experiment the laser was operated at 10 Hz and the pulse separation was chosen as \(\Delta\) t = 30  \(\upmu\)s. This represented a compromise between suitable spacing for the range of velocities sought, yet sufficiently high energies to excite the fluorescing particles. A photodiode (PD) was installed to monitor the energy of each pulse. The position of the PD was fixed during the calibration and all experiments to enable the correlation between PD signal and pulse energy.

Four lenses were used to form a collimated laser sheet. The combination of FL\(= -\)25 mm and a FL \(=\)150 mm cylindrical lenses produces an approximately 40 mm tall non-diverging laser sheet. A following combination of FL \(=\)150 mm and FL \(= -\)25 mm cylindrical lenses reduced the thickness of the light sheet. The thickness of the formed laser sheet above the jet nozzle was about 0.3 mm. A slit was used to remove the top and bottom edges of the laser sheet, where the intensity was too low for robust signals, resulting in a final height of the light sheet of about 35 mm. Unlike in previous studies, a collimated rather than diverging light sheet was used to obtain thermographic PIV for two reasons. First, the intensity of phosphorescence is generally much weaker than that of Mie scattering, so that a high laser fluence is preferred to excite phosphor particles before they are saturated. Second, neglecting the light absorption by ZnO particles, the laser fluence distribution F of a collimated laser sheet is a function of the vertical direction z and can be measured easily. As shown further on, considering the intensity ratio of the fluorescence emission by the phosphor particles is slightly dependent on laser fluence, so that measurements of temperature require a correction based on the local laser light intensity.

Fig. 1
figure 1

Experimental setup. BD beam dump, BS beam splitter, CL cylindrical lens, F short bandpass filter, FL focal length, M mirror, PD photodiode. Cameras are non-intensified

Full size image

The phosphorescence emitted from the seeded particles was imaged by two non-intensified low-speed PIV cameras (LaVision Imager Pro X 4M) both fitted with a AF Micro Nikkor 60 mm lens (f/2.8D). A 387 ± 5.5 nm interference filter (Edmund Optics 84094) and a 425 ± 25 nm filter (Edmund Optics 86961) were installed in front of cameras A and B, respectively. The combination of these two filters was used in Abram et al. (2015) and shown to yield high temperature sensitivity. A 50 mm diameter 50:50 beam splitter for UV light (Edmund Optics 48192) was mounted in front the cameras to separate the phosphorescent emission. During the calibration of ZnO, the set up was running in single-pulse/frame mode, and the exposure time was set to 90 ms, see timing diagram in Fig. 2a.

For thermographic PIV demonstration, the laser was operated in double-pulse mode, and the exposure times of the two images were 5 \(\upmu\)s and about 50 ms, for the first and second pulse, respectively. The minimum time on the first image is limited by the readout time of the first frame, as shown in timing diagram (b), and the second exposure time cannot be controlled. In the present experiments, the exposure times for ZnO calibration are set to a different value than that for thermographic PIV demonstration. However, there is negligible noise between the end of ZnO emission (of order 1  \(\upmu\)s) and the end of exposure, so that should not affect the results. However, for applications to flames, the exposure time for the calibration and actual experiment should be short and of the same order of the decay time, to avoid collection of undue flame luminosity during the interval.

To minimise the write out time and allow a sensible exposure time (or collection frequency) of 5 Hz, the experimental image was set to 1504 \(\times\) 1024 pixels, corresponding to a 33.2 mm \(\times\) 22.6 mm field of view and a pixel resolution of 22.1 \(\upmu\)m, according to the calibration using a target placed at the jet position. No hardware or software binning was applied. Many previous studies, such as Fond et al. (2012); Jovicic et al. (2012); Abram et al. (2015), used hardware binning to improve the signal to noise ratio. However, the downside of binning is the severe loss of spatial resolution. In the present study, no binning was applied to the raw images, because the measurements were conducted in the temperature range where the signal to noise ratio is reasonably high. The decision to perform in-chip or off-chip binning depends on the particular experimental conditions, i.e. whether SNR or resolution is most important.

Fig. 2
figure 2

Timing diagram for a calibration of ZnO; b thermographic PIV measurements

Full size image

The image pairs recorded by the first frames at time t and the second frames at time \(t+\Delta t\) were used to calculate the intensity ratio, while the two consecutive images recorded by each camera were used to produce the cross-correlation to calculate the velocity, as illustrated by sample images in Fig. 3. Although of course using the same camera for PIV and LIP can be desirable, this must be tempered by a trade-off: the strong PIV signal must be stopped down to a small aperture to avoid pixel-locking, yet the phosphorescence requires large aperture for high signal. The user must, therefore, perform controlled experiments to make sure experiments are not contaminated by pixel locking. For temperature imaging, the two images in a pair recorded by different cameras need to be overlapped exactly in order to determine the ratio. Translation stages were used to roughly adjust the position of two cameras before the experiment to guarantee that the shift of raw images was less than 10 pixels. Further image mapping was implemented by a program that shifts and rescales the images recorded by camera A and overlaps it onto the images recorded by camera B. The final overlap difference between two images was less than 1 pixel. For PIV, the two consecutive frames recorded by camera B were preferred because the quantum efficiency of CCD sensors is maximized within visible wavebands, and thus images recorded by camera B show higher signal to noise ratio. Since the decay time of ZnO is shorter than 1   \(\upmu\)s, particle images do not appear as streaks on either frame.

Fig. 3
figure 3

Single-shot intensities of first and second frames obtained with Cameras A and B at two different wavelength ranges as indicated. Upper row first frames recorded at time t; bottom row second frames recorded at time \(t+30 \, \upmu\)s. Images in the same row were used to calculate intensity ratio. Images on the right column were used to perform cross-correlation for PIV

Full size image

2.3 Timing optimization

The timing interval selected is a compromise between the following requirements: (a) a suitable mean displacement of the particles \(\Delta x\) to maximize the correlation peak detection probability, typically set to no larger than one-quarter of the interrogation window \(D_{I}\), \(\Delta x = U \Delta t \leqslant \frac{1}{4}D_{I}\), (b) a large enough energy per pulse delivered by the double pulsed Q-switch, which has an optimum timing to produce reasonably equal energies for both pulses, and (c) a suitably large flow rate and resulting bulk velocity U for the flow which produces sufficiently large seeding rate of particles. Figure 4 shows qualitatively how the signal and figures of merit vary with the chosen time interval. For the present system, using an interrogation window of 64 \(\times\) 64 pixels, corresponding to a displacement \(D_{I} = 1.4\) mm, the window of optimization produced a compromise of 40 slpm flow rate for a flow velocity of \(U = 23\) m/s at 410 K and 30 μs pulse separation. This produces a \(\Delta X\) of about half the interrogation volume, rather than one-quarter. However, the relatively high particle number density at the selected flow rate can partially compensate for the effects of out-of plane loss of particle images (Keane and Adrian 1990, 1992), so that acceptable 2D velocity measurements can still be achieved.

Fig. 4
figure 4

Schematic variation of normalized laser energy per pulse, probability of finding cross-correlation \(P_{c}\), as a function of timing interval \(\Delta t\) between images. For PIV, the total energy was evenly distributed between the two pulses (\(E_{1}=E_{2}\)). The particle seeding density, and hence the signal intensity, is proportional to the flow rate passing through the seeder

Full size image

3 Calibration

3.1 ZnO calibration curves as a function of laser intensity

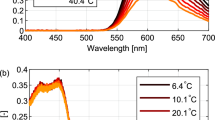
Calibration of ZnO fluorescence signal was conducted in the same jet flow for various temperatures ranging from room temperature to 424 K. Prior to the phosphorescence imaging, a K-type thermocouple of 0.5 mm diameter was placed in the jet core 5 mm above the nozzle to record the mean temperature, in a central region where the flow was stable. The exposure time of both cameras, operated in single-image mode and synchronized with the laser pulse at 10 Hz, was set to 90 ms. Since the intensity ratio of ZnO has been reported to be dependent on laser fluence, six levels of pulse energy were tested for each temperature. The mean pulse energy integrated over the whole region was measured (2.8, 6.4, 8.6, 11.6, 15.8, 34.6 mJ) at each energy level for over 900 pulses by a powermeter placed at the jet position. For each condition, the intensity ratio measured over the probed region and averaged spatially, over a 1.1\(\times\)1.1 mm\(^2\) square region is shown in Fig. 5a. The local and mean ratio was calculated for a total of 600 images. For 2.8 mJ pulse energy, the average signal to noise ratio in the square region is only about 2.0, which is too weak and would result in large errors. Hence, only higher energy levels were considered, as reported in Fig. 5b. The curves obtained show some discrepancies relative to those ones reported in Abram et al. (2015), possibly due to the use of a different beam splitter with a higher reflectivity for near UV light, and the use of higher laser fluences.

A key issue in producing a robust calibration is that the solid aerosol be as monodisperse and uniform as possible, and that the reference be obtained at similar conditions. The phosphorescence effect is a surface phenomenon, and its effectiveness is subject to the surface to volume ratio of the particle. As in many surface phosphorescence techniques, there is no expectation that the details of energy transfer will be entirely predictable for particles of different microscopic characteristics, so that calibration at relevant conditions is essential.

Fig. 5
figure 5

a Mean intensity ratio of wavelength range 450±25 nm to wavelength range 387±5.5 nm for a total laser energy of 8.6 mJ at a temperature 424 K in the marked region; b mean intensity ratio of marked the region shown in a, as a function of temperature and mean laser pulse energy (mJ). Intensity ratio variances are presented as vertical error bars. Lines are second-order polynomial fits for each energy

Full size image

The measured intensity ratios are an increasing function of temperature, and a weak function of the laser pulse energy. The weak dependency on laser energy is probably caused by two reasons: the particle absorption and the change of luminescence characteristics of ZnO due to increasing excitation fluences (Abram et al. 2015). To eliminate the effects of nonuniform spatial distribution of laser fluence, Abram et al. (2015) suggested that the dependence of the measured intensity ratio on fluence disappears once it is normalized by the room temperature intensity ratio. However, the fluence range they applied was 5–20 mJ/cm\(^{2}\), and a 7.2 K error caused by such normalization was reported at 475 K. Since a non-diverging Gaussian laser sheet was used in the present setup, in our case a much larger span of laser fluences (20–213 mJ/cm\(^{2},\) see Sect. 3.2) was applied to excite the particles. Hence, to achieve a better accuracy, instead of using the normalization method, the local laser fluence F is measured and introduced into the calibration function:

$$\begin{aligned} I_{r}=I_{r}( T,F ) \end{aligned}$$
(1)

where \(I_{r}\) is the intensity ratio, T the temperature, and F is the local laser light fluence at the calibration point.

3.2 Laser sheet profile

The local laser light fluence varies along the axial direction according to the laser light profile, denoted as F(z). The mean laser sheet profile F(z) along the axial distance z was measured by exciting diluted laser dye Coumarin 460 in a cuvette and imaging the fluorescence (435–485 nm) using camera B. To avoid saturation of the dye, the laser sheet was attenuated to approximately 1% of original energy using two pieces of glass and a prism. The mean laser intensity profile obtained over the highlighted rectangle shown in Fig. 6a was averaged over 900 shots. The laser intensity profile is assumed to be proportional to the fluorescence intensity obtained. Given the measured mean pulse energy (mJ) and the thickness of the laser sheet (0.3 mm), the intensity profile can be translated into laser fluence (mJ/cm\(^{2}\)), as shown in Fig. 6b. Corresponding laser fluences at the calibration point for the five energy levels are 20, 33, 51, 76, 213 mJ/cm\(^{2}\), respectively.

Fig. 6
figure 6

a Fluorescence from excited Coumarin 460 in a cuvette as recorded by camera B; b fluence obtained from highlighted region (1504\(\times\)50 pixels) in a and the measured mean energy (mJ/cm\(^{2}\)) for varying energy levels. The dashed line indicates the center of the calibration region, corresponding to fluences of 20, 33, 51, 76, 213 mJ/cm\(^{2}\)

Full size image

3.3 Final calibration function

The calibration function \(I_r = I_r (T, F)\) was finally obtained from the ratio of signals obtained in the region of interest shown in Fig. 5a, and the local fluence obtained at the same location using the profile in 6b. The plot of \(I_r(T, F)\) is shown in Fig. 7. The intensity ratio grows slowly for a fluence above 80 mJ/cm\(^{2}\), which matches well with the result reported in Abram et al. (2015). The calibration function was extrapolated to F \(=\) 250 mJ/cm\(^{2}\), in case the maximum laser fluence during the thermographic PIV demonstration falls beyond the calibration range. The final calibration grid was refined to 0.1 mJ/cm \(^{2}\times\) 0.1 K by interpolation to guarantee the accuracy of temperature measurement. The surface shows a distortion at higher temperatures and low laser fluences, owing to the low signal to noise ratio and was avoided during the experiment.

Fig. 7
figure 7

Calibration function \(I_r = I_r (T, F)\)

Full size image

3.4 Laser sheet profile for double pulse mode

Since we can use either the first or second pulse to obtain the intensity ratio, it is necessary to characterize the local laser fluence for both the first and second laser pulse. The laser fluence profiles F(z) measured for both pulses are shown in Fig. 8a. During the experiment, the energy released by the flashlamp charge also fluctuates from pulse to pulse. If the normalized mean shape function of the fluence profile \(\hat{F} (z)\) remains the same for all individual pulses, the fluence profile for an instantaneous profile F(z) is assumed to be proportional to the mean profile \(\hat{F} (z)\), and proportional to the total energy of the pulse E:

$$\begin{aligned} F (z)= \frac{E}{\overline{E}}\hat{F}(z) \end{aligned}$$
(2)

where \(\overline{E}\) is the mean energy over all laser pulses, and E is the energy of individual pulse, both of which are monitored by the PD. The measured temporal energy fluctuations of the first pulse and the second pulse are about 15% and 12% respectively. Figure 8b shows that the normalized shape function \(\hat{F}(z)\) does not change significantly from pulse to pulse, even though the pulse shapes are different. The single-shot intensity ratio obtained in this manner was translated into temperature according to the calibration function \(I_r(T,F)\) and the local mean laser fluence for the first or second laser pulse.

Fig. 8
figure 8

a Laser fluence profile F(z) for the first (blue) and second (red) pulses; b normalized shape function of the fluence profile. Averages represented by the solid line, variances by the error bars

Full size image

4 Operating conditions

A flow rate of 53 lpm of air for a bulk velocity of 23 m/s at a measured outlet temperature of 410 K, was used to generate the test flow field of a jet mixing layer. The two cameras were running in double-frame mode at 5 Hz, a frequency was limited by the storage speed. A total of 900 double-frame images were recorded by each camera. The temperature results obtained by thermography were compared to a traverse of a thermocouple at 5 and 10 mm above the jet nozzle.

5 Data processing

5.1 Thermography

Data processing for 2-color thermography was completed by a Matlab program. The background image was recorded and subtracted from all raw images and a 5 \(\times\) 5 pixel moving average filter was used to increase the signal to noise ratio and smooth the image, resulting in a spatial resolution of 110.5   \(\upmu\)m. A threshold of 10 counts was considered as the threshold of noise to be removed from the images, for a maximum signal of 5000 counts (large aggregates) and mean signal intensity of about 300. In most of the raw images there are a few large aggregates, whose intensity appears significantly higher than those of small particles. The intensity ratio of these large aggregates is also higher than the surrounding intensity ratio, as illustrated in Fig. 9a, because the temperature response time of large particles is significantly longer than for the small ones (Fond et al. 2012). To remove the large aggregates, all pixels with intensity higher than 500 counts in the raw images were removed, and the corresponding regions excluded from the processing. The resulting intensity ratio field is shown in Fig. 9b, where the edge of large aggregates can still be seen due to diffraction. The area removed was extended by 3 pixels outwards to remove the diffraction of those large aggregates, as shown in Fig. 9c. The values for the removed regions were determined by interpolation, Fig. 9d. We note that the problem of large aggregates is less likely to happen if commercial coated phosphor particles are used.

Fig. 9
figure 9

Resulting sample temperature fields (K) after each image processing step for removing large aggregates. The area of the shown region is 150 \(\times\) 150 pixel (3.3 \(\times\) 3.3 mm)

Full size image

After large aggregates were removed from raw images, the intensity ratio field was translated into temperature via the following process: the laser fluence profile for each pulse was calculated from the mean fluence profile and the individual pulse energy recorded by the PD based on Eq. (2); the laser fluence corresponding to each row of pixels was extracted from the profile, and the closest value \(I_{r}\) to the measured intensity ratio was searched to determine the temperature. The main advantage of this data processing method is that the laser fluence does not need to be uniform in order to guarantee the accuracy of temperature measurements, but the data processing time is long (approximately 4 minutes per image).

5.2 Particle image velocimetry

The phosphorescence in the 400–450 nm bandwidth was recorded by camera B and used for cross-correlation for PIV, as the CCD sensors are much less effective for the lower selected spectral line (381–393 nm). However, the signal to noise ratio of the phosphorescent PIV images is significantly lower than PIV images recorded at 532 nm, and the resulting detectability of cross-correlation peak can be relatively poor. The most efficient way to increase pixel intensity under the present conditions is to increase the seeding density, as the former is a linear function of the latter (Fond et al. 2015a). Hence, an efficient seeder that can provide enough particles dispersed into the flow is essential for high-quality cross-correlation of phosphorescent PIV image pairs. However, it should be noted that the high seeding density can also cause multiple scattering effects and bias the temperature measurement (Lipzig et al. 2013; Fond et al. 2015a; Lee et al. 2016), hence there is a compromise between guaranteeing a sufficiently high signal-to-noise ratio and avoiding severe multiple-scattering effects.

The images were processed by the Davis 7.2 software from LaVision. Vectors were calculated using a multipass cross-correlation, with a constant 64 \(\times\) 64 pixel window size and an overlap of 75% in three passes, which gives 91 \(\times\) 61 vectors in total. Vectors with a Q-factor below 1.2 were removed, and a 3 \(\times\) 3 pixel moving average filter was applied to smooth the vector field. The final nominal vector spatial resolution is approximately 0.37 mm/vector.

6 Results and discussion

6.1 Temperature imaging

Figure 10 shows single shot 2D temperature fields extracted from the calibrated and corrected image ratios for times t and \(t+30\; \upmu\)s. The entrainment structures can be observed clearly and the temporal change of temperature field during the time interval is also clear by comparing the two frames. The horizontal streaks are a result of CCD charge transfer noise. This was confirmed, as the streak direction changes 90 degrees for a corresponding different camera orientation.

Fig. 10
figure 10

Single shot of temperature field at time a t, b \(t+30\;\upmu\)s based on calibration function \(I_r(T,F)\)

Full size image

Figure 11 shows the mean temperature fields over the first and second frames. To eliminate the effects of CCD transfer noise, the mean temperature fields were smoothed by a 30-pixel (0.66 mm) 1D moving average filter along the vertical direction. The images on Fig. 11, the temperature on the left half of the jet appears higher than the right half. This could be a result of laser light absorption, as the laser beam is emitted from left to the right on the figure: the absorption can affect the local particle temperature, as well as the local fluence on the far side of the laser sheet. However, as remarked further on, the temperature field measured by the thermocouple is not entirely symmetric, and that accounts for part of the difference.

Fig. 11
figure 11

Mean temperature field obtained for the first pulse at time t (a) and second pulse at time \(t+30\;\upmu\)s (b). The laser sheet enters from the left side. To eliminate the effects of the CCD transfer noise, the mean temperature fields were smoothed by a 30-pixel (0.66 mm) 1D moving average along the vertical direction

Full size image

A comparison between the mean thermographic results and an average thermocouple sweep is shown in Fig. 12. The profile measured by the thermocouple is not symmetric, and the maximum temperature appears 1 mm to the left of the geometric centre of the jet. The heating was generated by wrapping tape heaters around the tube, so that it is possible that the heat transfer rate might not have been uniform. Results show that for an axial distance 10 mm from the base of the jet, the temperature profiles extracted from both frames are in good agreement with that measured by the thermocouple. The discrepancy increases on both sides because of the increasingly poor signal to noise ratio due to the dilution of the seeded jet by the unseeded co-flow. In a turbulent flow, this biases the mean temperature measured by the thermographic measurements towards the hot side of the jet, as the probability of signal from the seeded hot region is larger than that of the unseeded part. At an axial distance of 5 mm, the temperature profile processed from the first frame is biased to a lower value. The reason for the temperature bias is probably due to the low laser fluence (see Fig. 8a) and thus the poor signal to noise ratio at this height in the first frame.

Fig. 12
figure 12

Mean temperature profiles processed from the first frame (red) and the second frame (blue), compared to values measured by a thermocouple (dashed line with circles) for an axial distance 10 mm (upper) and 5 mm (bottom)

Full size image

The root mean square variation of the temperature field processed from the first and the second frames are shown in Fig. 13. In the core region, the temperature variance is estimated as 15 K for a 410 K outlet temperature. The high variance on the outer zone is clearly because of the combination of low signal to noise ratio due to particle dilution, combined with the actual high variance due to turbulent mixing. The high values at the bottom of the image arise due to the lower fluence. Better quantification of the variance should be made by seeding the outer flow for more uniform signal to noise ratio.

Fig. 13
figure 13

Temperature variance processed from the a first frames; b second frames

Full size image

6.2 Simultaneous velocity and temperature imaging

Figure 14 shows two sample images of simultaneous temperature and velocity fields. The white contour on Fig. 14a, c corresponds to the 2D vorticity calculated based on the velocity field shown in b, d. The vorticity contours match well with the expected entrainment structures, and the velocity field shows similarities to the temperature field, as expected for a heated simple jet. In Fig. 14b, d, there are some empty zones where the vectors were removed, as the quality factor was lower than 1.2, with the the presence of spurious vectors which significantly deviated from its surrounding vectors (see Fig. 14b). The uncertainty in velocity measurements arise due to: (i) long pulse separation due to the optimization of laser energy: this limits the detectability of cross-correlation peaks, (ii) the presence of large aggregates which cannot fully follow the flow, and (iii) low particle number density in the mixing regions. The first factor can only be improved using a two-cavity PIV system with a third harmonic generator, while the remaining two can be solved by using coated particles and seeding the co-flow as well.

In general, separating the PIV and LIP measurement using more lasers and cameras makes the system more flexible: (a) the SNR of the PIV image becomes independent of the phosphorescence emission and thus does not depend on temperature, (b) pixel-locking can be more easily avoided, and (c) higher temperatures can be detected by LIP, as hardware binning can be applied. There is, however, a compromise between the cost and the versatility of the system. The results shown here demonstrate that the concept can realise temperature and velocity images at low cost, without sacrificing too much in accuracy and dynamic range for both velocity and temperature.

Fig. 14
figure 14

Two examples (top and bottom) of simultaneous temperature (left column) and velocity (right column) imaging. The vorticity contours are superimposed onto the temperature field. As expected, the temperature structures show similarities to the velocity structures

Full size image

7 Conclusions

Simultaneous 2D temperature and velocity measurements were demonstrated by thermographic PIV based on ZnO particles, using a single laser, and two non-intensified cameras. The phosphorescence from excited ZnO particles proved to be suitable for conducting PIV and hence the experimental setup was to a large extent simplified comparing with previous studies (Omrane et al. 2008; Fond et al. 2012; Jovicic et al. 2012; Neal et al. 2013). A single-cavity YAG:Nd laser installed with third harmonic generator was operated in double-pulse mode (enabling the Q-switch twice during one flash-lamp charge) and two non-intensified CCD cameras were running in double-frame mode to record the phosphorescence signal, eliminating the need of using another PIV laser at 532 nm and an extra camera for recording the Mie scatter.

To compensate for the effects of laser fluence on the intensity ratio, a non-diverging laser sheet was arranged, and the profiles of the laser sheet were measured for both calibration and experiments. Calibration was conducted at various temperatures and different laser energies, to yield a calibration function of intensity ratio to temperature and laser fluence \(I_{r}(F,T)\). The intensity ratio field was transferred into temperature according to \(I_{r}(F,T)\) and measured local laser fluences F. A comparison with mean temperatures obtained by a thermocouple showed that the accuracy of ZnO thermography was within 3 K at 410 K in the jet core region.

Compromises were made in the time separation \(\Delta\) t to allow sufficiently high energies for both PIV and phosphorescence. However, reasonable velocity measurements were obtained due to large particle number density in each interrogation window. Higher spatial resolution temperature and velocity imaging (110.5 \(\upmu\)m \(\times\) 110.5 \(\upmu\)m) are demonstrated compared with previous studies. Unsurprisingly, the velocity structures show similarities to the temperature structures, and the vorticity contour is correlated with the entrainment structures shown on the temperature field. This shows the potential of thermographic PIV for investigating fundamental problems in fluid mechanics. Future work will aim to improve the quality of the data via optimized timing, resolution and seeding of the co-flow streams.

Due to several limitations on hardware, the experimental parameter settings are sitting on the edge of the optimum conditions for both PIV and thermography. The data quality could be largely improved if (a) a dual-cavity PIV laser with UV capabilities is made available so that the pulse energy is not limited by the pulse separation time, (b) commercial phosphor particles with coating can be used, to remove particle aggregation, (c) high quantum yield sensors are used for fluorescence cameras near the UV, and (d) an effective seeding mechanism can be guaranteed for various ranges of flow rate. If these conditions can be satisfied, the thermographic PIV technique can be readily applied and optimized to investigate various problems of turbulent heat transport and mixing.